Least Square based Multi-spectral Color Interpolation Algorithm

for RGB-NIR Image Sensors

Ji Yong Kwon, Chul Hee Park and Moon Gi Kang

Institute of BioMed-IT, Energy-IT and Smart-IT Technology (BEST), Yonsei University,

50 Yonsei-Ro, Seodaemun-Gu, Seoul, South Korea

Keywords:

Color Interpolation, Demosaicking, Least Square, Near-Infrared, Multi-spectral Filter Array.

Abstract:

The use of near-infrared (NIR) band gives us additional invisible information to discriminate objects and

enables us to recognize objects more clearly under low light conditions. To acquire color and NIR bands

together in a single image sensor developed from a conventional color ﬁlter array (CFA), we use a multi-

spectral ﬁlter array (MSFA) in the RGB-NIR sensors and design a color interpolation algorithm to ﬁll the

information about the multi-spectral (MS) bands from the subsampled MSFA image. Aliasing in the MSFA

image caused by the subsampled bands is minimized by balancing the energy of the bands. A panchromatic

(PAN) image is generated by ﬁltering the low-pass kernel to the MSFA image. This PAN image without

chrominance signals, which contains the most high-frequency in the MSFA image, is used to reconstruct the

MS images by solving the least square cost function between the PAN and MS images. The experiments show

that the proposed algorithm estimates the high-resolution MS images very well.

1 INTRODUCTION

Security camera safety issues are increasing because

many accidents and events take place abruptly. Espe-

cially at night, it is difﬁcult to see and discriminate

objects in dark areas. General digital cameras pre-

vent a spectrum longer than 700 nm such as a near-

infrared (NIR) band by using an infrared cutoff ﬁl-

ter (IRCF) in front of the image sensors to preserve

color information. However, a NIR band is invisible

to the human eye and it provides additional informa-

tion about objects in low light conditions. From these

reasons, a NIR band is useful in ﬁelds such as vi-

sion, digital photography,and remote sensing (Zhang,

1999)(Schaul et al., 2009).

In the ﬁrst study, to acquire three color bands to-

gether in one sensor, a conventional color ﬁlter array

(CFA) was designed by the sub-sampled periodic pat-

terns to reduce the cost and size of the sensors. To

interpolate the missing color values, the method to re-

construct the color images with a frequency selective

technique using luminance and chrominance was pre-

sented in (Alleysson et al., 2005). Based on an ex-

tension of the conventional CFA, to acquire several

bands together, a multi-spectral ﬁlter array (MSFA)

was described in (Lu et al., 2009). From this MSFA,

the binary tree-based demosaicking method was pro-

posed in (Miao et al., 2006). Also, multi-spectral de-

mosaicking by upsampling using an adaptive kernel

was introduced in (Monno et al., 2011). To reduce

the demosaicking artifacts, vector based median ﬁlter-

ing was presented in (Wang et al., 2013). To acquire

color and NIR images using a single sensor, Zahara et

al. designed a CFA pattern and demosaicing matrices

in (Sadeghipoor et al., 2011). Also, a CFA that ac-

quired color and a NIR image was designed by solv-

ing the spatial domain optimization problem in (Lu

et al., 2009).

To acquire visible and invisible bands together, we

use the RGB-NIR sensor presented in (Koyama et al.,

2008). Theis sensor consist of four multi-spectral

(MS) bands : red (R), green (G), blue (B), and NIR

according to the MSFA pattern, as depicted in Fig.

1. Each four bands are sub-sampled within one quar-

ter of the sensor. However, to acquire the NIR band

in an image sensor, the IRCF has to be removed. This

produces a color shift problem because color informa-

tion as well as the NIR band is absorbed in the sensor.

To solve this problem, a multi-layer decomposition

method was explained in (Park et al., 2012).

In this paper, a least square based multi-spectral

color interpolation algorithm for RGB-NIR sensors

is presented. To minimize aliasing in the MSFA

image, the energies of the MS bands are balanced.

Kwon J., Park C. and Kang M..

Least Square based Multi-spectral Color Interpolation Algorithm for RGB-NIR Image Sensors.

DOI: 10.5220/0005265000380045

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 38-45

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

+NIR

NIR

+NIR

NIR

+NIR

Figure 1: The RGB-NIR sensor pattern.

A panchromatic (PAN) image without chrominance

is generated from the MSFA image. The high-

frequency of each MS image is retrieved using the

high-frequency of the estimated PAN image with the

least square minimization process. Experiments show

that the proposed algorithm produces high quality re-

sults.

2 PROPOSED ALGORITHM

To obtain high-resolution R, G, B, and NIR images,

we designed the algorithm as shown in Fig. 2. A two-

step algorithm to reconstruct full resolution images is

proposed. This paper is based on the assumption that

the high-frequencies of the MS bands are highly cor-

related according to the spectral sensitivity described

in (Koyama et al., 2008). First, the energies of the

bands are balanced according to the band energy anal-

ysis process and the PAN image is obtained by ﬁlter-

ing a low-pass kernel to the MSFA image. Second,

the high-frequency of the MS bands is estimated us-

ing the high-frequency of the generated PAN image

by ﬁnding the solution of the least square function.

2.1 Panchromatic Image Generation

Let m[n

] represent the MSFA image with size

× N

, a pixel location of horizontal direction n

0,··· ,N

−1 and vertical direction n

= 0,··· ,N

−1,

as the pattern illustrated in Fig. 1. Let R, G, B, and

NIR bands be m

] where b ∈ {1, 2, 3,4}, respec-

tively. The MSFA image is as follow,

m[n

] =

](1+ (−1)

)(1+ (−1)

)

](1− (−1)

)(1+ (−1)

)

](1+ (−1)

)(1− (−1)

)

](1− (−1)

)(1− (−1)

). (1)

HR Image Estimation

Aliasing

Analysis

Least

Square

Minimize

PAN Image Generation

PAN

Signal

Filtering

Band

Energy

Analysis

PAN Image

MSFA

Image

High Resolution

Multi-spectral

Image

Figure 2: Overall block diagram of the proposed algorithm.

The four bands are acquired with sub-sampled in the

MSFA image as,

m[n

] =

] + m

]

] + m

])

] − m

]

−m

] + m

])(−1)

] − m

]

] − m

])(−1)

] + m

]

−m

] − m

])(−1)

. (2)

To see the Fourier spectrum of the MSFA image in

the Fourier domain, the MSFA image is decomposed

as a PAN signal m

and three chrominance signals,

, m

, and m

. In terms of the signal decompo-

sition to matrix notation, the relationship between the

PAN signal and three chrominance signals, and the R,

G, B, and NIR bands is,



















1 1 1 1

1 −1 −1 1

1 −1 1 −1

1 1 −1 −1



















(3)

Using the signal decomposition as (3), (1) is rewritten

m[n

] = m

] + m

](−1)

)

+ m

](−1)

+ m

](−1)

. (4)

LeastSquarebasedMulti-spectralColorInterpolationAlgorithmforRGB-NIRImageSensors

Noting that −1 = exp(jπ) and taking the Fourier

transform to (4), the MSFA image is rewritten as

M(u,v) = M

(u,v) + M

(u− π,v− π)

(u− π,v) + M

(u,v− π). (5)

This means that the Fourier spectrum of three chromi-

nance signals M

(u,v), M

(u,v), and M

(u,v) are

modulated at the frequencies (π, π), (π,0), and (0,π).

According to the spectral sensitivity of the sensor in

(Koyama et al., 2008), the NIR pixel is designed to ab-

sorb only the NIR band but the other color is also ab-

sorbed actually. In other words, all bands contain sim-

ilar information. Also, basically, the color bands R,

G, and B are highly correlated as mentioned in (Gun-

turk et al., 2002). Based on this, we suppose that the

high-frequencies of the R, G, B, and NIR bands are

highly correlated. Therefore, the aliasing invading the

PAN signal from the chrominance signals is removed

by balancing the energies of the bands because each

chrominance signal is composed of two plus signals

and two minus signals as discussed in (3).

We decompose the MS bands as low- and high-

frequency as

(u,v) = M

(u,v) + M

(u,v), (6)

where b ∈ {1,2,3,4}. The mean values of the bands

are calculated as

= E(m

]). (7)

The maximum mean value µ

max

is determined among

the mean values of the four bands. Using this, the

gain of each band is calculated according to the ra-

tio between the maximum mean value and the mean

value of each band as

max

, (8)

where b ∈ {1, 2, 3,4}. Applying the gains to each MS

band, the modiﬁed bth MS band M

′

] is com-

puted as

′

(u,v) = g

(u,v), (9)

where b ∈ {1,2,3,4}. The mean values of the bands

are adjusted to a similar magnitude. This makes the

high-frequency of the bands similar as

(u,v) = g

(u,v)

= g

(u,v) = g

(u,v). (10)

By using this process, the high-frequency of the

chrominance signals are eliminated. That is to say,

the chrominance signals invading the PAN signal are

minimized.

′

(u,v) =

′

(u,v) −

′

(u,v)

−

′

(u,v) +

′

(u,v)

′

(u,v) =

′

(u,v) −

′

(u,v)

′

(

u,v) −

′

(u,v)

′

(u,v) =

′

(u,v) +

′

(u,v)

−

′

(u,v) −

′

(u,v). (11)

The three modiﬁed chrominance signals are obtained

and the energy balanced MSFA signal m

′

] is ac-

quired as

′

] = m

′

] + m

′

](−1)

)

+ m

′

](−1)

+ m

′

](−1)

. (12)

With one PAN signal and three chrominance sig-

nals in the MSFA image overlapping, there is a trade-

off between the signals when extracting one signal

from the MSFA image. Therefore, we have to de-

termine the adequate cutoff frequency of the low-pass

kernel to acquire the PAN signal from the MSFA im-

age. According to (Fang et al., 2012a), the majority

of the spectrum energy of a typical signal is highly

concentrated at a lower frequency, and the Lapla-

cian probability density function is a good model

to approximate the magnitude of the Fourier spec-

trum. Generally, the Fourier spectrums of the PAN

and chrominance signals are approximated with the

Laplacian model with each mean and variance. The

cutoff frequencies are determined by matching two

probability density functions between the Laplacian

model of the PAN signal from (0,0) and the Laplacian

models of the chrominance signal from (0,π), (π,0),

and (π,π). In other words, the cutoff frequency of

the low-pass kernel h

] used to extract the PAN

image can be determined. The process of conducting

a convolution with a low-pass kernel h

] to the

energy balanced MSFA signal m

′

] can be writ-

ten as

ˆm

] = m

′

] ∗ h

]. (13)

The PAN image is generated without chrominance

signals containing the most high-frequency in the

MSFA image, as illustrated in Fig. 3. The MSFA

images are shown in Figs. 3(a) and (d). From this, the

MSFA images with balanced energy are depicted in

Figs. 3(b) and (e). By applying the low-pass kernel to

the MSFA images with balanced energy in Figs. 3(b)

and (e), the PAN images are generated as in Figs. 3(c)

and (f).

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

(a) (b) (c)

(d) (e) (f)

Figure 3: (a), (b), and (c) are parts of the Sample1 image.

(d), (e), and (f) are parts of the Sample2 image. (a) and (d)

MSFA pattern image. (b) and (e) Energy balanced MSFA

pattern image. (c) and (f) Generated PAN image from (b)

and (e), respectively.

2.2 HR Image Estimation

In this section, we estimate the high-resolution MS

images by using the PAN image generated in the pre-

vious section. We denote the PAN image m

]

and the MS images m

] by P and M

in a N ×1

lexicographical order where N = N

× N

, respec-

tively. According to the formation of the synthetic

PAN image (Zhang, 1999), the PAN images can be

generated by a weighted sum with the coefﬁcients of

their MS images. The PAN image acquirement pro-

cess can be represented as follows:

P =

∑

b=1

+ w, (14)

where the blur matrix B is an assumed linear blur

model and w refers to the Gaussian random noise. N

represents the number of the spectral bands. The bth

band coefﬁcient of each band α

according to the pix-

els is obtained through regression analysis using the

relationship between the MS bands.

The low-frequency regions are important since

they express the characteristics of the objects in the

scene. Also, aliasing occurs mostly in high-frequency

regions in the images. And we assume that each

high-frequency of MS bands is highly correlated. For

this reason, in this paper, we focused on the high-

frequency reconstruction of the MS images. There-

fore, the high-frequency of the MS images is esti-

mated using the high-frequency of the PAN image.

The PAN and MS images are decomposed into low-

and high-frequency as

P = P

+ P

= M

+ M

. (15)

Using the high-frequency signals only, (14) is rewrit-

ten as follows,

∑

b=1

+ w. (16)

The estimated bth band MS image is denoted by

. Also, the generated PAN image is denoted by

P. Both the PAN image and the MS images from

the MSFA image estimated in the previous section are

used. In other words, the PAN image

P whose original

expression is ˆm

] and the MS images from the

energy balanced MSFA m

′

] are used to estimate

the high-resolution MS images. To minimize the dif-

ference between the high-frequencyof the PAN image

and those of the MS images, the least square problem

is expressed as

= argmin

−

∑

b=1

. (17)

Since the square error function (17) is convex,

ﬁnding the minimization is equivalent to ﬁnding the

zero value of its gradient. To ﬁnd the minimization

solution, the conjugate gradient descent method (Lu-

enberger and Ye, 1984) is applied. Then, the high-

frequency of the MS images is estimated in iterations

as follows,

h(n+1)

h(n)

+ ε

(n)

(

− α

h(n)

)}, (18)

where ε and n refer to the iteration step and the iter-

ation number, respectively. Estimating the MS bands

in (18) refers to the fact that the high-frequency of

the MS images are substituted by the that of the PAN

image. The iteration ends when the relative differ-

ence energy ||

−

∑

b=1

h(n)

between the high-

frequency of the PAN image

and those of the es-

timated MS band images with nth iteration

h(n)

smaller than the given threshold. The energy of high-

frequency of the PAN image ||

is used to normal-

ize the relative difference energy. Finally, iteration

ends when it satisﬁes the following condition,

−

∑

b=1

h(n)

< T, (19)

where T represents the speciﬁed threshold value.

From (19), the high-frequency of the MS images are

estimated. These images contain the high-frequency

from the PAN image. As a result, the bth band high-

resolution MS image is obtained as

+ M

. (20)

LeastSquarebasedMulti-spectralColorInterpolationAlgorithmforRGB-NIRImageSensors

Figure 4: Rate of convergence for the Sample3 image ac-

cording to the step size.

The high resolution MS images are estimated by com-

bining the low-frequency of the original MS images

and the estimated high-frequency of the MS images.

By estimating the high-frequencies of the MS images

only, the high-frequencydetails of MS images are im-

proved and the low-frequencies of the original MS

images are preserved.

3 EXPERIMENTAL RESULTS

The results of the proposed algorithm are compared

both objectively and subjectively with the results of

the bilinear interpolation method and the BTES (Miao

et al., 2006). First, the images acquired by the RGB-

NIR sensors are used, Sample1, Sample2, Sample3,

and Sample4, along with a resolution chart and ob-

jects with details. The R, G, B, and NIR bands of

these images are sub-sampled by the MSFA pattern

in Fig. 1. We tested the performance of the proposed

algorithm by measuring the high-frequency energy

(HFE) in (Fang et al., 2012b). Also, we obtained sev-

eral original images using CCD sensors with change-

able R, G, B, and NIR ﬁlters (Sample5, Sample6,

Sample7, and Sample8) and measure the color-peak

signal-to-noise ratio (CPSNR) of the resulting im-

ages. We generated the MSFA pattern image accord-

ing to the pattern in Fig. 1 because each pixel con-

tains the intensity values of the four bands (R, G, B,

and NIR).

In the experiments, we assumed the variance of

the blur kernel is 0.2 with a low blur condition and

set the iteration step size ε at 0.5 in (18). The esti-

mated MS images convergedabout 40 iterations when

T is 10

−3

in (19). The bth band coefﬁcient α

is 1/4

equivalent for all bands. To decompose signals as

low- and high-frequency, we use wavelet ﬁlters like

the low-pass ﬁlter [1,2,1]/4 and the high-pass ﬁlter

(a) (b)

(e) (f)

Figure 5: Part of the Sample1 image. (a) Color result of the

bilinear interpolation. (b) Color result of the BTES method.

of the bilinear interpolation. (e) NIR result of the BTES

method. (f) NIR result of the proposed algorithm.

[−1,2, −1]/4. The initial value of the iterative esti-

mation method is the results of the bilinear interpola-

tion method.

The rate of convergenceto the minimized solution

of the cost function is compared according to the it-

eration step sizes ε which are 0.5, 0.25, and 0.125.

Fig. 4 describes the convergence of the iterations fol-

lowing the relative difference energy. The rate of con-

vergence when ε is 0.5 is faster than that when ε are

0.25 and 0.125. From this, the proposed algorithm

converges to ﬁnd a solution.

3.1 Images Captured by RGB-NIR

Sensors

The results of the proposed algorithm and other meth-

ods are shown for subjective image quality compar-

ison. The results of the algorithms using the im-

ages captured by the RGB-NIR sensors are shown in

Figs. 5-8. Figs. 5(a)-(d) and Figs. 6(a)-(d) show

that the results obtained by the bilinear interpolation

and the BTES methods contain aliasing artifacts such

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

(a) (b)

(e) (f)

Figure 6: Part of the Sample2 image. (a) Color result of the

bilinear interpolation. (b) Color result of the BTES method.

of the bilinear interpolation. (e) NIR result of the BTES

method. (f) NIR result of the proposed algorithm.

as false colors and zipper effects in the resulting im-

ages. However, the results of the proposed algorithm

in Figs. 5(e) and (f) and Figs. 6(e) and (f) show that

the image resolution improved greatly when using the

proposed algorithm. In Figs. 7(a)-(d), the edges of

the images are corrupted. However, Figs. 7(e) and

(f) show that the proposed algorithm produces cor-

rect edges without any aliasing artifacts. While it is

hard to recognize the letters in Figs. 8(a)-(d), Figs.

8(e) and (f) show the resulting edges to be well con-

nected with clear letters. Finally, the amount of false

colors and zipper effects in the high-frequency details

decreased.

To objectively measure the improvement of the

high-frequency details, the high-frequency energy

(HFE) value is used in (Fang et al., 2012b). An im-

age with a larger HFE is generally sharper. In this

paper, this means that image resolution improved and

the high-frequencydetails are reconstructed well. The

image is convolved with two ﬁlters, h

, with k = 1,2.

The two ﬁlters are high-pass ﬁlters [1,−2, 1] applied

in horizontal (k = 1) and vertical (k = 2) directions.

(a) (b)

(e) (f)

Figure 7: Part of the Sample3 image. (a) Color result of the

bilinear interpolation. (b) Color result of the BTES method.

of the bilinear interpolation. (e) NIR result of the BTES

method. (f) NIR result of the proposed algorithm.

Then, the HFE for the bth band image m

] is

given by

∑

k=1

||(h

∗ m

)[n

]||

/2. The average HFE

of the image is calculated as,

HFE

−1

∑

−1

∑

k=1

||(h

∗ m

)[n

]||

. (21)

We applied the HFE measurement to four images. Ta-

ble 1 shows the HFE values of the resulting images for

the four Sample images. The HFE values of the im-

ages produced by the proposed algorithm are higher

than those of the other results. That is, the edges

and high-frequency details of each image are recon-

structed well.

3.2 Simulated Images

The results of the algorithms with the original image

are illustrated in Fig. 9. We show the color images

among the R, G, B, and NIR bands. Figs. 9(b) and

LeastSquarebasedMulti-spectralColorInterpolationAlgorithmforRGB-NIRImageSensors

(a) (b)

(e) (f)

Figure 8: Part of the Sample4 image. (a) Color result of the

bilinear interpolation. (b) Color result of the BTES method.

of the bilinear interpolation. (e) NIR result of the BTES

method. (f) NIR result of the proposed algorithm.

the false colors. However, by the proposed algorithm,

the edges and high-frequency details in Fig. 9(d) are

reconstructed well without leaving aliasing artifacts

such as false colors.

To show a comparison of the objective image

quality measurements, the CPSNR (in dB) is used as

a performance measurement. We apply the CPSNR to

four MS bands,

CPSNR’ = 10log

(

255

MSE

), (22)

where

MSE =

∑

b=1

−1

∑

−1

∑

||m

] − ˆm

]||

(23)

Table 2 lists the CPSNR’ values of the algorithms

when applied to the four test images. In all instances,

the proposed algorithm outperforms the other algo-

rithms since high-frequency information is well re-

constructed by the proposed least square method with

the PAN image.

(a)

(b)

(c)

(d)

Figure 9: Part of the Sample5 image. (a) Original image. (b)

Result of the bilinear interpolation. (c) Result of the BTES

method. (d) Result of the proposed algorithm.

4 CONCLUSIONS

In this paper, we presented a multi-spectral color in-

terpolation algorithm for the RGB-NIR sensor that

acquires invisible NIR band and visible color bands.

This made objects clearer in dark conditions. The en-

ergies of the bands were compared and balanced sim-

ilarly. From the balanced MSFA image, a PAN image

was generated using a low-pass kernel with a high

cutoff frequency. Our algorithm estimated the high-

frequencyof the MS images from the PAN image con-

taining the high-frequency details without aliasing.

The proposed algorithm can be adapted for any type

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

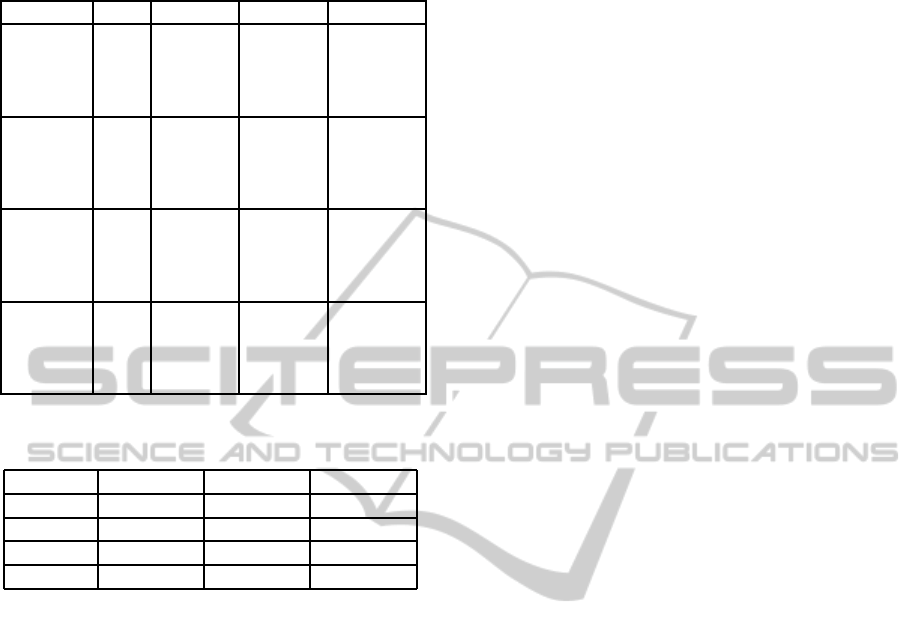
Table 1: HFE Performance Comparison For Four MSFA

Images.

Bilinear BTES Proposed

Sample1

R 5.76 6.77 9.16

G 5.14 5.96 9.14

B 4.07 4.65 9.16

NIR 4.79 5.54 9.14

Sample2

R 3.06 3.46 5.55

G 3.92 4.43 5.56

B 2.45 2.69 5.54

NIR 2.61 2.87 5.54

Sample3

R 7.54 8.99 13.51

G 8.84 10.10 13.61

B 8.26 9.63 13.56

NIR 7.10 8.15 13.45

Sample4

R 9.24 10.64 17.98

G 10.39 12.05 17.99

B 9.95 11.51 17.99

NIR 8.41 9.67 17.97

Table 2: CPSNR’ (in decibels) Performance Comparison

For Four Color Images.

Bilinear BTES Proposed

Sample5 22.80 23.18 24.16

Sample6 22.93 23.12 25.12

Sample7 21.79 21.71 24.44

Sample8 21.84 21.38 24.10

of sub-sampled regular patterns because the method

of reconstructing the high-frequency of the MS im-

ages is not related to any speciﬁc patterns.

ACKNOWLEDGEMENTS

This work was supported by the National

Research Foundation of Korea (NRF) grant

funded by the Korea government (MSIP) (No.

2012R1A2A4A01003732).

REFERENCES

Alleysson, D., Susstrunk, S., and Herault, J. (2005). Lin-

ear demosaicing inspired by the human visual system.

Image Processing, IEEE Transactions on, 14(4):439–

449.

Fang, L., Au, O., Tang, K., and Katsaggelos, A. (2012a).

Antialiasing ﬁlter design for subpixel downsampling

via frequency-domain analysis. Image Processing,

IEEE Transactions on, 21(3):1391–1405.

Fang, L., Au, O., Tang, K., Wen, X., and Wang, H.

(2012b). Novel 2-d mmse subpixel-based image

down-sampling. Circuits and Systems for Video Tech-

nology, IEEE Transactions on, 22(5):740–753.

Gunturk, B., Altunbasak, Y., and Mersereau, R. (2002).

Color plane interpolation using alternating projec-

tions. Image Processing, IEEE Transactions on,

11(9):997–1013.

Koyama, S., Inaba, Y., Kasano, M., and Murata, T. (2008).

A day and night vision mos imager with robust

photonic-crystal-based rgb-and-ir. Electron Devices,

IEEE Transactions on, 55(3):754–759.

Lu, Y., Fredembach, C., Vetterli, M., and Susstrunk, S.

(2009). Designing color ﬁlter arrays for the joint cap-

ture of visible and near-infrared images. In Image Pro-

cessing (ICIP), 2009 16th IEEE International Confer-

ence on, pages 3797–3800.

Luenberger, D. G. and Ye, Y. (1984). Linear and Nonlinear

Programming. Addison-Wesley.

Miao, L., Qi, H., Ramanath, R., and Snyder, W. (2006).

Binary tree-based generic demosaicking algorithm for

multispectral ﬁlter arrays. Image Processing, IEEE

Transactions on, 15(11):3550–3558.

Monno, Y., Tanaka, M., and Okutomi, M. (2011). Multi-

spectral demosaicking using adaptive kernel upsam-

pling. In Image Processing (ICIP), 2011 18th IEEE

International Conference on, pages 3157–3160.

Park, B. K., Choe, W., Lim, J., Lee, S., and Kim, C. (2012).

Color correction with edge preserving and minimal

snr decrease using multi-layer decomposition. volume

8296, pages 829613–829613–7.

Sadeghipoor, Z., Lu, Y., and Susstrunk, S. (2011).

Correlation-based joint acquisition and demosaicing

of visible and near-infrared images. In Image Process-

ing (ICIP), 2011 18th IEEE International Conference

on, pages 3165–3168.

Schaul, L., Fredembach, C., and Susstrunk, S. (2009). Color

image dehazing using the near-infrared. In Image Pro-

cessing (ICIP), 2009 16th IEEE International Confer-

ence on, pages 1629–1632.

Wang, X., Thomas, J.-B., Hardeberg, J. Y., and Gouton, P.

(2013). Median ﬁltering in multispectral ﬁlter array

demosaicking.

Zhang, Y. (1999). A new merging method and its spectral

and spatial effects. International Journal of Remote

Sensing, 20(10):2003–2014.

LeastSquarebasedMulti-spectralColorInterpolationAlgorithmforRGB-NIRImageSensors