Fractal Image Compression using Hierarchical Classiﬁcation of

Sub-images

Nilavra Bhattacharya

, Swalpa Kumar Roy

, Utpal Nandi

and Soumitro Banerjee

Dept. of Computer Sc.& Tech., Indian Institute of Engineering Science & Technology, Shibpur, India

Dept. of Computer Science, Vidyasagar University, Midnapore, India

Dept. of Physical Sciences, Indian Institute of Science Education and Research, Kolkata, India

Keywords:

Fractal Image Compression, Fisher Classiﬁcation, IFS, PIFS, Hierarchical Classiﬁcation, Block Classiﬁcation.

Abstract:

In fractal image compression (FIC) an image is divided into sub-images (domains and ranges), and a range

is compared with all possible domains for similarity matching. However this process is extremely time-

consuming. In this paper, a novel sub-image classiﬁcation scheme is proposed to speed up the compression

process. The proposed scheme partitions the domain pool hierarchically, and a range is compared to only those

domains which belong to the same hierarchical group as the range. Experiments on standard images show that

the proposed scheme exponentially reduces the compression time when compared to baseline fractal image

compression (BFIC), and is comparable to other sub-image classiﬁcation schemes proposed till date. The

proposed scheme can compress Lenna (512x512x8) in 1.371 seconds, with 30.6 dB PSNR decoding quality

(140x faster than BFIC), without compromising compression ratio and decoded image quality.

1 INTRODUCTION

The theory of fractal based image compression us-

ing iterated function system (IFS) was ﬁrst proposed

by Michael Barnsley (Barnsley, 1988). A fully auto-

mated version of the compression algorithm was ﬁrst

developed by Arnaud Jaquin, using partitioned IFS

(PIFS) (Jacquin, 1992). Jaquin’s FIC scheme is called

the baseline fractal image compression (BFIC). Frac-

tal compression is an asymmetric process. Encod-

ing time is much greater compared to decoding time,

since the encoding algorithm has to repeatedly com-

pare a large number of domains with each range to

ﬁnd the best-match.

Plenty of research has focused on how to speed-

up the compression process, and almost all of them

explored how to reduce the number of domain blocks

in the domain pool. Fisher (1994) divided the domain

pool into 72 classes according to certain combinations

of the four quadrants of a block. His work proved the

efﬁciency of the classiﬁcation schemes: the searching

time got reduced to the order of magnitude of sec-

onds without great loss of image quality. Tong and Pi

(2001) and later Wu et al. (2005) used standard devi-

ation to classify blocks. Wang et al. (2000) and Duh

et al. (2005) used the edge properties of the blocks to

group them into three or four classes, and this resulted

in a speedup ratio of 3 to 4. Xing et al. (2008) re-

ﬁned Fisher’s scheme and obtained 576 classes based

on a block’s mean pixel value and its variance. Han

(2008) used a fuzzy pattern classiﬁer to classify im-

age blocks. Tseng et al. (2008) used Particle Swarm

Optimization to classify image blocks. Jayamohan

and Revathy (2012) classiﬁed domains based on Lo-

cal Fractal Dimensions and used AVL trees to store

the classiﬁcation. Wang and Zheng (2013) used Pear-

son’s Correlation Coefﬁcient as a measure of similar-

ity between domains and ranges, and classiﬁed image

blocks based on it.

In this paper a novel sub-image classiﬁcation

scheme is proposed, which greatly improves the com-

pression time (when compared to BFIC), and is com-

parable to other sub-image classiﬁcation schemes

proposed till date, in terms of speed. The layout

of this paper is as follows: the mathematical back-

ground of Fractal Image Compression is brieﬂy out-

lined in section 2, while Fisher’s classiﬁcation scheme

is explained in section 3. The proposed classiﬁcation

scheme (abbreviated as P-I) is explained in section 4.1

and a further optimization technique (abbreviated as

P-II) is given in section 4.2. Experimental results are

given in section 5. The conclusions are made in sec-

tion 6, which are followed by acknowledgements, and

ﬁnally the references.

Bhattacharya N., Roy S., Nandi U. and Banerjee S..

Fractal Image Compression using Hierarchical Classiﬁcation of Sub-images.

DOI: 10.5220/0005265900460053

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 46-53

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 FRACTAL COMPRESSION

2.1 The Theory

A typical afﬁne transform from a domain to a range

is shown in Equation (1). Constants a

i, j

represent the

scaling factors from the domain to the range, while

constants d

i, j

represent the top-left corner of the do-

main. Constants s

and o

control the contrast and the

brightness of the transformation respectively. Hence,

an afﬁne map is basically a collection of constants.













i,1

i,2

i,3

i,4

0 0 s

















i,1

i,2





(1)

A domain and a range is compared using an RMS

metric (Fisher, 1994). Given two square sub-images

containing n pixel intensities, a

, . . . , a

(from the do-

main) and b

, . . . , b

(from the range), with contrast

s and brightness o between them, the RMS distance

between the domain and the range is given by

R =

∑

i=1

(s · a

+ o − b

)

(2)

Detailed mathematical description of IFS theory

and other relevant results can be found in (Barnsley,

1988; Edgar, 2007; Falconer, 2013).

2.2 The Pain

As mentioned in section 1, an enormous number of

domain-range comparisons is the main bottleneck of

the compression algorithm. E.g., consider an image

of size 512 × 512. Let the image be partitioned into

4 × 4 non-overlapping range blocks. There will be

= 16384 range blocks. Let there be 8×8 overlap-

ping domain blocks (most implementations use do-

main sizes that are double the size of range). Then, for

a complete search, each range block has to be com-

pared with 505 × 505 = 255025 domain blocks. The

total number of comparisons will be around 2

. The

time complexity can be estimated as Ω(2

3 FISHER’S CLASSIFICATION

Fisher’s classiﬁcation scheme (Fisher, 1994) is as

follows: A square sub-image (domain or range) is

divided into upper-left, upper-right, lower-left, and

lower-right quadrants, numbered sequentially.

On each quadrant, values A

(proportional to mean

pixel intensity) and V

(proportional to pixel intensity

variance) are computed. If the pixel values in quad-

rant i are r

, r

, . . . , r

, then

∑

j=1

(3)

and

∑

j=1

)

− A

(4)

Then it is possible to rotate the sub-image (do-

main or range) such that the A

are ordered in one of

the following three ways:

Major Class 1: A

≥ A

Major Class 2: A

≥ A

Major Class 3: A

≥ A

These orderings constitute three major classes and

are called canonical orderings. Under each major

class, there are 24 subclasses consisting of

= 24

orderings of the V

. Thus there are 72 classes in all.

Fisher noted that the distribution of domains across

the 72 classes was far from uniform. So he went on

to further simplify the scheme. 24 classes were de-

rived by combining the three major ﬁrst-classes in the

above classiﬁcation. Fisher concluded: ”the improve-

ment attained by using 72 rather than 24 classes is

minimal and comes at great expense of time” (Fisher,

1994). In this paper, we refer to this 24-class classiﬁ-

cation scheme as FISHER24.

4 PROPOSED HIERARCHICAL

CLASSIFICATION SCHEME

Fisher used values proportional to the mean and the

variance of the pixel intensities to classify a sub-

image. In our proposed schemes, we use only the sum

of pixel intensities of various parts of a sub-image to

classify the sub-image.

4.1 Proposed Technique - I (P-I)

After selecting the square sub-image (domain / range)

(Figure 1(a)), the proposed hierarchical classiﬁcation

algorithm works as follows:

1. Divide the sub-image into upper-left, upper-right,

lower-left, and lower-right quadrants.

2. For each quadrant i (i = 0, 1, 2, 3) calculate the

sum of pixel values S

. If the pixel values in quad-

rant i are r

, r

, . . . , r

, then

∑

j=1

(5)

FractalImageCompressionusingHierarchicalClassificationofSub-images

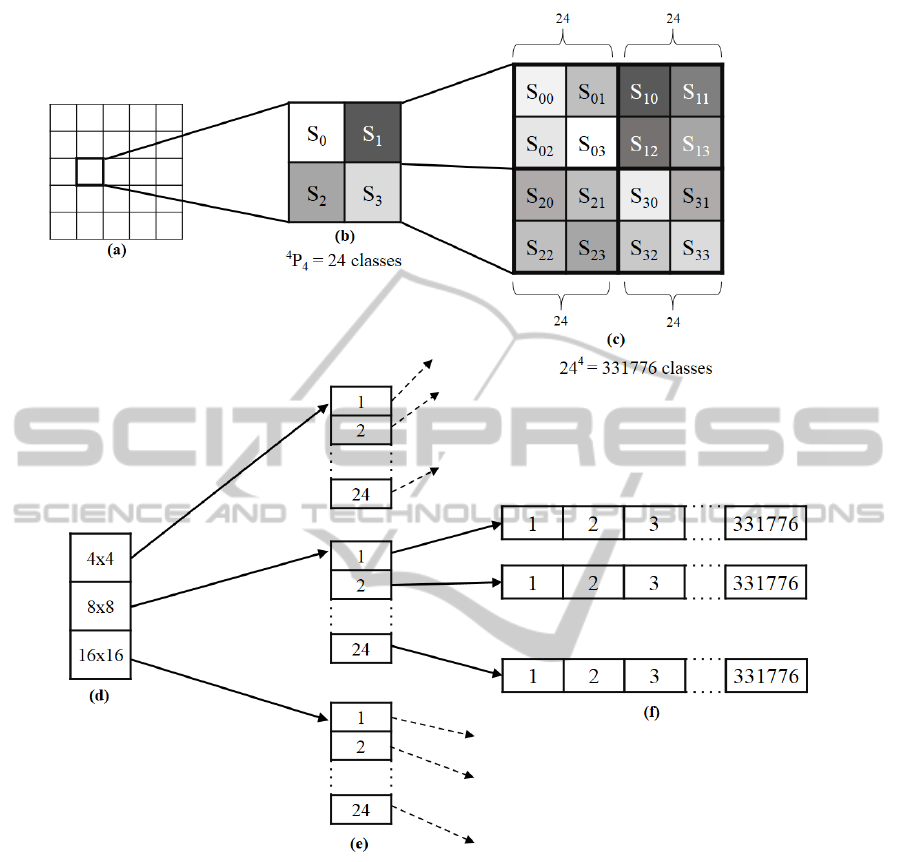
Figure 1: Proposed classiﬁcation scheme and data structures used: (a) Square sub-images (overlapping domains or non-

overlapping ranges) (b) Level I classiﬁcation - 24 classes based on relative ordering of pixel intensity sums S

, S

(c)

Level II classiﬁcation - 4 quadrants of Level I further subdivided into 4 sub-quadrants each; each quadrant i assigned a value

between 1 and 24 based on relative ordering of sub-quadrant pixel intensity sums S

, S

(i = 0, 1, 2, 3). 4 quadrants,

each having a value between 1 and 24 gives 3311776 classes. (d) Domain pool has domains of 3 sizes - 4 × 4, 8 × 8 and

16 × 16 (e) 24 Level I classes for all 3 domain sizes (f) 331776 Level II classes for every Level I class. Each of the 331776

array cells point to a list of domains falling in that class.

3. Based on the relative ordering of S

, S

(calculated in Step 2), there can be

= 24 per-

mutations. A number between 1 and 24, that

uniquely identiﬁes this particular permutation is

assigned to this sub-image. This number is the

Level I class for this sub-image (Figure 1(b)).

4. Divide each of the quadrants of Step 1 again, into

4 sub-quadrants (16 sub-quadrants in total).

5. Calculate the sum of pixel values S

i j

(i =

0, 1, 2, 3, j = 0, 1, 2, 3) for each sub-quadrant.

6. Based on the relative ordering of sub-quadrant

pixel-value sums S

, S

for each quad-

rant i = 0, 1, 2, 3, each quadrant can be assigned

a number between 1 and 24 (similar to step 3).

Four quadrants, each being assigned a number be-

tween 1 and 24 gives 24

= 331776 cases in to-

tal, for the entire sub-image. A number between 1

and 331776, that uniquely identiﬁes this particular

case is assigned to this sub-image. This number is

the Level II class for this sub-image (Figure 1(c)).

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

During compression, when the domain pool is be-

ing created, data structures are deﬁned as shown in

Figure 1(d), Figure 1(e) and Figure 1(f). Domains

are ﬁrst classiﬁed by their size, then into Level-I, ac-

cording to pixel-value-sum of 4 quadrants, and ﬁnally

into Level-II, according to pixel-value sum of 16 sub-

quadrants. After two rounds of classiﬁcation, the do-

main is placed in a list pointed to by the array cell

corresponding to the Level-II class (Figure 1(f)).

Later in the compression algorithm, when search-

ing the domain pool for a best-match with a particular

range, only those domains that are in the same Level-

II class as the range are considered for comparison.

4.2 Proposed Technique - II (P-II)

This is an add-on for the proposed P-I technique (sec-

tion 4.1) to further reduce the number of domain-

range comparisons. The main idea is to keep track of

the domains that are getting selected as the best-match

more than once, and offering those domains for com-

parison in subsequent searches, before others, hoping

that these will again be a best-match, and searching

will be over quickly. This is implemented as follows:

Along with each domain, a counter named

timesUsed is also maintained, which indicates how

many times that particular domain was already se-

lected as the best-match. During the creation of

the domain pool, all timesUsed counters of all do-

mains are initialized to zero. Later, when search-

ing the domain-list of a Level-II class for the best-

match, if a domain gets selected as the best-match, its

timesUsed counter value is incremented.

On subsequent searches in the same Level-II class,

domains are selected for comparison in the decreasing

order of their timesUsed value. Searching gets over

as soon as a domain is found whose RMS distance

from the range is less than a predeﬁned threshold.

Once again the timesUsed value of this best-match

domain is incremented.

The domain-lists of each Level-II class are imple-

mented as max-heaps which support O(logn) time in-

serts and O(1) lookups (Cormen et al., 2009).

4.3 Elementary Analysis

4.3.1 FISHER24

Let total number of domains in domain-pool = D

Number of classes = 24

∴ Average number of domains per class =

Let total number of ranges = R

∴ Number of domain-range comparisons =

· R (6)

4.3.2 P-I

Let total number of domains in domain-pool = D

Number of Level-I classes = 24

Number of Level-II classes = 24

∴ Total number of classes = 24 · 24

= 24

∴ Average number of domains per class =

Let total number of ranges = R

∴ Number of domain-range comparisons =

· R (7)

4.3.3 P-II

Let total number of domains in domain-pool = D

Number of Level-I classes = 24

Number of Level-II classes = 24

∴ Total number of classes = 24 · 24

= 24

∴ Average number of domains per class =

Let total number of ranges = R

∴ Number of domain-range comparisons

≤

· R (8)

In Equation (8), the less-than condition occurs be-

cause searching is over as soon as a domain is found

whose RMS distance from the range is less than the

predeﬁned threshold. Equality occurs in the worst-

case, when only the last domain of a class is selected

every time.

It is evident from the above analysis that since

· R 

(9)

the proposed classiﬁcation schemes reduce the do-

main search space exponentially, when compared to

FISHER24. This is bound to speed up the compres-

sion algorithm, and is corroborated by the experimen-

tal results in section 5.

FractalImageCompressionusingHierarchicalClassificationofSub-images

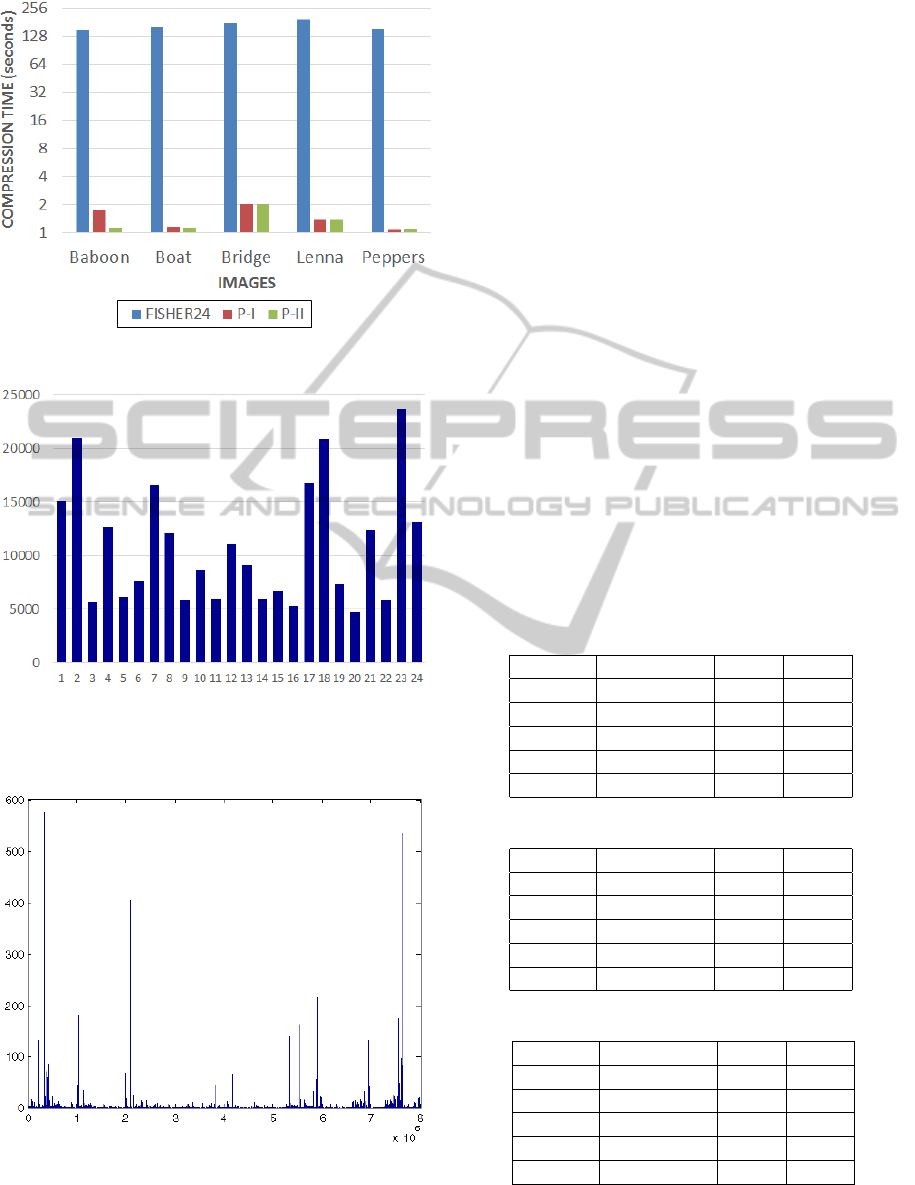
Figure 2: Graphical comparison of compression time.

Figure 3: Histogram of ”Lenna” showing the number of do-

mains in each of the 24 classes of FISHER24 classiﬁcation

scheme (summed across all the domain sizes).

Figure 4: Histogram of ”Lenna” showing the number of

domains in each of the 24

classes of the proposed classiﬁ-

cation scheme (summed across all the domain sizes).

5 RESULTS AND DISCUSSIONS

5.1 Tools

Five standard 512 × 512 × 8 images have been used to

test the proposed techniques P-I (section 4.1) and P-II

(section 4.2) and also for comparison with FISHER24

classiﬁcation scheme (section 3). The algorithm was

implemented in Java, running on a PC with Intel Core

i7 2630QM 2.0 GHz Processor, 8 GB DDR3 RAM,

and running Windows 8 x64.

5.2 Research Results

The comparison of compression time (in seconds),

PSNRs (in dB) and space savings (in percentage) for

the ﬁve image ﬁles have been made in Table 1, Table 2

and Table 3 respectively. The pictorial representations

of compression times, PSNRs and space savings are

illustrated in Figures 2, 5 and 6 respectively. Figures

7, 8, 9 and 10 show the close up of Lenna original,

decoded after using FISHER24, decoded after using

proposed P-I technique and decoded after using pro-

posed P-II technique respectively. Figure 11 shows

the result of the techniques on the other test images.

Table 1: Comparison of compression time (seconds).

Image FISHER24 P-I P-II

Baboon 147.441 1.737 1.137

Boat 160.214 1.161 1.133

Bridge 175.924 2.035 1.995

Lenna 193.066 1.371 1.374

Peppers 150.112 1.082 1.102

Table 2: Comparison of PSNR (in dB).

Image FISHER24 P-I P-II

Baboon 22.22 22.22 22.22

Boat 28.44 28.44 28.44

Bridge 25.55 25.55 25.56

Lenna 30.60 30.60 30.60

Peppers 28.01 28.01 28.02

Table 3: Comparison of Space Savings (%).

Image FISHER24 P-I P-II

Baboon 89.26 89.26 89.26

Boat 89.39 89.39 89.39

Bridge 86.88 86.88 86.88

Lenna 89.58 89.58 89.58

Peppers 89.43 89.43 89.43

The proposed two techniques exponentially re-

duce the compression time compared to FISHER24.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

It is because the total number of domain-range com-

parisons is reduced, as shown by Equation (9).

Figures 3 and 4 show the distribution of domains

across all classes for FISHER24 and the proposed

classiﬁcation scheme respectively, for the Lenna im-

age. Figure 3 shows that each class contains at least

5000 domains. So each range is compared to a mini-

mum of 5000 domains. However, Figure 4 shows that

in the proposed scheme, most classes contain less than

100 domains, while the maximum number domains

in a class is less than 600. So the total number of

domain-range comparisons is greatly reduced in the

proposed schemes. Between the two proposed tech-

niques, P-II takes less time for 3 out of 5 test-images.

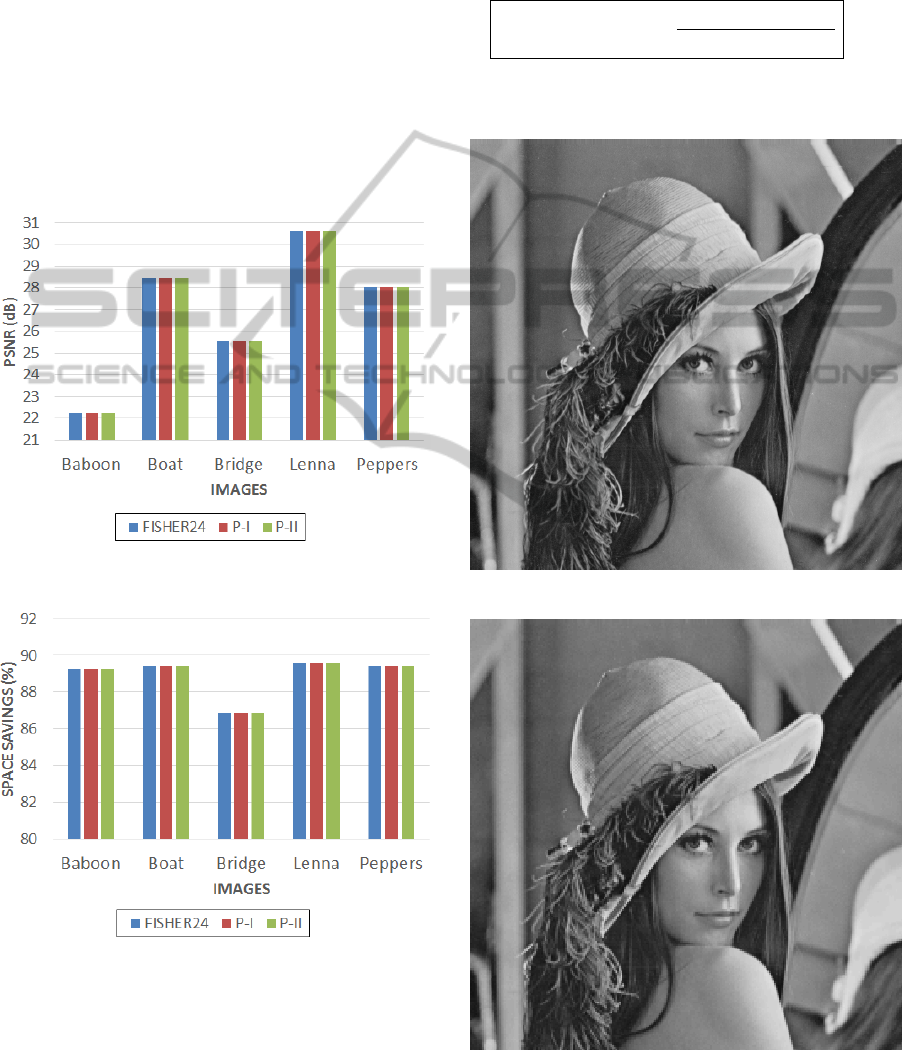
Figure 5: Graphical comparison of PSNR.

Figure 6: Graphical comparison of Space Savings (%).

Regarding decoded image quality, Table 2 and

Figure 5 shows that the proposed techniques offer the

same quality as FISHER24, for all the test-images.

The PSNR values are identical for all the recon-

structed images, even for P-II, where the search is

being terminated as soon as a domain with domain-

range RMS distance less than a predeﬁned threshold

is found. This means that the best domains are being

used maximum number of times.

Space Savings is the reduction in size relative to

uncompressed size, and is given as

Space Savings = 1 −

Compressed Size

Uncompressed Size

(10)

The proposed two techniques offer almost the

same percentage of space-savings as FISHER24.

Figure 7: Lenna - original.

Figure 8: Lenna - using FISHER24 classiﬁcation.

FractalImageCompressionusingHierarchicalClassificationofSub-images

Figure 9: Lenna - after using proposed technique P-I.

Figure 10: Lenna - after using proposed technique P-II.

6 CONCLUSION

The proposed techniques of Fractal Image Com-

pression by using hierarchical classiﬁcation of do-

main/range viz. P-I and P-II improve the compres-

sion time of images signiﬁcantly, when compared

to existing FISHER24 classiﬁcation. PSNRs of de-

coded images using both techniques are identical to

FISHER24, which means that image quality is not

degraded by the proposed techniques. The compres-

sion ratios (denoted by space savings in this paper)

for both P-I and P-II are also equal to FISHER24. Be-

tween the two proposed techniques, P-II is marginally

faster than P-I in 3 out of 5 test-images. In terms of

PSNR and space savings, they give identical results.

ACKNOWLEDGEMENTS

The ﬁrst author acknowledges the support of the

AICTE-INAE Travel Grant Scheme for Engineering

Students, Govt. of India, which enabled him to attend

the conference.

The ﬁrst-author also thanks the German Missions

in India for offering a free Schengen VISA to attend

the conference.

REFERENCES

Barnsley, M. F. (1988). Fractals Everywhere. Academic

Press, New York.

Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,

C. (2009). Introduction to Algorithms. MIT press,

Cambridge, MA, U.S.A.

Duh, D.-J., Jeng, J., and Chen, S.-Y. (2005). Dct based sim-

ple classiﬁcation scheme for fractal image compres-

sion. Image and vision computing, 23(13):1115–1121.

Edgar, G. (2007). Measure, topology, and fractal geometry.

Springer.

Falconer, K. (2013). Fractal geometry: mathematical foun-

dations and applications. John Wiley & Sons.

Fisher, Y., editor (1994). Fractal Image Compression: The-

ory and Application. Springer-Verlag, New York.

Han, J. (2008). Fast fractal image compression using fuzzy

classiﬁcation. In Fuzzy Systems and Knowledge Dis-

covery, 2008. FSKD’08. Fifth International Confer-

ence on, volume 3, pages 272–276. IEEE.

Jacquin, A. E. (1992). Image coding based on a fractal the-

ory of iterated contractive image transformations. Im-

age Processing, IEEE Transactions on, 1(1):18–30.

Jayamohan, M. and Revathy, K. (2012). An improved do-

main classiﬁcation scheme based on local fractal di-

mension. Indian Journal of Computer Science and

Engineering (IJCSE), 3(1):138–145.

Tong, C. S. and Pi, M. (2001). Fast fractal image encoding

based on adaptive search. Image Processing, IEEE

Transactions on, 10(9):1269–1277.

Tseng, C.-C., Hsieh, J.-G., and Jeng, J.-H. (2008). Frac-

tal image compression using visual-based particle

swarm optimization. Image and Vision Computing,

26(8):1154–1162.

Wang, J. and Zheng, N. (2013). A novel fractal image com-

pression scheme with block classiﬁcation and sorting

based on pearson’s correlation coefﬁcient.

Wang, Z., Zhang, D., and Yu, Y. (2000). Hybrid image

coding based on partial fractal mapping. Signal Pro-

cessing: Image Communication, 15(9):767–779.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

Figure 11: Test images and results - Baboon, Boat, Bridge and Peppers. (a) Original image (b) Result of using FISHER24

classiﬁcation (c) Result of using proposed P-I technique (d) Result of using proposed P-II technique.

Wu, X., Jackson, D. J., and Chen, H.-C. (2005). A fast frac-

tal image encoding method based on intelligent search

of standard deviation. Computers & Electrical Engi-

neering, 31(6):402–421.

Xing, C., Ren, Y., and Li, X. (2008). A hierarchical classi-

ﬁcation matching scheme for fractal image compres-

sion. In Image and Signal Processing, 2008. CISP’08.

Congress on, volume 1, pages 283–286. IEEE.

FractalImageCompressionusingHierarchicalClassificationofSub-images