Drawing Georeferenced Graphs

Combining Graph Drawing and Geographic Data

Giordano Da Lozzo

, Marco Di Bartolomeo

, Maurizio Patrignani

Giuseppe Di Battista

, Davide Cannone

and Sergio Tortora

Engineering Department, Roma Tre University, Rome, Italy

Product Innovation & Advanced EW Solutions, Elettronica S.p.a., Rome, Italy

Keywords:

Graph Visualization, Visual Interfaces, Networked and Geospatial Data.

Abstract:

We consider the task of visually exploring relationships (such as established connections, similarity, reacha-

bility, etc) among a set of georeferenced entities, i.e., entities that have geographic data associated with them.

A novel 2.5D paradigm is proposed that provides a robust and practical solution based on separating and then

integrating back again the networked and geographical dimensions of the input dataset. This allows us to

easily cope with partial or incomplete geographic annotations, to reduce cluttering of close entities, and to ad-

dress focus-plus-context visualization issues. Typical application domains include, for example, coordinating

search and rescue teams or medical evacuation squads, monitoring ad-hoc networks, exploring location-based

social networks and, more in general, visualizing relational datasets including geographic annotations.

1 INTRODUCTION

We address the problem of exploring a georeferenced

graph, i.e., a graph with some geographic information

associated to it. Typical applications include for ex-

ample, coordinating search and rescue teams, super-

vising medical evacuation squads, monitoring ad-hoc

networks, visualizing Internet routing events, and, on

a more familiar and playful side, exploring location-

based social networks.

The requirements of the interface are the follow-

ing: the area of interest consists of a terrain where

a number of entities are located, and possibly move.

Figure 1: A snapshot of the proposed 2.5D interface. The

logical layer, above, shows the networked data, while the

geographic layer, below, displays actual locations of the

entities contained in the logical layer, whenever available.

Their geographic position may be declared by the en-

tities themselves, tracked by radar stations, inferred

from their transmissions, or, in some cases, com-

pletely unknown. Entities have a number of rela-

tionships, such as established connections, similarity,

reachability, etc. The purpose of the interface is to

represent in the most intuitive and unambiguous way

both the relationships among the entities and their po-

sitions, conveying at the same time the degree of un-

certainty associated with the geographic information.

User’s tasks involve the analysis of both the net-

worked and the geographic dimensions of the infor-

mation. Let’s suppose, for example, that the data rep-

resented come from a social network. Typical queries

may be: What is the shortest friendship chain lead-

ing from a friend of mine living in London to any-

one located in Berlin? Is it possible to ﬁnd a friend-

ship chain from London to Berlin without involving

any person living in Rome? How many friends of my

friends are currently in the same location as I am now?

We propose an innovative 2.5D paradigm to visu-

ally explore data with both a relational and a geolocal-

ized nature. Our proposal is based on ﬁrst separating

and then integrating back again the networked and the

geographic information. Namely, the geographic in-

formation is shown within a map, called geographic

layer, while a second logical layer is devoted to the

relational information. The two equally-sized rect-

109

Da Lozzo G., Di Bartolomeo M., Patrignani M., Di Battista G., Cannone D. and Tortora S..

Drawing Georeferenced Graphs - Combining Graph Drawing and Geographic Data.

DOI: 10.5220/0005266601090116

In Proceedings of the 6th International Conference on Information Visualization Theory and Applications (IVAPP-2015), pages 109-116

ISBN: 978-989-758-088-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

angular layers are placed one above the other, and

viewed from a side in a 2.5D fashion, so that there

is no overlap among them, i.e., no ambiguity between

the two types of information (see Figure 1).

Entities are placed on the logical layer in such a

way to reduce cluttering and to make their relation-

ships readable and clear, while leaders are used to re-

late each entity on the logical layer to its known loca-

tion on the geographic layer, whenever available.

All the screenshots in this paper are taken from a

JavaScript demonstrative prototype, implemented us-

ing the WebGL graphics library (The Khronos Group,

2013), that runs within any compatible web browser.

2 VISUALIZING NETWORKED

AND GEOGRAPHIC DATA

In this section we describe a visualization system,

based on a novel graphic metaphore, that overcomes

the limitations of traditional solutions with respect to

user tasks that are typical of the visualization of geo-

referenced networks.

2.1 Problem Statement

Our visualization problem has two different inputs:

the ﬁrst one is from the user, who controls a rectangu-

lar area on a map, which is the current area of interest

to be monitored and that can be translated, rotated,

and zoomed. The second one comes from the out-

side world and is, essentially, a set of relationships

among the entities of the considered domain. Each

entity comes equipped with its type, its position, and

the degree of uncertainty of such geographic infor-

mation, which is provided by specifying the size of a

geometric shape (usually a circle) that approximates

the area where the entity is assumed to be.

The available data deﬁnes a network, whose nodes

are the entities and whose edges are the relationships

among entities. The purpose of the system is to show

both the networked and the geographic information,

meeting the following high-level requirements.

Effectiveness. The visualization should show in a

clear and readable way the number of entities located

on the selected area, their current position, and their

relationships.

Intuitiveness. The graphic metaphors and the inter-

action primitives should be natural and intuitive, with

low cognitive load.

Robustness. The visualization should support incom-

plete information, handling, in particular, missing and

uncertain geographic data.

Unambiguity. The representation should be accurate

and unambiguous. For example, the degree of uncer-

tainty of the geographic information should be clear.

2.2 User’s Tasks

When exploring a georeferenced graph relevant user’s

tasks involve both the networked and the geographic

dimensions of the information. Some of these tasks

address simple quantitative queries, as estimating

what is the amount of entities that share some target

location, ﬁnding the location that hosts the more in-

terconnected entities, determining whether a speciﬁc

location hosts unconnected clusters of entities, etc.

We also identify more complex tasks that strongly

rely on the analysis of the structure of the networked

information. For example, ﬁnding the shortest chain

of entities leading from a source placed in location A

to any target located in B; ﬁnding a chain from lo-

cation A to location B that does not involve any en-

tity located in C; determining how many entities are

reachable with two edges and are placed in a spe-

ciﬁc location; determining how strong are the connec-

tions among entities placed in location A and entities

placed in location B, etc.

All these high level tasks primarily require the

ability of the user to explore the structure of the rela-

tionships among the entities on the logical layer. Sec-

ondarily, the user needs to quickly grasp the area that

hosts a given entity or, conversely, the set of entities

that are located in a given area. These basic opera-

tions are complicated by the fact that some entities

may not have a location associated and that a number

of entities may share the same location.

2.3 Limitation of 2D Interfaces

The simple approach of placing icons on a 2D map

based on the entities’ geographic coordinates would

not meet the requirements. In particular, since some

entities share the same location, any 2D map would

fail to unambiguously show both the location of the

entities and their relationships. Also, entities on a ge-

ographic map are rarely equispaced. Instead, it is of-

ten the case that they gather in speciﬁc points (e.g.,

cities). Long and short distances among entities have

to be simultaneously represented in the same view.

When some entities have very close locations, their

icons overlap unless the user zooms in on them. This

zooming in and out has a dramatic effect on the us-

ability of the interface due to focus-and-context is-

sues: when some speciﬁc details are on focus the

whole picture is no longer in sight and vice versa.

To complicate this scenario, some entities may

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

110

have unknown geographic position. For example,

users of a geolocated social network may disallow

their applications to take advantage of GPS data;

some devices of an ad-hoc network may not host

a ground positioning circuit; routers of a computer

network may not have an associated administrative

site; end-points of a phone or radio conversation may

be unknown; etc. Wherever such entities would be

placed on a 2D map, it would result in an ambiguous

representation since the user would assume that those

positions are the actual positions of the entities.

Finally, a 2D map does not convey in a natural way

the degree of uncertainty of the geographic informa-

tion. Placing icons on the map at the center of the area

where the entity is supposed to be may result in the

user’s false conﬁdence about the actual position of the

entity. Drawing on the map some shadowed shapes,

rectangles or circles, proportional to the degree of un-

certainty on the position of the corresponding enti-

ties yields a representation that is not self-evident and

that is confusing when several entities, with different

shapes and different degree of uncertainty, are close

one to the other.

2.4 Exploiting a 2.5D Visualization

Our strategy is to separate and simultaneously visual-

ize the networked and the geographic information of

the input dataset. Namely, the geographic information

is represented on the geographic layer, which is in the

bottom part of the interface, while the networked in-

formation is represented on the logical layer, which

is parallel to the geographic layer and placed in the

upper part of the interface. Leaders among the two

layers relate nodes with their geographic locations, if

any. The interface is shown in Fig. 1. In order to

avoid overlaps between the two layers, which would

give occlusion among the two types of information,

we restrict their size to two equally-sized rectangles

and suitably place the point of view on the longest

side of the rectangles as shown in Fig. 2.

It has to be pointed out that the size and the ori-

entation of the rectangles representing the logical and

geographic layers are ﬁxed with respect to the screen

coordinates. Panning, zooming and rotating will have

the effect of changing what is represented in the geo-

graphic and logical layers, but will not move the point

of view with respect to the layers themselves. This de-

sign choice allows for a very simple and intuitive nav-

igation of the scenario, that does not require the user

to cope with fully 3D navigation primitives. Hence,

in spite of its 3D ﬂavor, our representation is a 2.5D

one, both because the graph is actually drawn on the

2D surface offered by the logical plane and because

camera

(a)

Figure 2: The position of the geographic and logical layers

with respect to the point of view (we used l

= 1600, l

900, l

= 650, c

= 2000, c

= 1600, p

= 260).

the user interaction is limited to the 2D primitives of

panning, zooming, and rotating. From a practical per-

spective, this is realized with four clipping planes that

move together with the point of view and that cut out

the world scene lying beyond the prescribed area.

Nodes are placed on the logical layer with the pur-

pose of conveying as effectively as possible the struc-

ture of the graph, reducing cluttering and crossings

among edges (see Fig. 3). To this purpose, we devised

a specialized force-directed algorithm, described in

Section 4. The computed layout tries to achieve both

evenly-spaced distribution of nodes and few crossings

among edges, while seeking to minimize the distance

of each node from the corresponding position on the

geographic layer. The goal of the geographic layer,

instead, is that of displaying the current position of

each node shown on the logical layer. Such a position

is represented by means of a marker on the map with

a straight-line leader connecting it to the correspond-

ing node on the logical layer. When the position of

the node is affected by uncertainty the marker on the

map is a geometric shape, usually a circle, enclosing

the area where the corresponding object is supposed

to be, and the leader consists of a cone with its apex

on the node. Nodes with no geographic information

associated have no marker on the map (see Fig. 4).

Therefore, in our approach, we have two types

of links: (i) the edges on the logical layer and (ii)

the leaders connecting the two layers. We privilege

the readability of the graph induced by the ﬁrst type

of links, by trying to reduce crossings on the logical

layer, which severely jeopardize the comprehension

of the graph structure (Purchase et al., 1997; Pur-

chase, 2000). Crossings among leaders have lower

impact on readability, since the structure of the graph

induced by them is of limited interest to the user. In

fact, each leader establishes a connection between an

DrawingGeoreferencedGraphs-CombiningGraphDrawingandGeographicData

111

(a) (b)

Figure 3: Two snapshots of the interface showing (a) crossings are reduced in the layout in the logical layer (the edges on the

geographic layer are drawn for comparison) and (b) entities with common locations are clearly shown in the logical layer.

entity and a geographic location, and paths of lead-

ers are never considered by the user. Also, when the

mouse hovers a vertex on the logical layer, the in-

terface highlights its incident leader to help the user

identify the leader endpoint on the geographic layer.

Figure 4: A georeferenced graph where the position of

some entities is unknown and the position of other entities

is known with some approximation.

The graph represented in the logical layer is com-

posed by all the entities inside the area of interest of

the user (in-sight entities) and all the entities that have

links with such entities (linked entities). When the

user zooms, rotates, or translates the area of interest

(for example by pressing keyboard combinations or

by dragging the mouse) the system updates the graph.

Appearing nodes are placed on the border of the log-

ical layer, in the point which is nearer to their actual

geographic position or in the point which is nearer to

the position of one of the nodes they are linked to (in

case of linked entities with no geographic position).

3 RELATED WORK

Visual Links in 2.5D Visualizations. The use of vi-

sual links (i.e., edges) to highlight relationships be-

tween multiple views has been pioneered in the two-

dimensional setting in (Weaver, 2005; Aris and Shnei-

derman, 2007; Shneiderman and Aris, 2006) and fur-

ther explored in (Steinberger et al., 2011; Hadlak

et al., 2011). The third dimension has been often used

to add extra information to a traditional 2D layout. In

particular, the use of inter-plane edges accounting for

the relationships between nodes of separate 2D visu-

alizations of the same graph has been proposed by the

authors of VisLink (Collins and Carpendale, 2007).

The VisLink system allows the user to change the po-

sition of the planes hosting the drawings of the graph,

stacking them horizontally, placing them side-by-side

vertically, viewing them from the top, etc. In (Streit

et al., 2008; Lex et al., 2010) a similar approach has

been used for the exploration of interconnected path-

ways. In this case, the planes are usually more than

two, and the system does not rely on the user ability

for arranging the planes and for efﬁciently using the

available screen space. Instead, the planes are placed

on ﬁve sides of a cube and the user looks at them from

the remaining side.

Spatial and Non-Spatial Data in Cartography. Our

target visualization problem can be viewed as a par-

ticular case of integrated spatial and non-spatial data

visualization, where the non-spatial data can be mod-

eled as a graph composed of entities and relationships

among pairs of entities. Providing an integrated visu-

alization of spatial and non-spatial data is a traditional

topic in cartography where thematic maps are used to

visualize the distribution of statistical variables. The

values associated with the points on the maps can

be represented, for example, by colors (choropleth

maps), by the sizes of suitable symbols (proportional

symbols maps), by the density of dots (dotted maps),

etc. Although thematic maps may go so far as to rep-

resent a small chart for each location (Wood et al.,

2011), usually the non-spatial data represented has a

very simple structure.

Reducing the Visual Clutter in Spatial Data. The

problem of reducing the visual clutter of symbols on

interactive maps has been approached with different

techniques. Google Earth (Google Inc., 2013) auto-

matically collapses into a single symbol spatially co-

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

112

incident placemarks, which are exploded again in a

cluster when clicked. Spatial dithering and changes

in symbology (e.g., colour, opacity, line thickness and

size) can be used to reﬂect the existence of unseen or

coincident data (Wood et al., 2007).

4 THE Retina LAYOUT

ALGORITHM

In this section we describe the algorithm that com-

putes the network layout on the logical layer. Spring

embedders are natural candidates for our application,

since they grant, besides good quality results, the ﬂex-

ibility needed by our interactive system.

Although spring embedders are standard force-

directed graph layout algorithms, our visualization

problem is somehow special, as the logical layer is

viewed from a side by the user, who, therefore, sees a

picture distorted by the perspective. This has the ef-

fect of increasing the cluttering of the objects in the

background with respect to those in the foreground.

Hence, we conceived a variant of the spring embed-

der algorithm that computes the layout directly on the

view plane, which is essentially the user’s retina. This

is why we dubbed it Retina layout algorithm.

A spring embedder boils down to be a very simple

iterative process that, given the conﬁguration at iter-

ation i, computes the conﬁguration at iteration i + 1

by summing up, for each node, the forces acting on

it, and then translating the node in the direction of

the resulting force and proportionally to its magni-

tude. Such process then stops as soon as the sum of

the forces acting on the nodes drops below a certain

minimum threshold. Like (traditional) spring embed-

ders, Algorithm Retina searches for an equilibrium

conﬁguration of a physical model obtained by replac-

ing nodes with equally charged particles and edges

with springs. On the one hand, since particles have

the same charge, the Coulomb force, decreasing with

the square of their distance, pushes them apart. On

the other hand, as edges are replaced by springs, the

Hooke force tends to keep adjacent particles close to-

gether (our springs have natural length zero and never

exert a repulsive force). Further, in order “to keep

the node close” to its geographic position, we intro-

duced a geographic force that attracts each node to

the point on the logical layer corresponding to the

node geographic position. Algorithm Retina intro-

duces a major, although conceptually simple, differ-

ence with respect to standard spring embedders. The

forces and their sums are computed on the projections

of the nodes’ positions on the view plane, so to avoid

the perspective distortion perceived by the user. Once

(a)

(b)

Figure 5: The effect of the Retina algorithm is apparent

when grid graphs are represented. (a) A grid graph drawn

by a traditional spring embedder. The perspective distortion

is apparent. (b) A grid graph with the Retina algorithm.

the sum of the forces is computed for each node pro-

jection, the translation vectors are unprojected again

from screen to world coordinates, yielding the new

positions for the nodes. Boundary constraints are not

implemented as forces, but rather as restrictions on

the nodes’ translations.

Figure 5 shows a drawing of a 5 × 4 grid graph

with and without the Retina algorithm. The perspec-

tive distortion of the traditional spring embedder that

computes the layout on the logical plane is apparent

in Fig. 5(a). Such distortion is reduced in Fig. 5(b).

5 EXPERIMENTAL EVALUATION

We evaluated the effectiveness of the proposed 2.5D

visualization and of Algorithm Retina by contrast-

ing them with “traditional 2D visualization” where

entities are place in their geographic position and the

screen is fully devoted to a 2D representation of the

area of interest. With respect to the problem require-

ments, we claim the following statements.

1. The interface allows us to unambiguously repre-

sent networked data enriched with geographic in-

formation which may be missing or uncertain for

some entity (Req. Unambiguity, Robustness).

2. The interface allows us to clearly represent enti-

ties that have coincident or very close locations

DrawingGeoreferencedGraphs-CombiningGraphDrawingandGeographicData

113

(Req. Unambiguity).

3. The logical and the geographic layers allow us to

represent the networked information in a readable

way (Req. Effectiveness, Unambiguity).

4. Algorithm Retina improves the readability of the

drawing with respect to a traditional spring em-

bedder run on the logical layer (Req. Effective-

ness, Unambiguity).

The ﬁrst claim, in our opinion, is self-evident, as

we are not aware of alternative visualization tech-

niques to represent in an unambiguous way geolo-

cated networks where part of the entities have miss-

ing or uncertain geographic information. Therefore,

we will give evidence of the other three claims by as-

suming that all the entities have a known position. To

this end, we set up the experimental setting described

in the following subsections. In all the experiments

we allowed the on-line layout algorithm to reach an

equilibrium conﬁguration.

5.1 Quality Measures

To assess the effectiveness of the interface we adopted

the following readability measures.

Crossings Percent Reduction (cpr). There is strong

evidence in the literature that reducing the number

of edge crossings is by far the most important aes-

thetic to improve the readability of a drawing (Pur-

chase et al., 1997; Purchase, 2000). This metric esti-

mates the ability of the interface to reduce the num-

ber of edge crossings in the representation of the net-

worked data. In particular, we measured the average

percent reduction of the number of crossings on the

logical layer with respect to the number of crossings

that would occur if the nodes were placed at their ac-

tual location, as in a traditional 2D visualization.

Homogeneous Edge Length (hel). This measure

is based on the average percent deviation of edge

lengths using a mean central tendency (Fowler and

Kobourov, 2013). We compute this metric on the pro-

jections of the edges on the view plane:

hel = 1 −

∑

j=1



| − |e|

avg

max{|e|

avg

, |e|

max

− |e|

avg

}



where m is the size of the edge-set of the graph,

| is the length of the jth edge, |e|

avg

is the average

edge length, and |e|

max

is the maximum edge length.

Observe that 0 ≤ hel ≤ 1. A value of hel = 0 could

indicate that half of the edges have length zero while

the other half have length 2|e|

avg

. A value of hel = 1

indicates all the edges have the same length.

Node Separation (ns). Our purpose is to measure

how well the interface is able to separate close nodes.

Metric ns is the minimum distance between the pro-

jections of the nodes on the view plane divided by the

length of the diagonal of the viewport

We remark that our 2.5D visualization is unfa-

vored by measures hel and ns as it uses only a portion

of the viewport to distribute nodes, whereas in a 2D

visualization the whole viewport is used by the map.

We also observe that our readability measures do not

take into account the crossings among the edges that

link the entities on the logical layer to their geo-

graphic positions. Such crossings are due to the 3D

perspective and remain in the background when the

user explores the network on the logical layer. Hence,

they may have a reduced effect on the comprehension

of the structure of such a network.

5.2 Testsuite

For our experiments we adopted a mix of real-life

and synthetic data. In particular, we obtained real-

life data about geolocalized entities from the maritime

data collected by the Automatic Identiﬁcation System

(AIS), which is an onboard navigation safety device

that broadcasts time-labeled messages with the loca-

tion and characteristics of vessels in real time. We

used a historic dataset of AIS data collected by the

U.S. Bureau of Ocean Energy Management and by the

U.S. National Oceanic and Atmospheric Administra-

tion (NOAA Coastal Services Center, ). Precisely, we

used the dataset relative to the Zone 14 of the Gulf of

Mexico area, collected during January 2009. Starting

from this dataset, we produced 300 test instances of

increasing size and density.

First, we chose an arbitrary rectangular region

whose aspect ratio is 16:9. We selected ten time in-

stants uniformly distributed in the available time win-

dow. For each time instant, we selected in the area of

interest the last s vessels broadcasting their position

and considered their last update, with s ranging from

10 to 100 with a step of 10. This produced 100 sets of

geolocated entities with distinct geographic positions.

AIS data are not provided with information about

relationships between the vessels. Therefore, we cre-

ated graph instances with different edge densities as

follows. We randomly added edges to each set of n

vertices, among all the possible

n∗(n−1)

edges, until

we reached the density of 5%, 10%, and 15%. This

produced 300 geolocated graphs, which compose the

testsuite for our experiments.

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

114

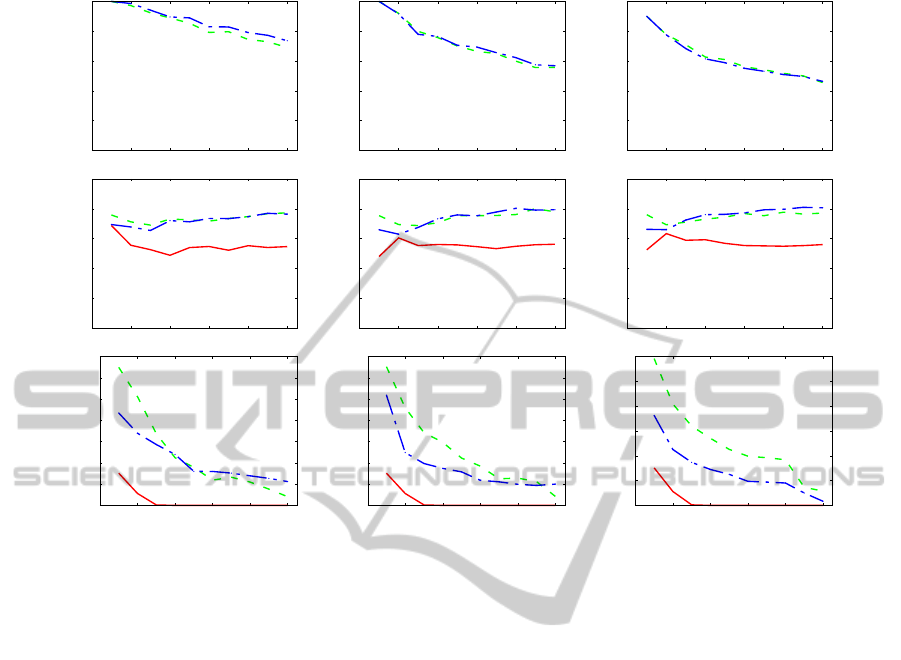
EDGE DENSITY = 5% EDGE DENSITY = 10% EDGE DENSITY = 15%

cpr

0.2

0.4

0.6

0.8

0 20 40 60 80 100

0.2

0.4

0.6

0.8

0 20 40 60 80 100

0.2

0.4

0.6

0.8

0 20 40 60 80 100

hel

0.2

0.4

0.6

0.8

0 20 40 60 80 100

0.2

0.4

0.6

0.8

0 20 40 60 80 100

0.2

0.4

0.6

0.8

0 20 40 60 80 100

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0 20 40 60 80 100

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0 20 40 60 80 100

0.005

0.01

0.015

0.02

0.025

0.03

0 20 40 60 80 100

Figure 6: Results of the experiments. Charts in the ﬁrst row report cpr measure; the second row is devoted to hel; and the third

row to ns. The density of the graphs varies over the columns. The x-axis shows the size of the graphs, while the y-axis reports

the measure of interest. The solid red line is the measure for the 2D visualization. The dashed green line is the measure for

Algorithm Retina. The dash-dotted blue line is the measure for the traditional spring embedder with no Retina distorition.

5.3 Results and Discussion

Figure 6 shows the results of the experiments. Each

dot corresponds to the average over ten values. Re-

garding measure cpr (Figs. 6, ﬁrst row), crossings are

completely removed for sparser and smaller graphs

and are greatly reduced both by the traditional spring

embedder and by Algorithm Retina, with the latter

performing negligibly worse for sparse graphs (see

Fig. 6, ﬁrst row, ﬁrst column). Even for bigger and

denser instances of our dataset crossings are reduced

of more than 40%. We remark that the number of

crossings on the geographic map for the denser graphs

is huge (for example, the last point of Fig. 6, ﬁrst row,

last column, corresponds to more than 6, 000 cross-

ings). The second row of Fig. 6 is devoted to metric

hel. For all the tested densities and sizes the readabil-

ity of the layout is steadily improved both by the tra-

ditional spring embedder and by Algorithm Retina,

which appears to behave better for small graphs. The

advantage of using a 2.5D interface is conﬁrmed by

these charts. It should be also noted that georefenced

graphs coming from many real-life applications have

the property that adjacencies are more likely among

nodes that are geographically close. However, in or-

der to prove the effectiveness of Algorithm Retina

with respect to metric hel, we decided to perform our

tests against unfavorable instances that do not exhibit

this property. Algorithm Retina performs better than

the traditional spring embedder with respect to met-

ric ns (see Fig. 6, last row), while the 2D visualiza-

tion has very unsatisfactory results. Denser graphs

are more effectively handled by Algorithm Retina.

Overall, our experiments conﬁrm that the 2.5D in-

terface meets the system requirements. In partic-

ular, it allows us to represent the networked infor-

mation in way that is considerably more readable

than a traditional 2D interface. The adoption of Al-

gorithm Retina is justiﬁed by its improvement on

measures hel and ns at the expenses of a negligible

worsening of the cpr measure. When the user fo-

cuses on smaller instances, the superiority of Algo-

rithm Retina is apparent.

6 CONCLUSIONS AND FUTURE

WORK

We described a 2.5D visualization technique for ex-

DrawingGeoreferencedGraphs-CombiningGraphDrawingandGeographicData

115

Figure 7: A georeferenced graph with 76 entities and 96

edges. The size of the graph makes cluttering hard to avoid.

ploring networked data enriched with geographic in-

formation, where the latter may have uncertain or

missing values. Adapting, to our knowledge, for the

ﬁrst time a force-directed algorithm to a 2.5D setting,

we conceived a variant of a spring embedder algo-

rithm that directly computes the layout on the view

plane (i.e., on the user’s screen).

We measured the effectiveness of the proposed vi-

sualization and layout algorithm by contrasting them

with a traditional 2D visualization with respect to

three relevant readability measures. Both the experi-

mentation and our experiences with the interface sup-

port our conﬁdence about the effectiveness of the pro-

posed techniques for small instances of geolocalized

graphs. In fact, when the entities are more than a few

dozens the readability measures show very poor per-

formances and the drawing on the logical layer be-

comes too cluttered to be clearly readable (see Fig. 7).

Although the results are promising, our experi-

ments only evaluate the static setting and do not ac-

count for the dynamic scenario, where changes occur

both in the area of interest selected by the user and in

the environment. An evaluation of the effectiveness of

the dynamic scenario would be much more complex

and could not leave aside a thorough user study. An

interesting evolution of the Retina algorithm could

consider additional forces to take into account cross-

ings among leaders. One line of further investigation

is given by the possibility of representing on the logi-

cal layer further information. A simple idea is to show

a network that is wider than the area of interest (we

call it neighborhood visualization), so to enhance the

situational awareness of the user. Our preliminary ex-

periments in this direction are encouraging.

ACKNOWLEDGEMENTS

We wish to thank Francesco Elefante, Marco Pas-

sariello, and Maurizio Pizzonia for their friendship

and help with this project. This work is partially

supported by the MIUR project AMANDA “Algo-

rithmics for MAssive and Networked DAta”, prot.

2012C4E3KT 001, and by EU FP7 STREP “Leone:

From Global Measurements to Local Management”,

no. 317647.

REFERENCES

Aris, A. and Shneiderman, B. (2007). Designing semantic

substrates for visual network exploration. Information

Visualization, 6(4):281–300.

Collins, C. and Carpendale, S. (2007). VisLink: Revealing

relationships amongst visualizations. IEEE Trans. on

Visual. and Comp. Graph., 13(6):1192–1199.

Fowler, J. J. and Kobourov, S. (2013). Planar preprocess-

ing for spring embedders. In Graph Drawing GD ’12,

volume 7704 of LNCS, pages 388–399. Springer.

Google Inc. (2013). Google Earth. http://earth.google.com.

Hadlak, S., Schulz, H., and Schumann, H. (2011). In situ

exploration of large dynamic networks. IEEE Trans.

on Visual. and Comp. Graph., 17(12):2334–2343.

Lex, A., Streit, M., Kruijff, E., and Schmalstieg, D. (2010).

Caleydo: Design and evaluation of a visual analysis

framework for gene expression data in its biological

context. In PaciﬁcVis 2010.

NOAA Coastal Services Center.

http://www.marinecadastre.gov (acc. 2014).

Purchase, H. C. (2000). Effective information visualisation:

a study of graph drawing aesthetics and algorithms.

Interacting with Computers, 13(2):147–162.

Purchase, H. C., Cohen, R. F., and James, M. I. (1997).

An experimental study of the basis for graph drawing

algorithms. J. Exp. Algorithmics, 2.

Shneiderman, B. and Aris, A. (2006). Network visualiza-

tion by semantic substrates. IEEE Trans. on Visual.

and Comp. Graph., 12(5):733–740.

Steinberger, M., Waldner, M., Streit, M., Lex, A., and

Schmalstieg, D. (2011). Context-preserving visual

links. IEEE Trans. on Visual. and Comp. Graph.,

17(12):2249–2258.

Streit, M., Kalkusch, M., Kashofer, K., and Schmalstieg, D.

(2008). Navigation and exploration of interconnected

pathways. Comput. Graph. Forum, 27(3):951–958.

The Khronos Group (2013). WebGL, Web Graphic

Library – OpenGL ES 2.0 for the Web.

http://www.khronos.org/webgl/ (acc. 2014).

Weaver, C. (2005). Visualizing coordination in situ. In IN-

FOVIS 2005.

Wood, J., Dykes, J., Slingsby, A., and Clarke, K. (2007). In-

teractive visual exploration of a large spatio-temporal

dataset: Reﬂections on a geovisualization mashup.

IEEE Trans. Vis. and C. Graph., 13(6):1176–1183.

Wood, J., Slingsby, A., and Dykes, J. (2011). Visualizing

the dynamics of London’s bicycle hire scheme. Car-

tographica, 46(4):239–251.

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

116