
Contextual Saliency for Nonrigid Landmark Registration and
Recognition of Natural Patterns
Luke Palmer
1
and Tilo Burghardt
2
1
The Institute of Cognitive Neuoscience, University College London, London, U.K.
2
The Visual Information Laboratory, University of Bristol, Bristol, U.K.
Keywords: Point-matching, Saliency, Registration, Recognition, Non-rigid, Biometrics, Regularity.
Abstract: In this paper we develop a method for injecting within-pattern information into the matching of point
patterns through utilising the shape context descriptor in a novel manner. In the domain of visual animal
biometrics, landmark distributions on animal coats are commonly used as characteristic features in the
pursuit of individual identification and are often derived by imaging surface entities such as bifurcations in
scales, fur colouring, or skin ridge minutiae. However, many natural distributions of landmarks are quasi-
regular, a property with which state-of-the-art registration algorithms have difficulty. The method presented
here addresses the issue by guiding matching along the most distinctive points within a set based on a
measure we term contextual saliency. Experiments on synthetic data are reported which show the contextual
saliency measure to be tolerant of many point-set transformations and predictive of correct correspondence.
A general point-matching algorithm is then developed which combines contextual saliency information with
naturalistic structural constraints in the form of the thin-plate spline. When incorporated as part of a
recognition system, the presented algorithm is shown to outperform two widely used point-matching
algorithms on a real-world manta ray data set.
1 INTRODUCTION
Registering sets of image locations between various
visual captures or models is an important stage in
many computer vision applications including optical
character recognition (Belongie, Malik, & Puzicha,
2002) and medical image registration (Rueckert &
Schnabel, 2011).
Solving this registration problem essentially
requires the derivation of a correspondence mapping
between two point sets which are related by some
initially unknown geometric transform. This is
difficult due to the combinatorial explosion of
possible between-image point correspondences and
usually very large transformation parameter spaces,
especially in cases of non-rigid transformation,
position noise and partial occlusion.
Here we consider the point set registration
problem in the context of animal biometrics (Kühl &
Burghardt, 2013), specifically with regard to the
identification of individual animals utilizing their
characteristic coat markings as identifiers.
Prominent examples of unique coat patterns include
spot or blob configurations on cheetahs or manta
rays, and the alignment of stripes on zebras.
Animal biometrics is widely used to enable non-
invasive ecological monitoring and conservation-
relevant population modelling (e.g. Gamble et al.,
2008). Such systems often combine landmark
distribution information with local appearance and
textural cues to form descriptors of animal identity.
However, here we analyse natural point-set
registration in isolation of these other factors that
may also contribute to identity recovery.
The difficulty in natural point-set registration is
two-fold: firstly, transformations between point-sets
are generally non-rigid and sometimes incomplete
due to the wide range of possible animal poses and
occlusion; and secondly, the stochastic
morphogenesis (Turing, 1952) of coat patterning can
often lead to a dense, widely homogenous layout of
landmarks from which points are extracted. We
address these difficulties through introducing a
transform-persistent and noise-robust intra-pattern
ordering of points, which is used to guide the
registration process alongside traditional inter-
pattern distance measures. We formally define this
ordering measure using the shape context descriptor
403
Palmer L. and Burghardt T..
Contextual Saliency for Nonrigid Landmark Registration and Recognition of Natural Patterns.
DOI: 10.5220/0005268604030410
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 403-410
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

(SC, Belongie et al, 2002) and name it contextual
saliency, Ψ.
First, experiments on synthetic point-sets are
reported which investigate the robustness of point
ordering on Ψ to noise and perspective
transformation and whether this ordering is
associated with correct correspondence. A general
non-rigid point-matching algorithm, Ψ-Match, is
then described which incorporates an ordering of
points on Ψ in iteratively building a correspondence
set between point-sets. Finally, results from an
identification experiment on a real-world manta-ray
data set are reported, comparing the performance of
a recognition setup using the Ψ-Match algorithm to
the same setup when employing two widely-used
registration algorithms.
2 RELATED WORK
In the general case of gauging similarity between
two sets of points in
,
,
,…,
and
,
,…,
, a common approach is to
apply a normalising transform to one or both sets,
e.g. →, followed by the application of a
similarity measure in that space, ,. This
value then quantifies the variation between the sets
which was not captured by the transformation.
Deriving a suitable normalising transformation
between the sets can be seen as a counterpart to the
correspondence problem: to indicate for points in
one set the corresponding points in the other. Point-
matching has therefore been approached from both
perspectives.
Methods which solve for the transformation, for
example the Hough transform (Ballard, 1981), have
proven successful in estimating rigid deformations,
however the concept is unsuitable for highly non-
rigid domains due to the associated dimensional
explosion of the parameter space. Other methods
concerned with deriving a correspondence set aim to
construct higher-order structures from the point-sets
(e.g. curves or surfaces; Metaxas et al., 1997),
drastically reducing the parameter space at the
expense of curve-fitting complexity when data are
noisy due to reliance on accurate feature extraction
and curve smoothness.
Shape contexts (SC, Belongie et al., 2002) are a
different approach to the construction of higher
order features; here each point in a set is represented
by its spatial relationship to all other points, and
correspondences are computed by comparing these
descriptors between sets. SC utilises a circular
histogramming approach where bins are uniform in
log-polar space, making the descriptor more
sensitive to local structure, capturing the intuition
that more proximate point pairs are likely to undergo
more similar transformations when compared to
more distal pairs.
Other approaches have adopted an iterated
estimation framework. The iterated closest point
algorithm (ICP; Zhang, 1994) operates on roughly
aligned sets and assigns correspondence based on a
simple nearest-neighbour criterion which is then
used to update the transformation between the sets.
The thin-plate spline robust point matching
algorithm (TPS-RPM; Chui & Rangarajan, 2003)
combines correspondence and transformation into a
single objective function, and uses an EM-like
optimisation routine to iteratively solve for both
variables. The routine leverages softassign
(Rangarajan et al., 1997), a loosening of the binary
correspondence criterion such that correspondences
can take on probabilistic values; and course-to-fine
deterministic annealing, where constraints on
transformation non-rigidity and correspondence
binarity are gradually reduced as the algorithm
progresses. Other methods in this vein have
approached point-matching through relaxation-
labelling as a graph-matching problem constrained
by neighbourhood relations (Zheng & Doermann,
2006) or as probability density estimation where
point positions define centroids in Gaussian mixture
models (Myronenko & Song, 2010).
3 THE CONTEXTUAL
SALIENCY HYPOTHESIS
There are limitations with the above approaches in
the domain of landmark-based animal biometrics
due to the stochastic morphogenesis that underpins
animal patterning (Turing, 1952). This process often
leads to a dense, quasi-regular arrangement of
landmarks across the animal surface. The lack of
discernible shape in these patterns makes
correspondence mapping between instances difficult,
which becomes especially clear in the case of partial
occlusion, where the aim is superimposing a subset
of a point pattern upon the full pattern, a common
occurrence in ecological imagery.
Here we demonstrate failures of TPS-RPM and
SC approaches in this scenario using controlled,
synthetic, quasi-regular point-sets. A first model set,
Y, is depicted in Figure 1. It is a regular grid of
equally spaced points with two points being slightly
displaced, while the probe set is a rectangular subset,
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
404

⊂, which includes those displaced points and is
shown in red.
Figure 1: Top Left: Synthetic point-sets. The smaller set
(red) is a subset of the larger (blue); a correct
correspondence is shown as a superposition of the two
sets. Results of TPS-RPM (top right) and SC (bottom left)
algorithms on the synthetic data. Points in X are shown
superimposed on Y according to the correspondences
found: red points refer to correct and yellow points refer to
incorrect assignments. Bottom Right: Contextual saliency
calculated for each point, scaled to the range [0, 1],
represented by colour.
Application of the TPS-RPM algorithm results in
only a single correct correspondence between the
sets (see Figure 1, top right).The algorithm favoured
(incorrect) global characteristics and scaled X to
cover Y, resulting in incorrect correspondences
transformation. In this example SC performed better,
yet still only aligned a few central points.
The present work aims to address this
demonstrated shortcoming by developing a method
of ordering points within sets across a measure we
term contextual saliency. In the above example, the
cluster of points centred near and including the
displaced points is salient in comparison to the more
distal points forming part of the regular grid: we
therefore develop a procedure for biasing matching
processes in favour of these points.
The intuitive reasoning is two-fold: points which
are contextually salient are likely to remain
contextually salient after distortion or deformation,
and correspondences based on locally
distinguishable points across patterns are more likely
to be correct than correspondences drawn from the
remaining pool of regular points. In Section 6 these
intuitions are substantiated with experiments on
controlled data.
4 FORMALISING CONTEXTUAL
SALIENCY
We now utilise the shape context (SC) descriptor as
a means for quantifying contextual saliency. For a
given point
∈, the SC descriptor is defined as a
histogram
of the remaining point positions, and is
populated according to
#
:
∈
bin
, where bins are uniform in log-polar space.
In the original application of SC, correspondences
between point-sets X and Y are estimated by
minimising an assignment problem of SC histogram
distances based on the
statistic (Belongie et al.,
2002). However, here we apply this distance
measure within a set, such that it reflects similarity
of a point to another point within the same set based
on local structure. This similarity between two
points,
∈ and
∈, is given by
1
2
,
where
and
represent the Q-bin
normalised SC histograms of each point. To define
the contextual saliency of a point
we compute the
similarity measure between
and all other points in
X giving a vector
,
,…,
of
similarities. The minimum value of this vector is
termed the contextual saliency of point
:
Ψ
min
∈/
.
A point with a large minimum similarity to other
points within the set is therefore relatively dissimilar
from all other points, and has high contextual
saliency. Applied to the synthetic data set from
Section 3, we see in Figure 1 (bottom right) that the
contextual saliency measure has numerically
captured this notion.
5 CHARACTERISTICS OF
CONTEXTUAL SALIENCY
Here we investigate by controlled experiment the
tolerance of the contextual saliency measure to
point-set noise and perspective distortion, and then
investigate whether contextual saliency is predictive
of correspondence.
ContextualSaliencyforNonrigidLandmarkRegistrationandRecognitionofNaturalPatterns
405

5.1 Synthetic Data Generation
Quasi-regular point-sets were constructed by the
addition of Gaussian noise to each point in a fully
regular grid of points. For each initial grid point
∈
, the regularity of the point-set X can
then be controlled by the variance parameter,
. To
preclude point-set boundary information, we define
a central subset of points, ⊂,such that a shape
context descriptor placed at the extreme outer points
of Q will not overlap edges of the complete set X. Q
is the set with which inferences regarding the
contextual saliency measure are made, whilst the
remainder of points in X are not studied in
themselves. In the following experiments, the initial
point-set
is comprised of 900 points in a 30
30 regular grid. Set Q is a 1010 central subset
of X. We used a shape context descriptor with 12
equally spaced orientation bins and 5 log-linear
radial bins with the inner bin extending to 1/16 units
and outer bin extending to 1.
5.2 Distribution
The initial variance of the point-sets was varied in
the range [110
: 1.810
] in 5 equal steps.
For each setting, 200 separate point-sets were
generated and the contextual saliency of the points
calculated. Figure 2 presents the mean Ψdistribution
across point-sets for each variance parameter.
Figure 2. Mean Ψdistributions at given variances.
Critically, a pronounced peak is evident in Ψ for the
most salient points at all probed variance values,
indicating that a subset could be usefully isolated
based on this measure.
5.3 Preservation
We investigated whether contextual saliency values
and point-ordering based on Ψ are tolerant to further
addition of Gaussian noise and the application of
perspective transformations. We calculated initial Ψ
values and within-set rankings for point-sets with an
initial variance of
510
. Point-sets then
underwent either the addition of Gaussian noise or
perspective transformation, in the form of a plane
rotation about the -axis in 3D space, at 5
manipulation levels. For each level results were
again averaged 200 point-sets.
Figure 3: An example of perspective transformation; a
rotation of 10° (set Q in black, set X in red).
The Ψ values of points after point-set degradation,
Ψ
, were plotted against the original ordering of
points. As shown in Figure 4, for both types of set
manipulation, highly salient points remain salient.
Figure 4: Ψvalues of points after (left) noise addition and
(right) rotation plotted according to their initial Ψranking.
The preservation of ordering is shown in Figure 5:
initially highly ranked points are more likely to
remain in the same rank than other points within the
pattern. We also see a marked peak at very low
ranks which is explained as a form of group saliency
whereby small groups of points are remarkable in
their similarity and as such that points in this group
remain similar after manipulation
Figure 5: Average ranking by Ψof points within point-sets
after (left) further noise addition and (right) rotation. The
x-axis again refers to the point’s initial ranking.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
406

5.4 Predictor of Correspondence
Using the same experimental procedure, the
relationship between contextual saliency ranking and
correct correspondence was investigated. True
correspondence between initial and transformed sets
was known a priori, while experimental
correspondences were derived as the global
minimum over all pairwise SC histogram costs using
the Hungarian method (Munkres, 1957).
Results are shown in Figure 6. While
correspondence accuracy is generally reduced in
more extreme transformations, initial contextual
saliency is positively correlated with correspondence
accuracy. Furthermore, this trend becomes stronger
as the manipulation becomes more extreme.
Figure 6: Correct correspondence proportion as a function
of initial contextual saliency rank under (left) additional
noise, and (right) perspective transformation.
6 A NEW ALGORITHM:
Ψ-MATCH
We now introduce a novel algorithm for registering
a test point-set X to a model set Y. The procedure
iteratively builds a correspondence set comprised of
a contextually salient subset of Y.
6.1 Ψ-Biased Matching Approach
Our approach is to extract subsets of the point-sets,
⊂ and
⊂, such that the transformation
between the two is representative of the
transformation between the whole sets. Given an
initial assumed correspondence set of n points
~
,
,
,
,…,
,
, the
transformation mapping between them
:
→
is applied to the test set such that ←
.
An additional correspondence pair is then added to
~
: the most contextually salient point in Y is
paired with that point in X which elicits the lowest
SC cost. The transformation is found between this
expanded correspondence set, and the process
repeated until some stopping criterion is reached.
For continuation, define the nested
transformation function
…
,
then on the nth iteration the subsets defining the
correspondence set are given by
∪
∈/
Ψ
where the second term represents the point
, the
newest addition to the correspondence set, and
∪
∈/
,
,
where , represents the shape context distance
between the points a and b.
In our case study, we initialise the
correspondence set
~
using manually
tagged reference points common to a particular
species: the edges of gills on manta ray bellies.
However, a fully automatic system could be
initialised using the most probable correspondences
using SC, or if image data were available, a robust
method such as SIFT or ASIFT (Yu & Morel, 2011).
The necessary size of this initial correspondence set
is dependent on the class of transformation used.
6.2 Transformation Parameterisation
To ensure a naturalistic and smooth interpolation
between the point-sets the transformation is
parameterised by the thin-plate spline (TPS), which
models a thin metal plate with certain resistance to
bending. The TPS fits a mapping function, ,
between corresponding point-sets X and Y through
minimising the energy function:
‖
‖
.
While the first term quantifies the spatial distance
between corresponding points, the second is a
measure of the total curvature of the function, the
importance of which can be controlled with the
regularising parameter, , such that high strictly
penalises non-affine warping. For a given
regularisation parameter, , there exists a unique
minimiser, f, of the form
,,
⋅
⋅
where d is a 11 affine
transformation matrix, w is a1 matrix
of non-rigid warping coefficients, and
is a 1
vector related to the TPS kernel where each entry
log
. The TPS kernel
ContextualSaliencyforNonrigidLandmarkRegistrationandRecognitionofNaturalPatterns
407

effectively contains information regarding the point-
set’s internal structure. Least-squares solutions for d
and w are arrived at through minimising the QR
decomposition of the energy function into separate
affine and non-affine warping spaces according to
the procedure described in (Wahba, 1990).
6.3 The Constancy Heuristic
The definite nature of the algorithm as introduced
here is problematic in the case where a false
correspondence is incorrectly admitted to
~
.
Therefore we admit a new correspondence pair only
if that pair is chosen in two successive iterations: if
in a subset of time during the dynamic fitting
process we encounter a constant, this implies a
meaningful correspondence since both the spline and
SC matching are in agreement. There is however,
the scenario where the algorithm does not produce
consecutive matching correspondence pairs; to
tackle this we build a history of previous candidate
pairs and when a history limit is reached, the
candidate pair with the most entries in the history is
admitted to the permanent correspondence set (we
use a limit of 5 in our case study and informal
experimentation suggests that recognition
performance is quite tolerant of this parameter). The
number of pairs to admit to the set in total is
explored experimentally in the case study
7 CASE STUDY: MANTA RAY
RECOGNITION
Manta rays (Manta birostris and Manta alfredi) are
suitable subjects for landmark-based matching
systems due to a characteristic blob-pattern present
on the underside which is thought to be a uniquely
identifying biometric feature (Kitchen-Wheeler,
2011). Figure 7 below shows sample blob
distributions of two different identity manta rays.
Figure 7: Examples of manually tagged manta rays. Red
tags are placed on belly spots, while blue tags represent
reference points placed at the end point of gills and the
base of the tail; these form the initial known
correspondence set.
We benchmark performance of our algorithm
against TPS-RPM and SC in a recognition context.
7.1 Dataset and Analysis Details
Images of 67 individual manta rays were taken in
waters off the Maldives, most showing non-linear
deformation and partial occlusion. Three-hundred
images were used in the study; a mean of 4.5 images
per individual ray, with a minimum of 2 and
maximum of 7 instances per individual. Individual
manta ray belly spots were tagged by experts, who
also tagged reference points corresponding to the
endpoints of the two most ventral gills and the base
of the tail. The average number of points per pattern
across all instances was 36.5 with standard
deviation 20.4, and all point-sets were scaled to
the range [0,1] in both the x and y-axes.
Recognition performance was compared for
systems using SC, TPS-RPM, or Ψ-Match point-
matching methods. For each method, the associated
similarity measure was derived for each possible
pair of manta instances, resulting in a 300300
similarity matrix; a correct recognition was declared
when, for a given instance, the most similar pattern
in a different image was of the same identity. We
also investigated whether a same identity pattern
was within the top N most similar patterns, useful
information for a semi-automatic system providing
the top N matches to an expert for ultimate
recognition
7.2 Algorithm Parameters
For each comparison an initial scaling and alignment
phase was conducted by recovering and applying the
TPS transformation between the reference points.
The a priori known correspondence between these
points was enforced throughout for each algorithm
(i.e. these assignments were always present in the
correspondence set).Parameters for the TPS-RPM
algorithm were taken from (Chui & Rangarajan,
2003). For the SC method, SC descriptors were
constructed using 12 equally spaced orientation bins
and 5 log-linear radial bins with inner radius of 1/16
and outer radius of 1, normalised through division
by the mean pair-wise distance between points
within each set. Correspondences were assigned
based on the global minimum of all SC costs using
the Hungarian method (Munkres, 1957). A TPS
transformation was recovered between sets using
these correspondences and applied to the
transforming point-set before the application of a
similarity measure; the TPS regularisation parameter
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
408
was set at the squared pair-wise Euclidean distance
between points within the transforming set,
, such
that
, as in Belongie et al. (2002).
For the Ψ-Match approach, SC histograms and
the TPS transformation were parameterised
identically to the SC method. In this experiment we
utilise the ratio of points incorporated into the
correspondence set to the maximum number of
points possible to incorporate (i.e. the number of
points in the lowest cardinality point-set) as a means
to parameterise Ψ-Match; we term this ratio .
7.3 Similarity
Similarity was measured following point-set
transformation using the modified Hausdorff
distance, a variant of the Hausdorff distance which
has been shown to outperform the standard measure
in the presence of position noise (Dubuisson & Jain,
1994):
1
,
,
∈
1
,
∈
where
,
is the directed distance between point
∈and all points in and is here defined as
,
∈
‖
‖
.
7.4 Results
The recognition accuracy of the system using the Ψ-
Match algorithm was first compared with
performance without saliency information. This
configuration was identical to the Ψ-Match
procedure; however the choice of model point
to
incorporate into the correspondence set was random
instead of being biased by Ψ. We calculated
similarity at each iteration of the matching
algorithms, allowing an investigation of the
tolerance to the parameter .
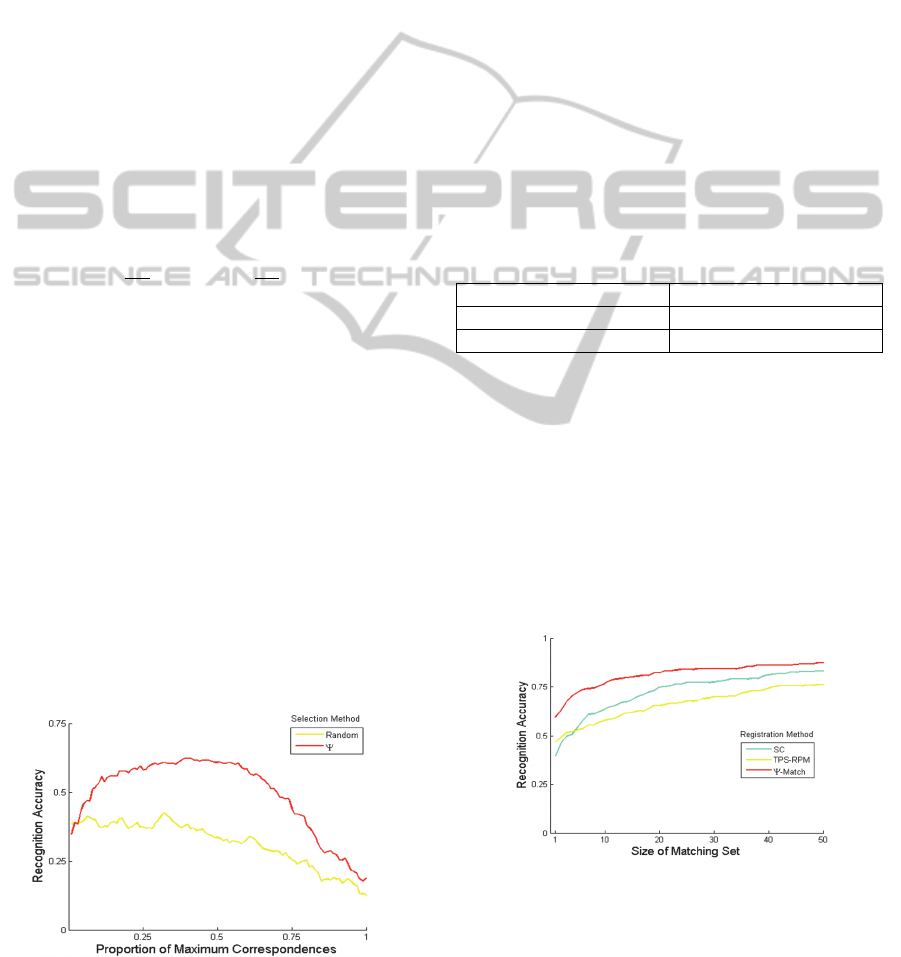
Figure 8: Recognition accuracy as a function of
(proportion of maximum correspondences) for the Ψ-
Match algorithm and a randomly ordered variant.
Ψ-Match exhibits expected behaviour, in that
recognition accuracy is rapidly improved as the
correspondence set is expanded - indicating more
accurate transformations for matching instances –
until a fairly stable performance is attained between
0.1 and 0.6. The dip after this is likely due
to the greater chance of false correspondences being
introduced and degrading transformation quality.
This performance pattern is not seen for the
algorithm disregarding saliency information, where
accuracy steadily declines throughout the process,
confirming the utility of contextual saliency in
pattern recognition.
Recognition performance using the SC and TPS-
RPM registration algorithms was calculated in an
identical manner; results are seen in Table 1 in
comparison to the Ψ-Match algorithm with
0.25.
Table 1: Recognition accuracy of the biometric system
across landmark-based registration methods.
Re
g
istration Method Reco
g
nition Accurac
y
SC 0.41
TPS-RPM 0.46
Ψ-Match 0.59
Ψ-Match is shown to outperform SC and TPS-RPM
by wide margins. Note that although the stopping
criterion was chosen here a posteriori, Ψ-Match
performance was improved over other methods for
in the range [0.06, 0.71], indicating the algorithm’s
robustness with respect to this parameter on our data
set.
Performance was then assessed within the
context of a semi-automatic recognition system
through looking at whether a correct identity was
produced within the N most similar patterns.
Figure 9: Recognition accuracy across validation matching
set size N for systems using SC, TPS-RPM, or
Ψ
-Match
(0.25) registration.
Ψ-Match outperforms other methods across the
range of matching set size. At a practical set size of
10, the system incorporating Ψ-Match registration
ContextualSaliencyforNonrigidLandmarkRegistrationandRecognitionofNaturalPatterns
409

produced a correct identity instance in 75% of cases,
in comparison to 61% and 54% for TPS-RPM and
SC methods, respectively; confirming the usefulness
of saliency-biased registration in animal biometrics.
8 CONCLUSIONS
A method for ordering points in a set on a measure
of distinguishability, contextual saliency, has been
introduced in this paper. Ordering on this basis is
shown to be tolerant of noise and perspective
transformation, as well as be predictive of
correspondence, in synthetic experiments.
This information is leveraged in an iterative non-
rigid registration algorithm, Ψ-Match. A case study
on a difficult real-world manta ray data set found
improved performance for a recognition system
using Ψ-Match registration in comparison to the
same setup using either shape context (Belongie et
al., 2002) or TPS-RPM (Chui & Rangarajan, 2003)
registration algorithms.
ACKNOWLEDGEMENTS
We thank Fit4Change Ltd for funding this work. We
would also like to acknowledge Guy Stevens and the
Manta Trust for image provision, and Mike Preager
for help with ground truth annotations.
REFERENCES
Ballard, D. H. 1981. Generalizing the Hough transform to
detect arbitrary shapes. Pattern recognition, 13(2),
111-122.
Belongie, S., Malik, J., & Puzicha, J. 2002. Shape
matching and object recognition using shape
contexts. Pattern Analysis and Machine Intelligence,
IEEE Transactions on, 24(4), 509-522.
Chui, H., & Rangarajan, A. 2003.A new point matching
algorithm for non-rigid registration.Computer Vision
and Image Understanding, 89(2), 114-141.
Dubuisson, M. P., & Jain, A. K. 1994. A modified
Hausdorff distance for object matching.In Pattern
Recognition, 1994. Vol. 1-Conference A: Computer
Vision & Image Processing., Proceedings of the 12th
IAPR International Conference on (Vol. 1, pp. 566-
568).
Gamble, L., Ravela, S., & McGarigal, K. 2008. Multi
scale features for identifying individuals in large
biological databases: an application of pattern
recognition technology to the marbled salamander
Ambystomaopacum. Applied Ecology, 45(1), 170-180.
Kitchen-Wheeler, A. M. 2011. Visual identification of
individual manta ray (Manta alfredi) in the Maldives
Islands, Western Indian Ocean. Marine Biology
Research, 6(4), 351-363.
Kühl, H. S., & Burghardt, T. 2013. Animal biometrics:
quantifying and detecting phenotypic
appearance. Trends in ecology & evolution, 28(7),
432-441.
Metaxas, D., Koh, E., & Badler, N. I. 1997. Multi-level
shape representation using global deformations and
locally adaptive finite elements.International journal
of computer vision, 25(1), 49-61.
Munkres, J. 1957. Algorithms for the assignment and
transportation problems. Journal of the Society for
Industrial and Applied Mathematics, 5, 32-38.
Myronenko, A., & Song, X. 2010. Point set registration:
Coherent point drift. Pattern Analysis and Machine
Intelligence, IEEE Transactions on, 32(12), 2262-
2275.
Rangarajan, A., Chui, H., & Bookstein, F. L. 1997. The
softassignprocrustesmatching
algorithm.In Information Processing in Medical
Imaging. Springer Berlin Heidelberg.
Rueckert, D., & Schnabel, J. A. 2011. Medical image
registration. In Biomedical Image Processing (pp.
131-154).Springer Berlin Heidelberg.
Turing, A. M. 1952. The chemical basis of
morphogenesis. Philosophical Transactions of the
Royal Society of London. Series B, Biological
Sciences, 237(641), 37-72.
Wahba, G. (1990). Spline models for observational
data (Vol. 59). Siam.
Yu, G., & Morel, J. M. 2011. ASIFT: an algorithm for
fully affine invariant comparison. Image Processing
OnLine, 1.
Zhang, Z. 1994. Iterative point matching for registration of
free-form curves and surfaces. International Journal
of Computer Vision, 13, 119-152.
Zheng, Y., & Doermann, D. 2006. Robust point matching
for nonrigid shapes by preserving local neighborhood
structures. Pattern Analysis and Machine Intelligence,
IEEE Transactions on, 28(4), 643-649.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
410
