Improvement of Phase Unwrapping Algorithms by Epipolar Constraints

Johannes K

ohler, Jan C. Peters, Tobias N

oll and Didier Stricker

German Research Center for Artiﬁcial Intelligence, Trippstadter Str. 122, 67663 Kaiserslautern, Germany

Keywords:

Structured Light, Fringe Projection, Phase Shifting, Phase Unwrapping.

Abstract:

Phase unwrapping remains a challenging problem in the context of fast 3D reconstruction based on structured

light, in particular for objects with complex geometry. In this paper we suggest to support phase unwrapping

algorithms by additional constraints induced by the scanning setup. This is possible when at least two cameras

are used, a likely case in practice. The constraints are generalized for two or more cameras by introducing the

concept of a candidate map. We claim that this greatly reduces the complexity for any subsequent unwrapping

algorithm, their performance is thereby strongly increased. We demonstrate this by exemplarily integrating

the candidate map into a local path following and a global minimum norm unwrapping method.

1 INTRODUCTION

Phase shifted structured light is a well known and

widely used method in the ﬁeld of 3D reconstruc-

tion. In this technique, a linear phase function is en-

coded by shifted sine waves and the resulting fringe

patterns are projected onto an object. If these pro-

jections are recorded by a camera, the corresponding

phase values can be recovered from the captured im-

ages. The resulting phase images induce pixel-wise

correspondences of very high quality among all in-

volved devices. These correspondences then can be

used for depth recovery. One of the biggest advan-

tages of phase shifting is its robustness towards the

projector’s narrow depth of ﬁeld. The projected si-

nusoidal fringe patterns can still be robustly decoded

even if they are out of the projector’s focus range.

However, the desired phase function can only be

recovered modulo-2π. This is an inevitable con-

sequence of the involved trigonometric functions,

whose inverse functions are always restricted to the

principal branch. Phase unwrapping denotes the res-

olution of these ambiguities (Figure 1).

Although this problem has been studied for

decades (Gorthi and Rastogi, 2010), a fully robust

and reliable solution has yet to be found for a sin-

gle frequency level. A successful unwrapping heavily

depends on the object scanned and is particularly dif-

ﬁcult near depth discontinuities. Most everyday ob-

jects are not convex, depth maps of the corresponding

object consequently will contain such discontinuities

(Figure 2 (a)). Perspective projection causes unrelated

(a) (b)

Figure 1: Individual steps for transmitting a phase from the

projector to a camera. (a) The projector’s phase before si-

nusoidal encoding into a fringe pattern. (b) Projected fringe

pattern. (c) Wrapped phase recovered from multiple fringe

patterns captured by a camera. (d) Unwrapped phase.

phase intervals to seamlessly blend into each other at

such regions, which poses a great challenge to phase

unwrapping algorithms (Figure 2 (b)). The transition

can be more or less smooth, which is very hard to de-

tect.

In this paper we follow the recent trend to uti-

472

Köhler J., Peters J., Nöll T. and Stricker D..

Improvement of Phase Unwrapping Algorithms by Epipolar Constraints.

DOI: 10.5220/0005271404720479

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 472-479

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b)

Figure 2: (a) Prominent foreground/background discontinu-

ity (the green line separates foreground (object) and back-

ground (wall). Two exemplary parts that belong to the same

wrap count (i.e. to the same stripe) are colored red. (b)

Stripes with different wrap counts seamlessly blending into

each other (red) at a depth discontinuity (enclosed by blue

lines).

lize the geometry of multiple cameras for unwrapping

(Br

auer-Burchardt et al., 2008; Br

auer-Burchardt

et al., 2011; Br

auer-Burchardt et al., 2013; Garcia

and Zakhor, 2012). In these publications, the epipo-

lar geometry of two cameras was used to constrain

the potential unwrapping possibilities. However, the

epipolar geometry alone is not sufﬁcient for unwrap-

ping, many ambiguities remain and further steps are

necessary. In this paper, we propose a more general

approach to use the epipolar geometry. We generalize

its use to more than two cameras and introduce the

candidate map, which stores all geometrically feasi-

ble unwrapping possibilities for a single camera. In

contrast to state of the art methods, we do not focus

on a single method to resolve the remaining ambigu-

ities. Instead, we suggest to use the candidate map

as an appropriate support for any classic phase un-

wrapping algorithm. The candidate map can drasti-

cally improve their performance, we demonstrate this

by including it into two exemplary state of the art un-

wrapping methods.

2 RELATED WORK

Existing phase unwrapping approaches can be

roughly grouped into temporal and spatial methods.

Temporal methods use additional patterns to remove

the ambiguity. All temporal methods have in com-

mon, that the additional patterns encode the period

of the desired phase. (Wang et al., 2010) proposes

sinusoidal patterns with different frequencies for this.

The method starts with a phase function whose encod-

ing yields no wrapping but poor phase quality. The

frequency is consecutively increased while the wrap-

ping is resolved using the previous levels. With the

correct frequency gain, this method yields correctly

unwrapped phases even for objects with many dis-

continuities and has the same advantages than phase

shifting itself. Other authors propose binary codes for

this task (Bergmann, 1995). Temporal methods are

fully local, i.e. the unwrapping decision for a single

pixel does not depend on his neighbors and are thus

robust even for complex objects with many depth dis-

continuities. However, they require a large amount

of additional images to be captured, which might not

be possible in application domains such as real time

scanning.

Spatial methods require less projected patterns

and try to unwrap the phase using neighborhood in-

formation. Existing spatial approaches can be roughly

grouped into two categories: Path following and min-

imum norm.

Path following methods (Goldstein et al., 1988;

Herr

aez et al., 2002; Abdul-Rahman et al., 2007; Lof-

feld et al., 2008; Martinez-Espla et al., 2009) start at

at a given pixel and unwrap the phase along a path

in the image by adding or subtracting multiples of 2π

to the current pixel’s phase value. The path to follow

can be ﬁxed or dynamically guided by a phase quality

measure. Algorithms of this kind are also called local

methods, since at every step they just inspect pixels

near the current position.

In contrast to this, minimum norm methods

(Ghiglia and Romero, 1996; Costantini, 1998; Dias

and Leito, 2002; Bioucas-Dias and Valado, 2007)

globally minimize an unwrapping cost function de-

ﬁned for each pair of neighboring pixels. Both ap-

proaches suffer from inaccuracies at depth discontinu-

ities, where unrelated phase intervals can seamlessly

blend into each other (Figure 2).

The aforementioned methods are purely image

based and rely on a single viewpoint. Several authors

recently proposed to use two viewpoints and their cor-

responding epipolar geometry for phase unwrapping.

This allows to deduce local (i.e. pixelwise) contraints.

Common to all methods is the fact, that epipolar con-

straints alone are not sufﬁcient for a correct unwrap-

ping, many ambiguities remain. It is thus important

to apply additional steps for computing the desired

phase. (Br

auer-Burchardt et al., 2008) were the ﬁrst

to use epipolar geometry. They use a disparity map

to resolve the remaining ambiguities, which is also

related to the epipolar geometry. In their follow up

paper (Br

auer-Burchardt et al., 2011), they use com-

binatorial considerations, but unwrapping ambiguities

can still remain. (Br

auer-Burchardt et al., 2013) tries

to resolve the ambiguities with a special hardware

and parameter arrangement. However, this reduces

the generality of the hardware setup, these restrictions

ImprovementofPhaseUnwrappingAlgorithmsbyEpipolarConstraints

473

might thus not be admissible in every scenario. (Gar-

cia and Zakhor, 2012) also use a stereo camera setup

and propose two approaches to resolve the remaining

ambiguities. The temporal approach is not relevant in

our context, as we focus on static scene reconstruc-

tion. The energy minimization approach can be con-

sidered as special case of our proposed framework.

In contrast to state of the art methods, which usu-

ally use only two cameras, we generalize the use of

epipolar geometry to n cameras by introducing the

candidate map in this paper. The candidate map does

not unambiguously unwrap the phase, but it strongly

constrains the available possibilities. We believe that

existing unwrapping methods can be used to achieve

this and thus suggest to use the candidate map as rea-

sonable preprocessing step for any classical phase un-

wrapping method.

3 PHASE GENERATION

In the context of this paper, phases are generated with

phase shifted structured light. A phase is thus deﬁned

in the image plane of a projector as a linear function

Φ(x, y) ∈ [0..2πN] (Figure 1 (a)). Φ can be projected

onto an object and recovered from the point of view

of a camera by encoding it with a sine or cosine func-

tion and shifting it K times. This results in shifted

fringe patterns captured in K camera images, an ex-

emplary camera image with a pattern projected onto

an object is illustrated in Figure 1 (b). For each pixel

it is then possible to compute tan(φ) using e.g. (Guo

et al., 2007), where φ is the desired object phase seen

from the respective camera. The tangent results from

the periodicity of the involved trigonometric functions

and the inverse tangent thus does not yield φ, but the

wrapped object phase ψ = φ mod 2π (Figure 1 (b)).

Note that the parameter N deﬁnes the amount of peri-

ods and thus also the wrap count of φ.

Without loss of generality, we restrict Φ to have a

constant gradient ∇Φ = d, d ∈ R

. This simply con-

strains the isocurves of Φ to be straight lines, as op-

posed to e.g. (Peng and Gupta, 2008). For d = (1, 0),

Φ would thus correspond to e.g. Figure 1 (a) and we

would project vertical fringes. We use this property in

Section 4 to relate the phase to the camera geometry.

4 CANDIDATE MAP

GENERATION

Depth reconstruction based on structured light can

be accomplished with a video projector and a single

camera. If more cameras are present, they naturally

restrict the unwrapping possibilities. In practice it is

likely to have more than one camera, because trian-

gulation with only cameras does not require a gamma

calibration (Guo et al., 2004) in contrast to triangula-

tion with a camera and the projector (Han and Huang,

2009).

In the following, we consider a scanning setup

with one projector and n ≥ 2 cameras and derive

phase constraints from the devices’ epipolar geome-

try. Our method requires only the fundamental ma-

trix, it is thus not stringently required to fully calibrate

the cameras by estimating their poses and intrinsic pa-

rameters (focal length, principal point and distortion

coefﬁcients). However, a structured light scanner is

usually calibrated and especially a prior calibration of

the camera’s distortion coefﬁcients and undistortion

of the respective images greatly improves the accu-

racy of the method. For an uncalibrated setup, the

fundamental matrix is easily computed from 2D cor-

respondences (Hartley and Zisserman, 2004).

The method sketched in Section 3 yields a

wrapped object phase ψ

for each camera (Figure

1 (c)). For every wrapped phase value ψ

(x, y) ∈

[0..2π] there is exactly one w ∈ {0..N − 1} such that

(x, y) + w · 2π = φ

(x, y). w is the desired period or,

in other words, the index of the correct stripe (Figure

1 (c)). It adds the multiple of 2π required for unwrap-

ping and we consider it as the wrap count.

The task of each unwrapping algorithm thus is to

ﬁnd the correct w for each pixel of ψ

. To formally

handle all possible values of w, we deﬁne the candi-

date map C

: N

→ P {0, ..., N − 1} (1)

where P is the power set operator. For each pixel of

a primary view there are N unwrapping possibilities

and the candidate map stores a subset of geometri-

cally feasible wrap counts for each pixel: C

(x, y) ⊆

{0,...,N − 1}.

is called consistent at position (x,y), if the cor-

rect wrap count w is present in C

(x, y). Pixels (x, y)

with |C

(x, y)| = 1 are called singletons. If a singleton

is consistent, it correctly unwraps the phase without

ambiguities.

Since the correct unwrapping must be consistent

among the devices, secondary views can drastically

reduce the feasible amount of unwrapping possibili-

ties |C

(x, y)| (Figure 3).

In the following we compute a candidate map C

by enforcing epipolar phase consistency among mul-

tiple secondary views. Given n ≥ 2 views, a primary

view i, fundamental matrices F

i j

from the primary

view i to each secondary view j, F

from the primary

view to the projector and F

p j

from the projector to

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

474

primary view (ψ

)

projector (Ψ)

secondary view (ψ

)

epipolar line l

pN-1

jN-1

epipolar line

Figure 3: Geometry of all unwrapping candidates for N =

4. If |ψ

) − ψ

)| > ε, the corresponding candidate

can be excluded before an unwrapping algorithm is applied

(zoom in for details). At the dotted lines, Ψ = ψ

each secondary view, we can restrict the unwrapping

candidates C

) for each primary view pixel p

applying the following steps:

• Compute epipolar line l

= F

,1)

in the pro-

jector image plane. The periods of the projector’s

phase touched by this line are relevant for unwrap-

ping. In Figure 3, all 4 exemplary periods are thus

relevant.

• Compute intersections p

..p

N−1

of l

with each

phase isoline corresponding to φ

). These are

the projector pixels with a phase value of φ

)

that could have illuminated p

• Each of these intersections deﬁnes a unique point

in a secondary view: We propagate the phase line

intersection points p

to each secondary view j

by computing the intersection points p

of the

epipolar line pairs (F

i j

,1)

p j

,1)

). The

resulting pixels potentially perceive the same ob-

ject point and thus should have the same phase

value than the primary view (ψ

)).

• if |ψ

) − ψ

)| < ε, it can be assumed, that

the secondary view j perceives the same wrapped

phase value. Due to occlusions, this will not hold

for all secondary views. We thus add the cor-

responding wrap count to C

(x, y), if this condi-

tion holds for m ≤ n − 1 secondary views, which

means that m secondary views agree on the per-

ceived phase value.

Remark: It is required for numerical stability, that

the angle enclosed by a phase line and an epipolar line

is not too low. As a rule of thumb for two cameras

and a projector setup, the devices should be placed on

a straight line that has ∇Φ as directional vector. E.g.

for cameras placed on a table to the left and right of a

projector such that the image planes are parallel, the

epipolar lines are parallel to the image planes’ x-axis.

A phase with ∇Φ = (1, 0) would then be optimal, as

the phase’s isolines and the epipolar lines are perpen-

dicular.

5 PHASE UNWRAPPING

In general, the performance of most phase unwrap-

ping algorithms can be greatly enhanced by augment-

ing them with a candidate map. This does not only re-

duce the amount of unwrapping possibilities per pixel

but can also directly constrain the starting pixels to

the correct phase value. This is in fact a serious dis-

advantage shared by many unwrapping methods: The

unwrapped phase produced by the respective algo-

rithm might be consistent in itself but shifted with

respect to the original phase projected onto the ob-

ject. This is caused by the fact that a wrap count

w needs to be assigned to the starting pixels for ini-

tialization. Subsequent pixels are unwrapped relative

to this w. Since an initial w cannot be correctly de-

termined without additional information it must later

be corrected, which might not always be possible.

The singletons of the candidate map, which are un-

wrapped correctly, implicitly solve this problem. In

the following, we sketch how to integrate the candi-

date map into a local path following algorithm and

outline a new global minimum norm algorithm based

on graph labeling.

5.1 Local Unwrapping by Region

Growing

As an exemplary local unwrapping algorithm we

choose the region growing method of (Xu and Cum-

ming, 1999). This algorithm starts growing regions

from multiple pixels of high data quality and prop-

agates the phase along paths with high unwrapping

conﬁdence. A pixel p is unwrapped using a weighted

mean of predictions based on extrapolations of neigh-

bouring pixels that are already unwrapped in a 5x5

window centered at p. The process is illustrated in

Figure 4. Predictions are made following K straight

lines originating from p. If in a direction k there is

only one unwrapped pixel, the corresponding predic-

tion is constant and the associated weight is set to 0.5.

In case there are two already unwrapped pixels along

the prediction line, a linear extrapolation is used and

= 1 since these predictions are more reliable than

the constant ones. Then a composite prediction

φ(p)

is formed as weighted average of the individual pre-

dictions. This composite prediction is used in an un-

wrapping attempt for p:

φ(p) = Ψ(p)+ 2πs with s =



φ(p) − Ψ(p)

2π



(2)

ImprovementofPhaseUnwrappingAlgorithmsbyEpipolarConstraints

475

0.5

unwrapped region

growth pixels

currently unwrapped pixel

pixels used for unwrapping

0.5

prediction lines with weights

Figure 4: Unwrapping by region growing and phase predic-

tion. This ﬁgure is based on an illustration in the original

paper (Xu and Cumming, 1999).

The operator [·] denotes rounding to the nearest in-

teger. The essence of this approach is the same as for

the level based temporal unwrapping, note the strik-

ing similarity of Equation 2 and Equation 7 of (Wang

et al., 2010). However, the wrap count in our case is

estimated from the neighborhood instead from addi-

tional patterns. The unwrapping is accepted after ad-

ditional reliability checks, please refer to the original

paper for more details.

Although the method starts from multiple local

positions, we found that it cannot fully cope with

discontinuities where the phase values with different

wrap counts seamlessly blend into each other (Figure

1 (d)). Integration of the candidate map can resolve

this and is straightforward: We start growing regions

only from singletons, the phase is thus directly un-

wrapped without having to deal with the relative shift

problem. In addition to the original reliability checks,

we allow an unwrapping at p only, if the correspond-

ing wrap count is found in the candidate map. In our

evalutaion we show that this greatly stabilizes the un-

wrapping process.

5.2 Global Unwrapping by Graph

Labeling

The application of graph cut based optimization to la-

beling problems had a large impact on image process-

ing during the last decade (Kolmogorov and Zabin,

2004; Boykov et al., 2001). Given an undirected

graph G = (V, E) and a set of labels L = {l

,..., l

}, a

(graph) labeling of G is a mapping ` : V → L. Further-

more there are weights placed on vertices and edges

of the graph. First order weighting functions are de-

ﬁned for the vertices and depend on the label of the

respective vertex. Second order weighting functions

are deﬁned for each edge, they depend on the weights

of the associated vertices. The ultimate goal then is

to compute a labeling of the graph that minimizes the

sum of all weights.

The graph labeling technique was also used for

phase unwrapping (Bioucas-Dias and Valado, 2007).

(a)

(b)

Figure 5: Parts of the graph G

for N = 5. Left: Representa-

tives of a single pixel from G. The dashed lines illustrate the

possible cuts and the associated wrap-counts. Right: Repre-

sentatives of two pixels u,v and their connections. The blue

dashed line is a possible graph-cut, the vertices are colored

according to the side of the cut they are on.

It relates to unwrapping in the following way: Each

pixel yields a vertex and neighboring pixels are con-

nected by an edge which results in a graph G. Each

w ∈ {0..N − 1} represents a label and each pixel of a

wrapped phase is unwrapped by labeling it with one

w. The costs for a certain labeling are deﬁned only

by second order weighting functions for each pair of

neighboring pixels. Minimization can then be accom-

plished using a graph cut. Since graph cuts optimize

binary labeling problems however, we follow the “k

to 2” method of (Schlesinger and Flach, 2006) to

transform our N-ary labeling problem to a binary one.

In the corresponding new graph G

, each vertex (i.e.

each pixel) of the old one is represented by N − 1 ver-

tices. Where there is an edge (u,v) in G, the represen-

tatives of u and v are fully interconnected in G

. More-

over, there are two special vertices s and t in G

which

provide the source and sink for the graph-cut calcula-

tion and are connected to the ﬁrst and last representa-

tives of each pixel, respectively. The spaces between

representatives themselves and between them and s

and t stand for the labels or here wrap-counts which

are identiﬁed with possible graph-cuts in G

. The sit-

uation is illustrated in Fig. 5.

Our cost function for the edges is

f (p

, p

) = k2πw

+ψ(p

)−(2πw

+ψ(p

))k

(3)

for a wrapped phase ψ, pixels p

and p

and wrap

counts w

and w

. This function in particular pe-

nalizes unwrapping over discontinuities, where |w

−

| > 1.

After computing a min-cut on G

the wrap-count

for each pixel is determined by assigning each repre-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

476

(a) (b)

Figure 6: The two objects used for evaluation. “Krusty” is

a gum ﬁgure with smooth geometry, it yields rather smooth

phases. The “Allegorie” is mostly made from metal and

marble, it yields rather noisy phases. Moreover, its highly

non-convex nature yields many self-occlusions. The respec-

tive discontinuities make the phases very hard to unwrap.

sentative the side of the cut it is on and by ﬁnding the

gap with the transition from source to sink, as indi-

cated in Figure 5. However, the sheer size of the graph

results in high memory consumption and high com-

putation time. Especially for high camera resolutions,

the computation of a min-cut becomes intractable.

The advantage of this method is the straightfor-

ward application of the candidate map: The struc-

ture of the candidate map is directly reﬂected in the

graph and all geometrically unfeasible labelings can

be omitted. This relaxes the problems mentioned

above: The number of representatives for each pixel

and thus the memory consumption is drastically re-

duced, which also speeds up the process considerably.

Similar to the region growing approach, singletons

ﬁx the relative shift problem in this context, too. In

our evaluation, we apply the method to 15 megapixel

phase images, which is not possible without the can-

didate map.

6 RESULTS

To prove the validity of the suggested methods, we

apply them to scans of two objects with very different

texture and geometric complexity (Figure 6). The ﬁrst

object (“Krusty”) is a ﬁgurine made of gum. Its color-

ing is simple, every region features one hue. The ob-

ject geometry is also quite simple, there are only few

rough edges and the surface is mostly smooth. From

most viewpoints, it yields phases with low noise, that

are rarely disrupted by discontinuities. The second

object (“Allegorie”) is a statue made from different

materials, mostly brass and marble. These materials

produce a phase with more noise. The complex geom-

etry causes many self-occlusions and depth disconti-

nuities from most view points, which makes the phase

signiﬁcantly harder to unwrap.

Both objects were scanned with multi-frequency

phase shifting with a setup of one Sanyo



Z 4100

projector (1920x1080) and seven Canon



EOS



500D cameras (4752x3168). We used ﬁve frequency

levels N = {1, 5, 11, 27, 91} with three shifts for the

ﬁrst four levels and ten shifts for the ﬁfth level for bet-

ter noise reduction. With these parameters, the multi-

frequency unwrapping algorithm of (Wang et al.,

2010) is able to correctly unwrap each level, we thus

use this phase as ground truth. Note that this unwrap-

ping algorithm requires substantially more input im-

ages due to the additional levels, which is intractable

in some application domains such as real time scan-

ning. In all experiments, the amount of required sec-

ondary views (m) is two.

Figure 7 (top row) shows the candidate maps and

the results of the proposed unwrapping algorithms for

N = 27 and N = 91. For both objects, large parts

of the candiate maps are ﬁlled with singletons. As

one would expect, the amount of candidates is larger

for N = 91. The second row of Figure 7 shows the

results of the region growing algorithm without can-

didate map. Since the algorithm does not know the

correct phase period at its starting pixels, it assigns

a ﬁxed w. Regions blending into each other are then

merged, i.e. the wrap count of one unwrapped region

is shifted to be consistent with the other region. How-

ever, consistent merging is not possible anymore as

soon as an unwrapping path crosses a depth discon-

tinuity that has a smooth phase (Figure 1 (d)). This

causes multiple self-consistent patches, whose phase

is shifted (unicolored, non-green regions). An aug-

mentation of this algorithm with the candidate map

almost fully resolves this problem (Figure 7, third

row). This is a remarkable result, in particular for the

“Allegorie” dataset, whose complex geometry with

many depth discontinuities yield phases that are very

hard to unwrap. Since the unwrapping is restricted

to |C

(p)| > 0 however, the unwrapped regions are

smaller for both objects. This could be improved by

applying classic approaches to regions with |C

(p)| =

0 after unwrapping with the candidate map, if the cor-

responding region is connected to an unwrapped part.

At N = 91, the performance of the augmented algo-

rithms is worse than at N = 27, but still better than

ImprovementofPhaseUnwrappingAlgorithmsbyEpipolarConstraints

477

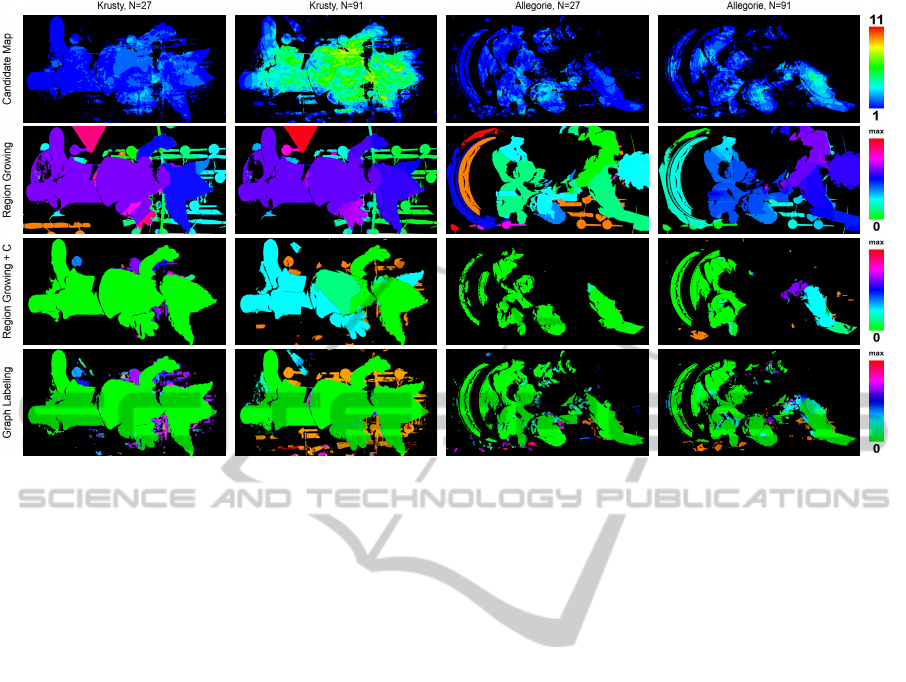
Figure 7: Candidate maps and results of the enhanced unwrapping algorithms. For the unwrapping results (row 2-4) we

visualize the period difference to the reference phase. Green corresponds to correct unwrapping, red to the highest measured

difference for this dataset. Everything but green yields wrong depth values.

without the candidate map. In case of the gum ﬁgure,

this is caused by the presence of only few singletons,

that are distributed along the border. In this region,

the surface normal is almost orthogonal to the view

direction and the reliability of C

decreases. The same

holds for the arm region of the “Allegorie” dataset.

The globally operating graph labeling algorithm

in general performs signiﬁcantly better than the lo-

cal path integration method. It also handles the few

singletons at N = 91 well and propagates the correct

phase over almost the full objects. In theory, the graph

labeling method can also be applied without the can-

didate map. In this case, each label is available per

pixel and the relative phase position is ﬁxed by as-

signing a ﬁxed label to some pixel(s). We tried this

but memory consumption and processing time of this

approach are unfeasible.

7 CONCLUSION

In this paper we proposed a general approach for us-

ing the epipolar geometry of multiple cameras in the

context of phase unwrapping. We introduced the con-

cept of the candidate map to aggregate all geometri-

cally feasible unwrapping possibilities. In contrast to

state of the art methods, we understand the candidate

map as a preprocessing step, that can support any sub-

sequent phase unwrapping algorithm.

The effect of the candidate map was illustrated by

augmenting two exemplary unwrapping methods: A

local path following and a global minimum norm ap-

proach. Our results illustrate, that both algorithms

greatly beneﬁt from the additional constraints pro-

vided by our candidate map. This is particularly im-

portant for application domains that require fast ac-

quisition speed and thus a low amount of captured

images such as real time scanning. Robust, temporal

unwrapping cannot be applied here. Together with the

fact that additional cameras also relax the need for a

gamma calibration we thus suggest to use at least two

cameras for such a respective system.

ACKNOWLEDGEMENTS

The work presented in this paper has been partially

funded by the project DENSITY (01IW12001).

REFERENCES

Abdul-Rahman, H., Gdeisat, M., Burton, D., Lalor, M., Lil-

ley, F., and Moore, C. (2007). Fast and Robust Three-

Dimensional Best Path Phase Unwrapping Algorithm.

Applied Optics, 46(26):6623–6635.

Bergmann, D. (1995). New approach for automatic surface

reconstruction with coded light. volume 2572.

Bioucas-Dias, J. M. and Valado, G. (2007). Phase unwrap-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

478

ping via graph cuts. IEEE Transactions on Image Pro-

cessing, 16(3):698–709.

Boykov, Y., Veksler, O., and Zabih, R. (2001). Fast approxi-

mate energy minimization via graph cuts. IEEE Trans.

Pattern Anal. Mach. Intell., 23(11):1222–1239.

auer-Burchardt, C., K

uhmstedt, P., and Notni, G. (2013).

Phase unwrapping using geometric constraints for

high-speed fringe projection based 3d measurements.

volume 8789.

auer-Burchardt, C., Munkelt, C., Heinze, M., K

uhmstedt,

P., and Notni, G. (2008). Phase unwrapping in fringe

projection systems using epipolar geometry. In Blanc-

Talon, J., Bourennane, S., Philips, W., Popescu, D.,

and Scheunders, P., editors, Advanced Concepts for

Intelligent Vision Systems, number 5259 in Lecture

Notes in Computer Science, pages 422–432. Springer

Berlin Heidelberg.

auer-Burchardt, C., Munkelt, C., Heinze, M., K

uhmstedt,

P., and Notni, G. (2011). Using geometric constraints

to solve the point correspondence problem in fringe

projection based 3d measuring systems. In Maino,

G. and Foresti, G., editors, Image Analysis and Pro-

cessing ICIAP 2011, volume 6979 of Lecture Notes

in Computer Science, pages 265–274. Springer Berlin

Heidelberg.

Costantini, M. (1998). A novel phase unwrapping method

based on network programming. Geoscience and Re-

mote Sensing, IEEE Transactions on, 36(3):813–821.

Dias, J. M. B. and Leito, J. M. N. (2002). The zm algo-

rithm: a method for interferometric image reconstruc-

tion in sar/sas. IEEE Transactions on Image Process-

ing, 11(4):408–422.

Garcia, R. and Zakhor, A. (2012). Consistent stereo-assisted

absolute phase unwrapping methods for structured

light systems. Selected Topics in Signal Processing,

IEEE Journal of, 6(5):411–424.

Ghiglia, D. C. and Romero, L. A. (1996). Minimum Lp-

norm two-dimensional phase unwrapping. J. Opt. Soc.

Am. A, 13(10):1999–2013.

Goldstein, R. M., Zebker, H. A., and Werner, C. L. (1988).

Satellite radar interferometry: Two-dimensional phase

unwrapping. Radio Science, 23(4):713–720.

Gorthi, S. S. and Rastogi, P. (2010). Fringe projection tech-

niques: whither we are? Optics and Lasers in Engi-

neering, 48:133–140.

Guo, H., He, H., and Chen, M. (2004). Gamma correction

for digital fringe projection proﬁlometry. Appl. Opt.,

43(14):2906–2914.

Guo, H., Zhao, Z., and Chen, M. (2007). Efﬁcient itera-

tive algorithm for phase-shifting interferometry. Op-

tics and Lasers in Engineering, 45(2):281–292.

Han, X. and Huang, P. (2009). Combined stereovision and

phase shifting method: a new approach for 3d shape

measurement. volume 7389, pages 73893C–73893C–

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521540518, second edition.

Herr

aez, M. A., Burton, D. R., Lalor, M. J., and

Gdeisat, M. A. (2002). Fast two-dimensional phase-

unwrapping algorithm based on sorting by reliabil-

ity following a noncontinuous path. Applied Optics,

41(35):7437–7444.

Kolmogorov, V. and Zabin, R. (2004). What energy func-

tions can be minimized via graph cuts? Pattern Anal-

ysis and Machine Intelligence, IEEE Transactions on,

26(2):147–159.

Loffeld, O., Nies, H., Knedlik, S., and Wang, Y. (2008).

Phase unwrapping for sar interferometry - a data fu-

sion approach by kalman ﬁltering. IEEE T. Geo-

science and Remote Sensing, 46(1):47–58.

Martinez-Espla, J. J., Martnez-Marn, T., and Lopez-

Sanchez, J. M. (2009). A particle ﬁlter approach for

insar phase ﬁltering and unwrapping. IEEE T. Geo-

science and Remote Sensing, 47(4):1197–1211.

Peng, T. and Gupta, S. K. (2008). Algorithms for generat-

ing adaptive projection patterns for 3d shape measure-

ment. Journal of Computing and Information Science

in Engineering, 8(3):031009.

Schlesinger, D. and Flach, B. (2006). Transforming an ar-

bitrary minsum problem into a binary one. Technical

Report TUD-FI06-01, Technische Universit

at Dres-

den.

Wang, Z., Nguyen, D. A., and Barnes, J. C. (2010). Some

practical considerations in fringe projection proﬁlom-

etry. Optics and Lasers in Engineering, 48(2):218 –

225. Fringe Projection Techniques.

Xu, W. and Cumming, I. (1999). A region-growing algo-

rithm for InSAR phase unwrapping. IEEE Transac-

tions on Geoscience and Remote Sensing, 37(1):124–

134.

ImprovementofPhaseUnwrappingAlgorithmsbyEpipolarConstraints

479