
Deep Learning for Facial Keypoints Detection
Mikko Haavisto, Arto Kaarna and Lasse Lensu
Machine Vision and Pattern Recognition Laboratory, Department of Mathematics and Physics,
Lappeenranta University of Technology, Lappeenranta, Finland
Keywords:
Deep Learning, Deep Belief Net, Restricted Boltzmann Machine, Denoising Score Matching.
Abstract:
A new area of machine learning research called deep learning has moved machine learning closer to one of its
original goals: artificial intelligence and feature learning. Originally the key idea of training deep networks
was to pretrain models in completely unsupervised way and then fine-tune the parameters for the task at hand
using supervised learning. In this study, deep learning is applied to a facial keypoints detection. The task is to
predict the positions of 15 keypoints on grayscale face images. Each predicted keypoint is specified by a real-
valued pair in the space of pixel coordinates. In the experiments, we pretrained a Deep Belief Network (DBN)
and finally performed discriminative fine-tuning. We varied the depth and size of the network. We tested both
deterministic and sampled hidden activations, and the effect of additional unlabeled data on pretraining. The
experimental results show that our model provides better results than the publicly available benchmarks for
the dataset.
1 INTRODUCTION
A feature learning algorithm could be described as a
way of automatically learn features from data at mul-
tiple levels of abstraction. The learned features might
be different depending on the task, even for the same
data. For example, a classification task requires dis-
tinctive features between classes whereas more gener-
ative features are needed in an image inpainting task.
In the case of images, the first abstraction level could
contain simple filters like straight lines with different
orientations. The level above the first one forms more
complex shapes, such as polygons, based on the ab-
stractions from the layer below.
There are at least three reasons why a feature
learning is of interest to researchers. First, higher-
level abstractions often become hard for humans to
specify in terms of raw data. Second, learned features
are adapted for the task at hand. To obtain features
for a specific task normally requires a huge amount
of domain knowledge, for example features used in
image processing are quite different from features in
speech recognition. Third, a feature learning scales
and adapts to the data compared to the traditional fea-
ture extractor methods. The last one is a fascinating
property: More data will provide better features. For
smaller problems, the lack of sufficient data might
also be a crucial limitation.
The depth of the architecture refers to the num-
ber of levels of composition of non-linear operations
in the learned function. Most current supervised
learning algorithms correspond to shallow architec-
tures (1, 2 or 3 levels), such as neural networks with
one hidden layer, support vector machines and ran-
dom forests. In addition to the limitations caused by
the shallow architectures (Bengio, 2009), these algo-
rithms are trained using only labeled data and they are
unable to benefit from unlabeled data. Even though
researchers have put huge effort on labeling data sets,
this underlying problem still remains in every ma-
chine learning application using supervised learning.
On the contrary, for example, object recognition
in the visual cortex, uses many layers of nonlinear
processing and requires very little labeled input (Lee
et al., 1998). Object recognition, which is a common
example of artificial intelligence (AI) related task, is
still a difficult task in computer vision research. This
is because the image of an object vary in different
view points, scale and sizes or when an object is trans-
lated or rotated into a different pose. Objects can
also be partially occluded from the view, which is ex-
tremely common in video sequences and real world
images.
The goal of this study is to find out how well a
deep learning model called Deep Belief Net (DBN)
can learn features from small grayscale images to de-
tect facial keypoints. The facial keypoints dataset
available through the Kaggle competition, was used
289
Haavisto M., Kaarna A. and Lensu L..
Deep Learning for Facial Keypoints Detection.
DOI: 10.5220/0005272202890296
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 289-296
ISBN: 978-989-758-090-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

in the experiments.
Section 2 gives a brief overview of deep learning
and its success on different application areas. Sec-
tion 3 gives a detailed description of methods used in
this study. The experiments that were done are ex-
plained in Section 4. The results are discussed in Sec-
tion 5 and a short conclusion of this study is given in
Section 6.
2 DEEP LEARNING
Increased computing power and massive data sets
have made the implementation of larger and more
complex machine learning systems feasible. These
factors have had a huge impact on the development
of artificial neural networks research, which is now
commonly referred as deep learning.
In 2006, Hinton et al. (Hinton et al., 2006) intro-
duced unsupervised learning algorithm for deep gen-
erative models called Deep Belief Net. The building
block for DBN is an energy-based graphical model
called restricted Boltzmann machine (RBM) that can
learn a probability distribution over its set of inputs.
Recently in 2012, Hinton et al. (Hinton et al.,
2012) developed an interesting biology-inspired
method to prevent overfitting by randomly omitting
half of the feature detectors on each training case.
This prevents complex co-adaptations in which a fea-
ture detector is only helpful in the context of several
other specific feature detectors. This method, referred
as “dropout”, can be seen as an efficient way of per-
forming model averaging.
Experiments in speech recognition show that pre-
training the model with DBNs can significantly out-
perform the conventional context-dependent Gaus-
sian mixture model (GMM) (Dahl et al., 2012)(Jaitly
et al., 2012). In the field of object recognition,
large, deep Convolutional Neural Network (CNN)
was considerably better than the previous state-of-the-
art methods in classification and localization tasks in
ImageNet Large Scale Visual Recognition Challenge
2012 (Krizhevsky et al., 2012). The network con-
tained 60 million parameters and 650,000 neurons,
and was trained on raw RGB pixel intensities.
High-dimensional data can be converted to low-
dimensional codes by training a multilayer neu-
ral network with a small central layer to recon-
struct high-dimensional input vectors. This deep
autoencoder network significantly outperforms com-
mon methods, such as Principal Component Analy-
sis (PCA) and Latent Semantics Analysis (LSA), and
autoencoder networks can be used for data visual-
ization purposes (Hinton and Salakhutdinov, 2006).
Also, a technique called “semantic hashing”, pro-
vides very fast method for document and image re-
trieval (Salakhutdinov and Hinton, 2009).
An important notion is that deep learning methods
do not necessarily require domain specific knowledge
of the particular task at hand. Deep learning moves
machine learning closer to one of its original goals:
artificial intelligence and automatic feature learning.
Deep learning models have been applied successfully
to a wide variety of machine learning competitions in
Kaggle (Kaggle, 2010), for example, molecular ac-
tivity prediction (Dahl, 2012) and job salary predic-
tion (Mnih, 2013).
Hierarchical face parsing (Luo et al., 2012) is an
interesting method on how to combine prior knowl-
edge on facial parts and components with deep learn-
ing strategy for several face-related tasks. Another in-
teresting work in the domain is the convolutional net-
work cascade model (Sun et al., 2013), which fuses
CNNs with multi-level regression. While the results
of both studies are very good, one drawback is that
the architectures used are carefully designed requir-
ing a lot of tedious manual engineering.
3 MODELING OF DEEP BELIEF
NETS
3.1 Binary RBM
A Restricted Boltzmann machine is a particular type
of Markov random field that has a two-layer architec-
ture (Smolensky, 1986). In the machine the visible,
binary stochastic units v ∈ {0,1}
V
are connected to
hidden binary stochastic units h ∈ {0, 1}
H
. The en-
ergy of the model with V visible units and H hidden
units is defined as follows:
E(v,h) = −
V
∑
i=1
H
∑
j=1
v
i
h
j
W
i j
−
V
∑
i=1
v
i
b
i
−
H
∑
j=1
h
j
a
j
, (1)
where W
V ×H
represents the symmetric weights
and b
V
and a
H
are bias terms. The conditional dis-
tribution over the hidden units is as follows:
P(h
j
= 1|v) = g
V
∑
i=1
v
i
W
i j
+ a
j
!
, (2)
where g(x) = 1/(1+exp(−x)) is the logistic func-
tion. Since v and h play a symmetric role in the energy
function,
P(v
i
= 1|h) = g
H
∑
j=1
h
j
W
i j
+ b
i
!
. (3)
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
290

3.1.1 Contrastive Divergence
Because the maximum likelihood learning for energy
based models is often infeasible (Lecun et al., 2005),
an approximation is needed. Contrastive Divergence
(CD) (Hinton, 2002) is an efficient learning algorithm
for such models and in the case of binary RBMs, this
equals to the following learning rule:
∆W = α
E
P
data
v
T
h
− E
P
T
v
T
h
(4)
∆a = α
E
P
data
[h] − E
P
T
[h]
(5)
∆b = α
E
P
data
[v] − E
P
T
[v]
, (6)
where α is the learning rate, P
data
is the training set
empirical distribution and P
T
represents a distribution
defined by running a Gibbs sampling, initialized at the
data, for T full steps. Setting T = ∞ recovers max-
imum likelihood learning. However, the CD learn-
ing with T = 1 has been shown to work well (Hinton,
2002).
3.2 Gaussian RBM
With the usual parameterization of the energy func-
tion for Gaussian RBM, it is difficult to learn vari-
ances from natural images using Contrastive Di-
vergence. Therefore, variances are often fixed to
unity (Cho et al., 2011) (Wang et al., 2012). To over-
come this limitation, we introduce a modified energy
function for Gaussian RBM that can be trained with
Denoising Score Matching (DSM) algorithm.
3.2.1 Denoising Score Matching
Score matching (SM) is another approach to esti-
mate parameters of probability models whose parti-
tion functions are intractable. SM minimizes the ex-
pected squared distance between the gradient of the
log-density given by the model, referred as score ψ,
and the gradient of the log-density of the observed
data (Hyv
¨
arinen, 2005).
Pascal Vincent showed that there is an equivalence
between Denoising Autoencoder (DAE), a successful
alternative to RBM that reconstructs the input from
a corrupted version of it (Vincent et al., 2008), and
Gaussian RBM trained using denoising score match-
ing (Vincent, 2011):
J
DSM
= E
q
σ
( ˜v,v)
"
1
2
ψ( ˜v) −
∂logq
σ
( ˜v|v)
∂ ˜v
2
#
. (7)
E
q
σ
( ˜v,v)
[·] is the expectation with respect to a noise
model and using additive Gaussian noise model, the
latter term in the squared distance corresponds to
∂logq
σ
( ˜v|v)
∂ ˜v
=
1
σ
2
(v − ˜v). (8)
By introducing the following energy function of
Gaussian RBM, we achieve the equivalence:
1
E(v,h) = −
1
σ
2
(v
T
b + v
T
W h + h
T
a −
1
2
v
T
v) (9)
P(h|v) = g
W v + a
σ
2
(10)
P(v|h) = N
W h + b,σ
2
(11)
ψ(v) = −
1
σ
2
(v − b − g
W v + a
σ
2
W
T
), (12)
where {W , b,a,σ} are the model parameters similar
to binary RBM with an added variance term σ
V
for
visible units. Substituting Eq. 8 and Eq. 12 in Eq. 7,
leads to the final objective function, which can then
be minimized by using gradient descent.
3.3 Deep Belief Nets
To extract higher-level features, a Deep Belief Net-
work combines a set of RBMs that are learned se-
quentially (Hinton et al., 2006). The greedy layer-
wise algorithm trains one RBM at a time, using the
previous layer’s activations as inputs.
Finally, a normal feed-forward neural network can
be initialized using the weights learned by the pre-
trained RBMs. For output, a softmax regression layer
is usually chosen for a classification task. For con-
tinuous values, a linear Gaussian layer can be used to
model conditionally Gaussian data. The full neural
network can be then fine-tuned with Stochastic Gra-
dient Descend (SGD) algorithm. The gradients for
the parameter updates are obtained using the standard
backpropagation algorithm (Rumelhart et al., 1988).
3.4 Momentum
Nesterov’s Accelerated Gradient (NAG) is a
momentum-based acceleration method that is capable
of accelerating directions of low-curvature, which
is particularly useful in training deep networks. It
explores new regions of the parameter space that
are local minima of better quality (Sutskever et al.,
2013). The NAG update rule for parameters θ is
given by:
v
t+1
= µv
t
− α∇ f (θ
t
+ µv
t
) (13)
θ
t+1
= θ
t
+ v
t+1
, (14)
1
This is not the same energy function as presented in
Eq. 4.3. in (Vincent, 2011) because in that energy function
there is no hidden variables and therefore is not an RBM.
Parameterization in Eq. 9 is proposed by Ian Goodfellow
in Pylearn2 (Goodfellow et al., 2013) implementation of
Gaussian RBM.
DeepLearningforFacialKeypointsDetection
291

where α > 0 is the learning rate, µ ∈ [0, 1] is the mo-
mentum coefficient, and ∇ f (x) is the gradient at x.
Intuitively, this tells us first to take a step in the di-
rection of the velocity v
t
, which is the direction of
the previous parameter update, and then calculate the
gradient update. By setting µ = 0, this becomes the
normal gradient descent update rule.
3.5 Regularization
While layer-wise generative pretraining itself is a
powerful regularizer, we introduce three regulariza-
tion methods that improve generalization of large
models even further.
3.5.1 L1 Weight-decay
Sparse features effectively lower the dimensions and
mitigates the curse of dimensionality. An easy way to
increase sparsity in a model is to use the L1 weight-
decay (Bach et al., 2012). By penalizing weights with
the L1-norm, the weight-decay induces sparsity to the
model in the sense that it forces many of the weights
to become exactly zero while allowing a few of the
weights to grow large.
3.5.2 Dropout
Dropout is a technique that prevents overfitting and
provides an efficient way of doing model averaging.
The first phase corresponds to dropping out units dur-
ing training: Each unit in a layer, with all its incom-
ing and outgoing connections, is dropped out with a
fixed probability p independent of other units. With
p = 0.5, a neural net with n units can be seen as
a collection of 2
n
possible thinned networks that all
share weights. At test time, a very simple approxi-
mate model averaging method is used: Using network
without dropout and multiplying weights by p. This
ensures that the expected output of any hidden unit is
the same as the actual output at test time (Srivastava
et al., 2014).
3.5.3 Data Augmentation
A very fundamental approach to improve generaliza-
tion is getting more training data. If a training set is
scarce and has some transformation-invariance prop-
erties, generating additional data may be useful. In
this particular case, we assume that the facial images
are extracted using standard face extractor. Thus, we
assume frontal faces with some rotational variance
and for example images in much smaller scale are er-
rors of the extractor and they are considered as out-
liers. This analysis is also supported by the distortion
intervals that produced the best generalization error
on the validation set.
We randomly added small variations to the train-
ing set, corresponding to rotation and scale. The
amount of variation for each distortion were uni-
formly sampled from the interval, which were deter-
mined using the validation set. In supervised fine-
tuning, the keypoints were also transformed accord-
ingly. Small distortions provided additional training
data that is consistent with the original data distribu-
tion. For images, even small random rotation could be
enough to prevent deep network to memoize its input.
4 EXPERIMENTS
In this section, we experimentally evaluated different
DBN architectures to find out a suitable model for fa-
cial keypoints detection. We varied the depth and the
size of an architecture. In unsupervised pretraining,
we tested sampled and expected activations and the
effect of additional unlabeled data.
4.1 Facial Keypoints Dataset
The facial keypoints dataset available through Kag-
gle competition (Kaggle, 2013) was used in exper-
iments. The task was to predict keypoint positions
on 96×96 pixel grayscale facial images. The prob-
lem is challenging because facial features vary from
one individual to another. Environmental conditions
such as illumination, viewing angle and pose express
a large amount of variation as well. Features learned
to predict the keypoints can also be suitable in several
other applications, such as tracking faces, analyzing
facial expressions, detecting dysmorphic facial signs
for medical diagnosis and face recognition.
The dataset was divided into a training set and a
public test set. Each predicted keypoint is specified
by an (x,y) real-valued pair in the space of pixel co-
ordinates. There are 15 keypoints
2
, which represent
locations of eyes, eyebrows, nose and mouth. 1783
images in the public test set do not have keypoint val-
ues annotated and the set is used to test performance
against other competitors through the Kaggle plat-
form. There are also two benchmarks in the public
leaderboard: Averages benchmark and patch search
2
Keypoint ids: left eye center, right eye center, left
eye inner corner, left eye outer corner, right eye inner
corner, right eye outer corner, left eyebrow inner end,
left eyebrow outer end, right eyebrow inner end, right
eyebrow outer end, nose tip, mouth left corner, mouth
right corner, mouth center top lip and mouth center
bottom lip.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
292
benchmark. Even though the training set size is 7049
images, only 2140 samples have all the 15 keypoints
and the rest have only 4 keypoints labeled. To make
use of all the training data, algorithms need to some-
how handle this missing label information.
4.2 Setup for Experiments
We used Pylearn2 (Goodfellow et al., 2013) machine
learning research library to implement the models.
It is built on top of Theano (Bergstra et al., 2010)
which can compile code for both CPU and GPU
backends. Many deep learning algorithms, like Con-
trastive Divergence for RBM, can be parallelized for
GPU which significantly speeds up the learning.
In data preprocessing, we first downsampled the
images by a factor of 3 which decreased the input di-
mensions to 32×32 = 1024. This common practise in
image processing is usually applied to achieve reason-
able memory usage and faster training times. Then
we applied global contrast normalization so that the
images became to have zero mean and unit variance.
The set of 2140 fully labeled images was split into
a training, validation and a test set. The test and the
validation sets consisted of 300 fully labeled exam-
ples. Images with imperfect label information gave
a convenient way to test the effect of additional un-
labeled data. The additional data were used in unsu-
pervised pretraining. Training epochs were fixed and
the best model was selected based on results on the
validation set.
4.3 Architectures
We varied the size of the network, more specifically
the number of hidden units in each layer. These three
hidden layer configurations were tested: 1000–1000–
4000 (small), 1500–1500–6000 (medium) and 2000–
2000–8000 (large). The linear Gaussian output layer
has 30 units which corresponds to (x,y) pixel coordi-
nates of 15 keypoints. The medium size architecture
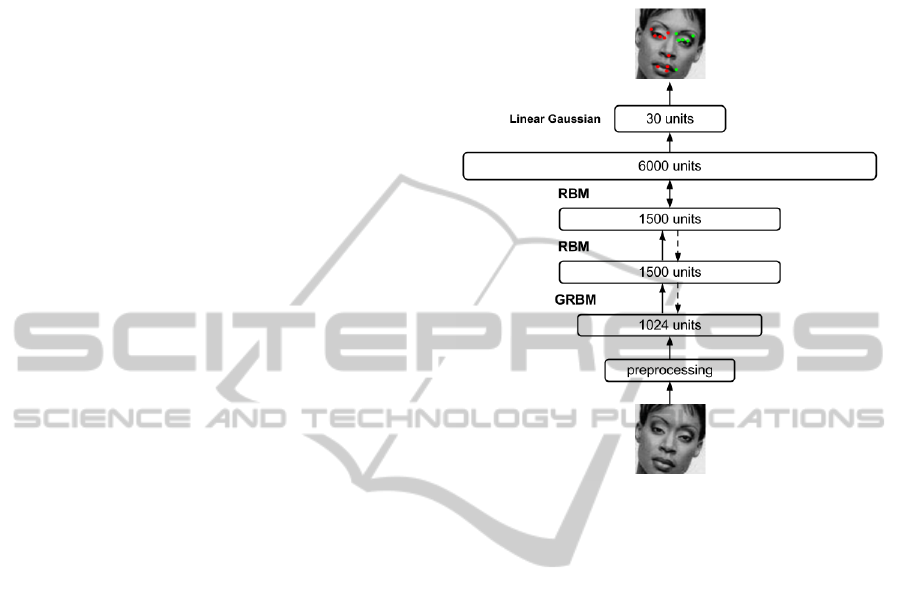
used in experiments is outlined in Figure 1.
The surrounding feed-forward neural network
with a linear Gaussian output layer was the same for
each pretrained DBN. To test the effect of increasing
the depth, we trained a new RBM above the previ-
ous DBN. We fine-tuned each DBN separately, which
led to the total of three DBNs per architecture. We
transformed the data from the lower layer by calcu-
lating the expectations of the hidden units. These de-
terministic activations can be considered as features
that the layer can extract. Because the hidden units
are binary stochastic units, it is natural to interpret the
activations to include a sampling from the Bernoulli
distribution. We also ran tests by using sampled ac-
tivations from deterministic expectations each time a
training example is shown to the model.
Figure 1: The architecture of medium size Deep Belief Net
used in experiments.
4.4 Pretraining
We trained the first layer Gaussian RBM with 1024
visible units (32 × 32 pixels) using Denoising Score
Matching with 0.4 Gaussian corruptor and 0.01 learn-
ing rate. The second and third layers are normal
binary RBMs which we trained using CD-1 algo-
rithm with 0.001 learning rate. The coefficient for L1
weight-decay was set to 0.0001. Momentum constant
for NAG was initialized at 0.5 and after 300 epochs
it reached its maximum value of 0.7. The data distor-
tion intervals of scale [1.1, 0.9] and rotation [−8
◦
,8
◦
]
in data augmentation were used. The values for hy-
perparameters were determined using the validation
set. We trained the models for 300 epochs. We used
the objective function on validation set to select the
best model with Denoising Score Matching and re-
construction error with Contrastive Divergence.
4.5 Fine-Tuning
The same values for the momentum constant, data
distortion and L1 weight-decay coefficient were used
as in pretraining. We used the dropout probability of
0.8 for the input layer and 0.5 for the other layers.
0.001 was used as the learning rate. We trained the
DeepLearningforFacialKeypointsDetection
293

models for 3000 epochs. In supervised fine-tuning,
the best model was selected on Mean Squared Error
of predictions on validation set.
4.6 Results
We followed the convention from the Kaggle platform
and used Root Mean Squared Error (RMSE) between
the ground truth and the predicted (x,y) points as a
performance metric.
The experiments showed that there were a little
difference on performance whether deterministic or
sampled activations were used on pretraining. Also,
the results did not provide decisive evidence that ad-
ditional unlabeled data on pretraining improves the
performance. However, the largest model was able
to benefit from the additional unlabeled data. There is
also a trend that increasing the size and depth of the
network improved the performance.
Our best model was the large size DBN-3, trained
using extended training set and deterministic activa-
tions between layers. The best DBN-3 in each size
category overcame the reference benchmarks in Kag-
gle competition (Table 1). Test results are summa-
rized in Table 2.
Table 1: Comparison to Kaggle benchmarks. “(e)” denotes
the usage of extended training set and “(s)” denotes sampled
hidden activations between layers on pretraining.
Model RMSE
Averages Benchmark 3.96244
Patch Search Benchmark 3.80685
DBN-3 (Small) (s) 3.25079
DBN-3 (Medium) (s) 3.23646
DBN-3 (Large) (e) 3.21211
Table 2: Prediction metrics (in RMSE) for various DBNs.
“(e)” denotes the usage of extended training set and “(s)”
denotes sampled hidden activations between layers on pre-
training.
Model Small Medium Large
DBN-1 1.71733 1.62732 1.60542
DBN-2 1.58002 1.54632 1.51221
DBN-3 1.53438 1.50519 1.50385
DBN-2 (s) 1.56710 1.56018 1.49564
DBN-3 (s) 1.53192 1.49432 1.49945
DBN-1 (e) 1.67990 1.63921 1.63162
DBN-2 (e) 1.59267 1.52828 1.51318
DBN-3 (e) 1.53839 1.50037 1.47267
4.7 Visualizations
Figure 2 shows some of the filters learned by the first-
level Gaussian RBM. Example keypoint predictions
by the best model are shown in Figure 3. Keypoints
from faces, which match the dominant scale in the
dataset, were predicted well. The mouth keypoints
were causing some error on these images when the
face was not aligned. When an image was in no-
tably smaller scale, predictions were clearly wrong
and somewhat corresponded to an average guess. The
model tolerated quite well occlusions like glasses,
hair and beard.
Figure 2: Some of the weights learned by Gaussian RBM
in the first layer.
5 DISCUSSION
The filters in Figure 2 show that modeling the real-
valued input data using Gaussian RBM and Denois-
ing Score Matching gave meaningful results. The first
layer plays an important role in the whole network
because the upper layers are trained based on its hid-
den activations. Filters clearly corresponds to recog-
nizable face images. This is due the fact that images
in the dataset have roughly the same scale and align-
ment. These weights are clearly better than random
values to initialize a feed-forward network. We want
to emphasize that these useful filters were learned in
completely unsupervised way. Experiments showed
that using the extended training set improved the re-
sults on the largest model and we are intrigued by the
possibility to exploit large databases such as Google
image search. There were no significant difference
between the deterministic and sampled activations,
when transforming the data from the lower layer dur-
ing pretraining.
Analysis of keypoint predictions tells us that our
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
294

Figure 3: Keypoint predictions. Green color indicates point
positions from the left side and red color from the right side
of the face relative to subject.
model can predict meaningful keypoint positions on
facial images which have the same scale. Faces with
small rotations got some error typically on one side,
but the prediction is probably still good enough for
tracking, for example. The largest errors were on
images that are at a completely different scale. Pre-
dictions for those cases are useless and can be inter-
preted that the model just made an educated guess.
We found that the model tolerated well occlusions that
were caused by glasses, hair and beard. That is a use-
ful feature to have because real-world use cases most
certainly contain noisy data.
There is a relatively large bias between the test re-
sults and Kaggle benchmarks. Some of that is prob-
ably caused by the fact that for the 4-keypoint im-
ages, the nose tip is systematically labeled below the
nose. These partially labeled images were only used
in the pretraining when testing the effect of additional
data and 4-keypoint images were not used in the more
powerful supervised training stage. The public test set
contained more examples with a smaller scale. Simi-
lar scale variance were present in particular in the 4-
keypoints dataset. This imbalance did not cause error
on our local tests because we only used the fully la-
beled examples in the supervised learning and tests.
The fully connected neural network architectures
used in our experiments does not scale linearly with
respect to the number of parameters. For example,
the small architecture had about 6 million parameters
while the large architecture had over 22 million pa-
rameters. If we increased the size further, for exam-
ple to 3000–3000–12000 architecture, it would cor-
respond to 48 million parameters. This suggests that
a different network architecture would have to be ex-
ploited to train even larger models.
6 CONCLUSIONS
The goal of this study was to find out how well Deep
Belief Nets can learn features from small grayscale
images to detect facial keypoints. We introduced
the main building block of deep learning, an energy-
based generative model called Restricted Boltzmann
Machine and an unsupervised learning algorithm
called Contrastive Divergence. A novel approach,
Denoising Score Matching, was introduced to train
Gaussian RBM to model real-valued data. We de-
scribed how Deep Belief Nets can be constructed by
using the greedy layer-wise training.
The facial keypoints dataset available through the
Kaggle competition, was used in the experiments.
The analysis of predicted keypoints showed that the
proposed deep model was able to predict meaning-
ful keypoints on facial images which have a similar
scale. It also overcame the reference benchmarks in
the Kaggle competition. The model tolerated occlu-
sions that were caused by glasses, hair and beard,
well. On pretraining, the largest model was able to
benefit from the extended unlabeled training set.
The results of this work imply that a Gaussian
RBM trained with DSM can successfully model real-
valued pixel intensities, and increasing the depth and
the size of the network improves the performance.
To further improve the model, a small amount of
translation invariance could be added to the archi-
tecture by using a combination of convolutional and
max-pooling layers. The weight sharing principle of
the convolutional layer will significantly decrease the
number of parameters, which makes it feasible to train
larger networks using images with realistic sizes. The
scale invariance is harder to achieve and it would re-
quire larger changes in the presented network archi-
tecture.
REFERENCES
Bach, F., Jenatton, R., Mairal, J., and Obozinski, G. (2012).
Optimization with sparsity-inducing penalties. Foun-
dations and Trends in Machine Learning, 4(1):1–106.
Bengio, Y. (2009). Learning deep architectures for AI.
DeepLearningforFacialKeypointsDetection
295

Foundations and Trends in Machine Learning, 2(1):1–
127.
Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu,
R., Desjardins, G., Turian, J., Warde-Farley, D., and
Bengio, Y. (2010). Theano: a CPU and GPU math
expression compiler. In Proceedings of the Python for
Scientific Computing Conference (SciPy).
Cho, K., Ilin, A., and Raiko, T. (2011). Improved learning
of gaussian-bernoulli restricted boltzmann machines.
In Proceedings of the 21th international conference
on Artificial neural networks - Volume Part I, pages
10–17, Berlin, Heidelberg. Springer-Verlag.
Dahl, G. (2012). Deep learning how I did it:
Merck 1st place interview. http://blog.kaggle.
com/2012/11/01/deep-learning-how-i-did-it-merck -
1st-place-interview/. Accessed September 29, 2014.
Dahl, G., Yu, D., Deng, L., and Acero, A. (2012).
Context-dependent pre-trained deep neural networks
for large-vocabulary speech recognition. Audio,
Speech, and Language Processing, IEEE Transactions
on, 20(1):30–42.
Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin,
V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F.,
and Bengio, Y. (2013). Pylearn2: a machine learning
research library. arXiv preprint arXiv:1308.4214.
Hinton, G. and Salakhutdinov, R. (2006). Reducing the di-
mensionality of data with neural networks. Science,
313(5786):504–507.
Hinton, G. E. (2002). Training products of experts by min-
imizing contrastive divergence. Neural Computation,
14(8):1771–1800.
Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006). A fast
learning algorithm for deep belief nets. Neural Com-
putation, 18(7):1527–1554.
Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. R. (2012). Improving neural
networks by preventing co-adaptation of feature de-
tectors. arXiv preprint arXiv:1207.0580.
Hyv
¨
arinen, A. (2005). Estimation of non-normalized statis-
tical models by score matching. In Journal of Machine
Learning Research, pages 695–709.
Jaitly, N., Nguyen, P., Senior, A. W., and Vanhoucke, V.
(2012). Application of pretrained deep neural net-
works to large vocabulary speech recognition. In IN-
TERSPEECH.
Kaggle (2010). Machine learning competitions.
http://www.kaggle.com. Accessed September
29, 2014.
Kaggle (2013). Facial keypoints detection.
http://www.kaggle.com/c/facial-keypoints-detection.
Accessed September 29, 2014.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in Neural Information Pro-
cessing Systems 25, pages 1097–1105. Curran Asso-
ciates, Inc.
Lecun, Y., Jie, F., and Jhuangfu (2005). Loss functions
for discriminative training of energy-based models. In
Proc. of the 10-th International Workshop on Artificial
Intelligence and Statistics.
Lee, T. S., Mumford, D., Romero, R., and Lamme, V. A.
(1998). The role of the primary visual cortex in higher
level vision. Vision Research, 38(15/16):2429–2454.
Luo, P., Wang, X., and Tang, X. (2012). Hierarchical face
parsing via deep learning. In Conference on Com-
puter Vision and Pattern Recognition, pages 2480–
2487. IEEE.
Mnih, V. (2013). Q&A with job salary pre-
diction first prize winner Vlad Mnih.
http://blog.kaggle.com/2013/05/06/qa-with-job-
salary-prediction-first-prize-winner-vlad-mnih/.
Accessed September 29, 2014.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1988).
Learning representations by back-propagating errors.
In Neurocomputing: Foundations of Research, pages
696–699. MIT Press, Cambridge, MA, USA.
Salakhutdinov, R. and Hinton, G. (2009). Semantic hash-
ing. International Journal of Approximate Reasoning,
50(7):969–978.
Smolensky, P. (1986). Information processing in dynami-
cal systems: foundations of harmony theory. In Par-
allel distributed processing: explorations in the mi-
crostructure of cognition, vol. 1, pages 194–281. MIT
Press, Cambridge, MA, USA.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: A Simple
Way to Prevent Neural Networks from Overfitting.
Journal of Machine Learning, 15:1929–1958.
Sun, Y., Wang, X., and Tang, X. (2013). Deep convolutional
network cascade for facial point detection. In Com-
puter Vision and Pattern Recognition (CVPR), 2013
IEEE Conference on, pages 3476–3483. IEEE.
Sutskever, I., Martens, J., Dahl, G. E., and Hinton, G. E.
(2013). On the importance of initialization and mo-
mentum in deep learning. In Proceedings of the
30th International Conference on Machine Learning,
pages 1139–1147.
Vincent, P. (2011). A connection between score match-
ing and denoising autoencoders. Neural Computation,
23(7):1661–1674.
Vincent, P., Larochelle, H., Bengio, Y., and Manzagol, P.-
A. (2008). Extracting and composing robust features
with denoising autoencoders. In Proceedings of the
25th International Conference on Machine Learning,
pages 1096–1103, New York, NY, USA. ACM.
Wang, N., Melchior, J., and Wiskott, L. (2012). An analy-
sis of gaussian-binary restricted boltzmann machines
for natural images. In Proceedings of the 20th Euro-
pean Symposium on Artificial Neural Networks, Com-
putational Intelligence and Machine Learning, pages
287–292.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
296
