Indoor Sensor Placement for Diverse Sensor-coverage Footprints

Masoud Vatanpour Azghandi, Ioanis Nikolaidis and Eleni Stroulia

Computing Science Department, University of Alberta, T6G 2E8, Edmonton, Alberta, Canada

Keywords:

Wireless Sensor Networks, Indoor Localization, Optimization, Sensor Placement, Smart Homes, Genetic

Algorithms.

Abstract:

Single occupant localization in an indoor environment can be accomplished by the deployment of, properly

placed, motion sensors. In this paper, we address the problem of cost-efﬁcient sensor placement for high-

quality indoor localization, taking into account sensors with diverse coverage footprints, and the occlusion

effects due to obstructions typically found in indoor environments. The objective is the placement of the

smallest number of sensors with the right combination of footprints. To address the problem, and motivated

by the vast search space of possible placement and footprint combinations, we adopt an evolutionary technique.

We demonstrate that our technique performs faster and/or produces more accurate results (depending on the

application) when compared to previously proposed greedy methods. Furthermore, our technique is ﬂexible

in that adding new sensor footprints can be trivially accomplished.

1 INTRODUCTION

Because of their low cost, infrared motion sensors

are being used in research and industry for a vari-

ety of localization purposes including military appli-

cations, target tracking, environment monitoring, in-

dustrial diagnostics, etc. One concern in using motion

sensors for localization is their placement. Subopti-

mal placement may result in inefﬁcient usage of the

equipment, and correspondingly, waste of equipment

cost and deployment effort. Pre–deployment simu-

lation to evaluate the anticipated performance of po-

tential deployment alternatives is a useful methodol-

ogy for systematically obtaining high-quality sensor

placements. The question then becomes how to de-

cide which placements to simulate, i.e., how many

sensors should the potential deployment include, of

what type, and where exactly these sensors should

be placed. In principle, a desirable placement should

have the smallest number of contributing sensors (in

order to minimize equipment cost, deployment effort,

and operating energy consumption) at locations such

that the overall space is sufﬁciently covered and the

target’s location can be inferred with a desirable de-

gree of accuracy and precision.

The work described in this paper builds on our

previous work, in the context of the Smart-Condo

(Boers et al., 2009; Ganev et al., 2011) project, where

we examined placement of same-type sensors, under

a cardinality constraint (i.e., a limited budget of sen-

sors) (Vlasenko et al., 2014) for the purpose of rec-

ognizing the location of an individual in a home en-

vironment. We adopt a similar formulation in this pa-

per. Namely, the formulation includes the represen-

tation of space as a line drawing (ﬂoorplan), and the

possible locations for the sensor place are from a set

which is expressed as a (ﬁne) grid of points over the

ﬂoorplan.

The placement is assumed to take place on the

ceiling (facing “down”). While alternative place-

ments can be accommodated, experience from prac-

tical deployments has reinforced that ceiling place-

ment is the most convenient for indoor deployments.

Our set of motion sensors include a variety of differ-

ent volumetric shapes, namely a cone, a square based

pyramid, and a rectangular based pyramid. Consid-

ering only orthogonal placement with respect to the

ﬂoor the projection of each of these shapes becomes

a disk, a square and a rectangle, respectively. More-

over, the projection of any sensor might be effected by

walls, doors or obstacles around the house depending

on where the sensor is placed (explained more in Sec-

tion 3.2).

Given the above description for the varieties of

sensors we consider, we expand the problem formu-

lation presented in (Vlasenko et al., 2014) to include

the various sensor footprints (from a ﬁnite set of foot-

prints) and to determine the optimal number of sen-

Vatanpour Azghandi M., Nikolaidis I. and Stroulia E..

Indoor Sensor Placement for Diverse Sensor-coverage Footprints.

DOI: 10.5220/0005273700250035

In Proceedings of the 4th International Conference on Sensor Networks (SENSORNETS-2015), pages 25-35

ISBN: 978-989-758-086-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

sors (not just their placement). The immediate impli-

cation of this more general problem formulation is a

signiﬁcantly enlarged search space, due to increased

number of possible combinations of placements and

footprints. We address the increase in complexity us-

ing genetic algorithms (GAs). Evolutionary methods,

based on GAs, are frequently employed to explore

large problem spaces in order to identify high-quality

solutions. Our sensor placement problem naturally

belongs to this category. The GA technique elabo-

rated in this paper outperforms the greedy algorithm

in (Vlasenko et al., 2014) in two different aspects.

First it efﬁciently delivers placements with acceptable

coverage accuracy. For example, we have noted that it

reaches 94.81 percent coverage after just 50 seconds

of execution on an off-the-shelf personal computer.

Second, it delivers placements with higher-accuracy

when efﬁciency is not a factor. It is able to eventually

reach coverage of 100, whereas the greedy algorithm

can do no better that 98.58 percent.

The remainder of this paper is organized as fol-

lows. In Section 2 we review earlier relevant research

in the same area. Section 3 presents details of our

mobility and sensor coverage model, as well as the

objective function. Section 4 provides a comprehen-

sive discussion of the GA methodology in the context

of our problem, and its parameters. Section 5 presents

simulation results. Finally, we conclude with a sum-

mary of the contributions of this work and some fu-

ture plans in Section 6.

2 RELATED WORK

The sensor placement problem is relevant to many

wireless sensor network (WSN) applications. Kang,

Li, and Xu (Kang et al., 2008) use a virus coevolution-

ary parthenogenetic algorithm (VEPGA) to optimize

sensor placement in large space structures (i.e., por-

tal frame and concrete dam) for modal identiﬁcation

purposes. They concluded that their method outper-

forms the sequential reduction procedure. Rao and

Anandakumar (Rao and Anandakumar, 2007), also

addressing the sensor placement problem in large-

scale civil-engineering structures, developed a solu-

tion based on particle swarm optimization, another

evolutionary technique. Poe and Schmitt adopt a GA

approach to sensor placement for worst-case delay in

minimization (Poe and Schmitt, 2008). Comparing

their results against a exhaustive and a Monte-Carlo

method, they found out that these methods serve as an

upper and lower bound, respectively. Their method is

a fast and near-optimum solution for optimized place-

ment. These papers show that evolutionary methods

are preferred over the exhaustive search approaches.

However none of them consider as an objective that

of optimizing the number of sensors placed.

Yi, Li and Gu (Yi et al., 2011) compared evolu-

tionary methods for sensor placement and described a

generalized genetic algorithm (GGA) approach for a

predeﬁned number of sensors. According to them the

GGA can get better results than the simple version

of the GA. They also describe a number of different

exhaustive and evolutionary methods to sensor place-

ment.

As we have already mentioned, the work concep-

tually closest to the method described in this paper is

our own previous work (Vlasenko et al., 2014) also

conducted in the context of the Smart-Condo

and

aiming at inexpensive placements for high-accuracy

localization of a individual in a home environment.

The greedy approach of (Vlasenko et al., 2014) iden-

tiﬁed sensor locations one at a time, resulting in ex-

ploring a large number of potential locations and, in

some cases, requiring a large amount of time. Our

method adopts evolution-based techniques to address

exactly these shortcomings.

3 MOBILITY AND SENSOR

COVERAGE MODEL

In this section we detail the mobility and coverage

models and we introduce the terminology, notation,

and deﬁnitions (Table 1) used in the remaining of the

study.

3.1 Basics of Localization

In order to improve localization accuracy, coverage

areas of the sensors are allowed to overlap. By having

the sensor coverage areas overlap the detection areas

will be reduced because the space is segmented into

new, smaller, polygons deﬁned by the intersection of

the coverage areas. We consider as location of the

individual to be the center of mass of the polygon oc-

cupied by the individual. To illustrate this, Figure 1

is presented. In this ﬁgure A12 is the new polygon

that has been created as a result of the overlap of the

coverage areas A1 and A2. A12 has the least amount

of localization error among the regions (because R3

is less than R1, R2, and R4).

With respect to representation conventions, we

can consider each polygon (or, more generally, over-

lap area) to be deﬁned by a speciﬁc signature signi-

fying the sensors that are “on” when an individual is

in that polygon. The signature can be represented by

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

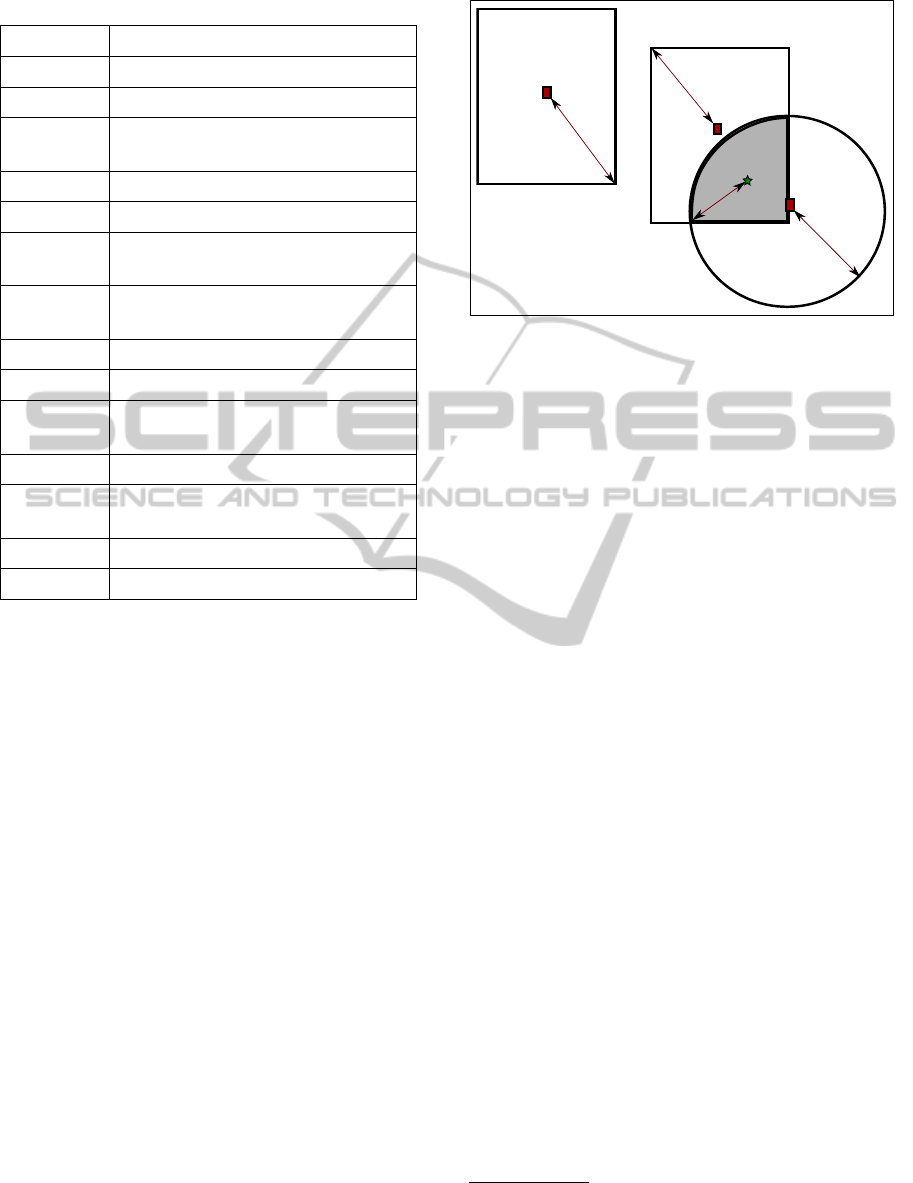
Table 1: Table of notation.

Symbol Deﬁnition

Coverage utility at point i

Heat-map value at point i

max

Maximum desired coverage score

)

t(c

max

) Threshold value

Points in space covered by sensor s

Points in space that are “seen

through” the doorway by sensor s

s→o

Probability of detection at point o

by sensor s

door open

Probability of doors being open

K Budget of sensors

Probability of detection at point o

by the sensors in set Z

C Chromosome

Coverage percentage metric of

chromosome C

Fitness function for chromosome C

Collective information utility

a series of 1s and 0s. If the e

motion sensor cov-

ers the polygon, its value of the signature at position

e will be 1, otherwise it is set to 0. For example in

Figure 1 each of the four regions have distinct signa-

tures which are (1, 0, 0), (0, 1, 0), (1, 1, 0) and (0, 0, 1)

for A1, A2, A12 and A3, respectively. The signature

also represents the sensor readings that we will get if

a person is present in the corresponding region.

Trying to ﬁnd good combinations of sensors to

overlap in certain “important” areas brings complica-

tions too. In Section 5 we show how our proposed

method handles overlaps, and places sensors where

their usefulness is maximized.

3.2 Sensor Coverage Model

As mentioned in our introduction section, walls,

doors and obstacles around the house can restrict sen-

sor footprints. Figure 2 presents an example where

two sensors (marked with green) with originally rect-

angular footprints (depicted with blue lines) are re-

stricted because of obstruction by walls (thick black

lines) and doors (painted in yellow). Some parts of

the polygon fall “behind” a door and the sensor may

cover these areas if the door is open, otherwise the

door restricts the sensor’s projection even further. The

probability of doors being open (p

door open

) directly

A12

R12

Figure 1: Example overlapping sensor coverage areas.

translates into probability of detection in the afore-

mentioned parts of the polygon.

A sensor’s coverage model is:

s→o











1, if o ∈ A

door open

, o ∈ D

0, otherwise

(1)

In this equation z is a point in space, A

is the set

of points sensor s covers, and D

is a set of points seen

by the sensor through the doorway. A

is represented

by:

: {a

, a

, . . . , a

} (2)

For our experiments we will set p

door open

to 0 in

order the avoid complexity. Therefore, we can rewrite

our coverage model, which now becomes a boolean

coverage model, as in Equation 3.

s→o

(

1, if o ∈ A

0, otherwise

(3)

If all of the sensors in the set of sensors Z cover

o, the joint sensing probability at that speciﬁc point is

(Wang et al., 2006):

= 1 −

∏

s∈Z

(1 − p

s→o

) (4)

3.3 Mobility Model

In this research, we adopt the environment model

developed in (Vlasenko et al., 2014). We consider

a ﬂoorplan and a corresponding “heat-map” created

through observation of the paths traversed by an in-

dividual in this space over time. Figures 3 and 4

In most cases, as in our evaluation section, this will be

a “sharp” probability, i.e., either 1 or 0, but the formulation

is applicable to general coverage probabilities.

IndoorSensorPlacementforDiverseSensor-coverageFootprints

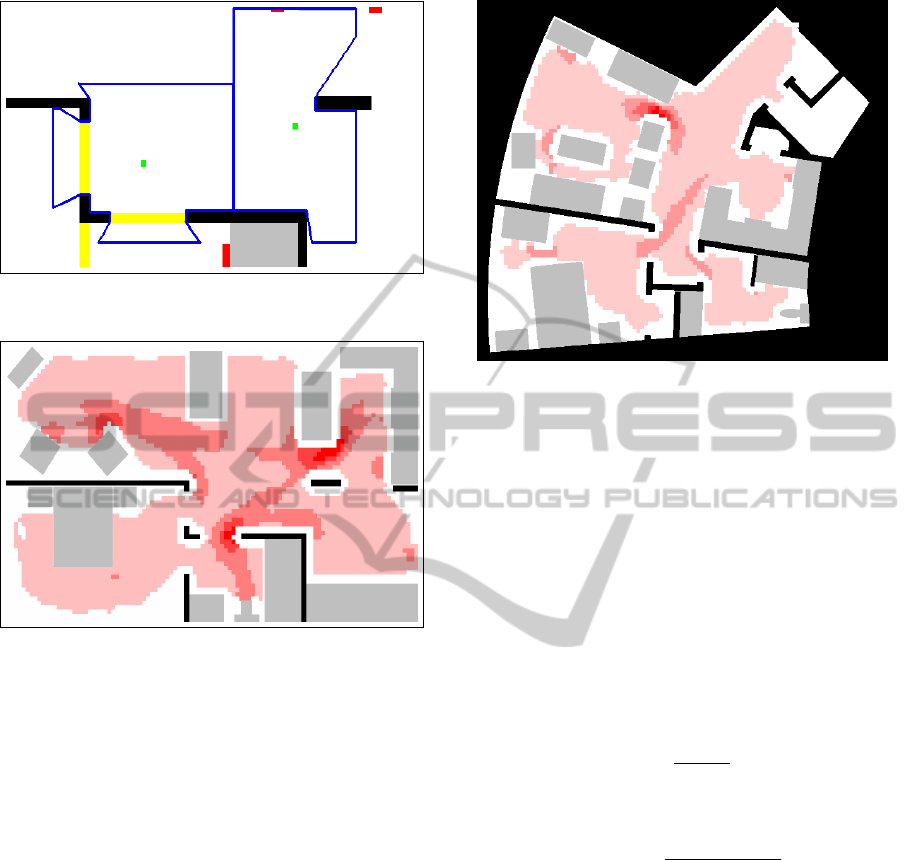
Figure 2: Real shape of sensor coverage projections

(Vlasenko et al., 2014).

Figure 3: Coverage utility heat-map of a person walking in

the Smart-Condo

show such ﬂoorplans with the heat-map represented

as various intensities of the same colour. The (approx-

imation of this) heat-map can be constructed without

a-priori observations of the occupant, but solely by

knowing the points of interest (e.g. locations in the

environment that form the origin/destination of an oc-

cupant’s paths).

The points of interest must include all potential

destinations in order to cover important areas. Failing

to doing so, will result in data loss and system deﬁ-

ciency. There are various parameters regarding how

to produce the heat-map, and depending on the oc-

cupant, different conﬁgurations can be adopted. In

cases were the user tends to choose more random and

unusual paths to traverse, the corresponding param-

eter(s) can be altered to accommodate exactly this.

For more information on how to produce the heat-map

please refer to (Vlasenko et al., 2014).

The heat-map is produced only once, at the pre-

deployment phase. It is at this phase that all the

planning has to be completed. After the sensors are

mounted on the ceiling, redeployment is consider-

ably expensive and time consuming. Thus, we should

make sure that the quantity of sensors in need agree

Figure 4: Coverage utility heat-map of a person walking in

the Independent Living Suit (ILS).

with our cost/accuracy trade-off, and that the place-

ment is optimal.

Next, using the two-dimensional heat-map that

contains N points of interest, (x

, y

), . . . , (x

, y

where each point has an information utility of v

construct a coverage utility map (with the same di-

mensions) which is the mapping of intensities from

the heat-map into numerical values. This is done

using a conﬁgurable application-speciﬁc parameter

called c

max

that indicates the upper bound of values

in the coverage utility map. Equations 5 and 6 show

how the translation between heat-map values (v

) and

coverage utility values (c

) are calculated.



t(c

max

)



(5)

Here, c

max

is the maximum desired coverage

score.

t(c

max

) =

max

i∈{1,...,N}

max

(6)

The coverage utility map will be used throughout

the rest of the study, mainly during the optimized sen-

sor placement.

3.4 Objective Function

Given the notation given in Table 1, the placement

problem can be formulated as follows:

Given (a) the coverage utility map and (b) K, the

set of sensors available, where k K k≤ N, the objec-

tive is to ﬁnd the combination of sensors, Z, that max-

imizes the collective information utility:

∑

i=1

) (7)

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

4 THE EVOLUTIONARY MODEL

GA solutions are represented as a population of chro-

mosomes, where each chromosome consists of genes.

In our model, the genes are a sensor’s type and its

location. In each evolution, new, and hopefully im-

proved, solutions are developed by applying a number

of different operators on the population. The criterion

for deciding whether a particular chromosome is bet-

ter than another is deﬁned through a ﬁtness function,

also known as the cost function. The classical GA

methodology that we use deﬁnes the following steps:

• Start. Generate an initial random population of

chromosomes representing potential problem so-

lutions, which in our case is sensor combina-

tions. Section 4.1 discusses the encoding of sen-

sor placements as chromosomes and the construc-

tion of the initial population.

• Loop. Create a new population by:

– selecting a percentage of the current population

as parents, and performing crossover to pro-

duce new offsprings,

– performing mutation of the new offsprings,

– applying elitism, i.e., including the new off-

springs in the new population but reducing the

population to its original size, keeping only the

best solutions for the next iteration.

Section 4.2 discusses the process of population re-

newal.

• Termination Check. If an end condition has been

reached,

– return the best solution in the current popula-

tion,

– else, go to Loop.

Section 4.3 discusses the termination conditions

of our method.

We note that the GA methodology requires a num-

ber of parameters for its conﬁguration, which must be

designed taking into account the speciﬁcs of the prob-

lem domain. A list of these parameters is given in

Table 2.

4.1 Chromosome Encoding

Each chromosome in the population contains a num-

ber of genes. In the context of our sensor placement

problem, genes are sensors with coverage models in-

troduced in Section 3.2. A chromosome is therefore

represented by a set of sensors:

C : {s

, s

, . . . , s

kCk

} (8)

Table 2: GA parameters.

Parameter Description

m Population size

u Number of children produced in

each iteration

n Number of sensors in each initial

chromosome

max Maximum number of sensors that

each solution can have (k K k)

The probability of crossover for the

parents

The probability of mutation on each

child

l Number of iterations for the whole

process

By combining equation 4 and 3, we can conclude

that P

= 1 whenever there is at least one sensor in C

that covers o.

In order to evaluate the performance of a solution

found by the genetic algorithm, we divide the chro-

mosomes collective information gain (calculated ac-

cording to Equation 7) by the summation of positive

coverage utility values. This will give a metric that

we call the coverage percentage metric, formulated

as follows:

∑

i=1

)

∑

i=1

≥0

)

∗ 100% (9)

In the Start step, we have to create the initial pop-

ulation for the algorithm to use as its ﬁrst evolution.

This is done by randomly creating m chromosomes,

i.e., sensor placement solutions. The initial length

of the chromosomes must be set to a value less than

or equal to a user-speciﬁed upper bound called max

i.e., (n ≤ max).

4.2 Selection, Crossover, Mutation and

Elitism

To produce children two parents must be selected for

a crossover procedure. The parents are chosen ran-

domly from the population, according to a selection

percentage also known as the crossover probability,

). For example, if the population consists of 100

chromosomes, and p

= 0.2, then approximately 20

parents are randomly chosen to participate. From the

chosen parents, two parents are randomly selected to

create two children. A second parameter, u, decides

the total number of children that will be produced in

IndoorSensorPlacementforDiverseSensor-coverageFootprints

each iteration. We continue the procedure until we

have all u children.

We use the “cut and splice” crossover method

(Banzhaf et al., 1998). In this method, the crossover

point for each parent is chosen separately and ran-

domly. As shown in Figure 5, the ﬁrst part of the ﬁrst

parent and the second part of the second parent are

used to construct the genes in the ﬁrst child, and the

rest construct the second child. Figure 5 shows how

cut and splice is performed to produce two children

from two parents. This crossover method leads to off-

springs with different chromosome lengths, which in

our case implies different numbers of sensors placed.

As we are seeking the number of sensors to use, as

well as the sensor locations, this method helps achieve

this. In addition, throughout the whole process of the

GA, chromosome lengths must remain less than or

equal to max.

Random Position in the Chomosome

Parents

Children

Figure 5: “Cut and splice” crossover method for producing

children chromosomes.

Once u children chromosomes have been pro-

duced through the parent-population crossover, ac-

cording to the mutation probability (p

), they might

be mutated. The chromosome mutation operation that

we use in our experiments is called a uniform muta-

tion (Banzhaf et al., 1998), which involves randomly

choosing a gene from the chromosome and perform-

ing the mutation operation on that gene. For this, we

either use relocating the sensor to a new random loca-

tion or we change its type, for example, turn its cov-

erage footprint from a disk to a square.

The last step of this phase involves adding the new

children in the population, and selecting the best chro-

mosomes from the combined population for the next

iteration so that the population cardinality always re-

mains stable. This selection is accomplished through

the ﬁtness function.

The ﬁtness of each chromosome is evaluated ac-

cording to the following three criteria. Sensors should

cover as much heat as possible. Sensors are penalized

for covering “restricted” areas, i.e., areas known to

not require coverage. For example sensors should not

be placed directly on top of a table, simply because

people don’t tend to walk there. Finally, the number

of contributing sensors should be minimized, there-

fore shorter chromosomes are preferable to longer

chromosomes. In order to capture these three crite-

ria, we have formulated the ﬁtness function to be:

= w1 ∗

∑

i=1

) − w2 ∗

kCk

∑

i=1

k A

k (10)

Where w1 and w2 are ﬁxed values, P

can be com-

puted using equation 4. Here, because the c

for points

in the restricted area is negative, the second criterion

is embedded in the ﬁrst summation.

4.3 The Termination Criterion

In principle, the evolutionary process terminates if (a)

the maximum number of iterations or execution time

has been reached, or (b) the average ﬁtness of the pop-

ulation does not change over a certain number of evo-

lutions, or (c) 100% accuracy is achieved. When the

genetic algorithm terminates, the best solution in the

current population is returned as the ﬁnal solution.

5 SIMULATION AND RESULTS

The evolutionary process described above is con-

trolled by the parameters listed in Table 2. As it is

a convention for users of evolutionary algorithms, pa-

rameter tuning needs to be performed based on ex-

perimental comparisons on a limited scale (Smit and

Eiben, 2009). We follow this requirement by ﬁne-

tuning the GA model parameters on a simple artiﬁcial

scenario. In the heat-map of Figure 6, the overlap-

ping footprints of several sensors are shown. The dif-

ferent footprint shapes correspond to three different

sensor types; the ﬁrst type projects a square footprint

(edge = 175 points); the second type projects a rect-

angle (length = 200 and width = 150 points); and the

third type projects a disk (radius = 100 points). The

darker the colour, the higher the signiﬁcance of the

area, i.e., the higher the utility of the area. The envi-

ronment shown in this simple heat-map consists of 6

different regions to be covered by the sensors, and the

ideal solution should place exactly 6 sensors of the

right types in exactly the right locations. Given this

desired solution, we proceeded to identify the param-

eter conﬁguration that results in the solution at hand.

Because of the implicit randomness of the evolu-

tionary GA process, we cannot predict the exact re-

sulting amounts for coverage percentage. So, the ex-

periments

conducted in this section are tested mul-

tiple times (i.e., 50 times), and the average is taken.

All experiments are run on Mac OS X, Processor: 1.7

GHz Intel Core i5, Memory: 4 GB 1600 MHz DDR3, plat-

form: Java.

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

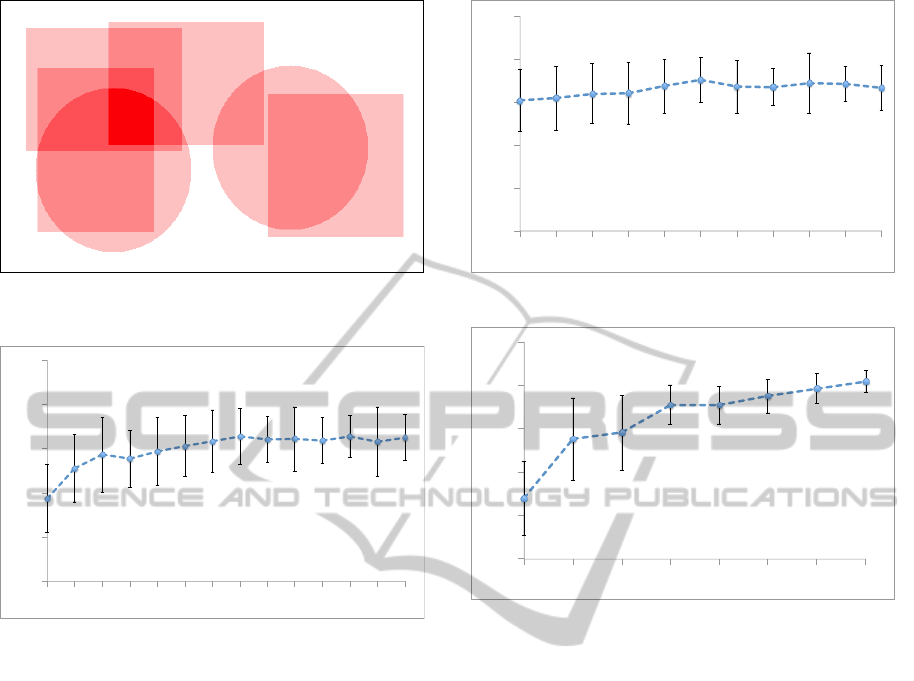
Figure 6: Artiﬁcial input with 6 overlapping regions to

cover.

80#

84#

88#

92#

96#

100#

0.02# 0.06# 0.1# 0.3# 0.5# 0.7# 0.9#

Figure 7: Coverage percentage for different values of p

To conﬁgure the algorithm parameters, we started

by optimizing p

, with the following initial settings:

m = 50, n = 10, u = 50, l = 50 and p

= 0.2. Fig-

ure 7 shows how the coverage percentage changes

for different values of p

. Lower p

values result

in lower accuracy. This is because, when there is

little crossover in the evolutionary process, the po-

tential parents are less likely to pair with each other

to produce better solutions. On the other hand, a

high crossover probability also threatens accuracy,

because good subsets of sensors inside the chro-

mosomes have a high risk of getting involved in a

crossover procedure and being separated from each

other; in these cases, the good subset, which should

have been passed to the next generation of chromo-

somes, is lost. We notice that the coverage percentage

at p

= 0.4 yields the best result. We used this value

for the remainder of the experiments and proceeded

to select p

through the experiments shown in Figure

As p

increases, more mutations occur and, as a

result, the diversity of the chromosomes increases.

However, too much mutation may result in los-

ing good chromosomes generated through crossover.

Based on the data of Figure 8, p

was set to 0.5 for

80#

84#

88#

92#

96#

100#

0# 0.1# 0.2# 0.3# 0.4# 0.5# 0.6# 0.7# 0.8# 0.9# 1#

Figure 8: Coverage percentage for different values of p

80#

84#

88#

92#

96#

100#

5# 10# 20# 50# 100# 200# 500# 1000#

Figure 9: Coverage percentage for different values of l.

the rest of the experiments.

Figures 9, 10 and 11 show the impact of l, m and u,

respectively. According to Figure 9, higher number of

iterations lead to better coverage percentages. Also,

as Figure 10 suggests the value of m should be set to

be the same as u, which in this case is 50. In Figure

11, we note that increasing the value of m (which is

equal to u) will result in higher accuracy. This is be-

cause, more children are produced in each iteration,

increasing the likelihood of ﬁnding a better solution.

Further, as the number of iterations increases, the like-

lihood of identifying a better solution increases since

more of the solution space is explored.

However, the downside to increasing m, u and l is

that execution time will also increase. So the question

becomes how to decide the tradeoff between m, l and

accuracy versus time consumption.

To answer this question we experimented with dif-

ferent conﬁgurations of m during different time pe-

riods. As shown in Figure 12 a larger population

size results in better accuracy, given the same amount

of execution time. Note that, because more execu-

tion time is consumed to produce children through

crossover in each iteration, there will be fewer iter-

ations in total.

In addition to running the same algorithm multiple

IndoorSensorPlacementforDiverseSensor-coverageFootprints

80#

84#

88#

92#

96#

100#

50# 100# 250# 500# 750# 1000# 1250# 1500# 1750# 1974#

m=100#

m=200#

m=300#

m=400#

m=500#

Greedy#

Figure 12: Results from GA for different values of m.

80#

84#

88#

92#

96#

100#

5# 10# 25# 50# 100# 250# 500#

Figure 10: Coverage percentage for different values of m.

80#

84#

88#

92#

96#

100#

10# 25# 50# 75# 100# 150# 200#

Figure 11: Coverage percentage for different values of u.

times, we also illustrate a logarithmic trend line func-

tion in order to visualize how different conﬁgurations

of the GA are performing. The trends in Figure 13 in-

dicate that although m = 500 performs slightly worse

than m = 100 at the beginning, it catches up and ﬁ-

nally exceeds the accuracy achieved with m = 100. In

conclusion, the process of parameter ﬁne-tuning re-

ported in this section produced the following param-

eter conﬁguration: m = 500, u = 500, p

= 0.4 and

= 0.5. When m is higher than 500, results deteri-

orate because the time spent in each iteration on pro-

ducing children increases and in a given amount of

time the algorithm cannot perform enough iteration

to achieve acceptable results.

5.1 Comparison Against the Greedy

Method

Let us now compare our GA method against the

greedy algorithm by (Vlasenko et al., 2014). In the

greedy method, sensors are placed one after the other,

in a location which optimizes the additional “heat”,

i.e., utility, covered. Once a sensor is placed, the heat

in the area covered by the sensor is reduced, since

gaining more localization accuracy in a given area

is becoming increasingly less useful as the area gets

covered. This procedure continues until the desired

number of sensors has been reached. It is important to

note here that, in the greedy method (Vlasenko et al.,

2014; Wang et al., 2006), the number of sensors to

be placed is assumed to be decided a-priori, based on

the cost that can be afforded. Near-optimal results are

guaranteed in this method when certain types of sen-

sors are used (Vlasenko et al., 2014). Although re-

alistic, this problem formulation does not address the

cases where the budget is ﬂexible and the users desire

to explore the cost/accuracy tradeoff. Another fun-

damental shortcoming of the greedy method is that it

consumes exponentially more processing time as the

types of available sensors increase.

Running the greedy algorithm on the simple heat-

map of Figure 6 always returns the same result of

98.58 percent coverage, after an average time of 1974

seconds. Figure 13 shows that after approximately

1800 seconds the GA surpasses the greedy method.

The greedy does not reach 100 percent accuracy with

the simple case heat-map, because it fails to exactly

match every area with the right sensor (Figure 14);

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

80#

84#

88#

92#

96#

100#

50# 100# 250# 500# 750# 1000# 1250# 1500# 1750# 1974#

Greedy#

Log.#(m=100)#

Log.#(m=500)#

Figure 13: Trend lines shown for m = 100 and m = 500.

Figure 14: Sensor placement on a simple case heat-map

with the greedy method.

Figure 15: Sensor placement on a simple case heat-map

with the GA method.

it always starts by covering the highest-utility area,

i.e., the darkest area in the heat-map, and gets stuck

in a local optimum. This phenomenon does not hap-

pen with the genetic algorithm. The GA can get even

100 percent accuracy thanks to its ability to ﬁnd the

best combination of sensors and not focusing on one

at a time (Figure 15). Although the process may take

time for very high accuracy (i.e., 37333.55 seconds

for 99.81%) but in time critical applications, it can

achieve very high accuracy in short time periods. Ac-

curacy as high as 94.81 % can be reached within the

ﬁrst 50 seconds.

In order to compare the two methods more real-

istically, we use the two complicated and larger scale

heat-maps, shown in Figures 3 and 4. The scale of the

Smart-Condo

heat-map is 629 × 1060 points and

for the ILS it is 573×651 points. Moreover, the value

of c

max

is set to 4 while producing these heat-maps. It

is noteworthy that the data reported throughout the re-

mainder of this section for the GA is the average of 10

runs.

The comparison methodology here is to ﬁrst see

how the greedy method is preforming with a desig-

nated budget of sensors and mark its coverage per-

centage (calculated using equation 9) for that budget

as the “desired accuracy”. After that, we give the GA

the same budget and see how fast we can achieve cov-

erage percentages higher than or equal to the desired

accuracy.

In the ﬁrst experiment conducted, we only use one

type of sensor footprint, the rectangle. Say the bud-

get for covering the ILS is 15 sensors, we would like

to know how much coverage each method achieves

having this budget. It turns out that greedy can get

81.48% coverage percentage in 466.7 seconds. This

value becomes our desired value, that the GA aims to

reach. The GA can achieve this accuracy in just 41.5

seconds on average.

Now, let us use a sensor set consisting of more

than one type of sensor. In the second experiment we

will use a budget of 5 squares, 5 disks, and 5 rectan-

gles (all with the same sizes as before). The same pro-

cedure as in the ﬁrst experiment is adopted to ﬁll ta-

bles 3 and 4 which show the results for both methods

when dealing with heat-maps 3 and 4, respectively. In

addition, we record the ﬁtness (calculated according

to Equation 10) of the solution as well as the average

Number of sensors.

IndoorSensorPlacementforDiverseSensor-coverageFootprints

Table 3: Comparison of different methods in the Smart-Condo

layout.

Desired Accuracy (%)

Greedy GA

nos

time (s) nos time (s) Average Cost Best Cost σ of Cost

74.29 10 3725 10 185 11933.41 12104.76 49.73

76.82 11 4231 11 275 12744.75 12873.20 44.36

79.93 12 4622 12 391 13313.95 13450.34 53.05

83.69 13 5023 13 387 14401.83 14488.54 47.51

84.50 14 5380 14 372 14389.32 14467.30 45.90

85.25 15 5572 15 348 14453.41 14595.90 51.05

Table 4: Comparison of different methods in the ILS layout.

Desired Accuracy (%)

Greedy GA

nos time (s) nos time (s) Average Cost Best Cost σ of Cost

72.45 10 643 10 56 2442.19 2487.82 16.55

73.77 11 741 11 35 2313.08 2432.68 34.65

76.80 12 837 12 52 2433.45 2504.76 22.44

77.60 13 912 13 62 2461.45 2529.08 26.86

79.43 14 967 14 58 2442.21 2557.78 31.65

80.80 15 996 15 50 2406.02 2524.48 28.05

and standard deviation of chromosome ﬁtness in the

population in which that solution was found (namely

solution cost, average cost, and cost STD).

According to these tables, the GA reached the de-

sired accuracy checkpoint with the same budget of

sensors in considerably less time. Comparing the

results from experiments one and two, we notice

that increasing sensor types affects the greedy’s time

consumption substantially, while increasing the GA’s

only slightly.

The GA can continue beyond this point and ﬁnd

even better solutions which brings us to our third and

ﬁnal experiment. In this experiment, again we get

back to only having 15 rectangles and want to see

how much accuracy we can achieve if we let the GA

consume the same amount of time that the greedy

has used. The GA reaches an average coverage per-

centage of 83.55% and shows is superiority when is

comes to hitting high accuracy, too.

6 CONCLUSION

Sensor placement can greatly impact the effective-

ness of sensor-based systems. In our work, in the

context of sensor-based indoor localization, we de-

veloped an evolutionary technique for sensor place-

ment. Our simulation experiments demonstrate that

our method achieves excellent coverage utility (close

to 100%) when time efﬁciency is not a factor; it also

delivers acceptable accuracy for applications that are

time sensitive. An important feature of our method is

that it does not require an a-priori number of sensors

as input, which is the case with an earlier greedy algo-

rithm developed by our group for this problem. Fur-

thermore, although a larger number of sensor types

tends to increase the run-time of the greedy algorithm,

it does not affect the genetic algorithm described in

this paper.

In the future, we plan to design a hierarchical

framework in the context of which to embed our al-

gorithm. The core idea is to decide sensor locations

for each utility level, starting from the highest level

and progressively descending to lower levels.

We also plan to extend the localization algorithm

with additional information sources, such as dead-

reckoning for a more accurate estimation of the per-

sons location, while this person moves between the

sensor regions.

ACKNOWLEDGEMENTS

This work has been partially funded by IBM, the Nat-

ural Sciences and Engineering Research Council of

Canada (NSERC), Alberta Innovates - Technology

Futures (AITF), and Alberta Health Services (AHS).

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

REFERENCES

Banzhaf, W., Francone, F. D., Keller, R. E., and Nordin, P.

(1998). Genetic Programming: An Introduction: on

the Automatic Evolution of Computer Programs and

Its Applications. Morgan Kaufmann Publishers Inc.,

San Francisco, CA, USA.

Boers, N. M., Chodos, D., Huang, J., Gburzynski, P., Niko-

laidis, I., and Stroulia, E. (2009). The smart condo:

Visualizing independent living environments in a vir-

tual world. In Pervasive Computing Technologies for

Healthcare, 2009. PervasiveHealth 2009. 3rd Interna-

tional Conference on, pages 1–8. IEEE.

Ganev, V., Chodos, D., Nikolaidis, I., and Stroulia, E.

(2011). The smart condo: integrating sensor networks

and virtual worlds. In Proceedings of the 2nd Work-

shop on Software Engineering for Sensor Network Ap-

plications, pages 49–54. ACM.

Kang, F., Li, J.-j., and Xu, Q. (2008). Virus coevolution

partheno-genetic algorithms for optimal sensor place-

ment. Advanced Engineering Informatics, 22(3):362–

370.

Poe, W. Y. and Schmitt, J. B. (2008). Placing multiple

sinks in time-sensitive wireless sensor networks us-

ing a genetic algorithm. In Measuring, Modelling and

Evaluation of Computer and Communication Systems

(MMB), 2008 14th GI/ITG Conference-, pages 1–15.

VDE.

Rao, A. R. M. and Anandakumar, G. (2007). Optimal

placement of sensors for structural system identiﬁca-

tion and health monitoring using a hybrid swarm in-

telligence technique. Smart materials and Structures,

16(6):2658.

Smit, S. K. and Eiben, A. E. (2009). Comparing parameter

tuning methods for evolutionary algorithms. In Evolu-

tionary Computation, 2009. CEC’09. IEEE Congress

on, pages 399–406. IEEE.

Vlasenko, I., Nikolaidis, I., and Stroulia, E. (2014). The

smart-condo: Optimizing sensor placement for indoor

localization. Systems, Man, and Cybernetics: Sys-

tems, IEEE Transactions on, PP(99):1–1.

Wang, Q., Xu, K., Takahara, G., and Hassanein, H.

(2006). Wsn04-1: deployment for information ori-

ented sensing coverage in wireless sensor networks.

In Global Telecommunications Conference, 2006.

GLOBECOM’06. IEEE, pages 1–5. IEEE.

Yi, T.-H., Li, H.-N., and Gu, M. (2011). Optimal sensor

placement for structural health monitoring based on

multiple optimization strategies. The Structural De-

sign of Tall and Special Buildings, 20(7):881–900.

IndoorSensorPlacementforDiverseSensor-coverageFootprints