
Using Inertial Data to Enhance Image Segmentation
Knowing Camera Orientation Can Improve Segmentation of Outdoor Scenes
Osian Haines, David Bull and J. F. Burn
University of Bristol, Bristol, U.K.
Keywords:
Vision Guided Locomotion, Segmentation, Image Interpretation, Scene Understanding, Inertial Sensors,
Oculus Rift, Mobile Robotics.
Abstract:
In the context of semantic image segmentation, we show that knowledge of world-centric camera orientation
(from an inertial sensor) can be used to improve classification accuracy. This works because certain structural
classes (such as the ground) tend to appear in certain positions relative to the viewer. We show that orientation
information is useful in conjunction with typical image-based features, and that fusing the two results in
substantially better classification accuracy than either alone – we observed an increase from 61% to 71%
classification accuracy, over the six classes in our test set, when orientation information was added. The
method is applied to segmentation using both points and lines, and we also show that combining points with
lines further improves accuracy. This work is done towards our intended goal of visually guided locomotion
for either an autonomous robot or human.
1 INTRODUCTION
Locomotion is fundamental to the survival of humans
and most other land-dwelling animals, in order to find
food, escape danger, or find mates, for example. One
of the primary senses used to guide locomotion is vi-
sion, enabling animals to perform complex tasks such
as avoiding obstacles, route planning, adjusting to
different terrains and building cognitive maps (Patla,
1997), which would be impossible with other senses.
This has inspired many applications in computer vi-
sion and robotics, which also attempt to use vision
to guide vehicles – either wheeled or legged – over
rough terrain using visual sensors (see for example
(DeSouza and Kak, 2002; Lorch et al., 2002)).
However, another sense available to animals is
from the vestibular system, allowing both relative ac-
celeration and absolute orientation (with respect to
gravity) to be perceived (Angelaki and Cullen, 2008).
This is combined with other senses, such as vision,
and is essential for the accurate balance required for
more agile motions. Interestingly, it has been sug-
gested that the central nervous system dynamically
controls the relative importance of visual and vestibu-
lar signals (Deshpande and Patla, 2007), and that
vestibular sensing may have a larger effect when vi-
sion is impaired. Vestibular sensing is also able to
ameliorate effects due to head motion when fixating
Figure 1: Typical results of our algorithm, showing how
segmentation results using only vision (left) can be im-
proved by taking into account the camera orientation (right).
In both examples knowledge of the camera orientation
avoids misclassifying vertical walls as ground (yellow). See
Fig. 7 for full colour legend. All images are best viewed in
colour.
on an object (Virre, 1996), and its absence causes se-
vere problems in interpreting visual information.
The use of orientation information in interpreting
scene content has been less well studied in the context
21
Haines O., Bull D. and Burn J..
Using Inertial Data to Enhance Image Segmentation - Knowing Camera Orientation Can Improve Segmentation of Outdoor Scenes.
DOI: 10.5220/0005274000210032
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 21-32
ISBN: 978-989-758-090-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

of mobile robotics however, and is something which
we believe can be put to good use alongside vision.
This is based on the observation that different types
of surface or structure are more likely to be observed
when the camera is facing in different directions: for
example, a camera pointing straight ahead is unlikely
to see the ground in the top half of the image; or a
camera pointing straight downward is very unlikely
to be looking at the sky.
In this paper we show that by using information
about the real-world orientation of a camera obtained
from an inertial sensor, it is possible to improve the
performance of algorithms designed to segment im-
ages into distinct semantic/structural regions, with the
aim of facilitating autonomous navigation through ur-
ban environments – see for example Fig. 1.
While vision is a suitable sensing modality for
such tasks, most solutions focus on using only vi-
sual features. While the location of a point/region in
an image has previously been used to alter likelihood
of predicting certain geometric classes (Hoiem et al.,
2007), to our knowledge the orientation of the camera
itself has not been used to facilitate segmentation in
this way.
Visual navigation is an important topic in robotics,
where the ability to navigate through unknown en-
vironments without human guidance is essential for
tasks such as disaster relief and search-and-rescue
(Kleiner and Dornhege, 2007), planetary exploration
(Maimone et al., 2007), or for self-driving cars
(Dahlkamp et al., 2006).
On the other hand, algorithms such as ours have
the potential to be used to guide humans, as we ex-
plore in this work. We do this primarily because a hu-
man makes a convenient test-bed for evaluating vision
guidance algorithms without the constraints of robot
locomotor capability, and give a useful proxy for how
well robots might be guided. Moreover, such algo-
rithms could also be applicatied as navigation aids for
the visually impaired, where recovering the structure
of a scene is important (Brock and Kristensson, 2013;
Tapu et al., 2013). This paper uses as an example the
goal of designing an algorithm able to guide a human
through an urban environment while wearing a head-
mounted display, through which the result of our seg-
mentation is shown.
The next section discusses related work in the
field. A brief overview of our method is given in
Section 3, followed by Section 4 which describes the
data acquisition process. Section 5 gives full details of
how our algorithm works. We then present extensive
results and examples in Section 6, before concluding
in Section 7.
2 RELATED WORK
Combining inertial sensors with computer vision al-
gorithms has been known to improve performance in
a variety of tasks. One of these is visual simultaneous
localisation and mapping, in which the pose of a cam-
era with respect to a map, and the unknown map itself,
must be recovered while it is being traversed. Since
inertial sensors provide an estimate of heading inde-
pendent of that derived from the image stream, these
estimates can be fused to improve robustness (N
¨
utzi
et al., 2011), and help to mitigate scale drift (Pini
´
es
et al., 2007). A rather different example from (Joshi
et al., 2010) uses inertial information for blur reduc-
tion, by using estimates of the camera’s motion de-
rived from inertial sensor during an exposure to guide
deconvolution.
More related to our application are tasks such as
segmenting an image into geometrically consistent
regions (Hoiem et al., 2007) and segmenting road
scenes into areas which are driveable or hazardous
(Sturgess et al., 2009). The former uses the position
of a segment within the image as a feature during clas-
sification, so that the expectation that the sky is near
the top of the image, for example, is learnt from data
– although in this work the camera is assumed to be
in an upright position with no roll. (Sturgess et al.,
2009) and more recently (Kundu et al., 2014) show in-
teresting examples of combining visual segmentation
with 3D information, which respectively use features
extracted from a point cloud to help classify objects
in road scenes, and fuse 2D segmentations and point
clouds to semantically label structure in 3D. While the
orientation of the camera may effect the result via the
3D map, this is not directly investigated, and further-
more is estimated from the image stream itself. Use
of 3D information in the form of depth data is also
useful in semantic segmentation (Gupta et al., 2014).
The use of inertial data for terrain classification
was investigated by (Sadhukhan et al., 2004). Rather
than use knowledge of gaze direction to guide seg-
mentation, the inertial data themselves are used as
features to encode the vehicle vibration and accelera-
tions for different terrains, in order to predict the ter-
rain type which the vehicle is currently traversing.
While these show interesting uses of information
not directly present in the image to aid labelling, they
are not making use of the information potentially
provided by the camera orientation itself. Similarly,
while some of the above mentioned works use inertial
data to aid vision tasks, this is generally in a purely
geometric sense, and they have not exploited the rele-
vance to semantic attributes in the image. We investi-
gate ways to do this in the following sections.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
22

3 OVERVIEW
In this paper we present an algorithm able to take
a single image with associated 3D orientation, mea-
sured with an inertial measurement unit (IMU), as in-
put, and produce a segmentation of the image into
distinct regions, corresponding to classes relevant to
the task of locomotion. The classes used are: ground
(walkable), plane (non-walkable, usually vertical),
obstacle (non-walkable and not planar), stairs, fo-
liage, and sky (coloured yellow, red, magenta, cyan,
green and blue respectively in all examples). These
were chosen as a reasonably minimal set of necessary
classes to facilitate locomotion through different en-
vironments. The reason we use more than two classes
(simply walkable/non-walkable) is to give more in-
formation to the human (or equivalently, robot) being
guided – for example, stairs can be traversed, but with
caution; foliage may be walkable but may require a
different gait; and a sky region should be interpreted
very differently from an impending obstacle, despite
the fact neither facilitate locomotion. Of course, our
algorithm is not specific to the classes we use.
To demonstrate the use of orientation in enhanc-
ing segmentation, we developed a relatively simple
means of classifying and segmenting images. We seg-
ment each image by describing a grid of points with
a collection of feature vectors, comprised of visual
and orientation information. These are used to predict
the most likely class for the point, using a pre-trained
classifier. Since each point is classified independently,
this initial segmentation exhibits much noise. To mit-
igate this, we use a Markov random field algorithm
to enforce the assumption of smoothness. With this
framework we show that fusing visual and orientation
information can substantially improve segmentation
accuracy over using either alone.
We also show that using both visual and orienta-
tion features improves performance when classifying
lines in the image. As above, these are described with
a combination of vision and orientation features, plus
features encoding some properties of the line itself.
Finally, we show that combining the results from both
point and line classification can improve performance
over either in isolation.
The result of our method is a segmentation of the
image, comprised of sets of contiguous points with
the same classification. This is not a per-pixel seg-
mentation, due to the resolution of the grid we use, but
every pixel in the image is covered, and every pixel is
used for the description. As shown in Fig. 1, this is
able to divide the image into regions appropriate for a
navigation task.
4 DATA ACQUISITION
To develop and evaluate the algorithms in this paper,
we gathered long video sequences (totalling around
90 minutes of footage) using an IDS uEye USB 2.0
camera
1
fitted with a wide-angle lens (approximately
80° field of view). This provides images at a resolu-
tion of 640 ×480, at a rate of 30 Hz.
Our aim is to use this method to guide humans
through outdoor environments. Therefore, all our data
are gathered from a camera mounted on the front of
a virtual reality headset, worn by a person travers-
ing various urban environments. While walking, the
subject sees only the view through the camera. This
was done so that the data are as close as possible to
what would be observed in a real application – both
in terms of height from the ground and viewing an-
gle, but also the typical movements and gaze direc-
tions made by a person wearing such a headset, with
somewhat limited visibility.
The hardware we used for this was the Oculus
Rift
2
(Dev. Kit 1), which has a large field of view and
sufficiently high framerate (up to 60 Hz). The cam-
era was mounted sideways, so that the images have a
portrait orientation – this is because the view for each
eye is higher than it is wide. We correct for barrel dis-
tortion introduced by the lens to produce an image ap-
proximating a pinhole camera, using camera parame-
ters obtained with the OpenCV calibration tool.
3
To gather orientation information we used the in-
ertial sensor built into the Oculus Rift. This com-
prises a three-axis accelerometer, gyroscope and mag-
netometer, which are combined with a sensor fusion
algorithm to give estimates of orientation in a world
coordinate frame at 1000 Hz. We retrieve the orienta-
tion as three Euler angles, and discard the yaw angle
(rotation about the vertical axis), since in general this
will not have any relationship to semantic aspects of
the world. Conversely, pitch and roll are important
since they encode the camera pose with respect to the
horizon line, and thus whether the camera is looking
up/down or is tilted. This has an influence on the like-
lihood of different classes being observed.
From these videos, a subset of frames are chosen
manually for labelling, either for training/validation
or testing. They are divided into disjoint regions, built
from straight-line segments. Each region is assigned
a ground truth label from our set of classes. This is by
nature a subjective task, since image content is often
ambiguous, but the labelling is as consistent as possi-
ble. Some truly ambiguous regions are not labelled,
1
en.ids-imaging.com
2
www.oculus.com
3
www.docs.opencv.org
UsingInertialDatatoEnhanceImageSegmentation-KnowingCameraOrientationCanImproveSegmentationofOutdoor
Scenes
23

Figure 2: Example ground truth – the manual labelling of
regions (left) and ground truth segmentation (right).
which are omitted from all training and testing.
Examples of ground truth data can be seen in Fig.
2. The labelling is independent of the points and
lines which are later created in the image. We also
show ground truth segmentations derived from these,
in which a grid of points has been assigned labels ac-
cording to the the underlying ground truth (where the
blockiness due to the grid is clearly visible). This
is the best possible segmentation, against which we
evaluate our algorithms in Section 6.
5 CLASSIFICATION AND
SEGMENTATION
In this section we describe the process by which
an image is segmented, according to either the vi-
sual features, orientation features, or both; and where
these features are created in regions surrounding grid
points, detected lines, or both. An overview of the
whole system is presented in Fig. 3.
5.1 Features
To describe a point, we build feature vectors from the
pixels in a square patch surrounding the point. We use
two types of visual feature: histograms of gradients,
and colour histograms.
Histograms of gradients are used to represent the
texture of the patch. The image is convolved with gra-
dient filters in the x and y directions, to obtain at each
pixel gradient responses g
x
and g
y
. For each pixel in
a patch we calculate θ = tan
−1
g
y
g
x
and m =
q
g
2
x
+ g
2
y
,
which are the gradient angle and magnitude respec-
tively. These are used to build the gradient histogram
by quantising the angle into bins, and weighting the
contribution to each bin by the magnitude. Rather
than creating a single orientation histogram for each
patch, we follow the example of (Haines and Calway,
2012) and create four separate histograms for each
quadrant of the patch, and concatenate them together
in order to encode richer structure information. This
is similar to the way HOG descriptors are built from
multiple cells (Dalal and Triggs, 2005), but without
the overlapping blocks.
Colour has also been shown to be beneficial when
classifying and segmenting images (Hoiem et al.,
2007; Kr
¨
ahenb
¨
uhl and Koltun, 2011). The colour
features we use are histograms built in HSV space,
which combine a histogram of quantised hue values,
weighted by the saturation (since the saturation repre-
sents the degree to which the hue is relevant), and a
separate histogram of the intensity values, to encode
the distribution of brightnesses within the patch.
We shall henceforth refer to the above as ‘vision
features’. The other type of features are the ‘orien-
tation features’. To compute these, we use the pitch
and roll values from the Oculus Rift IMU, each nor-
malised to the range [0, 1]. In addition to these, the
feature vector contains the position in the image of
the point (normalised by the image size). This is im-
portant, since otherwise the orientation feature would
be the same for all points in the image: it is the inter-
action between image position and camera orientation
which gives rise to cues of different types of structure
at different locations in the image.
5.2 Line Regions
An alternative form of the algorithm uses a set of
lines detected in the image. This is done in order to
represent high-frequency image content, and distinc-
tive texture and colour occurring over discontinuities,
which would be missed by the much smaller point
features. To detect lines we use the LSD line seg-
ment detector
4
(Von Gioi et al., 2010). The regions
are created around these lines, extending along their
length and covering a region of fixed width on either
side (we discard lines under 6 pixels long and 3 pix-
els wide (LSD gives a width value for each line) since
these are likely to be noise).
Line regions too are endowed with both visual and
orientation features. In order to create a description
better suited to lines, for both gradient and colour we
create pairs of histograms, from the pixels in rectan-
gular regions either side of the line, and concatenate
4
Code available at www.ipol.im/pub/art/2012/gjmr-lsd
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
24

Create points
Create vision
features
Create orientation
features
Detect lines
Assign points
to lines
Create vision
features
Create orientation
features
Classify
Classify
Combine
Combine
MRF
Extract Connected
Components
Create graph
Segments
Image
Orientation
(pitch and roll)
Camera
Oculus Rift
Classify
Classify
Combine
Create line-shape
features
Figure 3: Block diagram showing how the system as a whole works. The different algorithms discussed in this work corre-
spond to all or some of this. The ‘combine’ blocks can be interpreted as applying meta-learning, or concatenating features
before classification, as appropriate.
them. Thus, the gradient descriptor has half the di-
mensionality compared to the point case, while the
colour descriptor is twice as long.
We also add a line shape descriptor, which com-
prises simply its length, width, and orientation in the
image, each appropriately normalised. Finally, we use
the same orientation descriptor, using the line’s mid-
point and the pitch and roll of the camera as above (we
will refer to these together as the orientation features
unless otherwise stated). The use of these features
separately and together is evaluated in Section 6.
In order to combine lines with the rest of the seg-
mentation, we assign points to lines if they lie within
the region enclosed by the line feature (a point may
be assigned to multiple lines). It is this assignment of
points to lines which later allows line classifications
to be transferred to points for segmentation; similarly,
the ground truth label of a line is obtained via the
points, whose label in turn comes from the marked
ground truth regions (thus a line’s label vector is the
mean label vector of all points inside the area used to
describe it).
5.3 Classification
Having extracted features for all points and lines in
our training set, each being paired with a ground truth
label, we train a set of classifiers, with which we can
then predict labels for points and lines in new images.
For learning and prediction, we represent each label
as a 1-of-K vector (for the K = 6 classes), where di-
mension k is 1 for class k, and zero otherwise. The
outputs of the classifiers, after normalising to sum to
1, are treated as estimated probabilities for each class.
The classifier we use for this work is multivariate
Bayesian linear regression (Bishop, 2006), chosen be-
cause it is both fast to train, and very fast to evaluate
for a new input. It is similar to standard regularised
linear regression, except that the optimal value for the
regularisation parameter can be chosen directly, under
the assumption that the data have a Gaussian distribu-
tion. Since it is multivariate regression (predicting the
K dimensions of the label vector), an M × K weight
matrix is learnt, for M data. Prediction with the linear
regressor is simply a matter of multiplying the fea-
ture vector by the weight matrix. Rather than the raw
feature vector – which would allow for learning only
linear combinations of the inputs – we use fourth or-
der polynomial basis functions.
5.4 Combining Information
We can easily run the algorithm using points (P) or
lines (L) with either vision (V) or orientation (O) fea-
tures in isolation. This leads to the four baseline meth-
ods (denoted P-V, P-O, L-V and L-O respectively,
where L-O combines both orientation and line-shape
features as discussed above). The main theme of this
paper is to combine information from multiple fea-
ture types (vision/orientation) and from different im-
age entities (points/lines), which we describe here.
When classifying points, we can combine the fea-
tures in one of two ways. First and most obviously, we
simply concatenate the vision and orientation features
into one longer feature vector, and train/test with this
(algorithm P-VO-Cat). Or, we train separate classi-
fiers for the two feature types, and combine them af-
terwards. This is achieved by concatenating the out-
put K-dimensional label vectors from each classifier
for a point and treating this as a new feature vector.
This is input to a second round of classification, the
output of which is another K-d label vector, represent-
UsingInertialDatatoEnhanceImageSegmentation-KnowingCameraOrientationCanImproveSegmentationofOutdoor
Scenes
25

ing the final probability estimate for each class. This
process is known as ‘meta-learning’ (or sometimes
‘stacked generalisation’) (Bi et al., 2008). To train the
meta-classifiers, we run the classifiers whose outputs
we wish to combine on all points in the training data,
to gather example outputs. These predicted label vec-
tors are concatenated (to make the ‘meta-features’),
and paired with the known ground truth label for each
point to train the meta-learner. We refer to this algo-
rithm as P-VO-Meta.
The above can also apply to line regions, i.e. we
can combine line features either by concatenation
or meta-classification (L-VO-Cat and L-VO-Meta).
However, we cannot combine points with lines by
simply concatenating their features, because the point
and line features are created over different areas. In-
stead, we again use meta-learning, applied at the
points. Each point which lies in at least one line re-
gion is assigned the mean label vector from all lines
in which it lies (again normalised to sum to 1). Then a
final meta-classifier is trained using the predicted fea-
tures from the points and lines as inputs, to predict the
final label vector assigned to the point.
There are still two ways in which this could be
done, depending on how the features were combined
for the entities: either we concatenate the results of P-
VO-Cat and L-VO-Cat to make the meta-feature (PL-
VO-Cat); or use meta-classifiers for everything, and
concatenate the outputs of all predicted vectors from
P-V, P-O, L-V and L-O into a meta-feature, which
we call PL-VO-Meta. In either case, we need to deal
with points which are not in any lines: for PL-VO-Cat
we simply use the existing result of P-VO-Cat; for PL-
VO-Meta we train yet another meta-classifier, which
fuses the results of only P-V and P-O, i.e. fall back
to P-VO-Meta (the converse is not necessary, since
there are no points belonging to lines without their
own classifications). The performance of all of these
combinations is compared in Section 6.
5.5 Segmentation
The result of any of the above algorithms is a set of
points in the image, each having a predicted label
vector, from which we choose the most likely class
assignment as the dimension with the highest value.
Since each point is classified individually, there is no
guarantee that neighbouring points will have similar
labels, even if they belong to perceptually similar re-
gions of the image; this is especially true when using
line regions, as adjacent points may be assigned to
different lines.
To address this, we follow what has become fairly
standard practice in such tasks (Delong et al., 2012)
and formulate the problem as a Markov random field
(MRF). This allows us to choose the best label for
each point according to its observation (i.e. classifi-
cation result), while also incorporating a smoothness
constraint imposed by its neighbours.
We create a graph connecting all the points in the
image – this is simply a grid connecting a point to its
4-neighbours. The aim when optimising a MRF is to
maximise the probability of the configuration of the
field (i.e. an assignment of labels to points); this is
equivalent to minimising an energy function over all
cliques in the graph (Li, 2009). We define the neigh-
bourhood to include up to second-order cliques, i.e.
unary and pairwise terms.
A configuration of the MRF is represented as
p = (p
1
... p
N
), where p
i
∈ L is the class assigned to
point i of N and L is the set of possible labels. The
goal is to find the optimal configuration p
∗
, such that
p
∗
= argmin
p
E(p), where E(p) is the posterior en-
ergy of the MRF. We define this as:
E(p) = α
N
∑
i=1
ψ
d
(p
i
) +
P
∑
i=1
∑
j∈N
i
ψ
s
(p
i
, p
j
) (1)
where the first term sums over all points in the graph,
and the second sums over all neighbours N
i
for each
point i. α is a weight parameter, trading off the effects
of the data and the smoothness constraints. The unary
and pairwise potentials are:
ψ
d
(p
i
) = kp
i
− c
i
k
ψ
s
(p
i
, p
j
) = V
i j
T (p
i
6= p
j
)
(2)
Here, p
i
denotes the label p
i
represented as a 1-of-
K vector, and c
i
is the K-d output of the classifier. The
Euclidean distance means the predicted probability
for all the labels is taken into account. T (.) is an indi-
cator function, returning 1 iff its argument is true, and
V
i j
is a pairwise interaction term, controlling the de-
gree to which label dissimilarity is penalised at sites i
and j. This is set to V
i j
= β−min(β, |m
i
−m
j
|), where
m
i
is the median intensity over the patch at point
i. This penalises differences in label more strongly
between points with similar appearance, in order to
adapt the segmentation to the underlying image con-
tours. We set the parameters to α = 60 and β = 90
empirically based on observations on the training set
(note the pixel intensities are in the range [0, 255]).
We optimise the MRF using graph cuts with alpha-
expansion
5
(Delong et al., 2012).
Once the MRF has been optimised, each point has
one label, and points with the same label should be
spatially grouped together. To extract the final seg-
ments, we perform connected component analysis,
so one segment is created for each contiguous graph
component with the same label.
5
Using the ‘gco-v3.0’ code at vision.csd.uwo.ca/code
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
26

6 RESULTS
To evaluate our algorithms, we gathered two datasets
in the manner described in Section 4. All data were
obtained from the same camera, having a (rotated)
resolution of 480 × 640, and were corrected for barrel
distortion due to a wide-angle lens.
The first dataset was designated the training set,
and contained 178 manually labelled images. This set
was used for cross-validation experiments, to demon-
strate the claims made above. The second set of 156
images was the test set – this was obtained from dif-
ferent video sequences, from physically distinct loca-
tions to the training set to ensure there was no over-
lap during training and testing. This was done to ver-
ify that the algorithms generalise beyond the training
set, and to show example images (all examples in the
paper come from this set). All our labelled data are
available online.
6
Our algorithm has a large number of parameters
which will effect its operation. The most important
ones are described here, with typical values given.
The grid density (distance between points) was set
to a value of 15 pixels (making a grid of approxi-
mately 30×40 points), to give a compromise between
an overly coarse representation/segmentation, and the
quadratic increase in computational time for denser
grids. The patches around every pixel, from which
visual features are built, were squares of side 20 pix-
els. The width of line regions was set to 30. The
basic gradient histogram was 12-d, making the con-
catenated quadrant feature on points 48-d; and HSV
histograms had 20 dimensions each for the hue and
intensity parts. As described earlier, point-orientation
features had four dimensions, while lines had those
four, plus the three for line shape.
These parameters were set to values which appear
sensible or are supported by related literature. How-
ever, we make no claim that these were the optimal
parameters, and much further tuning could be done,
although the best settings would depend on the dataset
used. We emphasise that this does not alter the cen-
tral claims of this work, i.e. that making use of ori-
entation information, using either points or lines, can
improve segmentation. All parameters were kept con-
stant across evaluations, so all results are relative.
6.1 Cross-validation
We begin with results obtained through cross-
validation on our training set. This was done by
running five independent runs of five-fold cross-
validation on the data (to mitigate artefacts due to par-
6
Out dataset can be found at www.cs.bris.ac.uk/˜haines
Figure 4: Adding orientation features to vision features for
points. All error bars show a 95% confidence interval.
ticular choices of training/test splits). We use classi-
fication accuracy as our error measure, i.e. the aver-
age number of times a point was assigned the correct
class (we also looked at the diagonal of the confusion
matrix, or the mean of F-measures over all classes,
and observed the same trends). We evaluated seg-
mentation point-wise, i.e. looking at every point in-
dividually, since for the time being we are not con-
cerned with the issue of true segments being wrongly
split or merged. For this reason, and because it may
mask some of the differences between algorithms, all
evaluations were performed without using the MRF
segmentation; instead we directly used the labels as-
signed to points by the classifiers (we found the MRF
generally improved accuracy by a few percent).
First, we ran an experiment to compare classifica-
tion using only points, with vision features (P-V) or
orientation features (P-O) only, and combinations of
the two. The results are shown in Fig. 4. The bars in-
dicate the average accuracy over all the runs of cross-
validation, and the error bars are drawn to show a 95%
confidence interval, based on the average standard er-
ror over all runs of cross-validation.
As one might expect, using only orientation fea-
tures performs much worse than using only vision,
since it is utterly unable to predict foliage, for exam-
ple. Nevertheless, it can be surprising what orienta-
tion alone can tell us about what an image is expected
to contain, as we will show in the next section.
One of the key results of this paper is that either
of the combination methods (P-VO-Cat, P-VO-Meta)
are clearly better than either vision or orientation fea-
tures alone. It is interesting to note that classifying
separately followed by meta-learning improves per-
formance somewhat (consistently albeit perhaps not
significantly). This may be because it is able to learn
interactions between the classifiers not apparent when
UsingInertialDatatoEnhanceImageSegmentation-KnowingCameraOrientationCanImproveSegmentationofOutdoor
Scenes
27
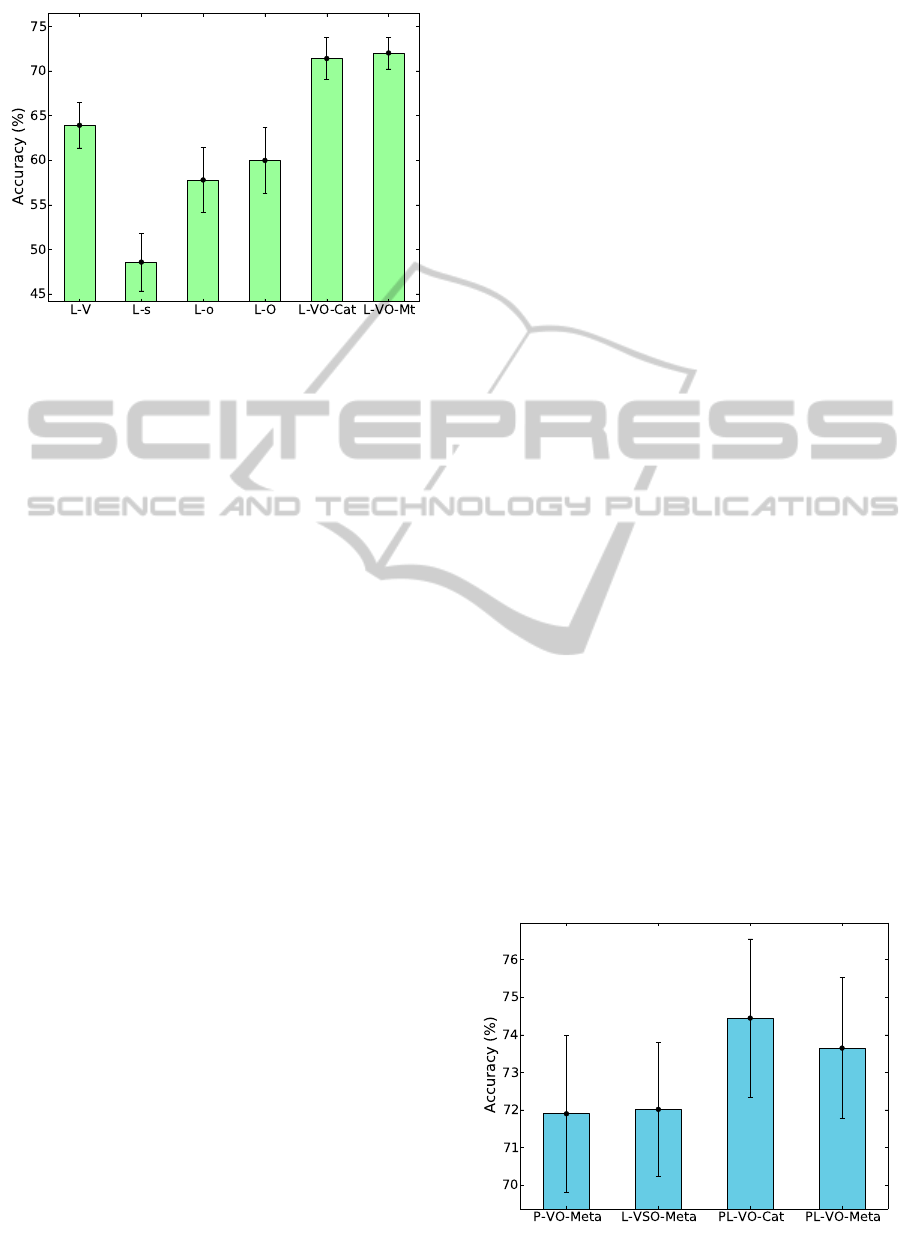
Figure 5: Using orientation with vision features for lines. L-
s and L-o respectively denote shape and orientation features
individually, and L-O concatenates both.
only one long feature vector is used; or because a
4-d orientation vector added to a 88-d vision feature
has difficulty making a large difference. However,
we cannot exclude the possibility that this is a con-
sequence of our choice of classifier.
The next experiment was the same as the above,
but for line regions instead. Note that these evalua-
tions were done using the points which were assigned
labels from classified lines, not on the lines them-
selves (points not in lines were excluded from the
evaluation). We also tested the use of orientation (L-
o) and shape (L-s) features separately, then together
(L-O), showing that knowledge of the lines’ size and
orientation in the image, combined with the camera
orientation, is better than using the camera orienta-
tion alone. As Fig. 5 shows, the same trend as in the
points experiment is observed: orientation and shape
alone (L-O) cannot compete with vision only (L-V),
but once again combination by concatenation (L-VO-
Cat) or meta-classification (L-VO-Meta) improve per-
formance (the latter two, like V-O, concatenate the
shape features with the orientation)
Finally, we investigated the effect of combining
point and line features. Figure 6 shows both point
and lines separately, using both types of feature (we
show the individual meta-classifier versions because
they are better; points and lines appear to perform
similarly, though note that the lines were evaluated
at only a subset of points). The two methods of com-
bining entities (PL-VO-Cat and PL-VO-Meta) lead to
an improved accuracy, suggesting that combining in-
formation from multiple types of patch/region is in-
deed beneficial, albeit by a smaller margin than the
above experiments. Strangely, the best performance
is achieved by PL-VO-Cat, which concatenates the
result of the less-good concatenation versions of the
individual entities, though the difference is small.
In Fig. 7 we show a confusion matrix, obtained
as the mean confusion matrix over all runs of cross-
validation, for PL-VO-Cat, the best performing vari-
ant. The diagonal is pleasingly prominent, though
there is significant confusion between stairs and
ground (when the true class is stairs), which is some-
what unfortunate from a safety point of view. Vertical
surfaces also tend to be confused with other obstacles
and foliage, which is less of a concern. For our task,
ground identification is perhaps the most important
criterion, which appears to be the strongest result.
6.2 Independent Data and Examples
After the cross-validation experiments, we trained
sets of (meta-)classifiers corresponding to different
variants of the algorithm, using the training set above
(plus copies obtained by reflecting across the verti-
cal image axis). We used these to evaluate perfor-
mance on the independent test set. Results are shown
in Table 1. This confirms the important result of the
paper: that combining orientation information is ben-
eficial, exhibiting around 10% increase in overall ac-
curacy. Adding line information did confer a further
improvement, although this was only slight. We also
show results after applying the MRF, which increased
accuracy by a few percent in each case.
We now show example results taken from the
test set, showcasing the differences between the al-
gorithms presented above. These images were chosen
to be representative examples of what the algorithms
can achieve, and where applicable, we choose the -Cat
or -Meta versions which gave the best performance in
the tests above. In all example images in the paper,
the MRF segmentation has been run, to remove noise
and give a tidier segmentation.
First, Fig. 8 shows side by side examples of the
Figure 6: Combining predictions from both points and lines.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
28

Sky
Foliage
Obstacle
Plane
Ground
Stairs
Figure 7: Confusion matrix over all runs of cross-validation,
for the best-performing algorithm PL-VO-Cat. Rows corre-
spond to the true classes, while columns represent the pre-
dicted classes. Colours correspond to those used through all
segmentation examples.
basic vision version (P-V), and the effect of adding
orientation (P-VO-Meta). In the top example, the
building fac¸ade is partly mistaken for the ground by
the visual features, whereas knowing the camera is
pointing upwards corrects this. In the bottom exam-
ple, the mis-classification of the road as stairs is also
corrected.
In the next example (Fig. 9) we show the effect
of adding line classifications to the points-only seg-
mentation, in both cases using both visual and ori-
entation features (P-VO-Meta, PL-VO-Cat, respec-
tively). These examples show how the information
gleaned from the lines can aid segmentation, for ex-
ample by disambiguating stairs and planes, or find-
ing non-planar objects. However, as our results below
will show, lines can sometimes be detrimental.
It is interesting to see what effect the orientation
features have, independently of the vision features,
so in Fig. 10 we show results generated using P-O
and PL-O, i.e. there are no visual features at all be-
ing used in these segmentations (image information
is being used only for line detection). Figure 10(a)
appears to be correctly segmented, but only because
this is a common and rather empty configuration of
ground and walls; whereas the cars in (b) are obvi-
ously ignored. (c) is interesting since it shows that
with the camera looking down at a certain angle, stairs
Table 1: Comparison of the different algorithms on inde-
pendent test data. Using a MRF to smooth away spurious
local detections increases accuracy slightly in all cases.
Algorithm Accuracy With MRF
P-V 61.0% 64.7 %
P-VO 71.1% 73.8 %
PL-VO-Cat 71.5% 74.6 %
PL-VO-Meta 72.0% 74.3 %
Figure 8: Example results, showing segmentation using
only vision features (left) and combined with orientation
features in (right). See colour legend in Fig. 7.
Figure 9: Examples showing how adding line classifica-
tions (centre) in conjunction with point features (P-VO-
Meta, left) can help improve segmentation results (PL-VO-
Cat, right).
are predicted – in this case correctly. This raises the
interesting issue that stairs are predicted here not just
because they are likely to be below the viewer, but
because the viewer is likely to look downward when
walking up stairs. In 10(d) and (e) the use of lines
has altered the segmentation, to give the impression it
is seeing the bollards and the sky (the points assume
there is sky above, but lines even at such a height are
rarely labelled as sky in the training set). In (f) the
lines themselves are shown, and it can be seen how
their orientation in the image has an effect, since the
bollards and paving stones are classified differently,
despite being at around the same image height.
UsingInertialDatatoEnhanceImageSegmentation-KnowingCameraOrientationCanImproveSegmentationofOutdoor
Scenes
29

(a) (b) (c) (d) (e) (f)
Figure 10: Example segmentations using only orientation information features – points only (a-c) and points with lines (d-f).
(f) shows the lines themselves, showing the effect of the lines’ orientations within the image, aiding detection of vertical posts.
More examples are shown in Fig. 11. Here, we
show the input image for clarity, plus the ground truth
segmentation which we are aiming for. The contri-
butions from vision (P-V), orientation (P-VO-Meta),
and lines (L-VO) to the final segmentation (PL-VO-
Cat) are shown. Figures 11(a) and 11(b) again show
orientation information being used to improve clas-
sifications, the latter being an interesting example
where adding lines improves segmentation even in the
presence of motion blur. Note that the different orien-
tations of the camera, such as in (c) and (d), mean that
using only position in the image as a prior would fail.
The segmentation in Fig. 11(e) also benefits from
classification of lines along the steps. Similarly in
Fig. 11(c) lines help in correctly identifying the step-
edges, but the step faces are classified as ground.
In a way this is correct, since stairs are made up
of periodic walkable regions, but this result would
be marked mostly incorrect compared to our ground
truth, which is labelled at a coarser resolution. This
echoes our comment in Section 4 about the world be-
ing ambiguous; but also that some regions may belong
to multiple classes simultaneously at different scales.
The example in 11(g) also shows orientation in-
formation being used to correctly identify the non-
ground surface; however, the addition of lines in this
case degrades the result. The final two rows show ex-
amples where our augmented algorithms fail to pro-
vide any benefit. In 11(h), the initial P-V segmenta-
tion is correct, and is unchanged by the addition of
orientation or lines (of course, if we could achieve
perfect segmentation, no amount of prior knowledge
would help). On the other hand, this illustrates why
it is so important that orientation does not impose a
hard constraint on surface identity: even when ori-
entation features are added, the grass (foliage class)
remains. In 11(i), none of the versions of the algo-
rithm are able to detect either the ground plane or the
foliage, perhaps due to the lower level of illumination.
Our implementation, comprising unoptimised
C++ code running on a Sony Vaio laptop (Intel i5,
2.40 GHz), processes one image in 1.7 seconds on
average (around 6 Hz). This is well below the cam-
era rate, but fast enough for some real-time use, when
moving at low speeds; further improvements could be
made by parallelising the code or using a GPU.
7 CONCLUSION
We have presented a way of combining information
about the real-world orientation of a camera, obtained
through inertial measurements, with more traditional
vision features, for an image segmentation algorithm.
This focused on our example application of scene seg-
mentation for locomotion in outdoor environments,
but we would expect the results to be applicable to
other types of classification, segmentation, scene un-
derstanding and image parsing tasks where the orien-
tation of the camera is likely to effect the likelihood of
observations. We have also shown that adding orien-
tation information is beneficial for line regions; and
that combining points and lines in a similar manner
can lead to some further improvement.
In our experiments it was not our intention to show
whether our method can compete with the state-of-
the art in image or scene segmentation, for example
(Gould et al., 2009) or (Domke, 2013). Rather, we
used a comparatively basic design of segmentation al-
gorithm to highlight the effect of using extra prior in-
formation, avoiding the complexity of advanced sta-
tistical techniques. An interesting avenue of further
research however to see how orientation priors can
be combined with powerful techniques such as condi-
tional random fields (Kr
¨
ahenb
¨
uhl and Koltun, 2011).
Other future work will look at ways to create more
accurate and detailed segmentations, and to imple-
ment this in a real-time setting. It would also be in-
teresting to combine this method with temporal in-
formation, enforcing consistency across frames; or to
combine with depth or 3D data.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
30

Input Ground Truth P-V P-VO-Meta L-VO-Cat PL-VO-Cat
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Figure 11: Example results of the various algorithms. After the input and ground truth, we show the baseline result, of points
with only vision features (P-V), followed by adding orientation information (P-VO-Meta). Detected and vision-classified
lines are shown, before the final result, combining everything (PL-VO-Cat).
UsingInertialDatatoEnhanceImageSegmentation-KnowingCameraOrientationCanImproveSegmentationofOutdoor
Scenes
31

ACKNOWLEDGEMENTS
This work was funded by the UK Engineering and
Physical Sciences Research Council (EP/J012025/1).
The authors would like to thank Austin Gregg-Smith
for advice on hardware and graphics, and Dr David
Hanwell for help with maths and text.
REFERENCES
Angelaki, D. and Cullen, K. (2008). Vestibular system: The
many facets of a multimodal sense. Annual Review of
Neuroscience, 31:125–150.
Bi, Y., Guan, J., and Bell, D. (2008). The combination of
multiple classifiers using an evidential reasoning ap-
proach. Artificial Intelligence, 172(15):1731–1751.
Bishop, C. (2006). Pattern Recognition and Machine
Learning. Springer.
Brock, M. and Kristensson, P. (2013). Supporting blind
navigation using depth sensing and sonification. In
Proc. Conf. Pervasive and ubiquitous computing ad-
junct publication.
Dahlkamp, H., Kaehler, A., Stavens, D., Thrun, S., and
Bradski, G. (2006). Self-supervised monocular road
detection in desert terrain. In Proc. Robotics Science
and Systems. Philadelphia.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In Proc. IEEE Conf.
Computer Vision and Pattern Recognition.
Delong, A., Osokin, A., Isack, H. N., and Boykov, Y.
(2012). Fast approximate energy minimization with
label costs. International journal of computer vision,
96(1):1–27.
Deshpande, N. and Patla, A. (2007). Visual–vestibular in-
teraction during goal directed locomotion: effects of
aging and blurring vision. Experimental brain re-
search, 176(1):43–53.
DeSouza, G. and Kak, A. (2002). Vision for mobile robot
navigation: A survey. IEEE Trans. Pattern Analysis
and Machine Intelligence, 24(2):237–267.
Domke, J. (2013). Learning graphical model parame-
ters with approximate marginal inference. IEEE
Trans. Pattern Analysis and Machine Intelligence,
35(10):2454.
Gould, S., Fulton, R., and Koller, D. (2009). Decomposing
a scene into geometric and semantically consistent re-
gions. In Proc. IEEE Int. Conf. Computer Vision.
Gupta, S., Arbel
´
aez, P., Girshick, R., and Malik, J.
(2014). Indoor scene understanding with rgb-d im-
ages: Bottom-up segmentation, object detection and
semantic segmentation. Int. Journal of Computer Vi-
sion, pages 1–17.
Haines, O. and Calway, A. (2012). Detecting planes and
estimating their orientation from a single image. In
Proc. British Machine Vision Conf.
Hoiem, D., Efros, A., and Hebert, M. (2007). Recovering
surface layout from an image. Int. Journal of Com-
puter Vision, 75(1):151–172.
Joshi, N., Kang, S., Zitnick, C., and Szeliski, R. (2010).
Image deblurring using inertial measurement sensors.
ACM Trans. Graphics, 29(4):30.
Kleiner, A. and Dornhege, C. (2007). Real-time localization
and elevation mapping within urban search and rescue
scenarios. Journal of Field Robotics, 24(8-9):723–
745.
Kr
¨
ahenb
¨
uhl, P. and Koltun, V. (2011). Efficient inference in
fully connected crfs with gaussian edge potentials. In
Advances in Neural Information Processing Systems,
pages 109–117.
Kundu, A., Li, Y., Dellaert, F., Li, F., and Rehg, J. (2014).
Joint semantic segmentation and 3d reconstruction
from monocular video. In Proc. European Conf. Com-
puter Vision.
Li, S. (2009). Markov Random Field Modeling in Image
Analysis. Springer-Verlag.
Lorch, O., Albert, A., Denk, J., Gerecke, M., Cupec, R.,
Seara, J., Gerth, W., and Schmidt, G. (2002). Experi-
ments in vision-guided biped walking. In Proc. IEEE
Int. Conf. Intelligent Robots and Systems.
Maimone, M., Cheng, Y., and Matthies, L. (2007). Two
years of visual odometry on the mars exploration
rovers. Journal of Field Robotics, 24(3):169–186.
N
¨
utzi, G., Weiss, S., Scaramuzza, D., and Siegwart, R.
(2011). Fusion of imu and vision for absolute scale
estimation in monocular slam. Journal of Intelligent
and Robotic Systems, 61(1-4):287–299.
Patla, A. (1997). Understanding the roles of vision in
the control of human locomotion. Gait & Posture,
5(1):54–69.
Pini
´
es, P., Lupton, T., Sukkarieh, S., and Tard
´
os, J. (2007).
Inertial aiding of inverse depth slam using a monoc-
ular camera. In Proc. IEEE Int. Conf. Robotics and
Automation.
Sadhukhan, D., Moore, C., and E., C. (2004). Terrain esti-
mation using internal sensors. In Proc. Int. Conf. on
Robotics and Applications.
Sturgess, P., Alahari, K., Ladicky, L., and Torr, P. (2009).
Combining appearance and structure from motion fea-
tures for road scene understanding. In Proc. British
Machine Vision Conf.
Tapu, R., Mocanu, B., and Zaharia, T. (2013). A computer
vision system that ensure the autonomous navigation
of blind people. In Proc. Conf. E-Health and Bioengi-
neering.
Virre, E. (1996). Virtual reality and the vestibular appara-
tus. Engineering in Medicine and Biology Magazine,
15(2):41–43.
Von Gioi, R., Jakubowicz, J., Morel, J., and Randall, G.
(2010). Lsd: A fast line segment detector with a false
detection control. IEEE Trans. Pattern Analysis and
Machine Intelligence, 32(4):722–732.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
32
