
A Nano-opto-mechanical Pressure Mapping Sensor via Bragg
Structure Waveguide for Biomedical Sensing
Xin Zhao
College of Physical Science and Technology, Sichuan University, China
Institute of Microelectronics, A*STAR (Agency for Science, Technology and Research), 11 Science Park Road, Science
Park II, Singapore117685, Singapore
School of Electrical & Electronic Engineering, Nanyang Technological University, Singapore 639798, Singapore
Keywords: Nano-electro-mechanical Systems, Bragg Structure Waveguide, Mapping Sensor.
Abstract: This paper reports a nano-opto-mechanical mapping sensor based on Bragg structure waveguide. The
pressure is measured by monitoring the output spectrum shift which is induced via mechanical deformation
of the period of the Bragg structure. In experiments, it measures that the shifting of the output spectra
linearly red shift under different position of the Bragg structure when the pressure is increasing. Compared
with traditional optical mapping sensor based on Mach-Zehnderinterferometer, the nano-opto-mechanical
mapping sensor has merits such as high sensitivity and fine resolution which are 1.55pm/kPa and 1.29kPa,
respectively. The nano-opto-mechanical mapping sensor has potential applications such as highly accurate
measurement of pressure waves, mass sensors array and bio-medical sensors.
1 INTRODUCTION
Optical pressure sensors have advantages such as
immunity to electromagnetic interference (EMI),
lightweight, small device scale, high sensitivity, and
ease in signal transmission, etc, compared with
electrical pressure sensors which are sensitive to
almost everything such as light, temperature,
pressure, electromagnetic (EM) field and humidity.
During the past thirty years, various ideas have been
developed based on optical pressure sensors. Most
of the optical pressure sensors are based on either
optical fibers, or single waveguide. However, optical
fibers pressure sensor occupy large area, the fibers
are not easy to be integrated with silicon based
photonic chips and cannot be fabricated using
standard complementary metal–oxide–
semiconductor (CMOS) technology. In MZI
structure pressure sensor, the waveguide branches or
3-dB directionalcouplers making the optical devices
long. The single waveguide pressure sensors need
additional input and output polarizers to form TM-
TE intermodal interference in a single-mode
waveguide. Single waveguide structure pressure
sensor as well as MZI structure pressure sensors
suffer from nonlinear optical intensity output.
Pressure sensors have been fabricated using many
different technologies such as glass, piezoelectric
quartz crystals, II–VI compound photoconductors,
and metal diaphragm. However silicon based
pressure sensors are most likely to be
commercialized due to their feasibility in mass
production and low cost. Although the introduction
of silicon cannot guarantee the improvements of the
performances, it definitely has great advantage in
producing micro-scaled or even nano-scale pressure
sensors which can be integrated in photonic circuits.
In this paper, the Bragg structure in silicon
waveguide is induced in the pressure sensor. A novel
nano-opto-mechanical pressure sensor based on
Bragg structure waveguide is proposed to provide a
reliable optical pressure sensor with high sensitivity,
good linearity of the output, CMOS compatibility
and ease in constructing sensors array.
2 DESIGN AND THEORETICAL
ANALYSIS
The design of the proposed pressure sensor is shown
in Fig. 1(a). The pressure sensor consists of a 820 ×
820 µm
2
diaphragm, five waveguides with Bragg
structure. The coordinate (0,0) is set at the center of
the diaphragm with the unit length as 1 μm. The
138
Zhao X..
A Nano-opto-mechanical Pressure Mapping Sensor via Bragg Structure Waveguide for Biomedical Sensing.
DOI: 10.5220/0005274101380143
In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2015), pages 138-143
ISBN: 978-989-758-071-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

centers of the Bragg structures are located at (0, 0),
(45, 45), (-45, -45), (84, -84), (-84, 84), respectively.
The period of the Bragg structure a is 0.6 µm. The
diameter of the hole d is 0.3 µm as shown in Fig.
1(b). The diaphragm consists of SiO
2
layer and Si
layer with thickness of 2 µm and 18 µm,
respectively as shown in Fig.1(c).
The pressure applied to the diaphragm causes the
shear stress displacement. The shear stress
displacement results in the change of the period of
the Bragg structure Δa as shown in the Fig 1(b). The
Δa influences the effective refractive index of the
Bragg structure Δn
eff
. Both the Δa and the Δn
eff
results in the resonant wavelength shift of the Bragg
structure Δλ. The Δλ could be read out from the
output spectrum of the waveguide. The pressure
applied to the diaphragm is detected by the Δλ.
(a)
(b)
(c)
Figure 1: (a) Schematic of the nano-opto-mechanical
pressure sensor, (b) Bragg structure, and (c) cross-section
of the pressure sensor.
2.1 Mechanical Design
The deformation of the diaphragm in x, y and z
direction is necessary to calculate the period change
of the Bragg structure Δa due to the applied pressure
on the diaphragm. The deflection of diaphragm
along z- direction w, the displacement along x-
direction u, and displacement along y- direction v
are the solution of the differential equation of
diaphragm are expressed as,
422
eq
P
ww
D
(1a)
2
2
12 1 1
2
2
22
uv w w
xx x y
h
(1b)
3
2
1
12 1
n
ii
eq
i
i
Eh
D
(1c)
where γ is the constant of integration, P is the
uniform pressure, D
eq
is the bending rigidity of the
equivalent single-layer, n is the number of the layer,
E
i
is the Young’s modulus of the i layer material, i
equate 1 or 2 in our design for SiO
2
layer or Si layer,
h
i
is the thickness of i layer, ν
i
is Poisson’s ratio of i
layer, h is the thickness of the whole diaphragm.
Finite Element Method is used to calculate the
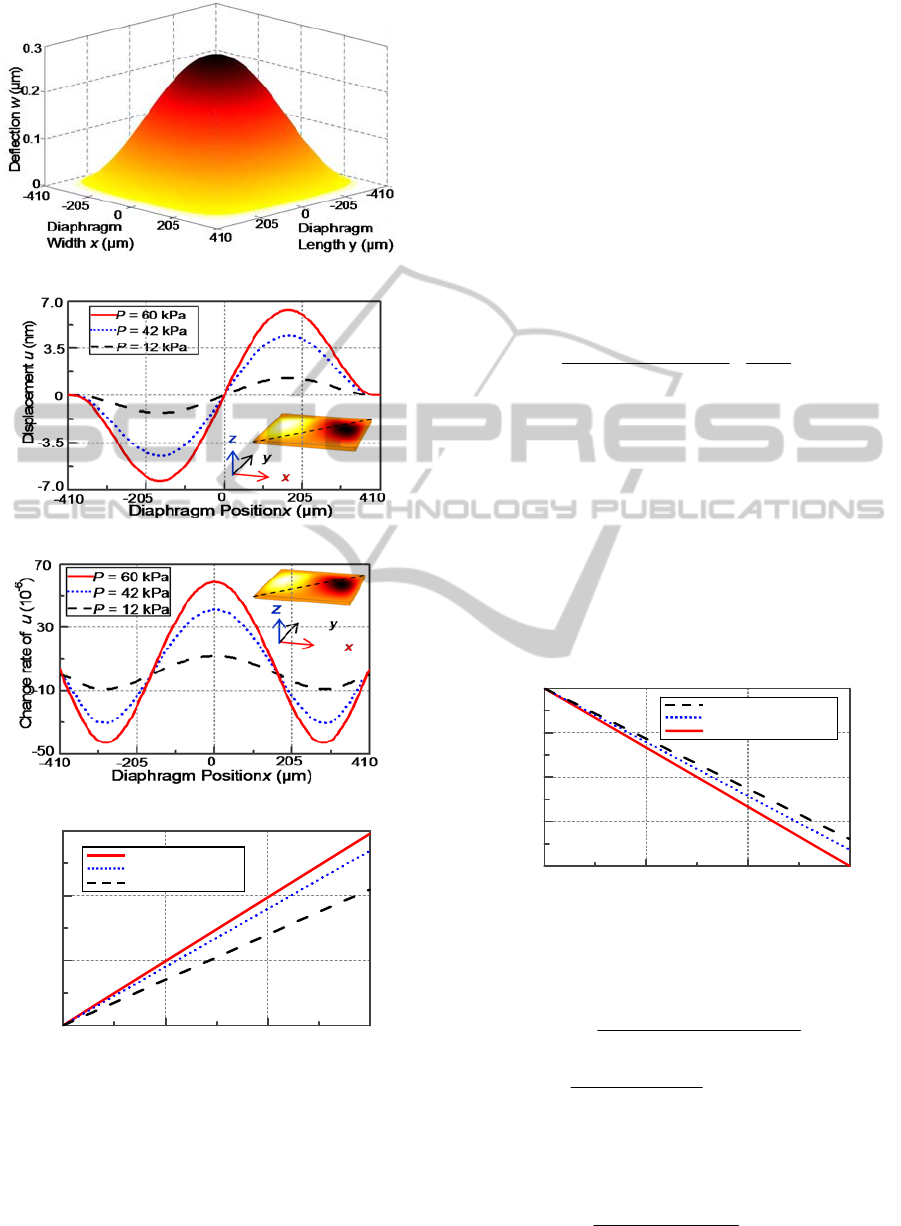
membrane deformation. Fig 2(a) shows the
deflection of diaphragm w along z-direction, when
the P is 60 kPa. Fig2(b) illustrates the displacement
along x direction u. The P is 12 kPa, 42 kPa, and 60
kPa, respectively. The diaphragm position is along
the diagonal of the diaphragm plane. Fig. 2(c) shows
the relation between the change rate of u and the
position of the diaphragm along diagonal of the
diaphragm. The change rate of u reaches the
maximum 58.9×10
-6
when the position of the
diaphragm is (0,0). The P is 12 kPa, 42 kPa, and 60
kPa, respectively. The thickness of the waveguide is
0.22 µm, which is much less than 20 µm. Therefore,
the shear stress of the diaphragm could influence
both the top and bottom edges of the air holes in the
Bragg structure. In this condition, the value of Δu
between edges of the two adjacent air holes equal to
Δa along x direction.
The relation between the Δa and P is shown in the
Fig 2(d). The Δa is proportional linearly to the
change of pressure ΔP for different position of the
Bragg structure.
1
aCP
(2)
where C
1
are 0.592 pm/kPa, 0.539 pm/kPa and 0.412
pm/kPa, respectively, when the centre position of the
Bragg structure are (0, 0), (45, 45), and (-84, 84) as
shown in Fig. 2 (d).
d = 0.3 a = 0.6
a+
Waveguide
Si
S
SiO
2
Dia
p
hra
g
m
ANano-opto-mechanicalPressureMappingSensorviaBraggStructureWaveguideforBiomedicalSensing
139
(a)
(b)
(c)
(d)
Figure 2: (a) The deflection along z-direction, and (b) the
displacement along x-direction of the diaphragm when the
applied pressure is 60 kPa. The different y value are 0 µm,
45 µm, and 84 µm, respectively. (c) The change rate of
displacement along x-direction (d) The period change of
Bragg structure Δa, when the centre position of the Bragg
structures are (0, 0), (45, 45), and (-84, 84). The applied
pressure is from 0 to 60kPa.
2.2 Optical Design
The pressure applied on the diaphragm can be read
out by the wavelength shift. The resonant
wavelength λ can be inferred from the following
equation based on the coupling condition of the
Bragg waveguide,
2
eff
na m
(3)
where m is the mode number. Calculated by the
Finite-difference-time-domain (FDTD) method, n
eff
is 2.6553, when a is 0.6 µm, and pressure is zero.
The resonant wavelength shift Δλ as a function of
Δn
eff
and Δa can be written as
2
2
eff eff
eff
nnaa
na
mm
(4)
The Δa causes the change of the horizontal hole
radius ratio to the lattice period r/a which results in
the change of the Bragg structure Δn
eff
. Calculated
by Finite Element Method, The relation between the
Δn
eff
and Δa can be written as:
2eff
nCa
(5)
where C
2
are -0.071
×
10
-6
/pm, -0.064
×
10
-6
/pm
and -0.060
×
10
-6
/pm, respectively, when the centre
position of the Bragg structure are (0, 0), (45, 45),
and (-84, 84) as shown in Fig. 3. The relation
between the Δn
eff
and Δa is linear.
Figure 3: Change of effective refractive index Δn
eff
due to
the change of period Δa.
The Eq. (4) can be expressed as:
2
2
eff eff eff
eff eff
na na na
m
na na
m
(6)
Δn
eff
Δa is 9.2
×
10
-17
which can be ignored. The
relationship between Δλ and P is obtained by
substituting Eq. (2) and Eq. (5) into Eq. (6).
112
3
2
eff
nC CCaP
CP
m
(7)
36
0 20 40
Pressure P(kPa)
Change of period Δa (pm)
12
0
24
0.592 pm/kPa
0.412
0.539
Position (0, 0)
Position
(
45
,
45
)
Position
(
-84
,
84
)
60
0
0
12
24
36
Change of period Δa (pm)
Δn
eff
(10
-6
)
-
1.28
-1.92
-
0.64
Position
(
45
,
45
)
Position
(
0
,
0
)
Position
(
-84, 84
)
-0.064×10
-6
/pm
-0.071×10
-6
/pm
-0.060 ×10
-6
/pm
-2.56
BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices
140

where C
3
= ∆λ/P is the sensitivity of the nano-opto-
mechanical pressure sensor, m is 2. Here, transverse
electric (TE) and transverse magnetic (TM) mode is
defined as the propagating mode with the electrical
field parallel and perpendicular to the diaphragm
plane, respectively. Only TE mode polarization
exists in the ring resonator and the bus waveguide
since the thickness of the waveguide is designed to
be smaller than the cutoff width of TM mode.
Therefore, n
eff
refers to the effective index of TE
mode only. The variation of n
eff
caused by the photo-
elastic effect is approximately 10
-7
which has trivial
effect, compared with the change of the period, on
Δλ.
3 EXPERIMENTAL RESULTS
AND DISCUSSIONS
The SEM images of the fabricated nano-opto-
mechanical pressure sensor are shown in Fig. 4. All
structures are fabricated on a standard silicon-on-
insulator (SOI) wafer with a silicon structure layer
of 220 nm. The thickness of silicon dioxide (SiO
2
)
layer and back side substrate is 2 µm and 720 µm,
respectively. The waveguide and the Bragg structure
are patterned by deep UV lithography, followed by
Reactive Ion Etching to transfer the photo resist
pattern into the silicon structure layer. Potassium
hydroxide (KOH) wet etching is used to form the
backside open of diaphragm with thickness of 20 µm.
For comparison, five different parameters are used
for the fabrication of the nano-opto-mechanical
pressure sensors which are the center position of the
Bragg structure: (0, 0), (45, 45), (-45, -45), (-84, 84),
and (84, -84).
(a)
Figure 4: SEM images of (a) pressure sensor, and (b)
zoom view of the Bragg structure.
(b)
Figure 4: SEM images of (a) pressure sensor, and (b)
zoom view of the Bragg structure (cont.).
Fig. 4(a) shows the overview of the pressure sensor
with a footprint of 1.8 mm × 1.8 mm which is the
same size as the etching window of backside open.
Fig. 4(b) shows the zoom view of the the Bragg
structure of the waveguide. The cross-section of the
Bragg structure is 800 nm × 220 nm. The period of
the Bragg structure is 0.6 µm. The diameter of the
air hole is 0.3 µm. These nano-scaled structures are
used to keep the single-mode propagation of the
light.
The nano-opto-mechanical pressure sensor is tested
by using the fiber-to-chip alignment system PS-1000
from SURUGA SEIKI CO.,LTD. The incident
broadband source is Amplified Spontaneous
Emission which has 8-mW output power over the
spectrum ranging from 1570 nm to 1608 nm. The
light is input from one end of the bus waveguide and
monitored from the other end using an optical
spectrum analyzer AP2052A from Apex
Technologies.
The output spectra of the nano-opto-mechanical
pressure sensor at different pressures applied to the
diaphragm is shown in Fig. 5(a). Here, the
diaphragm thickness is 20 µm. The measured
propagation loss of the waveguide is approximately
1.9 dB/cm. The resonance dip wavelength red shifts
from 1593.194 nm to 1593.287 nm when the
pressure on the diaphragm is increasing from 0 kPa
to 60 kPa. The quality factor of the resonance peak
is around 8.92×10
3
which is slightly broadened
because of the deformation of the ring resonator and
the bus waveguide induced by the pressure applied
to the diaphragm. Fig. 5(b) shows the wavelength
shift Δλ versus pressure P measured from three
different samples. The symbols and the lines
45
µ
m
84
µ
m
45
µ
m
84
µ
m
30 µm
Bragg waveguide
0.8 µm
0.3 µm
diameter
0.6 µm
period
0.3 µm
ANano-opto-mechanicalPressureMappingSensorviaBraggStructureWaveguideforBiomedicalSensing
141
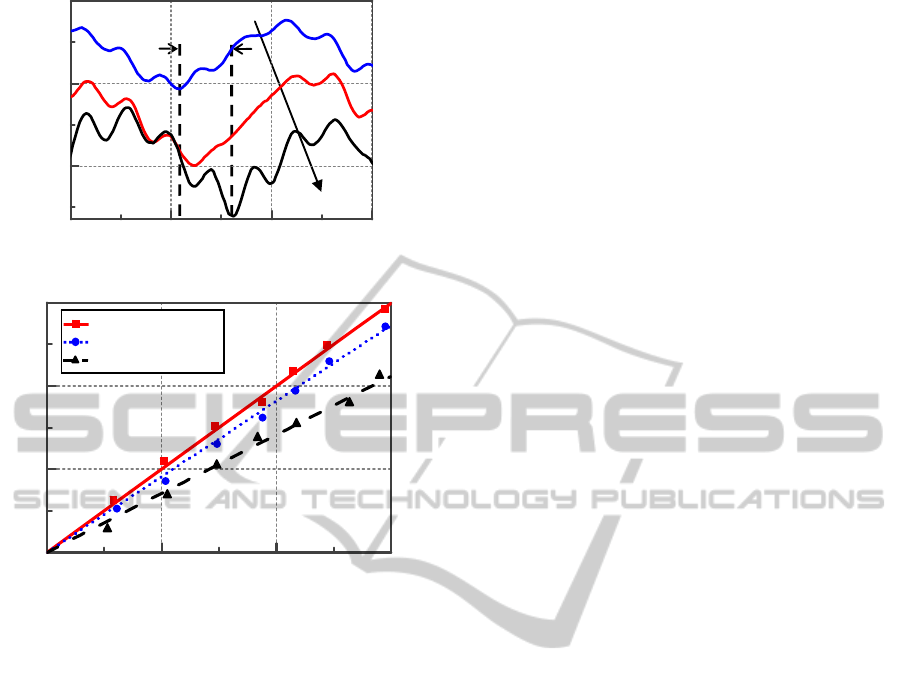
(a)
(b)
Figure 5: Transmission spectra at various applied
pressures on the diaphragm. The centre position of the
Bragg structures are (0, 0), and (b) wavelength shift
versus the pressure when the centre position of the Bragg
structure are (0, 0), (45, 45), and (-84, 84).
represent the measured and simulated results,
respectively. The solid, dotted and dashed line show
the Δλ as the function of P when the center position
of the Bragg structure is (0, 0), (45, 45), and (-84,
84), respectively which shows a good linearity
between the output of the pressure sensor and the
measured pressure. The slopes of the lines C
3
= Δλ/P
is equal to the sensitivity of the nano-opto-
mechanical pressure sensor. C
3
is 1.55×10
-3
nm/kPa,
when the center position of the Bragg structure is (0,
0) which is at least 1.42 times larger than that of the
(-84, 84). The resolution of the nano-opto-
mechanical pressure sensor is limited by the
resolution of the optical spectrum analyzer used in
the experiment. The optical spectrum analyzer
allows for a spectral resolution of approximately 2
pm. Consequently, the pressure resolution is 1.29
kPa which can be obtained by the Eq. (7).
4 CONCLUSIONS
In summary, a highly sensitive nano-opto-
mechanical pressure mapping sensor based on Bragg
structure is designed, fabricated and characterized
for pressures ranging from 0 kPa to 60 kPa. The
sensitivity as high as 1.55 pm/kPa has been
experimentally achieved which is in good agreement
with numerical prediction. The pressure sensor
structure make it possible to detect the shear stress
displacement distribution in highly accurate
measurement with low-cost advantages. The
characteristics indicate potential for various
applications such as mass sensor, bio-medical
sensors and optical integrated circuits etc.
REFERENCES
D. Donlagic and E. Cibula, 2005.All-fiber high-sensitivity
pressure sensor with SiO
2
diaphragm. Opt. Lett.
G. T. Kanellos, G. Papaioannou, D.Tsiokos, C.
Mitrogiannis, G. Nianios and N. Pleros, 2010.Two
dimensional polymer-embedded quasi-distributed
FBG pressure sensor for biomedical applications.
Opti. Express.
Y. C. Chao, W. J. Lai, C.Y. Chen, H. F. Meng, and H W
Zan, 2009."Low voltage active pressure sensor based
on polymer space-change-limited transisitor. Appl.
Phys. Lett.
M. Esashi, H. Komatsu, and T. Matsuo, 1983.Biomedical
pressure sensor using buried piezoresistors. Sens.
Actuators A.
C. S. Sander, J. W. Knutt and J. D. Meindl, 1980.A
monolithic capacitive pressure sensor with pulse-
period output.IEEE Trans. Electron Devices.
D. D. Bruyker, and R. Puers, 2000.Thermostatic control
for temperature compensation of a silicon pressure
sensor.Sens. Actuators A.
M. C. Oh, J. W. Kim, K. J. Kim, and S. S. Lee,
2009.Optical pressure sensors based on vertical
directional coupling with flexible polymer waveguides.
IEEE Photonics Technol. Lett.
M. Shimada, Y. Kinefuchi, and K. Takahashi,
2008.Sleeve-type ultra miniature optical fiber pressure
sensor fabricated by DRIE. IEEE Sensors J.
Y. Zhu and A. Wang, 2005.Miniature fiber-optic pressure
sensor, IEEE Photon. Technol. Lett.
B.J. Luff, J.S.Wilkinson, J. Piehler, U. Hollenbach, J.
Ingenhoff, N. Fabricius, 1998.Integrated optical
Mach–Zehnder biosensor. J. Light. Technol.
M. Ohkawa, M. Izutsu, and T. Sueta. 1989.Integrated
optic pressure sensor on silicon substrate, Appl. Opt.
N. Pelletier, B. Bêche, N. Tahani, J. Zyss, L. Camberlein,
and E.Gaviot, 2007.SU-8 waveguiding interferometric
micro-sensor for gage pressure measurement. Sens.
Actuators A.
1593
-45.0
-46.6
Output transmission (dBm)
60 kPa
0 kPa
1593
15931593
Wavelen
g
th
(
nm
)
0.093 nm
-40.0
-42.5
Pressure P
(
kPa
)
Wavelength shift (pm)
93
31
0
40
20 0
62
Position (0, 0)
Position (45, 45)
Position (-84, 84)
1.55 pm/kPa
1.09 pm/kPa
1.41 pm/kPa
60
BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices
142

Y. S. Hsu, L. Wang, W.-F. Liu, and Y. J. Chiang,
2006.Temperature compensation of optical fiber Bragg
grating pressure sensor. IEEE Photon.Technol. Lett.
T. H. Ning,1997.Trends in CMOS technology and
application development,Mater. Chem. Phys. W. P.
Eaton, and J. H. Smith.Micromachined pressure
sensors: review and recent developments. Smart
Mater. Struct.
X. P. Wu, M. F. Hu, J. Y. Shen and Q. H. Ma, 1993.A
miniature piezoresistive catheter pressure sensor. Sens.
Actuators A.
C. T. Peng, J. C. Lin, C. T. Lin and K. Ning. Chiang,
2005.Performance and package effect of a novel
piezoresisitive pressure sensor fabricated by front-side
etching technology. Sens. Actuators A.
M. T. C. Silva, and S. K. Manfrin, 1995.Silicon integrated
optical pressure sensor based on distributed Bragg
reflector structure. SPIE.
H. M. Berger, 1954.A new approach to the analysis of
large deflections of plates.
K. Okamoto, 2006.Fundamentals of optical waveguides.
Second edition.
ANano-opto-mechanicalPressureMappingSensorviaBraggStructureWaveguideforBiomedicalSensing
143
