
Mathematical Modelling and Numerical Simulations in Nerve
Conduction
N. J. Ford
1
, P. M. Lima
2
and P. M. Lumb
1
1
University of Chester, CH1 4BJ Chester, U.K.
2
Johannes Kepler University, 4040 Linz, Austria
Keywords:
Nerve Conduction, Myelinated Axon, Discrete FitzHugh-Nagumo Equation, Newton Method, Finite Differ-
ence Method.
Abstract:
In this paper we are concerned with the numerical solution of the discrete FitzHugh-Nagumo equation. This
equation describes the propagation of impulses across a myelinated axon. We analyse the asymptotic be-
haviour of the solutions of the considered equation and numerical approximations are computed by a new
algorithm, based on a finite difference scheme and on the Newton method. The efficiency of the method is
discussed and its performance is illustrated by a set of numerical examples.
1 INTRODUCTION
In the present work we analyse a functional-
differential equation, sometimes known as the dis-
crete FitzHugh-Nagumo equation, arising in nerve
conduction theory. The history of this equation began
in 1952, when A. Hodgkin and A. Huxley (Hodgkin
and Huxley, 1952) introduced a mathematical model
that describes the excitation and flow of electrical cur-
rent through the surface of a giant nerve fibre from a
squid. This investigation was continued in the works
of FitzHugh (FitzHugh, 1960), (FitzHugh, 1962) and
Nagumo (Nagumo et al., 1962).
During its evolution the FitzHugh-Nagumo equa-
tion has taken different forms. The case of myelinated
axons deserves special attention.
In a myelinated nerve axon the myelin completely
insulates the membrane, so that the potential change
jumps from node to node (pure saltatory condition).
According to Bell (Bell, 1984) two basic proper-
ties of the myelinated axon are the following:
• it possesses threshold behaviour; this means that
there are conditions which guarantee either the de-
cay of a solution (subthreshold response) or non-
decay of a solution (suprathreshold response);
• it is able to conduct pulses.
On the other hand, with the purpose of obtaining
a mathematical model that can be analysed and lead
to numerical solutions, some theoretical assumptions
have been imposed: a) the axon is infinite in extent, b)
the Ranvier nodes are identical and uniformly spaced;
c) the electric signals propagate with constant speed.
These assumptions make sense when considering the
propagation of signals not at the central, but at the
peripheral nervous system.
The mathematical model for myelinated axons de-
veloped in (Chi et al., 1986), based on these assump-
tions, leads to the discrete FitzHugh-Nagumo equa-
tions:
v
0
(t) = v(t + τ) − 2v(t) + v(t − τ)+
bv(t)(v(t) − 1)(α −v(t)),
(1)
where v(t) represents the potential at a Ranvier node
of the axon at the moment t (in this case, the poten-
tial at the neighbouring nodes is denoted by v(t − τ)
and v(t + τ); the constant τ is the time that a signal
takes to be transmitted from a node to the neighbour-
ing one (in other words, τ is inversely proportional
to the propagation speed of the signal). The constant
b reflects the resistance and the conductance in the
nerve axon, while α is the threshold potential.
From a mathematical point of view, an impor-
tant feature of equation (1) is that it contains both
negative and positive deviations of the argument (de-
layed and advanced terms); this is the reason why it
is called a mixed type functional differential equa-
tion (or an advance-delay-differential equation). Im-
portant contributions to the analysis of this type of
equation have been introduced in the literature in
the last two decades of the past century, by Rusti-
chini (Rustichini, 1989), Mallet-Paret and Verduyn-
283
J. Ford N., M. Lima P. and M. Lumb P..
Mathematical Modelling and Numerical Simulations in Nerve Conduction.
DOI: 10.5220/0005274702830288
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2015), pages 283-288
ISBN: 978-989-758-069-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Lunel (Mallet-Paret, 1999). More recently, Hupkes
and Verduyn-Lunel studied the behaviour of solu-
tions to nonlinear autonomous MTFDEs in the neigh-
bourhood of an equilibrium solution (Hupkes and
Verduyn-Lunel, 2007). Concerning boundary value
problems for MTFDEs, contributions to their analysis
and numerical methods for their solution have been
introduced in (Ford and Lumb, 2009), (Lima et al.,
2010) and (Ford et al., 2010). Computational meth-
ods for nonlinear MFTDEs, which includes equations
of the form (1), were introduced by Abell et al. (Abell
et al., 2005) and then by the authors of the present
paper in (Lima et al., 2013) and (Ford et al., 2014).
Comparing with previous contributions, the present
paper describes more robust and efficient methods,
which are able to produce accurate results for a wider
choice of the input parameters. The outline of this
paper is as follows. In section 2 we investigate the
asymptotic behaviour of solutions at infinity. In sec-
tion 3 we describe some computational methods used
for numerical approximation. In section 4 we provide
some numerical results and we finish with some con-
clusions in section 5.
2 BOUNDARY CONDITIONS AND
ASYMPTOTIC ANALYSIS
Let us rewrite equation (1) in the following form:
v
0
(t) = f (v(t)) + v(t −τ) − 2v(t)+ v(t + τ), (2)
where
f (v) = bv(v − α)(1 − v); (3)
this function is the nonlinear part of (2) and is called
the current voltage function. Due to the form of f ,
given by (3), equation (2) has two stable equilibrium
points: v = 0 (resting potential) and v = 1 (fully ac-
tivated potential). Therefore, we are interested in a
solution of (2), increasing on ] − ∞, ∞[, which satis-
fies the boundary conditions
lim
t→−∞
v(t) = 0, lim
t→+∞
v(t) = 1. (4)
These conditions will be satisfied by the potential at
any node. In order to guarantee uniqueness of solu-
tion, we add the condition
v(0) = 1/2. (5)
We are interested in a monotone solution of problem
(2)-(5), that is, we assume that once the signal starts
propagating, the potential will increase at every node,
tending to its maximal value (v(t) = 1). Such a so-
lution exists for a certain value of τ, which must be
computed. An extensive analysis of this behaviour
has been provided in (Chi et al., 1986), so here we will
just recall the main results from that paper. Based on
the Taylor expansion of f , as v tends to 0, we assume
that v has the form
v
−
(t) = ε
−
e
λ(t+L)
, (6)
where L is a sufficiently large parameter and ε
−
is
an estimate for v
−
(−L). In this way we obtain the
equation
λ + 2 − f
0
(0) − 2 cosh(λτ) = 0. (7)
This equation has two real roots; since we are inter-
ested in a function v
−
that tends to 0 at −∞, we choose
the positive one, which we denote by λ
+
.
The case where t → ∞ can be handled in an analo-
gous way. In this case, we assume that v has the form
v
+
(t) = 1 − ε
+
e
λ(t−L)
, (8)
where ε
+
is an estimate of 1 − v
+
(L). In this way we
obtain the characteristic equation
λ + 2 − f
0
(1) − 2 cosh(λτ) = 0 (9)
Here we choose the negative root of the characteris-
tic equation, which we will denote by λ
−
, in order to
have v
+
(t) → 1, as t → +∞.
Now we have obtained two representations for the
solution of our problem, (6) and (8), which we shall
use to approximate the solution, for t < −L and t > L,
respectively, where L is a sufficiently large number.
According to the form of equation (2), L must be a
multiple of the delay τ; in our computations we have
used L = kτ, where 2 ≤ k ≤ 9, depending on the spe-
cific problem (as discussed in Sec. 4).
These representations of the solution are used in
the computational methods to replace the boundary
conditions (4). In the next section we will show how
this can be achieved.
3 COMPUTATIONAL METHODS
In this section we will describe and compare some
computational methods that can be applied to obtain
approximate solutions of the problem (2), (4), (5).
Since the problem is nonlinear, some of the methods
considered require initial approximations, which must
be sufficiently close to the true solution, to guarantee
the convergence of the iterative process. Thus we be-
gin by presenting some preliminary results, which can
help us to build a rough approximation of the solution.
3.1 Finding an Initial Approximation
We now present an approach that results from ap-
proximating the solution by a piecewise differentiable
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
284

function. In this case, we search for an approximate
solution of the considered problem in the form
v
0
(t) =
ε
−
e
λ
+
(t+2τ)
, i f t < −2τ;
a
0
+ a
1
t + a
2
t
2
, i f − 2τ ≤ t < −τ;
1
2
+ b
1
t + b
2
t
2
+ b
3
t
3
, i f − τ ≤ t < 0;
1
2
+ c
1
t + c
2
t
2
+ c
3
t
3
i f 0 < t < τ;
d
0
+ d
1
t + d
2
t
2
, i f τ ≤ t < 2τ;
1 − ε
+
e
λ
−
(t−2τ)
, i f t ≥ 2τ;
(10)
From the form of v
0
if follows that this function
satisfies the boundary conditions (4) and (5). We
easily see that v
0
depends on 17 parameters: τ,ε
−
,
ε
+
,λ
−
,λ
+
, a
0
,a
1
,a
2
,b
1
,b
2
,b
3
,c
1
,c
2
,c
3
,d
0
,d
1
, d
2
. These
coefficients are computed from a system of 17 equa-
tions. (for details, see (Ford et al., 2014)). The nonlin-
ear system of equations can be solved by the Newton
method. Note that in this case the number of equa-
tions in the system is not so high as when we apply
the finite difference method, and therefore it is not so
difficult to find an initial approximation for the New-
ton method. For example, if we know the solution
for a cetain set of values a, b, we can use this soution
as initial approximation to solve the system and find
the solution for close values of a,b. The estimates
for λ
−
,λ
+
and τ from above can be used as initial ap-
proximations. As follows easily from the construc-
tion, v
0
∈ C
1
(IR). Some examples of application of
this approximation will also be given in section 4. As
we shall see, though these results have relative errors
which may attain 0.1, the corresponding approximate
solutions have the correct qualitative behaviour and
this explains that they provide good initial approxi-
mations for the more refined method we describe in
the next subsection.
3.2 A Finite Difference Approach
In this section we describe a finite difference scheme
for the solution of problem (2), (4), (5). This scheme
has some common features with the one described
in (Chi et al., 1986), but it has the advantage that it
can be easily solved by the Newton iterative method,
without using the continuation algorithm. As an ini-
tial approximation for the Newton method we have
used the function v
0
, defined by (10).
In order to approximate the solution we introduce
on [−Kτ,Kτ] a uniform mesh with stepsize h = τ/N.
Let t
i
= −Kτ + ih, i = 0, ...,2KN be the nodes of this
mesh. Here K is a sufficiently large integer so that
ε
1
= v(−Kτ) is comparable with h
2
(the reason for
this choice will be explained below). As in (Chi et al.,
1986), the first derivative is approximated by a 4-th
order finite difference:
v
0
(t
i
) ≈ L
h
(v)
i
=
1
h
2
3
(v(t
i+1
) − v(t
i−1
)) −
1
12
(v(t
i+2
) − v(t
i−2
))
.
(11)
By using this approximation at each node t
i
we obtain
2KN + 1 equations of the form:
L
h
(v)
i
= v(t
i
+ τ) + v(t
i
− τ) − 2v(t
i
) + f (v(t
i
)) + r
h
i
,
(12)
where kr
i
h
k = O(h
4
) . Note that for t
i
> (K − 1)τ and
t
i
< −(K −1)τ equation (12) involves the value of v at
one or more points that do not belong to the interval
[−Kτ, Kτ]. In this case the boundary conditions (4)
are applied, by considering the fact that v satisfies (6)
or (8), when v < −Kτ or v > Kτ, respectively. In this
way, we write
v(−Kτ − x) = v(−Kτ)e
−λ
+
x
, (x > 0), (13)
1 − v(Kτ + x) = (1 − v(Kτ))e
−λ
−
x
, (x > 0).
(14)
Finally, by ignoring r
h
i
in (12), we obtain (2K − 2)N
finite difference equations of the form:
L
h
(v)
i
= v
i+N
+ v
i−N
− 2v
i
+ f (v
i
), (15)
i = N + 1, ...,(2K − 1)N + 1.
Here as usual v
i
represents the approximate value
of v(t
i
). For 0 ≤ i < N + 1 and (2K − 1)N + 1 <
i ≤ 2KN + 1, we have modifications of equation (15)
which result from applying formulae (13) or (14), re-
spectively. This gives a system of 2KN + 1 equa-
tions, which is then completed with the equation
v
KN
= 1/2, resulting from (5). Moreover, we have
the characteristic equations (7) and (9), making a to-
tal of 2KN + 4 equations. Note that the number of
unknowns is also 2KN + 4: 2KN + 1 entries of the
vector v = (v
0
,...,v
2KN
) , λ
−
, λ
+
and τ.
This nonlinear system is then solved by the New-
ton method.
4 NUMERICAL RESULTS
We first compare the estimates of τ, λ
−
, and λ
+
, ob-
tained by the two methods described in Sec. 3. In
both cases we consider the problem (2), (4), (5). We
denote by τ
0
the estimate of τ obtained when using the
approximating function v
0
, defined by (10); τ
1
stands
for the value obtained by the finite difference method
with N = 64. Table 1 contains the values of τ
0
and τ
1
,
for b = 15, with different values of a. The values of
τ
0
and τ
1
, obtained in the case a = 0.05, for different
values of b, are displayed in Table 2.
The errors of τ
0
can be obtained by comparing
these estimates with τ
1
, which can be considered as
MathematicalModellingandNumericalSimulationsinNerveConduction
285

Table 1: Estimates of τ, λ
−
and λ
+
for different values of
a, with b = 15.
a τ
0
τ
1
λ
−
λ
+
0 0.3101 0.38029 −6.22752 5.1007
0.05 0.3461 0.43511 −5.44866 4.5111
0.1 0.3910 0.5056 −4.6909 3.9297
0.15 0.4485 0.5993 −3.95523 3.3586
0.2 0.5250 0.73001 −3.32594 2.6073
0.25 0.6318 0.92525 −2.55197 2.2691
0.3 0.7916 1.2515 −1.88069 1.66568
0.35 1.0575 1.9371 −1.2111 1.08772
Table 2: Estimates of τ, λ
−
and λ
+
for different values of
b, with a = 0.05.
b τ
0
τ
1
λ
−
λ
+
1 1.652 1.6250 −0.4333 0.4096
5 0.6639 0.7229 −2.0677 1.8678
11 0.4325 0.5008 −4.1869 3.5574
16 0.3296 0.4227 −5.7499 4.7354
21 0.2656 0.3744 −7.1795 5.7840
51 0.1216 0.1200 −14.0692 10.6338
the most accurate value for this purpose. Notice that
the presented values of τ
1
coincide with those ob-
tained in (Chi et al., 1986), within the given precision.
The approximate values of λ
−
and λ
+
obtained by
the finite difference method, with N = 64, are given
in the two last columns of the mentioned tables.
All the estimates preserve the main characteristics
of τ, as a function of a and b: they increase with a and
decrease as b increases. This behaviour agrees with
the physical meaning of the variables. Since a is the
threshold potential, the propagation speed is supposed
to decrease as a increases, and therefore we observe τ
increasing. On the other hand, increasing b means a
higher potential at the nodes and this leads to a greater
propagation speed and the decreasing of τ.
It is worth remarking that for values of a, greater
than 0.3 large discrepancies between the different es-
timates arise. This is connected with the numerical
instability of the different methods which is observed
for the values of a we considered. In particular, in
the case a ≥ 0.3, the value τ obtained by the finite
difference method seems to have a larger error than
the other approximations (and this does not arise else-
where). The explanation for this may be the instabil-
ity which is also visible in the graph of Figure 3. Note
that according to the available theoretical results, ex-
istence of a solution can be proved only for a < 0.5.
The accuracy of the results is also reduced for values
of b, greater than 21.
According to Keener (Keener, 1987), the discrete
Nagumo equation has a “propagation failure” for suf-
ficiently small coupling coefficient. When the equa-
tion is written in the form (2), a small coupling cor-
responds to high values of b. Thus when b is large
the problem (2),(4),(5) becomes unsolvable. This ex-
plains why for high values of b estimates obtained by
different methods differ signifficantly.
In Tables 3 and 4 numerical approximations for
v
0
(0), obtained by the two considered methods, are
given for a set of values of a and b. In agreement
with the notation used in Tables 1 and 2, we denote
by v
0
0
(0) (resp. v
0
1
(0)) the estimate obtained by the
method, corresponding to τ
0
(resp. τ
1
). In this case
the differences between the estimates obtained by dif-
ferent methods are not so large as in the case of the
evaluation of τ. Even for a > 0.3 or b > 21, these dif-
ferences are not greater than 5 per cent. This suggests
that the gradient of the solution at the origin is not so
sensitive to computational errors as the value of τ.
Table 3: Estimates of v
0
(0) for different values of b, with
a = 0.05.
b v
0
0
(0) v
0
1
(0)
1 0.1224 0.112695
5 0.6045 0.58339
11 1.2821 1.2774
16 1.83603 1.84116
21 2.39174 2.40116
51 5.7504 5.76174
Table 4: Estimates of v
0
(0) for different values of a, with
b = 15.
a v
0
0
(0) v
0
1
(0)
0 1.9171 1.9181
0.05 1.72515 1.72889
0.1 1.53326 1.53918
0.15 1.34141 1.34891
0.2 1.1496 1.1580
0.25 0.957907 0.96647
0.3 0.76624 0.774237
0.35 0.57463 0.58131
Note that, for all the approximations, the largest
errors occur close to t = 0, where the solution changes
faster. In this region the error can reach about 10 per
cent of the solution value.
We remark that by differentiating v
0
we obtain a
reasonable approximations of v
0
. The derivatives of
v
0
and v
1
are plotted in Figure 1.
We will now focus on the numerical results for
the problem (2)-(5), obtained by the finite difference
method. We have tested numerically the convergence
order of the method. When the exact solution is not
known, an estimate of the convergence order can be
obtained from three finite difference solutions, ob-
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
286
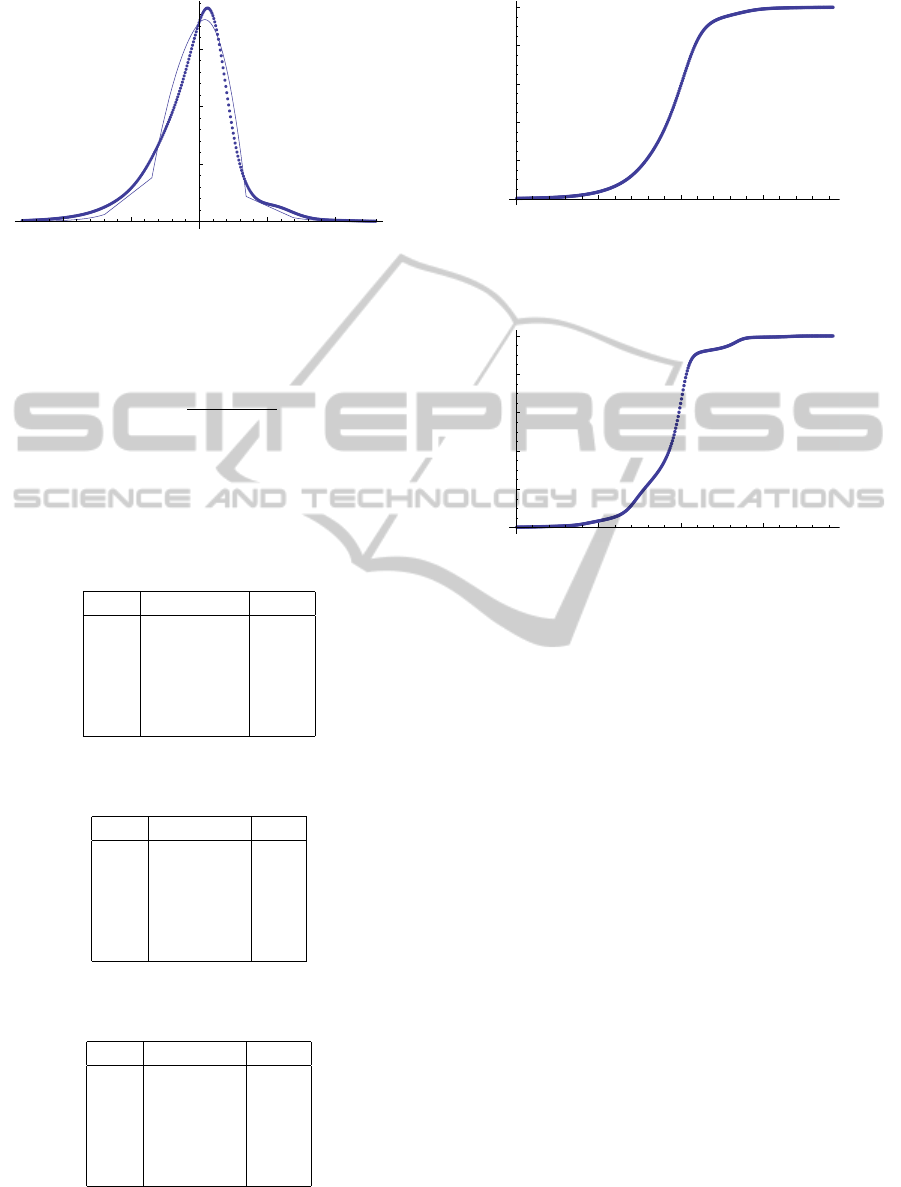
-1.0
-0.5
0.5
1.0
0.5
1.0
1.5
Figure 1: Approximation of the solution derivative: by the
finite difference method (thick line); using v
0
(thin line).
tained with different stepsizes: v
2h
,v
h
,v
h/2
, where
h > 0. The estimate of the convergence order is then
given by
p = log
2
kv
h
− v
2h
k
kv
h
− v
h/2
k
,
where the maximum norm is used. The numerical re-
sults displayed in Tables 5,6,7 suggest that the method
has 4-th order of convergence, as could be expected.
Table 5: Estimates of convergence order in the case a =
0.05,b = 5, with K = 9.
h kv
h
− v
2h
k p
τ/2
4
1.51E − 5 6.22
τ/2
5
2.03E − 7 3.981
τ/2
6
1.29E − 8 3.994
τ/2
7
0.07E − 10 3.998
τ/2
8
5.05E − 11
Table 6: Estimates of convergence order in the case a =
0.05,b = 15, with K = 6.
h kv
h
− v
2h
k p
τ/2
4
0.015 7.42
τ/2
5
8.80E − 5 5.11
τ/2
6
2.55E − 6 3.97
τ/2
7
1.63E − 7 3.99
τ/2
8
1.02E − 8
Table 7: Estimates of convergence order in the case a =
0.05,b = 21, with K = 6.
h kv
h
− v
2h
k p
τ/2
4
0.00041 6.518
τ/2
5
4.48E − 6 3.973
τ/2
6
2.85E − 7 3.992
τ/2
7
1.79E − 8 3.998
τ/2
8
1.12E − 9
The large differences between the estimates of τ,
obtained by the two methods, for certain values of a
100
200
300
0.2
0.4
0.6
0.8
1.0
Figure 2: Graph of the numerical solution obtained by the fi-
nite difference method with N = 64, in the case a = 0.1, b =
15. Here the numerical solution preserves the smoothness
of the true solution.
100
200
300
0.2
0.4
0.6
0.8
1.0
Figure 3: Graph of numerical solutions obtained by the
finite difference method with N = 64, in the cases a =
0.35,b = 15 (right side). Here the effect of numerical in-
stability is even mor evident than in the previous figure.
and b, suggest that some of the computational meth-
ods may become unstable for such values, in particu-
lar, when a is close to 0.5 or b is large. This is true, in
particular, in the case of the finite difference method,
as is shown by the graphs of the approximate solu-
tions plotted in Figures 2 and 3.
As mentioned in subsection 3.2, the finite differ-
ence method developed in this work was inspired by
the method described in (Chi et al., 1986) . However,
the algorithm described in that work relies on the con-
tinuation method, that is, a numerical solution is first
computed for a test problem and then, by a contin-
uous change of a parameter, a sequence of auxiliary
equations is solved, until reaching the target problem.
Possibly following on from this, the results reported
in (Chi et al., 1986) are limited to the cases where
a ≤ 0.2 and b ≤ 20. In our numerical experiments, the
initial approximations for the Newton method were
obtained by the numerical method described in sub-
section 3.1; this enabled us to solve the problem for a
wider range of values of a and b. Moreover, our algo-
rithm worked with stepsizes as small as 0.001, while
in the case of the numerical results reported in (Chi
et al., 1986) the typical stepsize was h = 0.05.
MathematicalModellingandNumericalSimulationsinNerveConduction
287

5 CONCLUSIONS
We have applied two computational approaches to the
solution of the problem (2)-(4), analysed and com-
pared the numerical results. The more accurate re-
sults are obtained by the finite difference method, de-
scribed in Sec. 3.2. The numerical results suggest
that this method has fourth order of convergence, as
it could be expected. Highly accurate results can
be obtained, within a reasonable computational ef-
fort, when the parameters satisfy 0 ≤ a < 0.3 and
5 ≤ b ≤ 51. However, for other values of the parame-
ters computational instability arises.
Another approximation method was discussed in
Sec. 3.1 . The computational effort required by this
method is very small and the algorithms are very sim-
ple. Although its accuracy is reduced, it can provide
good initial approximations for the finite difference
method.
The numerical results obtained in our paper con-
firm the main features of the considered mathematical
model. In particular, it was observed that the propa-
gation speed (1/τ) increases as the threshold potential
a decreases (see table 1) and as the intensity of the
ionic currents (represented by b) increases (see table
2). The typical S-shaped form of the solution graphic
(illustrated by figure 2) means that the potential value
changes slowly when it is close to its resting or fully
activated value; and changes fast, when it is close to
the average value. As a consequence, the solution
derivative takes its highest values when t is close to
0, and these values are particularly high when a is
small and b is large (as it follows from tables 3 and
4). In conclusion, the numerical results obtained by
the described methods can be useful for applications,
because they help to interpret experimental results on
the propagation of nervous signals through axons.
The proposed numerical techniques can be
easily extended to more general forms of the
Fitzhugh-Nagumo equations, in particular, systems
of differential-difference equations describing other
physical variables than the membrane potential (Bell,
1984). This will be the subject of future work.
ACKNOWLEDGEMENTS
P. M. Lima acknowledges support by a Marie Curie
Intra European Fellowship, through grant PIEF-GA-
2013-629496.
REFERENCES
Abell, K., Elmer, C., Humphries, A., and Vleck, E. V.
(2005). Computation of mixed type functional differ-
ential boundary value problems. SIAM J. Appl. Dyn.
Syst., 4:755–781.
Bell, J. (1984). Behaviour of some models of myeli-
nated axons. IMA Journal of Mathematics Applied in
Medicine and Biology, 1:149–167.
Chi, H., Bell, J., and B.Hassard (1986). Numerical solu-
tion of a nonlinear advance-delay-differential equa-
tion from nerve conduction theory. J. Math. Biol,
24:583–601.
FitzHugh, R. (1960). Impulses and physiological states in
theoretical models of nerve membrane. Biophysical
J., 1:445–466.
FitzHugh, R. (1962). Computation of impulse initiation and
saltatory condition in a myelinated nerve fiber. Bio-
physical J., 2:11–21.
Ford, N., Lima, P., and Lumb, P. (2014). Computational
methods for a mathematical model of propagation
of nerve impulses in myelinated axons. Appl. Num.
Math., 85:38–53.
Ford, N. and Lumb, P. (2009). Mixed-type functional dif-
ferental equations: a numerical approach. J. Comput.
Appl. Math., 229:471–479.
Ford, N., Lumb, P., Lima, P., and Teodoro, M. (2010).
The numerical solution of forward-backward equa-
tions: decomposition and related issues. J. Comput.
Appl. Math., 234:2745–2756.
Hodgkin, A. and Huxley, A. (1952). A quantitative descrip-
tion of nerve current and its application to conduction
and excitation in nerve. J. Phisiology, 117:500–544.
Hupkes, H. and Verduyn-Lunel, S. (2007). Center manifold
theory for functional differential equations of mixed
type. J. Dyn. Diff. Eq., 19:497–560.
Keener, J. (1987). Propagation and its failure in coupled
systems of discrete excitable cells. SIAM J. Appl.
Math., 47:556–572.
Lima, P., Teodoro, M., Ford, N., and Lumb, P. (2010).
Analytical and numerical investigation of mixed-type
functional differential equations. J. Comput. Appl.
Math., 234:2826–2837.
Lima, P., Teodoro, M., Ford, N., and Lumb, P. (2013). Anal-
ysis and computational approximation of a forward-
backward equation arising in nerve conduction. In
Differential and Difference Equations with Applica-
tions, pages 475–483. Springer.
Mallet-Paret, J. (1999). The fredholm alternative for func-
tional differential equations of mixed type,. J. Dyn.
Diff. Eq., 11:1–47.
Nagumo, J., Arimoto, S., and Yoshizawa, S. (1962). An
active pulse transmission line simulating nerve axon.
Proceedings of the IRE, 50:2051–2070.
Rustichini, A. (1989). Functional differential equations of
mixed type: the linear autonomous case. J. Dyn. Diff.
Eq., 1:121–143.
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
288
