Direct and Inverse Models of Human Arm Dynamics

Andr´e Ventura

, In´es Tejado

, Duarte Val´erio

and Jorge Martins

IDMEC, Instituto Superior T´ecnico, Universidade de Lisboa, Lisboa, Portugal

Industrial Engineering School, University of Extremadura, Badajoz, Spain

Keywords:

Human Arm Models, Surgical Robots, Fractional Calculus, Neural Networks.

Abstract:

This paper uses experimental data to model the human arm at the elbow joint. Direct models have been pub-

lished before; this papers addresses inverse models (i.e. relating the force at the hand with the arm angle).

Models used were integer, fractional commensurable and fractional non-commensurable order transfer func-

tions, as well as neural networks (used as a term of comparison). Results show the superiority of fractional

models, simpler, more exact, and with less parameter uncertainty.

1 INTRODUCTION

Dynamic models for the human arm are needed to

replicate its behaviour by a robot (Ta¨ıx et al., 2013;

Fu and Cavusoglu, 2012). And controlling a robotic

arm so that it will behave as much as possible as a

human arm is no idle experience. It seems to be a

good option for surgical robots (Park et al., 2006).

Such robots can achieve, if properly designed, per-

formances with an accuracy that represent a valuable

assistance even to the most seasoned surgeons. But,

for this to happen, the surgeon has to be comfortable

working with the robot, and that is where the repli-

cation of a human arm comes in. A robot that feels

more like another person’s hand has shown to be a

better companion than a robot with some other type

of behaviour.

Third-order linear models are a usual assumption

for this system; experimental data can be reasonably

ﬁtted, and there is furthermore a very reasonable ra-

tionale argument in favour of this structure, shown in

Figure 1. More accurate results can be obtained with

more complicated identiﬁcation techniques and struc-

tures (Adewusi et al., 2012; Nagarsheth et al., 2008;

Mobasser and Hashtrudi-Zaad, 2006; Venture et al.,

2006); whether this pays off or whether the simpler

linear option is better because it is good enough de-

pends, of course, on the intended use.

In a previous paper we presented fractional order

linear models for the human arm, obtained from ex-

perimental data with the measured force at the hand

as model input and the measured arm angle as out-

put, and compared them with the above mentioned

third order models (Tejado et al., 2013). There are

reasons to expect this type of models here, because

the dynamics of muscles of several animal species

(including humans) have been modelled using frac-

tional derivatives (Sommacal et al., 2008; Sommacal

et al., 2007b; Sommacal et al., 2007a; Djordjevic

et al., 2003), and because muscles show viscoelastic

behaviour, that can also be modelled using fractional

derivatives (Mainardi, 2010; Magin, 2004). In their

turn, fractional derivatives are expectable here given

the fractal nature of muscular tissue.

In this paper, we present inverse (i.e. using now

the measured arm angle as model input and the mea-

sured force at the hand as output) models for the hu-

man arm, using the same data from (Tejado et al.,

2013), comparing fractional and third order (integer)

linear models with neural networks. Neural networks

provide nonlinear models that often obtain excellent

performances (Jang et al., 1997; Nørgaard et al.,

2003; Haykin, 1999): hence the pertinency of the

comparison with fractional models, to see if they can

stand the test. Parameter variability is checked and

held as an important indicator of model suitability.

The contents of the paper are as follows: section 2

explains how data was obtained, and section 3 which

models were used. Then, section 4 presents the re-

sults, and section 5 offers comments and conclusions.

2 EXPERIMENTAL DATA

As mentioned above, the experimental data is that of

(Tejado et al., 2013); further details can be got in that

156

Ventura A., Tejado I., Valério D. and Martins J..

Direct and Inverse Models of Human Arm Dynamics.

DOI: 10.5220/0005276701560161

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2015), pages 156-161

ISBN: 978-989-758-071-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

force applied

by motor

position measured

by motor encoder

(analogous with

motor angle)

position analogous

with elbow angle

model of the arm

(mass–spring–damper)

model of the hand

(spring–damper; mass

assumed neglectable)

Figure 1: Third order translation analog to elbow dynamics.

paper.

Nine female and nine male volunteers, with ages

ranging from 25 to 66, without any known musculo-

skeletal injuries of the higher limbs, kneeled or sat

holding a horizontal robotic arm and tried to keep it

steady, while it moved randomly. The robotic arm

was moved by a Kollmorgen direct drive D061M-

23-1310 motor, able to produce 5.3 N·m continuous

torque and 16.9 N·m peak torque, in current con-

trol mode. The rotation range was limited to ±0.9

rad for safety reasons. The measured angle was ob-

tained from an encoder with a resolution of 65, 535

pulses/revolution. At the end of the aluminium hori-

zontal robotic arm there was a handle for the volun-

teers to grab, a JR3 12-degree-of-freedomDSP-based

force sensor, and a laser pointer which should be kept

inside a target. Data was recorded with a 2 kHz sam-

pling frequency.

Experiments (shown in Figure 2), which lasted

40 s to avoid fatigue, could be of three types:

• Type I — Oscillations in both directions around

the zero-point;

• Type II — Oscillations only in the positive side of

the zero-point (ﬂexion of the elbow);

• Type III — Oscillations only in the negative side

of the zero-point (extension of the elbow).

The oscillations were random to avoid anticipatory re-

ﬂexes, which would interfere with the modelling of

the arm dynamics. So the forces generated by the

motor were a sum of sinusoids with frequencies in the

[0.12, 15] Hz range (chosen because the bandwidthfor

the human arm is approximated to 10 Hz), limited to

not exceed 4 N. Eight voluntaries of either sex per-

formed two experiment of type I, one experiment for

type II, and one experiment for type III (68 data sets

in total). The two other voluntaries performed 16 ad-

ditional experiments: six of type I, seven of type II,

and seven of type III. The force measured by the men-

Figure 2: Robotic arm used to obtain experimental data of

human arm dynamics (Tejado et al., 2013).

tioned sensor was practically identical to the force in-

put.

3 TYPES OF MODELS

This section describes which models were used to ﬁnd

transfer function G

arm,inverse

(s) =

measured

(s)

θ(s)

, where θ

is the measured arm angle, F

measured

is the measured

force at the hand, and s is the Laplace transform vari-

able.

3.1 Third-order Integer Linear Models

These have already been mentioned in section 1, and

the reasoning behind their choice in Figure 1. The

identiﬁcation methods were the same described below

for fractional transfer functions, restricting differenti-

ation orders to natural numbers.

3.2 Fractional Linear Models

If initial conditions are zero, fractional derivatives,

denoted by

, α ∈ R, have Laplace transforms

given by L [

f(t)] = s

F(s). Consequently, from

a differential equation with fractional derivatives,

DirectandInverseModelsofHumanArmDynamics

157

fractional transfer functions arise. Those in which all

orders share a least common multiple (the commensu-

rability order) are called commensurate. Commensu-

rate transfer functions with a commensurability order

of 1 are integer transfer functions. Interested readers

can ﬁnd ample information on fractional derivatives

in several books and papers, among which (Val´erio

and S´a da Costa, 2013; Val´erio and S´a da Costa, 2011;

Podlubny, 1999; Miller and Ross, 1993; Samko et al.,

1993; Magin, 2004).

To identify a fractional transfer function from the

measured data, rather than using a method to do this

directly from a time response (Malti et al., 2008;

Val´erio and S´a da Costa, 2013), a frequency response

was estimated ﬁrst (using Welch’s method on the ﬁl-

tered output), and then Levy’s method was applied, as

this leads to less noisy results. Levy’s method ﬁts to

frequency response G( jω

), p = 1, . . . , f, a commen-

surable fractional model with a frequency response

given by

G( jω

) =

∑

k=0

( jω

)

kα

∑

k=1

( jω

)

kα

N( jω

)

D( jω

)

(1)

minimising (G( jω)D( jω) − N( jω))

(which is eas-

ier than the more obvious alternative of minimising



G( jω) −

N( jω)

D( jω)



, which leads to a nonlinear prob-

lem). Commensurable orders of fractional models

were found sweeping the α ∈ [0, 2] range (outside

which no transfer function is stable) with a 0.1 step,

and keeping the α for which results are better, using

a heuristic which is better described below in section

4 after performance indexes are introduced. For more

details on identiﬁcation procedures of transfer func-

tions for this plant, see (Tejado et al., 2013). Levy’s

method for fractional transfer functions is covered in

(Val´erio et al., 2008).

3.3 Neural Networks

The (artiﬁcial) neural network (NN) models used be-

low have a particular architecture—neural network

auto-regressive with exogenous inputs (NNARX)

models—represented in Figure 3. Notice how the

model dynamics appear through the delay operator

−1

to make use of past values of both the input and

the output of the system. Maximum input and out-

put delays, respectively m and n, determine the mem-

ory that the model has of the input and output signals.

Neurons are arranged in layers; as input, each neuron

i in layer n receives a signal y

n,i

that is a linear com-

bination of every output signal of the neurons in the

previous layer n− 1:

n,i

= b

n,i

n−1

∑

i=1

n−1,i

. (2)

Here x

n−1,i

is the ith input of the neuron coming from

the previous layer, w

n−1,i

is a weight associated with

that input, N

n−1

is the number of such inputs, and

n,i

is a bias. Obviously, layer number 0 (which does

not exist) corresponds to the neural network’s inputs

themselves. The neuron’s output x

n,i

is determined

by its transfer function f

n,i

, usually known as activa-

tion function. Activation functions may be transfer

functions, but if the neural network already includes

a dynamic elsewhere activation functions will proba-

bly be static; the hyperbolic tangent sigmoid function

n,i

= f

n,i

) =

1−e

−y

n,i

1+e

−y

n,i

is commonly used. Neural

networks employed below use the activation function

y(x) = x in the output layer; in other words, their out-

put is a biased linear combination of all the inputs.

For more details on neural network architecture, see

the references in section 1.

Training a neural network is an optimization pro-

cess in which weights w

n,i

and bias factors b

n,i

are

iteratively updated in order to minimize the mean

square error between the model output signals and

the output data. Numbers of delays m and n are to

be identiﬁed along with the weights and bias of the

neural network. For the system at stake NNARX,

models were trained using the Levenberg-Marquardt

backpropagation algorithm, chosen for speed and ac-

curacy. It is, actually, a local minimization method:

therefore it is not guaranteed that a global optimal

set of networks parameters is achieved. Because of

this and the fact that the algorithm initialization has a

random basis, the probability of two networks having

equal ﬁnal weights and biases is very low, even when

trained with the same data. The data, after being re-

sampled at 500 Hz (the robot’s communication fre-

quency), was then actually split into three parts: 60%

for training, 20% for validation, and 20% for testing.

The best results were consistently obtained for neu-

ral networks with 4 input delays, 2 output delays and

a single neuron in the hidden layer: this was thus the

conﬁguration chosen. Indeed, architectures with more

than one neuron in the hidden layer were tested, show-

ing insigniﬁcantly better or weaker overall results, de-

pending on the number of input and output delays. As

to the number of input and output delays, it was de-

termined as discussed below in section 4. That is why

only networks with a single neuron in the hidden layer

are considered below. (Mandic and Chambers, 2001;

Marquardt, 1963) further elaborate on neural network

training.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

158

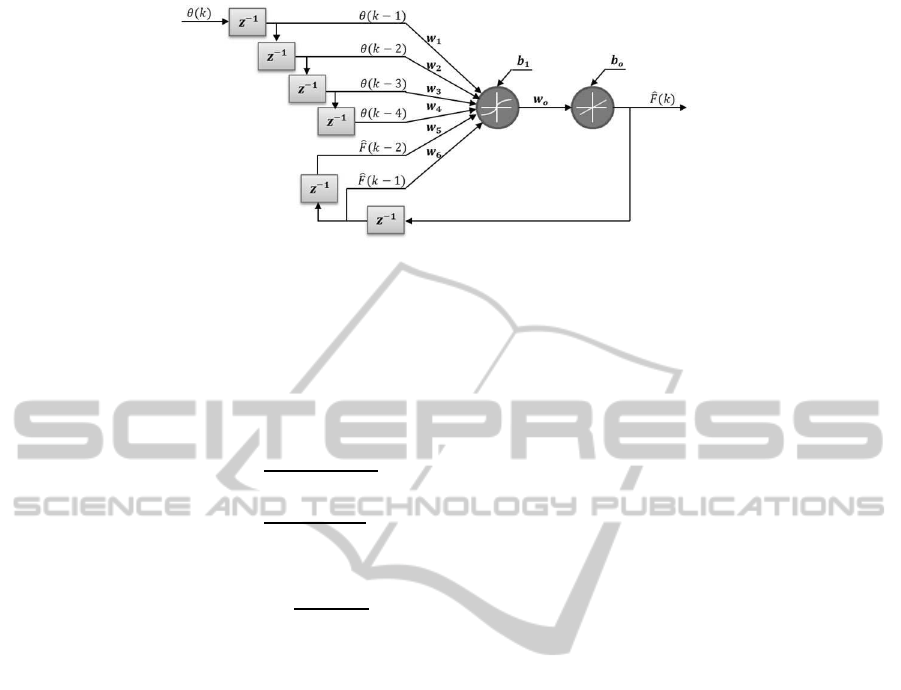
Figure 3: Neural network auto-regressive with exogenous inputs (NNARX) model, with one input and one output, one hidden

layer, n = 2 output delays and m = 4 input delays.

4 PERFORMANCE ASSESSMENT

Results were assessed with the following four perfor-

mance indexes:

Mean Squared Error, MSE =

∑

j=1

− ˆy

)

(3)

Mean Absolute Deviation, MAD =

∑

j=1

− ˆy

(4)

Maximum Deviation, MD = max

− ˆy

| (5)

Variance Accounted For, VAF = 1−

y−

(6)

The meaning of the variables for frequency and time

responses is shown in Table 1. With three series to

compare (gain, phase, time response) and four in-

dexes, there are in all 12 values to assess a model’s

performance.

Recall that in (Tejado et al., 2013) we have shown

that fractional models are better than integer order

models, inasmuch they achieve a performance which

is similar or even slightly better, with one parame-

ter less, and with clearly less parameter uncertainty.

Since identiﬁed integer direct models have 2 zeros

and 3 poles, inverse models with 3 poles and 3 ze-

ros were considered, as they ought to be causal. In

the case of fractional order models, the same princi-

ple as above was applied: since fractional order direct

models have 1 zero and 2 poles, causal inverse mod-

els with 2 zeros and 2 poles were considered. But this

time there is the commensurability factor. So, in a

ﬁrst stage, the best commensurable order was found

sweeping this factor in the [0.1, 1.9] range with a 0.1

step, keeping the model’s dynamical structure (2 ze-

ros and 2 poles). The output of this process is a set of

19 models to compare using the 12 aforementioned

performance indexes. The following heuristic, es-

sentially a multi-criteria optimisation algorithm, was

used to choose the commensurate order:

1. Initialize P = 12 lists with a length L = 1;

2. Select the best L models according to each perfor-

mance index;

3. Model by model, check for its presence in any

of the P lists with length L and compute a his-

togram that shows the number of presences of ev-

ery model in all the lists;

4. If one model is found to be present in every single

list, that is the best choice and the heuristic stops;

5. Otherwise, increment the value of L by 1 and re-

peat from step 2.

It may happen that more than one model comes to

appear at all P lists at the same time. In that case, ei-

ther may be selected as convenient. With this heuris-

tic a good value for the commensurability order may

be got, but a 0.1 step may be a little too rough, so

a second stage search was performed. In this stage,

the best model was found sweeping the commensu-

rable order, with a 0.01 step, in a range deﬁned by a

neighborhood, with a 0.1 radius, centred on the best

commensurability value (or values) obtained on the

ﬁrst stage. From this sweeping process, another set of

models arise and are, consequently, compared, again,

using the same heuristic. Therefore, this second stage

is essentially a reﬁned search around the best solution

(or solutions) of the ﬁrst stage.

In the case of NNARX models, training algo-

rithms are rather blind when it comes to the best val-

ues of m and n. Models with an unrealistically large

(and unnecessary) number of input and output delays

may still provide good results. So we might assume,

initially, an unrealistically large number of input and

output delays and analyze the corresponding weights,

comparing them to decide if m and n should be decre-

mented, until none of the weights is lower than a cer-

tain threshold value. But in this case it is possible to

use prior knowledge of the system to be identiﬁed,

assume a maximum value for the number of input

DirectandInverseModelsofHumanArmDynamics

159

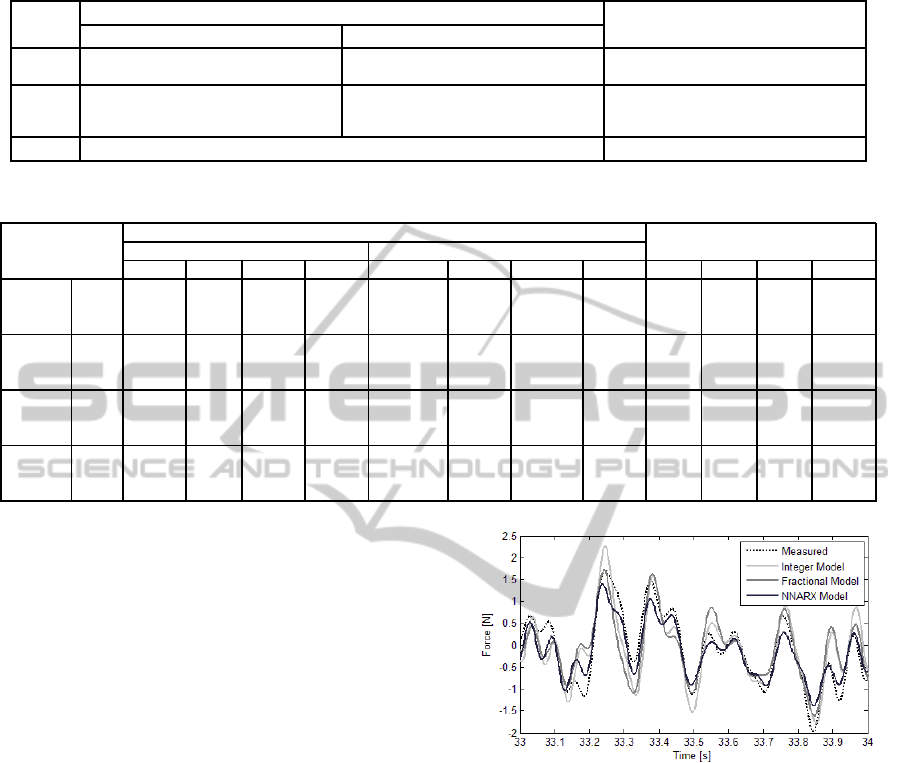
Table 1: Variables in equations (3)–(6).

Variables Frequency response Time

Gain Phase response

y Gain curve estimated from measured data for a

certain frequency vector

Phase curve estimated from measured data for a

certain frequency vector

Time series of measured input data

Gain curve estimated from measured input and

identiﬁed inverse model for the same frequency

vector of y

Phase curve estimated from measured input and

identiﬁed inverse model for the same frequency

vector of y

Time series of inverse model output

N Length of the frequency vector length, that must be the same for y

y and

y Length of the time series

Table 2: Performance comparison between identiﬁed inverse models of the human arm (best values in bold).

Frequency response Time response

Model Magnitude (dB) Phase (

◦

)

MSE MAS MD VAF MSE MAS MD VAF MSE MAS MD VAF

Int. 15.410 2.903 11.994 92.545 1007.274 28.486 69.760 74.125 0.272 0.371 1.819 41.508

All Frac. 21.632 3.455 14.352 88.903 628.689 18.032 58.400 86.449 0.266 0.354 1.658 47.888

NN 23.028 3.807 18.378 90.812 559.089 16.279 101.135 87.496 1.616 1.096 2.335 57.827

Int. 12.294 2.587 11.398 92.703 764.852 24.454 62.375 82.033 0.421 0.490 2.440 51.515

Type I Frac. 18.769 3.274 12.803 89.150 404.851 14.437 42.690 90.971 0.423 0.477 2.284 55.144

NN 25.354 4.094 14.948 90.574 467.089 16.026 76.924 88.489 0.286 0.415 2.001 63.803

Int. 15.315 2.842 12.230 93.656 1146.667 30.209 69.054 68.563 0.143 0.280 1.408 39.239

Type II Frac. 23.264 3.483 17.098 88.926 624.472 17.813 59.324 85.727 0.136 0.269 1.267 45.956

NN 22.443 3.908 14.337 93.456 920.851 17.971 157.716 81.771 0.086 0.227 1.086 57.492

Int. 16.032 3.089 10.971 93.165 1318.925 31.813 80.725 65.715 0.126 0.271 1.363 31.355

Type III Frac. 21.802 3.507 14.387 89.999 687.664 19.075 67.334 84.818 0.096 0.239 1.143 45.007

NN 24.498 4.129 12.308 93.450 647.907 17.872 128.764 84.132 0.098 0.250 1.041 54.529

and output delays and try every dynamical structural

combination within that maximum number of delays;

from this process, results a set of models that should

be compared, keeping the best one. It was shown

that linear inverse models are of 2nd or 3rd order, so

a maximum of 6 input and output delays was con-

sidered, to give some margin for possible additional

nonlinear dynamics to be identiﬁed in measured data.

With this maximum value, one gets a set of 36 neural

networks to compare and a heuristic similar to the one

described above for fractional plants was employed.

The only difference here is that, as mentioned previ-

ously, very complex networks can have slightly better

results, but at the cost of a lower computational ef-

ﬁciency. Therefore, to the 12 values of performance

indexes mentioned above, two more were added: m

and n themselves, thus providing for a neural network

which is a compromise between model performance

and model complexity.

5 COMMENTS AND

CONCLUSIONS

Performance results in Table 2 show that integer mod-

els often get better results in what the gain of the

transfer function is concerned, but not the phase, or

above all the time response; NN models, even though

nonlinear, do not consistently perform better, and,

Figure 4: Part of the responses of the several models, com-

pared with experimental data.

when they do, only slightly. Normalising all perfor-

mance indexes between 0 (worst) and 1 (best), and

averaging the results, we obtain the following results:

integer models, 0.6224; fractional models, 0.6847;

NNARX models, 0.3770. It can be seen that frac-

tional models achieve their performance being linear,

continuous (and thus ﬁt for every sampling time) and

using one parameter less than integer models. They

are thus the simplest possible model.

So again we ﬁnd a dynamic behaviour which we

can conclude is best described by fractional transfer

functions, just as was seen in (Tejado et al., 2013) for

direct models. Figure 4 shows some seconds of the re-

sponses obtained with the different models, compared

with experimental data.

Future work consists in using these models to

make a KUKA LWR 4+ 7–degree of freedom light

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

160

weight robot behave like a human arm, and check this

behaviour against the experimental data collected.

ACKNOWLEDGEMENTS

This work was partially supported by Fundac¸˜ao para

a Ciˆencia e a Tecnologia, through IDMEC under

LAETA, and under the joint Portuguese–Slovakian

project SK-PT-0025-12.

REFERENCES

Adewusi, S., Rakheja, S., and Marcotte, P. (2012). Biome-

chanical models of the human hand-arm to simulate

distributed biodynamic responses for different pos-

tures. International Journal of Industrial Ergonomics,

42(2):249–260.

Djordjevic, V. D., Jaric, J., Fabry, B., Fredberg, J. J., and

Stamenovic, D. (2003). Fractional derivatives embody

essential features of cell rheological behavior. Annals

of Biomedical Engineering, 31:692–699.

Fu, M. J. and Cavusoglu, M. C. (2012). Human-arm-and-

hand-dynamic model with variability analyses for a

stylus-based haptic interface. IEEE Transactions on

Systems, Man, and Cybernetics, Part B: Cybernetics,

PP(99):1–12.

Haykin, S. (1999). Neural Networks—A Comprehensive

Foundation. Prentice Hall International, Inc, New Jer-

sey, U.S.A., 2nd edition.

Jang, J.-S. R., Sun, C.-T., and Mizutani, E. (1997). Neuro-

fuzzy and soft computing. Prentice-Hall, Upper Saddle

River. chapters 8 to 11.

Magin, R. L. (2004). Fractional Calculus in Bioengineer-

ing. Begell House.

Mainardi, F. (2010). Fractional Calculus and Waves in Lin-

ear Viscoelasticity. An Introduction to Mathematical

Models. Imperial College Press, London.

Malti, R., Victor, S., and Oustaloup, A. (2008). Advances in

system identiﬁcation using fractional models. ASME

Journal of Computational and Nonlinear Dynamics,

3:021401–021401.

Mandic, D. and Chambers, J. (2001). Recurrent Neural Net-

works for Prediction—learning algorithms, architec-

tures and stability. John Wiley & Sons, LTD, Chich-

ester, England.

Marquardt, D. (1963). An algorithm for least squares es-

timation of nonlinear parameters. SIAM Journal on

Applied Mathematics, 11:431–441.

Miller, K. S. and Ross, B. (1993). An introduction to the

fractional calculus and fractional differential equa-

tions. John Wiley and Sons, New York.

Mobasser, F. and Hashtrudi-Zaad, K. (2006). A method for

online estimation of human arm dynamics. In Pro-

ceedings of th 28th Annual International Conference

of the IEEE Engineering in Medicine and Biology So-

ciety (EMBS’06), pages 2412–2416.

Nagarsheth, H., Savsani, P., and Patel, M. (2008). Modeling

and dynamics of human arm. In Proceedings of the

2008 IEEE International Conference on Automation

Science and Engineering (CASE’08), pages 924–928.

Nørgaard, M., Ravn, O., Poulsen, N. K., and Hansen,

L. K. (2003). Neural networks for modelling and con-

trol of dynamic systems: a practitioner’s handbook.

Springer-Verlag, London.

Park, S., Lim, H., Kim, B.-S., and Song, J.-B. (2006). De-

velopment of safe mechanism for surgical robots us-

ing equilibrium point control method. In Larsen, R.,

Nielsen, M., and Sporring, J., editors, MICCAI 2006,

pages 570–577. Springer Berlin / Heidelberg.

Podlubny, I. (1999). Fractional differential equations: an

introduction to fractional derivatives, fractional dif-

ferential equations, to methods of their solution and

some of their applications. Academic Press, San

Diego.

Samko, S. G., Kilbas, A. A., and Marichev, O. I. (1993).

Fractional integrals and derivatives. Gordon and

Breach, Yverdon.

Sommacal, L., Melchior, P., Cabelguen, J.-M., Oustaloup,

A., and Ijspeert, A. J. (2007a). Advances in Frac-

tional Calculus: Theoretical Developments and Ap-

plications in Physics and Engineering, chapter Frac-

tional Multimodels of the Gastrocnemius Muscle for

Tetanus Pattern, pages 271–285. Springer.

Sommacal, L., Melchior, P., Dossat, A., Petit, J., Ca-

belguen, J.-M., Oustaloup, A., and Ijspeert, A. J.

(2007b). Improvement of the muscle fractional mul-

timodel for low-rate stimulation. Biomedical Signal

Processing and Control, 2:226–233.

Sommacal, L., Melchior, P., Oustaloup, A., Cabelguen, J.-

M., and Ijspeert, A. J. (2008). Fractional multi-models

of the frog gastrocnemius muscle. Journal of Vibra-

tion and Control, 14(9-10):1415–1430.

Ta¨ıx, M., Tran, M. T., ares, P. S., and Guigon, E. (2013).

Generating human-like reaching movements with a

humanoid robot: A computational approach. Journal

of Computational Science, 4(4):269–284.

Tejado, I., Val´erio, D., Pires, P., and Martins, J. (2013).

Fractional order human arm dynamics with variabil-

ity analyses. Mechatronics, 23:805–812.

Val´erio, D., Ortigueira, M. D., and S´a da Costa, J. (2008).

Identifying a transfer function from a frequency re-

sponse. ASME Journal of Computational and Nonlin-

ear Dynamics, 3(2):021207–021207.

Val´erio, D. and S´a da Costa, J. (2011). An introduction

to single-input, single-output Fractional Control. IET

Control Theory & Applications, 5(8):1033–1057.

Val´erio, D. and S´a da Costa, J. (2013). An Introduction to

Fractional Control. IET.

Venture, G., Yamane, K., and Nakamura, Y. (2006). Identi-

ﬁcation of human musculo-tendon subject speciﬁc dy-

namics using musculo-skeletal computations and non

linear least square. In BioRob’06, pages 211–216.

DirectandInverseModelsofHumanArmDynamics

161