Fault Modeling of Implantable MEMS Sensors

J. A. Miguel

, Y. Lechuga

, M. Martinez

and J. R. Berrazueta

Microelectronics Group, TEISA Department, University of Cantabria, Avda de los Castros s/n, Santander, Spain

Department of Medicine, Faculty of Medicine, University of Cantabria, Avda de Valdecilla s/n, Santander, Spain

Keywords: MEMS Testing, Fault Injection, Biomedical Transducers, Implantable Biomedical Devices, Cardiology.

Abstract: The aim of this work is to analyse the fault-injection problem of implantable capacitive micro-electro-

mechanical pressure sensors intended to be used as a part of smart stents for in-stent restenosis monitoring.

The development of accurate fault models is mandatory in order to create a Design-for-Test methodology

compatible with MEMS-based sensors as well as with its related CMOS electronic circuitry. Rigorous

behavioural descriptions of both circular and square-shaped fault-free pressure sensors can be obtained from

analytical expressions and numerical approximations. However, the deflection vs. pressure response of

faulty sensors, suffering from contamination-based defects growth during the fabrication process, require

the use of finite-elements analysis to be modelled, allowing the fulfilment of a realistic fault model library.

1 INTRODUCTION

During the last decade, the fast development of

Micro-Electro-Mechanical Systems (MEMS), in

conjunction with the build-up of new fabrication

technologies compatible with CMOS processes has

made possible the production of heterogeneous

systems, integrating MEMS structures and electronic

circuits on the same silicon substrate. In this way, a

miniaturization of implantable electronic devices has

been achieved, increasing their capabilities and uses.

Nowadays, Atherosclerosis, affecting cardiac,

cerebral, renal or peripheral vascular vessels, is the

most prevalent disease in developed countries,

responsible for nearly 47% of deaths in Europe. The

related treatment costs reach about 9% of the total

healthcare expenditure from countries across the EU,

with inpatient hospital care comprising 49% of these

costs (Nichols et al., 2012).

Percutaneous Coronary Interventions (PCI),

allow an accurate diagnosis of obstructive lesions

using arteriography, as well as a reliable treatment

through balloon angioplasty, generally accompanied

by stenting. In Spain, nearly 124.000 diagnostic

coronary angiograms are performed annually. In

66.000 of these cases an angioplasty is performed,

and in 55.000 cases 100.000 stents are implanted,

trying to avoid restenosis, the most important

sequela of this technique (Garcia B. et al., 2013).

Severe and symptomatic carotid lesions have a

similar treatment by neuroradiologists. In general

population, total severe carotid stenosis is estimated

in less than 1%. However the prevalence of lesions

greater than 50% in population younger than 70

years is 4.8% in men and 2.2% in women, rising to

12.5% for males and 6.9% for women over 70 years

(Wolff T. et al., 2007).

The prevalence of lower extremity Peripheral

Artery Disease (PAD) ranges from 3% to 12%, with

202 million people affected in 2010 (Fowkes F.G. et

al., 2013). The annual incidence of critical ischemia

of the lower extremities varies from 500 to 1.000

new cases per million population, being higher for

patients with diabetes (Tendera M. et al., 2011).

During angioplasty, a flexible balloon catheter is

threaded into the blockage location and inflated,

applying a controlled pressure which compresses the

plaque deposition against the artery walls.

Angioplasty is usually accompanied by stents placed

surrounding the tip of the balloon catheter. Once the

balloon tip is inflated, the stent spring is opened and

attached to the vessel walls, remaining in place after

the balloon is deflated and removed. Thus, the stent

holds the vessel open, lessening the risk of re-

narrowing due to elastic recoils and spasms.

However, In-Stent Restenosis (ISR), a process of

neointimal tissue growth inside the stent, supposes a

major drawback to angioplasty reliability.

ISR monitoring is carried out nowadays using

expensive techniques, like angiography and

intravascular ultrasound. Smart stents, implantable

electronic devices able to sense and transmit real-

162

A. Miguel J., Lechuga Y., Martinez M. and R. Berrazueta J..

Fault Modeling of Implantable MEMS Sensors.

DOI: 10.5220/0005278801620167

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2015), pages 162-167

ISBN: 978-989-758-071-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

time data from physiological signals related to the

vessel condition, have positioned themselves as an

economic alternative to ISR follow-up.

Smart stents, as implantable electronic devices,

must fulfil certain design constraints, including

small size, low power requirements, output stability,

and reliability over time without recalibration. This

last challenge makes testing and fault modelling

critical issues to validate the fabricated device.

Generally, MEMS testing has been limited to a

set of electrical, optical and mechanical analyses,

used to check the functionality of the device.

However, the correlations between the detected

failures and their underlying physical causes are

usually missing. These relationships are needed to

allow an accurate modelling of complex fabrication

defects, and can be useful in the generation of

realistic faults models, as well as in the development

of capable testing techniques. For this reason, fault

models must include real defective behaviours in

order to reach high fault coverage and test quality.

This work focuses on the generation of a fault

model for an implantable MEMS capacitive pressure

sensor. Finite Elements (FE) tools have been proven

to be necessary to model those faults whose

complexity makes analytical descriptions inapt. The

results from FE analysis will give rise to a realistic

fault model library, and to the development of a

comprehensive Design-for-Test (DfT) methodology.

In Section 2, the most common failure

mechanisms affecting MEMS devices are described.

Section 3 introduces the proposed heterogeneous

system, focusing on the analytical modelling of its

MEMS sensors under fault-free conditions. Section

4 illustrates the need of FE analysis to model the

behaviour of MEMS sensors under the presence of

certain faults. Finally, in Section 5 conclusions are

presented.

2 MEMS FAULT CLASSES AND

FAILURE MECHANISMS

Several failure mechanisms or defects can appear

during the fabrication process of heterogeneous

devices, being possible to distinguish between

defects arising during the CMOS process and defects

occurring during micromachining.

Microelectronic and MEMS components can be

created on the same silicon substrate by means of a

set of conductor, semiconductor and dielectric

layers. Each one of the technological operations

used to grow these layers, such as oxidation,

deposition, photolithography or etching, is a

potential source of defects, where contaminants can

appear, degrading the succeeding fabrication steps.

In the particular case of CMOS-compatible

MEMS, failure mechanisms can be classified

according to the physical property being affected.

MEMS faults can be initially grouped into

parametric or catastrophic types, in the same way as

for analog testing. However, the nature of MEMS

devices gives rise to new types of manufacturing

defects, which require an extended classification

scheme. Thus, it is necessary to distinguish between

faults affecting the microsystem gauge and those

affecting the supporting structure. Each of these

faults can be again classified as a parametric fault,

changing the physical properties of the device and

altering its performance; or as a catastrophic fault,

preventing any use of the system.

In this work, the case of impurities appearing

during the anisotropic wet etching process used to

create diaphragms is analysed in detail. Impurities in

the form of small crystal lattice defects located in the

bulk material during this process can cause the

growth of pyramids on top of the diaphragm.

Depending on their size and location, these pyramids

can strongly change the properties of the diaphragm.

As can be seen in Fig. 1, the sidewall slope of the

pyramids is a fixed parameter which depends on the

angles between the main crystal planes of a single

silicon crystal. For instance, this slope presents a

value of 54.7º in the case of anisotropic wet etching

of a {100} oriented wafer, corresponding to the

angle between the {100} and {111} planes. It must

be noticed that the height of the pyramid can be

obtained from the sidewall slope, so a change in the

base length of the pyramid will alter its size (Rosing,

Reichenbach, Richardson, 2002) (Landsberger,

Nashed, Kahrizi, Paranjape, 1996).

Figure 1: Pyramid defect growth during anisotropic wet

etching process.

3 MEMS PRESSURE SENSOR

MODELLING

One of the simplest and more reliable smart stent

FaultModelingofImplantableMEMSSensors

163

designs for ISR monitoring is made up of two

MEMS capacitive pressure sensors attached at

opposite sides of a regular stent. In this way, the

pressure gradient along the device (implanted in a

distal pulmonary artery) can be measured and

wirelessly transmitted outside the patient body by

means of an LC tank formed by the sensors and the

body of the stent (Takahata, Gianchandani, Wise,

2006).

The proposed MEMS capacitive pressure sensor

to be included in the above-mentioned smart stent

can be split into two different parts: a fully-clamped

suspended flexible top diaphragm anchored to the

substrate, and a fixed back plate. The principle of

operation governing the behaviour of this kind of

sensors is based on the concept of a two parallel

plate capacitor, where the resultant capacitance is

inversely proportional to the distance between the

plates.

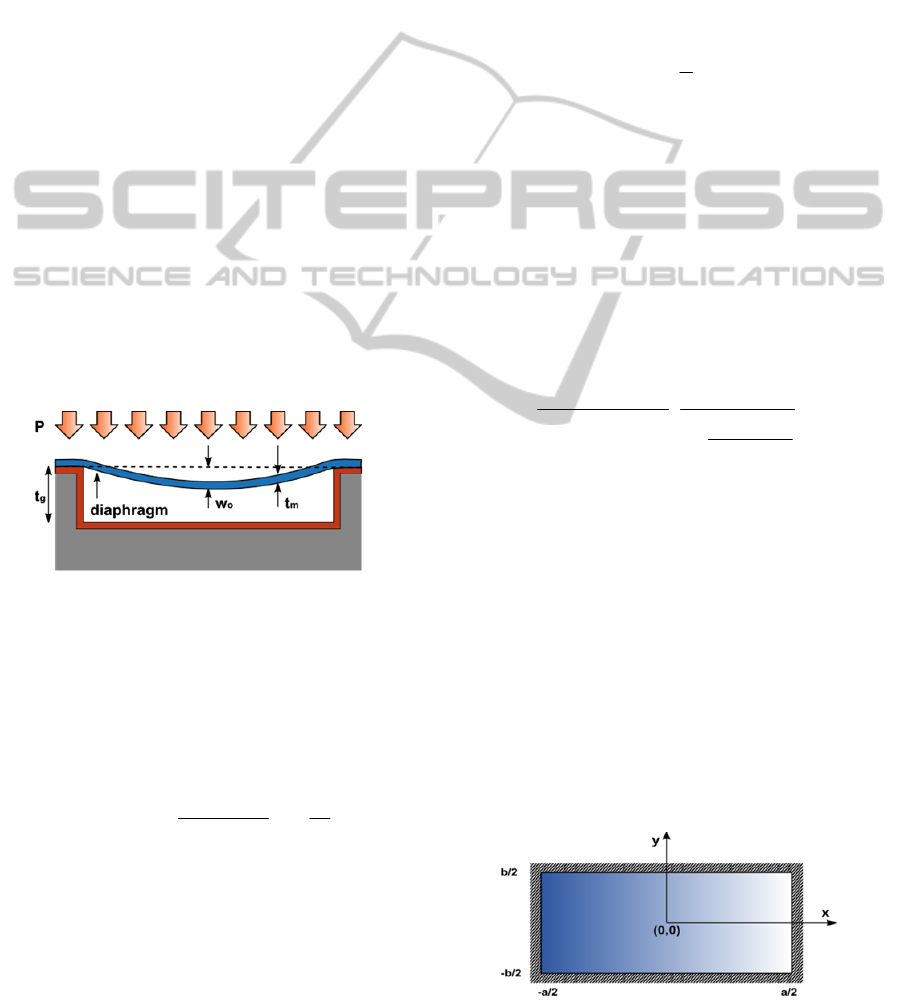
Fig. 2 shows a simplified cross-sectional view of

a MEMS capacitive pressure sensor with an air-

filled cavity. When a certain pressure P is uniformly

applied to the top plate, with a thickness t

, a

deflection is induced, reducing the initial gap t

between the plates and increasing the sensor

capacitance. The parameter w

refers to the

maximum deflection of the plate.

Figure 2: Cross-sectional view of a MEMS capacitive

pressure sensor.

The equivalent capacitance of a MEMS pressure

sensor can be analytically calculated by the

expression stated in (1), where C

is the capacitance

of the undeformed sensor, ε

is the dielectric

permittivity of the void, and A is the overlapped area

between both plates.

y)w(x,-t

dydxε

CCΔC 







(1)

3.1 Circular Sensor

An analytical behavioural modelling of a fully-

clamped diaphragm can be achieved only when

certain conditions are fulfilled: (a) the fabrication

material of the top diaphragm must have isotropic

mechanical properties; (b) the thickness of the

metallic electrode on the top plate is required to be

smaller than the thickness of the plate in order to be

neglected; (c) the initial gap between the plates must

be small compared to the lateral extents of the

plates, so that the influence of the field fringing

effects could be neglected; (d) the residual stresses

in the flexible diaphragm are not considered. Once

all the requirements have been met, the plate

deflection at radius r, of a fully clamped circular

diaphragm, can be expressed as:

1ww(r)



























(2)

Where r is the distance of the point of interest to

the centre of the diaphragm, a is the radius of the

diaphragm and w

is the maximum centre deflection.

Depending on the sensor deflection-to-thickness

ratio, the maximum centre displacement can be

analytically modelled using different expressions, as

described in (Timoshenko, Woinowsky-Krieger,

1959). The centre displacement vs. pressure

relationship for both small and large deflection

conditions can be approximated as (Timoshenko,

Woinowsky-Krieger, 1959):





w0.488

tE16

ν1aP3













(3)

Where P is the pressure applied to the

diaphragm, a is its radius, and υ and E are the

Poisson’s ratio and Young’s modulus of elasticity of

the diaphragm material respectively.

3.2 Rectangular Sensor

The deflection of a rectangular flexible diaphragm,

as shown in Fig. 3, can be analytically modelled by a

set of differential equations (4) and (5). Some

conditions have to be fulfilled to validate the model:

(a) the diaphragm must be fully clamped at its edges;

(b) the bending of the diaphragm must be elastic; (c)

the deflection has to remain smaller than half the

thickness of the diaphragm.

Figure 3: Coordinate system of a rectangular diaphragm.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

164

Thus, the fully clamped rectangular diaphragm

deflection vs. pressure relationship can be

approximated by the following differential equation

and its boundary conditions:

















(4)

y;x

0;y

y;xw

0;y





































































(5)

Where

)υ1(E2

υα





(6)

)υ1(12





(7)

and a, b, E, E

and υ are the diaphragm x-length

and y-length, the Young’s elasticity modulus, the

shear modulus and Poisson’s ratio, respectively.

The following changes in variable are introduced

to limit the integration domain to a square of unit

side:

1Y1;

1X1;



(8)

The system of differential equations can be

approximated via several mathematical methods.

The Galerkin method has been applied

(Timoshenko, Woinowsky-Krieger, 1959), leading

to the following analytical result:

)r,Y,X(fw)P,y,x(w





(9)

tD16

bak(r)







(10)











Y(r)Xk)Y)(1X(1

r)Y,f(X,

(11)

Where n is an even positive integer; i, j=0, 2, 4,

6, …, n; r=b/a; k(r) and k

(r) are tabulated shape

factors, whose values are shown in Table 1.

Table 1: Coefficients of the polynomial solution for a

rectangular fully clamped diaphragm.

r 1 2 3

k(r) 0.02019 0.01035 0.00469

k00 1 1 1

k20 0.233 0.01837 0.00510

k02 0.233 1.27 1.82

k22 0.252 0.195 -0.183

k40 -0.00166 -0.00253 -0.00033

k04 -0.00166 0.475 3.030

k42 0.13 0.00181 0.0306

k24 0.13 0.636 1.46

k44 -0.235 0.0495 0.0844

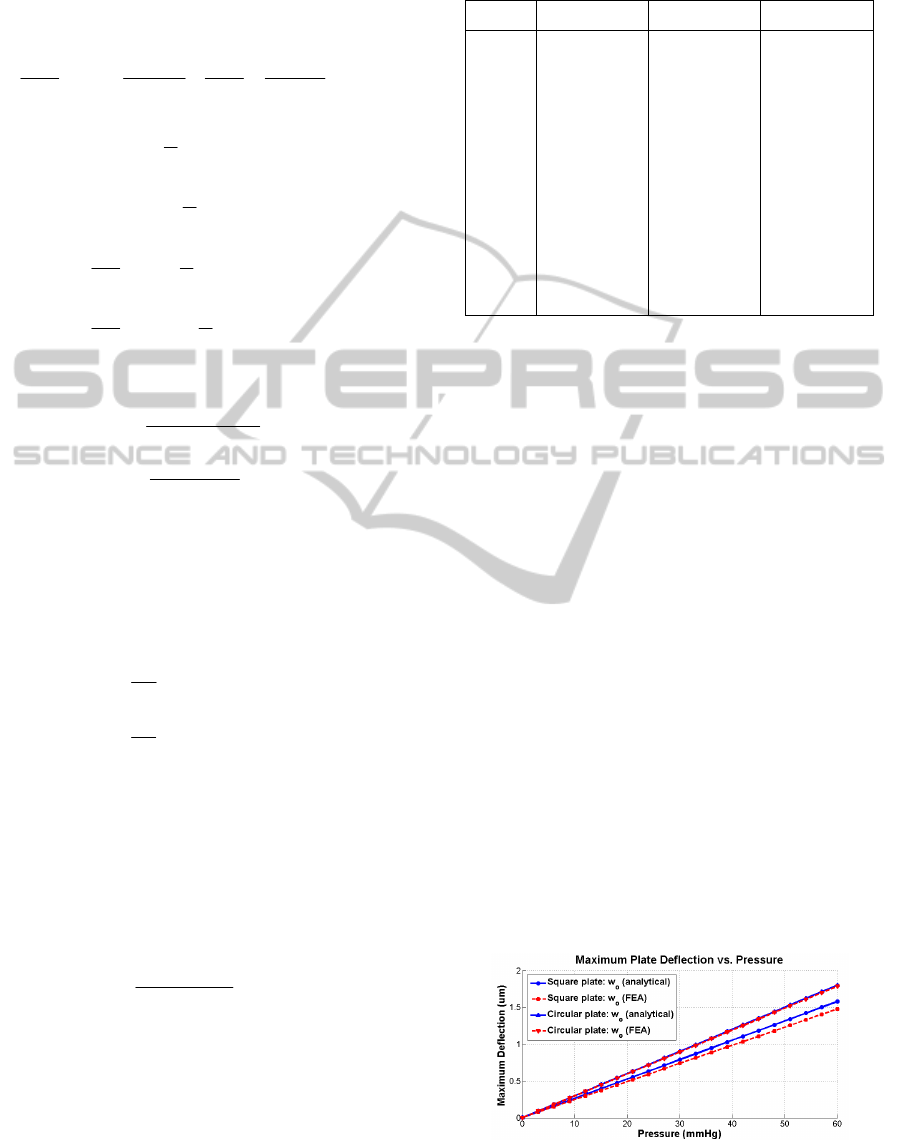
3.3 Results Comparison

A behavioural model for circular and square

diaphragms has been developed based on the

previously-mentioned analytical expressions. Both

sensors have been designed to present identical

capacitance for zero pressure difference between the

sealed cavity and the environment surrounding the

device.

The sensors are based on PolyMUMPs

technology provided by MEMSCAP. The diaphragm

is made of polysilicon (Young Elasticity Modulus:

E=169GPa; Poisson’s ratio: υ=0.22) with a thickness

of 4µm, and a 2µm gap between the plates, filled

with air sealed at ambient pressure. The circular

sensor presents a radius of 350µm, while the square-

shaped sensor has a side length of 620.35µm.

Pressures up to 60mmHg have been simulated,

corresponding to conditions of moderate stenosis.

These two sensors have been modelled in Ansys

. In

this way, it is possible to compare results from

analytical and FEA simulations, as shown in Fig. 4.

It can be noticed that in the case of a square sensor,

the error induced by the analytical formulation is

proportional to the pressure. This is explained

considering the numerical approximation used to

Figure 4: Analytical vs. FEA centre deflection response

for circular and square-shaped diaphragms.

FaultModelingofImplantableMEMSSensors

165

solve the differential equation in (4), so a certain

deviation is inevitable. Other numerical methods can

be used to enhance the accuracy of the model, at the

expense of higher complexity and computing times.

4 FE FAULT INJECTION

A complete library of accurate fault models, based

on real defects, needs to be developed to enable fault

simulations with a realistic estimation of the fault

coverage of the test method. The use of FE tools is

proposed to analyse the influence of defects

occurring during the fabrication or the lifetime of the

sensor. The detection and description of defects that

give rise to faults will ease the generation of an

electrical-compatible behavioural model where new

test methodologies could be evaluated.

In this case, FE models of fully-clamped circular

and square diaphragms have been built in Ansys

Defects with different sizes and locations have been

inserted on the top plate, where a uniformly

distributed pressure is applied. For each particular

fault, the capacitance and centre deflection are

measured, enabling the evaluation of their influence.

Pyramids grown during the anisotropic wet

etching process have been chosen as the case under

study. Fig. 5a and Fig. 5b show the capacitance

results for circular and square sensors respectively,

with pyramids of base areas up to 2500 µm

located

at the centre of their diaphragms. As expected, the

influence of a pyramid is proportional to its size,

with bigger pyramids compromising the reliability

of the sensor due to strong sensitivity losses. It can

be noticed that the sensitivity loss is higher for

circular plates (8.77% loss for a 50x50µm

pyramid)

than for their square counterparts (4.8% loss). In Fig

6a and Fig. 6b the capacitance results for both

sensors, under the influence of a pyramid of 50µm

base side placed at different locations, are shown. In

a fault-free case, the centre and anchoring locations

of a circular plate present the maximum bending

conditions. On the other hand, a square diaphragm

has its critical stress density spots located at its

centre, at its side midpoint (θ=0º) and at the

midpoint of the semi-diagonal of the plate (θ=45º).

The presence of rigid pyramids at these locations

prevents any bending of the plate, reducing the

sensitivity of the sensor.

In order to probe the accuracy of the simulation

results, several prototype PolyMUMPs capacitive

pressure sensors have been designed and fabricated.

These sensors have been conceived to be part of an

ISR monitoring smart stent device, designed to be

Figure 5a: Capacitance vs. pyramid base area: circular

sensor.

Figure 5b: Capacitance vs. pyramid base area: square

sensor.

Figure 6a: Capacitance vs. pyramid location: circular

sensor.

Figure 6b: Capacitance vs. pyramid location: square

sensor.

implanted in a distal ramification of the pulmonary

artery. Hence, the sensors must be capable of

bearing pressure ranges between light (Pmin =

30mmHg) to moderate (Pmax = 60mmHg) stenosis

conditions. Both fault-free (Fig. 7) and fault-injected

(Fig.8) sensors have been fabricated, and are

expected to be measured under in-vitro conditions

once coated with the biocompatible materials.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

166

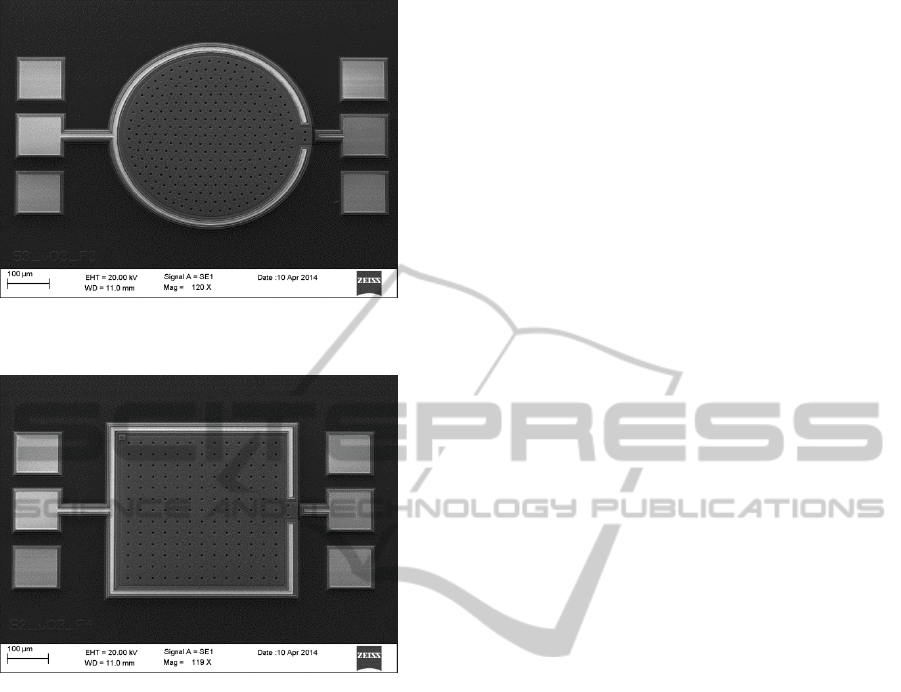
Figure 7: SEM picture of a fault-free PolyMUMPs circular

capacitive pressure sensor.

Figure 8: SEM picture of a fault-injected PolyMUMPs

square capacitive pressure sensor (injected fault located on

the top left corner of the sensor).

5 CONCLUSIONS

In this work, fault modelling problems affecting

MEMS capacitive pressure sensors for ISR detection

have been analysed. The most common failure

mechanisms and defects that generate faulty

behaviours have been introduced.

The deflection modelling of circular and

rectangular diaphragms has been proven to be

solvable via analytical expressions and numerical

approximations for the fault-free case. However,

these mathematical methods are no longer valid to

describe the behaviour of MEMS sensors under

certain faulty conditions, where their material

properties and geometry are affected. In order to

obtain a realistic fault model in all these cases, the

use of FE tools is required.

The development of a realistic fault model

library, as well as a comprehensive MEMS testing

approach, depends on the methodology extension of

to any other faulty conditions detected during

MEMS fabrication process and its useful lifetime.

REFERENCES

Nichols M. et al., Cardiovascular Disease Statistics 2012,

European Heart Network, Brussels. European Society

of Cardiology, Sophia Antipolis, 2012.

Garcia Blanco B. et al., Spanish Registry on Cardiac

Catheterization and Interventional Cardiology: XXII

Official Report of the Working Group on Cardiac

Catheterization and Interventional Cardiology of the

Spanish Society of Cardiology (1990-2012), Revista

Española de Cardiología, vol. 66, pp. 894-904, 2013.

Wolff T. et al., Screening for carotid artery stenosis: an

update of the evidence for the US Preventive Services

Task Force, Annals Internal Medicine, vol. 147,

pp.854-859, 2007.

Fowkes F.G. et al., Comparison of Global Estimates of

Prevalence and risk factors for peripheral artery

disease in 2000 and 2010: a systematic review and

analysis, Lancet, vol. 382, pp. 1329-1340, 2013.

Tendera M. et al., ESC Guidelines on the diagnosis and

treatment of peripheral artery diseases. Document

covering atherosclerotic disease of extracranial carotid

and vertebral, mesenteri, renal, upper and lower

extremity arteries: the Task Force on the Diagnosis

and Treatment of Peripheral Artery Diseases of the

European Society of Cardiology (ESC), European

Heart Journal, vol. 32, pp. 2851-906, 2011.

Rosing R., Reichenbach R., Richardson A., Generation of

component level fault models for MEMS,

Microelectronics Journal, vol. 33, pp. 861-868, 2002.

Landsberger L. M., Nashed S., Kahrizi M., Paranjape M.,

On Hillocks Generated During Anisotropic Etching of

Si in TMAH, Journal of Microelectromechanical

Systems, vol. 5, no. 2, pp. 106-116, 1996.

Takahata K., Gianchandani Y. B., Wise K.D.,

Micromachined antenna stents and cuffs for

monitoring intraluminal pressure and flow, Journal of

Microelectromechanical Systems, vol 15(5), pp. 1289-

1298, October 2006.

Timoshenko S., Woinowsky-Krieger S., Theory of Plates

and Shells, McGraw-Hill, New York, 1959.

FaultModelingofImplantableMEMSSensors

167