
High Dimensional Similarity Search
with Bundled Query Processing on Hilbert R-Tree
∗
Yohei Nasu
1
, Naoki Kishikawa
1†
, Kei Tashima
1‡
, Shin Kodama
1§
, Yasunobu Imamura
1
,
Takeshi Shinohara
1
, Kouichi Hirata
1
and Tetsuji Kuboyama
2
1
Department of Artificial Intelligence, Kyushu Institute of Technology, Kawazu 680-4, Iizuka 820-8502, Japan
2
Computer Center, Gakushuin University, Mejiro 1-5-1, Toshima, Tokyo 171-8588, Japan
Keywords:
High Dimensional Similarity Search, Bundled Query Processing, Hilbert R-tree.
Abstract:
Hilbert R-tree is an R-tree, which is a B-tree-like multiway balanced tree, such that data objects with high
dimensions are sorted along the Hilbert curve. In this paper, we first point out that the compact Hilbert
R-tree, which is a Hilbert R-tree without preserving Hilbert values, realizes the same performance as the
standard Hilbert R-tree, by using the Hilbert sort and the Hilbert merge. Then, to improve search time for high
dimensional objects in the compact Hilbert R-tree, we propose a bundled query processing. Furthermore, we
introduce two methods, the pre-processing by the Hilbert merge and the control for the order of visiting nodes.
From experimental results, we observe that, in the similarity search of sound and image data, the bundled
query processing is about 30% faster than the combinations of individual query processing.
1 INTRODUCTION
In information retrieval for multimedia data, it is a
general method to extract feature data from objects
and to construct hierarchical spatial index structure.
An R-tree (Guttman, 1984) is an extension of a B-
tree to treat high dimensional objects, and many vari-
ations of the R-tree have been developed (cf., (Samet,
2006)). Almost all of the variations have been de-
signed for a dynamic environment.
A Hilbert R-tree (Kamel and Faloutos, 1993;
Kamel and Faloutos, 1994) is an adequate R-tree for
high dimensional objects to impose a linear ordering
on the data along the Hilbert curve, which is one of
the space filling curves (Bader, 2013). The ordering
on nodes in an R-tree by using the Hilbert curve has
to be good, in the sense that it should group simi-
lar data rectangles together, to minimize the area and
perimeter of the resulting minimum bounding rectan-
gles (MBRs).
We can apply the Hilbert R-tree to both static and
∗
This work is partially supported by Grant-in-Aid
for Scientific Research 24240021, 24300060, 25540137,
26280085, 26280090 and 26370281 from the Ministry of
Education, Culture, Sports, Science and Technology, Japan.
†
Current affiliation: PFU Limited
‡
Current affiliation: Kumahira Co., Ltd.
§
Current affiliation: SCSK Cooporation
dynamic environment. In particular, to realize dy-
namic operations such as insertion or deletion of ob-
jects, every entry of the Hilbert R-tree has a Hilbert
value of an object. On the other hand, the explicit con-
struction of the Hilbert curve to obtain the Hilbert Val-
ues falls into the inefficient construction of the Hilbert
R-tree.
To solve this problem, in this paper, we adopt the
Hilbert sort introduced by Tanaka (Tanaka, 2001).
The Hilbert sort is a method which sort objects along
the Hilbert curve without constructing Hilbert curves
explicitly nor using Hilbert values. Furthermore,
Tashima (Tashima, 2011) has introduced a variation
of Hilbert R-tree without Hilbert values, which is
constructed by using the Hilbert sort, named com-
pact Hilbert R-tree. He has also designed the Hilbert
merge to realize the insertion of objects in the com-
pact Hilbert R-tree with the similar performance as
the standard Hilbert R-tree.
In this paper, to improve search time for high
dimensional objects in the compact Hilbert R-tree,
we propose a bundled query processing, which is
a method to reduce the IO costs to read nodes in
the compact Hilbert R-tree from files with spatial in-
dices. In particular, we introduce two effective meth-
ods into the bundled query processing, called the pre-
processing by the Hilbert merge and the control for
the order of visiting nodes. In the former, we com-
354
Nasu Y., Kishikawa N., Tashima K., Kodama S., Imamura Y., Shinohara T., Hirata K. and Kuboyama T..
High Dimensional Similarity Search with Bundled Query Processing on Hilbert R-Tree.
DOI: 10.5220/0005279503540359
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 354-359
ISBN: 978-989-758-076-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

pute data objects adjacent to queries along the Hilbert
curve, and then obtain the initial radius for each query
in the similarity search. In the latter, by computing the
minimum distances between the bundle of queries and
the nodes, we determine the order of visiting nodes.
Finally, as experiments, we apply the bundled
query processing to similarity search of image and
sound data. We observe that our bundled query pro-
cessing is faster than the combinations of individual
query processing about 30% for the search time.
This paper is organized as follows. In Sec-
tion 2, we introduce some notions for later discus-
sion. In Section 3, we explain the Hilbert curve,
the Hilbert sort, the compact Hilbert R-tree and the
Hilbert merge. In Section 4, we investigate the bun-
dled query processing for the compact Hilbert R-tree.
In Section 5, we give experimentalresults for the bun-
dled query processing. Section 6 concludes this paper.
2 PRELIMINARIES
Let U = R
N
be a space of objects, where R is the
set of real numbers and N is a dimension of objects.
Also let d : U × U → R
+
be a distance function on
U and D = (U, d) a distance space. In this paper,
we assume that d is a metric, that is, d satisfies the
following conditions for every x, y, z ∈ U.
1. d(x, y) ≥ 0.
2. d(x, y) = 0 ⇐⇒ x = y.
3. d(x, y) = d(y, x).
4. d(x, z) ≤ d(x, y) + d(y,z) (triangle inequality).
Let x, y ∈ U, where x = (x
1
, . . . , x
N
) and y =
(y
1
, . . . , y
N
). In this paper, as a distance func-
tion on U, we adopt the L
1
-distance d
1
(x, y) =
N
∑
i=1
|x
i
− y
i
|,which is more natural than L
2
-distance for
many multimedia data. We use Simple-Map (Shino-
hara and Ishizaka, 2002) as a dimension reduction
technique which is applicable to any metric.
In the similarity search in this paper, we use near-
est neighbor queries (NN-queries, for short). The
NN-query searches for an object in U nearest to a
given query (point) with respect to d
1
. In the imple-
mentation of NN-queries, we first set the radius r of a
query q to ∞ and then update r to the distance between
q and an object within the current radius r of q.
In NN-queries, it is not necessary to compute the
exact distances between a query q and objects out-
side the radius of q. In other words, for a query
q = (q
1
, . . . , q
N
) with the radius r and an object x =
(x
1
, . . . , x
N
), if there exists a K (1 ≤ K ≤ N) such that
K
∑
i=1
|q
i
− x
i
| > r, then it is not necessary to compute the
distance between q and x. Then, with incrementing K
from 1 to N, we can break off computing the distances
between q and x when the above inequality holds. By
using this method, we can reduce the number of com-
puting distances. In experimental results represented
in Section 5, we will use such breaking off computing
distances implicitly.
3 COMPACT HILBERT R-Tree
In this paper we adopt the compact Hilbert R-tee sup-
ported by two algorithms Hibert-sort (Tanaka, 2001)
and Hilbert-merge (Tashima, 2011), which are also
used in our algorithms for bundled query process-
ing. However, there are no English papers for them.
Therefore, here, we briefly introduce them.
3.1 Hilbert Curve
A space filling curve (Bader, 2013)visits all the points
in a high dimensional grid exactly once and never
crosses itself. The Hilbert curve (Bader, 2013; Butz,
1971; Lawder and King, 2001a; Lawder and King,
2001b) is one of the space filling curves. The Hilbert
curve of order 1 on a 2×2 grid is shown in Figure 1 in
2-dimensional case. To derive a curve of order i, each
vertex of the basic curve is replaced by the curve of
order i−1, which may be appropriately rotated and/or
reflected. Figure 1 also shows the Hilbert curves of
order 2 and 3. The Hilbert curve can be generalized
for higher dimensions.
order 1 order 2 order 3
Figure 1: The Hilbert curves in 2 dimension.
3.2 Hilbert Sort
For a space U with N dimension, we can construct the
Hilbert curve by repeating the procedure that divides
a subspace of U into 2
N
subspaces and then sorts ob-
jects recursively, until all of the objects are sorted. We
call the value representing the order of an object on
the Hilbert curve the Hilbert value of it. Then, for n
objects in U and the m division of U, we compute the
Hilbert value in O(n2
N
m) time (cf., (Bader, 2013)),
which is very expensive in general.
HighDimensionalSimilaritySearchwithBundledQueryProcessingonHilbertR-Tree
355
In order to solve this problem, Tanaka (Tanaka,
2001) has introduced the Hilbert sort, which is a
method to sort data objects with high dimensions
along the Hilbert curve, without constructing the
Hilbert curve explicitly. The Hilbert sort repeats the
procedure that divides a subspace of U into two for
some coordinate, not 2
N
subspaces, with dividing ob-
jects in subspaces, recursively, until a subspace con-
tains at most one object.
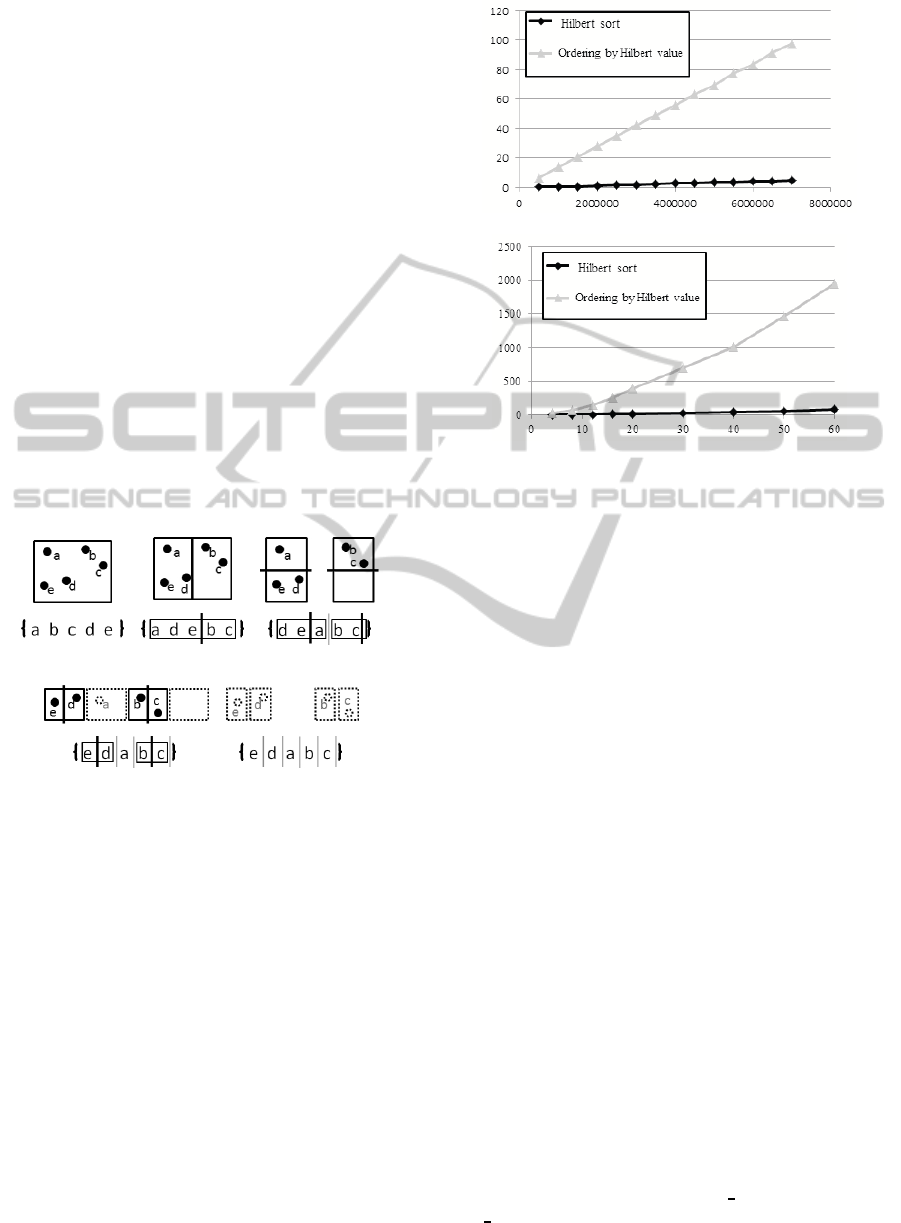
Figure 2 illustrates the running image of the
Hilbert sort applied to five objects from a to e in xy-
plane. In Step 1, the Hilbert sort divides a whole
space into two for the y-axis with dividing objects into
{a, d, e}, { b, c}. In Step 2, it divides two subspaces
containing {a, d, e} and {b, c} into two for the x-axis
with dividing objects into {d, e}, {a} and {b, c},
/
0, re-
spectively. In Step 3, it divides two subspaces con-
taining {d, e} and {b, c} into two for the y-axis with
dividing objects into {e}, {d} and {b}, {c}. Here, the
Hilbert sort halts the division of subspacesfor the sub-
spaces containing {a} and no object, illustrated by
dotted boxes in Step 3 and 4.
Initial state Step 1 Step 2
Step 3 Step 4
Figure 2: The running image of the Hilbert sort.
In contrast to the above O(n2
N
m) time, by using
the Hilbert sort, we can sort n objects in N dimen-
sional space in O(nNm
′
) time, where m
′
is the num-
ber of divisions such that m
′
< m in general. Figure 3
illustrates the running time (sec) of the Hilbert sort
(black line) and the ordering by Hilbert values (grey
line) when varying the number of data under fixed 8
dimensions (upper) and varying the number of dimen-
sions under fixed 7,000, 000 data (lower) pointed by
the x-axis. Hence, the Hilbert sort is more efficient
than the ordering by Hilbert values.
3.3 Compact Hilbert R-tree
The R-tree, introduced by Guttman (Guttman, 1984),
is an extension of the B-tree for high dimensional
objects. A geometric object is represented by its
minimum bounding rectangle (MBR). Then, internal
8 dimensions
7, 000,000 data
Figure 3: The running time of the Hilbert sort and the or-
dering by Hilbert values.
nodes in an R-tree contain entries of the form (R, ptr),
where ptr is a pointer to a child nodes in the R-tree
and R is the MBR that covers all rectangles in the
child nodes; leaf nodes contain entries of the form
(obj, R), where obj is a pointer to the object descrip-
tion and R is the MBR of the object. The R-tree is
known to be adequate to both static and dynamic en-
vironment (Guttman, 1984).
The Hilbert R-tree (Kamel and Faloutos, 1993;
Kamel and Faloutos, 1994) is an R-tree such that
data objects with high dimensions are sorted along the
Hilbert curve. Then, internal nodes in a Hilbert R-tree
contain entries of the form (R, ptr, LHV), where LHV
is the largest Hilbert value among the data rectangles
enclosed by R; leaf nodes contain entries of the form
(obj, HV), where HV is the Hilbert value of objects.
We can apply the Hilbert R-tree to both static and dy-
namic environment.
Note that, since the explicit construction of the
Hilbert curve to obtain the Hilbert values falls into the
inefficient construction of the Hilbert R-tree. On the
other hand, by using the Hilbert sort, we can construct
the Hilbert R-tree without constructing the Hilbert
curve explicitly.
The compact Hilbert R-tree, introduced by
Tashima (Tashima, 2011), is a Hilbert R-tree con-
structed from the Hilbert sort without using Hilbert
values. Internal nodes in a compact Hilbert R-tree
contain entries of the form (des
obj, R, ptr), where
des
obj is the leftmost object obj in the leftmost child
node; leaf nodes contain entries of the form (obj).
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
356

Figure 4: The compact Hilbert R-tree.
Figure 4 illustrates the outline of the compact
Hilbert R-tree omitting R and ptr. Here, every alpha-
bet from
A
to
Z
is an object such that the alphabetical
order coincides with the order along the Hilbert curve.
3.4 Hilbert Merge
The remained problem for the compact Hilbert R-
tree is to design the method for insertion of ob-
jects in the Hilbert R-tree with the similar perfor-
mance as the standard Hilbert R-tree. Also we can-
not apply the method of mass update to the Hilbert
R-tree, because the objects are stored by ordering
along the Hilbert curve. In order to solve these prob-
lems, Tashima (Tashima, 2011) introducedthe Hilbert
merge to insert a group of objects ordered by the
Hilbert sort in a mass like as merging leaf nodes in
the compact Hilbert R-tree.
We explain the Hilbert merge by us-
ing an example to insert a group
INS
=
{
ins 1
,
ins 2
,
ins 3
,
ins 4
,
ins 5
} of objects to
the compact Hilbert R-tree illustrated in Figure 4.
Here, suppose that INS is ordered by the Hilbert sort
from left to right. We call the order along the Hilbert
curve a Hilbert order simply.
In Step 1, the Hilbert merge adds
ins 1
to the left-
most descendant group {A, J, S} of objects in the node
(i) and determines the position of
ins 1
in the group
as the Hilbert order. As a result, suppose that the or-
der is given as {A, J,
ins 1
, S}. Then,
ins 1
is inserted
to the descendant nodes (viii), (ix) and (x) of
J
.
In Step 2, the Hilbert merge adds
S
as the right of
J
to
INS
and determines the position of
S
in
INS
as
the Hilbert order. As a result, suppose that the order
is given as {
ins 1
,
ins 2
,
ins 3
, S,
ins 4
,
ins 5
}. Then,
not only
ins 1
but also
ins 2
and
ins 3
are inserted to
the descendant nodes(viii), (ix) and (x) between
J
and
S
.
In Step 3, the group {
ins 1
,
ins 2
,
ins 3
} is sent
to the child node (iii) of
J
as the group of insertion
objects. Suppose that the Hilbert merge determines
the position of
ins 1
in the leftmost descendant group
{J, M, P} of objects in the node (iii) as {J,
ins 1
, M, P}.
In Step 4, the Hilbert merge determines the posi-
tion of
M
in {
ins 1
,
ins 2
,
ins 3
} as the Hilbert order
similar as Step 2.
As a result, suppose that the order is given as
{
ins 1
,
ins 2
, M,
ins 3
}. In this case, both
ins 1
and
ins 2
are inserted to the leaf node (viii).
The Hilbert merge has the following properties.
1. The Hilbert merge visits every node in the Hilbert
R-tree at most once.
2. The Hilbert merge arranges the MBR of a node in
the Hilbert R-tree after finishing the insertion to
all of its children nodes.
3. When it is necessary to divide a node in the
Hilbert R-tree, the Hilbert merge inserts the ob-
ject that the node is a child node to an upper level
in the Hilbert R-tree as a new object.
Hence, by using the Hilbert sort and the Hilbert
merge, the compact Hilbert R-tree realizes the same
performance as the standard Hilbert R-tree.
4 BUNDLED QUERY
PROCESSING
In the remainder of this paper, we call an NN-query a
query simply, and assume that a query is set to some
radius. In this section, we discuss the processing for
the bundle of queries, called a bundled query pro-
cessing, to search for high dimensional objects on the
compact Hilbert R-tree. In contrast, we call the com-
binations of query processing for every query in bun-
dles an individual processing.
In the remainder of this section, we denote the
bundle consisting of queries q
1
, . . . , q
n
by hq
1
, . . . , q
n
i.
For a bundle Q of queries and a query q
i
, we denote
that Q contains q
i
by q
i
∈ Q. Also we denote the ra-
dius of q
i
by r
i
.
HighDimensionalSimilaritySearchwithBundledQueryProcessingonHilbertR-Tree
357

4.1 Naive Bundled Query Processing
In the naive bundled query processing, the bundle of
queries visits nodes in the compact Hilbert R-tree by
using the depth-first search from the root node. Note
that naive processing does not consider the order of
visiting nodes.
When Q visits an internal node whose entry is
(des
obj, R, ptr), we determine whether q
i
∈ R for ev-
ery q
i
∈ Q, and, if such a q
i
exists, then Q visits the
children of the node. When Q visits a leaf node whose
entry is (obj), we compute the distance d(o, q
i
) be-
tween each o ∈ obj and each q
i
∈ Q, and, if the radius
r
i
of q
i
is greater than d
i
= min{d(o, q
i
) | o ∈ obj},
then we set r
i
to d
i
.
The number of visiting nodes in the naive bundled
query processing is much smaller than one in the in-
dividual processing. Hence, the naive bundled query
processing reduces the IO costs for reading files.
4.2 Pre-processing by Hilbert Merge
On the other hand, the number of distance com-
putaions in the naive bundled query processing is pos-
sible to be larger than one in the individual process-
ing. To avoid this situation, we introduce the pre-
processing by the Hilbert merge, which follows from
the following two properties.
1. Two objects such that one is near to the other in
the Hilbert order are that one is near to the other
in a space of objects with high probability. Hence,
an object near to a query within the Hilbert order
is contained in the radius of the query with high
probability.
2. By using the Hilbert merge, we can insert the
group of objects to the nodes in the Hilbert order
simultaneously.
In the pre-processing by Hilbert merge, first we
sort the bundle Q of queries in the Hilbert order by us-
ing the Hilbert sort. Next, we simultaneously search
for nodes where each query q
i
∈ Q is inserted by using
the Hilbert merge. Then, after computing distances
d(o, q
i
) between each q
i
∈ Q and each o ∈ obj in the
searched leaf node whose entry is (obj), we set the
initial radius r
i
of q
i
to min{d(o, q
i
) | o ∈ obj}.
Hence, the number of distance computaions in the
bundled query processing with the pre-processing by
the Hilbert merge is smaller than one in the naivebun-
dled query processing.
4.3 Control for the Order of Visiting
Nodes
In order to reduce the number of distance com-
putaions, in the bundled query processing, we control
the order of visiting nodes in the compact Hilbert R-
tree as similar as the R-tree, by using the ABL (Active
Branch List) L.
When Q visits an internal node, we determine
whether or not Q must visit its child nodes, and, if
so, then we insert the set C of such child nodes to L.
Here, let Q
′
be a sub-bundle Q
′
of Q which will visit
C and R
c
an MBR of c ∈ C. Then, C in L is sorted by
ascending order of min{d(q
i
, R
c
) | q
i
∈ Q
′
}. Hence,
by visiting nodes in the first element of L, Q can visit
a node c ∈ L such that d(q
i
, R
c
) is minimum for every
q
i
∈ Q.
5 EXPERIMENTAL RESULTS
In this section, we give experimental results for the
bundled query processing in similarity search on the
compact Hilbert tree.
For image data, data objects consist of about
7, 000, 000 pictures extracted from about 2, 800 video
data whose features have 64 dimensions, and queries
consist of 90, 000 pictures extracted from 100 video
data. On the other hand, for sound data, data ob-
jects consist of about 7, 000, 000 sound fragments ex-
tracted from about 1, 500 musical data whose features
are 96 dimensions and queries consist of 90, 000 frag-
ments extracted from 30 musical data. Here, 90, 000
queries consist of near queries to far queries. Queries
is not intended to completely match in the database.
The number of queries in bundles varies 10, 100 and
1, 000. The computer environment is Intel Core i7-
3770 3.40GHz CPU with 16GB RAM.
Table 1 and 2 describe the results of the bundled
query processing for image data and sound data, re-
spectively. Here, #queries, #nodes and #distance de-
note the number of queries in bundles, the number of
visiting nodes and the number of distance computa-
tions, respectively. The individual processing adopts
the pre-processing of the Hilbert merge and the con-
trol for the order of visiting nodes.
As shown in row (3) in Table 1 and 2, in the bun-
dled query processing with the control for the order
of visiting nodes, increasing the number of queries
decreases the number of visiting nodes, as well as in
rows (1) and (2). Also, the search time is shortest
when the number of queries in bundles is 100, not
1, 000, for both image data and sound data.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
358

Table 1: The results for image data.
method #queries #nodes #distance search time
(min)
(0) individual processing @ 1.11× 10
9
5.99× 10
10
138.17
(1) naive bundled 10 3.50× 10
8
1.33× 10
11
196.07
query processing
100 5.45× 10
7
1.33× 10
11
187.60
1,000 6.39× 10
6
1.33× 10
11
186.32
(2) (1) with 10 2.93× 10
8
9.34× 10
10
135.87
pre-processing
100 5.11× 10
7
9.34× 10
10
128.29
by Hilbert merge
1,000 6.32× 10
6
9.34× 10
10
127.02
(3) (2) with control 10 2.14× 10
8
6.05× 10
10
101.03
for the order
100 4.12× 10
7
6.23× 10
10
95.51
of visiting nodes
1,000 6.17× 10
6
6.73× 10
10
104.42
Table 2: The results for sound data.
method #queries #nodes #distance search time
(min)
(0) individual processing @ 7.98× 10
8
4.59× 10
10
138.76
(1) naive bundled 10 2.57× 10
8
7.79× 10
10
166.52
query processing
100 4.23× 10
7
7.79× 10
10
158.12
1,000 5.62× 10
6
7.79× 10
10
156.97
(2) (1) with 10 2.08× 10
8
5.99× 10
10
123.99
pre-processing
100 3.81× 10
7
5.99× 10
10
117.24
by Hilbert merge
1,000 5.42× 10
6
5.99× 10
10
115.94
(3) (2) with control 10 1.78× 10
8
4.66× 10
10
106.68
for the order
100 3.35× 10
7
4.79× 10
10
100.61
of visiting nodes
1,000 5.04× 10
6
4.95× 10
10
102.69
As shown in rows (2) and (3) when the search time
is shortest denoted by bold faces, the number of dis-
tance computations decreases about 30% and 20% to
the bundled query processing without the control (in
the row (2)) in the bundled query processing with the
control (in the row (3)) for image data and sound data,
respectively. Also the search time decreases about
20% and 10%, respectively.
As shown in the rows (0) and (3) when the search time
is shortest denoted by bold faces, the number of vis-
iting nodes much decreases to the individual process-
ing (in the row (0)) in the bundled query processing
with the control for image data and sound data, re-
spectively. However, the number of distance compu-
tations increases 10% for both data. Nevertheless, the
search time decreases about 30% for both data.
6 CONCLUSION
In this paper, we have proposed the bundled query
processing on compact Hilbert R-trees for high di-
mensional data and, in particular, introduced two
methods that the pre-processing by the Hilbert merge
and the control for the order of visiting nodes. Then,
we have given the experimental results for the bun-
dled query processing in similarity search of image
and sound data. Hence, we have succeeded that our
bundled query processing is more efficient than the
individual processing about 30% for the number of
visiting nodes and the search time.
However, the number of distance computations in
our bundled query processing is larger than one in the
individual processing. It is a future work to design an
appropriate method for bundled query processing to
reduce the number of distance computations.
In addition, it is necessary to verify this technique
for other tree structures such as M-tree (Ciaccia and
M. Patella, 1997).
REFERENCES
Bader, M. (2013). Space-filling curves. Springer.
Butz, A. R. (1971). Alternative algorithm for Hilbert’s
space-filling curves. IEEE Trans. Computers, C-
20:424–426.
Ciaccia, P. and M. Patella, P. Z. (1997). M-tree: An efficient
access method for similarity search in metric spaces.
Proc. 23rd Int. Conf. on Very Large Data Bases, pages
426–435.
Guttman, A. (1984). R-trees: A dynamic index structure for
spatial searching. In Proc. SIGMOD’84, pages 47–57.
Kamel, I. and Faloutos, C. (1993). On packing R-trees. In
Proc. CIKM’93, pages 490–499.
Kamel, I. and Faloutos, C. (1994). Hilbert R-tree: An im-
proved R-tree using fractals. In Proc. VLDB’94, pages
500–509.
Lawder, J. K. and King, P. J. H. (2001a). Querying multi-
dimensional data indexed using the Hilbert space-
filling curve. ACM SIGMOD Record, 30:19–24.
Lawder, J. K. and King, P. J. H. (2001b). Using state dia-
grams for Hilbert curve mappings. Internat. J. Com-
puter Math., 78:327–342.
Samet, H. (2006). Foundations of multidimentional and
metric data structures. Morgan Kaufmann.
Shinohara, T. and Ishizaka, H. (2002). On dimension re-
duction mappings for approximate retrieval of multi-
dimensional data. Progress in Discovery Sciencer
(LNCS 2281), pages 224–231.
Tanaka, A. (2001). Study on a fast ordering of high dimen-
sional data to spatial index. Master Thesis, Kyushu
Institute of Technology.
Tashima, K. (2011). Study on efficient method of insertion
for spatial index structure by using Hilbert sort. Mas-
ter Thesis, Kyushu Institute of Technology.
HighDimensionalSimilaritySearchwithBundledQueryProcessingonHilbertR-Tree
359
