
Formalizing the Qualitative Superposition of Rectangles in
Proof Assistant Isabelle/HOL
Fadoua Ghourabi and Kazuko Takahashi
Graduate School of Science and Technology, Kwansei Gakuin University, Nishinomiya, Japan
Keywords:
Knowledge Representation and Reasoning, Qualitative Spatial Reasoning, Theorem Proving, Isabelle/HOL,
Rectangle Superposition.
Abstract:
We formalize and verify the superposition of rectangles in Isabelle/HOL. The superposition is associated with
the arrangement of rectangular software windows while keeping some regions visible and other hidden. We
adopt a qualitative spatial reasoning approach to represent these rectangles and the relations between their
regions. The properties of the model are formally proved and show some characteristics of superposition
operation. Although, this work is limited to 29 structures of rectangles, the superpositions produce hundreds
of cases that are tedious to tackle in Isabelle/HOL. We also explain our strategy to optimize the proofs.
1 INTRODUCTION
Qualitative spatial reasoning (QSR) methods describe
the objects of the space qualitatively. Such approach
provides a low demand in numerical computation
and, furthermore, contains enough expressiveness to
teach a program to reason about the spatial objects.
QSR methods target various applications, such as ge-
ographical information systems and robotics (Liu and
Daneshmend, 2004; Bennett, 1996). The importance
of QSR methods leads us to address their reliability
and correctness. While various research works focus
on developing QSR methods, little attention is given
to their formal verification.
On the other hand, proof assistants are increas-
ingly used to formalize mathematical models (Avi-
gad and Harrison, 2014). With the help of proof
assistants, mathematical proofs are formally verified
where each step is transparent and, thus, the involved
logical reasoning can be checked. In the case of the
field of QSR, there are two major approaches: the
topological knowledge about objects (e.g. RCC calcu-
lus (Randell et al., 1992b)), and the positional knowl-
edge about objects (e.g. direction relations (Frank,
1991; Clementini et al., 1997)). Both of RCC and di-
rection relations are formalized using first-order logic
and relation algebra, which motivate us to use them in
automated reasoning by a proof assistant such as Is-
abelle/HOL (Nipkowet al., 2002). The only work that
tackle the formal verification in QSR of which we are
aware dates back to early 90s. The OTTER proof sys-
tem for first-order logic has been used to assist pen-
and-paper proofs of theorems in RCC (Randell et al.,
1992a). As far as we know, there is no (full) formal
presentation of QSR methods using proof assistant.
The purpose of this research is to extend the use of
proof assistants to the field of QSR. We focus on win-
dow allocation problem. When using software, we
often rearrange windows by dragging, resizing, su-
perposing, etc. until obtaining better visibility. A su-
perfluous information in a window can be hidden and
superposed by a relevant information in another win-
dow. A systematic method of superposing windows is
proposed in (Konishi and Takahashi, 2012). The win-
dow parts that should be visible are pre-specified by
the user. The window and its parts form a rectangu-
lar structure. The problem of arranging software win-
dows is regarded as the problem of superposing rect-
angles while keeping some pre-specified parts visible.
The rectangles are regarded as spatial objects, and the
superposition is examined from a QSR point of view.
This paper is based on the method presented
in (Konishi and Takahashi, 2012), and the contribu-
tion that we seek is twofold.
1. The original qualitative representation of rectan-
gles is simple but not expressive enough. When
checking properties about superposition, extra
conditions are defined to detect degenerate situ-
ations. Due to the numerous cases of superpo-
sition, the question is whether all the degenerate
situations are covered. We therefore propose a
more expressive representation based on matrices
530
Ghourabi F. and Takahashi K..
Formalizing the Qualitative Superposition of Rectangles in Proof Assistant Isabelle/HOL.
DOI: 10.5220/0005280005300539
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 530-539
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

of direction relations. The matrix representation
is more natural as the correspondence between
the parts of a rectangular structure and the ele-
ments of its matrix representation is straightfor-
ward. Furthermore, the extra conditions are not
required and a single set membership test is suffi-
cient.
2. We formalize our revised method of superposition
in Isabelle/HOL. Proof assistants are interactive
systems. The formal proofs are, consequently, te-
dious to do if the model present hundreds of cases.
We therefore take into consideration the practical-
ity of proving in Isabelle/HOL despite the numer-
ous cases of superposition. Our proof strategy re-
lies on establishing equivalence relations between
the qualitative representations of rectangles and
grouping them into classes.
The structure of the rest of the paper is as follows. In
Section 2, we summarize the notations that we use.
In Section 3, we define matrices in Isabelle/HOL. In
Section 4, we explain the operations over matrices. In
Section 5, we give matrix representation to rectangu-
lar units. In Section 6, we apply matrix superposition
to compute the superposition of units. In Section 7,
we introduce properties about superposition of units
and explain how we proceed in order to prove them.
In Section 8, we conclude with remarks on future di-
rections of research.
2 NOTATION
A matrix
m
of dimension
p
×
q
has
p
rows and
q
columns, where
p
,
q
∈ N. We write for short “
p
×
q
matrix
m
”. The expression
m
(
i
,
j
) denotes the ele-
ment of
m
at the
i
-th column and the
j
-th row, where
0 ≤
i
<
q
and 0 ≤
j
<
p
. Let S be the set of matrices,
m
be a matrix in S and
f
:S → S be an unary function,
we use
m
f
to mean the term
f
(
m
) and
f
n
to denote
the n(∈ N) compositions of
f
. We recurrently use the
notation
m
f
n
for
f
n
(
m
).
The formalization presented in this paper is done
in the proof assistant Isabelle/HOL (Nipkow et al.,
2002). The choice of the tool is made principally due
to the availability of powerful libraries for reasoning
with equivalence classes (Paulson, 2006) and mathe-
matical operations on matrices (Sternagel and Thie-
mann, 2010) on which the proposed qualitative rep-
resentation depends. In the following, we present the
elements of syntax used in this paper. Isabelle/HOL
provides a rich collection of formalized theories, use-
ful proof tactics (e.g. natural and structural induction,
and case splitting), elaborate techniques for pattern
matching and term rewriting, etc. Furthermore, Is-
abelle/HOL is a strongly typed system. The expres-
sion “
m::
′
a
list
” is a type constraint over a variable
m
. The variable
m
is of type list whose elements are
of variable type
′
a
. The type of a function
f
is writ-
ten “
f::
τ
1
⇒ . . . ⇒ τ
n
⇒ τ
n+1
”. In this paper, we use
Isabelle/HOL expression “
f x
1
. . .
x
n
” to denote the
term
f
(
x
1
, .. .,
x
n
). A list is represented by a sequence
of elements between square brackets, i.e. [e
0
, e
1
, . . .,
e
n
]. The constructor “#” adds an element to a list, i.e.
v#[e
0
, e
1
, . . ., e
n
] = [v, e
0
, e
1
, . . ., e
n
]. The i-th element
of a list m is given by “
m
! i”. For an equivalence rela-
tion r, the expression r‘‘{
x
} in Isabelle/HOL denotes
the equivalence class [
x
]
r
.
The formulas that we prove are written using com-
mon mathematical symbols. We explain some of the
proof in Isabelle/HOL using natural language. We
use Isar, which is an extension of Isabelle/HOL, to
write structured and human-readable proofs (Wenzel,
1999). The proofs in the classical Isabelle/HOL proof
style intertwines with Isar proofs.
1
3 FORMALIZATION OF
MATRICES
In Isabelle/HOL, no type is defined for matrix. We
use the types “
’a vec
” and “
’a mat
” provided by the
Matrix
Arith theory (Sternagel and Thiemann, 2010).
type
synonym ’a vec = ’a list
type
synonym ’a mat = ’a vec list
A matrix is implemented as a list of lists, i.e. a
list of columns. For example, list [[
a
,
b
],[
c
,
d
],[
e
,
f
]]
is of type “
′
a mat
”, and represents the 2×3 matrix
a c e
b d f
.
3.1 Dimension
The following issues arise when working with matri-
ces as list of lists. First, a matrix of type “’a mat”
has a dimension
p
×
q
, i.e. the length of the whole list
is
q
, and each column list has
p
elements. To make
sure that we work with mathematically valid matrices,
we use predicate
mat::nat
⇒
nat
⇒
’a mat
⇒
bool
(Ster-
nagel and Thiemann, 2010).
mat p q m
,
(
length m
=
q
) ∧ (∀ x ∈
set m
.
length x
=
p
),
(1)
1
For a closer look at the proofs, our Isabelle/HOL
theory files are available at http://ist.ksc.kwansei.ac.jp/
∼ktaka/SuperpositionTheory/.
FormalizingtheQualitativeSuperpositionofRectanglesinProofAssistantIsabelle/HOL
531

where
length
and
set
are Isabelle/HOL functions that
compute the length of a list and the set of elements of
a list, respectively.
Second, empty matrix (i.e. [ ]) and matrices with
empty columns (i.e. [[ ]], [[ ],[ ]], etc.) are of type
“
′
a mat
”. We want to exclude these matrices for the
following reasons. In the case of empty matrix, the
second part of the conjunction in definition (1) causes
vacuous truth that we wish to avoid (i.e. “
mat p
0 [ ]”
holds for any
p
). Moreover, the transpose of a matrix
with empty columns gives rise to the empty matrix,
hence we wish to avoid these cases too. We there-
fore restrict ourselves to a set
M
of type “
′
a mat set
”
whose elements satisfy the following condition.
m
∈
M
, ∃
p q::nat
.
mat
(
Suc p
) (
Suc q
)
m
The theorems that we prove in this work are defined
for matrices
m
∈
M
. In the premises, we impose the
condition
m
∈
M
from which we can deduce the di-
mension
p
×
q
by adding the following Isar line.
from ‘m ∈ M‘ obtain p q
where mat p q m and 0 < p and 0 < q
by (rule M.cases, simp)
The command “by (rule M.cases, simp)” proves
that the dimension of m is
p
×
q
and that
p
and
q
are
strictly positive.
3.2 Matrix Equality
The equality is established between two matrices of
the same dimension. In order to assert that two matri-
ces are equal, we either check that all their respective
elements are equal or that their respectivecolumn lists
are equal, depending on the proof strategy. Lemmas
about the equality of matrices are provided by the Ma-
trix
Arith theory.
4 OPERATIONS ON MATRICES
We explain two operations on matrices, namely rota-
tion
2
and superposition.
4.1 Rotation
Before giving a formal definition of rotation, we first
examine what does rotation of a matrix intuitively
mean. An operation of rotation has a spatial con-
notation. It involves a circular movement of objects
2
Here, operation of rotation over matrices is not to be
confused with “rotation matrix” used to compute the new
coordinates of a geometrical object that undergoes rotation
in Euclidean space.
defined by parameters such as the center of rotation,
angle of rotation, etc. If we picture a matrix as an ob-
ject (not only as data-structure), we can perform a
π
2
counter-clockwise rotation. For instance, if we rotate
the matrix
a c e
b d f
!
by
π
2
in a counter-clockwise
direction, we obtain
e f
c d
a b
.
From a computational point of view, function ρ =
R
◦
T
represents the rotation operation over matrices.
Functions
T
and
R
denote the transpose and the re-
verse. For a matrix
m
∈
M
,
m
ρ
=
m
R
◦
T
is obtained by
reversing the columns of
m
T
. In the previous exam-
ple, the transpose is
a b
c d
e f
. Then, the result of
reversing the columns of the transpose is
e f
c d
a b
.
Functions
transpose
,
reverse
and ρ implement
T
,
R
and ρ in Isabelle/HOL. We use function
transpose
::
nat
⇒
′
a mat
⇒
′
a mat
given in the Matrix Arith
theory, and we define functions
reverse
and ρ (both
of type
′
a mat
⇒
′
a mat
) as follows.
reverse m
,
map rev m
ρ
m
,
reverse (transpose (nr mat m) m)
Function
rev
reverses a list, and function
reverse
applies
rev
to all the column lists. Note that function
transpose
has two arguments. The first argument is
a natural number that corresponds to the number of
rows, which is computed by the function call “
nr mat
m
”.
Furthermore, we can perform n successive rota-
tions of matrix
m
by computing
m
ρ
n
, where n ∈ N. In
Isabelle/HOL, we use the notation for function power,
i.e. “ρ ˆˆn”, to implement successive rotations. We
prove a collection of useful properties about rotation
operation that are stated as inference rules in (2) − (7)
depicted in Fig. 1.
The variables in the rules (2) − (7) are universally
quantified, and their types are understood from the
context. Rule (5) expresses the transitivity of ρ
n
. A
matrix is invariant by a number of rotations multiple
of 4 (c.f. rules (4) and (6)). If matrix
m
2
is obtained
by n rotations of matrix
m
1
, then
m
1
can be obtained
back by 3× n rotations of
m
2
(c.f. rule (7)).
Based on rotation, we establish a relation
rot rel
.
In other words, if a matrix
m
2
is obtained by n rota-
tions of matrix
m
1
, then we write (
m
1
,
m
2
) ∈
rot rel
.
rot rel
,{(
m
1
,
m
2
)|∀
m
1
m
2
.∃
n::nat
.
m
1
∈
M
∧
m
2
∈
M
∧
m
2
=
m
1
ρ
n
}
(8)
We furthermore prove that the relation
rot rel
is an
equivalence relation over the set
M
.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
532

m
∈
M mat p q m even n
mat p q m
ρ
n
(2)
m
∈
M mat p q m
¬
even n
mat q p m
ρ
n
(3)
m
∈
M
m
ρ
n
=
m
ρ
n mod 4
(4)
m
∈
M
m
ρ
n
1
+
n
2
=
m
ρ
n
1
◦ρ
n
2
(5)
m
∈
M
m
ρ
4×n
=
m
(6)
m
1
∈
M m
2
∈
M m
2
=
m
1
ρ
n
m
1
=
m
2
ρ
3×n
(7)
Figure 1: Rules on rotations of matrices.
lemma equiv M rot_rel
Relation
rot rel
is obviously reflexive over
M
since
m
=
m
ρ
4×
n
. From property (5), we deduce that
rot rel
is transitive, and from property (7) that
rot rel
is symmetric.
4.2 Superposition
The other operation that we consider is superposition
of matrices. Intuitively, we superpose two matrices
m
1
and
m
2
by “putting”
m
2
onto
m
1
. The super-
position requires that both of
m
1
and
m
2
are of the
same dimension
p
×
q
. The superposition amounts to
“putting” elements of
m
2
onto elements of
m
1
.
Let
f
and
s
be two functions of type
′
a mat
⇒
′
a
mat
⇒
′
a mat
and
′
a
⇒
′
a
⇒
′
a
, respectively. We
define predicate
is superposition
as follows.
same dimension p q m
1
m
2
,
mat p q m
1
∧
mat p q m
2
is superposition f s
,
∀
m
1
m
2
∈
M
. ∀
p q i j::nat
.
(
same dimension p q m
1
m
2
) →
i
< q →
j
< p →
(
f m
1
m
2
)(
i
,
j
) =
s m
1
(
i
,
j
)
m
2
(
i
,
j
)
If “
is superposition f s
” holds then we write that
f
is a superposition with respect to
s
. For instance,
addition over matrices is a superposition with respect
to addition operation.
lemma is_superposition mat_plus plus
The implementation of
f
that we use in this paper
is the function
map thread
defined as follows.
fun map_thread::(’a ⇒’a ⇒’a)⇒’a mat⇒
’a mat⇒ ’a mat
where map_thread s m1 m2 =
map (λ(v1,v2). map (λ(a1,a2). s a1 a2)
(zip v1 v2)) (zip m1 m2)
Since matrices are implemented as lists, the super-
position “
map thread
” applies function
s
to pair-wise
combinations of elements of
m
1
and
m
2
. Function
s
is applied to elements of
m
1
and
m
2
that have the
same position (i.e. same column and row numbers).
For instance, calling “(
map thread s
) [[a
1
, a
2
, a
3
], . . .]
[[b
1
, b
2
, b
3
], . . .]” gives rise to the matrix “[[s a
1
b
1
, s
a
2
b
2
, s a
3
b
3
], . . .]”. We show that “
map thread s
” is
a superposition with respect to
s
.
3
lemma is_superposition (map_thread s) s
Furthermore, we prove properties about superpo-
sition of rotation of matrices shown in rules (9) −
(11). In the left-side of the equation in (9), we com-
pute the superposition of matrices
m
1
and
m
2
rotated
by the same number n. We can take ρ
n
outside as
shown in the right-side of the equation in (9), i.e. we
first superpose
m
1
and
m
2
then rotate the result by n.
More relevant to our formalization is showing how
superposition behaves when we rotate
m
1
and
m
2
by
distinct numbers
n
1
and
n
2
, respectively. Depending
on whether
n
1
is less than
n
2
, we distinguish the two
cases in (10) and (11). In case
n
1
≤
n
2
, we can take
ρ
n
1
outside as shown in the right-side of (10). There-
fore, matrix
m
2
is rotated by
n
2
−
n
1
. Rules (10) and
(11) are used as substitution rules to replace the occur-
rence of left-side of the equality by the right-side of
the equality. The two rules are important to optimize
the proofs which we will explain later in Sect. 7.2.
Recall that from properties (2) and (3), the dimen-
sion of matrix
m
1
ρ
n
1
depends on whether
n
1
is even.
Hence,
m
1
ρ
n
1
and
m
2
ρ
n
2
are not necessary of the same
dimension, and therefore we cannot always perform
superposition. A sufficient condition, but not neces-
sary, is to consider only
p
×
q
square matrices, where
p
=
q
. So far, all the lemmas that we have proved are
for arbitrary
p
×
q
matrices, but, as we see in next sec-
tions, only square matrices are used to formalize the
superposition of rectangles.
The qualitative spatial reasoning approach to the
problem of superposition of software windows is
based on operations of rotation and superposition of
matrices. First, a window is given a qualitative rep-
resentation using matrices, which is the subject of the
next section.
3
The type of function
s
is not specified in the statement
of the lemma since it is inferred by Isabelle/HOL.
FormalizingtheQualitativeSuperpositionofRectanglesinProofAssistantIsabelle/HOL
533
m
1
∈
M m
2
∈
M
(
map thread s
)
m
1
ρ
n
m
2
ρ
n
= ((
map thread s
)
m
1
m
2
)
ρ
n
(9)
m
1
∈
M m
2
∈
M n
1
≤
n
2
mat p p m
1
mat p p m
2
(
map thread s
)
m
1
ρ
n
1
m
2
ρ
n
2
= ((
map thread s
)
m
1
m
2
ρ
n
2
−n
1
)
ρ
n
1
(10)
m
1
∈
M m
2
∈
M n
2
<
n
1
mat p p m
1
mat p p m
2
(
map thread s
)
m
1
ρ
n
1
m
2
ρ
n
2
= ((
map thread s
)
m
1
m
2
ρ
3×(n
1
−n
2
)
)
ρ
n
1
(11)
Figure 2: Inference rules on matrix superposition.
5 QUALITATIVE
REPRESENTATION OF UNIT
The spatial object that we investigate is the software
window modelled as a rectangle, called unit. Some
parts of a unit are required to be visible, which are
modelled as white rectangular plates. The parts that
can be hidden are black rectangular plates. The size
of a unit is unfixed, and changes in a fashion similar
to the way software windows are shrunk or expanded.
We explain the qualitative representation of a unit that
reflects its structure, i.e. locations of its black and
white plates.
5.1 Black Plates
Let U be a rectangular unit of unfixed length l and un-
fixed height h, i.e. of size l × h. In this paper, we use
units with at most two black plates, and we consider
the following two assumptions about the black plates
of a unit U.
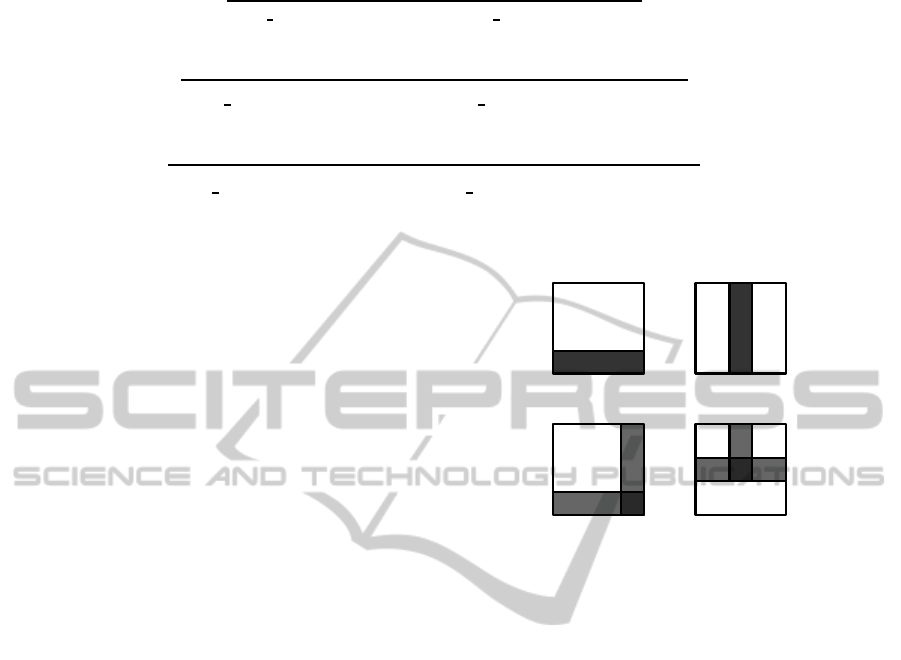
1. If U has one black plate p, then the size of p is
either l × v or u× h, where u ≤ l and v ≤ h. Each
of the units in Fig. 3(a) and 3(b) has one black
plate that stretches along the length/height of the
unit.
2. If U has two black plates p
1
and p
2
, then they are
perpendicular, and at least one of them is of size
u×h or l ×v, where u ≤ l and v ≤ h. Furthermore,
p
1
and p
2
must be overlapping. The overlapping
part forms a rectangular shared area denoted by
p
1
⊓ p
2
(e.g. the units in Fig. 3(c) and 3(d)).
5.2 Regions of Unit
We work with units that are located on the 2D plane.
The 2D plane is the grey region, simply denoted by
g
.
From the white and black plates, we compute regions
(a) (b)
(c) (d)
Figure 3: Examples of units with one black plate ((a)
and (b)) and with two perpendicular and overlapping black
plates ((c) and (d)).
of unit, namely white and black regions that we de-
note
w
and
b
, respectively. We define the datatype
rg
as follows.
datatype rg = w | b | g | N
The region N is called undefined region that is rel-
evant for checking the success of superposition which
we explain in Sect. 6. The regions
w
and
b
of a unit
U are determined as follows.
(a) A white plate of U is a
w
region.
(b) If p is the only black plate of U, then p is also the
only
b
region of U.
(c) If p
1
and p
2
are two distinct black plates of U,
then together they generate 3, 4 or 5
b
regions de-
pending on their placements (cf. Fig. 4). Note that
the area p
1
⊓ p
2
is one of the
b
regions generated
by p
1
and p
2
.
Next, we define the core of a unit. The core region
of unit U, denoted by C
U
, is a
b
region. If U has only
one black plate p, then p is the coreC
U
. Otherwise, let
p
1
and p
2
be the two black plates of U, then the core
of U is the shared area between p
1
and p
2
, i.e. C
U
=
p
1
⊓ p
2
. Since a unit has at most two black plates as
established in the assumptions in the previous section,
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
534

b b
b
(a)
b b
b
b
(b)
b b b
b
b
(c)
Figure 4: Black plates,
b
regions and the core regions.
then a unit has one and only one core. In our figures,
the cores are highlighted in darker black (cf. Figs. 3
and 6).
5.3 Representation
One common approach to represent positional know-
eledge is the use of matrix representation. In particu-
lar, the object interaction matrix (OIM) (Chen et al.,
2010) encodes the direction relations between spa-
tial objects. In this paper, we use OIM matrix to
represent the positions of the unit regions w.r.t. the
core region. Recall that the core C
U
is a rectangu-
lar black area, thus it has 4 edges and 4 vertices.
Extending the edges of C
U
divides the plane into 9
tiles where the central tile is bounded and 8 are un-
bounded (e.g. the tiling in Fig. 5). The tiles decom-
pose the plane into the 9 regions of direction rela-
tions, i.e.
up left
,
left
,
bottom left
,
up
,
center
,
bottom
,
up right
,
right
,
bottom right
. The core region occu-
pies the central bounded tile. The intersection of the
tiles and the rectangular unit determines the direction
relations between the coreC
U
and the 8 regions of the
unit that are connected to the core.
4
The reference of direction system, being the core,
is the center of the matrix representation. The remain-
ing elements of the matrix are the values of the inter-
sections of the unit and the 8 unbound tiles. We use
the following 3×3 matrix to represent the positions of
the 8 regions that surround the core.
up
le ft up up right
le ft core right
bottom
le ft bottom bottom right
We place a unit in the 2D plane and we substitute
the values
g
,
b
,
w
for the elements of the above ma-
trix. The obtained matrix is the qualitative represen-
tation of the unit. For instance, the qualitative rep-
resentations of the units in Fig. 3 are
g w g
g b g
g g g
,
g g g
w b w
g g g
,
w b g
b b g
g g g
and
w b w
b b b
w w w
, re-
spectively.
4
Regions that share a point are considered connected.
w b w
b b b
w w w
Figure 5: Tiling of the plane and the OIM matrix of a unit.
In Isabelle/HOL, we provide a set
rgM
of all the
3×3 matrices with
b
core region, and prove that
rgM
is a subset of
M
defined in Sect. 3.1.
definition core::rg mat ⇒ rg
where core m = m!1!1
definition rgM ::rg mat set where
rgM = {m. (mat 3 3 m)∧(core m = b)}
lemma rgM ⊂ M
5.4 Valid Units
There are 29 possible cases of fitting one or two black
plates in a rectangular unit. They are depicted in
Fig. 6. We call them valid units. Since we deal with
qualitative representation of units where size does not
matter, we observe that some units are obtained by
rotating others.
6 SUPERPOSITION OF UNITS
Superposition of units is a non-symmetric binary op-
eration. Superposing two units U
1
and U
2
means that
we put U
2
onto U
1
while keeping the
w
regions of
U
1
visible. The superposition, that we define in this
paper, operates by putting the core C
U
2
onto the core
C
U
1
. The cores C
U
1
and C
U
2
are not necessarily of
the same size. Operations of shrinking, expanding,
lengthening are performed on U
1
and U
2
so that their
cores fit. Consequently, the sizes of the units and their
regions change. Such operations may also affect the
amount of visible information. We assume that the
operating system or the software application automat-
ically generates scrollbars for the viewing. For the
simplicity of our examples, we only modify the size
of U
2
and its core. The changes in the size do not af-
fect the matrix representation since it is a qualitative
representation.
FormalizingtheQualitativeSuperpositionofRectanglesinProofAssistantIsabelle/HOL
535
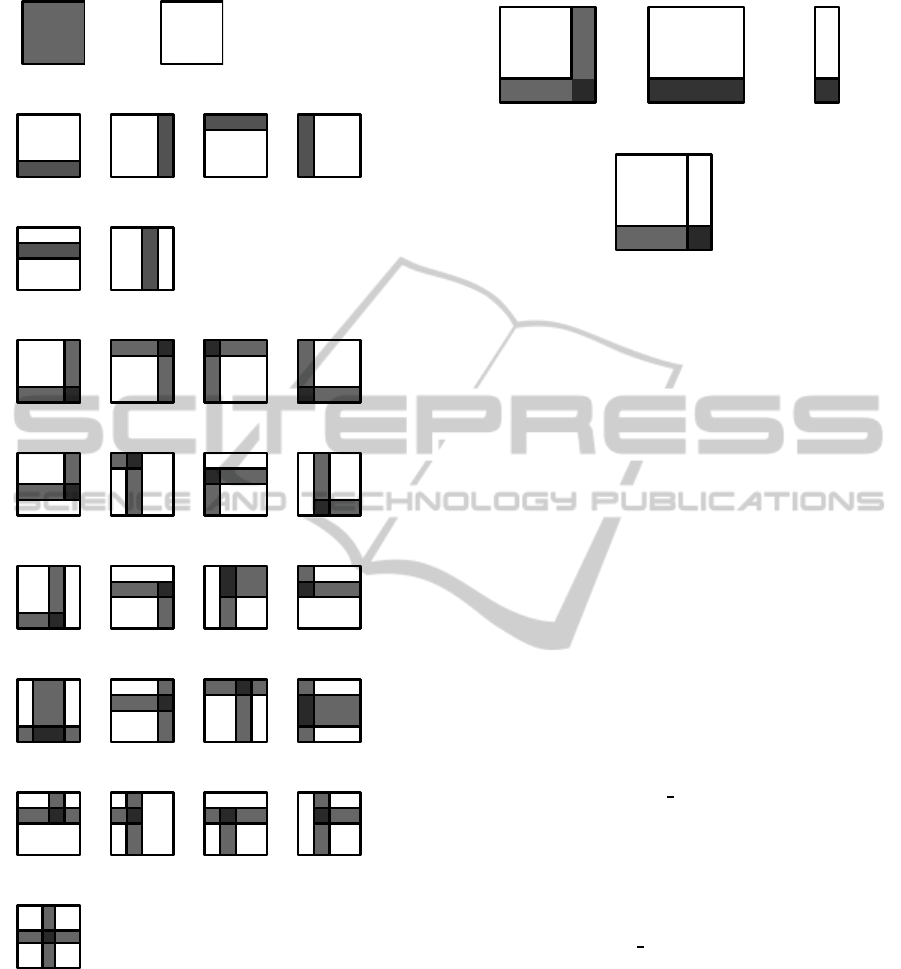
(a) Class B (b) Class W
(c) Class I1
(d) Class I2
(e) Class L1
(f) Class L2
(g) Class L3
(h) Class T1
(i) Class T2
(j) Class PLUS
Figure 6: Valid units grouped into 10 equivalence classes.
The result of superposition is a unitU
3
whose core
is C
U
3
= C
U
2
= C
U
1
. The superposition of U
1
and U
2
is computed from the superposition of their respective
matrix representations. In Sect. 4.2, we introduced
superposition of matrices where function
s
has not yet
been defined. In the following section we discuss an
implementation of
s
.
(a) Unit L1
(b) Unit I1
(c) Result of I1 on L1
Figure 7: Superposition of unit I1 onto unit L1.
6.1 Function
on
We define a function
on
that computes superposition
of regions.
fun on::rg ⇒ rg ⇒ rg
where
on g u = u | on u g = u |
on N _ = N | on _ N = N |
on w _ = N | on _ w = w | on _ b = b
The equation “
on x y = z
” means that region
y
is to
be put on region
x
, and the result is region
z
. Function
on
is defined using Isabelle/HOL function definition
fun. The order of appearance of the equations “
on x y
= z
” matters. The pattern matching of “
on w b
” suc-
ceeds first with the 5th equation and thus gives rise to
N
, i.e. the superposition should not be allowed since
a
w
region is hidden.
The superposition of two matrices
m
1
and
m
2
is
achieved by calling “
(map thread on) m
1
m
2
”.
Example. We take the two units of type L1 and
I1 in Fig. 7(a) and 7(b) with matrix representations
m
1
=
w b g
b b g
g g g
and
m
2
=
g w g
g b g
g g g
, respec-
tively. We resize I1, then we put C
I1
onto C
L1
. The
computation of “(
map thread on
)
m
1
m
2
” gives rise
to
w w g
b b g
g g g
which corresponds to the unit in
Fig. 7(c).
The unit in Fig. 7(c) has one more
b
regionbesides
the core. The
b
region is adjacent to the core to the
left. In other words, it shares an edge with the core.
We merge it with the core to form one
b
region. The
conditions for the merge as well as its impact on the
matrix representation of a unit are discussed in the
next section.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
536

(a) (b)
b b
(c)
Figure 8: The result of putting I2 type unit on L1 type unit.
6.2 Merging Black Regions
The merge is necessary only if the following two con-
ditions apply.
1. There is only one
b
region that is connected to the
core by an edge. In other words, there is a unique
b
region located either up or left or bottom or right
to the core. Fig. 7(c) illustrates such situation. Be-
sides the core, only left region is black.
2. If the above condition holds, then we check
whether the
b
region and the core are connected to
the same regions. Referring to Fig. 7(c) with ma-
trix representation
w w g
b b g
g g g
, both
b
region
and core are connected to the same upper
w
re-
gion, and to the same bottom
g
region. In that
case we can merge the left, up left and bottom
left regions into one
g
region. Hence, the matrix
representation becomes
g w g
g b g
g g g
. In the ex-
ample illustrated by Fig. 8, we put I2 unit on L1
unit. The result of superposition (cf. Fig. 8(c))
has the matrix representation
g w w
g b b
g w g
. The
right region is the only
b
region besides the core.
The core is connected to a
w
bottom region while
the right region is connected to a
g
bottom region.
We, therefore, cannot merge the right, up right and
bottom right regions into one
g
region.
The final result is merging the superposition (if appli-
cable) which is given by function
puton
=
merge
◦
(
map thread on
).
7 ON PROVING PROPERTIES
ABOUT
puton
7.1 The Properties
We define properties to answer questions about the
final result of superposing two units. Let
m
1
and
m
2
be matrices in
rgM
, the properties of applying “
puton
m
1
m
2
” that we want to check are the following.
Success. Are all the
w
regions visible?
Effectiveness. Does the final result of superposition
has only one
b
region?
Validity. Is the final result of the superposition a
valid unit?
The superposition proceeds by putting the core of a
unit onto the core of another one. This does not guar-
antee that all the
w
regions are visible. In order to
judge whether a superposition is successful, we com-
pute the occurrence of
N
in the matrix representation
obtained by
puton
.
definition successful::rg mat ⇒ bool where
successful m ≡ (occurs N (concat m))=0
Naturally, effectiveness and validity are checked
for successful
puton
. “
puton m
1
m
2
” is said effective
if its result has only one
b
region.
definition effective::rg mat ⇒ bool where
effective m ≡ (occurs b (concat m)) = 1
“
puton m
1
m
2
” is valid if its result is one of the
29 units in Fig. 6.
definition valid::rg mat ⇒ bool where
valid m ≡ ∃V::rg mat. V ∈ U0 ∧
(m ∈ rot_rel‘‘{V})
7.2 Proof Strategy
Given the units in Fig. 6, the number of all the
pairwise combinations is 29 × (29 − 1) + 29 = 841.
Checking properties of success, effectiveness and va-
lidity for all possible superpositions involves numer-
ous computations of
puton
. It is crucial to design
an efficient proof strategy to prove a large number of
properties.
Earlier in Sect. 4.2, we explained the results (10)
and (11) about superposition of rotations of matrices.
Namely, if
m
1
and
m
2
are two square matrices of the
same dimension, and given that “
map thread on
” is
a superposition with respect to function
on
, then we
FormalizingtheQualitativeSuperpositionofRectanglesinProofAssistantIsabelle/HOL
537

Table 1: Computation of “
map thread on
” for elements of the classes C
1
and C
2
.
H
H
H
H
H
C
1
C
2
m
2
m
2
ρ
m
2
ρ
2
m
2
ρ
3
m
1
f m
1
m
2
f m
1
m
2
ρ
f m
1
m
2
ρ
2
f m
1
m
2
ρ
3
m
1
ρ
f m
1
ρ
m
2
f m
1
ρ
m
2
ρ
f m
1
ρ
m
2
ρ
2
f m
1
ρ
m
2
ρ
3
m
1
ρ
2
f m
1
ρ
2
m
2
f m
1
ρ
2
m
2
ρ
f m
1
ρ
2
m
2
ρ
2
f m
1
ρ
2
m
2
ρ
3
m
1
ρ
3
f m
1
ρ
3
m
2
f m
1
ρ
3
m
2
ρ
f m
1
ρ
3
m
2
ρ
2
f m
1
ρ
3
m
2
ρ
3
Note: Function
f
stands for “
map thread on
”.
Table 2: Results of applying (12) on the entries of Table 1.
H
H
H
H
H
C
1
C
2
m
2
m
2
ρ
m
2
ρ
2
m
2
ρ
3
m
1
f m
1
m
2
f m
1
m
2
ρ
f m
1
m
2
ρ
2
f m
1
m
2
ρ
3
m
1
ρ
(
f m
1
m
2
ρ
3
)
ρ
(
f m
1
m
2
)
ρ
(
f m
1
m
2
ρ
)
ρ
(
f m
1
m
2
ρ
2
)
ρ
m
1
ρ
2
(
f m
1
m
2
ρ
6
)
ρ
2
(
f m
1
m
2
ρ
3
)
ρ
2
(
f m
1
m
2
)
ρ
2
(
f m
1
m
2
ρ
)
ρ
2
m
1
ρ
3
(
f m
1
m
2
ρ
9
)
ρ
3
(
f m
1
m
2
ρ
6
)
ρ
3
(
f m
1
m
2
ρ
3
)
ρ
3
(
f m
1
m
2
)
ρ
3
Note: Function
f
stands for “
map thread on
”.
have the following.
(
map thread on
)
m
1
ρ
n
1
m
2
ρ
n
2
=
(
((
map thread on
)
m
1
m
2
ρ
n
2
−n
1
)
ρ
n
1
, if n
1
≤ n
2
((
map thread on
)
m
1
m
2
ρ
3×(n
1
−n
2
)
)
ρ
n
1
, otherwise
(12)
Suppose that we want to check properties of all
the possible applications of
puton
on elements of two
equivalence classes C
1
and C
2
. We need to compute
“(
map thread on
)
m
1
m
2
” for all
m
1
∈ C
1
and
m
2
∈ C
2
as shown in Table 1. By applying the result in (12),
the entries of Table 1 are equivalent to those depicted
in Table 2.
The 16 entries in Table 2 can be grouped into
equivalence classes using relation
rot rel
. Namely, we
have the following 4 equivalence classes [
f m
1
m
2
],
[
f m
1
m
2
ρ
], [
f m
1
m
2
ρ
2
] and [
f m
1
m
2
ρ
3
]. Note that
due to rule (4), the entries (
f m
1
m
2
ρ
6
)
ρ
2
and (
f m
1
m
2
ρ
9
)
ρ
3
in Table 2 are equal to (
f m
1
m
2
ρ
2
)
ρ
2
and
(
f m
1
m
2
ρ
)
ρ
3
, respectively, and therefore elements of
the classes [
f m
1
m
2
ρ
2
] and [
f m
1
m
2
ρ
], respectively.
Now to finish computing
puton
, we need to ap-
ply function
merge
. To that end, we introduce (in-
fix) predicate “
preserves
”. A function
g
preserves an
equivalence relation r if the image of all the elements
in [x]
r
by
g
are in [
g
x]
r
.
g preserves
r , ∀
x y
. (
x
,
y
) ∈ r → (
g x
,
g y
) ∈ r
We prove that
merge
preserves relation
rot rel
.
lemma merge preserves rot_rel
Applying
merge
gives rise to the 4 equivalence
classes [
merge
(
f m
1
m
2
)], [
merge
(
f m
1
m
2
ρ
)],
[
merge
(
f m
1
m
2
ρ
2
)] and [
merge
(
f m
1
m
2
ρ
3
)].
Next, we use (infix) predicate “
respects
” defined
in the Equiv Relations theory (Paulson, 2006). A
function
g
respects an equivalence relation r if
g
re-
turns the same value for all the elements of an equiv-
alence class generated by r.
g respects
r , ∀
x y
. (
x
,
y
) ∈ r →
g x
=
g y
The properties that we want to check, namely
successful
,
effective
and
valid
can be regarded as
boolean functions. We prove that they respect
rot rel
.
If a property P(∈{
successful, effective, valid
}) holds
for one element of a class then it holds for all the re-
maining elements, otherwise it gives False for all the
remaining elements.
lemma successful respects rot_rel
lemma effective respects rot_rel
lemma valid respects rot_rel
In order to check properties of
puton
applied to
all the 16 pairwise combinations of two equivalence
classes C
1
and C
2
, it is sufficient to check them for 4
puton
computations that are the
putons
applied to a
representative of C
1
and all the elements of C
2
.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
538

8 CONCLUSION
We covered the formalization of superposition of rect-
angular units in Isabelle/HOL. A unit is given a quali-
tative matrix representation. The superposition of two
units is regarded as superposition function applied to
their respective matrix representations. Function
pu-
ton
is defined to refine the result of superposition
by merging black regions. We defined properties of
success, effectiveness and validity, and explained our
proof strategy to tackle the numerous cases of super-
position. We can think of two directions for future
work of this research.
First, we plan to relax all the assumptions on the
unit structure that are enumerated in Sect. 5.1. We
would like to include more complex unit structures
such as the ones depicted in Fig. 9. To that end, we
need to extend the set of direction relations to ex-
press the locations of regions that are not directly con-
nected. The refinement to higher granularity level al-
lows representing any unit structure. We also plan to
formalize the generalization in Isabelle/HOL.
(a) (b) (c)
Figure 9: Unit structures whose qualitative representations
require extending direction relations.
Second, QSR theories, such as direction relations,
rely on composition tables that are relevant for de-
ciding whether QSR constraints are consistent (Renz,
2002; Frank, 1991). In order to construct the com-
position tables, the work presented in (Randell et al.,
1992a) uses OTTER proof system for first-order logic
to assist pen-and-paper proofs. The authors have enu-
merated the challenge of such proofs because of the
number of the entries of a composition table. We plan
to investigate the proof of the correctness of the com-
position tables using proof assistant.
ACKNOWLEDGEMENTS
This work is supported by JSPS KAKENHI Grant
No. 25330274.
REFERENCES
Avigad, J. and Harrison, J. (2014). Formally Verified Math-
ematics. Communications of the ACM, 57(4):66–75.
Bennett, B. (1996). The Application of Qualitative Spatial
Reasoning to GIS. In Proceedings of The 1st Inter-
national Conference on GeoComputation, volume I,
pages 44–47.
Chen, T., Schneider, M., Viswanathan, G., and Yuan, W.
(2010). The Objects Interaction Matrix for Modeling
Cardinal Directions in Spatial Databases. In Database
Systems for Advanced Applications, volume 5981 of
LNCS, pages 218–232. Springer Berlin Heidelberg.
Clementini, E., Felice, P. D., and Hern´andes, D. (1997).
Qualitative Representation of Positional Information.
Artificial Intelligence, 95(2):317 – 356.
Frank, A. U. (1991). Qualitative Spatial Reasoning about
Cardinal Directions. In Proceedings of the Inter-
national Symposium on Computer-Assisted Cartogra-
phy, pages 148–167. ACSM-ASPRS.
Konishi, T. and Takahashi, K. (2012). Superposition of
Rectangles with Visibility Requirement: A Qualita-
tive Approach. International Journal On Advances in
Software, 4(4):422–433.
Liu, J. and Daneshmend, L. (2004). Spatial Reasoning and
Planning: Geometry, Mechanisms, and Motion. Ad-
vanced Information Processing. Springer.
Nipkow, T., Paulson, L. C., and Wenzel, M. (2002).
Isabelle/HOL: A Proof Assistant for Higher-Order
Logic, volume 2283 of LNCS Tutorial. Springer.
Paulson, L. C. (2006). Defining Functions on Equivalence
Classes. ACM Transactions on Computational Logic,
7(4):658–675.
Randell, D. A., Cohn, A. G., and Cui, Z. (1992a). Comput-
ing Transitivity Tables: A Challenge for Automated
Theorem Provers. In Proceedings of Automated De-
duction (CADE-11), volume 607 of LNCS, pages 786–
790. Springer.
Randell, D. A., Cui, Z., and Cohn, A. G. (1992b). A Spatial
Logic based on Regions and Connection. In Proceed-
ings of the 3rd International Conference on Knowl-
edge Representation and Reasoning, pages 165–176.
Renz, J. (2002). Qualitative Spatial Reasoning with Topo-
logical Information, volume 2293 of LNCS. Springer.
Sternagel, C. and Thiemann, R. (2010). Executable
Matrix Operations on Matrices of Arbitrary Di-
mensions. In The Archive of Formal Proofs.
http://afp.sf.net/entries/Matrix.shtml.
Wenzel, M. (1999). Isar - A Generic Interpretative Ap-
proach to Readable Formal Proof Documents. In The-
orem Proving in Higher Order Logics, volume 1690
of LNCS, pages 167–183. Springer.
FormalizingtheQualitativeSuperpositionofRectanglesinProofAssistantIsabelle/HOL
539
