
The Critical Feature Dimension and Critical Sampling Problems
Bernardete M. Ribeiro
1
, Andrew H. Sung
2
, Divya Suryakumar
3
and Ram Basnet
4
1
Department of Informatics Engineering, University of Coimbra, Coimbra, 3030-290 Coimbra, Portugal
2
School of Computing, University of Southern Mississippi, Hattiesburg, MS 39406, U.S.A.
3
Apple, Inc., Sunnyvale, CA, U.S.A.
4
Department of Computer Science, Colorado Mesa University, Grand Junction, CO 81501, U.S.A.
Keywords: Data Mining, Knowledge Discovery, Critical Feature Dimension, Critical Sampling Random Selection.
Abstract: Efficacious data mining methods are critical for knowledge discovery in various applications in the era of
big data. Two issues of immediate concern in big data analytic tasks are how to select a critical subset of
features and how to select a critical subset of data points for sampling. This position paper presents ongoing
research by the authors that suggests: 1. the critical feature dimension problem is theoretically intractable,
but simple heuristic methods may well be sufficient for practical purposes; 2. there are big data analytic
problems where the success of data mining depends more on the critical feature dimension than the specific
features selected, thus a random selection of the features based on the dataset’s critical feature dimension
will prove sufficient; and 3. The problem of critical sampling has the same intractable complexity as critical
feature dimension, but again simple heuristic methods may well be practicable in most applications.
1 INTRODUCTION
One of the many challenges of “big data” is how to
reduce the size of datasets in tasks such as data
mining for knowledge discovery. In that regard,
effective feature ranking and selection algorithms can
guide us in data reduction by eliminating features
that are insignificant, irrelevant, or useless. In some
bio- or medical informatics datasets, for example, the
number of features can reach tens of thousands. This
is partly because that many datasets constructed
today for intended data mining purposes, without
prior knowledge about what is to be specifically
explored or derived from the data, likely have
included measurable attributes that are actually
insignificant or irrelevant, which inevitably results in
large numbers of useless features that can be deleted
to reduce the size of datasets without negative
consequences in data analytics or data mining (Blum
1997, Guyon 2003).
We investigate in this paper the general question:
Given a dataset with p features, is there a Critical
Feature Dimension (CFD, or the smallest number of
features that are necessary) that is required, say, for a
particular data mining or machine learning process,
to satisfy a minimal performance threshold? That is,
any machine learning, statistical analysis, or data
mining, etc. tasks performed on the dataset must
include at least a number of features no less than the
CFD or it would not be possible to obtain
acceptable results. This is a useful question to
consider since feature selection methods generally
provide no guidance on the number of features to
include for a particular task; moreover, for many
poorly understood and complex problems to which
big data brings some hope of breakthrough there is
very little useful prior knowledge which may be
otherwise relied upon in determining this number of
CFD.
In this position paper, the question is analyzed in
a very general setting in the next section and shown
to be intractable. Next, an ad-hoc method is proposed
in section 2 as a first attempt to approximately solve
the problem; and experimental results on selected
datasets are presented to demonstrate the existence of
a CFD for most of them. Section 3 presents the
authors’ second position that for some data mining
problems, it is the CFD that matters; in other words,
random feature selection will be sufficient for
satisfactory performance in data mining
tasksprovided that the number of features selected
meets the CFD. In section 4 the critical sampling
problem is analyzed and shown to be of the same
complexity as the CFD problem; and heuristic
360
Ribeiro B., Sung A., Suryakumar D. and Basnet R..
The Critical Feature Dimension and Critical Sampling Problems.
DOI: 10.5220/0005282403600366
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 360-366
ISBN: 978-989-758-076-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

methods for critical sampling are suggested as likely
to be sufficient for practical purposes. Conclusions
and discussions are given in section 5.
2 THE CFD PROBLEM
The feature selection problem has been studied
extensively; and feature selection to satisfy certain
optimal conditions have been proved to be NP-hard
(Guyon 2003). Here we consider the problem from a
different perspective by asking the question whether
there exist a CFD, i.e., a minimum number of
features, that must be included for a data analytic
task to achieve “satisfactory” results (e.g., building a
learning machine classifier to achieve a given
accuracy threshold), and we show the problem is
intractable as it is in fact both NP-hard and coNP-
hard.
Assume the dataset is represented as the typical n
by p matrix D
n,p
with n objects (or data points,
vectors, etc.) and p features (or attributes, etc.) The
intuitive concept of the CFD of a dataset with p
features is that there may exist, with respect to a
specific “machine” M and a fixed performance
threshold T, a unique number
≤ p such that the
performance of M exceeds T when a suitable set of
features is selected and used (and the rest p
features discarded); further, the performance of M is
always below T when any feature set with less than
features is used. Thus,
is the critical (or absolute
minimal) number of features that are necessary to
ensure that the performance of M meets the given
threshold T.
Formally, for dataset D
p
with p features (the
number of objects in the dataset, n, is considered
fixed here and therefore dropped as a subscript of
the data matrix D
n,p
), a machine M (a learning
machine, a classifier, an algorithm, etc.) and
performance threshold T (the classification accuracy
of M, etc.), we call
(an integer between 1 and p)
the T-Critical Feature Dimension of (D
p
, M) if the
following two conditions hold:
There exists D
, a
-dimensional projection
of D
p
(i.e., D
contains
of the p features) which
lets M to achieve a performance of at least T, i.e.,
(D
∝ D
p
) [P
M
(D
) T], where P
M
(D
) denotes the
performance of M on input dataset D
.
For all j <
, a j-dimensional projection of D
p
fails to let M achieve performance of at least T, i.e.,
(∀D
j
∝ D
p
) [j <
P
M
(D
j
) < T]
To determine whether a CFD exists for a D
p
and M
combination is a very difficult problem. It is shown
below that the problem belongs to complexity class
D
P
= {L
1
∩ L
2
| L
1
NP, L
2
coNP}
(Papadimitriou 1984). In fact, it is shown that the
problem is D
P
-hard.
Since NP and coNP are subclasses of D
P
(Note
that D
P
is not the same as NP ∩ coNP), the D
P
-
hardness of the CFD problem indicates that it is both
NP-hard and coNP-hard, and likely to be intractable.
2.1 CFDP Is Hard
The Critical Feature Dimension Problem (CFDP) is
stated formally as follows: Given a dataset D
p
, a
performance threshold T, an integer k (1 < k ≤ p),
and a fixed machine M. Is k is the T-critical feature
dimension of (D
p
, M)?
The problem to decide if k is the T-critical
feature dimension of the given dataset D
p
belongs to
the class D
P
under the assumption that, given any D
i
∝D
p
, whether P
M
(D
i
) T can be decided in
polynomial (in p) time, i.e., the machine M can be
trained and tested with D
i
in polynomial time.
Otherwise, the problem may belong to some larger
class, e.g.,
p
2
(Garey 1979). Note here that (NP ∪
coNP) D
P
p
2
in the polynomial hierarchy of
complexity classes.
To prove that the CFDP is a D
P
-hard problem,
we take a known D
P
-complete problem and
transform it into the CFDP. We begin by considering
the maximal independent set problem: In an
undirected graph, a Maximal Independent Set
(MIS) is an independent set (Garey 1979) that is not
a subset of any other independent set; a graph may
have many MIS’s.
EXACT-MIS Problem (EMIS) – Given a graph
with n nodes, and k ≤ n, decide if there is a MIS of
size exactly k in the graph is a problem known to be
D
P
-complete (Papadimitriou 1984). Due to space
limitations, we only sketch how to transform the
EMIS problem to the CFDP.
Given an instance of EMIS (a graph G with p
nodes, and integer k ≤ p), to construct the instance of
the CFDP, let dataset D
p
represent the given graph G
with p nodes (e.g., D
p
can be made to contain p data
points, with p features, representing the symmetric
adjacency matrix of G), let T be the value “T“ from
the binary range {T, F}, let
= k be the value in the
given instance of EMIS, and let M be an algorithm
that decides if the dataset represents a MIS of size
exactly
, if yes P
M
= “T“, otherwise P
M
= “F“, then
a given instance of the D
P
-complete EMIS problem
is transformed into an instance of the CFDP.
Detailed examples that explain the proof can be
found in (Suryakumar 2013).
TheCriticalFeatureDimensionandCriticalSamplingProblems
361

The D
P
-hardness of the CFDP indicates that it is
both NP-hard and coNP-hard; therefore, it’s most
likely to be intractable (that is, unless P = NP).
2.2 Heuristic Solution for CFDP
From the analysis above it is clear that even deciding
if a given number k is a CFD (for the given
performance threshold T) is intractable, so, to
determine what that number is for a dataset is
certainly even more difficult. Nevertheless, a simple
heuristic method is proposed in the following, which
represents a practical approach in attempting to find
the CFD of a given dataset and a given performance
threshold with respect to a fixed learning machine.
Though the heuristic method described below
can be seen as actually pertaining to a different
definition of the CFD, we argue that it serves to
validate the concept that
, the CFD, if not for all
datasets; and we show that for most datasets with
which experiments were conducted a CFD indeed
exists. Finally, the
determined by this heuristic
method is hopefully close to the theoretically-
defined CFD.
In the heuristic method, the CFD of a dataset is
defined as that number (of features) where the
performance of the learning machine would begin to
drop notably below an acceptable threshold, and
would not rise again to exceed the threshold. The
features are initially sorted in descending order of
significance and the feature set is reduced by
deleting the least significant feature during each
iteration of the experiment while performance of the
machine is observed. (For cross validation purposes,
therefore, multiple runs of experiments can be
conducted: the same machine is used in conjunction
with different feature ranking algorithms; and the
same feature ranking algorithm is used in
conjunction with different machines; then we can
compare if different experiments resulted in similar
values of the CFDif so the notion that the dataset
possesses a CFD becomes arguably more apparent.).
2.2.1 Critical Dimension Empirically
Defined
Let A = {a
1
, a
2
, …, a
p
} be the feature set where a
1
, a
2
,
…, a
p
are listed in order of decreasing importance as
determined by some feature ranking algorithm R.
Let A
m
= {a
1
, a
2
, …, a
m
}, where m ≤ p, be the set of
m most important features. For a learning machine M
and a feature ranking method R, we call µ (µ ≤ p) the
T-Critical Dimension of (D
p
, M) if the following
conditions are satisfied: when M uses feature set Aµ
the performance of M is T, and whenever M uses
less than µ features its performance drops below T.
2.2.2 Learning and Ranking Algorithms
In the experiments the dataset is first classified by
using six different algorithms, namely Bayes net,
function, rule based, meta, lazy and decision tree
learning machine algorithm. The machine with the
best prediction accuracy is chosen as the classifier to
find the CFD for that dataset.
For the experiments reported below, the ranking
algorithm is based on chi-squared (
2
) statistics,
which evaluates the worth of a feature by computing
the value of the
2
statistic with respect to the class.
Note that in the heuristic method the performance
threshold T will not be specified beforehand but will
be determined during the iterative process where a
learning machine classifier’s performance is
observed as the number of features is decreased.
2.3 Results
Three large datasets are used in the experiments, each
is divided into 60% for training and 40% for testing.
Six different models are built and retrained to get the
best accuracy. The model that achieves the best
accuracy is used to find the CFD.
2.3.1 Amazon 10,000 Dataset
The Amazon commerce reviews dataset (Frank 2013)
is a writeprint dataset useful for purposes such as
authorship identification of online texts, etc.
Experiments were conducted to identify fifty
authors in the dataset of online reviews. For each
author 30 reviews were collected, totaling 1500.
There are 10,000 attributes and they include authors’
linguistic style, such as usage of digit, punctuation,
words and sentences’ length and usage frequency of
words and so on. This becomes a multiclass
classification problem with 50 classes, where the
dataset contains numerical values for all features.
The results are shown in Figure 1, where a CFD
is found at 2486 features. The justifications that this
is the CFD are, firstly, from 2486 downward, the
performance drops quickly andunlike the situation
at around 9000the performance never rises
thereafter; secondly, the performance at feature size
2486 is only slightly lower than the highest observed
performance (at around 9000 features). Another point
at around 6000 may also be taken as the CFD;
however, 2486 is deemed more “critical” since there
is a big difference between 6000 and 2486 but very
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
362
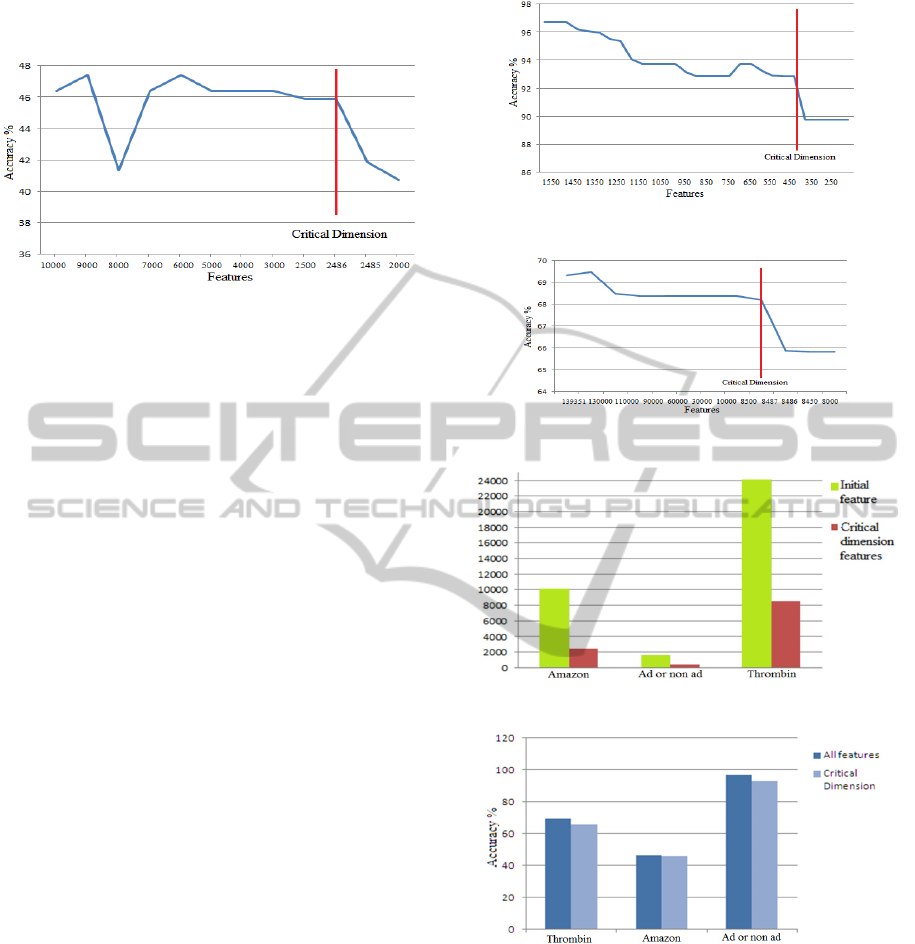
little difference between the performances at these
two points.
Figure 1: The CFD of the Amazon 10,000 dataset.
2.3.2 Amazon Ad or Non-Ad Dataset
The Amazon commerce reviews Internet
advertisement dataset is a set of possible
advertisements on web pages (Frank 2013). The task
is to predict whether an image is an advertisement
(“ad”) or not advertisement (“non-ad”). The dataset
includes 459 ad and 2820 non-ad images. Only 3 of
the 1558 attributes of the dataset are continuous
values and the remaining are binary. It is also
noteworthy that one or more of the three continuous-
valued features are missing in 28% of the instances.
The classification results of the ad and non-ad dataset
are shown in Figure 2 below, where a CFD at feature
size 383 is seen.
2.3.3 Thrombin Dataset
The training set consists of 1909 compounds tested
for their ability to bind to a target site on thrombin, a
key receptor in blood clotting (Frank 2013). Of these
compounds, 42 are active and the others inactive.
Each compound is described by a feature vector
containing a class value (A for active, I for inactive)
and 139,351 binary features describing 3-
dimensional properties of the molecule. Biological
activity in general and receptor binding affinity in
particular, correlate with various properties of small
organic molecules. The task is to determine which
properties are critical and to learn to accurately
predict the class value.
The classification results are shown in Figure 3,
where a CFD of 8487 is apparent.
Figures 4 and 5 summarize the results of
experiments done on the three large datasets.
We observe that each of the three datasets shows
an apparent CFD, which is much smaller than the
original feature dimension in each case while an
acceptable level of performance is maintained.
Figure 2: The CFD of the Amazon ad or non-ad dataset.
Figure 3: The CFD of the thrombin dataset.
Figure 4: Reduction in feature size of three large datasets.
Figure 5: Prediciton accuracy at the CFD and at intial
feature dimension (all features included).
For additional reference, the results of 16
different datasets that were studied earlier can be
found in (Suryakumar 2013).
3 RANDOM FEATURE
SELECTION
For certain data mining problems with large
TheCriticalFeatureDimensionandCriticalSamplingProblems
363
numbers of features, it is suspected that performance
depends more on the number of features used, than
the specific features that are selectedprovided that
the number of features used meets or exceeds the
CFD. In other words, if the dataset possesses a CFD
of µ, then a random selected feature set with µ
features will guarantee satisfactory performance in
model building. In particular, the text classification
problem is suspected to be such a problem where
random feature selection may well be sufficient.
3.1 Preliminary Results
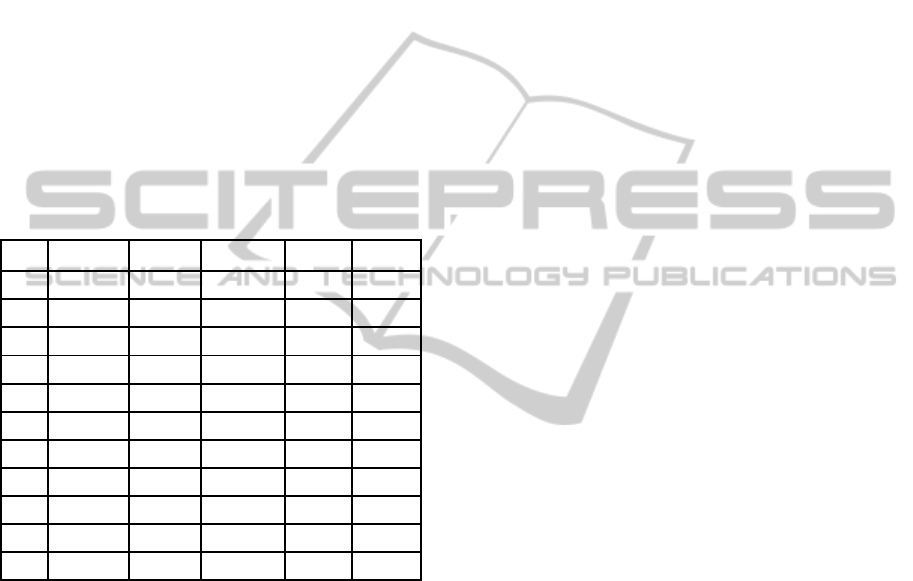
Experiments are carried out on a set of 4 well-known
corpuses of texts, using C4.5, KNN, and NB. Each
time a different set of µ randomly selected features
is
Table 1: Results of random feature selection in text mining
of four datasets.
Set R8(C4.5) R8(kNN) WebKB R52 News
group
1
70.86 87.11 82.43 58.37 63.82
2
58.61 82.46 76.34 57.26 52.96
3
64.84 82.2 72.05 55.26 55.28
4
68.01 80.71 72.28 58.66 57.28
5
69.33 84.22 75.43 55.61 57.28
6
68.85 78.91 77.44 55.03 51.08
7
68.51 85.26 73.5 49.28 51.2
8
60.39 81.01 70.12 54.98 52.34
9
66.5 80.13 72.65 55.78 57.28
10
58.26 80.46 72.65 54.75 51.94
Ave 65.42 81.75 74.49 55.5 55.05
used, and the performance is measured, the average
of 9 experiments is considered the performance of
the respective learning machine for the dataset. The
results are summarized in Table 1 above, where row
1 lists results of using the top µ features, rows 2-10
are 9 experiments using randomly selected µ
features, and the last row is the average of 9
experiments.
To conclude, it would appear that text mining is
an example of data mining problems where the
number of features used is more important than the
specific features selected.
4 THE CRITICAL SAMPLING
SIZE PROBLEM
In this section, we consider the other problem of data
reduction in big data mining: how to select a
minimal sample of data points that will guarantee
good performance? Assume again the dataset is
represented as an n by p matrix D
n,p
. The concept of
the Critical Sampling Size (CSS) of a dataset with n
points is that there may exist, with respect to a
specific machine M and a given performance
threshold T, a unique number
≤ n such that the
performance of M exceeds T when some suitable
sample of
data points is used; further, the
performance of M is always below T when any
sample with less than
data points is used. Thus,
is
the critical (or absolute minimal) number of data
points required in any sample to ensure that the
performance of M meets the given threshold T.
Formally, for dataset D
n
with n points (the
number of features in the dataset, p, is considered
fixed here when only sample size is concerned, and
therefore dropped as a subscript of the data matrix
D
n,p
),
(an integer between 1 and n) is called the T-
Critical Sampling Size of (D
n
, M) if the following
two conditions hold:
1. There exists D
, a
-point sampling of D
n
(i.e., D
contains
of the n vectors in D
n
) which lets
M to achieve a performance of at least T, i.e.,
(D
D
n
) [P
M
(D
) T], where P
M
(D
) denotes the
performance of M on dataset D
.
2. For all j <
, a j-point sampling of D
n
fails to
let M achieve performance of at least T, i.e.,
(∀D
j
D
n
) [j <
P
M
(D
j
) < T]
In the above, the specific meaning of P
M
(D
), the
performance of machine (or algorithm) M on sample
D
, is left to be defined by the user to reflect a
consistent setup of the data analytic (e.g. data
mining) task and the associated performance
measure. For examples, the setup may be to train
the machine M with D
and define P
M
(D
) as the
overall testing accuracy of M on a fixed test set
which is distinct from D
; or the setup may be to use
D
as training set and use D
n
D
as testing set. The
value of threshold T, which is to be specified by the
user as well, represents a reasonable performance
requirement or expectation of the specific data
analytic task.
To determine whether a CSS exists, for a D
n
and
M combination, is a very difficult problem.
Precisely, the problem of deciding, given D
n
, T, k (1
< k ≤ n), and a fixed M, whether k is the T-critical
sampling size of (D
n
, M) belongs to the class D
P
= {
L
1
∩ L
2
| L
1
NP, L
2
coNP} as well, where it is
assumed that the given machine M runs in
polynomial time (in n). In fact, it can be shown to be
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
364

D
P
-hard, exactly as the critical feature dimension
problem (CFDP) analyzed in Section 2, and by using
the same proof and merely selecting rows (instead of
columns) of the adjacency matrix of the graph to
construct a MIS. Due to space limitations, details of
the proof are omitted but can be found in
(Suryakumar 2013).
Due to the complete symmetry or similarity to
the CFD problem, it is suspected that simple
heuristic methods can be developed to be
sufficiently useful for practical purposes in solving
the CSS problem, in the same way heuristic methods
proved useful for finding the “critical features”
(even though the CFD found may be different from
the value based on the formal definition), as
illustrated in Section 2.
Therefore, proposed in the following is a heuristic
method for finding a critical sampling:
1. Apply a clustering algorithm (such as k-
means) to partition D
n
into k clusters.
2. Select, say randomly, m points from each
cluster to form a sampling D with mk points.
3. Apply M (learning machine, analytic
algorithm, etc.) on the sample, then measure
performance P
M
(D).
4. If P
M
(D) T, then D is a critical sampling,
and its size
is the critical sampling size for (D
n
,
M). Otherwise enlarge D by randomly select
another m points from each cluster, and repeat until
a critical sampling is found, or the whole D
n
is
exhausted and procedure fails to find
.
The values of the parameters k and m are to be
decided in consideration of the size and nature of the
dataset, the specific data analytic problem or task
being undertaken, and the amount of resource
available. As usual in all data analytic problems,
prior knowledge and domain expertise are always
helpful in designing the experimental setup.
Likewise, whether the random sampling is done with
or without replacement is a decision to be made
according to the dataset and the problem. Also,
progressive sampling techniques which possess nice
properties (Provost 1999, Domingo 2002) may be
incorporated into Step 4 instead of fixed increments
during each iteration.
The authors are conducting experiments for
validation of the concept that simple heuristic
methods are sufficient for application purposes in
dealing with the critical sampling size problem,
despite its high complexity.
5 CONCLUDING REMARKS
To meet some of the challenges in data mining
brought about by the big data (National Research
Council 2013), this paper presents some preliminary
results of the authors’ ongoing research:
Complexity analysis of the critical feature
dimension and critical sampling size problems.
Heuristic method for determining the critical
feature dimension.
Study of the effect of random selection of
critical features for the text classification problem.
Heuristic methods for finding critical sampling,
currently under study.
The corresponding positions of the authors being
proposed are the following:
The critical feature dimension problem is
intractable and requires heuristic solutions.
Simple heuristic methods are demonstrably
sufficient for applicational purposes in determining
the CFD of datasets.
Random selection of features that meets the
CFD may well be sufficient for data mining
purposes for certain problems whose associated
datasets have large number of features.
Heuristic methods are likely to be practicable
for finding critical sampling as well.
In view of the preliminary results, it is believed
that the ongoing research on heuristic methods for
determining critical feature dimensions and for
finding critical sampling, if successful, may lead to
the development of effective solutions to cope with
some of the challenges inherent in big data analytic
problems due to the large dimensions of feature sets
and the large number of samples in the big data.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the reviewer
whose most insightful comments point them to
fruitful study such as inter-feature correlations,
fractal dimension, the Hausdorff dimension, etc., in
explaining the results on feature selection/reduction.
REFERENCES
Blum, A., Langley, P., 1997. Selection of relevant
features and examples in machine learning, Artificial
Intelligence, vol. 97, pp.1-2.
Domingo, C., Gavaldà, R. and Watanabe, O. 2002.
Adaptive sampling methods for scaling up knowledge
TheCriticalFeatureDimensionandCriticalSamplingProblems
365

discovery algorithms, Data Mining and Knoledge
Discovery, Kluwer Academic Publishers, Vol. 6 No.
2, pp.131-152, 2002.
Frank, A., Asuncion, A., 2013. UCI Machine Learning
Repository, School of Information and Computer
Science, University of California, Irvine,
http://archive.ics.uci.edu/ml.
Garey, M.R., Johnson, D.S., 1979. Computers and
Intractability: A Guide to the Theory of NP-
Completeness, W. H. Freeman and Compnay.
Guyon, I., Elisseeff, A., 2003. An Introduction to Variable
and Feature Selection, Journal of Machine Learning
Research, Vol 3, pp.1157-1182.
National Research Council, 2013. Frontiers in Massive
Data Analysis, The National Academies Press.
Papadimitriou, C.H.,Yannakakis, M., 1984. The
complexity of facets (and some facets of complexity),
Journal of Computer and System Sciences 28:244-259.
Provost, F., Jensen, D. and Oates, T. 1999. Efficient
Progressive Sampling. Proceeding of the Fifth
International Conference on Knowledge Discovery
and Data Mining, ACM KDD-99, pp.23-32.
Suryakumar, D., 2013. The Critical Dimension Problem –
No Compromise Feature Selection, Ph.D. Dissertation,
New Mexico Institute of Mining and Technology.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
366
