Ofﬂine Evolution of Normative Systems

Magnus Hjelmblom

1,2

Faculty of Engineering and Sustainable Development, University of G

avle, SE-80176 G

avle, Sweden

Department of Computer and Systems Sciences, Stockholm University, Forum 100, SE-16440, Kista, Sweden

Keywords:

Norm-regulated Multi-Agent System, Normative MAS, DALMAS, Norm Evolution, Evolutionary Algorithm.

Abstract:

An approach to the pre-runtime design of normative systems for problem-solving multi-agent systems (MAS)

is suggested. A key element of this approach is to employ evolutionary mechanisms to evolve efﬁcient nor-

mative systems. To illustrate, a genetic algoritm is used in the process of designing a normative system for

an example MAS based on the DALMAS architecture for norm-regulated MAS. It is demonstrated that an

evolutionary algorithm may be a useful tool when designing norms for problem-solving MAS.

1 INTRODUCTION

Agent-based modeling and simulation is an active

ﬁeld of study which, for example, may offer meth-

ods for solving complex optimisation problems. In

this setting, agents are required to cooperate to solve

the problem at hand. In complex systems with ad-

justable agent autonomy, sophisticated planning can

often be replaced by norms; see for example (Verha-

gen and Boman, 1999). The study of norm-regulated

multi-agent systems, often referred to as normative

MAS, has also attracted a lot of attention. The Nor-

MAS roadmap (Andrighetto et al., 2013b) is a com-

prehensive introduction to and overview of the ﬁeld.

The combination of agent-based modeling and sim-

ulation and normative MAS is a promising ﬁeld of

study. (Balke et al., 2013)

It is often desirable to replace planning (and re-

planning), since it may be a complex and time-

consuming task, especially in collaborative environ-

ments. On the other hand, designing good normative

systems is also a challenge. The approach suggested

here, whose basic ideas were outlined in (Odelstad

and Boman, 2004, pp. 164f), is to use evolutionary

mechanisms, employed in a genetic algorithm, to aid

the ‘off-line’ (i.e., pre-runtime) design of normative

systems for problem-solving multi-agent systems.

The paper is structured as follows. In Sect. 1.2,

previous work on the DALMAS architecture for norm-

regulated MAS is brieﬂy presented. Sect. 2 intro-

duces an example DALMAS which is used in Sect. 3

to demonstrate how to employ evolutionary mecha-

nisms in the process of designing norms, by applying

an evolutionary algorithm to this example. Sect. 4

concludes and suggests some lines of future work.

1.1 Related Work

The runtime emergence of norms within artiﬁcial so-

cial systems has attracted the attention of many re-

searchers; see, e.g., (Andrighetto et al., 2013a). How-

ever, evolving normative systems as part of the pro-

cess of designing norm-regulated MAS is not as well

studied, but evolutionary approaches for learning be-

haviour patterns or strategies for coordination have

been successfully used in, e.g., the RoboCup

do-

main; see for example (Luke et al., 1998; Di Pietro

et al., 2002; Nakashima et al., 2004). In fact, the sim-

ple decision policies evolved by Di Pietro et al. for

the RoboCup Keepaway game can be regarded as sim-

ple normative systems consisting of production rules

which prescribe certain behaviours in certain situa-

tions.

1.2 Previous Work

DALMAS (Odelstad and Boman, 2004) is an abstract

architecture for a class of norm-regulated multi-agent

systems. A deterministic DALMAS is a simple multi-

agent system in which the actions of an agent are con-

nected to transitions between system states. In a de-

terministic DALMAS the agents take turns to act; only

one agent at a time may perform an action. By al-

lowing ‘do nothing’ actions and accelerating the turn-

taking, systems with close to asynchronous behaviour

can be obtained.

Formally, a DALMAS is an ordered 9-tuple, where

the components are various sets, operators and func-

tions which give the speciﬁc DALMAS its unique fea-

http://www.robocup.org

213

Hjelmblom M..

Ofﬂine Evolution of Normative Systems.

DOI: 10.5220/0005284102130221

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 213-221

ISBN: 978-989-758-074-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

tures. Of particular interest is the deontic structure-

operator, which for each situation of the system deter-

mines an agent’s deontic structure (i.e., the set of per-

missible acts) on the feasible acts in the current situa-

tion, and the preference structure-operator, which for

each situation determines the preference structure on

the permissible acts. A norm-regulated simple deter-

ministic DALMAS employs what is often referred to

as ‘negative permission’, by letting the deontic struc-

ture consist of all acts that are not explicitly prohibited

by a normative system. The preference structure con-

sists of the most preferable (according to the agent’s

utility function) of the acts in the deontic structure.

In short, a DALMAS agent’s behaviour is regulated by

the combination of a normative system and a utility

function; this ‘agent oeconomicus norma’

chooses

the most desirable act, according to the utility func-

tion, within the ‘room for manouver’ determined by

the norms. The DALMAS’s normative framework is

based on an algebraic version of the Kanger-Lindahl

theory of normative positions, in which normative

consequences are formulated by applying normative

operators to descriptive conditions. From these gen-

eral normative sentences on conditions follow nor-

mative sentences regarding speciﬁc states of affairs,

which in turn result in permission or prohibition of

individual actions in speciﬁc situations. (See for ex-

ample (Lindahl, 1977; Lindahl and Odelstad, 2004;

Odelstad and Boman, 2004; Odelstad, 2008) for an

introduction.) Hence, the norms in the DALMAS ar-

chitecture play a different role, and is represented in

a fundamentally different way, than, e.g., the decision

rules in the RoboCup setting (see Sect. 1.1).

Since the agents take turns to act, each individ-

ual step in a run of a DALMAS may be characterised

by an ordered 5-tuple S = hx, s, A, Ω, Si whose com-

ponents are a set of states S, a state s, an agent-set

Ω = {x

, ..., x

}, the acting (‘moving’) agent x, and

an action-set A = {a

, ..., a

In this setting, a may

be regarded as a function such that a(x, s) = s

means

that s

is the resulting state when x performs act a in

state s. In the following, the abbreviation s

will be

used for a(x, s) when there is no need for an explicit

reference to the action a and the acting agent x. Since

the action by the acting agent is deterministic and is

performed asynchronously, there is no simultaneous

action by other agents (including the ‘environment’,

which may be regarded as a special kind of agent).

Furthermore, we assume that a ν-ary condition d is

true or false on ν agents x

, ..., x

∈ Ω in s; this will

Cf. (Odelstad, 2008, Sect. 1.8.3).

In (Hjelmblom, 2013) such a tuple is called a transition

system situation.

be written d(x

, ..., x

;s).

To facilitate the presenta-

tion, X

will often be used as an abbreviation for the

argument sequence x

, ..., x

. Negations d

, conjunc-

tions (c ∧ d) and disjunctions (c ∨d) can be formed in

the following way:

) iff ¬d(X

(c ∧ d)(X

) iff c(X

) and d(X

), and

(c ∨ d)(X

) iff c(X

) or d(X

)

where ν = max(p, q).

Therefore, it is possible to

construct Boolean algebras of conditions.

Let the situation hx, si be characterised by the

moving agent x and the state s in a norm-regulated

simple deterministic DALMAS. In the following, we

assume that norms always apply to the moving agent

x in a situation hx, si, in order to facilitate the pre-

sentation. A norm in N is represented by an or-

dered pair hg, ci, where the (descriptive) condition g

on a situation hx, si is the ground of the norm and

the (normative) condition c on hx, si is its conse-

quence; see, e.g., (Odelstad and Boman, 2004). We

ﬁrst deﬁne a set of ‘transition type operators’ C

based on Table 2 in (Hjelmblom, 2014a), and a set of

corresponding ‘transition type prohibition operators’

, k ∈ {1, 2Λ, 2Ω, 4Λ, 4Ω, 5, 6Λ, 6Ω, 7}, such that

d(X

;x, s) is intended to mean that if C

d(X

;x, s)

holds, then a is prohibited for x in hx, si.

In effect,

d(X

;x, s) implies a prohibition of zero, one or two

of the four ‘basic transition types’ with regard to the

state of affairs d(X

For example, hc, P

di, where c

and d can have different arity, represents the sentence

∀x

, x

, ..., x

∈ Ω : c(x

, x

, ..., x

;x, s) →

d(x

, x

, ..., x

;x, s)

where Ω is the set of agents, x is the acting agent

(to which the norm applies) in the situation hx, si,

and ν = max(p, q). If the condition speciﬁed by the

ground of a norm for some agents in some situation,

then the (normative) consequence of the norm is in

effect in that situation. If the normative system con-

tains a norm whose ground holds in the situation hx, si

In the special case when the sequence of agents is

empty, i.e. ν = 0, d represents a proposition which is true

or false in s.

The free variables in c(x

, ..., x

) must be the same, and

in the same order, as the free variables in d(x

, ..., x

), but

it is not necessary that p and q have the same arity. Cf.

(Odelstad and Boman, 2004, p. 146).

The original set of operators in (Odelstad and Boman,

2004) contains seven operators, indexed 1-7. In (Hjelm-

blom, 2013), two new operators were added. See this paper

for an explanation of the somewhat peculiar indices.

See (Hjelmblom, 2014a, Sect. 2) for a description of

the basic transition types.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

214

and whose consequence prohibits the type of transi-

tion represented by x performing action a, then a is

prohibited for x in hx, si:

Prohibited

x,s

(a) according to N

if there exists a p-ary condition c

and a q-ary condition d

and a k ∈ {1, 2Λ, 2Ω, 4Λ, 4Ω, 5, 6Λ, 6Ω, 7},

such that hc, P

di is a norm in N,

and there exist x

, ..., x

such that

c(x

, ..., x

;x, s) & C

d(x

, ..., x

;x, s),

where ν = max(p, q).

Hence, if c(x

, ..., x

;x, s) for some sequence

of agents x

, ..., x

, then the normative condi-

tion P

d(x

, ..., x

;x, s) is ‘in effect’. Thus, if

d(x

, ..., x

;x, s) holds, then a is prohibited for x in

s. (Cf. the examples in Sect. 3.1.) Table 1 shows the

set of nine norm-building operators, together with (in

the rightmost column) the corresponding C

applied

to d(x

, ..., x

;s). Cf. Table VI in (Hjelmblom,

2014b), which also shows a suggested interpretation

of the P

operators in terms of an extended set of

types of one-agent normative positions, based on the

Kanger-Lindahl theory of normative positions.

A general-level Java/Prolog implementation of the

DALMAS architecture has been developed, to facil-

itate the implementation of speciﬁc systems. The

Colour & Form system, the Waste-collector system

and the Forest Cleaner system are three speciﬁc sys-

tems that have been implemented using this frame-

work. The reader is referred to (Odelstad and Boman,

2004; Hjelmblom, 2008; Hjelmblom and Odelstad,

2009; Hjelmblom, 2011) for a description of these

systems and their implementations.

The approach to normative systems employed in

this framework is ideally suited for evolution of nor-

mative systems, since the set of P

operators exhausts

the set of logical possibilities regarding prohibition of

transition types. Therefore each conceivable norma-

tive system, consisting of conditional norms based on

descriptive conditions selected from a set of potential

grounds and normative conditions selected from a set

of potential consequences, could become a candidate

for evaluation in the execution of an evolutionary al-

gorithm. This idea will be further explored in the fol-

lowing sections.

2 EXAMPLE: EXPLORER

DALMAS

Let us consider a class of systems of agents operat-

ing in an environment consisting of a grid of squares

ordered in rows and columns, in which each square

is assigned a pair of integer coordinates. Let us as-

sume that the joint goal of the agents is to explore as

much as possible of the grid using a ﬁxed number of

moves. An agent can stay in the current square, i.e.,

do nothing, or move one square in one of eight direc-

tions (east, northeast, north, northwest, west, south-

west, south, southeast) as long as it stays within the

boundaries of the grid. In other words, in a given

situation, an action is feasible if and only if it does

not move the agent off limits. It should of course be

noted that these simple systems (in the following re-

ferred to as Explorer DALMASes) in themselves are of

limited interest, but the idea here is to illustrate how

evolutionary mechanisms could be used in the process

of designing normative systems for problem-solving

MAS.

To simulate a situation with limited possibilites for

communication between agents and only local knowl-

edge of the environment, we further assume that an

agent only knows the status (visited or unvisited) of

the immediately surrounding squares, and the loca-

tion of other agents within two squares. An agent’s

preference is represented by a very simple utility

function such that moving to an unvisited square is

preferred over moving to a visited square, and stay is

the least preferred action. In the case of a tie between

equally preferred actions, one of them is randomly se-

lected. In other words, all agents have the same utility

function.

To make the situation more concrete, let us assume

that the size of the grid is 7×7 squares and place three

agents at square (1, 1), the leftmost lowest square.

Note that this system can be considered as an instance

of the Waste-collector system, in which visited (resp.,

unvisited) squares are represented by 0 (resp., 1) units

of ‘waste’. The higher number of ‘waste’ carried by

an agent, the higher number of unvisited squares have

been entered by that agent. It would not be a very

difﬁcult task to design a plan where the agents take

turns to act in such a way that all remaining 48 squares

are visited in 48 moves. But if the environment gets

changed, e.g., is resized or reshaped, the plan must

be recalculated. What if we let norms replace plans

in this class of environments? Let us investigate the

interplay between the agents’ utility functions, repre-

senting their ‘desires’, and a normative system which

determines their ‘room for manouvre’. One idea is

to base norms on the spatial relationship between

the agents, potentially restricting how the agents may

move in the proximity of other agents. We deﬁne

a condition Lap

, n ∈ {0, 1, 2, 3, 4, 6, 9}, with the in-

tended meaning that Lap

, x

;s) holds if and only

if the ‘protected spheres’ of agents x

and x

overlap

with i squares in a state s. The protected sphere con-

OfflineEvolutionofNormativeSystems

215

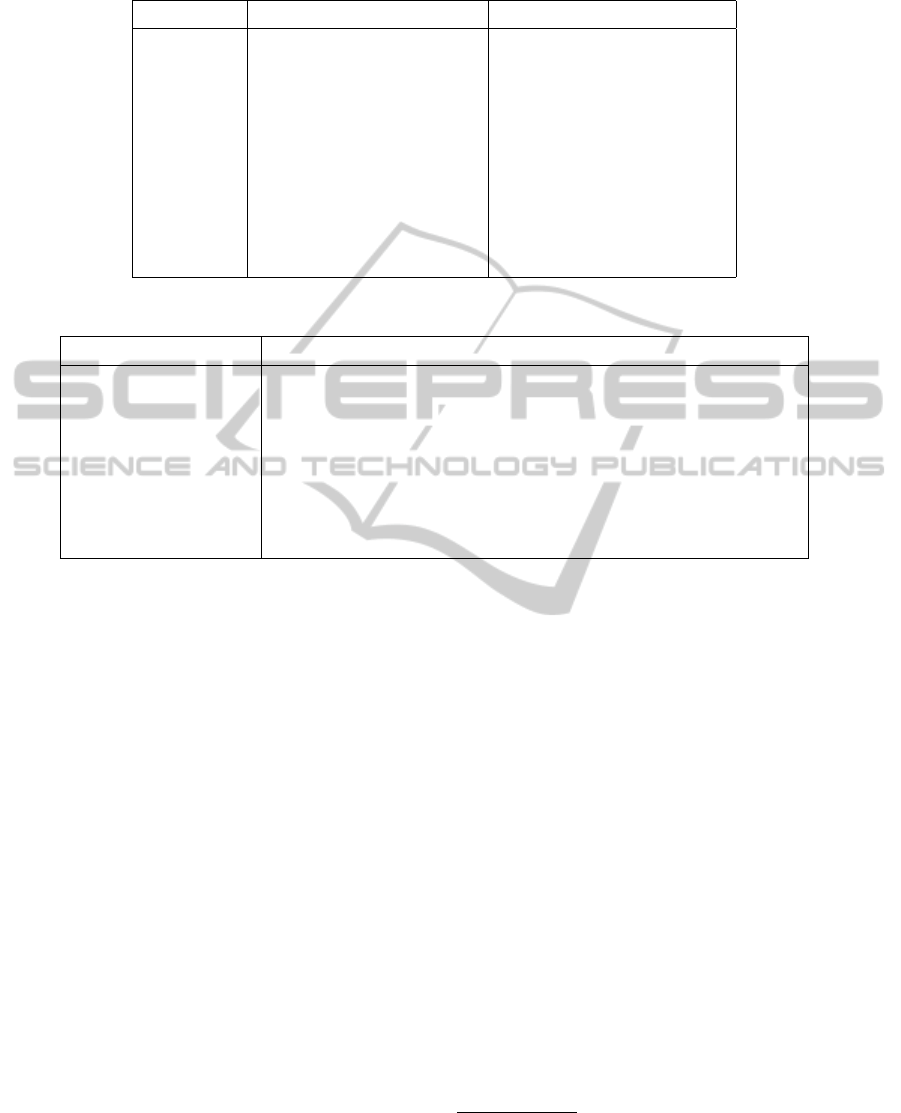
Table 1: Transition Type Conditions (Λ mnemonic for Leave and Ω for Oppose).

-operator Corresponding C

-operator Prohibited

(x, s) if

- -

2Λ

d(X

;s) ∧ ¬d(X

;a(x, s))

2Ω

¬d(X

;s) ∧ ¬d(X

;a(x, s))

4Λ

¬d(X

;s) ∧ d(X

;a(x, s))

4Ω

d(X

;s) ∧ d(X

;a(x, s))

¬d(X

;a(x, s))

6Λ

¬(d(X

;s) ↔ d(X

;a(x, s)))

6Ω

d(X

;s) ↔ d(X

;a(x, s))

d(X

;a(x, s))

Table 2: Possible changes of Lap

State of affairs Possible state of affairs in next state

Lap

, x

) Lap

, x

), Lap

, x

), Lap

, x

), Lap

, x

)

Lap

, x

) Lap

, x

), Lap

, x

), Lap

, x

)

Lap

, x

) Lap

, x

), Lap

, x

), Lap

, x

), Lap

, x

), Lap

, x

)

Lap

, x

) Lap

, x

), Lap

, x

), Lap

, x

), Lap

, x

)

Lap

, x

) Lap

, x

), Lap

, x

), Lap

, x

)

Lap

, x

) Lap

, x

), Lap

, x

), Lap

, x

), Lap

, x

)

6= x

&Lap

, x

) Lap

, x

), Lap

, x

)

sists of ω’s square plus the eight surrounding squares.

See Fig. 1 in (Hjelmblom, 2008) for an illustra-

tion. Table 2 shows how the overlap can change from

one state to another, given the nine available actions.

Note that since it is always the case that Lap

, x

Lap

, x

) (Odelstad and Boman, 2004) x

6= x

for n < 9, and x

= x

(Odelstad and Boman, 2004)

Lap

, x

). Furthermore, Lap

, x

) (Odelstad

and Boman, 2004) ¬Lap

, x

) for n 6= m. Now let

the ‘elementary’ conditions Lap

, Lap

Lap

, Lap

, together with the ‘non-elementary’ con-

dition (6= ∧Lap

), form a set of potential descrip-

tive grounds for conditional norms. The set of po-

tential normative consequences corresponding to each

ground is constructed by applying the norm-building

operators P

, P

2Λ

, ..., P

(see Sect. 1.2) to the con-

ditions listed in the corresponding rows in Table 2.

Thus, the potential consequences for, e.g., Lap

are

Lap

,..., P

Lap

, P

Lap

,..., P

Lap

, P

Lap

,...,

Lap

, and P

Lap

,..., P

Lap

. Note that it would

be meaningless to, e.g., let P

Lap

be a potential con-

sequence for Lap

, since none of the available acts

can change the state of the system in such a way that

Lap

, x

) holds in one state and Lap

, x

) holds

in the next state.

With these building blocks available, norma-

tive systems for Explorer DALMASes can be con-

structed. Let us use the following approach: For

each condition c in the leftmost column of Ta-

ble 2, one norm hM

c, P

di is added to the nor-

mative system for each condition d in the right-

most column.

E.g., for Lap

we add four norms:

hLap

, P

Lap

i, hLap

, P

Lap

i, hLap

, P

Lap

and hLap

, P

Lap

i. Note that, as regards the ground

(6= ∧Lap

), one of h(6= ∧Lap

), P

Lap

i and h(6=

∧Lap

), P

Lap

i is redundant (since the only condi-

tions that can follow Lap

are Lap

and Lap

) and can

therefore be removed. This gives a total of 24 norms.

Note, however, that not all normative systems formed

in this way are coherent. To begin with, some sets of

rules may be contradictory, according to the intended

meaning of the P

operators, but the problem of coher-

ence (sometimes referred to as ‘absence of conﬂicts’)

cannot simply be reduced to logical consistency; see

for example (Alechina et al., 2013). We will return to

this issue in Sect. 3.1.

We would now like to ﬁnd the ‘best’ normative

system, i.e., the normative system that, together with

the simple utility function described earlier, on aver-

age makes the Explorer system most efﬁcient. The

following measure of ‘efﬁciency’ will be employed:

The ‘move operator’ M

identiﬁes the agent to which

the normative condition applies with the acting agent and

with the ﬁrst agent in the argument sequence X

. See for

example (Hjelmblom, 2013) for an explanation. In the fol-

lowing, M

is omitted to facilitate reading.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

216

the normative system is applied to three different

Explorer DALMASes, operating on grids of (almost)

equal sizes but different shapes: 6 × 8 squares, 7 × 7

squares, and 10 × 5 squares, respectively. On each

grid, three agents are initially placed on square (1, 1).

A k-event run of each of these three systems will be

performed, where k is the number of unvisited squares

from the beginning. For each run, the ratio between

the total number of visited squares and the total num-

ber of unvisited squares in the beginning is calculated.

If the normative system is not coherent, in the sense

that at some point during the run all actions (includ-

ing stay) become prohibited for the acting agent, then

the evaluation score is set to 0. The score of the nor-

mative system under evaluation is then the average of

the three ratios obtained. We have now obtained an

optimisation problem which may be solved with the

help of an evolutionary algorithm.

3 EVOLUTION OF EXPLORER

NORMS

Evolutionary algorithms (EA), being a subﬁeld of

evolutionary computation, use the principles of bi-

ological evolution (such as reproduction, mutation,

recombination, and selection) to solve problems on

computers. For a comprehensive introduction to this

ﬁeld the reader is referred to, e.g., (Whitley, 2001).

In the Explorer DALMAS setting, there is some ran-

domness in the agents’ choices of actions, and in such

‘noisy’ domains, evolutionary algorithms are known

to work well. (Darwen, 2000) We thus implement

a basic genetic algorithm (one of the most common

forms of EAs) for Explorer DALMAS norms:

1. Genesis

Create an initial population of n candidate nor-

mative systems, half of which are entirely ran-

domly generated and half of which consist of

-consequences (the most permissive conse-

quences) only. Each candidate is represented by

a character string consisting of 24 characters from

{1, ..., 9}.

2. Evaluation

Evaluate each member of the population, by trans-

lating the character string to a normative system

according to the scheme presented in Sect. 2, run-

ning three different systems regulated by this nor-

mative system and using as ﬁtness function the av-

erage of the evaluation scores of the three runs.

3. Survival of the Fittest

Select a number of members of the evaluated pop-

ulation, favouring those with higher ﬁtness scores,

to be the parents of the next generation.

4. Evolution

Generate a new population of offspring by ran-

domly altering and combining elements of the

parent candidates. The evolution is performed by

the two basic evolutionary operators cross-over

and mutation.

5. Iteration

Repeat steps 2-4 until the termination condition

(see Table 3) is met.

The evolutionary algorithm was implemented us-

ing the Java-based Watchmaker framework for evolu-

tionary computation

together with a slightly adapted

Java/Prolog implementation of the Waste-collector

system (Hjelmblom, 2008; Hjelmblom and Odelstad,

2009).

The latter was used in step 2 to perform the

k-event runs of Explorer systems to be evaluated.

3.1 Result

The algorithm was run with the parameter values

shown in Table 3; the execution time on an ordinary

laptop was 5-6 hours. The graph in Fig. 1 shows the

ﬁtness values (evaluation scores) of the best norma-

tive system, as well as the average ﬁtness values, in

each generation. We can see that, initially, the best

ﬁtness (which is obtained by a normative system with

-consequences only, i.e., a normative system which

allows everything) is around 0.78. Up to around gen-

eration 25, we can see a slow but quite steady im-

provement in the best ﬁtness values, although the im-

pact of the slight randomness in the agents’ choices

of actions is clear. The highest scores, just above

0.86, which roughly corresponds to three more vis-

ited squares per run, are obtained in generations 41

and 78. After 25 generations there seems to be no

signiﬁcant improvement.

According to the log, the best normative system in

generation 41 (with P

-norms omitted for brevity) is

translated to

h(6= ∧Lap

), P

2Ω

Lap

i, hLap

, P

6Λ

Lap

hLap

, P

6Ω

Lap

i, hLap

, P

2Λ

Lap

hLap

, P

6Λ

Lap

i, hLap

, P

4Ω

Lap

hLap

, P

4Ω

Lap

i, hLap

, P

4Λ

Lap

http://watchmaker.uncommons.org/

The source code is available for download via

http://drp.name/norms/nrtssit, together with a log of a run

of the algorithm.

OfflineEvolutionofNormativeSystems

217

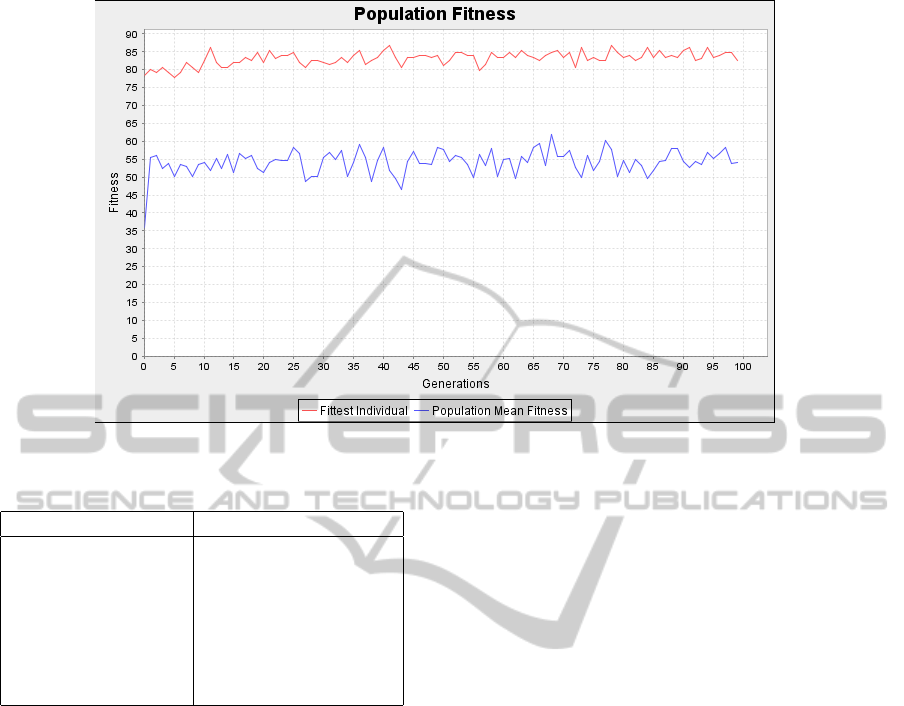
Figure 1: Evolution Progress. Lower curve shows mean ﬁtness.

Table 3: Choice of Parameter Values.

Parameter Value

Population size 100 individuals

Termination condition 100 generations evolved

Level of elitism 25%

Crossover probability 0.7

Crossover points 6

Mutation probability 0.05

Selection strategy Roulette wheel selection

A closer look at the log reveals that, of the best

candidates with a ﬁtness over 0.85, (1) all but

one (13 out of 14) contain either hLap

, P

6Λ

Lap

or hLap

, P

4Λ

Lap

i, and (2) all but three con-

tain hLap

, P

6Λ

Lap

i or hLap

, P

4Λ

Lap

i. Let

us ﬁrst consider (1). As we see in Table 1,

the intended meaning of hLap

, P

6Λ

Lap

i is

that if Lap

, x

) for some agents x

and

, then action a is prohibited for the moving

agent if ¬Lap

, x

;s) ∧ Lap

, x

;a(x, s)) or

Lap

, x

;s) ∧ ¬Lap

, x

;a(x, s)). Since Lap

implies Lap

, the second disjunct never becomes true

when Lap

, x

); hence a is prohibited for the mov-

ing agent if Lap

, x

;s) and Lap

, x

;a(x, s)).

The meaning of hLap

, P

4Λ

Lap

i is that if

Lap

, x

) for some agents x

and x

, then a is

prohibited if ¬Lap

, x

;s) ∧ Lap

, x

;a(x, s));

i.e., if Lap

, x

;s) and Lap

, x

;a(x, s)). Hence,

hLap

, P

6Λ

Lap

i and hLap

, P

4Λ

Lap

i are ‘opera-

tionally equivalent’ in the Explorer DALMAS setting,

in the sense that they prohibit the same actions in the

same situation. Furthermore, both are operationally

equivalent to hLap

, P

Lap

i with the intended

interpretation that if Lap

then the moving agent

shall see to it that not Lap

. A similar case can be

made for (2); hLap

, P

6Λ

Lap

i, hLap

, P

4Λ

Lap

i and

hLap

, P

Lap

i are operationally equivalent and thus

interchangeable in this setting.

(1) and (2) illustrate that, in many settings,

the set of consequences may contain redundancy.

This is an effect of the fact that, in this particu-

lar setting, the set of grounds and the set of con-

sequences are constructed from the same set of

conditions. Whether this is a problem or not is

probably dependent on the particular setting. We

may also note that, for example, the meaning of

hLap

, P

4Ω

Lap

i would be that if Lap

, x

) for

some agents x

and x

, then a is prohibited for the

moving agent if Lap

, x

;s) ∧ Lap

, x

;a(x, s)).

Now, since Lap

implies Lap

, Lap

, x

;s) ∧

Lap

, x

;a(x, s)) can never become true when

Lap

, x

). Hence, hLap

, P

4Ω

Lap

i will never pro-

hibit any actions, and is thus operationally equivalent

to, hLap

, P

Lap

i in this setting. This illustrates an-

other kind of redundancy. Another consequence of

employing negative permission is that normative sys-

tems may evolve which are incoherent (see Sect. 1.2)

according to the underlying logic of the P

opera-

tors, but still meaningful in an ‘operational’ sense. To

avoid or at least reduce redundancy and logical in-

coherence (and thus, potentially, signiﬁcantly reduce

the search space for the evolutionary algorithm) in

the setting at hand, a more precise representation of

genes and a more careful design (based on a more

thorough analysis of the relationships between poten-

tial grounds and consequences) of the genetic opera-

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

218

tors is required. For this purpose, the mechanisms for

norm addition and subtraction described in (Lindahl

and Odelstad, 2013, Sect. 4.3) might be very useful.

Based on the above analysis, the following set

of Explorer norms (again, P

-norms are omitted) is

suggested: {hM

Lap

, P

Lap

i,hM

Lap

, P

Lap

i}.

The intended interpretation is

(1) For all x,y: M

Lap

(x, y; x, s) →

Lap

(x, y; x, s)); and

(2) For all x,y: M

Lap

(x, y; x, s) →

Lap

(x, y; x, s)).

This represents the following simple set of ‘rules

of thumb’: (1) If you stand in the square next to

another agent’s square, you shall move so that you

do not end up in the same location as the other

agent, and (2) if your protected sphere overlaps an-

other agent’s protected sphere with two squares, you

shall move so that the overlap does not increase to

four. These rules may be expressed in logical form

using the deontic operator Shall and the action op-

erator Do: (1) ∀x, y: Lap

(x, y), and x is the mov-

ing agent, implies Shall Do(x, ¬Lap

(x, y)); and (2)

∀x, y: Lap

(x, y), and x is the moving agent, implies

Shall Do(x, ¬Lap

(x, y)). Cf. (Odelstad and Boman,

2004; Hjelmblom, 2014b).

Test runs indicate that the average improvement

with this very simple normative system compared

with a system with no restrictions is two to three

additional squares visited. As the Explorer DAL-

MAS example was chosen for demonstration purposes

only, we shall be content with the simple analysis per-

formed here. In more complex scenarios, other more

powerful (e.g., statistical) methods could be useful.

3.2 Discussion

Validation of the suggested approach to the design of

normative systems for problem-solving MAS is, of

course, a non-trivial problem. One aspect of this prob-

lem is the difﬁculty of applying this approach, but

most important is probably to focus on the quality of

the results it produces, i.e., to validate the systems ob-

tained by applying the approach. The performance of

norm-regulated MAS designed in this way could, for

example, be compared with the performance of sys-

tems (norm-regulated systems as well as, e.g., plan-

ning systems) designed ‘by hand’. Such compar-

isons require domain-speciﬁc performance measures,

which makes a general-level (i.e., domain indepen-

dent) validation very difﬁcult, if not impossible. Even

within a speciﬁc domain, validation is non-trivial and

sensitivity analyses are required. A good starting-

point is to consider every tool in the evolutionary tool-

box, together with a thorough analysis of the domain

at hand, to increase the chance of evolving the optimal

normative system. First, the parameters controlling

the evolutionary algorithm may be varied: the pop-

ulation size, the number of evolved generations, the

level of elitism (i.e., the portion of the best candidates

which are allowed to survive into the next generation),

the probability of crossover, the number of crossover

points, and the selection strategy (e.g., tournament se-

lection instead of roulette wheel). Other ideas include

using other representations of chromosomes, such as

tree-based representations to allow for normative sys-

tems with a variable number of norms, or (as has al-

ready been mentioned) more carefully designed evo-

lutionary operators that exclude redundant and/or in-

coherent candidates from evaluation. More advanced

schemes, such as island evolution (where several pop-

ulations are evolved in parallel, with a small probabil-

ity of ‘migration’ between such ‘islands’) or cooling

(where the crossover and mutation probabilities grad-

ually decreases), could also be tried.

Furthermore, the parameters for the particular set-

ting may also be varied. For example, one might

want to consider grounds and consequences based on

other conditions. In the Explorer DALMAS domain

one could try, e.g., Lap

conditions based on larger

protected spheres (since it seems reasonable to ex-

pect that a normative system based on small protected

spheres will be most ‘effective’ when the agents are

relatively close to each other), or generalised versions

of Lap

conditions involving three or more agents.

Other ideas are to allow individual utility functions

for each agent, or evolving the utility function and

the normative system in parallel. In general, spe-

cial treatment is required for domains such as the

Explorer DALMAS where the ﬁtness evaluations are

‘noisy’, i.e., subject to some degree of randomness.

To deal with noisy ﬁtness evaluations, a number of

techniques are available, for example increasing the

population size, and resampling and averaging the ﬁt-

ness. (Di Pietro et al., 2002, Sect. 3.3) As described

in Sect. 2, a variant of the latter technique is used

in the Explorer DALMAS ﬁtness evaluations. Another

option regarding the evaluation function is to allow

more or less variation regarding, e.g., grid sizes or

shapes, number of agents, number of events per run

and number of runs per normative system. However,

large populations, in combination with expensive ﬁt-

ness calculations in each generation, are computation-

ally challenging. The moving average approach by Di

Pietro et al. can be used to reduce the number of sam-

ples needed per generation, and thus allow for run-

ning more generations in a given run-time. When a

candidate is generated for the ﬁrst time, its ‘ﬁtness

array’ is initialised with n ﬁtness evaluations. For

OfflineEvolutionofNormativeSystems

219

each new generation, the evaluation score is calcu-

lated only once, and the oldest score in the ﬁtness

array is replaced with the new score. A candidate’s

ﬁtness is then the average of the evaluation scores in

the ﬁtness array.

4 CONCLUSION AND FUTURE

WORK

A sketch of a methodology for using evolutionary

mechanisms as part of the pre-runtime design of nor-

mative systems for problem-solving MAS was pre-

sented. The idea behind this methodology is to use

a ‘top-down’ approach of selecting (a subset of ) the

most ‘efﬁcient’ norms from an evolved normative sys-

tem, rather than a ‘bottom-up’ approach of designing

a normative system entirely from scratch. To illus-

trate the idea, a simple system, based on the DALMAS

architecture for norm-regulated MAS was employed

as part of the evaluation step of an evolutionary al-

gorithm. The results show that an evolutionary algo-

rithm has the potential of being a useful tool when de-

signing normative systems for problem-solving MAS.

Ideas for future work include trying to formalise

and further investigate the notion of operational

equivalence which was introduced in Sect. 3.1. Al-

sto left for future work is further validation of the

suggested methodology, for example by applying the

methodology in other domains in which the grounds

of the norms and the consequences are based on dif-

ferent sets of descriptive conditions, or by further

validating the evolved normative system for the Ex-

plorer DALMAS. One could experiment with differ-

ent domain-speciﬁc parameters as well as evolution-

ary algorithm parameters, as suggested in Sect. 3.2,

to see if better solutions can be found and thus gain

more support for the ideas suggested here. It could

be interesting to, e.g., explore variable-sized norma-

tive systems and evaluation functions which impose a

‘penalty’ for large normative systems, since in many

cases it could be desirable to rely on a small num-

ber of ‘rules of thumb’ and avoid overly complex

normative systems which may become expensive in

terms of calculations. Investigating the possibility

to design more ‘accurate’ evolutionary operators also

seems like a promising idea.

ACKNOWLEDGEMENTS

The author is very grateful to Jan Odelstad and Mag-

nus Boman for valuable ideas and suggestions.

REFERENCES

Alechina, N., Bassiliades, N., Dastani, M., Vos, M. D.,

Logan, B., Mera, S., Morris-Martin, A., and Scha-

pachnik, F. (2013). Computational Models for Nor-

mative Multi-Agent Systems. In Andrighetto, G.,

Governatori, G., Noriega, P., and van der Torre,

L. W. N., editors, Normative Multi-Agent Systems,

volume 4 of Dagstuhl Follow-Ups, pages 71–92.

Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik,

Dagstuhl, Germany.

Andrighetto, G., Castelfranchi, C., Mayor, E., McBreen, J.,

Lopez-Sanchez, M., and Parsons, S. (2013a). (So-

cial) Norm Dynamics. In Andrighetto, G., Gov-

ernatori, G., Noriega, P., and van der Torre, L.

W. N., editors, Normative Multi-Agent Systems, vol-

ume 4 of Dagstuhl Follow-Ups, pages 135–170.

Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik,

Dagstuhl, Germany.

Andrighetto, G., Governatori, G., Noriega, P., and van der

Torre, L. W. (2013b). Normative multi-agent systems,

volume 4 of dagstuhl follow-ups. Schloss Dagstuhl-

Leibniz-Zentrum fuer Informatik.

Balke, T., Craneﬁeld, S., Tosto, G. D., Mahmoud, S.,

Paolucci, M., Savarimuthu, B. T. R., and Verhagen,

H. (2013). Simulation and NorMAS. In Andrighetto,

G., Governatori, G., Noriega, P., and van der Torre,

L. W. N., editors, Normative Multi-Agent Systems,

volume 4 of Dagstuhl Follow-Ups, pages 171–189.

Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik,

Dagstuhl, Germany.

Darwen, P. (2000). Computationally intensive and noisy

tasks: co-evolutionary learning and temporal differ-

ence learning on backgammon. In Evolutionary Com-

putation, 2000. Proceedings of the 2000 Congress on,

volume 2, pages 872–879 vol.2.

Di Pietro, A., While, R. L., and Barone, L. (2002). Learning

in robocup keepaway using evolutionary algorithms.

In GECCO, volume 2, pages 1065–1072.

Hjelmblom, M. (2008). Deontic action-logic multi-agent

systems in Prolog. Technical Report 30, University of

avle, Division of Computer Science.

Hjelmblom, M. (2011). State transitions and normative

positions within normative systems. Technical Re-

port 37, University of G

avle, Department of Industrial

Development, IT and Land Management.

Hjelmblom, M. (2013). Norm-regulated transition system

situations. In Filipe, J. and Fred, A., editors, Proceed-

ings of the 5th International Conference on Agents

and Artiﬁcial Intelligence, ICAART 2013, pages 109–

117, Portugal. SciTePress.

Hjelmblom, M. (2014a). Instrumentalization of norm-

regulated transition system situations. In Filipe, J. and

Fred, A., editors, Agents and Artiﬁcial Intelligence,

volume 449 of Communications in Computer and In-

formation Science, pages 80–94. Springer Berlin Hei-

delberg.

Hjelmblom, M. (2014b). Normative positions within norm-

regulated transition system situations. In Web In-

telligence (WI) and Intelligent Agent Technologies

(IAT), 2014 IEEE/WIC/ACM International Joint Con-

ferences on, volume 3, pages 238–245.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

220

Hjelmblom, M. and Odelstad, J. (2009). jDALMAS: A

Java/Prolog framework for deontic action-logic multi-

agent systems. In H

akansson, A., Nguyen, N., Har-

tung, R., Howlett, R., and Jain, L., editors, Agent

and Multi-Agent Systems: Technologies and Applica-

tions, volume 5559 of Lecture Notes in Computer Sci-

ence, pages 110–119. Springer Berlin / Heidelberg.

doi:10.1007/978-3-642-01665-3 12.

Lindahl, L. (1977). Position and change: a study in law and

logic. Synthese library. D. Reidel Pub. Co.

Lindahl, L. and Odelstad, J. (2004). Normative positions

within an algebraic approach to normative systems.

Journal of Applied Logic, 2(1):63 – 91.

Lindahl, L. and Odelstad, J. (2013). The theory of joining-

systems. In Gabbay, D., Horthy, J., Parent, X., van der

Meyden, R., and van der Torre, L., editors, Handbook

of Deontic Logic, volume 1, chapter 9, pages 545–634.

College Publications, London.

Luke, S., Hohn, C., Farris, J., Jackson, G., and Hendler,

J. (1998). Co-evolving soccer softbot team coordina-

tion with genetic programming. In Kitano, H., edi-

tor, RoboCup-97: Robot Soccer World Cup I, volume

1395 of Lecture Notes in Computer Science, pages

398–411. Springer Berlin Heidelberg.

Nakashima, T., Takatani, M., Udo, M., and Ishibuchi, H.

(2004). An evolutionary approach for strategy learn-

ing in robocup soccer. In Systems, Man and Cyber-

netics, 2004 IEEE International Conference on, vol-

ume 2, pages 2023–2028. IEEE.

Odelstad, J. (2008). Many-Sorted Implicative Conceptual

Systems. PhD thesis, Royal Institute of Technology,

Sweden. QC 20100901.

Odelstad, J. and Boman, M. (2004). Algebras

for agent norm-regulation. Annals of Math-

ematics and Artiﬁcial Intelligence, 42:141–166.

doi:10.1023/B:AMAI.0000034525.49481.4a.

Verhagen, H. and Boman, M. (1999). Norms can replace

plans. In IJCAI’99 Workshop on Adjustable, Au-

tonomous Systems.

Whitley, D. (2001). An overview of evolutionary algo-

rithms: practical issues and common pitfalls. Infor-

mation and Software Technology, 43(14):817 – 831.

OfflineEvolutionofNormativeSystems

221