Ontology Selection for Semantic Similarity Assessment

Montserrat Batet and David Sánchez

Department of Computer Engineering and Mathematics, Universitat Rovira i Virgili,

Av. Països Catalans, 26, 43007, Tarragona, Catalonia, Spain

Keywords: Knowledge Representation, Ontologies, Semantic Similarity.

Abstract: The assessment of the semantic similarity between concepts is a key tool to improve the understanding of

text. The structured knowledge that ontologies provide has been extensively used to estimate similarities

with encouraging results. However, in many domains, several ontologies modelling the same concepts in

different ways are available. In such scenarios, the most suitable ontology for similarity calculation should

be selected. In this paper we tackle this task by proposing an unsupervised method to select the ontology

that seems to enable the most accurate similarity assessments. By studying the ontology features that most

influence the similarity accuracy, we propose a score that captures them in a mathematically coherent way.

Then, the most suitable ontology can be selected as that with the highest score. We also report the results of

the proposed method for several well-known ontologies and a widely-used semantic similarity benchmark.

1 INTRODUCTION

A key element to text understanding is the

assessment of the semantic similarity between the

concepts referred in the text (Resnik, 1995).

Semantic similarity is understood as the level of

taxonomic proximity between concepts (Batet and

Sánchez, 2014). To enable this assessment in an

automatic way, ontologies provide a formal and

machine-readable representation of the knowledge

related to a domain, from which similarities can be

estimated (Batet and Sánchez, 2014).

Traditionally, ontology-based similarity

measures relied on the knowledge modeled in a

single ontology (Wu and Palmer, 1994; Jiang and

Conrath, 1997; Resnik, 1995; Batet et al., 2011b).

Thus, the similarity results strongly depended on the

accuracy of the knowledge modeled in the ontology.

To overcome this limitation and, given the

availability of several complementary and

overlapping knowledge bases in many domains,

some authors have recently proposed methods to

exploit multiple ontologies for semantic similarity

assessment (Rodríguez and Egenhofer, 2003;

Petrakis et al., 2006; Al-Mubaid and Nguyen, 2009).

The motivation is that the additional knowledge and

the complementary views that several knowledge

sources provide of a certain domain could lead to

more accurate similarity estimations.

Semantic similarity computation from multiple

ontologies faces two main challenges. First, in many

situations, a single ontology does not model the

concepts to be compared, so that, their similarity

should be computed across different ontologies.

Second, in cases in which the pair of terms to be

compared belong to several ontologies at the same

time (and, thus, different similarity results can be

obtained for the several ontologies), it is necessary

to select the best knowledge source.

In this work we focus on the latter problem. This

situation is especially relevant in domains in which

several ontologies are available (e.g., in

biomedicine, we can find overlapping knowledge

bases such as MeSH (Nelson et al., 2001) or

SNOMED-CT (Spackman, 2004), which model the

same medical concepts). However, ontologies are

usually independently created from a wide variety of

sources and with different goals and quality criteria.

Thus, different ontologies can model the same

domain of knowledge in significantly different ways

because the scope of the ontology, and the point of

view and design principles followed by knowledge

engineers may differ. Consequently, overlapping

ontologies usually present different levels of detail,

completeness and semantic structure, thus enabling

more or less accurate similarity assessments.

Because of the many factors that are involved in the

knowledge modelling, it is difficult to select a priori

569

Batet M. and Sanchez D..

Ontology Selection for Semantic Similarity Assessment.

DOI: 10.5220/0005284205690576

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 569-576

ISBN: 978-989-758-074-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

the most suitable ontology (Al-Mubaid and Nguyen,

2009; Sánchez et al., 2012b).

In this paper, we tackle this issue by proposing a

method to assess the suitability of an ontology as a

source for similarity assessments. This is done by

analysing the taxonomic structure of the ontology

and results in a numerical score that enables the

selection of the ontology that seem to enable the best

similarity assessments. The theoretical premises

have been empirically evaluated by applying our

method to a set of well-known ontologies. Results

suggest that those ontologies with the highest score

also enable the most accurate similarity assessments.

The rest of the paper is organised as follows.

Section 2 discusses related works on semantic

similarity. Section 3 details the proposed

mechanism. Section 4 presents and discusses the

empirical results. The final section contains the

conclusions of the work.

2 RELATED WORK

In the literature, ontology-based semantic similarity

measures are usually classified in different

paradigms according to the knowledge sources they

exploit and the theoretical principles in which they

rely. In this work, we focus on methods that only

rely in the knowledge modelled in an ontology.

Earliest approaches measure the distance (i.e.,

the opposite to similarity) of a pair of concepts as a

function of the length of the shortest path

connecting those concepts by means of taxonomic

relationships (Wu and Palmer, 1994; Li et al., 2003).

One limitation of these approaches is that they omit

much of the knowledge represented in the ontology,

because only the shortest path is considered.

To overcome this limitation, some authors have

proposed measures in which different ontological

features are considered (Sánchez et al., 2012a; Batet

et al., 2011b; Pirró, 2009; Rodríguez and Egenhofer,

2003; Petrakis et al., 2006). They usually measure

similarity as a ratio between the number of features

that the concepts to be compared have or do not

have in common. Because these measures exploit

more ontological knowledge, feature-based methods

provide, in general, more accurate results than

measures based on taxonomic paths (Sánchez et al.,

2012a).

Other similarity paradigms rely, not only on the

taxonomic knowledge provided by an ontology, but

also on the Information Content of concepts, which

is computed as the inverse of the probability of

appearance of such concepts in a corpus (Jiang and

Conrath, 1997; Resnik, 1995). The main limitation

of these methods is that they require representative

textual corpora in which concepts have been tagged,

so that the probabilities required to compute their

information content and estimate similarities

assessed (Batet and Sánchez, 2014).

In any case, the results provided all these

methods depend on the coverage, completeness and

level detail of the ontology in which they rely (Al-

Mubaid and Nguyen, 2009; Sánchez et al., 2012b).

In recent years, researchers have tackled this

limitation by considering multiple ontologies.

In (Rodríguez and Egenhofer, 2003; Petrakis et

al., 2006) two ontologies are connected by means of

an imaginary root node that subsumes the root nodes

of each ontology. In (Rodríguez and Egenhofer,

2003) similarity is computed according to the

overlapping between a set of non-taxonomic features

(e.g. synonyms, meronyms). In (Petrakis et al.,

2006) the Jaccard index is used to calculate the

degree of overlapping between concept glosses and

synonym sets. Overlapping features are found by

means of the terminological matching of concept

labels. The simplistic solution used to join

ontologies is a main drawback of these approaches.

Moreover, they do not consider the case in which

concept pairs appear in different ontologies. Finally,

their dependency on the availability of non-

taxonomic features, which are rarely found in

ontologies (Ding et al., 2004), limit the practical

applicability of these methods, which are focused on

the more general notion of semantic relatedness

rather than strict taxonomic similarity.

In (Saruladha et al., 2010), the similarity is

assessed as a function of the concreteness of the

most specific concept in the taxonomy that

subsumes the pair of concepts to be compared.

When each concept belongs to a different ontology,

the common subsuming concept is obtained by

means of a terminological matching of the labels of

the subsumers of each concept. Similarly to the

previous approach, in (Al-Mubaid and Nguyen,

2009) authors retrieve concepts that act as bridges

between ontologies. First, the user selects a primary

ontology, which she believes it the most accurate

one. Then, if the pair of concepts are found in the

primary ontology or in an unique secondary

ontology, the similarity is computed using the

ontology to which the concepts belong; if one of the

concepts is found in the primary ontology and the

other one in a secondary ontology, the two

ontologies are connected using bridge nodes and the

resulting structure is used as if it was a unique

ontology; finally, when concepts appear in several

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

570

secondary ontologies, the similarity is computed

using the ontology with the highest alikeness to the

primary one. Because the method relies on a path-

based measure, the authors face the problem that

different ontologies may have different granularity

degrees. To solve this problem, they propose to

normalize similarity values by scaling the part of the

path corresponding to a secondary ontology taking

as reference the primary ontology. In all cases they

assume that the ontology that has been –manually-

selected as primary will lead to better similarity

estimations than any secondary ontology. However,

this requires the user to deeply understand the

knowledge structure of the ontologies.

3 ONTOLOGY SELECTION

In this section, we propose an unsupervised method

to quantify the suitability of an ontology to measure

semantic similarity. First, we analyse the semantic

and structural features of ontologies that seem to

most influence the accuracy of semantic similarity

assessments. Then, we propose a numerical score

that quantify the suitability of an ontology to guide

similarity assessments.

3.1 Problem Analysis

From the analysis of related works on semantic

similarity, one can realize that all of them rely on the

number of differences (which are inversely

proportional to similarity) and commonalities (which

are proportionally to similarity) that can be

identified in the semantic structures associated to the

concepts in their respective ontology/ies. Since we

are focusing on semantic similarity, which is a

function of taxonomic features, in the following we

will study the effect that the modelling of such

taxonomic structure in an ontology has over the

evaluation of similarities/distances.

In the simplest case, in which the taxonomy is

perfectly balanced, the root node is the geometric

centre and all concepts are direct specializations of

the root node, the distance between all pairs of

concepts is exactly the same. In figure 1 we show an

example of this scenario for a set of medical

concepts. Because all concepts are modelled in the

same way, in this taxonomy all concepts pairs will

appear to be equally distant/similar for any semantic

similarity measure, a result that would be unlikely

realistic. In fact a knowledge representation as

simple as this is not much different to a flat list of

concepts with any semantic structure at all.

Figure 1: Sample ontology O

In order to better represent the differences in

semantics inherent to the concepts and, coherently

with the principles of cognitive saliency (i.e.

concepts are specialised when they must be

differentiated from other ones), in figure 2 we have

added a new inner taxonomic level (mental disorder)

that separates the set paranoia, schizophrenia and

affective psychosis from the set melanosis, albinism

and vitiligo, which are subsumed by disorder of

pigmentation. Even though more taxonomic levels

have been included the taxonomy is still balanced

and, thus, the root node is still the geometric.

However, now the semantic distance between

paranoia and albinism will be larger than the

distance between paranoia and schizophrenia

because we are able to distinguish concepts that are

mental disorder from those that are disorder of

pigmentation. Thanks to the better differentiation

between concepts, distance/similarity results

obtained from this structure will be more diverse

than in the previous case and, assuming that the

representation is semantically coherent, results will

offer a better understanding concept semantics.

Figure 2: Sample ontology O

Finally, in figure 3 we show how these concepts are

represented in SNOMED-CT (Spackman, 2004).

Notice that in this case the concepts schizophrenia

and affective psychosis has been better differentiated

from paranoia by adding a new inner node

(psychotic disorder). As result, the root node is not

the geometric centre of the taxonomy anymore,

because the branch on the left goes deeper than the

OntologySelectionforSemanticSimilarityAssessment

571

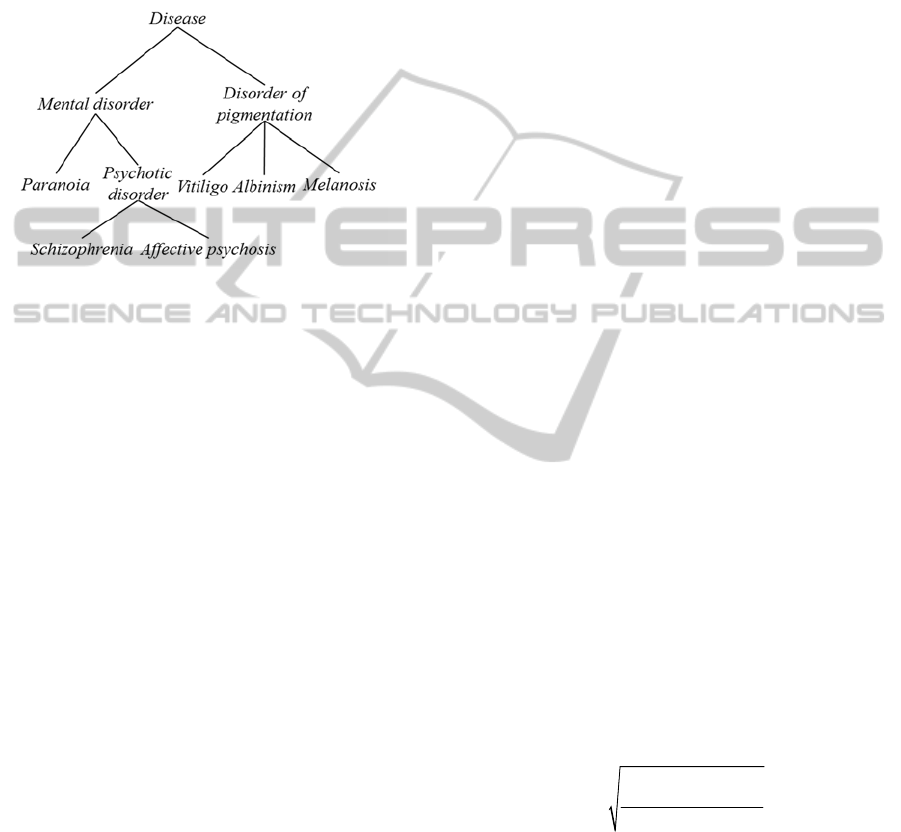
one on the right. This taxonomy better represents the

fact that, for example, albinism and schizophrenia

are more different than albinism and paranoia, a

dimension that can be captured by similarity

measures by evaluating the number of common and

disjoint subsumers (Batet et al., 2011b) and that

results in even more diverse similarity/distance

results than in the previous cases.

Figure 3: Sample ontology O

3.2 A Score for Ontology Selection

From the above discussion, we can conclude that a

taxonomy with an accurate knowledge modelling is

likely to better differentiate concepts from each

other. Inversely, an accurately modelled ontology

will unlikely have a homogenous taxonomy because,

in such structure, concepts are distributed uniformly

and, hence, they are hardly distinguishable. This

assumption is coherent with the principles of

knowledge modelling, whose main aim is to make

concepts well-differentiated in order to minimize the

ambiguity of the semantic inferences (Pirró, 2009).

Likewise, human judgements on semantic similarity

(which computerized measures try to mimic) are

rarely homogenous and tend to be highly diverse

because of the informal nature of semantics

(Pedersen et al., 2007).

Given these arguments, in the following we

propose a score that aims to measure the degree of

concept differentiation that the taxonomic structure

of an ontology provides. Since this level of

differentiation positively influences the diversity of

the similarity assessments, which we hypothesise as

an indication of accuracy in such assessments, our

score can be used to compare and select the most

suitable ontology for semantic similarity calculation.

To measure this level of differentiation, we

evaluate the dispersion of the taxonomic structure.

From a semantic point of view, the centre of an

ontology can be seen as the root of the taxonomic

tree. As shown in the previous section, in a perfectly

balanced ontology (figures 1 and 2), the root node

corresponds to the geometric centre of the

taxonomy. As stated in (Martínez et al., 2012), this

central node is the one that minimizes the distances

with respect to all the concepts in the ontology. In

such balanced structure, the level of differentiation

between concepts will tend to be low, because

“sibling” or “cousin” concepts will be all equally

distant/similar. On the contrary, in a taxonomy in

which the different branches have different depths

and branching factors, the root node will not match

with the geometrical centre of the structure (as in

figure 3). Here, the degree of differentiation between

concepts will tend to be higher than in the previous

case, thus producing more diverse similarities.

From a mathematical perspective the dispersion

of a sample quantifies the variability of the values of

that sample with regard to the central value. A high

dispersion indicates that values are very different

from each other. By considering the set of concepts

in an ontology as a sample of values and the root

node as their centre, we can adapt the mathematical

notion of dispersion to quantify to what extent the

concepts modelled in taxonomy are dispersed or

differentiated. Consequently, we propose a score

that quantifies that degree of differentiation by

measuring the dispersion of the taxonomic structure

of the ontology. For numerical values, the dispersion

of a sample is the normalized aggregation of their

distances towards the central value. When dealing

with ontologies, such distance should be a measure

of the semantic distance of each concept towards the

root node of the taxonomy. In particular, our score is

based on the standard numerical deviation, which

has the advantage that the results are expressed in

the same units as the distance.

Formally, we quantify to what extent the whole

set of concepts C of an ontology O

are

differentiated, as the square root of the average

squared semantic distance between each concept c

in C and the root node of O

()

(, ( ))

Score O

dc RootO







(1)

In the above expression, |C| is the number of

concepts in the ontology O

without considering the

root node, which does not contributes to the

numerator, and function d(.,.) is any semantic

distance measure to be applied between each

concept c

in C and the root node (Root(O

)). Notice

that the contribution of the most scattered concepts,

which are those that contribute most to the

unbalancing of the taxonomy, is greater because of

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

572

the squared semantic distances. Numerically,

equation (1) is zero when all the values are identical.

In contrast, a high Score suggests that concepts are

far apart from the root node and form each other,

and thus, that they are well differentiated.

By means of the proposed Score, we can select

the most suitable ontology O

to be used to compute

the similarity of a set of concepts (modelled in a set

of ontologies O) as the one with the max value.

arg max ),(()

sii

ScoreOOOO

(2)

The proposed method can also be applied only to

taxonomic branches of different ontologies. This is

relevant because the different scopes and goals by

which ontologies are designed can produce more or

less accurate or detailed taxonomic branches, even

in ontologies modelling the same domain. With our

method, this partial comparison can be done by

using the common generalization of that branch as

the root, and by computing the distances towards all

of its taxonomic specializations.

3.3 Measuring Distances

In order to apply the proposed Score, we should be

able to estimate the semantic distance (function

d(.,.)) between each concept c

and the root node.

The semantic distance should meet some

requirements in order to be suitable to compare

ontologies. First, it should not be affected by the size

of the ontology in order to fairly compare the degree

of concept differentiation of ontologies with

different sizes. On the other hand, the semantic

distance should only rely on taxonomic knowledge

because similarity assessment only relies on this

feature, and also because many ontologies does not

model other knowledge than taxonomic

relationships (Ding et al., 2004).

As stated in section 2, many different measures

have been proposed (Batet and Sánchez, 2014).

Since path-based approaches provide absolute

distance values between concepts, semantic

distances tend to be larger as the ontology size

increases. Thus, they cannot be used to compare

ontologies with different sizes. Moreover, since only

the shortest path is considered, they omit a lot of

knowledge explicitly modelled in the ontology

(Batet et al., 2011b).

Feature-based measures are able to overcome

these limitations. They compute similarity or

distance according to a normalized ratio of semantic

commonalities and differences between concepts

and, thus, they evaluate a larger number of semantic

evidences. In this work, we instantiate d(.,.) with the

feature-based measure defined in (Sánchez et al.,

2012a) because it solely relies on taxonomic

features. This measure computes the distance

d(c

) between two concepts

as the logarithm of the

number of non-common subsumers of c

and c

divided by their total number of subsumers:

12 12

12 2

() () () ()

(, ) log 1

() ()

Tc Tc Tc Tc

dc c

Tc Tc













(3)

where T(c

) is the set of taxonomic subsumers of

concept c

in the ontology, including itself.

This measure captures more knowledge than the

methods based on shortest paths, since it implicitly

considers all the paths connecting the two concepts,

which are represented by all their subsumers. As a

result, and according to a set of empirical

experiments, it approximates human judgments of

similarity better than other ontology-based measures

(Sánchez et al., 2012a; Batet et al., 2011b).

Numerically, thanks to the normalizing

denominator, this distance results in positive

normalized values in the [0,1] range, thus making it

suitable to compare the degree of concept

differentiation of ontologies with different sizes.

3.4 Example

Let us illustrate how the Score proposed in section

3.2 behaves with regard to the taxonomic structure

of an ontology. To do so, we will use the different

knowledge representations shown in figures 1, 2 and

3 for the same set of concepts. By applying the

Score to the taxonomy in figure 1 (the one in which

concepts are the least differentiated), we obtain:

222

()

(,)( ,)

( ,)( ,)/6

(,)(,)

111

log 1 log 1 log 1

222

Score O

d paranoia dis d schizophrenia dis

d affective psychosis dis d melanosis dis

d albinism dis d vitiligo dis





















  

  

  



  





222

/6 0.585

111

log 1 log 1 log 1

222





















  



  

  





  





By applying the same calculation to the taxonomy

shown in figure 2, which offers a better

differentiation between mental and pigmentation

disorders, the Score increases accordingly:

OntologySelectionforSemanticSimilarityAssessment

573

()

(,)( ,)

( ,)( ,)

(,)(,)

( ,)( ,)

6lo

Score O

d paranoia dis d schizophrenia dis

d affective psychosis dis d melanosis dis

d albinism dis d vitiligo dis

d mental dis dis d dis of pigmentation dis





























g1 2 log1

0.702



 

 

 



 





Finally, for the taxonomy shown in figure 3, which

offers the best differentiation between concepts, we

also obtain the highest Score.

()

(,)( ,)

( ,)( ,)

(,)(,)

( ,)( ,)

( ,

Score O

d paranoia dis d schizophrenia dis

d affective psychosis dis d melanosis dis

d albinism dis d vitiligo dis

d mental dis dis d dispigmentation dis

d psychotic disorder di







 



222

)

321

2log1 5log1 2log1

432

0.723













  



  



  





Thus, according to the method presented in section

3.2, the ontology O

shown in figure 3 will be

selected as the base to compute semantic similarities

between the modelled concepts.

4 EXPERIMENTS

The goal of the experiments is to show that, in

practice, the ontology (from a set of overlapping

ones) with the highest Score is also the one that

enables the most accurate similarity assessments.

We focused on the biomedical domain because, as

mentioned in the introduction, several standard

ontologies modelling the same concepts exist.

To measure the accuracy of similarity

assessments, that is, up to which level the similarity

results mimic human judgements, related works

measure the Pearson correlation between human

similarity ratings and computerized results for a

given set of concept pairs. In the literature, several

benchmarks providing human ratings for a set of

concepts of different domains have been proposed.

For the biomedical domain, the Pedersen et al.’s

benchmark (Pedersen et al., 2007) has become the

de facto standard for similarity evaluation. It

consists of 30 pairs of medical terms, whose

similarity has been assessed, in the range [1..4], by a

group of experts of the Mayo Clinic.

Table 1: Medical term pairs that can be found both in

SNOMED-CT and MeSH, with averaged experts’

similarity scores from the Pedersen et al. benchmark

(Pedersen et al., 2007). In boldface we represent those

pairs that specifically correspond to diseases.

Term 1 Term 2 Sim.

Renal failure Kidney failure 4.0

Heart Myocardium 3.3

Stroke Infarct 3.0

Abortion Miscarriage 3.0

Delusion Schizophrenia 3.0

Congestive heart

failure

Pulmonary edema 3.0

Metastasis Adenocarcinoma 2.7

Calcification Stenosis 2.7

Mitral stenosis Atrial fibrillation 2.3

Rheumatoid

arthritis

Lupus 2.0

Brain tumor Intracranial

hemorrhage

2.0

Carpal tunnel

syndrome

Osteoarthritis 2.0

Diabetes mellitus Hypertension 2.0

Acne Syringe 2.0

Antibiotic Allergy 1.7

Cortisone Total knee

replacement

1.7

Pulmonary

embolus

Myocardial

infarction

1.7

Pulmonary fibrosis Lung cancer 1.7

Cholangiocarcinoma Colonoscopy 1.3

Lymphoid

hyperplasia

Laryngeal cancer 1.3

Multiple sclerosis Psychosis 1.0

Appendicitis Osteoporosis 1.0

Xerostomia Alcoholic cirrhosis 1.0

Peptic ulcer disease Myopia 1.0

Depression Cellulitis 1.0

Varicose vein Entire knee meniscus 1.0

Hyperlipidemia Metastasis 1.0

As ontologies to be compared, we use SNOMED-

CT (Spackman, 2004) and MeSH (Nelson et al.,

2001), which semantically model biomedical

concepts with a large degree of overlapping. Since

we focus in the scenario in which concepts appear in

several ontologies at the same time, in table 1 we

show the pairs of terms of the Pedersen et al.’s

benchmark that can be found both in SNOMED-CT

and MeSH. The last column provides the averaged

similarity ratings provided by the experts. Moreover,

those pairs that are diseases in both ontologies are

shown in boldface. According to this set of terms,

we configured two scenarios:

(a) Scenario 1: ontology selection evaluation. All

the term pairs in table 1 are evaluated. Since

those terms are spread through the different

branches of SNOMED-CT and MeSH, in this

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

574

scenario we aim to select the ontology that is

best suited to compute semantic similarities.

(b) Scenario 2: branch selection evaluation. This

scenario is designed to show how our method

can also be applied to a particular branch of an

ontology. In this case, only the set of term pairs

that are diseases are considered. Likewise, only

the taxonomic branches of SNOMED-CT and

MeSH that model diseases have been

evaluated. The reference root nodes are now

the Disease (disorder) concept in SNOMED-

CT and C-Disease in MeSH.

Table 2 shows the Scores resulting from the

evaluation of each ontology/branch and also the

accuracy (Correlation) of the similarity assessments

obtained for the same ontology/branch in the two

scenarios detailed above. In all cases, distances and

similarities have been computed using equation (3).

From table 2, we can see that our Score and the

accuracy of the semantic similarity assessments are

positively correlated. This supports our hypothesis

and suggests that the most appropriate ontology to

compute semantic similarities would be the one that

better differentiates concepts, a dimension that our

Score quantifies. In fact, this better differentiation

provides semantic similarity measures with more

degrees of freedom to evaluate concepts and

produces more diverse similarity results that, as

shown in the experiments, better correlate with

human ratings of similarity.

Table 2: Pearson correlation coefficients for each scenario

and ontology/branch between the experts’ similarity

ratings in (Pedersen et al., 2007) and the measure from Eq.

(3). The last column shows the Score (Eq. (1)) for each

ontology/branch.

Ontology/branch Correlation

Scenario 1

Correlation

Scenario 2

Score

SNOMED-CT 0.69 0.938

MeSH

0.65 0.903

SNOMED-CT

disease

0.83 0.951

MeSH disease 0.77

0.886

Looking at the numeric scales, we can also see that,

thanks to the normalized values provided by

equation (3), Score values are not dependant on the

ontology size. Specifically, even though SNOMED-

CT models 300,000 concepts and MeSH just around

22,000, Score values do not differ proportionally to

these sizes (0.938 vs. 0.903). These Score values are

however quite proportional to the differences

observed in semantic similarity accuracies for both

ontologies (0.69 vs. 0.66). The same behaviour is

also observed for taxonomic branches.

5 CONCLUSIONS

In this paper we presented an unsupervised method

to assess the suitability of ontologies as sources to

measure semantic similarity in the scenario in which

the concepts to be compared appear in several

ontologies. Given that similarity measures benefit

from knowledge structures that better

(taxonomically) differentiate concepts, we propose a

quantitative Score that measures the degree of

taxonomic differentiation of concepts in an

ontology. To do so, the Score adapts to the semantic

domain the mathematical notion of numerical

dispersion of a sample. By means of this Score, we

can select the ontology that likely provides the most

accurate similarities from a set of overlapping ones.

The results of the empirical experiments carried

out using biomedical ontologies and a widely-used

semantic similarity benchmark, supported our

hypotheses: in all cases, those ontologies (or

taxonomic branches) with the highest Score also

enabled the most accurate similarity assessments.

As future work, we plan to evaluate the proposed

method in other domains in which multiple

overlapping ontologies are available. Moreover, we

will also evaluate the behaviour of other distance

functions in the Score calculus, such as those based

on word vectors (Mikolov et al., 2013). Finally, we

plan to study its suitability as a predictor of results

accuracy in specific tasks that require from semantic

similarity assessments and in which different

knowledge-bases are available, such as semantic

clustering (Batet et al., 2011a) or textual data

anonymisation (Batet et al., 2013).

ACKNOWLEDGEMENTS

This work was partly supported by the European

Commission under FP7 project Inter-Trust and

H2020 project CLARUS, by the Spanish Ministry of

Science and Innovation through project ICWT

TIN2012-32757 and by the Government of

Catalonia under grant 2014 SGR 537. This work was

also made possible through the support of a grant

from Templeton World Charity Foundation. The

opinions expressed in this paper are those of the

authors and do not necessarily reflect the views of

Templeton World Charity Foundation.

OntologySelectionforSemanticSimilarityAssessment

575

REFERENCES

Al-Mubaid, H. & Nguyen, H. A. 2009. Measuring

Semantic Similarity between Biomedical Concepts

within Multiple Ontologies. IEEE Transactions on

Systems, Man, and Cybernetics, Part C: Applications

and Reviews, 39(4), pp 389-398.

Batet, M., Erola, A., Sánchez, D. & Castellà-Roca, J.

2013. Utility preserving query log anonymization via

semantic microaggregation. Information Sciences,

242(1), pp 49-63.

Batet, M., Gibert, K. & Valls, A. Semantic clustering

based on ontologies: an application to the study of

visitors in a natural reserve. In: Filipe, J. & Fred, A. L.

N., eds. 3th International Conference on Agents and

Artificial Intelligence (ICAART'11), 2011a Rome,

Italy. SciTePress, 283-289.

Batet, M. & Sánchez, D. 2014. A review on semantic

similarity. Encyclopedia of Information Science and

Technology, Third Edition. IGI Global.

Batet, M., Sánchez, D. & Valls, A. 2011b. An ontology-

based measure to compute semantic similarity in

biomedicine. Journal of Biomedical Informatics,

44(1), pp 118-125.

Ding, L., Finin, T., Joshi, A., Pan, R., Cost, R. S., Peng,

Y., Reddivari, P., Doshi, V. & Sachs, J. Swoogle: A

Search and Metadata Engine for the Semantic Web.

In: Grossman, D. A., Gravano, L., Zhai, C., Herzog,

O. & Evans, D. A., eds. thirteenth ACM international

conference on Information and knowledge

management, CIKM 2004, 2004 Washington, D.C.,

USA. ACM Press, 652-659.

Jiang, J. J. & Conrath, D. W. Semantic Similarity Based

on Corpus Statistics and Lexical Taxonomy.

International Conference on Research in

Computational Linguistics, ROCLING X, Sep 1997

Taipei, Taiwan. 19-33.

Li, Y., Bandar, Z. & McLean, D. 2003. An Approach for

Measuring Semantic Similarity between Words Using

Multiple Information Sources. IEEE Transactions on

Knowledge and Data Engineering, 15(4), pp 871-882.

Martínez, S., Valls, A. & Sánchez, D. 2012. Semantically-

grounded construction of centroids for datasets with

textual attributes. Knowledge-Based Systems, 35(1),

pp 160-172.

Mikolov, T., Chen, K., Corrado, G. & Dean, J. Efficient

Estimation of Word Representations in Vector Space.

International Conference on Learning Representations,

2013. 1-12.

Nelson, S. J., Johnston, D. & Humphreys, B. L. 2001.

Relationships in Medical Subject Headings.

Relationships in the Organization of Knowledge. K.A.

Publishers.

Pedersen, T., Pakhomov, S., Patwardhan, S. & Chute, C.

2007. Measures of semantic similarity and relatedness

in the biomedical domain. Journal of Biomedical

Informatics, 40(3), pp 288-299.

Petrakis, E. G. M., Varelas, G., Hliaoutakis, A. &

Raftopoulou, P. 2006. X-Similarity:Computing

Semantic Similarity between Concepts from Different

Ontologies. Journal of Digital Information

Management, 4(1), pp 233-237.

Pirró, G. 2009. A semantic similarity metric combining

features and intrinsic information content. Data &

Knowledge Engineering, 68(11), pp 1289-1308.

Resnik, P. Using Information Content to Evalutate

Semantic Similarity in a Taxonomy. In: Mellish, C. S.,

ed. 14th International Joint Conference on Artificial

Intelligence, IJCAI 1995, 1995 Montreal, Quebec,

Canada. Morgan Kaufmann Publishers Inc., 448-453.

Rodríguez, M. A. & Egenhofer, M. J. 2003. Determining

semantic similarity among entity classes from different

ontologies. IEEE Transactions on Knowledge and

Data Engineering, 15(2), pp 442–456.

Sánchez, D., Batet, M., Isern, D. & Valls, A. 2012a.

Ontology-based semantic similarity: A new feature-

based approach. Expert Systems with Applications,

39(9), pp 7718-7728.

Sánchez, D., Solé-Ribalta, A., Batet, M. & Serratosa, F.

2012b. Enabling semantic similarity estimation across

multiple ontologies: An evaluation in the biomedical

domain. Journal of Biomedical Informatics, 45(1), pp

141-155.

Saruladha, K., Aghila, G. & Bhuvaneswary, A. 2010.

Computation of Semantic Similarity among Cross

Ontological Concepts for Biomedical Domain.

Journal of Computing, 2(8), pp 111-118.

Spackman, K. A. 2004. SNOMED CT milestones:

endorsements are added to already-impressive

standards credentials. Healthcare Informatics, 21(9),

pp 54-56.

Wu, Z. & Palmer, M. Verb semantics and lexical

selection. In: Pustejovsky, J., ed. 32nd annual Meeting

of the Association for Computational Linguistics,

1994 Las Cruces, New Mexico. Association for

Computational Linguistics, 133 -138.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

576