A Low-power Color Mosaic Image Compressor Based on Optimal

Combination of 1-D Discrete Wavelet Packet Transform and DPCM for

Wireless Capsule Endoscopy

Kinde A. Fante, Basabi Bhaumik and Shouri Chatterjee

Department of Electrical Engineering, Indian Institute of Technology Delhi, Hauz Khas, New Delhi-110016, India

Keywords:

Wireless Capsule Endoscopy, Discrete Wavelet Packet Transform, Mosaic Image Compressor, Low-power.

Abstract:

A novel low-power endoscopic image compressor is designed that occupies small silicon chip area, gives a

high compression rate and maintains acceptable image quality. By utilizing unique properties of human gas-

trointestinal tract images, computationally simple and elegant methods are employed. The employed methods

are lifting scheme based two level 1-D discrete wavelet packet transform, uniform quantization, chrominance

component sub-sampling, differential pulse code modulation and Golomb-Rice entropy encoder. All the mod-

ules are highly optimized from computational complexity, efﬁciency and memory requirement perspectives.

The proposed algorithm requires neither demosaicking nor de-interleaving operations that require large mem-

ory and consume a signiﬁcant amount of power. The proposed image compression scheme achieves a com-

pression rate of 81.31 % with peak signal to noise ratio of 39.45 dB. The implementation of the algorithm

in 130 nm standard CMOS process technology occupies a core area of 0.342 mm×0.342 mm. It consumes

48.4 µW of power for encoding two color mosaic frames, with a resolution of 512×512, per second. The

proposed endoscopic image compression scheme gives a power consumption reduction of about two orders

less than the realizations proposed in literature.

1 INTRODUCTION

Wireless Capsule Endoscope (WCE) (Idden et al.,

2000) was introduced by Given Imaging Ltd in 2000.

Since then it has been widely used to diagnose gas-

trointestinal abnormalities with minimal invasiveness.

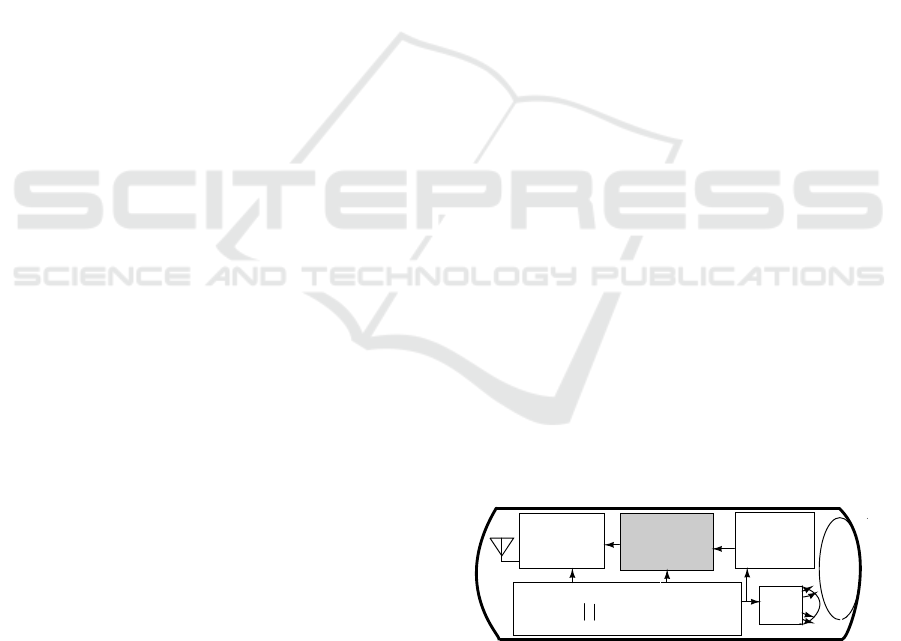
Its main electrical components are image sensor, RF

transmitter, button battery and structured light source

(LEDs) as shown in Figure.1. During the diagnos-

tic procedure, the capsule is swallowed by the patient

through the mouth. As it travels through the gastroin-

testinal(GI) tract with the aid of peristalsis, it cap-

tures high resolution color images of the GI tract wall

which cannot be reached by the wired conventional

endoscopy. The images are then transmitted by the

wireless RF transmitter to a receiver worn round the

patients waist for an average of eight hours before the

battery runs out (Moglia et al., 2008). The capsule

comes out of the digestive system along with the stool

and it is discarded. The images are downloaded onto

a workstation (PC) with appropriate image process-

ing software to make a video. The diagnosis is done

ofﬂine by Gastroentrologist.

transmitter

CMOS

image

LEDs

Battery

Image

compressor

sensor

Figure 1: Block diagram of the wireless capsule endoscopy.

In order to reduce the power consumption of the

RF transmitter without signiﬁcant overhead, the im-

age compressor inside WCE should have small chip

area, low power consumption and maintain high im-

age quality. Previous works on this topic were pre-

dominantly based on discrete cosine transform (DCT)

and differential pulse code modulation (DPCM). The

works in (Lin et al., 2006; Wahid et al., 2008; Dung

et al., 2008; Lin and Dung, 2011; Chen et al., 2009;

Turcza and Duplaga, 2011; Xie et al., 2007; Tur-

cza and Duplaga, 2013) have used block-based DCT

in order to encode endoscopic color mosaic images.

These block-based transforms require huge memory

to buffer data when they work with image sensor

190

Fante K., Bhaumik B. and Chatterjee S..

A Low-Power Color Mosaic Image Compressor Based on Optimal Combination of 1-D Discrete Wavelet Packet Transform and DPCM for Wireless

Capsule Endoscopy.

DOI: 10.5220/0005284701900197

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2015), pages 190-197

ISBN: 978-989-758-071-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

that sends the pixel values in raster scan fashion.

The DPCM based algorithms were proposed for both

mosaic and full color image formats. The works

proposed for mosaic image compression (Xie et al.,

2006; Cheng et al., 2010) have used JPEG-LS algo-

rithm which requires to store at least one row of the

previously encoded pixels for prediction. The context

variables also require 1.9KB of memory (Cheng et al.,

2010). The DPCM based algorithms which were pro-

posed for full color image compression (Khan and

Wahid, 2011b; Khan and Wahid, 2011a) are sim-

ple. However, these algorithms require the imple-

mentation of the demosaicing algorithms inside the

image sensor which consumes considerable amount

of power and need memory. Memory consumes high

power and occupies large silicon area which increases

the overhead of the image compressor. Demosaicing

the mosaic image increases its size by threefold which

reduces the effective compression rate by the same

amount. Despite its success in many applications,

wavelet based image compression algorithm has not

been explored for WCE application to the best of the

authors’ knowledge. In this work we present the study

and design of wavelet based mosaic image compres-

sion algorithm which does not require huge memory

buffer and is computationally simple.

The proposed image compressor combines mul-

tiple methods which are computationally simple to

achieve high compression efﬁciency. These meth-

ods are: lifting scheme based discrete wavelet packet

transform (DWPT), DPCM, uniform quantization,

sub-sampling and Golomb-Rice encoding. The nov-

elty of this work lies in modifying the wavelet ﬁl-

ter coefﬁcients to utilize the unique properties of hu-

man GI tract images. It also combines DWPT with

DPCM, uniform quantization and sub-sampling op-

timally to achieve its target. We have experimen-

tally determined the optimal combinations of the sub-

sampling and uniform quantization parameters that

can achieve the desired performance for WCE appli-

cation. The ﬁnal contributionof this work is optimiza-

tion of Golomb-Rice encoder from memory require-

ment and efﬁciency perspective. The Golomb-Rice

encoder parameter,k, is determined dynamically from

local image properties using only four contexts in or-

der to reduce the memory requirement and still main-

tain its adaptability property. The context variables

require only 34 bytes of memory. We get a mem-

ory reduction of about 1.866 KB as compared to the

method proposed in (Xie et al., 2006; Cheng et al.,

2010). The image compressor can elongate the life-

time of the WCE signiﬁcantly so that it can cover the

whole GI tract.

The rest of the paper is organized as follows. The

detailed discussion of the proposed algorithm is given

in section 2. The performance evaluation of the algo-

rithm is presented in section 3. The hardware imple-

mentation is discussed in the section 4. The conclu-

sion is given in the section 5.

2 ANALYSIS OF SUITABLE

METHODS FOR EFFICIENT

COMPRESSION OF WCE

IMAGE

Mosaic image is captured using color ﬁlter arrays

(CFA) (Bayer, 1976) shown in Figure 2 (a). The

spectral bands are interleaved in mosaic image. The

pixel values have high frequency content in its neigh-

borhood. Hence, conventional image compression

methods fails to give high compression efﬁciency for

mosaic images. In the following sections we will

showhowcomputationallysimple methods can be op-

timally combined to achieve high compression efﬁ-

ciency for WCE mosaic image.

2.1 Analysis of Color Mosaic Image

Using Wavelet

Consider a pair of rows of color mosaic image which

has six elements per row as shown in table 1, where

the spectral band samples are given as R (red), G

(green) and B (blue). Let’s apply 1-D DWPT on this

image using 5-3 integer wavelet (Angelopoulou et al.,

2007) with lifting scheme (Sweldens, 1995). We use

the horizontal ﬁltering operation as shown in Figure

Figure 2: The Bayer arrangement of color ﬁlters on the pixel

array of an image sensor (a), mosaic WCE image (b) and

typical WCE full color image (c).

Table 1: Two rows of color mosaic image.

0,0

0,1

0,2

0,3

0,4

0,5

1,0

1,1

1,2

1,3

1,4

1,5

If we directly apply the lifting scheme 1-D DWT

on the color mosaic image which is given in table 1,

we will get the followingoutputs. For the ﬁrst row, the

ALow-PowerColorMosaicImageCompressorBasedonOptimalCombinationof1-DDiscreteWaveletPacketTransform

andDPCMforWirelessCapsuleEndoscopy

191

Original

image

Level 0 Level 1

H LH HH

Level 2

L HLLL

Figure 3: Diagrammatic representation of dyadic decompo-

sition for two decomposition levels using horizontal ﬁlter-

ing.

high-pass ﬁlter (H

) and low-pass ﬁlter (L

) outputs

after horizontal ﬁltering are given by:

[2i, 2j+ 1] = R

2i,2j+1

− ⌊

2i,2j

+ G

2i,2j

+ 2

⌋ (1)

[2i, 2j] = G

2i,2j

⌊

[2i, 2j− 1] + H

[2i, 2j+ 1] + 2

⌋ (2)

where i and j are row and column indexes of the image

array. Similarly, for the second row of image given in

table 1, the high-pass ﬁlter (H

) and low-pass ﬁlter

) outputs after horizontal ﬁltering are given by:

[2i+ 1, 2j + 1] = G

2i+1,2j+1

− ⌊

2i+1,2j

+ B

2i+1,2j+2

⌋

(3)

[2i+ 1, 2j] = B

2i+1,2j

⌊

[2i+ 1, 2j − 1] + H

[2i+ 1, 2j + 1] + 2

⌋ (4)

Our simulation result on 120 endoscopic images taken

from Gastrolab (Gastrolab, 2014) shows that the

smoothness of the low-pass ﬁlter outputs (L

and L

)

are worse than the G and B color channels when they

are de-interleaved. For this reason, the low-pass ﬁl-

tering operation of (2) is modiﬁed as:

[2i, 2j] = G

2i,2j

(5)

Similarly, the low-pass ﬁltering operation given in (4)

is modiﬁed as:

[2i+ 1, 2j] = B

2i+1,2j

(6)

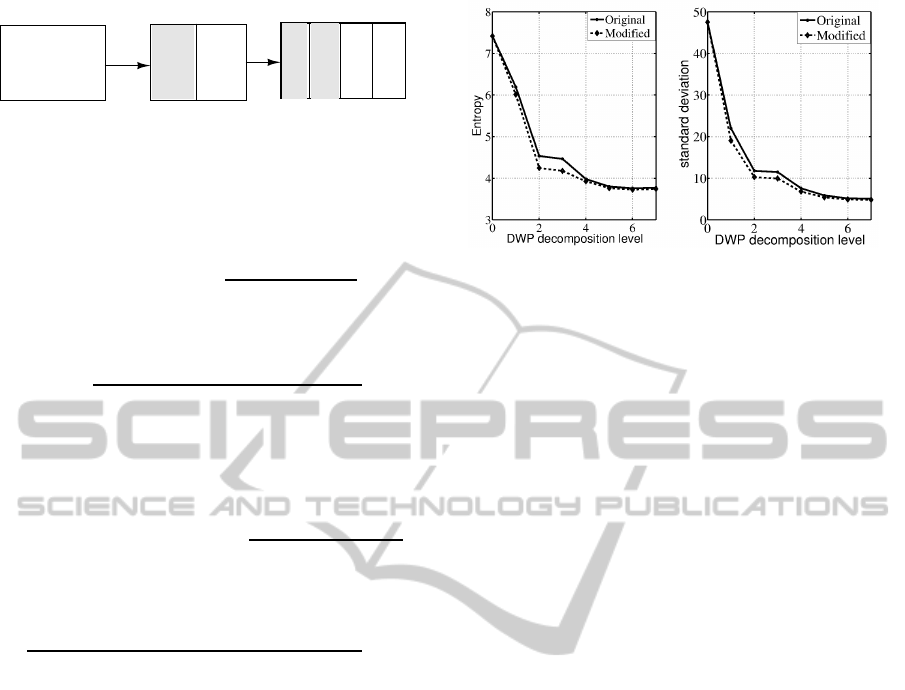
Figure 4 shows the statistical measurements (entropy

and standard deviation) of the decomposed mosaic

image given in Figure 2(b) using 1-D DWPT when

the low-pass ﬁltering operation is done using the orig-

inal equations (2) and (4), and the modiﬁed equations

(5) and (6). The modiﬁcation of the low-pass ﬁltering

operation gives two advantages: It reduces computa-

tional resources and improves the compression efﬁ-

ciency.

We observed from Figure 4 that the average sta-

tistical measurements of the subbands of the decom-

posed color mosaic image do not show signiﬁcant

change after second level decomposition. Therefore,

Figure 4: Average entropy (left) and standard deviation

(right) of 120 endoscopic images at different wavelet packet

decomposition level.

the level of decomposition is limited to two in order

to save computational resources.

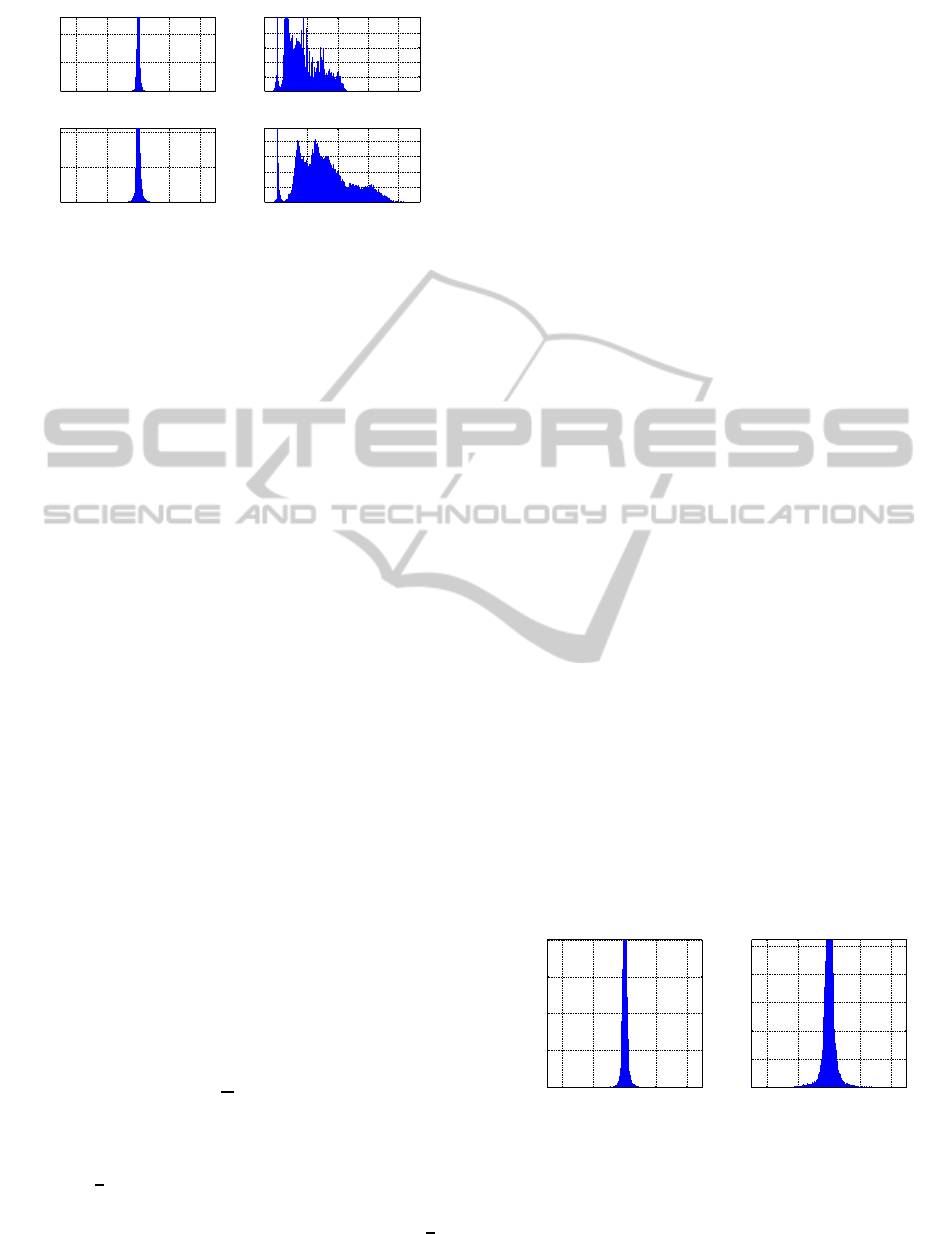
After the second level DWP decomposition, three

quarter of the subbands of the mosaic image are low-

pass signals. Figure 5 shows that the histogram of

detail subbands (HH and HL subbands) of the second

level DWPT is narrow and the values are small, near

zero with high probability. The LH subband shows

narrower histogram than the LL subband. The sub-

bands which have narrow histogram can be efﬁciently

encoded using computationally simple image com-

pression techniques such as DPCM.

The 2-D decomposition of color mosaic images

using Mallat wavelet packet was discussed in (Zhang

and Wu, 2004). The authors have shown the simul-

taneous de-correlation of spectral and spatial redun-

dancies of mosaic image using the convolution based

5-3 integer wavelet. The convolution based wavelet

decomposition has higher computational complexity

as compared to the lifting scheme (Sweldens, 1995).

The 2-D decomposition of the mosaic image enables

to de-correlate the image in both the vertical and hor-

izontal direction. Hence, it gives higher compression

efﬁciency than its 1-D counterpart. However, the 2-D

based operation requires huge memory to buffer data

during computation especially when the image com-

pressor works with image sensor which sends pixel

values in raster-scan fashion. Since memory occupies

large area and consumes high power we use the 1-

D based decomposition for this area and power con-

strained application. In the subsequent sections we

show that 1-D DWP decomposition of mosaic endo-

scopic image can be optimally combined with DPCM,

uniform quantization and sub-sampling to achieve a

high compression rate.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

192

−80 −40 0 40 80

2000

4000

(a) Histogram of HH band.

0 50 100 1250 200

250

500

750

1,000

−80 −40 0 40 80

2000

4000

(b) Histogram of HL band.

0 50 100 150 200

200

400

600

800

(d) Histogram of LL band.

Figure 5: Histogram of the subbands of mosaic image

shown in Figure 2 (b) after second level wavelet packet de-

composition.

2.2 Uniform Quantization and

Sub-sampling

The detail subbands of the ﬁrst level DWP decompo-

sition of color mosaic image, which are given by (1)

and (3), represent the chrominance component of a

color image. These subbands are the color difference

images (R-G and G-B) which are low-pass signals

because of the high correlation between RGB color

channels. Human GI tract has a reddish color. There

is a little sharp color transition in human GI tract. The

absence of sharp color transitions in human GI tract

enables to sub-sample chrominance components of

the GI tract images without much loss of information.

After ﬁrst level discrete wavelet decomposition of

color mosaic image, the high frequency wavelet sub-

bands (H

and H

) are down-sampled to reduce the

size of image. For example, image is down-sampled

by two by removing every other column from the im-

age. Sub-sampling is a computationally simple and

efﬁcient image compression technique.

In addition to DWPT, the high frequency content

of the mosaic image can be reduced using a compu-

tationally simple way of low-pass ﬁltering operation

(Pattanaik et al., 2006) which uses quantization. The

quantization operation can be done using only addi-

tion and shift operation if the quantizer is in the form

of power-of-two. It has very simple hardware realiza-

tion. For a given pixel value P and a quantizer value q,

where q is positive integer, the quantized pixel value

is given by:

= ⌊

+ 0.5⌋ (7)

From the statistics point of view it is obvious that the

standard deviation of the a set of pixel values is re-

duced by

when the set is uniformly quantized using

quantizer value q. Whereas the maximum error intro-

duced when the values are dequantized is limited to

If a set of pixels have low standard deviation, then it

will have higher spatial correlation which is important

for efﬁcientcompression. Note that the uniform quan-

tization supports the DWP decomposition in reducing

the high frequency components of mosaic image. As

shown in table 2, the proper combination of quantizer

and sub-sampler gives optimal performance in terms

of compression rate and image quality. We have cho-

sen quantizer value of four and the down-sampling

factor of four as optimal parameters.

2.3 Differential Pulse Code Modulation

(DPCM)

After second level DWP decomposition of color mo-

saic image, two subbands (LL and LH) have large

values and the other two subbands (HH and HL)

have small values near to zero as shown in Figure

5. The small values can be efﬁciently encoded us-

ing Golomb-Rice entropy encoder. We use DPCM

scheme subband-wise to remove spatial redundancy

in the LH and LL subbands. In DPCM scheme, the

current pixel, X, is estimated from previously en-

coded neighborhood pixels and then the estimated

pixel value, X p, is subtracted from current pixel value

to get prediction error, dX = X − X

. If the predic-

tion accuracy is high, then the prediction error will

be small and can be efﬁciently encoded. In baseline

lossless JPEG standard (JPEG, 1998), up to six dif-

ferent prediction modes are recommended. We have

chosen the simplest and static prediction mode which

estimates the current pixel from a previously encoded

pixel in the same row and same subband in order to

reduce the computational complexity and to avoid the

memory required to buffer one row of previously en-

coded pixels. As shown in Figure 6 the prediction er-

ror of LL and LH subbands have small values which

can can be efﬁciently encoded using computationally

simple entropy encoding techniques such as Golomb-

Rice encoder as shown in the next section.

−80 −40 0 40 80

1000

2000

3000

4000

(a)

−80 −40 0 40 80

500

1000

1500

2000

2500

(b)

Figure 6: Histogram of the DPCM prediction error of LH

(a) and LL (b) subbands for the mosaic image shown in Fig-

ure 2(b).

ALow-PowerColorMosaicImageCompressorBasedonOptimalCombinationof1-DDiscreteWaveletPacketTransform

andDPCMforWirelessCapsuleEndoscopy

193

2.4 Locally Adaptive Optimized

Golomb-Rice Encoder

After second level DWPT decompostion of mosaic

image, the detail subbands (HH and HL subbands)

have two-sided laplacian distribution around zero as

shown in Figure 5 (a) and (b). Similarly, the predic-

tion error of the DPCM scheme applied on approx-

imate subbands (LL and LH subbands) have a two-

sided laplacian distribution around zero as shown in

Figure 6. Golomb-Rice (GR) coding (Golomb, 1966;

Rice, 1991) is simple and efﬁcient for encoding pos-

itive integers that form two-sided geometric distri-

bution around zero (Gallager and Voorhi, 1975) and

has been implemented in baseline JPEG-LS standard

(JPEG, 1998). In JPEG-LS two modes of encoding

are employed: regular mode and run-length encoding

mode. Experiments show that the runs are too short

in endoscopic image except at the corners. Hence, we

do not use the run-length coding mode to save silicon

area and power consumption.

In the regular mode of JPEG-LS encoding, the

Golomb-Rice encoder parameter k, is determined

from the global image statistics using 365 contexts.

The context variable requires a memory of size

1.9 KB (Chen et al., 2009) which is potentially expen-

sive for power and area constrained device like WCE.

Non-adaptiveparameter k based Golomb-Rice encod-

ing was used in (Khan and Wahid, 2011b). The ﬁxed

parameter based Golomb-Rice encoding gives lower

compression rate than the adaptive one.

We have modiﬁed the regular mode of JPEG-LS

encoder in order to reduce the memory requirement.

In our case, we have used only a single context to

determine the parameter k for each subbands. By us-

ing single context for each subband, the Golomb-Rice

parameter, k, can adapt to local statistics of the pixel

values. We use two registers in order to store the ac-

cumulated values and to count the number of contexts

encountered so far for each of the subbands. By us-

ing single context in Golomb-Rice encoder we have

simpliﬁed the encoding process and still maintain its

adaptability property. Totally, we have used four con-

texts, one for each subband in order to make the pa-

rameter adaptation intra-subband. Each subband is

encoded separately because of the difference in their

statistical properties. The maximum number of pre-

viously encoded values to be stored for the param-

eter k estimation is determined using a constant N

This value is determined experimentally for the opti-

mal hardware cost and compression efﬁciency and it

is found to be 8 (64 in JPEG-LS). The context vari-

ables require only 34 bytes of memory which is very

small.

2.5 The Proposed Image Compression

Algorithm

The block diagram of the proposed image compres-

sor is depicted in Figure 7. Due to the square shape

of image sensor and circular shape of the lens inside

endoscopic capsule, the corner region pixels have no

important information as shown in Figure 2(b). This

regions can be cropped without any loss of informa-

tion. The corner pixels are cropped using the algo-

rithm proposed in (Khan and Wahid, 2011a). The

mosaic image pixel values are quantized to increase

the spatial correlation in the neighborhood pixels as

described in section 2.2. The the ﬁrst level DWPT

is applied on the quantized pixel values as described

in section 2.1. The chrominance (H subband) com-

ponents of the ﬁrst level wavelet decomposition of

the mosaic image is down-sampled to reduce the im-

age size. Then L subband of the ﬁrst level wavelet

decomposition and the down-sampled H subband are

further decomposed into four subbands (LL, LH, HH

and HL) by applying second level wavelet decompo-

sition. DPCM is applied on the LL and LH subbands

of the second level DWPT as given in section 2.3. Fi-

nally, locally adaptive Golomb-Rice encoder is used

as an entropy encoder as described in section 2.4. The

decoding operation is the inverse of the encoding pro-

cess.

3 PERFORMANCE EVALUATION

The performance of image compression algorithm is

evaluated using compression rate (CR) and given by:

CR = (1−

Image size after compression

Image size before compression

) × 100 % (8)

The proposed image compression algorithm is lossy

due to the quantization and sub-sampling operations.

The quality of the decompressed image is evaluated

using peak signal to noise ratio (PSNR)(Korhonen

and Junyong, 2012) which is given by:

PSNR = 10log

(

255

∑

x=1

∑

y=1

( f(x, y) −

f(x, y))

) (9)

where M and N are width and height of the original

image f(x, y) and the noisy image

f(x, y), x and y are

coordinates of the pixel. All the experiments in this

work are done using 120 endoscopic images obtained

from Gastrolab (Gastrolab, 2014). The test images in-

clude the images of the whole GI tract, from esopha-

gus to colon. Therefore, we believe that these images

are a good representative of the whole human diges-

tive system images. The images are originally avail-

able in RGB full color format. For our experiment, we

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

194

Corner

clipper

Uniform

quantizer 1D

DWPT

DPCM

AGR

Output

Input

Sub-

DWPT

Level 1 Level 2

encoder

sampling

Figure 7: Block diagram of the proposed endoscopic image compressor.

Table 2: The performance of the proposed image compres-

sion algorithm for different parameters.

Parameters

Quantizer

H subband

sub-sampling

factor

CR (%)

PSNR

(dB)

1 - 55.02 ∞

2 - 65.49 51.3719

4 - 73.57 46.6142

8 78.35 41.0004

- 2 63.22 46.2585

- 4 68.05 41.2555

- 8 71.01 36.75

4 2 78.59 40.6736

4 4 81.31 39.4471

4 8 82.95 36.6333

have convertedthe full color images into color mosaic

images using matlab. For visual comparison (subjec-

tive image quality assessment) both original mosaic

images and the decompressed images are converted

to full color images using a demosaicing algorithm

(Getreuer, 2011). The performance of the proposed

image compression algorithm is shown in table 2.

As shown in Table 2, the lossless mode of the

proposed image compressor gives a compression rate

of 55.02 %. The nearly-lossless and lossy versions

of the algorithm give up to 82.95 % compression

rate. This implies that the proposed image compres-

sor (quantizer=4 and H subband down-sampling by 4)

reduces the size of image by an average factor of 5.5.

It has an average peak signal to noise ratio (PSNR)

of 39.45 dB which is greater than minimum PSNR

(35dB)(Istepanian et al., 2008; Cosman et al., 1994)

required for accurate diagnosis of medical images.

4 HARDWARE REALIZATION

The block diagram of the proposed image compressor

is given in Figure 8. The image compressor takes 8-bit

pixel value from image sensor at every rising edge of

clock (or CLK) signal. The image sensor also sends

row (HSYNC) and frame synchronisation (VSYNC)

to indicate the end of a row and frame respectively.

The image compressor requires computationally sim-

ple methods such as adders, shift registers, counters

etc. The lifting scheme based 1-D wavelet decom-

position of mosaic image is done modifying the ar-

chitecture proposed in (Angelopoulou et al., 2007).

In the modiﬁed architecture the ﬁrst level wavelet de-

composition is done according to the equations given

in (5) and (6). The Golomb-Rice encoder generates

a codeword (CW) of length 32 and codeword index

(CWI). The codeword index holds the index to MSB

of the generated code in the 32-bit CW. No memory

buffer is used in the implementation, only few regis-

ters are employed.

The proposed endoscopic image compression al-

gorithm ( with quantizer q=4 and sub-sampling the

high frequency subband of ﬁrst level wavelet decom-

position by 4) has been implemented in both MAT-

LAB and VHDL for veriﬁcation. The image compres-

sor was implemented in MATLAB scripts and VHDL.

The image decompressor is implemented only in

MATLAB. After the functionality of the algorithm

is veriﬁed using 120 endoscopic images, the VHDL

code is synthesized and mapped to UMC 130 nm

Faraday high speed (HS) library using Synopsys De-

sign Compiler. After post-synthesis functional veriﬁ-

cation of the algorithm is done using QuestaSim and

MATLAB, the layout is generated using Cadence Soc

Encounter place and route tool. The layout view of

the core of the chip is shown in Figure.9. The pro-

posed image compression algorithm has core size of

0.342 mm x 0.342 mm. The power consumption of

the synthesized design is estimated using Synopsys

PrimeTime PX. The mean power consumption of the

image compressor is 48.4µW when operating at two

frames per second (fps) for encoding 512x512 color

mosaic image. The operating voltage is 1.2V.

The performance comparison of the proposed al-

gorithm with other existing works is given in table

3. We compare our proposed image compressor with

one algorithm which is based on JPEG-LS (Xie et al.,

2006) and two algorithms which are based on DCT

(Lin and Dung, 2011; Turcza and Duplaga, 2013).

All the competing algorithms included in the table

From

image

Image

compressor

HSYNC

VSYNC

CLK

DATA

sensor

CWL

To RF

transmitter

Figure 8: Block diagram of the proposed image compressor

implementation.

ALow-PowerColorMosaicImageCompressorBasedonOptimalCombinationof1-DDiscreteWaveletPacketTransform

andDPCMforWirelessCapsuleEndoscopy

195

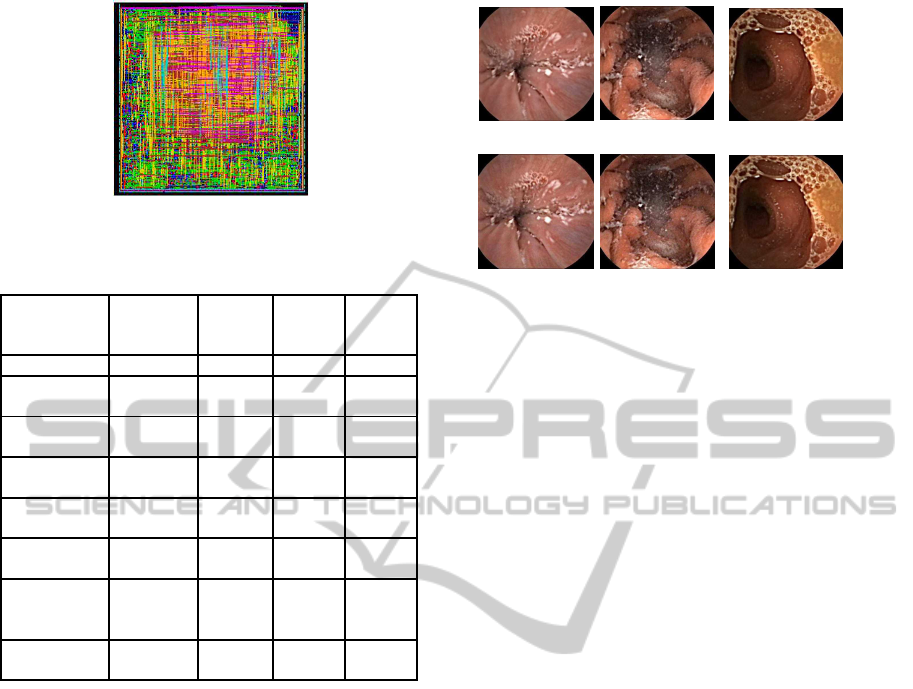
Figure 9: Layout view of the core of the proposed image

compressor implementation.

Table 3: The comparison results with previous works.

(Xie

et al.,

2006)

(Lin

et al.,

2011)

(Turcza

et al.,

2013)

This

work

Methods JPEG-LS DCT DCT DWPT

Compression

Rate (%)

72.7 82.0 91.2 81.31

Overall

PSNR (dB)

46.8 36.2 35.7 39.5

Technology

ASIC

0.18 µm

ASIC

0.18 µm

FPGA

65nm

ASIC

0.13µm

Core

size (µm

)

90K gates 318K - 117K

Memory

(byte)

93.81K YES 10.5K 0

Power

consumption

(mW)

1.55

(0.28 fps)

9.17

(2 fps)

(7 fps)

0.048

(2 fps)

Supply

Voltage(V)

1.8 1.8 1.2 1.2

were tested with similar images of 512 x 512 reso-

lution. The proposed image compression algorithm

doesn’t require memory and consumes about two or-

ders of less power than other algorithms as shown in

table 3. Our algorithm has also the lowest chip area

as compared to other works. The proposed algorithm

outperforms work in (Xie et al., 2006) in terms of

compression rate. It gives a comparable compression

rate with a work in (Lin and Dung, 2011) but has also

higher image quality. It achieves lower compression

rate than the work in (Turcza and Duplaga, 2013).

However, the work in (Turcza and Duplaga, 2013)

needs about 10.5 KB of memory which consumes

high powerand occupies large silicon area. Generally,

DCT based compression algorithms introduce block-

ing effect due to the quantization of DCT coefﬁcients.

The proposed algorithm doesn’t introduce blocking

effect which is indispensable for precise diagnosis of

medical images. As shown in Figure.10, the proposed

endoscopic image compression algorithm doesn’t in-

troduce noticeable artifacts in the reconstructed im-

age. The proposed endoscopic image compression al-

gorithm meets all the criterion to be a serious candi-

date for WCE.

(a) Cardia (b) Gastric Body (c) Jejunum

(i) 39.38 dB (ii) 39.04 dB (iii) 38.16 dB

Figure 10: Three endoscopic images out of 120 test images

that we have employed in the experimentation. The original

(top) and reconstructed images (bottom) with PSNR value.

5 CONCLUSION

In this paper, we have presented a low-power im-

age compression algorithm for WCE application.

The algorithm uses optimal combination of meth-

ods which are computationally simple. Utilizing

the combination of computationally simple methods

we have achieved a compression rate of 81.3 %.

The compressed image has a high image quality

(39.5 dB) which is greater than the minimum PSNR

(35 dB)(Istepanian et al., 2008; Cosman et al., 1994)

required for accurate medical image diagnosis. The

proposed image compression algorithm has relatively

high compression rate, small chip area, low power

consumption and high image quality which makes it

a good candidate for WCE application.

The future work includes the design of the whole

capsule system and testing its performance in real-

world. The impact of the distortion introduced due to

the image compressor on automatic disease detection

algorithms will be studied.

REFERENCES

Angelopoulou, M. E., Cheung, P. Y. K., Masselos, K., and

Andreopoulos, Y. (2007). Implementation and com-

parison of the 5/3 lifting 2d discrete wavelet transform

computation schedules on fpgas. Springer, Journal of

VLSI Signal Processing.

Bayer, B. E. (1976). Color imaging array.

Chen, X., X., Zhang, L., Li, X., Qi, N., Jiang, H., and

Wang, Z. (2009). A wireless capsule endoscope sys-

tem with low-power controlling and processing asic.

IEEE Transactions on,Biomedical Circuits and Sys-

tems, 3(1):11–22.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

196

Cheng, C., Liu, Z., Hu, C., and Meng, M. (2010). A novel

wireless capsule endoscope withjpeg compression en-

gine. In 2010 IEEE International Conference on, Au-

tomation and Logistics (ICAL), pages 553–558.

Cosman, P., Gray, R., and Olshen, R. (1994). Evaluating

quality of compressed medical images: Snr, subjective

rating, and diagnostic accuracy. Proceedings of the

IEEE, 82(6):919–932.

Dung, L., Wu, Y., Lai, H., and Weng, P. (2008). A mod-

iﬁed h.264 intra-frame video encoder for capsule en-

doscope. In BioCAS 2008, IEEE Biomedical Circuits

and Systems Conference, pages 61–64.

Gallager, R. and Voorhi, D. V. (1975). Optimal source

codes for geometrically distributed integer alphabets

(corresp.). IEEE Transactions on, Information The-

ory, 21(2):228–230.

Gastrolab (2014). http://gastrolab.net/ (Online avail-

able),last visited 2014.

Getreuer, P. (2011). Color demosaicing with contour sten-

cils. In 17th International Conference on, Digital Sig-

nal Processing (DSP), pages 1–6.

Golomb, S. (1966). Run-length encodings (corresp.). IEEE

Transactions on, Information Theory, 12(3):399–401.

Idden, G., Meron, G., Glukhovsky, A., and Swain, P.

(2000). Wireless capsule endoscopy. Nature.

Istepanian, R., Philip, N., Martini, M., Amso, N., and

Shorvon, P. (2008). Subjective and objective quality

assessment in wireless teleultrasonography imaging.

In EMBS 2008,3 0th Annual International Conference

of the IEEE Engineering in Medicine and Biology So-

ciety.

JPEG (1998). Lossless and near-lossless compression of

continuous-tone still images baseline. JPEG-LS,T.87.

Khan, T. and Wahid, K. (2011a). Low power and low

complexity compressor for video capsule endoscopy.

IEEE Transactions on, Circuits and Systems for Video

Technology, 21(10):1534–1546.

Khan, T. and Wahid, K. (2011b). Subsample-based image

compression for capsule endoscopy. Journal of Real-

Time Image Prococessing, 8(1):5–19.

Korhonen, J. and Junyong, Y. (2012). Peak signal-to-noise

ratio revisited: Is simple beautiful? In Fourth Inter-

national Workshop on, Quality of Multimedia Experi-

ence (QoMEX).

Lin, M. and Dung, L. (2011). A subsample-based low-

power image compressor for capsule gastrointestinal

endoscopy. EURASIP Journal on Advances in Signal

Processing, 2011.

Lin, M., Dung, L., and Weng, P. (2006). An ultra-low-power

image compressor for capsule endoscope. BioMedical

Engineering OnLine, 5(14).

Moglia, A., Menciassi, A., and Dario, P. (2008). Recent

patents on wireless capsule endoscopy. Recent Patents

on Biomedical Engineering.

Pattanaik, S., Mahapatra, K., and Panda, G. (2006). A

novel lossless image compression algorithm using

arithmetic modulo operation. In IEEE Conference on

Cybernetics and Intelligent Systems, pages 1–5.

Rice, R. F. (1991). Some practical universal noiseless cod-

ing techniques - part iii. Tech. Rep.JPL-91-3, Jet

Propulsion Laboratory.

Sweldens, W. (1995). Lifting scheme: A new philosophy

in biorthogonal wavelet constructions. In proc. SPIE,

volume 2569.

Turcza, P. and Duplaga, M. (2011). Low power fpga-based

image processing core for wireless capsule endoscopy.

Sensors and Actuators A: Physical, 172(2):552–560.

Turcza, P. and Duplaga, M. (2013). Hardware-efﬁcient low-

power image processing system for wireless capsule

endoscopy. IEEE Journal of Biomedical and Health

Informatics, 17(6):1046–1056.

Wahid, K., Ko, S., and Teng, D. (2008). Efﬁcient hardware

implementation of an image compressor for wire-

less capsule endoscopy applications. In IJCNN’08,

IEEE International Joint Conference on Neural Net-

works (IEEE World Congress on Computational In-

telligence).

Xie, X., Li, G., Chen, X., Li, X., and Wang, Z. (2006). A

low-power digital ic design inside the wireless endo-

scopic capsule. IEEE Journal of Solid-State Circuits,

41(11):2390–2400.

Xie, X., Li, G., and Wang, Z. (2007). A near-lossless image

compression algorithm suitable for hardware design

in wireless endoscopy system. EURASIP Journal on

Advances in Signal Processing.

Zhang, N. and Wu, X. (2004). Lossless compression of

color mosaic images. In ICIP ’04, International Con-

ference on Image Processing.

ALow-PowerColorMosaicImageCompressorBasedonOptimalCombinationof1-DDiscreteWaveletPacketTransform

andDPCMforWirelessCapsuleEndoscopy

197