
Multifactorial Dimensionality Reduction for Disordered Trait
Alexander Rakitko
Steklov Mathematical Institute, Russian Academy of Sciences, Moscow, Russia
Keywords:
GWAS, Multifactorial Dimensionality Reduction, Associated Factors, Disordered Response, Cross-validation
Procedure.
Abstract:
We develop our recent works concerning the identification of the factors associated with a certain complex
disease. The case of disordered discrete trait is studied. We build two models (3D and 2D) for the range
of response variable indicating the state of the health of a patient. In this work we consider the problem of
optimal forecast for response variable depending on a finite collection of factors with values in arbitrary finite
set. The quality of prediction is described by the error function involving a penalty function. The estimation
of the error requires some cross-validation procedure. The developed approach provides the basis to identify
the set of significant factors. Such problem arises naturally, e.g., in the genome-wide association study. Using
simulated data we illustrate the efficiency of our method.
1 INTRODUCTION
The problem of the high dimension arises naturally
in various stochastic models. For instance, in ge-
netics studies the number of explanatory factors (e.g.
SNP - single nucleotide polymorphism) X
1
,...,X
p
is
much more than the possible sample size. But nowa-
days the main part of specialists share the paradigm
that not all of them are significant for certain com-
plex disease provoking. So the challenging problem
is to find among huge number of factors the collection
X
k
1
,...,X
k
r
of factors associated with the disease.
In the previous works (Bulinski and Rakitko,
2014) we considered the case when response vari-
able Y (Y depends on a number of factors X
1
,...,X
p
and indicates disease status) takes values in the set
{−m,...,0,...,m} for some natural m ∈ N . How-
ever, in many applications it is impossible to intro-
duce a linear order for traits under consideration. In
this paper we study the model which assumes that Y
can take values in an arbitrary finite set with no as-
sumption about its serializability.
In medical and biological studies there exists a
special research domain called the genome-wide as-
sociation studies (GWAS). This branch of bioin-
formatics has already included a number of differ-
ent approaches for identification of significant fac-
tors. Among powerful statistical methods applied in
GWAS one can find the principal component anal-
ysis (Lee et al., 2012), logic and logistic regres-
sion (Ruczinski et al., 2003), (Sikorska et al., 2013),
LASSO (Tibshirani and Taylor, 2012) and various
methods of machine learning (Hastie et al., 2001). In
our work we concentrate on the development of mul-
tifactorial dimensionality reduction (MDR) method.
For the first time this method was implemented in the
paper by M. Ritchie (Ritchie et al., 2001). Our variant
of this method is based on the estimation of the error
functions. Details are given in the next section.
The paper is organized as follows. In the second
section we describe our method and build two mod-
els for response variable. Moreover, we introduce the
procedure of simulation of genetics data. Some sta-
tistical results for proposed estimations are given as
well. In the third section we discuss the results of ap-
plication of our method to the analysis of generated
data. Here we compare two different models and give
some recommendations about the choice of the size of
significant collection. Summary of the work is given
in conclusion.
2 MATERIALS AND METHODS
Let X = (X
1
,...,X
p
) be a random vector with com-
ponents X
k
: Ω → {0, 1, . ..,s} where k = 1,..., p and
s, p ∈ N. All random variables are defined on a prob-
ability space (Ω, F ,P). In general for different k
one could consider different s as it is of no impor-
tance. For instance, X
k
can characterizes single nu-
232
Rakitko A.
Multifactorial Dimensionality Reduction for Disordered Trait.
DOI: 10.5220/0005285302320236
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOSTEC 2015), pages 232-236
ISBN: 978-989-758-070-3
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

cleotide polymorphism (SNP) and takes values in the
set {0, 1, 2} (corresponding to the number of minor
alleles) whereas X
l
, l 6= k, can be binary and indicates
smoking addiction.
We assume that X : Ω → X (e.g.
X = {0,1,...,s}
p
) and Y : Ω → Y. In our
model a response variable Y depends on factors
X
1
,...,X
p
and describes the state of the health of a
patient. In some recent papers (Bulinski and Rakitko,
2014) the case of linearly ordered set Y was studied.
For example, if Y = {−1,0,1} then Y = 1 or Y = −1
mean that person is sick or healthy, respectively. The
value 0 one can interpret as ”intermediate”. In other
words, in this ”grey zone” corresponding to 0 one
cannot make conclusion whether disease appear or
not. However, in some applications it is difficult (or
even impossible) to introduce a linear order of the set
Y. For instance, Y can indicates the subtype of acute
ischemic stroke according TOAST classification
(Adams et al., 1993): large-artery atherosclerosis,
cardioembolism or small-artery occlusion. Besides,
we should take into account the other two groups
corresponding to stroke of other determined etiology
and stroke of undetermined etiology. So we add
an extra value of Y which is responsible for such
uncertainty.
2.1 2D and 3D Models
Here we consider two models for linearly unordered
set Y. The following theory with little effort could
be extend onto the case of any finite capacity of Y.
But for simplicity we assume that Y = {y
0
,y
1
,y
2
,y
3
}
where y
1
, y
2
, y
3
correspond, as example, to one of the
three subtypes of ischemic acute stroke and y
0
indi-
cates unclassified patient.
3D-Model. In this model all elements of Y are
equidistant from each other. It means that {y
i
}
4
i=0
are
located at the vertices of tetrahedron (Figure 1). With-
out loss of generality let edge of tetrahedron equals 1.
2D-Model. Let us put elements y
1
, y
2
, y
3
at the ver-
tices of the regular triangle with unit edge. The el-
ement y
0
is located in the middle of triangle (Figure
2).
2.2 Methods
In this subsection we describe new modification of
MDR-EFE method (Bulinski and Rakitko, 2014) con-
cerning introduced 2D- and 3D-Models.
MDR-EFE Method. To predict Y we use determinis-
tic function f : X →Y of factors X
1
,...,X
p
. The qual-
ity of such f is determined by means of error function
y
1
y
2
y
3
y
0
Figure 1: 3D-case.
y
1
y
2
y
3
y
0
Figure 2: 2D-case.
Err( f ) involving a penalty function ψ : Y → R
+
:
Err( f ) := E|Y −f(x)|ψ(Y). (1)
The trivial case ψ ≡ 0 is excluded. In fact, the choice
of penalty functions ψ gives an additional degree of
freedom. But for further analysis we take function
ψ(y) =
c
P(Y = y)
, y ∈ Y, c = const > 0, (2)
proposed by Velez (Velez et al., 2007). Assuming
here that P(Y = y) > 0 for y ∈ Y one can take c = 1
without loss of generality. In (Bulinski, 2014) it was
explained that this choice is natural.
For r = 1,..., p set X
r
= {0, 1 . . . , s}
r
. Then X =
X
p
. We write α = (k
1
,...,k
r
), X
α
= (X
k
1
,...,X
k
r
) and
x
α
= (x
k
1
,...,x
k
r
) where x
i
∈ {0, . . . , s}, i = 1,. . . , p.
In many models it is natural to assume that response
variable Y depends significantly only on a certain col-
lection of factors X
k
1
,...,X
k
r
where 1 ≤k
1
< . . . <
k
r
≤ p. In other words, for x ∈ X, P(X = x) > 0
and y ∈ Y the following relation holds true
P(Y = y|X = x) = P(Y = y|X
α
= x
α
). (3)
Here P(X = x
α
) ≥ P(X = x) > 0.
In medical and biological studies the factors
X
k
1
,...,X
k
r
can be viewed as essential for provoking
Multifactorial Dimensionality Reduction for Disordered Trait
233

complex disease whereas the impact of other can be
neglected. Any collection of such indexes {k
1
,...,k
r
}
from (3) is called significant.
Fortunately, it is possible to describe all functions
f : X
r
→ Y which are the solution of the problem
Err( f ) →inf. It is natural to approximate Y by means
of one of this optimal functions. So we take a certain
function f
β
opt
defined below from the whole class of
optimal functions.
Optimal function f
β
opt
in 3D-Model. Simple arith-
metic conversions conclude that in 3D-Model the fol-
lowing f
β
opt
is optimal. Let us define the system of
sets B
β
y
, y ∈ Y as shown
x ∈B
β
y
⇐⇒ P(X
β
= x
β
|Y = y) > P(X
β
= x
β
|Y = z)
for all z 6= y, z ∈ Y. If for some z 6= y, z,y ∈ Y and
x ∈ X one has P(X
β
= x
β
|Y = y) = P(X
β
= x
β
|Y = z)
then we add this x to one of B
β
y
or B
β
z
at one’s dis-
cretion. Augmented sets B
β
y
we denote as A
β
y
for any
y ∈ Y. Obviously, {A
β
y
}
y∈Y
is a partition of the set X.
Then the following function is optimal
f
β
opt
(x) =
∑
y∈Y
yI{x ∈A
β
y
}. (4)
Optimal function f
β
opt
in 2D-Model. In this case
let’s define the sets {B
β
y
}
y∈Y
by the following way
x ∈B
β
y
0
⇐⇒
P(X
β
= x
β
|Y = y
0
) >
(1 −
√
3)
P(X
β
= x
β
|Y = y
2
)+
P(X
β
= x
β
|Y = y
3
)
+
P(X
β
= x
β
|Y = y
1
),
P(X
β
= x
β
|Y = y
0
) >
(1 −
√
3)
P(X
β
= x
β
|Y = y
1
)+
P(X
β
= x
β
|Y = y
2
)
+
P(X
β
= x
β
|Y = y
3
),
P(X
β
= x
β
|Y = y
0
) >
(1 −
√
3)
P(X
β
= x
β
|Y = y
1
)+
P(X
β
= x
β
|Y = y
3
)
+
P(X
β
= x
β
|Y = y
2
).
(5)
And for i = 1, 2, 3 and k,l ∈ {1,2,3}\i, k 6= l
x ∈B
β
y
i
⇐⇒
P(X
β
= x
β
|Y = y
i
) >
(
√
3 −1)
P(X
β
= x
β
|Y = y
k
)+
P(X
β
= x
β
|Y = y
l
)
+
P(X
β
= x
β
|Y = y
0
),
P(X
β
= x
β
|Y = y
i
) >
P(X
β
= x
β
|Y = y
j
),
j ∈ {1, 2, 3}\i.
(6)
Then after augmentation of the sets {B
β
y
}
y∈Y
we come
to the sets {A
y
}
y∈Y
and the optimal function
f
β
opt
(x) =
∑
y∈Y
yI{x ∈A
β
y
}. (7)
In fact, function f
β
opt
depends only on x
β
. Moreover,
if the collection of indexes α is significant then the
property of optimality of f
α
opt
implys for any collec-
tion β = (m
1
,...,m
r
), where 1 ≤ m
1
≤ . . . ≤ m
r
≤ p
the following relation
Err( f
α
) ≤ Err( f
β
). (8)
Let ξ
1
,ξ
2
,... be a sequence of independent iden-
tically distributed (i.i.d.) random vectors having the
same law as (X,Y ). For N ∈ N, set ξ
N
= (ξ
1
,...,ξ
N
).
We will use approximation of Err( f ) by means of ξ
N
(as N → ∞) and a prediction algorithm (PA). This PA
employs a function f
PA
= f
PA
(x,ξ
N
) defined for x ∈X
and ξ
N
and taking values in Y. More exactly, we op-
erate with a family of functions f
PA
(x,v
p
) (with values
in Y) defined for x ∈X and v
t
∈(X ×Y)
t
where t ∈N,
t ≤ N. To simplify the notation we write f
PA
(x,v
t
) in-
stead of f
PA
(x,v
t
).
Following (Bulinski and Rakitko, 2014) we can
construct an estimate of Err( f ) involving ξ
N
, predic-
tion algorithm defined by f
PA
and K-cross-validation
(on cross-validation we refer, e.g., to (Arlot and
Celisse, 2010)).
Theorem 1. Let α = (k
1
,...,k
r
) where a significant
collection {k
1
,...,k
r
} ⊂ {1, . . . , n}. Then, for any
ε > 0 and each β = (m
1
,...,m
r
) with {m
1
,...,m
r
} ⊂
{1,...,n}, the following inequality holds
d
Err
K
(
b
f
α
PA
) ≤
d
Err
K
(
b
f
β
PA
) + ε a.s. (9)
for all N large enough.
Theorem 1 shows that it is quite natural to take
for further analysis as significant such collection of
indexes {k
1
,...,k
r
} ⊂ {1, . . . , n} that
d
Err
K
(
b
f
α
PA
,ξ
N
)
with α = (k
1
,...,k
r
) has the minimal value (or near
the minimal value) among all
d
Err
K
(
b
f
β
PA
,ξ
N
) where
β = (m
1
,...,m
r
) and {m
1
,...,m
r
} ⊂ {1, . . . , n}.
2.3 Simulation
Our following aim is to test MDR-EFE-algorithm on
generated data. So in this subsection we introduce the
way for simulation of genetic markers (X ) and corre-
sponding phenotypes (Y ).
First of all we generate an array of genotypes. We
define the marginal distributions of each factor by se-
lecting alleles’ frequencies in a certain way and add
prescribed correlation structure responsible for Link-
age Disequilibrium (LD). Let us assume that there are
BIOINFORMATICS 2015 - International Conference on Bioinformatics Models, Methods and Algorithms
234

Figure 3: Correlation matrix.
N patients and for each of them we observe p fac-
tors. Then set X
i
= (X
i,1
,...,X
i,p
) to be the genetic
information about the i-th person. And the disease
status for this patient we will defile below. Every
factor takes values in the set {0, 1, 2}. For all j ∈
{1,..., p}we generate numbers q
(1)
j
and q
(2)
j
such that
q
(1)
j
∼ U[0, 1] and q
(2)
j
∼ U[q
(1)
j
,1]. Let’s consider
the collections p
j
= (p
j,AA
, p
j,Aa
, p
j,aa
) = [q
(1)
j
,q
(2)
j
−
q
(1)
j
,1 −q
(2)
j
] (here square brackets [·] mean an order-
ing by ascending) as the marginal distribution of the
j-th factor. For any j we can write
p
j,A
= p
j,AA
+
p
j,Aa
2
.
Here ”A” and ”a” denote major and minor allele cor-
respondingly.
We sample matrix X of dimention N × p with in-
dependent elements such that A
i, j
∼ Ber(p
j,A
). To
obtain desired correlations between factors we ap-
ply Iman&Conovers’ (Iman and Conover, 1982) algo-
rithm to matrix A. We take block-diagonal correlation
matrix where different blocks could be corresponded
to different genes. For each block the correlations are
constructed by means of some positive defined func-
tion
LD(i, j) = exp{−|i − j|/c}∗(1 + |i − j|/c).
In such a way we get alleles on the first chromosome.
Using the same procedure we generate matrix B with
the only difference that B
i, j
∼ Ber(p
j,A|A
i, j
) where
p
j,A|A
i, j
is the conditional probability to find allele A
on the second chromosome given allele A
i, j
on the
first one. One can see that in this case
X
i, j
= A
i, j
+ B
i, j
=
0,with probability p
j,AA
,
1,with probability p
j,Aa
,
2,with probability p
j,aa
.
Parameters of Simulation:
1. N = 6000
2. p = 10
3. Correlation matrix consists of two blocks of the
size 5 ×5, c
1
= 2, c
2
= 1
4. Y ∈ {y
1
,y
2
,y
3
} with P(Y = y
k
) = θ
k
, k = 1,2,3.
To define θ = (θ
1
,θ
2
,θ
3
) we introduce
α
i,1
= exp{1 + 2X
i,1
−1.5X
i,2
+ X
i,3
},
α
i,2
= exp{1 + 0.5X
i,1
+ 2X
i,2
−1.5X
i,3
},
α
i,3
= exp{1 + 0.5X
i,1
+ 0.6X
i,2
+ 0.7X
i,3
}.
and assume that (θ
1
,θ
2
,θ
3
) ∼ Dir(α
i,1
,α
i,2
,α
i,3
).
To add more noise and uncertainty in our data we
change the disease status of each patient onto y
0
with
probability 0.1. After simulations the following dis-
tribution of response function Y were acquired: 611,
1856, 1169, 2364.
3 RESULTS
Here we demonstrate the results obtained by applying
our algorithm. In the Table 1 one can see the top 10
collections (with the minimal estimation of the error
function Err). The estimations are counted assuming
3D-model.
Table 1: 3D-case.
n
1
n
2
n
3
Error
1 2 3 2.3794
2 3 5 2.4929
2 3 9 2.4967
2 3 4 2.5034
2 3 6 2.5043
2 3 8 2.5088
2 3 10 2.5111
2 3 7 2.5285
1 2 10 2.6117
1 2 5 2.6178
In the Table 2 the results for 2D-model are listed.
In both models the significant collection is defined
correctly. But one can see that the gap between the
first and the second collection in the 2D-case almost
two times bigger than the gap in the 3D-case. It may
implicate that the model with triangle and its center
works better with the data involving uncertainty. It
should be noted that, in fact, we are interested not in
the minimization of the absolute value of error, but in
the growth of the gap between significant and other
collections.
Multifactorial Dimensionality Reduction for Disordered Trait
235
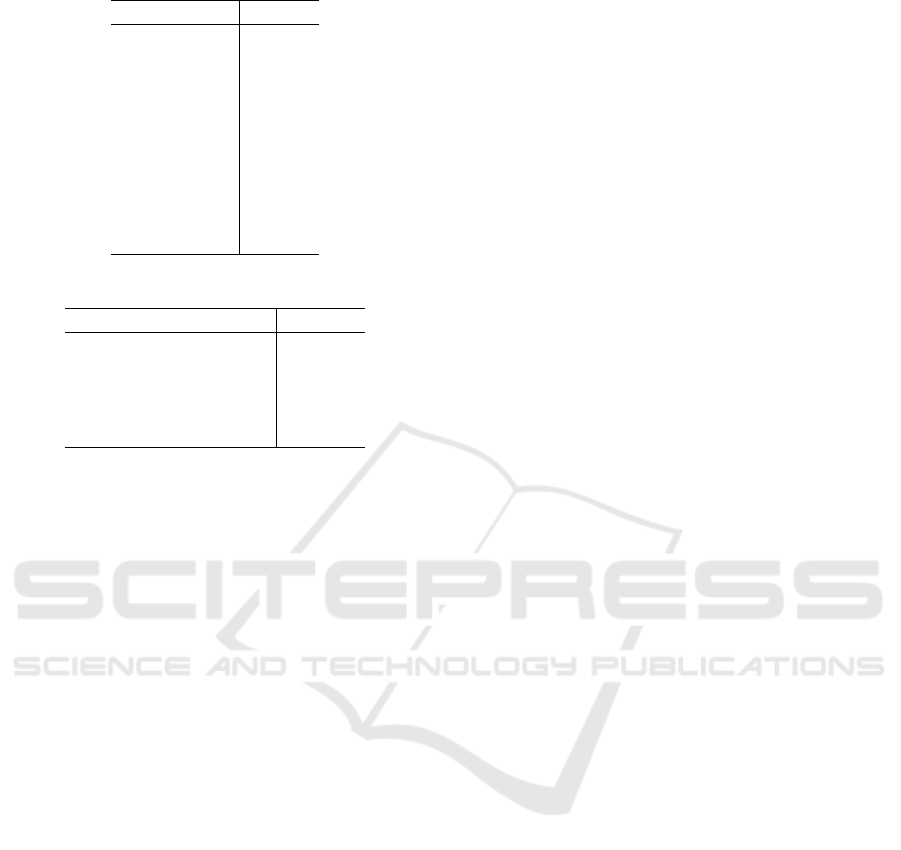
Table 2: 2D-case.
n
1
n
2
n
3
Error
1 2 3 2.5394
2 3 9 2.7503
2 3 8 2.7539
2 3 5 2.7595
2 3 10 2.7647
2 3 6 2.7662
2 3 7 2.7682
2 3 4 2.7697
1 2 5 2.7754
1 2 6 2.8143
Table 3: r-variation.
n
1
n
2
n
3
n
4
n
5
Error
3 2.95372
2 3 2.74907
1 2 3 2.56917
1 2 3 4 2.57371
1 2 3 5 9 2.56517
There is no formal rule for the choice of optimal r
(the size of significant collection). But it seems quite
natural to stop increase r if it doesn’t decrease the
estimation of the error. In the Table 3 one can find
the results for another one application of our method
to simulated data. In this table estimations of Err
for different r are listed. It is not difficult to con-
clude that the error does not decrease when r exceeds
3 (the number of significant factors). Besides, one
more reason to choose the r = 3 is that for r = 4 the
gap between the first and the second collections is just
0.0003 (the error of collection (X
1
,X
2
,X
3
,X
4
) equals
2.57371 and the error of collection (X
1
,X
2
,X
3
,X
6
) is
equal to 2.57396). It means that factors X
6
and X
4
are
not in strong association with the trait in contrast to
the factors X
1
, X
2
, X
3
.
4 CONCLUSIONS
In this paper we studied the problem of identifica-
tion of the collection of significant factors determin-
ing some disordered complex trait. We introduced
two models for the set of possible values of response
variable and developed multifactorial dimensionality
reduction approach based on estimation of error func-
tion. Using simulated data we demostrated the ef-
ficiency of our method. Further research remains a
comparison our algorithm with other methods of di-
mensionality reduction (e.g., Discriminant Principal
Component Analysis).
ACKNOWLEDGEMENTS
This work is partially supported by RSF grant 14-21-
00162.
REFERENCES
Adams, H. P., Bendixen, B. H., Kappelle, L. J., Biller, J.,
Love, B. B., Gordon, D. L., and Marsh (1993). Clas-
sification of subtype of acute ischemic stroke. Defi-
nitions for use in a multicenter clinical trial. TOAST.
Trial of Org 10172 in Acute Stroke Treatment. Stroke,
24(1):35–41.
Arlot, S. and Celisse, A. (2010). A survey of cross-
validation procedures for model selection. Statistics
Surveys, 4:40–79.
Bulinski, A. (2014). On foundation of the dimensionality
reduction method for explanatory variables. Journal
of Mathematical Sciences, 199(2):113–122.
Bulinski, A. and Rakitko, A. (2014). Estimation of
nonbinary random response. Doklady Mathematics,
89(2):225–229.
Hastie, T., Tibshirani, R., and Friedman, J. (2001). The
Elements of Statistical Learning. Springer Series in
Statistics. Springer New York Inc., New York, NY,
USA.
Iman, R. L. and Conover, W. J. (1982). A distribution-free
approach to inducing rank correlation among input
variables. Communications in Statistics - Simulation
and Computation, 11(3):311–334.
Lee, S., Epstein, M. P., Duncan, R., and Lin, X. (2012).
Sparse principal component analysis for identifying
ancestry-informative markers in genome-wide associ-
ation studies. Genetic Epidemiology, 36(4):293–302.
Ritchie, M. D., Hahn, L. W., Roodi, N., Bailey, L. R.,
Dupont, W. D., Parl, F. F., and Moore, J. H.
(2001). Multifactor-dimensionality reduction reveals
high-order interactions among estrogen-metabolism
genes in sporadic breast cancer. The American Jour-
nal of Human Genetics, 69(1):138 – 147.
Ruczinski, I., Kooperberg, C., and LeBlanc, M. (2003).
Logic regression. Journal of Computational and
Graphical Statistics, 12(3):475–511.
Sikorska, K., Lesaffre, E., Groenen, P. F. J., and Eilers, P.
H. C. (2013). Gwas on your notebook: fast semi-
parallel linear and logistic regression for genome-
wide association studies. BMC Bioinformatics, pages
166–166.
Tibshirani, R. J. and Taylor, J. (2012). Degrees of free-
dom in lasso problems. The Annals of Statistics,
40(2):1198–1232.
Velez, D. R., White, B. C., Motsinger, A. A., Bush, W. S.,
Ritchie, M. D., Williams, S. M., and Moore, J. H.
(2007). A balanced accuracy function for epista-
sis modeling in imbalanced datasets using multifac-
tor dimensionality reduction. Genetic Epidemiology,
31(4):306–315.
BIOINFORMATICS 2015 - International Conference on Bioinformatics Models, Methods and Algorithms
236
