
Spatial Mode Conversion by Non-degenerate Four Wave Mixing
Sh. Zandi
1
, A. Rostami
1,2
, Gh. Rostami
2
and M. Dolatyari
2
1
Photonics and Nanocrystal Research Lab. (PNRL), Faculty of Electrical and Computer Engineering, University of Tabriz,
Tabriz 5166614761, Iran
2
Photonics Group, School of Engineering-Emerging Technologies, University of Tabriz, Tabriz 5166614761, Iran
Keywords: Mode Conversion, Semiconductor Optical Amplifiers, Nonlinear Optics, Four-wave Mixing.
Abstract: We investigate coupling and power transfer between two transverse modes in a single quantum-well
traveling wave semiconductor optical amplifier (SOAs) by non-degenerate four wave mixing. By this
approach the mode purity achieve 99.99% at the end of active region of SOA and the mode conversion can
be controlled by the adjusting pump and probe power.
1 INTRODUCTION
The mode conversion recently has found
applications in optical communication, especially in
spatial mode division multiplexing, wavelength
filters, sensors, dispersion compensators, optical
switching (Tim Hellwig, Sep 2013) and generation
the orbital angular momentum (Yao, 2011). The
mode conversion by using the devices like spatial
light modulator, cylindrical lens (Yao, 2011), Bragg
grating (Dietmar Johlen, Nov 2000, Tim Hellwig,
Sep 2013), and multimode interference (Yutaka
Chaen, Oct. 27 - 30, 2013) are well-known. In this
paper, we demonstrate a new method for mode
converting and spatial mode modulating based on
the SOAs. The applicability of SOAs in optical
switching and optical processing and their capability
in integration are proved (Connelly, 2004). Here, we
obtain the efficient conversion on the conjugate
frequency between two excited modes in multi
modes geometry of active region by non-degenerate
four wave mixing.
2 THEORY
Due to the nonlinearity effect, coupling between two
or more light beams can occur in a single waveguide
(Yaron Silberberg, 1987). In our investigations we
have used the GaAs as active region (or waveguide).
First the modal analysis on the typical structure of
TW-SOAs has been performed and the obtained
results is used as a guided modes that can be excited
in the active region(Yamada, Sep 1983, Yaron
Silberberg, 1987). These guided modes and their
effective refractive index for pump, probe and
conjugate (or signal) frequency are shown in figure
1. The first and third order susceptibility that depend
on the carrier density are derived by density matrix
method and represented by(Yamada, 1989):
2
11
0pgm
Nk iNN b
11
.i
(1a)
2
2
3 3
4
in
pg
Nk M iNN
33
.i
(1b)
Where k and b are constant coefficient, for GaAs are
1.61×10
-26
m
3
and 3×10
19
m
-3
Å
-2
respectively.
α
p
is a
line width enhancement factor, N
g
(1)
and N
g
(3)
are
first order and third order transparency carrier
density, λ
p
is a peak wavelength, λ
m
is a wavelength
of interaction beam, τ
in
is an intra-band relaxation
time,
is a plank constant,
2
M
is a dipole
moment. Also the
3
N
like a simplified
susceptibility due to the spectral hole burning that
has been introduced in (A. Uskov, Aug 1994).
The optical field of guided modes in active
region can be expressed as:
1
,, ,
,2
exp , exp
iijij i
j
ji
E
it A zF xy i z
(2)
69
Zandi S., Rostami A., Rostami G. and Dolatyari M..
Spatial Mode Conversion by Non-degenerate Four Wave Mixing.
DOI: 10.5220/0005289500690072
In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 69-72
ISBN: 978-989-758-093-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

12
().exp
i
EE it
Where A is amplitude, β is the propagation
constant and F(x, y) is the normalized transverse
distribution of optical field. Subscribe i indicates the
pump, probe and conjugate optical field
respectively, and subscribe j indicates the
fundamental and second mode, respectively. Also
the relation between frequencies is
201
2
.
Figure 1: Electric Field (x component ) of Modes in
multimode geometry of Active region, Active region
width=1.1 μm, Active region thickness=0.7 μm. (a)-
(b) fundamental and second mode in signal
(Conjugate) frequency, 353 THz, n
eff2,1
= 3.5702, n
eff2,2
= 3.5438. (c)-(d) fundamental and second mode in
pump frequency, 371.5 THZ, n
eff0,1
= 3.572, n
eff0,2
=
3.5466. (e)-(f) fundamental and second mode in
probe frequency, 390 THZ, n
eff1,1
= 3.5737, n
eff1,2
=
3.5493.
The nonlinear coupling due to the nonlinear
polarization can be represented by(Jensen, Oct 1982,
P.Agrawal, 2001):
,
*
,
0
,
ij
NL
i
ij
ij
iz
P
e
F
Az
i P dxdy
z
∬
(3)
P
NL
is a perturbing nonlinear polarization that is the
summation of all nonlinear polarization in the
specific frequency and these perturbing nonlinear
polarization terms are defined in (.Boyd, 2008) and
P
0
is a normalized power. The carrier density
equation for SOA in time independent state is:
22
,i ,i
i,1 i,1 i,2 i,2
0,1,2
22
,i
i,1 i,1 i,2 i,2
0,1,2
ΓΓ
1
ΓΓ
ntr
i
n
s
i
i
i
N
I
AA
qAL
Nz
AA
(4)
Where V is the active region volume, α
n
is a
differential gain, τ
s
is spontaneous lifetime, Γ is a
confinement factor and N
tr
is a transparency carrier
density depends on wavelength, in other words
2
1
0m
tr g
NbN
.
Finally, we have a differential equations set that
include six coupled equations due to the SOA linear
rate equation and four wave mixing coupling
equations, these equations obtain the amplitude of
fundamental and second mode in pump, probe and
conjugate (or signal) frequency.
3 SIMULATION RESULTS
In this section, we demonstrate the coupling between
fundamental and second mode in pump, probe and
(2a)
(2b)
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
70
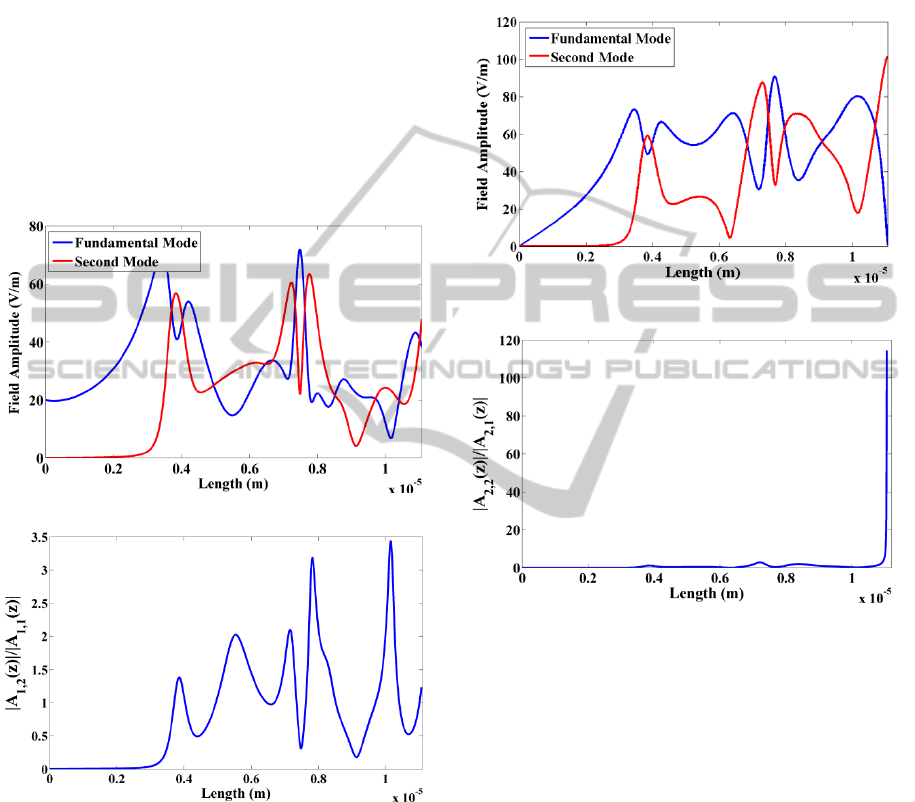
Figure 2: (2a) The coupling of amplitude of fundamental
and second modes in pump frequency. (2b) The ratio of
second mode amplitude to fundamental mode amplitude of
pump.
conjugate wave, due to the highly non-degenerate
four wave mixing, and dynamic gain, refractive
index grating (Agrawal, Jan 1988). Figure 2 shows a
coupling process between two transvers mode for
pump. As the figure (2a) shows, the second mode in
this frequency has been excited and coupling has
occurred on the length. The figure (2b) shows the
ratio of second mode amplitude to fundamental
mode amplitude on the length of active region, as
this figure shown, the efficiency of mode conversion
in pump frequency is insignificant.
(3a)
(3b)
Figure 3: (3a) The coupling of amplitude of fundamental
and second modes in probe frequency. (3b) The ratio of
second mode amplitude to fundamental mode amplitude of
probe.
Finally, figure 4 shows a coupling between
fundamental and second mode for signal (conjugate)
wave due to the non-degenerate four waves mixing
and a dynamic gain and refractive index grating. As
figure (4a) shows the coupling and mode conversion
has been occurred between fundamental and second
mode in conjugate frequency (ω
2
). Figure (4b)
shows the ratio of second mode amplitude to
fundamental mode amplitude in this frequency. As
this figure shows, this ratio at the end of active
region is about 115, and mode purity achieves 99.99
percent.
(4a)
(4b)
Figure 4: (4a) The coupling of amplitude of fundamental
and second modes in signal (conjugate) frequency. (4b)
The ratio of second mode amplitude to fundamental mode
amplitude of signal.
4 CONCLUSIONS
In this paper we demonstrate the efficient mode
conversion in TW-SOAs by highly non-degenerate
four wave mixing. This flexible mode conversion
can be occurred for both probe and conjugate wave
by adjusting pump and probe amplitude.
REFERENCES
Boyd, R. W. 2008. Nonlinear Optics, Academic Press.
A. Uskov, J. M., And J. Mark Aug 1994. Wave Mixing In
Semiconductor Laser Amplifiers Due To Carrier
SpatialModeConversionbyNon-degenerateFourWaveMixing
71

Heating And Spectral-Hole Burning. Ieee Journal Of
Quantum Electronics, 30.
Agrawal, G. P. Jan 1988. Population Pulsation's and
Nondegenerate Four-Wave Mixing In Semiconductor
Lasers And Amplifiers. J. Opt. Soc. Am. B, 5.
Connelly, M. J. 2004. Semiconductor Optical Amplifiers,
New York, Boston, Dordrecht, London, Moscow,
Kluwer Academic Publishers.
Dietmar Johlen, P. K., Hagen Renner, And Ernst
Brinkmeyer Nov 2000. Fiber Fabry–Perot
Interferometer With Mode-Converting Bragg
Gratings. Journal Of Lightwave Technology, 18.
Jensen, S. M. Oct 1982. The Nonlinear Coherent Coupler.
Ieee Transactions On Microwave Theory And
Techniques, Mtt-30.
P.Agrawal, G. 2001. Nonlinear Fiber Optics, Academic
Press.
Tim Hellwig, T. W., And Carsten Fallnich Sep 2013.
Optically Induced Mode Conversion In Graded-Index
Fibers Using Ultra-Short Laser Pulses. Applied
Physics B 112, 499-505.
Yamada, M. 1989. Theoretical Analysis Of Nonlinear
Optical Phenomena Taking Into Account The Beating
Vibration Of The Electron Density In Semiconductor
Lasers. Applied Physics, 66.
Yamada, M. Sep 1983. Transverse And Longitudinal
Mode Control In Semiconductor Injection Lasers Ieee
Journal Of Quantum Electronics, Qe-19.
Yao, A. M., And Padgett, M.J. 2011. Orbital Angular
Momentum: Origins, Behavior And Applications.
Advances In Optics And Photonics.
Yaron Silberberg, G. I. S. 1987. Nonlinear Coupling Of
Waveguide Modes. Applied Physics Letters, 50, 801.
Yutaka Chaen, R. T., And Kiichi Hamamoto Oct. 27 - 30,
2013. Optical Mode Converter Using Multimode
Interference Structure. 18th Microoptics Conference
(Moc’13). Tokyo, Japan.
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
72
