
A Particle-based Dissolution Model using Chemical Collision Energy
Min Jiang, Richard Southern and Jian Jun Zhang
National Centre for Computer Animation, Bournemouth University, Bournemouth, U.K.
Keywords:
Dissolution, Solute, Solvent, Collision Theory, Activation Energy, Particle Excitation, SPH, Erosion.
Abstract:
We propose a new energy-based method for real-time dissolution simulation. A unified particle representation
is used for both fluid solvent and solid solute. We derive a novel dissolution model from the collision theory
in chemical reactions: physical laws govern the local excitation of solid particles based on the relative motion
of the fluid and solid. When the local excitation energy exceeds a user specified threshold (activation energy),
the particle will be dislodged from the solid. Unlike previous methods, our model ensures that the dissolution
result is independent of solute sampling resolution. We also establish a mathematical relationship between
the activation energy, the inter-facial surface area, and the total dissolution time — allowing for accurate
artistic control over the global dissolution rate while maintaining the physical plausibility of the simulation.
We demonstrate applications of our method using a number of practical examples, including antacid pills
dissolving in water and hydraulic erosion of non-homogeneous terrains. Our method is straightforward to
incorporate with existing particle-based fluid simulations.
1 INTRODUCTION
The reliance of films and games on realistic fluid
simulations has led to the popularity of this research
topic, with most work in this field focused on the
behaviour of fluid itself, such as spray, waves and
bubbles (Ihmsen et al., 2012; Cleary et al., 2007;
Busaryev et al., 2012) or the interaction with solids
(Batty et al., 2007; Robinson-Mosher et al., 2008;
Schechter and Bridson, 2012; Akinci et al., 2013).
Comparatively few researchers have tackled the chal-
lenging problem of the chemical reaction between
fluid and solids, which, under the right conditions, can
lead to solid mixing with the liquid: a phenomenon
known as dissolution. The solid in this case is called
the solute and the liquid is the solvent.
Our paper proposes an energy–based dissolution
model to describe this complicated fluid–solid inter-
action. Dissolution is the result of physical and chem-
ical processes: our dissolution model follows colli-
sion theory which explains how the chemical reac-
tion happens. We introduce a kinetic energy func-
tion to measure the particle excitation of the so-
lute, which ensures the same dissolution results even
when the object sampling resolutions are different.
This approach is advantageous when performing pre-
visualization of the phenomena, allowing animators
to quickly preview the dissolution behaviour with a
low resolution sampling of the solute.
A solute particle will become dislodged if the lo-
cal energy exceeds a user specified activation energy.
While physically justified, this threshold does not pro-
vide a user with an intuition of the total dissolution
time. We demonstrate that the activation energy can
be approximated as a function of the inter-facial sur-
face area of the solvent/solute and the total dissolution
time, providing animators with a tool to more accu-
rately predict the total dissolution rate.
The key contributions of this paper include:
1. a unified particle framework which generates
physically and chemically plausible dissolution
behaviour that is simple to incorporate with an
existing particle–based fluid system;
2. an expression for measuring the local particle ex-
citation derived from kinetic energy which is in-
dependent of solute sampling resolution; and
3. a mapping between the global dissolution time
and local particle excitation based on the activa-
tion energy.
Our particle–based method enables real–time perfor-
mances using a parallel implementation. We demon-
strate plausible dissolution behaviours in different cir-
cumstances, such as rotating and translating solids in
fluids and pouring fluids onto dissolving objects. Due
to the similarity between hydraulic erosion and disso-
lution, our dissolution model is able to simulate ero-
sion without any additional computational overhead.
285
Jiang M., Southern R. and Zhang J..
A Particle-based Dissolution Model using Chemical Collision Energy.
DOI: 10.5220/0005290302850293
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 285-293
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
The simulation of natural phenomena is one of the
most studied areas in Computer Graphics, enabling
animators to generate complex and physically plau-
sible dynamics which would be impossible to create
manually. We only review work related to dissolution
since there is a large body of work in fluid simulation.
In most observable systems, the most frequent sol-
vent is fluid and solute is solid. There have been many
studies on the physical interaction between fluids and
solids. (Arash et al., 2003) studied the fluid–solid
interaction by representing solid with linked point
masses. (Batty et al., 2007) applied a pressure projec-
tion method with kinetic energy minimization to in-
corporate irregular boundary geometry into standard
grid–based fluid simulations. Their methods are yet
difficult to cooperate in dissolution simulation.
(Carlson et al., 2004) and (Amada, 2006) treated
the objects as if they were made of fluid. To main-
tain the object rigidity, (Carlson et al., 2004) identi-
fied the object by velocity field, and (Amada, 2006)
applied a corrective step to bring back the rigidity of
the solid. (Harada et al., 2007) simulated the inter-
action using collision detection. To prevent fluid par-
ticles intersecting the solid boundary, both (Amada,
2006) and (Harada et al., 2007) used penalty force
method, which took a few frames to push the particles
out. (Becker et al., 2009) also dealt with boundary
conditions to ensure no–penetration. However, they
required two additional neighbour queries for colli-
sion detection, which was expensive to compute.
(Schechter and Bridson, 2012) achieved the no–
separation and no–slip boundary condition by sam-
pling the air and solid surface as ghost particles. (Ak-
inci et al., 2012) used corrected density to compute
the pressure and viscosity force to avoid the sticking
artefacts. Both solved the boundary problem, mak-
ing an extension to support dissolution simulation. In
this paper we use the similar method with (Akinci
et al., 2012) to handle the boundary problem during
the fluid–solid interaction, but we sample the entire
object rather than just the surface since the boundary
changes as the shape dissolves.
The methods above tackled the problem of physi-
cal interaction between the fluid and solid, but did not
consider the chemical interaction between them. Rel-
atively few attempts have been made to simulate the
complex chemical reaction between fluid and solid.
(Solenthaler et al., 2007) used an elasticity model
for particle–based objects and modelled temperature
for phase changes, allowing them to simulate objects
melting in hot liquid. (Stomakhin et al., 2014) intro-
duced augmented MPM for phase-change and simu-
lated butter melting in pan. Melting offers a simi-
lar visual result with dissolution, but the underlying
function is a heat model, which is different from the
chemical model in this paper.
(Kim et al., 2010) simulated bubbles around dis-
solving objects. Their focus was on simulating the
dispersed bubble flow — the dissolution model was
approximated by generating offsets of a level–set rep-
resentation of the solute, which had little relationship
with actual dissolution behaviour. (Shin et al., 2010)
simulated solids dissolving in liquids by modelling
solid mass transfer. They treated the solvent and so-
lution as different fluids, and used multiple level–sets
to track mixing surfaces which needed to be updated
whenever the reactions and interactions occurred —
an expensive but necessary step. They also didn’t
consider about the object separation during dissolu-
tion. The latter problem is solved in (Wojtan et al.,
2007). However, they both use level–set represen-
tation to guide the object surface without additional
treatment which means their dissolution results will
largely depend on the level-set grid resolution. Fur-
thermore, all these previous approaches did not con-
sider the relationship between the dissolution time
and the mass transfer of the solute, meaning that pre-
dicting the overall dissolution time is an exercise in
trial and error. In this paper we propose a model for
predicting total dissolution time from activation en-
ergy, and our dissolution model is independent of so-
lute sampling resolutions.
Dissolution also shares many properties with hy-
draulic erosion. (Bene
ˇ
s et al., 2006) proposed a so-
lution for erosion simulation by using Navier–Stokes
equations, while (Wojtan et al., 2007) animated corro-
sion and erosion by driving the fluids with a finite dif-
ference simulation and presenting the solid by advect-
ing the level sets inward. (Kri
ˇ
stof et al., 2009) used
an SPH based method to simulate erosion, where the
erosion model is adapted from an Eulerian approach.
The erosion rate used in (Kri
ˇ
stof et al., 2009; Woj-
tan et al., 2007) is derived from the power law, which
unfortunately requires a large number of parameters
to control, making it impractical for use by an anima-
tor. In this paper we demonstrate two practical ero-
sion examples, including one which demonstrates the
specification of non–homogeneous solutes forming a
natural layering stratum.
3 DISSOLUTION MODEL
In the following sections we present a model for
simulating objects dissolving in fluid, derived from
the physics and chemistry behind the solute–solvent
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
286

interaction. Collision theory was firstly proposed
by (Trautz, 1916). It describes how chemical reac-
tions take place and why chemical reaction rates dif-
fer (McNaught and Wilkinson, 1997). Collision the-
ory is closely related to the kinetic-molecular theory:
molecules are in constant motion, occasionally col-
liding as they move. For a chemical reaction to occur,
molecules need to collide in the right orientation and
with sufficient energy (Clark, 2004). The energy re-
quired for the reaction to occur is referred to as the
activation energy — necessary to break the existing
chemical bonds between substrate molecules.
In our system we volumetrically represent both the
solute and the solvent with particles, with each parti-
cle becoming a representative component of the corre-
sponding substance. This unified particle representa-
tion removes the need for special handling of mixing
surfaces. When solute particles collide with the sol-
vent particles, energy is added to the solute particle.
Each solute particle carries the energy information
which is summed over all the collisions which have
occurred. When the energy is larger than a threshold
energy—the activation energy—the particle detaches
from the object. This activation energy becomes an
important factor in determining the dissolution rate.
This method allows us to model the dissolution pro-
cess in a physically and chemically correct manner.
3.1 Solvent Representation
Most fluid simulation methods are governed by the
Navier–Stokes equations (Foster and Metaxas, 1996).
From the viewpoints of the Lagrangian (particle–
based) and Eulerian (grid–based) methods, particle–
based methods seem to be a natural choice for dis-
solution because it is easy to implement with arbi-
trary boundaries and applied forces, while supporting
fluid mixing and interaction with arbitrary rigid bod-
ies. Smoothed Particle Hydrodynamics (SPH) was
first introduced as a mesh–free Lagrangian method in-
dependently by both (Gingold and Monaghan, 1977)
and (Lucy, 1977), and is being increasingly used for
fluid simulation due to its simplicity. In our model,
the physical and chemical reactions between fluid and
solid are elegantly simulated by a single SPH solver.
Our method is implemented within the framework
of SPH model of (M
¨
uller et al., 2003), but is com-
patible with other SPH models (Ihmsen et al., 2014),
such as PCISPH (Solenthaler and Pajarola, 2009), and
can be extended with other particle–based represen-
tations. We demonstrate the basic SPH model with a
short introduction which is required to understand our
dissolution method in the following sections. In SPH,
a scalar quantity A at location x is computed by
A(x) =
∑
j
m
j
A
j
ρ
j
W (x − x
j
, h), (1)
where W (x, h) is a smoothing kernel with smooth
core radius h which also decides the neighbour-
hood size. The kernel satisfies
R
W (x, h)dx = 1 and
W (x, h) = 0 when kxk > h. Particle j is the neigh-
bour of the particle at x. m
j
is the particle mass and
A
j
is the field quantity at x
j
.
The density and pressure force of the solvent are
calculated also based on (M
¨
uller et al., 2003). Neigh-
bour searching of the solvent simulation is GPU par-
alleled using framework of (Hoetzlein, 2014).
3.2 Solute Representation
The enclosing volume of the solute is sampled by
particles, each of which contributes to the fluid SPH
to ensure the correctness of the fluid–solid interac-
tion: (Akinci et al., 2012) and (Schechter and Brid-
son, 2012) are both good choices for this task. The
pressure between the fluid and solid automatically re-
pels the fluid particles and naturally produces the mix-
ing surface with more accuracy at lower computa-
tional cost than level–set methods. Since we focus on
the dissolution effect when the fluid interacts with the
solid, we need to sample the entire object rather than
boundary particles to produce the volume change.
For the examples used in this paper, a regular grid
sampling is used for the solute. While we have ex-
perimented with alternative sampling techniques, but
these did not alter our results significantly and are not
the focus of this paper.
3.2.1 Sampling Independent Dissolution
Our method ensures the same dissolution result
(within error tolerance) even when the sampling res-
olutions of the solute are different. This property
has important applications in computer graphics: for
the purposes of pre–visualisation, the dissolution of
a lower resolution or adaptively sampled object can
be used to predict the behaviour of a very densely
sampled object, or simply to improve performance for
real–time applications.
In previous methods (Wojtan et al., 2007; Shin
et al., 2010) shape alteration of a dissolving object
was achieved using mass transfer. Both methods used
level–sets to represent the solute, causing the dissolu-
tion result to be largely affected by the grid resolution.
In our method we use volume mass instead of mass
for each solute particle to ensure that our result is in-
dependent with the sampling resolution. The volume
mass of each solid particle is calculated by
AParticle-basedDissolutionModelusingChemicalCollisionEnergy
287

(a) solute – 6811 particles (b) solute – 2106 particles
(c) solute – 4085 particles (d) solute – 4085 particles
Figure 1: 2D bunny dissolving in fluid. Using our method
(in (a), (b) and (c)) the sampling density does not affect
the dissolution process, even when the sampling is non-
homogeneous. In (d) we demonstrate the result when using
previous methods (Wojtan et al., 2007; Shin et al., 2010).
All the images are taken from the same frame with the same
initial conditions. The solute particles with high energy are
coloured in red.
m
vs
= v
s
· ρ
s
=
V
N
∑
j
m
s
W (x
s
− x
j
, h), (2)
where v
s
and ρ
s
are respectively the volume and the
representative density of each solid particle. V is
the volume of the entire object and m
s
is the mass
of each particle: both of which are constant once
the object is initialised. N is the number of par-
ticles used to sample the object. It is easy to tell
that ρ
s
=
∑
j
m
s
W (x
s
−x
j
, h) originates from the basic
SPH density calculation in Equation 1. j is the object
particle within the solute neighbourhood h. The vol-
ume mass m
vs
must be updated in each frame due to
the changing shape of the object during dissolution.
Figure 1 demonstrates sampling independence
by using different sampling resolutions, as well as
non–homogeneous sampling resolutions, and com-
pare these against previous dissolution methods (Wo-
jtan et al., 2007; Shin et al., 2010). This property is
further discussed in Section 4.2.
3.2.2 Particle Excitation
Particle excitation is measured by local particle en-
ergy. Since collision itself is a kinetic process, we de-
rive our particle excitation equation from the kinetic
energy
1
2
mv
2
, where v is the relative velocity. This is
incorporated into Equation 1 to derive an expression
for particle excitation:
E
s
=
1
2
m
vs
∑
f
[
m
f
ρ
f
(v
l
+ v
w
+ ε)]
2
W (x
s
− x
f
, h), (3)
where m
vs
is the volume mass from Equation 2; f
is the solvent particle within the neighbourhood of
solid particle s; m
f
and ρ
f
are the mass and density
of fluid particle; v
l
is the relative linear velocity of
solid and fluid particles; and W (x
s
− x
f
, h) is poly6
kernel (M
¨
uller et al., 2003), which smooths out the
energy according to distance; other kernel may apply,
such as cubic spline (Ihmsen et al., 2014).
According to the collision theory, the detachment
of particles only occurs when particles collide with
right angle and enough strength. In SPH, however,
particles cannot collide as they will be repelled by the
pressure between particles. Instead, we consider two
particles to collide once one particle has entered the
neighbourhood of the other. Particles outside of the
neighbourhood are not computed. The size of the ve-
locity is affected by the angle of the collision, calcu-
lated by:
v
l
= max((v
f
− v
s
) · (x
s
− x
f
), 0), (4)
where v
s, f
represent the velocity of solid and fluid
particles respectively. The direction of v
l
is x
s
− x
f
.
This is illustrated in Figure 2, where only f
2
and f
3
contribute to the collision.
Figure 2: The collision domain. s represents a solid parti-
cle and f
1,2,3,4
are fluid particles. The blue arrows indicate
the actual relative velocity, while yellow ones indicate the
calculated linear relation velocity v
l
.
v
w
represents the angular velocity which con-
tributes to the local particle energy. v
w
is calculated
by w ×r, where w is the angular velocity and r is the
vector from the particle position to the centre of the
object. This is only needed when there is obvious rel-
ative rotational motion between the object and fluid.
Figure 3 shows the different dissolution behaviours of
the spinning bunny with and without angular velocity.
A small ε is also added to represent the random
thermal motion among molecules (ε = 0.00001 in
our model), which gives the possibility of dissolution
when there is no macroscopic relative motion between
the fluid and solid.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
288

(a) Dissolving without v
w
(b) Dissolving with v
w
Figure 3: A spinning bunny dissolves in water. Note that
(b) demonstrates separation behaviour (discussed in Sec-
tion 4.3). The fluid is not rendered in these examples.
E
s
accumulates by time: when it is larger than a
user specified activation energy, the particle dissolves
into the solution. As described by Equation 2, parti-
cles tend to have larger volume mass where the sam-
pling is more compact. This corrects the single par-
ticle energy by making the particle more active (i.e.
larger energy) in Equation 3, making it dissolve faster.
3.3 Activation Energy
The activation energy provides a physically correct
mechanism by which the dissolution rate of individ-
ual particle can be controlled. However, this offers no
control over the time taken for the object to be com-
pletely or partially dissolved: a property that is par-
ticularly important to animators seeking to control the
simulation without having to resort to trial and error.
In this section we provide the bridge to connect the
global dissolution time with the local particle excita-
tion. Dissolution depends on the nature of the solvent
and solute, the temperature of both, the inter–facial
surface area between them, and the presence of mix-
ing (McNaught and Wilkinson, 1997). In our method
the presence of mixing is implicitly solved by the par-
ticle excitation. For simplicity, we assume tempera-
ture to be a constant parameter θ (although this could
be varied within more complex simulations).
We determine the relationship between the total
dissolution time T , activation energy E
0
and the inter–
facial surface area S based on our simulation experi-
ments. In Figure 4, we show the results of dissolv-
ing objects with different inter–facial surface areas
and different activation energies. The three objects
(sphere, cube, spiky cube) have the same volume. The
Figure 4: The relationship between the total dissolution
time and activation energy for different immersed shapes.
Shapes with more surface area in contact with the fluid nat-
urally dissolve faster. The observed dissolution rates leads
us to use the exponential function to model the total disso-
lution time as a function of activation energy.
surface area is respectively 4.83, 6.0, and 8.20.
Each curve describes the dissolution times of cer-
tain object with different activation energies. The
shape of the curve is best approximated with the gen-
eral exponential function (α = 0.25 in our examples):
T ∝ exp(αE
0
), (5)
By observing the dissolution time of the different
objects with the same activation energy, the relation-
ship between dissolution time T and surface area S
matches:
T ∝
1
S
. (6)
This agrees with common sense: a larger surface area
results in shorter dissolution time.
According to Equations 5 and 6, we can con-
clude that the relationship between the total dissolu-
tion time, activation energy and the inter-facial sur-
face area can be described as:
T =
exp(αE
0
)
θS
, (7)
Using this experimental methodology, artists are
able to better estimate the total dissolution time for
objects based on the surface area and the local acti-
vation energy. An interactive tool could be developed
which uses preceding simulation results of a partic-
ular fluid configuration to calculate the coefficients
for better estimation. Once the coefficients are de-
termined, the inverse of this function can be used to
determine the activation energy for an artist specified
target dissolution time.
AParticle-basedDissolutionModelusingChemicalCollisionEnergy
289

3.4 Object Update
The positions of solutes are updated as rigid bod-
ies. Each disconnected component will be treated as
a rigid body, more detail discussed in Section 4.3.
No relative motion is expected among the particles
in one rigid body. The forces acted on the object are
the forces from the fluid, the gravity, and the support
force when the objects hit the boundary. The forces
from fluid, such as pressure and viscosity forces,
equal to the opposite of the corresponding forces from
the object to fluid. The rules updating the solid obey
the same with standard rigid body dynamics (Feath-
erstone, 2007).
4 IMPLEMENTATION AND
RESULTS
We ran our simulations on an Intel Xeon W3680 (8M
Cache, 3.33GHz) with 8GB RAM. The SPH fluid
simulation implemented in CUDA and executed us-
ing a GeForce 460Ti with 1GB onboard RAM. Real–
time results are rendered in OpenGL, and simulation
results were exported and rendered externally using
Houdini. The computational cost of our algorithm is
depending on the number of both solute and solvent
particles, the complexity of interaction between solute
and solvent and the update of solute positions. The
real–time performance of our technique is presented
in Table 1. In a same example, the performance can
be largely improved with less solute particles. There-
fore, our sampling independent dissolution model al-
lows animators to preview the dissolution behaviour
with a lower computational cost. Our method is very
efficient and advantageous for pre-visualization.
Table 1: The performance in average frames per second
(FPS) of our method in different examples. Solute and Sol-
vent represent the number of particles in each.
Example Solute Solvent FPS
Spinning bunny 28553 65535 27
Antacid pills 12745 80000 50
Spheres (low) 8538 100000 148
Spheres (high) 22274 100000 48
River Bed 15000 385948 19
Layered Terrain 169650 262140 20
4.1 Antacid Pills to Water
Antacid pills are a classic demonstration of dissolu-
tion behaviour for simulation. In Figure 5 we demon-
strate our effect on two Antacid pills dropped into
a glass of water. Bubbles caused by the release of
trapped air and chemical processes are recognisable
clues that dissolution is taking place. We add bubbles
at the dissolution site to increase the authenticity of
the simulation. The bubble motion is modelled using
basic Brownian motion similar in (Kim et al., 2010).
Figure 5: Two antacid pills dissolving in water.
4.2 Sampling Independent Dissolution
In Figure 6 we pour liquid over a sphere, demonstrat-
ing the effect of pouring fluid at a targeted area. We
also evaluate this example using two different sam-
pling resolutions in order to demonstrating that the
dissolution results are equivalent. We calculated the
percentage of the volume difference at each frame of
both spheres: with our method, this reaches a max-
imum of 3.4% of the sphere volume, while with the
method of (Wojtan et al., 2007; Shin et al., 2010)
the low sampled sphere dissolves completely before
the high sampled sphere halves in size. The adhesion
method of (Akinci et al., 2013) is used to ensure the
fluid realistically adheres to the sides of the sphere.
4.3 Separation
During dissolution, parts of object may break off and
form separate shapes. In order to track changes to the
topology of the shape, we use a region growing algo-
rithm to detect the object separation during dissolu-
tion, a method commonly used in image segmentation
(Hojjatoleslami and Kittler, 1995). We apply the tech-
nique to identify connected regions from amongst the
volumetric particles. Particles that are close enough
are grouped into clusters, each representing a separate
rigid body.
The main challenge in implementing this algo-
rithm is testing the proximity of particles, but as we
already have neighbourhood information as part of
the fluid simulation, this becomes trivial. We update
the neighbourhood information before evaluating the
region growing algorithm. The region grows from
a random seed particle p by adding it to cluster C.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
290

(a) Sphere sampled with 8538 particles
(b) Sphere sampled with 22274 particles
Figure 6: Fluid is poured over spheres with different sam-
pling resolutions, with almost identical results, except that
the sphere dissolves more smoothly with higher resolution.
Neighbours of p are added to C. Then all new parti-
cles in C become the new seeds for the next iteration.
Note that only neighbours that are not in C are added.
The algorithm proceeds until there are no more valid
particles that can be added to C — each resulting clus-
ter is a separate body. Implementing this algorithm in
parallel is an interesting area of future research. In
Figure 3(b) the bunny separates into pieces as a result
of the dissolution.
4.4 Erosion
We use our dissolution method to simulate complex
natural erosion phenomena. While we do not use the
actual physical properties of different terrain types,
these examples demonstrate the viability of using our
model for practical simulations. Figure 7 shows the
hydraulic erosion acting on the floor of a river bed.
As the fluid runs over the terrain, certain soil particles
become dissolved in the water. Note that more com-
plex properties of erosion, such as fluid carrying and
relocating sediment, are ignored in our simulation.
One advantage of our energy based model is that
we can simulate different terrain types by simply
modifying the activation energy of individual layers
of particles. This allows us to simulate erosion of
rocks consisting of different layers each with different
material properties, giving rise to natural formations
similar to those which can be found in mountainous
or coastal regions.
This is demonstrated in Figure 8, where a three
(a) Fluid simulation
(b) Resulting erosion
Figure 7: Hydraulic erosion with dissolution model. In (a)
we show the dissolution process, while in (b) the removed
soil particles are shown in red.
layered terrain is immersed in turbulent fluid to simu-
late coastal erosion. Different activation energies are
assigned to particles in each layer, with the lowest ac-
tivation energy assigned to the middle layer — lead-
ing to a natural arch formation.
5 CONCLUSION
In this paper we introduce a novel energy-based dis-
solution model based on the collision theory. We
demonstrate by way of examples that this method
achieves physically and chemically plausible dissolu-
tion and erosion behaviours. The key to this model
is a new expression for particle excitation based on
kinetic energy. By using the volume mass instead of
mass to update local particle energy, we are able to
ensure the same dissolution results independent of the
sampling density.
We also identify the relationship between global
dissolution time and the local particle activation en-
ergy, allowing animators to easily adjust the global
properties of the dissolution simulation by modify-
AParticle-basedDissolutionModelusingChemicalCollisionEnergy
291
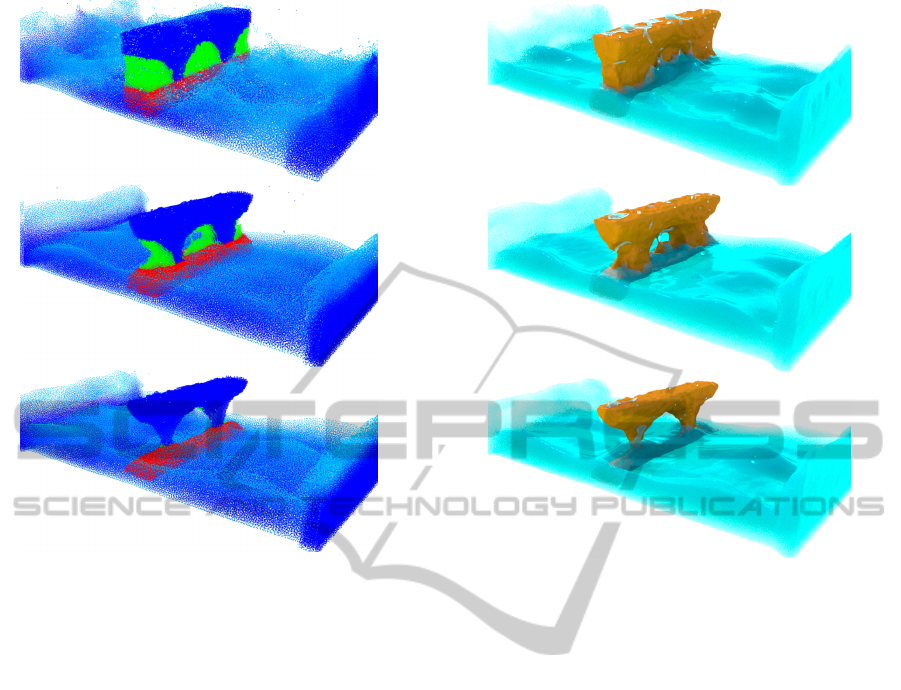
Figure 8: A simulation of layered terrain erosion using our
dissolution model. The solute consists of three different ma-
terial layers, each with a different activation energy. Forces
are added to the fluid to keep the fluid active. This simula-
tion consists of about 430k combined particles and runs as
20 frames per second on a commodity graphics card. Please
refer to Figure 9 for the rendered results.
ing a single parameter. In addition, our method is
straightforward to implement in an existing particle–
based fluid framework, and naturally lends itself to a
parallel implementation.
There are several exciting avenues for research
arising from our energy–based model. The indepen-
dence on sampling resolution implies that adaptively
refining solute representations or multi–grid methods
could be applied to improve the dissolution compu-
tation performance, the incorporation of temperature
into our model will allow for more accurate simula-
tion of melting effects, and the unified particle nature
of our dissolution model and other recently published
work hints at a unified representation for interacting
media, allowing gases, solvents and solutes to be sim-
ulated within a single framework.
ACKNOWLEDGEMENTS
We would like to thank Phil Spicer for fluid rendering,
Mathieu Sanchez for providing Signed Distance Field
library, Shujie Deng and Wei Wang for video editing.
Figure 9: Rendered results of layered terrain erosion using
our dissolution model.
REFERENCES
Akinci, N., Akinci, G., and Teschner, M. (2013). Versa-
tile surface tension and adhesion for sph fluids. ACM
Trans. Graph., 32(6):182:1–182:8.
Akinci, N., Ihmsen, M., Akinci, G., Solenthaler, B., and
Teschner, M. (2012). Versatile rigid-fluid coupling for
incompressible sph. ACM Trans. Graph., 31(4):62:1–
62:8.
Amada, T. (2006). Real-time particle-based fluid simulation
with rigid body interaction. In Dickheiser, M., editor,
Game Programming Gems 6, pages 189–205. Charles
River Media.
Arash, O. E., Gnevaux, O., Habibi, A., and michel Dischler,
J. (2003). Simulating fluid-solid interaction. In in
Graphics Interface, pages 31–38.
Batty, C., Bertails, F., and Bridson, R. (2007). A fast vari-
ational framework for accurate solid-fluid coupling.
ACM Trans. Graph., 26(3).
Becker, M., Tessendorf, H., and Teschner, M. (2009). Di-
rect forcing for lagrangian rigid-fluid coupling. IEEE
Transactions on Visualization and Computer Graph-
ics, 15(3):493–503.
Bene
ˇ
s, B., T
ˇ
e
ˇ
s
´
ınsk
´
y, V., Horny
ˇ
s, J., and Bhatia, S. (2006).
Hydraulic erosion. Computer Animation and Virtual
Worlds, 17(2):99 – 108.
Busaryev, O., Dey, T. K., Wang, H., and Ren, Z. (2012).
Animating bubble interactions in a liquid foam. ACM
Trans. Graph., 31(4):63:1–63:8.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
292

Carlson, M., Mucha, P. J., and Turk, G. (2004). Rigid
fluid: Animating the interplay between rigid bodies
and fluid. In ACM Trans. Graph, pages 377–384.
Clark, J. (2004). The Essential Dictionary of Science. New
York: Barnes & Noble Book.
Cleary, P. W., Pyo, S. H., Prakash, M., and Koo, B. K.
(2007). Bubbling and frothing liquids. ACM Trans.
Graph., 26(3).
Featherstone, R. (2007). Rigid Body Dynamics Algorithms.
Springer-Verlag New York, Inc., Secaucus, NJ, USA.
Foster, N. and Metaxas, D. (1996). Realistic animation of
liquids. Graph. Models Image Process., 58(5):471–
483.
Gingold, R. A. and Monaghan, J. J. (1977). Smoothed par-
ticle hydrodynamics-theory and application to non-
spherical stars. Monthly Notices of the Royal Astro-
nomical Society, 181:375–389.
Harada, T., Tanaka, M., Koshizuka, S., and Kawaguchi, Y.
(2007). Real-time coupling of fluids and rigid bodies.
APCOM in conjunction with EPMESC XI, (3-6).
Hoetzlein, R. C. (2010-2014). Fast fixed-radius nearest
neighbors: Interactive million-particle fluids.
Hojjatoleslami, S. and Kittler, J. (1995). Region growing:
A new approach. IEEE Transactions on Image Pro-
cessing, 7:1079–1084.
Ihmsen, M., Akinci, N., Akinci, G., and Teschner, M.
(2012). Unified spray, foam and air bubbles for
particle-based fluids. Vis. Comput., 28(6-8):669–677.
Ihmsen, M., Orthmann, J., Solenthaler, B., Kolb, A., and
Teschner, M. (2014). SPH Fluids in Computer Graph-
ics. pages 21–42.
Kim, D., young Song, O., and Ko, H.-S. (2010). A practical
simulation of dispersed bubble flow. In ACM SIG-
GRAPH 2010 papers, SIGGRAPH ’10, pages 70:1–
70:5.
Kri
ˇ
stof, P., Bene
ˇ
s, B.,
ˇ
Kriv
´
anek, J., and
ˇ
Stava, O. (2009).
Hydraulic erosion using smoothed particle hydrody-
namics. Computer Graphics Forum, pages 219–228.
Lucy, L. B. (1977). A numerical approach to the testing of
the fission hypothesis. Astron. J., 82:1013–1024.
McNaught, A. D. and Wilkinson, A. (1997). Collision the-
ory. Oxford: Blackwell Scientific Publications.
M
¨
uller, M., Charypar, D., and Gross, M. (2003).
Particle-based fluid simulation for interactive appli-
cations. In Proceedings of the 2003 ACM SIG-
GRAPH/Eurographics symposium on Computer ani-
mation, SCA ’03, pages 154–159.
Robinson-Mosher, A., Shinar, T., Gretarsson, J., Su, J., and
Fedkiw, R. (2008). Two-way coupling of fluids to
rigid and deformable solids and shells. ACM Trans.
Graph., 27(3):46:1–46:9.
Schechter, H. and Bridson, R. (2012). Ghost sph for ani-
mating water. ACM Trans. Graph., 31(4):61:1–61:8.
Shin, S.-H., Kam, H. R., and Kim, C.-H. (2010). Hybrid
simulation of miscible mixing with viscous fingering.
Comput. Graph. Forum, pages 675–683.
Solenthaler, B. and Pajarola, R. (2009). Predictive-
corrective incompressible sph. ACM Trans. Graph.,
28(3):40:1–40:6.
Solenthaler, B., Schl
¨
afli, J., and Pajarola, R. (2007). A uni-
fied particle model for fluid–solid interactions: Re-
search articles. Comput. Animat. Virtual Worlds,
18(1):69–82.
Stomakhin, A., Schroeder, C., Jiang, C., Chai, L., Teran,
J., and Selle, A. (2014). Augmented mpm for phase-
change and varied materials. ACM Trans. Graph.,
33(4):138:1–138:11.
Trautz, M. (1916). Das gesetz der reaktionsgeschwindigkeit
und der gleichgewichte in gasen. besttigung der
additivitt von cv-3/2r. neue bestimmung der in-
tegrationskonstanten und der molekldurchmesser.
Zeitschrift fr anorganische und allgemeine Chemie,
96(1):1–28.
Wojtan, C., Carlson, M., Mucha, P. J., and Turk, G.
(2007). Animating corrosion and erosion. In Proceed-
ings of the Third Eurographics conference on Natu-
ral Phenomena, NPH’07, pages 15–22, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
AParticle-basedDissolutionModelusingChemicalCollisionEnergy
293
