Inverse Light Design for High-occlusion Environments

Anastasios Gkaravelis, Georgios Papaioannou and Konstantinos Kalampokis

Department of Informatics, Athens University of Economics and Business, Athens, Greece

Keywords:

Computer Graphics, Light Design, Optimization, Inverse Light Positioning Problem.

Abstract:

Lighting design is a demanding but very important task in computer cinematography, games and architectural

design. Computer-assisted lighting design aims at providing the designers with tools to describe the desired

outcome and derive a suitable lighting conﬁguration to match their goal. In this paper, we present an automatic

approach to the inverse light source emittance and positioning problem, based on a layered linear / non-linear

optimization strategy and the introduction of a special light source indexing according to the compatibility

of each individual luminary position with the desired illumination. Our approach is independent of a partic-

ular light transport model and can quickly converge to an appropriate and plausible light conﬁguration that

approximates the desired illumination and can handle environments with high occlusion.

1 INTRODUCTION

Lighting design is a very important task in order to

correctly illuminate a scene, emphasizing individual

aspects of the scene or establishing a speciﬁc mood. It

plays an essential role, especially in the entertainment

industry, and more speciﬁcally in computer cine-

matographyand games. Also, it is a necessary process

in architectural modelling, where energy-efﬁcientand

well-balanced illumination from artiﬁcial luminaries

needs to be carefully devised. Despite its importance,

lighting design is also a tedious and - more often than

not - a counter-intuitive procedure. To manually il-

luminate a scene, the artist has to carefully and iter-

atively adjust the lighting parameters in a trial-and-

error basis, until the desired effect is achieved. Thus,

automatic methods have emerged, which compute the

lighting parameters to achieve a user-speciﬁed light-

ing result, requiring minimal or even no manual inter-

vention.

Due to the nature of light transport in an arbitrary

environment, the generalized inverse lighting prob-

lem is a very complex one to solve. Therefore, as

mentioned in (Patow and Pueyo, 2003), it is often

partitioned into sub-problems, such as the light emit-

tance problem (EP) and the light source positioning

(LSP) problem. First attempts only solved a simpler,

more tightly-constrained problem, such as the indi-

rect light adjustment via shadow manipulation (e.g.

(Poulin and Fournier, 1992), (Poulin et al., 1997)).

As researchers got more comfortable with the inverse

lighting problem, uniﬁed emittance/positioning solu-

tions were sought. Despite the progress in this ﬁeld,

the inverse lighting problem is still challenging and

it becomes increasingly more complex due to the de-

mand for increased realism by including global illu-

mination in the inverse lighting calculations and the

ability to handle dynamic environments.

In this paper, we present an algorithm that, given

a number of lights and the desired illumination, com-

putes their position and emittance by using optimiza-

tion techniques and heuristics to guide them (see ex-

ample in Figure 1). As usual, we describe the de-

sired illumination by using an irradiance goal at user-

speciﬁed sample locations, although any goal can be

used, such as a uniform lighting level across random

locations distributed within the environment.

Our inverse lighting algorithm consists of three

major steps. In the ﬁrst step, we discretize the param-

eter space of the possible light source positions into

a grid of cells and compute an emittance-independent

contribution or coverage of these potential light posi-

tions to the sampling points. We build a special index

that allows querying light positions based on a spe-

ciﬁc sampling point coverage pattern. We exploit this

index to efﬁciently ﬁnd the globally optimal combina-

tion of cells (coarse light positions) and emittance that

match the lighting goal, using Simulated Annealing

with an inner linear optimizer for the emittance. Fi-

nally, we deploy a non-linear optimization algorithm

to ﬁne-tune the light source positions in order to over-

come the discretization simpliﬁcation.

Gkaravelis A., Papaioannou G. and Kalampokis K..

Inverse Light Design for High-occlusion Environments.

DOI: 10.5220/0005291400260034

In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 26-34

ISBN: 978-989-758-087-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Inverse lighting pipeline, using the proposed

method.

The main contributions of this paper are:

• A novel indexing of light conﬁgurations based on

their contribution to the speciﬁed goal (coverage).

This index allows fast queries of alternative light

positions to satisfy a particular goal, correspond-

ing to a clustering in coverage space.

• A robust mapping of the EP/LSP problem to the

Simulated Annealing optimization method and a

respective practical algorithm using the light cov-

erage indexing.

The remainder of the paper is organized as fol-

lows. Section 2 places our method in the context of

the related work. Sections 3 and 4 provide a formu-

lation for our coverage-space solving strategy and a

description of the process. Section 5 presents com-

parative results and discusses the performance of our

method. Finally, in Section 6 we present our conclu-

sions and future research directions.

2 PREVIOUS WORK

For the inverse lighting problem, several methods

have been proposed. Similar to (Patow and Pueyo,

2003), here we partition the inverse lighting problem

into sub-problems and brieﬂy present some represen-

tative techniques and applications from each category.

For a more comprehensive, recent survey of the ﬁeld,

please refer to (Schmidt et al., 2014). Furthermore, at

the end of this section we provide more details on a

recent method that we compare our work with.

Light Source Emittance Problem. (Schoeneman

et al., 1993) proposed a method, in which the user

paints the desired illumination on a scene and the in-

tensity of a set of lights with known positions is de-

termined by a constrained least squares solver. The

method relied on the observation that the resulting

lighting on any surface location is a linear combina-

tion of the emittance levels of light sources, provided

the latter remain ﬁxed in space. A similar approach

was implemented by (Anrys et al., 2004) in order to

compute the intensity of a set of light sources by us-

ing and optimizing the luminance of real luminaries,

which were previously set up and their illumination

on a physical object captured in a set of photographs.

(Kawai et al., 1993) performed an optimization

over the intensities and directions of a set of lights as

well as the reﬂectivity of surfaces in order to best con-

vey the subjective impression of certain scene quali-

ties as expressed by the user and minimize the global

energy of the scene.

(Okabe et al., 2007) presented an algorithm to

manipulate and alter environment maps by directly

painting the outgoing radiance on the target model.

They used a constrained linear least square solver,

which minimizes the weighted squared difference of

the computed and desired illumination. It could han-

dle diffuse and specular reﬂections and relied on

the SRBF-based Precomputed Radiance Transfer ap-

proach to perform the computations interactively.

Light Source Positioning. (Poulin and Fournier,

1992) proposed a way to deﬁne light positions in

a scene by manipulating their shadows or resulting

highlights on both diffuse and specular surfaces. By

selecting a pair of points in a scene, they deﬁne the

illumination constraints, which are subsequently used

to position the light source accordingly. Later, (Poulin

et al., 1997) presented a system that controls the posi-

tion of a number of light sources by sketching strokes

where the shadow of selected objects should fall in

a scene. The proposed solution could also provide

feedback regarding the plausibility of a newly placed

stroke. To avoid solving the problem analytically, a

non-linear constraint optimization algorithm was uti-

lized. (Pellacini et al., 2002) developed a user in-

terface system that facilitated the design of shadows.

The shadows in the scene could be selected, trans-

formed or new ”fake” shadows could be introduced.

Inverse Lighting addresses both the emittance and

InverseLightDesignforHigh-occlusionEnvironments

positioning of light sources in a uniﬁed manner and

several architectures and systems havebeen proposed.

(Costa et al., 1999) introduced an IL system where a

custom scripting language was used to deﬁne the illu-

mination constraints. The system utilized the Adap-

tive Simulated Annealing algorithm to optimize the

light sources. (Pellacini et al., 2007) proposed a work-

ﬂow, where artists could directly paint the desired

lighting effects onto the geometry. With the use of

an importance map, obtained from the painted target

image, the system applies the non-linear simplex al-

gorithm (Nelder and Mead, 1965) to adjust the var-

ious parameters of the light sources by minimizing

the goal function, which is a weighted average of the

difference between the desired and computed illumi-

nation.

(Castro et al., 2009) solve the problem of light

positioning and emittance, while keeping the total

emission power at a minimum. They computed the

contribution of a user-deﬁned number of lights using

the radiosity algorithm and experimented with local

search algorithms, such as Hill Climbing and Beam

Search. As a goal, they tried to minimize total emis-

sion power. Later, (Castro et al., 2012) improved the

algorithm and used global approaches to solve the

problem in order to avoid getting stuck in a local op-

timum. They offered an implementation and experi-

mented with Genetic algorithms, Particle Swarm op-

timization and a hybrid combination of a global and

local search algorithm.

An interesting formulation of the ”opening” prob-

lem was suggested by (Fern´andez and Besuievsky,

2012), where skylights were treated as area light

sources and a uniﬁed skylight/luminaries optimiza-

tion was sought. They used the VNS metaheuristic

algorithm to solve the inverse lighting problem, while

keeping the energy consumption of the artiﬁcial light

sources to a minimum and/or maximize the contribu-

tion of the skylights.

Finally, (Lin et al., 2013) proposed a coarse-to-

ﬁne strategy to solve the inverse lighting problem,

given a set of user-painted lighting samples on sur-

faces. They spread unit-intensity lights in a volume

grid and conﬁgure their intensities using a constrained

linear least square solver. Dim lights are pruned and

the process is repeated with the remaining cells, after

subdividing them. Then, a light hierarchy is built and

traversed to obtain a good conﬁguration, which is sub-

sequently optimized using a non-linear least squares

method. Since this is the most recent method, closely

related to ours, in the remainder of the paper, we often

provide direct comparisons with it.

3 PROBLEM FORMULATION

Let I

goal

be an illumination goal over a scene and

P be a light conﬁguration consisting of k lights that

illuminates a scene producing an illumination result

res

(P). I

goal

, I

res

can be radiance, radiosity or irradi-

ance, depending on the measurement demands of the

underlying application (e.g. dependence on viewing

direction, material etc.). For a discrete set of surface

samples in the scene s

, I

res

(P, s

) and I

goal

) are the

resulting illumination from the lighting conﬁguration

P and the desired illumination at s

, respectively.

Using the above notations, an inverse lighting

problem can be deﬁned as the search for the optimal

lighting conﬁguration P

∗

, which minimizes some dis-

tance function D between the resulting and the desired

illumination at the sampling locations s

∗

= argmin

D(I

res

(P, s

), I

goal

)) (1)

Typically, D is expressed as the L

norm of the

measurement differences at all N

sampling points s

For real luminaries, although the dependence of

the emittance L

on direction or power consumption

cannot be considered linear, its dependence on a nom-

inal unit output power distribution can: L

, ω) =

c(l

)

, ω). In other words, the measured contribu-

tion of a light source l

to the illumination of a given

point is linearly dependent on its emittance scaling

c(l

). Therefore, the illumination from a set of n light

sources to a sampling point s

is the superposition of

all luminary contributions.

If we consider a general light transport operator

(path integral) LT(l

→ s

) to describe the total con-

tribution of each light source l

to a sampling point s

for n unit light sources, the lighting result on s

is the

linear combination of these contributions with coefﬁ-

cients c(l

Assuming now ﬁxed positions for n light sources

covering a discretization of the 3D environment, the

(discrete) LSP and EP problems can be solved simul-

taneously, by optimizing the emittance scaling factors

c(l

) of all n potential candidate lights so that the re-

sulting light conﬁguration P

∗

satisﬁes Equation 1. A

zero c(l

) implies the absence of a light source at l

4 METHOD OVERVIEW

(Lin et al., 2013) solve a simpliﬁed version of the

above problem by regarding all potential light sources

positioned on a discretized grid covering the entire

scene and solving a linear system of N

equations and

unknowns, N

being the number of light (goal)

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

sample points and N

the number of grid cells, i.e. po-

tential light positions. They evaluate the light contri-

bution using rasterization and solve the linear system

with a least squares method.

In order to make the light optimization problem

manageable, they use a hierarchical (coarse to ﬁne)

solving strategy, starting from a very rough initial dis-

cretization of the scene volume. The calculated emit-

tance scaling factors are clamped and the cells of non-

zero light intensity are further subdivided. The result-

ing lights are clustered in a light tree, whose graph

cut that satisﬁes an error margin, is reﬁned using a

non-linear optimization method to provide the ﬁnal

lighting conﬁguration. However, this strategy leads

to solutions that are unsuitable for environments with

dense geometry or heavy occlusion (e.g. typical ar-

chitectural spaces) since the sparsity of the initial po-

tential light locations results in single cells frequently

containing occluders, thus clustering potential lights

near walls, after the cell subdivision, or worse, plac-

ing lights only in one side of the barrier.

Since we needed to overcome this problem, we

strived for a solution that allows a ﬁner initial sub-

division of the space into cells. Solving the inverse

light problem using a linear system, would require a

set of N

equations with 3 × N

unknowns c

(RGB

coefﬁcients), N

being the number of cells (potential

lights) and N

being the number of sampling points,

where the desired illumination is given. 3 × N

can

reach several hundreds of thousands in some expan-

sive scenes and the problem can become practically

intractable. Additionally, to ﬁnd a stable and usable

solution would require deﬁning a large number of

sampling points, proportional to N

, which is imprac-

tical for all purposes. We exploit a discretized ini-

tial light placement, too, but propose a non-linear ap-

proach to light positioning with an inner linear solver

for the emittance adjustment (Figure 2), as follows.

4.1 Light Coverage Computation

We ﬁrst initialize a set of potential light source posi-

tions on a ﬁne grid (e.g. in the order of 64

cells or

more), the center of each cell l

representing a po-

tential light source. For each light and each sam-

pling point, we compute the light transport function

LT(l

→ s

), normalize it over all N

sampling points

and store the values as an (3 × N

)-dimensional at-

tribute vector f

(LT is a three-channel quantity).

Normalizing the attribute vector f

transforms the

EP/LSP to a sample coverage problem, because we do

not include the magnitude of the light’s contribution

to the sampling points but rather their ”reachability”

by a given source.

Scene

Goal

Illumination

Light Coverage

Computation

User

Input

Coarse-level

Optimization Loop

Candidate

Selection

Optimize

Emittance

Compute

Error

Final

Configuration

Light Coverage

Index

Refinement

Step

Figure 2: Our algorithm consists of an initialization step,

the main optimization strategy and a ﬁnal reﬁnement step.

Given as input the goal illumination, our algorithm ﬁnds a

lighting conﬁguration that satisﬁes the goal illumination.

In our current system, to estimate the path integral

LT(l

→ s

) for all light-sampling point paths, we use

bidirectional path tracing (BPT). This way, we avoid

rasterization problems, such as artifacts introduced by

shadow maps, and we can inherently include complex

global light transport phenomena. However, any path

integral estimator can be utilized instead. For this pa-

per, we use an NVIDIA Optix-based BPT implemen-

tation to compute all light position - sampling point

path integrals in parallel, with a Monte Carlo solver

and 20-100 samples per (l

, s

) pair.

An important novel step of our approach is that

the light attribute vectors are all together stored in a

k-d tree indexed by attribute vector dimension, i.e.

the structure is a (3× N

)-d tree. The normalized at-

tribute vector f

allows for a fast search of light posi-

tions with similar sample point coverage. We use the

Nanoﬂann k-d data structure implementation that al-

lows very fast queries using the Approximate Nearest

Neighbors algorithm. We show next how we exploit

this propertyto performmeaningful mutations of light

conﬁgurations P.

4.2 Coarse-level Optimization

To ﬁnd a light conﬁguration P of k sources that mini-

mizes the distance function D(I

res

(P, s

), I

goal

)), we

use a non-linear optimization algorithm and in par-

InverseLightDesignforHigh-occlusionEnvironments

Figure 3: Method comparison - Studio scene. Left: results

from the method by (Lin et al., 2013). Right: our method

optimizes goal point coverage (global path throughput) and

results in more acceptable solutions with better light cover-

age. The preview on the top row shows the direct paths to

the sample (goal) points. The bottom row shows the path-

traced results of the two light conﬁgurations.

ticular, Simulated Annealing, with random mutations

over a k-dimensional state vector equal to the cur-

rent choice of light positions. The reason for uti-

lizing a non-linear solver is that although the com-

bined EP/LSP is linear with respect to light contri-

butions, we want to rapidly investigate solutions in

sample coverage space, a non-linear domain and ex-

ploit the fact that light sources in completely different

locations may indeed provide similar coverage to the

sampling points, thus explore seemingly disjoint, al-

beit increasingly favourable solutions.

Separating the coverage problem from the light

source emittance has the additional beneﬁt of produc-

ing more usable solutions, regardless of the explicit

goals provided by the user. For example, in Figure 3

both our method and the method by (Lin et al., 2013),

produce visually similar irradiance near the goal po-

sitions. However, due to better coverage, our method

reduces shadowing, as it better handles occlusion.

Mutation Strategy. For a given light conﬁguration,

we select and remove one light source at random. The

remaining k − 1 lights, constitute an incomplete light

conﬁguration P

(k−1)

for which we compute the con-

tribution I

res

(k−1)

, s

) to the N

sampling points (see

Emittance Estimation below).

Next, the residual I

goal

) − I

res

(k−1)

, s

)) is

computed and the resulting normalized attribute vec-

tor f

dif f

is used to locate a number of light sources

with similar attributes in the k-d tree. Simply put,

we use the normalized lighting residual from remov-

ing a light source to locate other source positions

that would better complement the remaining lights in

achieving the goal.

Figure 4: The mutation strategy. After the removal of one

light source (middle), we compute the optimal emittance of

the remaining light sources and estimate the residual illu-

mination that is required to match the goal illumination at

all points. Finally, we locate a light that better matches this

residual (right).

Given the resulting set of nearest lights (in terms

of coverage complementarity, i.e. attribute vector

dif f

), we pick one candidate location at random and

replace the missing light source, in order to gener-

ate a new improved light conﬁguration P. The opti-

mal emittance for this new conﬁguration is estimated

and the resulting evaluation of D(I

res

(P, s

), I

goal

))

is the outcome of the cost function. The entire muta-

tion procedure is illustrated in Figure 4.

When the SA algorithm accepts mutations with a

potentially higher cost, a random mutation of the state

P occurs and the above mutation strategy is omitted.

Emittance Estimation. According to the preceding

discussion, we have decoupled the light position se-

lection strategy from the emittance problem, by esti-

mating the intensities L(l

) of a conﬁguration P (i.e.

a set of k ﬁxed light sources) within each position op-

timization step. This is a linear system (Schoeneman

et al., 1993) with only a few unknowns (3× k), which

can be rapidly solved, especially since all F(s

, l

)

path integrals have been estimated.

For our implementation we chose a non-negative

linear least square solver (Lawson and Hanson, 1987)

since the intensity of a light source could not have a

negative value.

The use of this hybrid non-linear / linear strategy

has a signiﬁcant impact on convergence, especially

when coupled with our light coverage prioritization

strategy (see evaluation in Section 5).

4.3 Solution Reﬁnement

Similar to (Lin et al., 2013), to ﬁnd the ﬁnal, non-

discretized positions of the light sources and their re-

spective emittance, we reﬁne further the light conﬁg-

uration solution of the coarse-level optimization. This

is achieved by again running a hybrid non-linear / lin-

ear optimizer, only this time, the light - sample path

integrals need to be evaluated in each optimization it-

eration, although for only k light sources. Based on

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

0 50 100 150 200 250

35%

37%

33%

31%

29%

27%

25%

Error

Iterations

Renement Stage Convergence

Hybrid

Non-linear

Figure 5: Convergence rate of the reﬁnement stage using a

position/emittance non-linear optimization versus a hybrid

linear (emittance) / non-linear (position) strategy.

our experiments and the suggestion in (Pellacini et al.,

2007) and (Lin et al., 2013), as a non-linear optimizer

we use the nonlinear simplex algorithm (Nelder and

Mead, 1965), which performsvery well given that it is

initialized with an already near-optimal solution. The

parameter space of the non-linear optimizer (i.e. the

light positions) is very narrow, since the light posi-

tions only need to be jittered by at most the size of

one cell.

Again, after estimating the path integrals in each

iteration, we employ the non-negative linear least

square solver to adjust the emittance of the given light

conﬁguration.

Figure 5 demonstrates the faster convergence of

the hybrid algorithm when compared to a uniﬁed non-

linear optimization algorithm (non-linear simplex in

this case) to simultaneously optimize position as well

as source emittance.

5 EVALUATION AND RESULTS

We tested our method on scenes of varying geomet-

ric complexity. We mainly focused on environments

that have a high degree of shape and structure com-

plexity such as scenes consisting of separate regions

with high occlusion, since such complex scenes are

commonly found on cinematic imagery, games or ar-

chitectural designs. The tests were performed on an

Intel i7-4930 CPU and a Nvidia Geforce GTX 780

and we report times in seconds. The CPU side of

the algorithm was ran in a single thread without tak-

ing advantage of multi-core CPUs, although it can be

very easily parallelized to take advantage of multi-

threading systems by running concurrent instances of

the SA method or splitting the search space. In our

tests, we used 1000 iterations for the Simulated An-

nealing process, which were sufﬁcient since by us-

ing our mutation strategy and the fast clustered search

mechanism (via the coverage index), we were able to

obtain a good solution in only a few iterations.

Correctness. First, we evaluated the accuracy of our

Figure 6: Correctness experiment. Left: the user deﬁned

light sources, whose irradiance to sampling points is mea-

sured and used as a goal. Right: the computed light conﬁg-

uration produced by our algorithm (4.3% error).

method: We illuminated a scene with a known light-

ing conﬁguration and tried to re-establish the same

lighting conﬁguration by using our algorithm. The

scene we used was the Apartment environmentof Fig-

ure 6 that has 8 rooms and a hallway connecting them.

We manually placed 10 light sources at typical loca-

tions inside the scene and computed their contribu-

tion at random sampling positions s

(Figure 6 (left)).

Then, we ran our method using the computed con-

tribution as the goal illumination I

goal

). The com-

puted luminaries (Figure 6 (right)) were very close to

the manual conﬁguration. It took our algorithm 40

seconds to compute the result and the normalized il-

lumination difference between the goal and resulting

illumination was 4.3%.

Mutation Strategy. We tested the convergence rate

of our light conﬁguration mutation strategy against

the random selection approach. We conﬁrmed that re-

placing one of the k light sources with one that com-

plements the missing contribution to the sampling

points ensures a signiﬁcantly faster convergence to a

better solution than in the case of randomly select-

ing a new light source (Figure 7). Even if we choose

more iterations for the random selection method, it

is evident that the complementary coverage approach

always results in a better solution, due to its prioriti-

zation of regions that are inadequately illuminated.

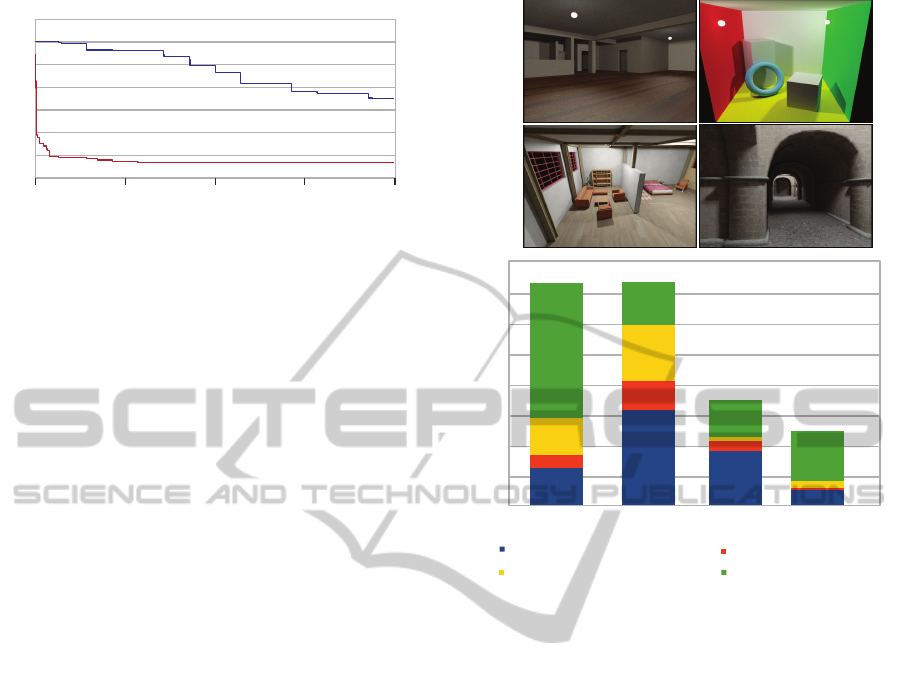
Performance. In Figure 8 we measure and present

the performance of the stages of our algorithm. We

selected various scenes with different structural com-

plexity (high or low occlusion) and polygon count.

We measured the initialization step, where we com-

pute the coverage of the light sources, the index con-

struction, the Coarse-Level optimization and the ﬁnal

InverseLightDesignforHigh-occlusionEnvironments

0 700 1400 2100 2800

60%

50%

40%

30%

20%

10%

Error

Iterations

Our mutation strategy

Random state selection

SA Convergence

Figure 7: Convergence rate of the coarse-level optimization

stage (simulated annealing) using standard state transitions

and our mutation strategy.

solution reﬁnement step.

Figure 8 conﬁrms that the initialization time de-

pends on the polygon count of the scene, since we

need to compute the coverage of every light source,

which involves tracing paths within a larger environ-

ment. In every scene we compute the global illumina-

tion of the light sources, except from the Sewers scene

where we only used direct illumination. It is obvious

that by only using direct illumination, the computa-

tion of the illumination is greatly reduced.

On the other hand, the Coarse-Level optimization

step does not depend on the polygon count of the

scene, since the light coverage of every light source

is already computed, but on the structural complexity

of the scene and the feasibility of the desired illumi-

nation. One example is the Studio scene where, given

a conﬁguration of two lights, there are many possible

light conﬁgurations that satisfy our goal, thus the op-

timizer takes more time to converge to a global opti-

mum. Another example is the Sewers scene, which is

a scene with high occlusion. However, the algorithm

can easily mark regions that need to be covered and

place light sources in positions that minimize the cost

function, locating a good conﬁguration very quickly.

Finally, the reﬁnement step does not only depend

on the polygon count of the scene, since we need

to compute the illumination of the evaluated con-

ﬁguration at every step, but it is also affected by

how close the current solution is to the optimal one.

Even though the Studio scene has the highest poly-

gon count, the solution reﬁnement step found a solu-

tion very quickly, because the conﬁguration from the

Coarse-Level Optimization step was very close to the

optimal solution. On the other hand, the reﬁnement

step took more time on the Apartment scene, since

there were more light sources to optimize, coupled

with the fact that small state changes of the light posi-

tions can signiﬁcantly alter the resulting illumination

due to high occlusion.

Comparative Evaluation. Below we compare our

Apartment Studio Cornell Sewers

Solution Refinement

Initialization

Index Construction

Coarse-Level Optimization

Time (Seconds)

Scenes

Apartment

Studio

Cornell

Sewers

Figure 8: Perfomance measurements of the various stages

of the algorithm with simple and complex scenes.

algorithm with the recently published lighting opti-

mization method of (Lin et al., 2013). We compare

their performance using complex environments with

high occlusion. First, we test both methods with the

Apartment scene, which has separate regions with

high occlusion. As a goal, in both experiments we

used the illumination produced by a known initial

light conﬁguration (see Correctness paragraph).

As we previously mentioned, our method per-

forms quite well for a conﬁguration of 10 lights, with

the normalized illumination difference to the desired

illumination being at 4.3%. In order to check the ro-

bustness of our algorithm, we tried to satisfy the illu-

mination goal by using fewer light sources. We chose

8 light sources since the scene has 8 separate rooms

(connected via a doorway to others). Figure 9 shows

a comparison of the two methods. On the right, we

show the results from our implementation with a nor-

malized illumination difference of 12%. In the left

inset, we present the lighting conﬁguration that the al-

gorithm by (Lin et al., 2013) found for an 8-light con-

ﬁguration, producing a normalized illumination dif-

ference of 36.7% in 35 seconds. The method by (Lin

et al., 2013) failed to compute the correct light con-

ﬁguration, resulting in luminaries with high error and

failure to include lights in certain spaces, because of

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

Figure 9: Lighting conﬁguration comparison - Apartment

scene. Left: the compared method. Right: our method.

The line segments represent the path throughput of domi-

nant path integrals (green: high, blue: low).

its hierarchical light placement strategy. A hierarchi-

cal (coarse-to-ﬁne) scheme fails, if the coarse can-

didate solutions cannot successfully represent their

neighborhood. In this case, large cells intersect the

boundaries of separate spaces and result in biased

placement of luminaries. In some scenes, a ﬁner grid

can be used, but this does not alleviate the problem,

unless the boundaries of the cells roughly coincide

with the occluding structures. Also, another problem

of using a ﬁner grid is that the linear least squares

solver tries to optimize lights that are near the sam-

pling points in order to minimize the error,which does

not work well with the clustering method (light tree),

despite our effort to optimize the parameters and grid

size to give the best results.

Next, we run experiments with the Studio scene

shown in Figure 3, which is a single space featuring

a large occluder and a lot of complex geometry. In

the Studio scene, we deﬁned the goal illumination at

the bedroom and the living room by manually paint-

ing the desired irradiance directly on the geometry

(Figure 3, top row) and then compute the emittance

and position of 2 light sources to satisfy this goal.

Even though, this scene is suitable to be solved with a

coarse-to-ﬁne method, the compared method achieves

a score of 44.5% normalized illumination difference

in 30 seconds, while our method achieves a score of

24.8%.

6 CONCLUSION

We have presented a method to solve the inverse light

positioning / emittance problem, which efﬁciently

computes the conﬁguration of a given number of light

sources, in order to satisfy the design goals. We pro-

posed a scheme for the efﬁcient representation of can-

didate light conﬁgurations to directly search and clus-

ter the light position space according to the light’s

contribution to the desired illumination. This, along

with a hybrid linear / non-linear optimizer that disas-

sociates the emittance and light positioning, lead to a

fast convergence to usable solutions for environments

with high occlusion.

Currently, our system handles only point light

sources, but with no restriction on the materials of

surfaces, while it also provides a user interface for

painting the desired irradiance on any surface. In the

future, we would like to address the problem of deter-

mining the number of lights to be used, by carefully

covering the geometry to be illuminated with the least

amount of light sources that will minimize the error in

a meaningful manner. Furthermore, we would like to

also support area luminaries and include sky lighting

in the calculations, so we can take into consideration

the contribution of natural light, which is very impor-

tant in architectural design.

ACKNOWLEDGEMENTS

This research has been co-ﬁnanced by the European

Union (European Social Fund - ESF) and Greek na-

tional funds through the Operational Program ”Edu-

cation and Lifelong Learning” of the National Strate-

gic Reference Framework (NSRF) - Research Fund-

ing Program: ARISTEIA II-GLIDE (grant no.3712).

REFERENCES

Anrys, F., Dutr´e, P., and Willems, Y. (2004). Image based

lighting design. In the 4th IASTED International Con-

ference on Visualization, Imaging, and Image Pro-

cessing, page 15.

Castro, F., Acebo, E., and Sbert, M. (2009). Heuristic-

search-based light positioning according to irradiance

intervals. In Proceedings of the 10th International

Symposium on Smart Graphics, SG ’09, pages 128–

139, Berlin, Heidelberg. Springer-Verlag.

Castro, F., del Acebo, E., and Sbert, M. (2012). Energy-

saving light positioning using heuristic search. Eng.

Appl. Artif. Intell., 25(3):566–582.

Costa, A. C., Sousa, A. A., and Ferreira, F. N. (1999). Light-

ing design: A goal based approach using optimisation.

InverseLightDesignforHigh-occlusionEnvironments

In Proceedings of the 10th Eurographics Conference

on Rendering, EGWR’99, pages 317–328, Aire-la-

Ville, Switzerland, Switzerland. Eurographics Asso-

ciation.

Fern´andez, E. and Besuievsky, G. (2012). Technical sec-

tion: Inverse lighting design for interior buildings

integrating natural and artiﬁcial sources. Comput.

Graph., 36(8):1096–1108.

Kawai, J. K., Painter, J. S., and Cohen, M. F. (1993). Ra-

dioptimization: Goal based rendering. In Proceedings

of the 20th Annual Conference on Computer Graphics

and Interactive Techniques, SIGGRAPH ’93, pages

147–154, New York, NY, USA. ACM.

Lawson, C. and Hanson, R. (1987). Solving Least Squares

Problems. PrenticeHall.

Lin, W.-C., Huang, T.-S., Ho, T.-C., Chen, Y.-T., and

Chuang, J.-H. (2013). Interactive lighting design with

hierarchical light representation. Comput. Graph. Fo-

rum, 32(4):133–142.

Nelder, J. A. and Mead, R. (1965). A simplex method

for function minimization. The computer journal,

7(4):308–313.

Okabe, M., Matsushita, Y., Shen, L., and Igarashi, T.

(2007). Illumination brush: Interactive design of all-

frequency lighting. In Proceedings of the 15th Paciﬁc

Conference on Computer Graphics and Applications,

PG ’07, pages 171–180, Washington, DC, USA. IEEE

Computer Society.

Patow, G. and Pueyo, X. (2003). A survey of inverse render-

ing problems. Computer Graphics Forum, 22(4):663–

687.

Pellacini, F., Battaglia, F., Morley, R. K., and Finkelstein,

A. (2007). Lighting with paint. ACM Trans. Graph.,

26(2).

Pellacini, F., Tole, P., and Greenberg, D. P. (2002). A

user interface for interactive cinematic shadow design.

ACM Trans. Graph., 21(3):563–566.

Poulin, P. and Fournier, A. (1992). Lights from highlights

and shadows. In Proceedings of the 1992 Symposium

on Interactive 3D Graphics, I3D ’92, pages 31–38,

New York, NY, USA. ACM.

Poulin, P., Ratib, K., and Jacques, M. (1997). Sketching

shadows and highlights to position lights. In Proceed-

ings of the 1997 Conference on Computer Graphics

International, CGI ’97, pages 56–, Washington, DC,

USA. IEEE Computer Society.

Schmidt, T.-W., Pellacini, F., Nowrouzezahrai, D., Jarosz,

W., and Dachsbacher, C. (2014). State of the art in

artistic editing of appearance, lighting, and material.

In Eurographics 2014 - State of the Art Reports, Stras-

bourg, France. Eurographics Association.

Schoeneman, C., Dorsey, J., Smits, B., Arvo, J., and Green-

berg, D. (1993). Painting with light. In Proceedings

of the 20th Annual Conference on Computer Graphics

and Interactive Techniques, SIGGRAPH ’93, pages

143–146, New York, NY, USA. ACM.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications