
Blind Watermarking using QIM and the Quantized SVD Domain based
on the q-Logarithm Function
Ta Minh Thanh
1,2
and Keisuke Tanaka
1,3
1
Dept. of Computer Science, Tokyo Institute of Technology, Tokyo, 152-8552, Japan
2
Dept. of Network Security, Le Quy Don Technical University, 236 Hoang Quoc Viet, Cau Giay, Ha Noi, Vietnam
3
CREST, JST., Tokyo, Japan
Keywords:
q-Logarithm SVD (q-SVD), Image Watermarking, Quantization Index Modulation (QIM).
Abstract:
We propose new image blind watermarking by using both the quantization index modulation (QIM) technique
and the quantized singular value decomposition (SVD) domain based on the q-logarithm function. In order to
reduce the distortion of the embedded image, we employ the q-logarithm transform on the Y component of the
original image after performing the SVD domain. We call this domain the q-SVD domain. In our proposed
method, the tradeoff of robustness and quality can be controlled by a predefined quantization coefficient Q of
QIM and a parameter q of the q-SVD domain. Several experiments are conducted to show the robustness of
our proposed method against processing attacks and geometric attacks.
1 INTRODUCTION
1.1 Background
Due to the advance of computer and network tech-
niques, e-business of digital contents has become the
most popular market for various types of digital con-
tents such as picture, audio, movie, and so on. How-
ever, since network applications have become very
popular, everyone can easily copy, alter, or even steal
digital content via network. Therefore, the protection
of digital content in e-business has become one of the
most important issue.
Digital watermarking is a promising technique in
order to protect the digital content by embedding the
watermark directly into digital content. The embed-
ded watermark can be extracted later for authentica-
tion, copyright protection, and traitor detection (Shih,
2008; Yeung, 1998; Nikolaidis and Pitas, 2003; Bao
and Ma, 2005; Liu and Tan, 2002).
In general, the invisibility, robustness, and capac-
ity of the watermark are important requirements for
the proposed watermarking. The watermark should
not make visible changes on digital content in order
to remain the quality of the original image. Addi-
tionally, the watermark must be robust against the im-
age attacks/distortions applied to the embedded con-
tent. Finally, the watermark must be easily extracted
to prove ownership and to detect the traitor.
There are two types of the digital watermarking
methods, the spatial domain watermarking and the
transform domain watermarking.
In the spatial domain watermarking, the water-
mark information is embedded directly into the com-
ponents of the original content, for example, an RGB
component by altering its values (Yeung, 1998). The
spatial watermarking domain has advantages such as
low complexity and simple implementation. How-
ever, the spatial domain watermarking methods are
not robust against image processing attacks, and geo-
metric attacks.
The transform domain watermarking methods em-
bed the watermark by modifying the magnitude of
coefficients in transform domain such as discrete
Fourier transformation (DFT), discrete cosine trans-
form (DCT), discrete wavelet transform (DWT), and
singular value decomposition (SVD) (Nikolaidis and
Pitas, 2003; Bao and Ma, 2005; Liu and Tan, 2002).
Also, there have been a lot of proposals of watermark-
ing methods that use the mixed domain. For instance,
the combination of DCT and SVD (Liu and Liu, 2008;
Lu et al., 2007; Yavuz and Telatar, 2006), that of SVD
and DWT (Cao et al., 2009; Yavuz and Telatar, 2007;
Zhang and Li, 2009), that of DWT and DCT (Deb et
al., 2012; Feng et al., 2010; Bei et al., 2011) are em-
ployed to embed the watermark into the digital con-
14
Thanh T. and Tanaka K..
Blind Watermarking using QIM and the Quantized SVD Domain based on the q-Logarithm Function.
DOI: 10.5220/0005291900140025
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 14-25
ISBN: 978-989-758-091-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

tent. Embedding on transform domain seems more
robust but rather complicated to compute because of
its high computation cost. Additionally, the previous
methods only focused on the robustness of the water-
mark by sacrificing the quality of the embedded con-
tent.
In particular, the SVD-based technique is used to
efficiently extract algebraic features from an image.
Based on the feature of SVD transform, the stable
SVD matrices feature of image can be easily obtained.
Therefore, when the image is degraded by several
image processing attacks, its singular values (SVs)
do not change significantly (Liu and Tan, 2002; Lai,
2011; Zhou and Chen, 2004). This feature is normally
used to embed the user’s information into the image
with less degradation.
As shown in the papers (Liu and Tan, 2002;
Lai, 2011; Zhou and Chen, 2004; Bhatnagar and
Raman, 2009), SVD-based watermarking algorithms
were proposed. In order to achieve the robustness,
Liu and Tan (Liu and Tan, 2002) presented a water-
mark method which embeds the watermark into the
SVD domain. They added the watermark bits into the
singular values of matrix S. Three matrices U
w
,S, and
V
w
are saved as the secret key. These matrices are
required in the watermark extraction. In order to ex-
tend the method of (Liu and Tan, 2002), Lai et al.
(Lai, 2011) demonstrated a watermarking technique
using SVD and a tiny genetic algorithm to achieve
the robustness of the watermark information. Un-
fortunately, both algorithms of (Liu and Tan, 2002)
and (Lai, 2011) are fundamentally flawed as men-
tioned in (Loukhaoukha, 2013). This bug of these
algorithms causes false positive detection even if the
attacker uses a different embedded watermark or the
secret key. In the method of Chandra et al. (Chandra,
2002), not only the original image is required but also
the original watermark during the watermark extrac-
tion process. Hence, their method is not suitable for
real applications. Bao (Bao and Ma, 2005) utilized
the quantization parameter for enhancing the quality
of the watermarked image. In the extraction process,
the quantization parameter is required as the private
key. However, the original image must to be trans-
formed to the wavelet and SVD domain. It requires
high computation cost.
As mentioned above, the previous SVD-based wa-
termarking techniques mainly focused on the robust-
ness of embedding methods but did not the quality of
the watermarked images.
1.2 Our Contributions
We consider that it is very important to improve the
quality of the embedded content, while maintaining
the robustness of watermarking methods.
We extend the original SVD domain to the q-
logarithm SVD domain in order to improve the qual-
ity of image and to retain the robustness of water-
marking method. In particular, we make the following
contributions in this paper:
(1) Inspired by the motivation of (Tsallis, 1998),
we present the novel frequency domain, called q-
logarithm SVD domain (q-SVD), for the image wa-
termarking that is not proposed before. – See Section
2.
(2) We investigate the efficiency of the combina-
tions of both parameters Q and q for our method. We
find out the appropriate values for Q and q suitable
for watermark embedding. By these combinations,
the tradeoff of the robustness and the quality can be
controlled by a predefined quantization coefficient Q
of QIM and a parameter q of the q-SVD transform. –
See Section 4.2.
(3) Various simulation experiments are conducted
to demonstrate the performance of our proposed
method. Experimental results show that the proposed
method has stronger robustness against most com-
mon attacks such as the JPEG compression, cropping,
swirl, and so on. – See Section 4.3.
Therefore, by using our method, we simultane-
ously improve the quality of embedded image also
achieve the robustness of the watermark.
1.3 Roadmap
The rest of this paper is organized as follows. The
proposed q-SVD domain is described in Section 2 and
we will explain why the q-SVD domain is suitable for
our watermarking method. Section 3 describes our
proposed watermarking method using QIM on the q-
SVD domain. Our simulation results are shown in
Section 4. Section 5 concludes our paper.
2 QUANTIZED SVD DOMAIN
BASED ON q-Logarithm
FUNCTION
2.1 q-Logarithm and q-Exponential
Function
q-logarithm and its inverse, q-exponential, are the
concept of non-extensive statistics which is intro-
BlindWatermarkingusingQIMandtheQuantizedSVDDomainbasedontheq-LogarithmFunction
15
!"
!#$"
!#%"
!#&"
!#'"
("
(#$"
("
(("
$("
)("
%("
*("
&("
+("
'("
,("
(!("
-./"
01-./203!#&4"
01-./203!#'4"
01-./203(#!4"
SVD coefficients
index
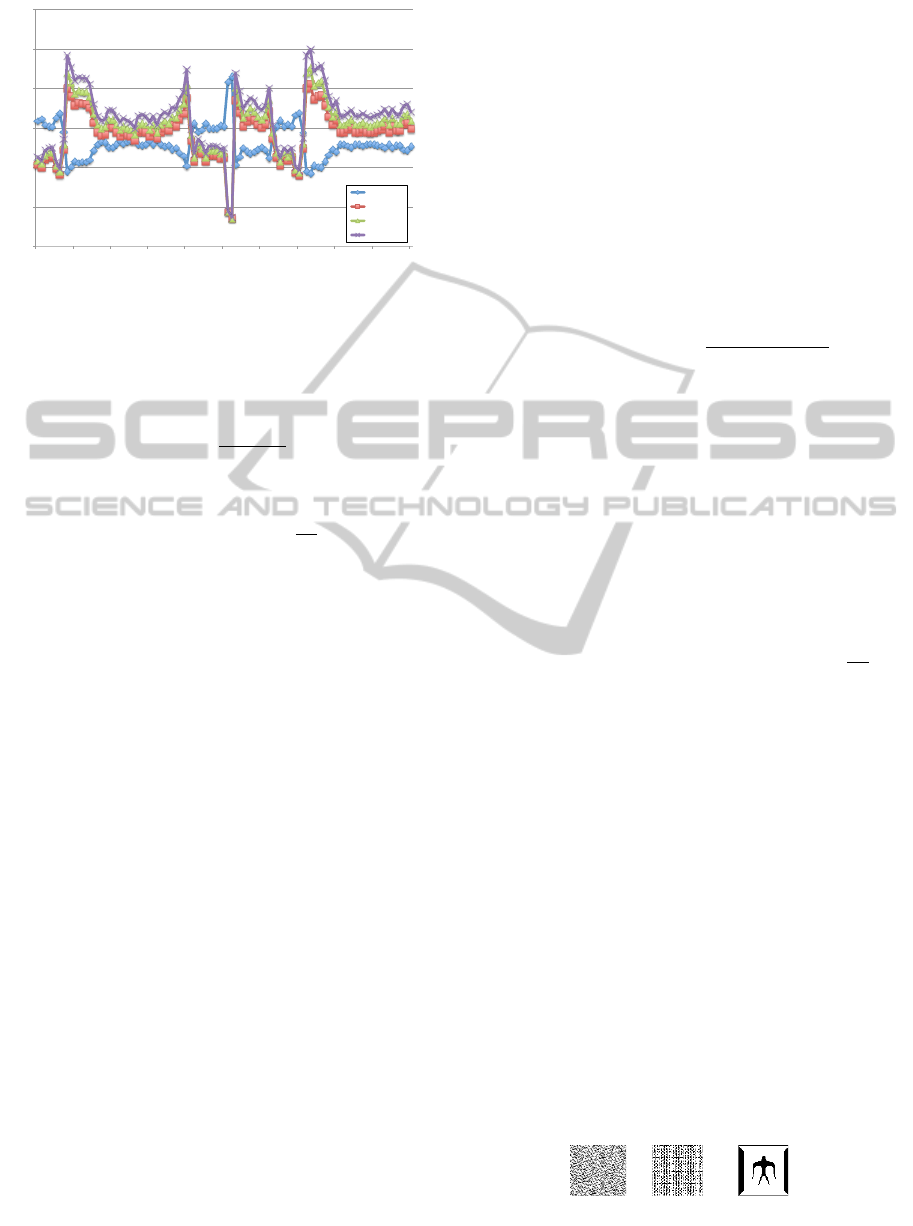
Figure 1: The comparison of SVD and q-SVD.
duced by Tsallis (Tsallis, 1998), a theory of non-
extensive statistics. The q-logarithm function is de-
fined as follows:
log
q
(x) =
x
1−q
− 1
1 − q
(1)
and its converse, q-exponential is defined as:
exp
q
(x) = (1 + (1 − q)x)
1
1−q
, (2)
where the parameter q is a real number that is prede-
termined and x is also a real number. In our work,
x can be a pixel of image or a coefficient of the fre-
quency domain.
Inspired by the theory of non-extensive statistics, we
propose q-SVD domain to provide a novel frequency
domain, which is very flexible by randomly choos-
ing q parameter to control the quality of image af-
ter inverse transform. We employ the feature of q-
logarithm and q-exponential in Eq. (1) and Eq. (2) to
construct q-SVD for image processing.
2.2 Proposed q-SVD Domain
Suppose that the image I with size N × N is divided
into non-overlapping blocks. Each block is a matrix,
called A, with size 8 × 8.
In general, the real matrix A can be decomposed
into three matrices SV D(A) = USV
T
, where U and V
are orthogonal matrices, such that UU
T
= E, VV
T
=
E and S = diag(λ
1
,λ
2
,···). Here, the singular values
λ
1
,λ
2
,··· of matrices A are sorted decreasingly, and
E is the unit matrix.
There are the following advantages when using
SVD in digital image processing:
(1) It is not necessary to fix the size of the matrix A
beforehand. Its size is x × x or x ×y for some x, y.
Therefore, we can choose the size of A suitable
for that of the watermark image.
(2) SVs of a digital image are less affected under the
general image processing such as blurring, noise
addition, slight rotation. Therefore the quality of
the watermarked image can be kept after embed-
ding.
Inspired by the theory of non-extensive statistics
(Tsallis, 1998), we propose the q-SVD domain, which
is very flexible by arbitrary choosing the parameter q
to control the quality of image. We employ the fea-
ture of q-logarithm and q-exponential (Tsallis, 1998)
to construct the q-SVD for image processing.
Suppose an image I is given. First, I is trans-
formed into q-logarithm as follows:
I
q
(i, j) = log
q
{I(i, j)} =
{I(i, j)}
1−q
− 1
1 − q
, (3)
where I(i, j) and I
q
(i, j) represent the pixel (coeffi-
cient) at coordinate (i, j) of the spatial domain and the
q-logarithm domain, respectively. The matrix A
q
from
I
q
can be transformed to q-SVD using the original
SVD. The q-SVD domain of I is defined as SV D(A
q
).
We call the resulting U, S, and V
T
as q-SVD domain.
After performing the SVD, we adjust the values of
U, S, or V
T
to control the quality of image. In order
to reconstruct the image I
0
, we apply SVD again to
obtain I
0
q
based on the adjusted values of U, S, and
V
T
. Finally, we perform the q-exponential function:
I
0
(i, j) = exp
q
(I
0
q
(i, j)) = (1 + (1 − q)I
0
q
(i, j))
1
1−q
.
(4)
Since the values of image pixels are slightly
changed after applying the q-logarithm transform, the
low-frequency of q-SVD domain is considered to be
very suitable for the image watermarking method.
Therefore, the watermarking based on q-SVD can be
expected not only to improve the quality of the em-
bedded image, but also to keep the robustness of the
watermark information.
2.3 Advantage of the q-SVD
In the previous watermarking researches, the water-
mark is directly added into the coefficient of the fre-
quency domain. Therefore, it causes the distortion
in quality of the embedded digital content. In our
proposed frequency domain, q-SVD, the coefficient
of the classical frequency domain is then quantized
by q-logarithm transformation. The modification of
(a) (b) (c)
Figure 2: Permuted watermark by the Torus permutation
after p times, where a) p=20, b) p=60, c) p=96.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
16

Original Image
RGB=>YCbCr
Conversion
Blocking
Y-component
SVD
q-logarithm
QIM
embedding
Watermark
Torus
permutation
q-exponential
Inverse
SVD
YCbCr=>RGB
Conversion
Last block?
Y
Next block
N
Watermarked Image
q
Q
p
CbCr-component
q-SVD
Figure 3: Embedding based on q-SVD.
the coefficient in q-SVD after watermark embedding
does not affect to the value of the coefficient of the
classical frequency domain after applying the inverse
transform of the q-logarithm transform. Based on this
feature, when the parameter q is changed, the loga-
rithm transformed coefficients are slightly changed.
Hence, the quality of the digital content can be con-
trolled flexibly.
To show the property of quality controlling based
on q-SVD, we employ the Lena image to implement
the classical frequency domain and our q-SVD. In
order to compare the quality of image after inverse
transform, we choose 100 coefficients of S(0,0) from
the same number of coefficients of SVs of the SVD
domain and q-SVD domain. The comparison of the
quality of image after inverse transformation is shown
in Figure 1.
As described in Figure 1, if we change the param-
eters q, its frequency coefficients are also changed.
Fortunately, such kind of change just affects slightly
the quality of image. This feature is suitable for the
watermark embedding. This is the reason why we
propose the q-SVD for watermark embedding tech-
nique.
3 PROPOSED WATERMARKING
TECHNIQUE
In this section, we explain the proposed watermarking
method based on the q-SVD domain.
3.1 Watermark Permutation
Before embedding, we prepare watermark informa-
tion W of size L × L and obtain a binary sequence bits
from W denoted by w
i
∈ {0,1}, the i-th bit of the wa-
termark. In order to achieve more security, W should
be scrambled before embedding into the original im-
age.
We employ the Torus permutation (Voyatzis and
Pitas, 1996) to scramble W and obtain the scrambled
W
0
as follows:
x
0
y
0
=
1 1
k k + 1
x
y
mod L. (5)
Here, each pixel at coordinate (x, y) of W is moved
to (x
0
,y
0
) of W
0
. W
0
is obtained by applying p times of
the Torus permutation to the watermark. k is chosen
from 1 to L−1. In our method, the choices of k and p
are unknown to the attackers. The Torus permutation
is periodic with period P which depends only upon
the parameters k ∈ [1,L − 1] and L. So, we set p ∈
[1,P]. Figure 2 shows the periodic property of the
Torus permutation where k = 1 and L = 64. It shows
that the period P of W is 96.
3.2 Watermark Embedding Algorithm
Figure 3 describes the detailed steps in our proposed
embedding method. The embedding process is de-
scribed in following.
Step 1. Convert the RGB image I to YCbCr color
space. Transform the Y-component by using the q-
logarithm transformation to obtain Y
q
. Divide Y
q
into
the non-overlapping blocks. The size of each block is
8 × 8.
Step 2. Perform SVD transformation on each
block A
q
divided from Y
q
to obtain the SVs in block S
of q-SVD domain.
Step 3. Embed the binary sequence {w
0
i
} from
W
0
into each SVs of S by QIM method (Chen and
Wornell, 2001) as:
BlindWatermarkingusingQIMandtheQuantizedSVDDomainbasedontheq-LogarithmFunction
17
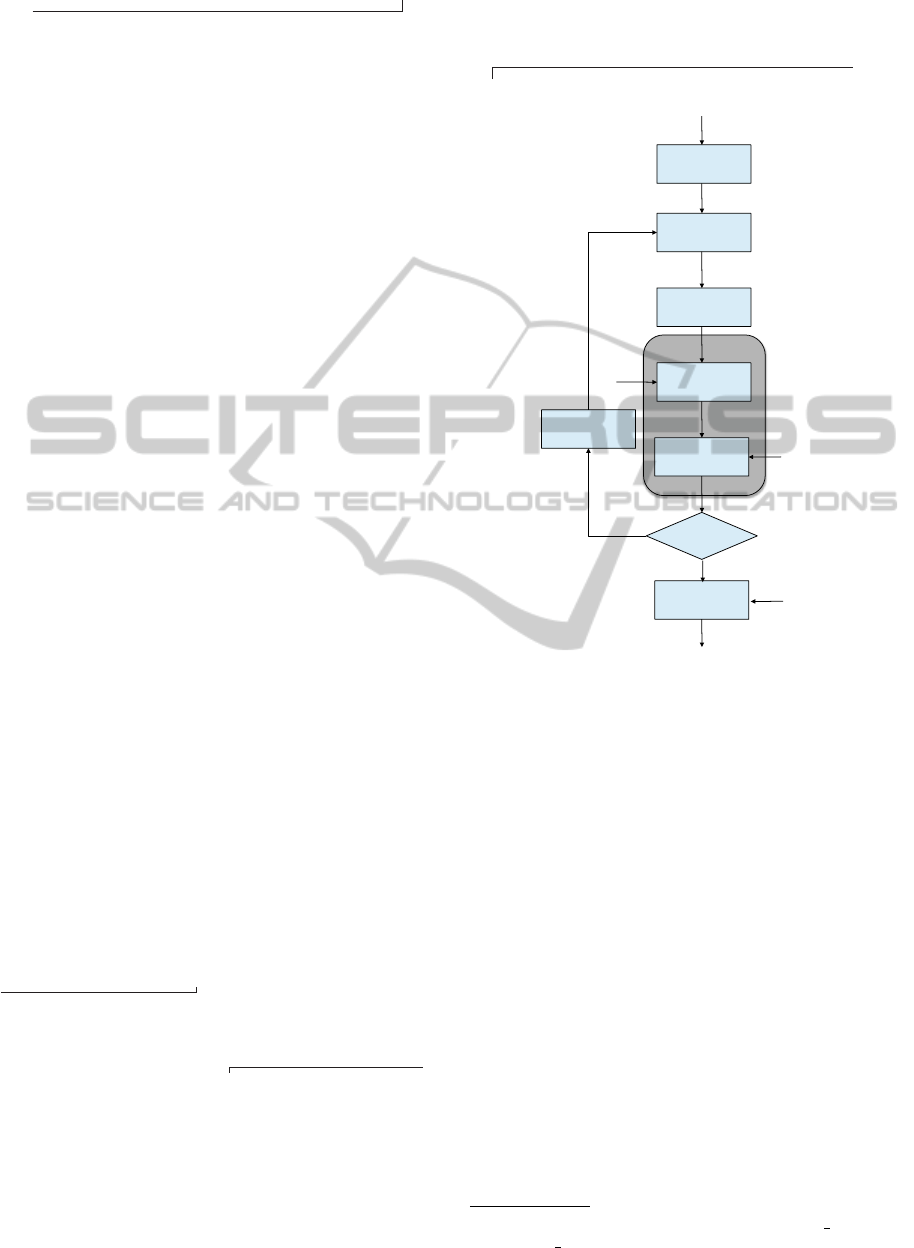
S
w
(u,v)=
S(u,v)/Q×Q + sgn(S(u, v)) × 3Q/4ifw
i
= 1,
S(u,v)/Q×Q + sgn(S(u, v)) × Q/4ifw
i
= 0,
where S(u,v) and S
w
(u,v) are the SVs of the block S
in the q-SVD domain at the coordinate (u, v) of the
original image and the watermarked image, respec-
tively. sgn function equals to “+” if S(u,v) > 0, “−”
if S(u,v) < 0. b c denotes the floor function. Q de-
notes the embedding strength chosen to maintain the
quality of embedded image.
Step 4. Perform the SVD again to make the wa-
termarked matrix A and to obtain Y
0
q
.
Step 5. Apply the q-exponential function for Y
0
q
to obtain Y
0
. Include Cb, Cr component with Y
0
and
transform YCbCr space to RGB color for reconstruct-
ing the watermarked image I
0
.
According to the embedding process, we embed
the watermark W
0
into the q-SVD domain of the Y
component. Thus, we can control the quality of the
embedded image based on two parameters: the pa-
rameter q for q-SVD domain, and the parameter Q for
watermark strength. Therefore, our proposed method
is more flexible than conventional methods using the
SVD domain.
3.3 Watermark Extraction Algorithm
The extraction is performed without using the origi-
nal image and those steps are described in following.
Basic steps involved in the watermarking extraction,
shown in Figure 4, are given as follows:
Step 1. Convert the RGB image I
∗
to YCbCr
color space. Transform Y
∗
component using the q-
logarithm transformation to obtain Y
∗
q
. Divide Y
∗
q
into
the non-overlapping blocks. The size of each block is
the size used in the embedding process.
Step 2. Perform SVD on each block A
∗
to obtain
the SVs of each block.
Step 3. Extract the binary sequence of the
watermark from matrices S
∗
based on the following
rule:
w
∗
i
=
(
1 if S
∗
(u,v) − bS
∗
(u,v)/Qc × Q ≥ sgn(S
∗
(u,v)) × Q/2,
0 if S
∗
(u,v) − bS
∗
(u,v)/Qc × Q < sgn(S
∗
(u,v)) × Q/2.
(6)
Step 4. From {w
∗
i
}, we can obtain the permuted
watermark W
∗
. Permute W
∗
with P − p times using
Torus permutation, we can obtain the extracted water-
mark W
00
.
Watermarked Image
RGB=>YCbCr
Conversion
Blocking
Y-component
DWT/SVD
q-logarithm
QIM
extraction
Torus
permutation
Last block?
Y
Next block
N
Watermark
q
Q
P - p
q-LFD
Figure 4: Extraction based on q-SVD.
4 SIMULATION RESULTS
4.1 Test Images and Evaluational
Measures
To assess the performance of the proposed algorithm,
we conduct four colors images of the well known
SIDBA (Standard Image Data-BAse) database
1
. All
test images have size 512 × 512 pixels. The water-
mark image is a binary image with size 64×64 shown
in Figure 2(c).
In order to evaluate the quality of watermarked
images, we employ PSNR (Peak Signal to Noise
Ratio) criterion (Thanh et al., 2014). The PSNR of
N × N pixels of image I(i, j) and
˙
I(i, j) is calculated
by:
1
www.vision.kuee.kyoto-u.ac.jp/IUE/IMAGE DATA
BASE/STD IMAGES/
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
18

Table 1: PSNR[dB], NC values using q and Q.
Q q 0.2 0.4 0.6 0.8 1.2 1.4 1.6 1.8 2.0
0.30 PSNR 38.4593 40.3052 41.9444 43.2561 45.5018 46.3084 47.0307 47.5226 48.1225
NC 0.971029 0.964782 0.956682 0.941818 0.918022 0.89495 0.885542 0.862428 0.85067
0.35 PSNR 36.8905 38.7757 40.4758 41.9163 44.2819 45.3985 46.1682 46.8607 47.2839
NC 0.977358 0.969377 0.963476 0.941196 0.938796 0.910206 0.883629 0.876834 0.860438
0.40 PSNR 35.4971 37.4385 39.1805 40.6326 43.2493 44.1945 45.214 46.0372 46.6467
NC 0.980723 0.974017 0.968718 0.94935 0.945882 0.92807 0.896696 0.880235 0.85553
0.45 PSNR 34.1959 36.205 37.9389 39.5019 42.0997 43.2704 44.178 45.13 45.8973
NC 0.984111 0.978375 0.969048 0.962175 0.943057 0.930975 0.903418 0.89034 0.871261
0.50
PSNR 33.0911 35.0678 36.8297 38.4515 41.1907 42.3449 43.3211 44.2749 45.1378
NC 0.984111 0.982753 0.975685 0.975763 0.94511 0.939008 0.917181 0.891637 0.877551
0.55 PSNR 32.0909 34.0549 35.8289 37.4512 40.2472 41.4019 42.568 43.3395 44.4058
NC 0.985472 0.985131 0.979374 0.970037 0.945847 0.943396 0.93117 0.900313 0.887457
0.60 PSNR 31.1681 33.1005 34.9007 36.5316 39.3755 40.5954 41.6975 42.716 43.5228
NC 0.98855 0.985131 0.981737 0.973684 0.945569 0.940174 0.928848 0.911775 0.887944
0.75 PSNR 30.2909 32.2614 34.0562 35.711 38.5476 39.9008 41.0083 42.0944 42.8494
NC 0.987179 0.985813 0.985131 0.97435 0.949017 0.945729 0.92867 0.913636 0.904137
PSNR = 20log
255
MSE
[dB]. (7)
MSE =
v
u
u
t
1
N × N
N−1
∑
i=0
N−1
∑
j=0
{I(i, j)−
˙
I(i, j)}
2
.
(MSE : Mean Square Error).
To judge the robustness, we use the normalized
correlation (NC) value between the original water-
mark W and the extracted watermark W
00
(Thanh et
al., 2014). The value of NC is calculated by:
NC =
63
∑
i=0
63
∑
j=0
[W (i, j)×W
00
(i, j)]
63
∑
i=0
63
∑
j=0
[W (i, j)]
2
, (8)
where W (i, j) and W
00
(i, j) are the original watermark
bit and the extracted bit at the position (i, j).
In our experiments, we calculate the PSNR value
for each embedded image and the NC value for each
watermark extracted from the embedded images and
the attacked images. In general, if the PSNR value
is over 37dB, the quality of the embedded image is
considered to be close to the original image. When the
NC value is close to 1, it means that the watermarking
method is robust against the attacks.
4.2 Quality Evaluation and
Optimization of Parameters Q and q
In our method, by increasing the parameter Q of QIM,
we can achieve the robustness of the watermarking
method. However, the visible distortion of the em-
bedded image is more conspicuous. Fortunately, by
increasing the parameter q of the q-SVD, we can im-
prove the quality of the embedded image with keeping
the robustness of the watermark.
In order to optimize the values of the parame-
ters q and Q, we estimate the parameters q and Q
for obtaining the visual quality of the embedded im-
age and the robustness of the watermark information.
To compare the average PSNR and the average NC
values obtained from the embedded images based on
{Q,q}, the watermark strength Q and the parameter q
of the q-SVD are increased with uniform steps until
we can achieve the minimum acceptable PSNR and
NC value. Those are 37 dB for the PSNR and 0.9 for
the NC, respectively.
The experimental results of the color image, Lena,
are given in Table 1. According to the results shown
in Table 1, it can be observed that we can control the
visual quality of the watermarked image and the ro-
bustness of the watermark information based on the
parameter q of q-SVD domain and the embedding
strength parameter Q. When q is larger, the PSNR
value is larger. It means that the visual quality of the
embedded image is better if q increases. When Q is
larger, the NC value is close to 1. It means that the ro-
bustness of watermark is better if Q increases. There-
fore, to achieve high quality of the embedded image
and the robustness of watermark, we can choose the
appropriate the parameters q and Q for the watermark-
ing method.
In order to find the appropriate values for the pa-
rameters Q and q, we set the upper bound and the
lower bound values of these parameters Q and q. In
our experiments, we cannot arbitrarily increase the
value of Q and decrease the value of q because the
quality of the embedded image may become worse in
the case of PSNR< 37 dB. On the other hand, we also
BlindWatermarkingusingQIMandtheQuantizedSVDDomainbasedontheq-LogarithmFunction
19
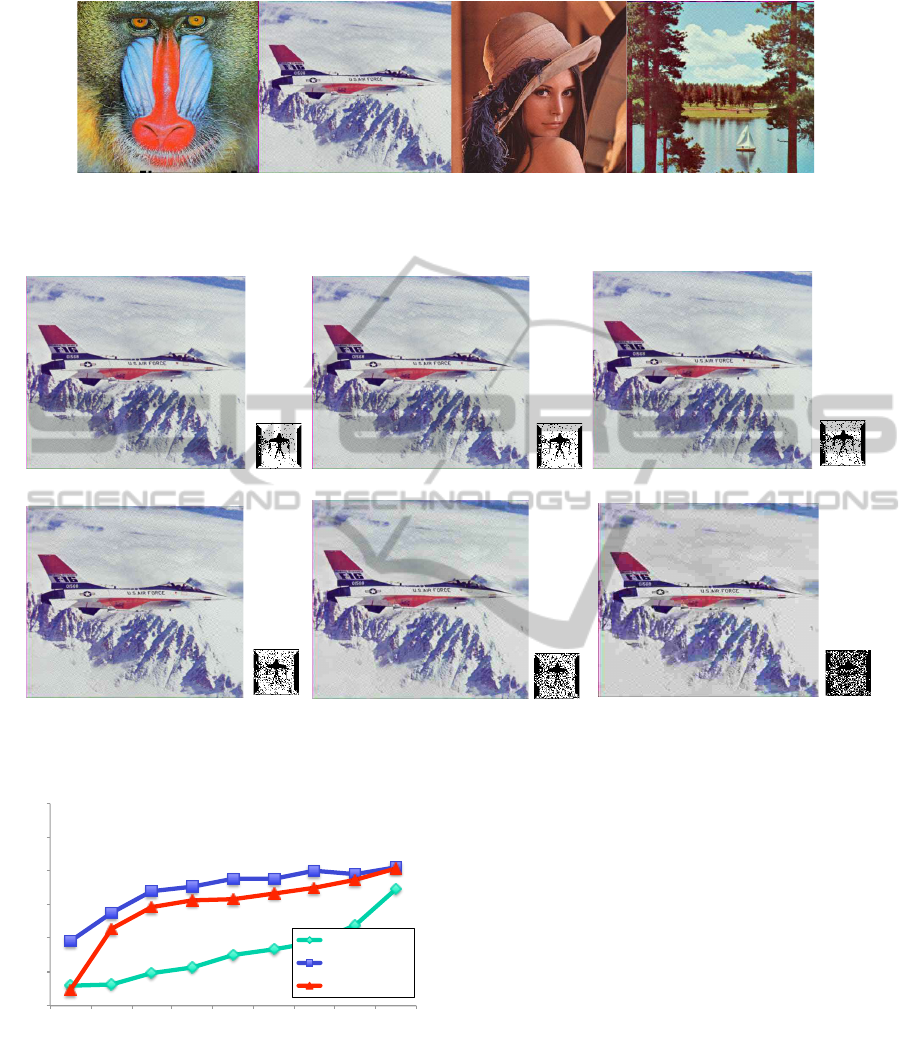
(a) (b) (c) (d)
Figure 5: The watermarked color images (q = 1.2,Q = 0.40). (a) Baboon, PSNR=33.39, (b) F16, PSNR=35.90, (c) Lena,
PSNR=43.67, and (d) Scene, PSNR=39.25.
(a) F16, JPEG compression with quality 60,
PSNR=30.42, NC=0.9426
(b) F16, JPEG compression with quality 50,
PSNR=29.99, NC=0.9187
(d) F16, JPEG compression with quality 30,
PSNR=29.05, NC=0.8420
(c) F16, JPEG compression with quality 40,
PSNR=29.52, NC=0.8869
(e) F16, JPEG compression with quality 20,
PSNR=28.16, NC=0.7542
(f) F16, JPEG compression with quality 10,
PSNR=26.44, NC=0.5552
Figure 6: Watermarks extracted from embedded image F16 after JPEG compression with quality factors 60, 50, 40, 30, 20,
and 10, respectively, when q = 1.2,Q = 0.40.
0.7$
0.75$
0.8$
0.85$
0.9$
0.95$
1$
10$
20$
30$
40$
50$
60$
70$
80$
90$
Jia's$method$
Ours(q=1.4,Q=0.6)$
Ours(q=1.2,Q=0.4)$
NC
Quality factor
Figure 7: JPEG compression attack.
cannot decrease the value of Q and increase the value
of q to obtain the better quality of the embedded im-
ages because this may decrease the robustness of the
watermark in the case of NC< 0.9. By considering
the upper bound and lower bound values, the appro-
priate values for the parameters Q and q are in the
gray region shown in Table 1.
4.3 Simulation Results and Comparison
Without loss of generality, we choose {q = 1.2,Q =
0.40} and {q = 1.4, Q = 0.60} to simulate the exper-
imental images. We embed the watermark into the
original image and try to extract the watermark from
the suspected image under intentional and uninten-
tional attacks.
In order to evaluate the robustness of our pro-
posed method, we compare our results with that of the
method of Jia (Jia, 2014). In the case of Jia’s method,
to be fair, we implement his method employing the
grayscale watermark instead of the color watermark.
4.3.1 Robustness Against JPEG Compression
Robust against JPEG compression is a basic require-
ment for the image watermarking. Therefore, we
test our proposed method against JPEG compression
with various quality factors. The simulation results
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
20
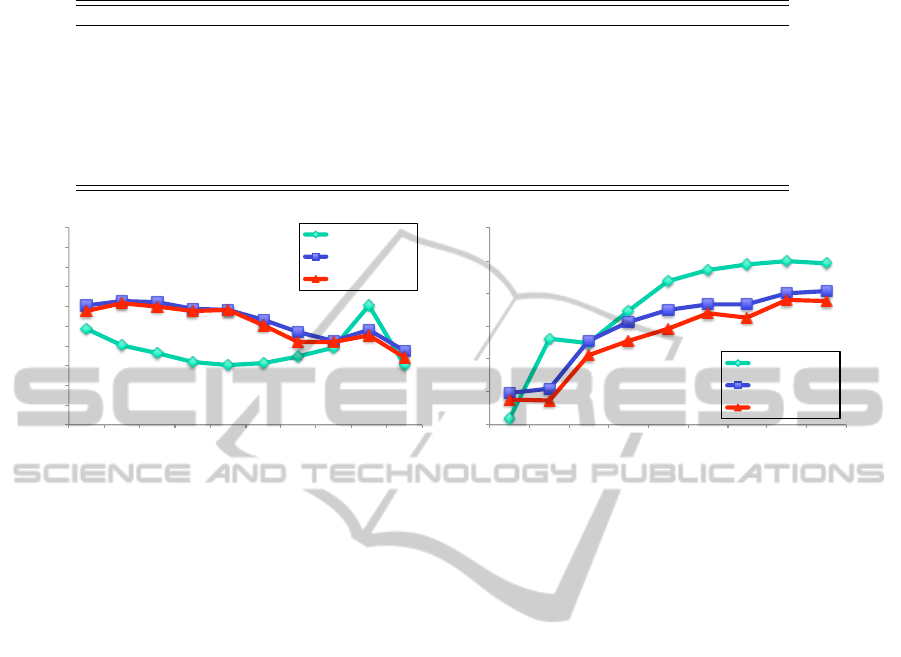
Table 2: PSNR[dB], NC values under JPEG compression with QF (q = 1.2,Q = 0.40)/(q = 1.4,Q = 0.60).
Image Quality factor No attack 90 80 70 60 50
Lena PSNR 43.67/41.08 37.04/36.35 32.75/32.47 31.92/31.70 31.37/31.17 30.96/30.78
NC 0.952/0.951 0.877/0.881 0.808/0.830 0.752/0.786 0.706/0.744 0.667/0.696
F16 PSNR 35.90/32.38 33.85/31.30 31.44/29.80 30.92/29.44 30.41/29.08 29.99/28.81
NC 0.996/0.994 0.989/0.986 0.982/0.978 0.963/0.974 0.943/0.961 0.919/0.946
Baboon PSNR 33.39/32.83 29.22/29.00 25.76/25.66 25.12/25.03 24.62/24.54 24.24/24.17
NC 0.961/0.966 0.906/0.911 0.814/0.823 0.761/0.795 0.725/0.766 0.686/0.725
Scene PSNR 39.25/35.73 31.82/30.86 28.52/28.00 28.09/27.55 27.77/27.34 27.44/27.17
NC 0.981/0.980 0.889/0.887 0.811/0.830 0.662/0.762 0.595/0.673 0.576/0.600
0.8$
0.82$
0.84$
0.86$
0.88$
0.9$
0.92$
0.94$
0.96$
0.98$
1$
10$
20$
30$
40$
50$
60$
70$
80$
90$
100$
Jia's$method$
Ours(q=1.4,Q=0.6)$
Ours(q=1.2,Q=0.4)$
NC
Angle
0.7$
0.75$
0.8$
0.85$
0.9$
0.95$
1$
0.3$
0.5$
0.7$
0.9$
1.1$
1.3$
1.5$
1.7$
1.9$
Jia's$method$
Ours(q=1.4,Q=0.6)$
Ours(q=1.2,Q=0.4)$
NC
Scaling
Figure 8: Geometric attack.
of the color images, Baboon, F16, Lena, and Scene,
are given in Figure 5 and Table 2. Table 2 shows
the NC values of the extracted watermarks and the
PSNR values of the watermarked images after attack-
ing by JPEG compression with different quality fac-
tors (QF). In the JPEG compression, the QF for the
compression process is ranged from 1 to 100, which
denotes the predetermined image quality of the JPEG
compression. When QF is larger, lower compression
ratio of the JPEG image is obtained and better visual
quality of the JPEG image is retained.
According to Table 2, we find that even if un-
der high compression ratios, high NC values can be
obtained. It means that our proposed method is ro-
bust against the JPEG compression attack. The im-
age watermarking needs to be robust against, at least,
JPEG compression to ensure for image transmission
via network. Note that, image is always compressed
to JPEG image with quality factor equals to 75∼80
before transmission. Figure 6 illustrates the water-
mark extracted from the embedded image F16 after
the JPEG compression with low quality factors 60, 50,
40, 30, 20, and 10. It is clear that the extracted water-
marks can be easily recognized by human eyes. Addi-
tionally, Figure 7 shows that our methods achieve bet-
ter performance compared to Jia’s method (Jia, 2014).
Therefore, according to the results of Table 2 and Fig-
ure 7, our proposed method is useful under the JPEG
compression and image transmission via network.
Comparing the results of Table 2, we find that
when we use {q = 1.4,Q = 0.60} instead of {q =
1.2,Q = 0.40}, the visual quality of watermarked im-
ages are remained, and the robustness of watermark
is improved. Normally, when the parameter Q is in-
creased, the quality of the embedded image is de-
graded. However, by using the larger q of the q-
SVD domain, the quality of the embedded image is
improved.
4.3.2 Robustness Against Geometric and
Processing Attacks
In our experiments, the embedded images are subject
to the following attacks.
Firstly, the geometric attacks are considered as the
first challenge because they destroy the synchroniza-
tion in the embedded image. The embedded images
are scaled with different scaling factors (scaling at-
tack). They are also rotated by several angles (rota-
tion attack). The scaling factors with ranging from
0.3 to 1.9 and the rotation angles with ranging from
10
o
to 100
o
are employed in our tests. In order to
obtain good extraction, the attacked image should be
rescaled or re-rotated by an estimated scaling factor
or an estimated rotation angle in the opposite direc-
tion. To be fair, the estimation algorithm in (Thanh et
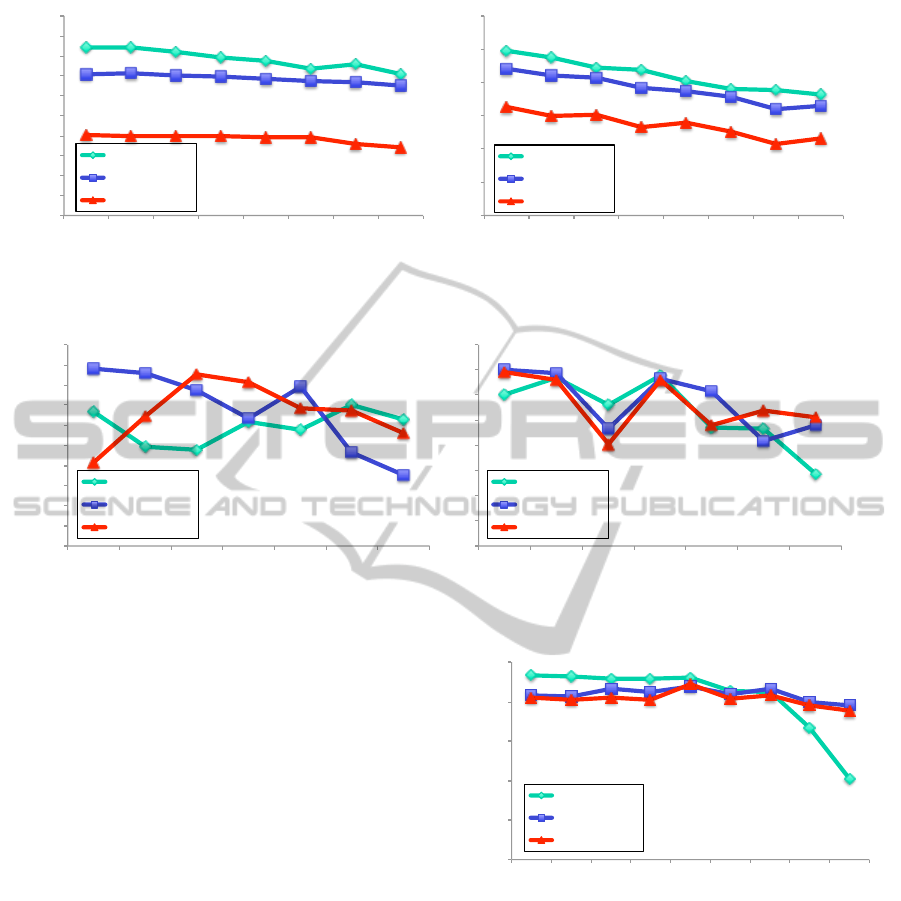
al., 2014) is performed. The results in Figure 8 shows
that our methods are better than the method of Jia (Jia,
2014) in the rotation attacks. However, our methods
in the scaling attacks are worse than the method in
(Jia, 2014).
Secondly, noise addition attack is common distor-
BlindWatermarkingusingQIMandtheQuantizedSVDDomainbasedontheq-LogarithmFunction
21
0.8$
0.82$
0.84$
0.86$
0.88$
0.9$
0.92$
0.94$
0.96$
0.98$
1$
0.1$
0.2$
0.3$
0.4$
0.5$
0.6$
0.7$
0.8$
Jia's$method$
Ours(q=1.4,Q=0.6)$
Ours(q=1.2,Q=0.4)$
0.7$
0.75$
0.8$
0.85$
0.9$
0.95$
1$
2%$
3%$
4%$
5%$
6%$
7%$
8%$
9%$
Jia's$method$
Ours(q=1.4,Q=0.6)$
Ours(q=1.2,Q=0.4)$
NC
NC
p
(a) Gaussian noise addition
(b) Pepper and salt noise addition
Figure 9: Noise addition attack.
0.65%
0.66%
0.67%
0.68%
0.69%
0.7%
0.71%
0.72%
0.73%
0.74%
0.75%
3x3%
5x5%
7x7%
9x9%
11x11%
13x13%
15x15%
Jia's%method%
Ours(q=1.4,Q=0.6)%
Ours(q=1.2,Q=0.4)%
0.58%
0.6%
0.62%
0.64%
0.66%
0.68%
0.7%
0.72%
0.74%
3x3%
5x5%
7x7%
9x9%
11x11%
13x13%
15x15%
Jia's%method%
Ours(q=1.4,Q=0.6)%
Ours(q=1.2,Q=0.4)%
NC
NC
Window size Window size
(a) Median filter
(b) Gaussian blur filter
Figure 10: Filtering attack.
tion in which the noise is added to the embedded im-
age. There are two types of noise, Gaussian white
noise and ‘pepper and salt’ noise, which are normally
added into the embedded images. For the purpose of
our experiments, Gaussian white noise of zero mean
and variance ranging from 0.1 to 0.9, and ‘pepper and
salt’ noise with percentage ranging from 2% to 9%
are added into the embedded image. As shown in Fig-
ure 9, our methods are not as robust against the Gaus-
sian noise and ‘pepper and salt’ noise as the method of
Jia (Jia, 2014). However, as we can see the watermark
image in Figure 6 with NC>0.8, the watermark image
has still good quality. Hence, our methods can be ac-
ceptable under the noise addition attacks since the NC
values of the extracted watermark are over 0.8.
Thirdly, the filtering attack is also tested in
our experiments. There are two kinds of the filter-
ing attacks, median filtering and Gaussian blur fil-
tering, are used and adopted with window sizes are
3 × 3, 5 × 5, 7 × 7,9 × 9,11 × 11,13 × 13,15 × 15. As
in Figure 10, we can assert our proposed methods are
better than the method in (Jia, 2014) under strong fil-
tering attacks.
Fourthly, we present the shearing attack on the
embedded images. In our experiment, the shearing
percentages in x axes with ranging from 10% to 90%
0.7$
0.75$
0.8$
0.85$
0.9$
0.95$
0.1$
0.2$
0.3$
0.4$
0.5$
0.6$
0.7$
0.8$
0.9$
Jia's$method$
Ours(q=1.4,Q=0.6)$
Ours(q=1.2,Q=0.4)$
NC
Shearing percentages
Figure 11: Shearing attack.
are applied. For re-shearing the attacked images, to be
fair, we also use the method in (Thanh et al., 2014).
After re-shearing, the watermark images are extracted
from the the re-sheared images. As shown in Fig-
ure 11, our methods achieve better performance com-
pared to (Jia, 2014) when the shearing percentages
become higher.
For showing the robustness of our proposed
method, we pick up several extracted watermark im-
age of Lena image compared to Jia’s method. It can
be seen from Figure 12, the robustness of watermark
in the proposed method is better than (Jia, 2014).
In order to show the robustness of our proposed
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
22

Attack type Jia’s method Ours (q=1.4, Q=0.6) Ours (q=1.2, Q=0.4)
NC=0.86
NC=0.92 NC=0.91
Rotation 40°
NC=0.88 NC=0.86
NC=0.94
Scaling 1.5
NC=0.86 NC=0.85
NC=0.88
NC=0.89 NC=0.86
NC=0.77
NC=0.73 NC=0.71
NC=0.69
NC=0.80 NC=0.87
NC=0.84
NC=0.93 NC=0.94
NC=0.95
Figure 12: Comparison of extracted watermarks in terms of visual perception, NC values for Lena image.
method against common image processing attacks,
we apply several attacks to the embedded Lena image
such as tampered attacks by text “TA MINH”, quar-
ter of cropping, center cropping with radius of cycle
equals to 100, 2/3 of cropping, grayscale and swirl
attack. Here, we extract the watermark image from
those attacked images and calculate the NC values.
The results are illustrated in Figure 13. We can also
easily recognize the watermark by human eyes.
5 CONCLUSION
A robust image watermarking based on the q-SVD
domain using QIM technique have been proposed in
this paper. As far as we know, it is the first scheme for
watermarking. The watermark is embedded into the
low-frequency of q-SVD domain in order to achieve
the robustness of watermark and to keep the quality of
embedded image. According to our experimental re-
sults, the embedded watermark can successfully sur-
vive after attacked by image processing attacks, es-
pecially for the JPEG compression. Moreover, since
we have employed QIM method for the watermark
embedding and extracting processes, our methods are
simple and the watermark can be extracted without
the original image. Beside, the tradeoff of robustness
and quality can be controlled by the parameter Q of
QIM and the parameter q of logarithm transform.
Our method requests neither the extra data nor
the original image during the extracting procedure.
Furthermore, since only the authenticator knows the
private key for extraction process, our method can
achieve more security.
BlindWatermarkingusingQIMandtheQuantizedSVDDomainbasedontheq-LogarithmFunction
23

Figure 13: Some examples of simulation results against common image processing attacks on Lena image with parameters
{q = 1.2,Q = 0.40}.
ACKNOWLEDGEMENTS
This work is supported by the Ministry of Edu-
cation, Science, Sports and Culture, Grant-in-Aid
for Scientific Research (A) No.24240001 and (C)
No.23500010, a grant of I-System Co. Ltd., NTT Se-
cure Platform Laboratories.
REFERENCES
F. Y. Shih (eds.), “Digital Watermarking and Steganogra-
phy: Fundamentals and Techniques,” Taylor & Fran-
cis Group, CRC Press., Inc., Boca Raton, FL, USA,
2008.
M. M. Yeung, “Digital watermarking,” Commun. ACM,
vol. 41, no. 7, 1998.
A. Nikolaidis, I. Pitas, “Asymptotically optimal detection
for additive watermarking in the DCT and DWT do-
mains,” IEEE Trans. Image Process., vol. 12, no. 5,
pp. 563–571, 2003.
P. Bao, X. Ma, “Image adaptive watermarking using
wavelet domain singular value decomposition,” IEEE
Trans. Circuits and Systems for Video Technology,
vol. 15, no. 1, pp. 96–102, 2005.
R. Liu, T. Tan, “An SVD-based watermarking scheme for
protecting rightful ownership,” IEEE Trans. Multime-
dia, vol. 4, no. 1, pp. 121–128, 2002.
F. Liu, Y. Liu, “A watermarking algorithm for digital image
based on DCT and SVD”, Proc. of CISP ’08, vol. 1,
pp. 380–383, 2008.
Z. Lu, H. Zheng, J. Huang, “A digital watermarking scheme
based on DCT and SVD,” Proc. of IIHMSP ’07, vol.
1, pp. 241–244, 2007.
E. Yavuz, Z. Telatar, “SVD adapted DCT domain DC sub-
band image watermarking against watermark ambigu-
ity,” Proc. of IW-MRCS2006, LNCS, vol. 4105, pp.
66–73, 2006.
W. Cao, Y. Yan, S. Li, “Robust image watermarking based
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
24

on singular value decomposition in DT-CWT do-
main,” Proc. of IST ’09, pp. 381–384, 2009.
E. Yavuz, Z. Telatar, “Improved SVD-DWT based digital
image watermarking against watermark ambiguity,”
Proc. of SAC ’07, pp. 1051–1055, 2007.
L. Zhang, A. Li, “Robust watermarking scheme based on
singular value of decomposition in DWT domain,”
Proc. of APCIP ’09, vol. 2, pp. 19–22, 2009.
K. Deb, M. Al-Seraj, M. Hoque, M. Sarkar, “Combined
DWT-DCT based digital image watermarking tech-
nique for copyright protection,” Proc. of ICECE ’12,
pp. 458–461, 2012.
L. P. Feng, L. B. Zheng, P. Cao, “A DWT-DCT based
blind watermarking algorithm for copyright protec-
tion,” Proc, of ICCSIT, vol. 7, pp. 455–458, 2010.
Y. Bei, D. Yang, M. Liu, L. Zhu, “A multi-channel wa-
termarking scheme based on HVS and DCT-DWT,”
Proc. of CSAE ’11, vol. 4, pp. 305–308, 2011.
C. C. Lai, “A digital watermarking scheme based on singu-
lar value decomposition and tiny genetic algorithm,”
Digital Signal Process., no. 21, vol. 4, pp. 522–527,
2011.
B. Zhou, J. Chen, “A Geometric Distortion Resilient Image
Watermarking algorithm Based on SVD,” Chinese J.
of Image and Graphics, vol. 9, pp. 506–512, 2004.
G. Bhatnagar, B. Raman, “A new robust reference wa-
termarking scheme based on DWT-SVD”, Computer
Standards and Interfaces, vol. 31, issue 5, pp. 1002–
1013, 2009.
K. Loukhaoukha, “Comments on “A digital watermarking
scheme based on singular value decomposition and
tiny genetic algorithm”,” Digital Signal Process., vol.
23, issue 4, p. 1334, 2013.
D. V. S. Chandra, “Digital image watermarking using sin-
gular value decomposition,” Proc. of the 45th Mid-
west Symposium on Circuits and Systems (MWSCAS
2002), vol. 3, pp. 264–267, 2002.
C. C. Chang, P. Tsai, C. C. Lin, “SVD-based digital image
watermarking scheme,” Pattern Recognition Letters,
vol. 26, no. 10, pp. 1577–1586, 2005.
S. Jia, “A novel blind color images watermarking based
on SVD,” Optik - International Journal for Light and
Electron Optics, vol. 125, issue 12, pp. 2868–2874,
2014.
C. Tsallis, “Possible generalization of Boltzmann Gibbs
statistics,” J.Stat. Phys. vol. 52, pp.479–487, 1998.
T. M. Thanh, P. T. Hiep, T. M. Tam, ”A New Spatial q-
log Domain for Image Watermarking,” International
Journal of Intelligent Information Processing (IJIIP),
ISSN 2093-1964, 2014.
G. Voyatzis and I. Pitas, “Chaotic mixing of digital images
and applications to watermarking,” European Conf.
on Multimedia Applications, Services and Techniques
(ECMAST96), vol. 2, pp. 687–695, 1996.
B. Chen, G. W. Wornell, “Quantization index modula-
tion methods for digital watermarking and informa-
tion embedding of multimedia,” J. VLSI Signal Pro-
cess. Syst., vol. 27, pp. 7–33, 2001.
T. M. Thanh, P. T. Hiep, T. M. Tam, K. Tanaka, “Robust
semi-blind video watermarking based on frame-patch
matching,” AEU - International Journal of Electronics
and Communications, ISSN 1434-8411, 2014.
BlindWatermarkingusingQIMandtheQuantizedSVDDomainbasedontheq-LogarithmFunction
25
