Partner Selection in Formation of Virtual Enterprises using Fuzzy

Logic

Shahrzad Nikghadam

, Bahram Lotfi Sadigh

, Ahmet Murat Ozbayoglu

, Hakki Ozgur Unver

and

Sadik Engin Kilic

Department of Mechanical Engineering, Middle East Technical University, Ankara, Turkey

Department of Computer Engineering, TOBB University of Economics and Technology, Ankara, Turkey

Department of Mechanical Engineering, TOBB University of Economics and Technology, Ankara, Turkey

Department of Mechanical Engineering, Atilim University, Ankara, Turkey

Keywords: Virtual Enterprise, Partner Selection, Fuzzy Logic.

Abstract: Virtual Enterprise (VE) is a temporary cooperation among independent enterprises to build up a dynamic

collaboration framework for manufacturing. One of the most important steps to construct a successful VE is

to select the most qualified partners to take role in the project. This paper is a survey of ranking the

volunteer companies with respect to four evaluation criteria, proposed unit price, delivery time, quality and

enterprises’ past performance. Fuzzy logic method is proposed to deal with these four conflicting criteria,

considered as input variables of the model. As each criterion is different in nature with the other criterion,

various membership functions are used to fuzzify the input values. The next step is to construct the logical

fuzzy rules combining the inputs to conclude the output. Mamdani’s approach is adopted to evaluate the

output in this Fuzzy Inference System. The result of the model is the partnership chance of each partner to

participate in VE. A partner with highest partnership chance will be the winner of the negotiation.

Implementation of this model to the illustrative example of a partner selection problem in virtual enterprise

and comparing it with fuzzy-TOPSIS approach verifies the feasibility of the proposed approach and the

computational results are satisfactory.

1 INTRODUCTION

In today’s increasingly competitive dynamic global

market, traditional manufacturing concepts cannot

satisfy the diverse customer demands. Small

companies are suffering from limited resources

while large companies are inflexible (Huang, et al.,

2004). Providing adequate resources for Small and

Medium Sized Enterprises (SMEs) are often very

costly and time consuming. Constructing a synergic

cooperation between these enterprises will aid

companies to share their resources without losing the

flexibility. Virtual Enterprise (VE) is proved to be

one of the effective cooperation platforms.

VE is a network based temporary alliance

between independent and geographically dispersed

enterprises to share skills, core competencies and

resources, in order to catch business opportunities

(Camarinha-Matos & Afsarmanesh, n.d.).This kind

of consortium will help companies for responding

quickly to unanticipated demands from customers.

Lifecycle of VE consists of three main phases;

Formation, Operation and Dissolution. The

Formation phase of a VE is usually triggered by a

request for quote from customer. Based on the

project, design specifications and manufacturing

requirements, production processes are decomposed

into individual task(s). The main step of VE

formation phase is to select the best partners to

participate in forthcoming VE consortium. In order

to fulfil the project, each individual task should be

completed by selected VE partner(s). After the

operation phase of VE which includes

manufacturing and assembly processes, getting

customer’s consent and achieving the goal(s) VE

project is finalized and it can be dissolved.

The most important part of VE formation phase

is the partner selection step. In order to form up a

successful VE consortium it is crucial to select the

most appropriate partners from list of potential

partners registered in virtual breeding environment.

This is why there are lots of researches conducted in

this field. However, due to neglecting the dynamic

Nikghadam S., Lotﬁ Sadigh B., Murat Ozbayoglu A., Ozgur Unver H. and Engin Kilic S..

Partner Selection in Formation of Virtual Enterprises using Fuzzy Logic.

DOI: 10.5220/0005293000820088

In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 82-88

ISBN: 978-989-758-075-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

nature of VE and heterogeneity of customer

preferences (decision making criteria), much of the

proposed methods are not generic solutions and

cannot be implemented directly in different decision

making problems.

Partner selection is not a simple optimization

problems (Sari, et al., 2007). Regarding the fact that,

it is very difficult to express the qualitative criteria

with precise values in digits and considering the

nature of quantitative criteria which are represented

in numbers, handling the quantitative criteria

mathematically is much easier than including

qualitative criteria in mathematical models (Ye,

2010).

The other difficulty of decision making is that it

involves conflicting criteria. If there is a potential

partner with best score in all criteria surely that

company is the best; however generally this is not

the case in practical applications. For instance a high

quality product usually comes with expensive price.

Hence there is an inevitable trade-off between

criteria which is done on the basis of customer’s

preferences.

Importance of partner selection problem along

with complexity of this subject drew the attention of

many researchers. Some approaches use Artificial

Intelligence techniques such as Genetic Algorithm to

solve the partner selection’s mathematical model

(Fuqing, et al., 2005), where Sari et al. propose

Analytic Hierarchy Process (AHP) to perform

pairwise comparisons between criteria and

alternatives (Sari, et al., 2007). In these

methodologies quantitative criteria are assigned with

a crisp value, neglecting the subjective nature of

them. In contrast, most of the papers in the literature

are hybrid fuzzy approaches which are capable of

handling the imprecision of input data. Mikhailov

and Fei propose Fuzzy-AHP and Fuzzy-TOPSIS

methods respectively (Ye, 2010), (Mikhailov, 2002).

In a study conducted by Bevilacqua and Petroni

fuzzy logic is employed in specifying the relative

importance (weight) given to criteria and in

determining the impact of each supplier on the

attributes considered (Bevilacqua & Petroni, 2010).

Yet this study is conducted in the field of supplier

selection of supply chain management (SC) and

there is insufficient research for applying fuzzy logic

approach in partner selection problem of VE.

Selection of partner enterprises in creation of

virtual enterprise has much in common with supplier

selection of supply chain management. They both

evaluate the companies and try to find the best

alternative with respect to number of factors.

However they are not completely identical. VE is

more dynamic in comparison to SC. Supplier

selection of SC designed for a specific set of

processes, while VE can emerge for fulfilling

different types of projects and customers so VE is

more dynamic in comparison to SC.

The method proposed in this paper is based on

applying fuzzy logic to deal with uncertainty of the

problem; in addition it considers “criteria-specific

membership functions” which is a fact neglected in

the literature to the best of our knowledge.

The remainder of this paper is organized as

follows: Section 2 reviews some background

information about fuzzy logic. Section 3 explains

and discusses the developed model in details. An

illustrative example is presented in section 4 and the

results of proposed model is compared with fuzzy-

TOPSIS model. Conclusions are discussed and

future research scopes are recommended in the last

section.

2 FUZZY LOGIC

Lotfi A. Zadeh published the theory of fuzzy set

mathematics in 1965 and fuzzy logic by extension.

(Zadeh, 1965). Fuzzy set is a valid supporting tool to

overcome uncertainty (Bevilacqua & Petroni, 2010).

Fuzzy Inference system is a popular reasoning

framework based on the concepts of fuzzy set

theory, fuzzy logic and fuzzy IF-THEN rules. Fuzzy

Inference systems make decisions based on inputs in

the form of linguistic variables derived from

membership functions. These variables are then

matched with the preconditions of linguistic IF-

THEN rules called fuzzy logic rules, and the

response of each rule is obtained through fuzzy

implication as a crisp value (Shing & Jang, 1993).

Mamdani fuzzy inference is the most commonly

used inference method introduces by Mamdani in

1975 (Mamdani & Assilian, 1975). The fuzzy

inference involves four steps: 1. Fuzzification of

input variables, 2. Rule Evaluation, 3. Aggregation

of the rule outputs, 4. Defuzzification.

The first step of fuzzy inference system is

calculating the membership degree of inputs to their

belonging fuzzy sets. In the second step fuzzified

values of inputs are used to evaluate fuzzy rules.

Fuzzy rules are contain fuzzy operators (AND or

OR). The next step is aggregating the fuzzy outputs

of all rules. The last step of fuzzy inference process

is defuzzifying the output, conclude the final crisp

value and rank the results.

PartnerSelectioninFormationofVirtualEnterprisesusingFuzzyLogic

3 PARTNER SELECTION

MODEL

Among tens of aspects to evaluate the partners to

join virtual enterprise, in this research, four main

criteria are taken into account; proposed unit price,

proposed delivery time, company’s products quality

and its past performance. According to the industry

experts, these four criteria are believed to be the

most essential aspects to evaluate the enterprises.

First two criteria are proposed by each enterprise

during negotiation process. The values of last two

criteria are imported from quality and performance

evaluation models which are available in the system.

The proposed values of price and delivery time are

normalized using Euclidean normalization method.

After calculating the values of enterprises for each

criterion, these values are fuzzified with respect to

the corresponding membership functions. Due to

different nature of each criterion, different sets and

membership functions are defined.

3.1 Input Variables of Fuzzy Logic

First step to implement the model is to translate the

linguistic variables into fuzzy numbers through

defining the appropriate membership functions.

Using different membership functions to calculate

the value of each criterion is the novelty introduced

in this paper, compared to the researches in the

literature. i.e. different types of membership

functions are selected in order to fit the actual

pattern of each factor.

3.1.1 Unit Price

Since the price proposals are absolute values, the

corresponding membership functions must be linear

in order to maintain the competitiveness between

candidates. Even a dollar less, means cheaper price.

This should not be ignored in fuzzification process.

So, three triangular membership function are used to

model the fuzzy behaviour of unit price proposed by

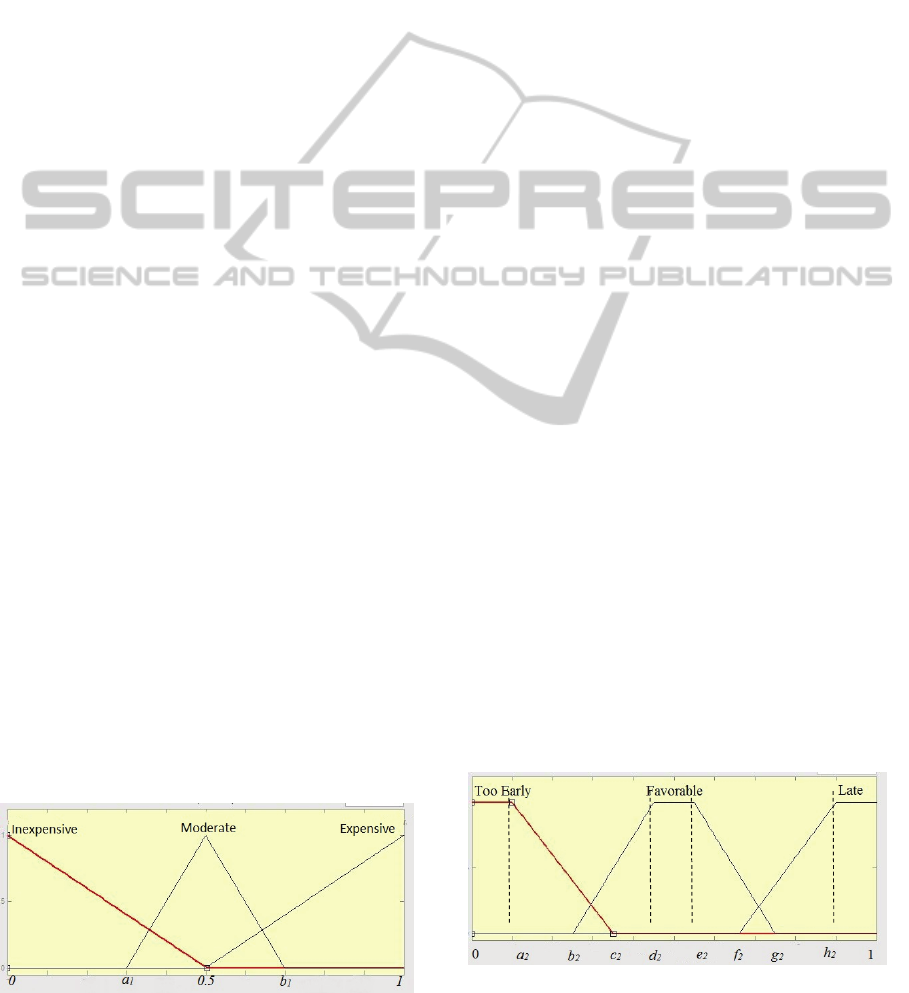
enterprises, as shown in Fig.1.

Figure 1: Unit Price’s membership functions.

The membership function are as follows:

Inexpensive (0; 0; 0.5)

Moderate (a

; 0.5; b

)

Expensive (0.5; 1; 1)

3.1.2 Delivery Time

The membership functions of delivery time are also

linear. However, they consist of domains which,

within that range, the fuzzified values of scores are

equal. Generally Project Evaluation Review

Technique (PERT) is used to calculate the Earliest

Finish and Latest Finish. The range between these

two due dates is a favourable domain.

If a task cannot be completed on time it will be

back order charging some penalties (Nikghadam, et

al., 2011). If lateness exceeds, the order will be lost

and it cannot be compensated, this is a domain

which membership function has a constant value

equal to one. As too early delivery imposes storage

costs its trend is similar to late delivery. Trapezoidal

membership function is providing all the

characteristics required to model the delivery time.

The membership functions are shown in Figure 2.

Too Early (0; 0; a

; c

)

Favourable (b

; d

; e

; g

)

Late (f

; h

; 1; 1)

3.1.3 Quality

Similar to delivery time, there are constant-valued

domains for membership functions of quality.

Quality specifications are generally defined by an

acceptable “range”, all the values within these limits

are satisfactory. Furthermore, considering the

marginality of human decisions bell-shaped

membership function are most suitable to model the

problem as shown in Figure 3. Parameters of a

and

are determining the shape of the curves.

Less than Required (a

; b

; 1.5; 0)

Satisfactory (a

; b

; 0.5)

More than Required (a

; b

; 1)

Figure 2: Delivery time’s membership functions.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

Figure 3: Quality’s membership functions.

3.1.4 Past Performance

Past performance of a company is a criterion

representing the customer’s satisfaction degree,

which is influenced by several factors such as after

sale service; respond to changes; communication

openness and etc. Similar to the nonlinear trend of

quality, past performance’s membership function is

not linear due to marginality. Increasing customer’s

consent is more demanding at higher scores. So two

simple Gaussian membership functions are defined.

These membership functions are shown in Fig. 4.

Parameter a

is specifying the shape of the curves.

Poor (a

; 0)

Good (a

; 1)

Figure 4: Past performance's membership functions.

3.2 Output Variable of Fuzzy Logic

Output variable of this model is partner’s acceptance

chance to join VE consortium. This model reveals a

method to calculate this value by getting two

bidding proposals (price and delivery time) and two

performance evaluation value from enterprise

background (quality and enterprise past

performance). An enterprise with competitive

proposals and good background will have higher

chance to be picked out as a winner to take role in

virtual enterprise rather than other rival enterprises.

3.2.1 Partnership Chance

As shown in Fig. 5 three triangular membership

functions are used to define fuzzy set of the output.

Usually enterprises violating the project

requirements belong to the first membership

function and their partnership chance are low. The

third membership function members are those which

can satisfy almost all the necessities of four inputs

and the enterprises belonging to this set are most

likely to be accepted as partner. While the members

of second membership function, are potential partner

enterprises which cannot be classified in first or

third membership function groups and have the

medium partnership chance.

Low (0; 0; 0.5)

Medium (a

; 0.5; b5)

High (0.5; 1; 1)

3.3 Fuzzy Logic Rules

Once the inputs are fuzzified, fuzzy rules should be

defined. Fuzzy rules are made up of linguistic

statements which describe how to make decisions

considering the inputs.

If (input 1 is membership function1) AND/OR

(input 2 is membership function 2) THEN (Output n

is membership function n)

Figure 5: Partnership chance’s membership functions.

Rules are established based on customer

preferences. By asking the decision maker(s) to fill

the questionnaire, the relative importance of each

criterion is extracted.

For instance an enterprise producing the low

quality product which do not met the system

predefined specifications or unable to get customer

consent about delivery time is not competitive, has

low partnership chance.

All the possible combinations should be

considered for constructing fuzzy rules to ensure the

validity of the model. More descriptive fuzzy rules

will be presented for the case of our study.

Establishing the IF-THEN rules are the most

important step of the method since even a single

improper rule will cause untrustworthy results.

According to these fuzzy rules, fuzzy inputs will

be combined and evaluated by Mamdani’s fuzzy

inference system to find the partnership chance as

this model’s output.

PartnerSelectioninFormationofVirtualEnterprisesusingFuzzyLogic

4 ILLUSTRATIVE EXAMPLE

In order to illustrate the application of fuzzy logic

method to partner selection problem in formation of

virtual enterprise a simplified example is considered.

A virtual enterprise has received an order from a

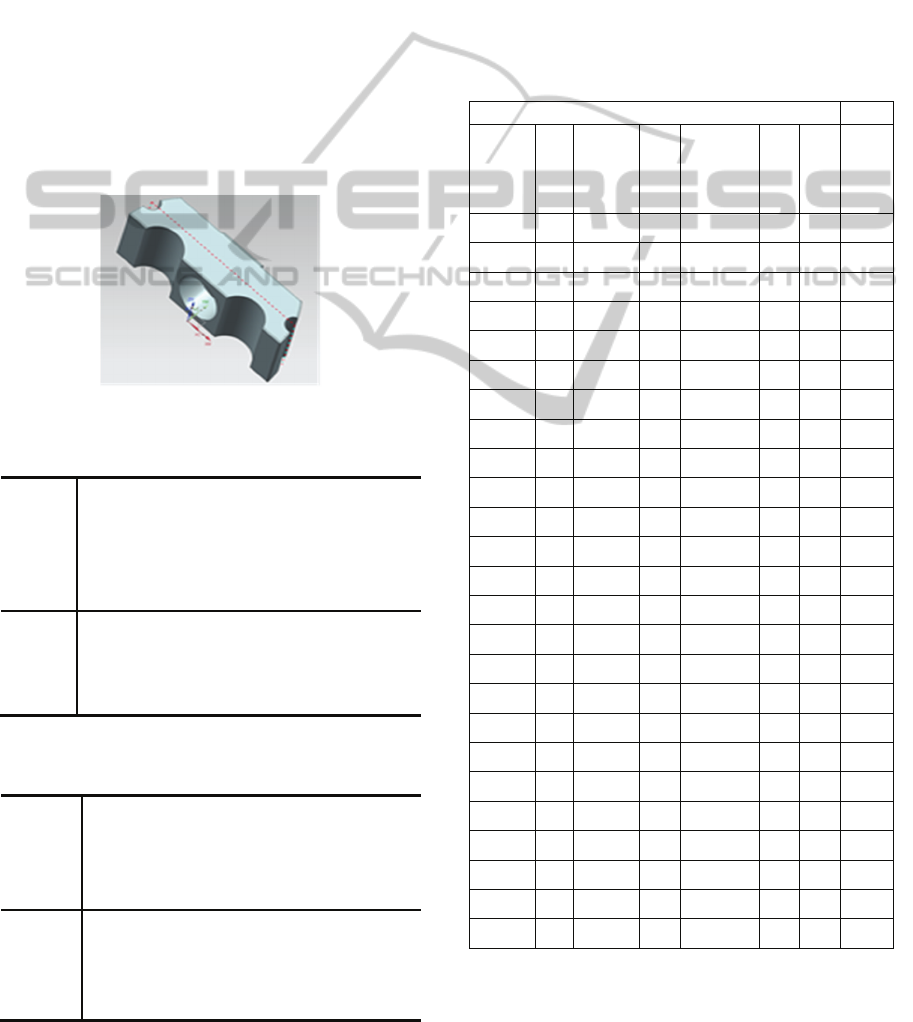
customer to manufacture the component shown in

Figure 6. There are four candidate enterprises eager

to take role in project. Bidding starts in order to

identify the best proposal from the best company.

The evaluation procedure is based on fuzzy logic

approach presented in previous section.

Bidding Proposals and candidates’ scores are

shown in Table 1. The values of input variables,

price and delivery time are proposed by each

company, while the scores of quality and past

performance which are feedback-oriented are out of

10. Table 2 shows the normalized values of Table 1.

Figure 6: Component sketch for illustrative example.

Table 1: Scores of enterprises with respect to criteria.

Unit Price

($)

Delivery Time

(days)

Quality

(Out of 10)

Past

Performance

(Out of 10)

Co. A 1700 8 4 5

Co. B 1700 10 5 4

Co. C 2000 12 5 3

Co. D 1500 10 6 5

Table 2: Normalized scores of enterprises with respect to

criteria.

Unit Price

Delivery

Time

Quality

Past

Performance

Co. A 0.49 0.396 0.396 0.577

Co. B 0.49 0.495 0.495 0.346

Co. C 0.577 0.594 0.495 0.462

Co. D 0.432 0.495 0.594 0.577

These values are fuzzified according to the

membership functions specified for each criterion.

Regarding the customer preference based- fuzzy

rules shown in Table 4, companies’ partnership

chance is evaluated and tabulated in Table 4.

With three levels for unit price, delivery time,

quality and two levels for past performance there are

total of 3×3×3×2=54 possible combinations if all the

rules are defined by ‘AND’ operator. Though, to

simplify the rule list, one rule is defined as below;

If (Delivery time is Late) OR (Quality is Less

than Required) THEN (Partnership Chance is Low)

Table 3: Set of fuzzy rules.

THEN

Price

Delivery

Time

Quality

Past

Performance

Partnership

Chance

- Late OR Less than req. - Low

inexpensive And too early And satisfactory And poor medium

inexpensive And too early And satisfactory And good medium

inexpensive And too early And more than req. And poor medium

inexpensive And too early And more than req. And good medium

inexpensive And favorable And satisfactory And poor high

inexpensive And favorable And satisfactory And good high

inexpensive And favorable And more than req. And poor high

inexpensive And favorable And more than req. And good high

average And too early And satisfactory And poor low

average And too early And satisfactory And good low

average And too early And more than req. And poor low

average And too early And more than req. And good medium

average And favorable And satisfactory And poor medium

average And favorable And satisfactory And good medium

average And favorable And more than req. And poor High

average And favorable And more than req. And good high

expensive And too early And satisfactory And poor low

expensive And too early And satisfactory And good medium

expensive And too early And more than req. And poor low

expensive And too early And more than req. And good medium

expensive And favorable And satisfactory And poor low

expensive And favorable And satisfactory And good medium

expensive And favorable And more Than req. And poor low

expensive And favorable And more Than req. And good medium

By doing this, just two levels are left for delivery

time and quality. As (3×2×2×2)+1= 25, all the

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

possible combinations are included by defining 25

rules to build up a reliable model for the case of our

study.

The output of the model is calculated using fuzzy

logic toolbox of MATLAB software. And tabled in

Table 4.

Table 4: Companies’ partnership chance based on fuzzy

logic.

Partnership Chance (%)

Co. A 53.5

Co. B 51.8

Co. C 39.9

Co. D 61.0

In order to verify the fuzzy logic based model,

the results are compared with Fuzzy-TOPSIS

method developed by Chen et al. (Chen & Tsao,

2008). Customer preferences are calculated using

pairwise comparisons and allocating fuzzy numbers

for their subjective terminations. The final results of

criteria weights for our sample are set to be 0.394,

0.277, 0.257, and 0.106 for unit price, delivery time,

quality and past performance respectively (The rules

of fuzzy logic are also constructed considering these

preferences). Using the normalized values of Table 2

and multiplying them by their corresponding

weights are results in weighted performance matrix.

Then applying the TOPSIS procedure step by step

companies are ranked based on their closeness to the

ideal solution as shown in Table 5. The closest

candidate to the positive ideal solution has higher

partnership chance.

Regarding Table 6 the ranking lists proposed by

these two methods are same and both choose

Company D as a winner. However, their partnership

chances are not equal. There are two main reasons

which explains these differences. First, for

constructing fuzzy logic model different types of

functions; constant, linear and nonlinear are used.

Table 5: Companies’ partnership chance based on fuzzy

TOPSIS.

Distance from

Positive Ideal

Solution

Distance from

Negative Ideal

Solution

Closeness

(%)

Co. A 0.056 0.069 55.3

Co. B 0.05 0.051 50.2

Co. C 0.084 0.028 25.2

Co. D 0.027 0.085 75.5

This ability makes the model to be more sensitive to

changes in specific domains. Moreover, for criteria

such as delivery time and quality which have the

predefined “acceptable domain” all of the values

within this domain are identically same and does not

affect the overall score of candidate. These are the

facts neglected in Fuzzy-TOPSIS approach.

Table 6: Candidates ranking based on Fuzzy Logic and

Fuzzy TOPSIS methods.

Fuzzy Logic

Ranking List

Fuzzy TOPSIS

Ranking List

Co. D Co. D

Co. A Co. A

Co. B Co. B

Co. C Co. C

5 CONCLUSIONS

In this study, a fuzzy logic based model is proposed

for formation of virtual enterprise. The developed

approach provides an effective tool for ranking the

enterprises with respect to both quantitative and

qualitative criteria and selecting the best partner to

participate in virtual enterprise.

Unless many other techniques in literature,

specific membership functions are defined for each

criterion regarding their characteristics in order to

acquire more reliable outcomes. Besides, the other

strength of this method is; it provides a flexible

model to change the policies in a way decision

maker prefers. Not only fuzzy rules can be edited

considering customer preferences, but also

membership functions of four inputs and output can

be modified corresponding to bidding properties. In

contrast, models reliability is highly dependent on

stablishing reasonable fuzzy rules. Thus, the way to

get more accurate results and enhanced models

trustworthy is to define precise fuzzy rules by

consulting experienced industrial experts.

This study is a preliminary validation of the

model for further implementations in industry. The

verified model will be implemented in partner

selection process of forthcoming VE platform which

is going to be established in OSTIM organized

industrial park in Ankara.

ACKNOWLEDGEMENTS

This study is being funded by SAN-TEZ project No.

00979.stz.2011-12 of Turkish Ministry of Science,

PartnerSelectioninFormationofVirtualEnterprisesusingFuzzyLogic

Technology and Industry. Authors are sincerely

thankful for continuous support of OSTIM Industrial

Park management.

REFERENCES

Bevilacqua, M. & Petroni, A., 2010. From traditional

purchasing to supplier management: A fuzzy logic

based approach to supplier selection. International

Journal of Logistics: Research and Application, pp.

235-255.

Camarinha-Matos, L. & Afsarmanesh, H., n.d. The virtual

enterprise concept. In: Infrastructure for virtual

enterprises: networking Industrial enterprises.

London: Kluwer Academic Publishers, pp. 3-14.

Chen, T.-Y. & Tsao, C.-Y., 2008. The interval-valued

fuzzy TOPSIS method and experimental analysis.

Fuzzy Sets and Systems, 159(11), pp. 1410-1428.

Fuqing, Z., Yi, H. & Dongmei, Y., 2005. A multi-

objective optimization model of the partner selection

problem in a virtual enterprise and its solution with

genetic algorithms. The International Journal of

Advanced Manufacturing Technology, 28(11-12), pp.

1246-1253.

Huang, X., Wong, Y. & Wang, J., 2004. A two-stage

manufacturing partner selection framework for virtual

enterprises. International Journal of Computer

Integrated Manufacturing, 17(4), pp. 294-304.

Mamdani, E. & Assilian, S., 1975. An experiment in

linguistic synthesis with fuzzy-logic-controller, Int.

Journal of Man-Machine studies, pp.1-13.

Mikhailov, L., 2002. Fuzzy analytical approach to

partnership selection in formation of virtual

enterprises. The international journal of management

science, Volume 30, pp. 393-401.

Nikghadam, S., Kharrati Shishvan, H. &

Khanmohammadi, S., 2011. Minimizing earliness and

tardiness costs in job-shop scheduling problems

considering job due dates, Proceedings of AIPE.

Sari, B., Sen, T. & Kilic, S. E., 2007. AHP model for the

selection of partner companies in virtual enterprises.

The International Journal of Advanced Manufacturing

Technology, 38(3-4), pp. 367-376.

Shing, J. & Jang, R., 1993. Adaptive-Network-Based

fuzzy inference system. s.l., Transactions on Systems,

Man and Cybernetics, pp. 665-685.

Ye, F., 2010. An extended TOPSIS method with interval-

valued intuitionistic fuzzy numbers for virtual

enterprise partner selection. Expert Systems with

Applications, 37(10), pp. 7050-7055.

Zadeh, L. A., 1965. Fuzzy Sets. Information and Control,

Volume 8, pp. 338-353.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems