
Sales Forecasting Models in the Fresh Food Supply Chain
Gabriella Dellino
1
, Teresa Laudadio
1
, Renato Mari
1
, Nicola Mastronardi
1
and Carlo Meloni
1,2
1
Istituto per le Applicazioni del Calcolo ”M. Picone”, Consiglio Nazionale delle Ricerche, Bari, Italy
2
Dipartimento di Ingegneria Elettrica e dell’Informazione, Politecnico di Bari, Bari, Italy
Keywords:
Fresh food supply chain, Forecasting, ARIMA, ARIMAX, Transfer function.
Abstract:
We address the problem of supply chain management for a set of fresh and highly perishable products. Our
activity mainly concerns forecasting sales. The study involves 19 retailers (small and medium size stores)
and a set of 156 different fresh products. The available data is made of three year sales for each store from
2011 to 2013. The forecasting activity started from a pre-processing analysis to identify seasonality, cycle
and trend components, and data filtering to remove noise. Moreover, we performed a statistical analysis to
estimate the impact of prices and promotions on sales and customers’ behaviour. The filtered data is used
as input for a forecasting algorithm which is designed to be interactive for the user. The latter is asked to
specify ID store, items, training set and planning horizon, and the algorithm provides sales forecasting. We
used ARIMA, ARIMAX and transfer function models in which the value of parameters ranges in predefined
intervals. The best setting of these parameters is chosen via a two-step analysis, the first based on well-known
indicators of information entropy and parsimony, and the second based on standard statistical indicators. The
exogenous components of the forecasting models take the impact of prices into account. Quality and accuracy
of forecasting are evaluated and compared on a set of real data and some examples are reported.
1 INTRODUCTION
Supply chain optimization is one of the most chal-
lenging tasks in operation management due to the
presence of multiple critical issues and multiple deci-
sion makers involved. Inventory management, order
planning, scheduling and vehicle routing are among
the most studied problems in the logistic field (Ja-
cobs and Chase, 2014) in order to reduce supply chain
and transportation costs, and to increase service level,
quality and sustainability.
The efficiency and effectiveness of quantitative
methods for optimizing a supply chain strictly depend
on the quality of available data. It is often assumed
that customer demand is available and/or it is deter-
ministic, while in real scenarios this assumption does
not hold and future sales are often a missing data. For
this reason, sales forecasting represents the first cru-
cial step for such an optimization process and may
affect the capacity to design a realistic supply chain
model.
In the market of fresh and highly perishable food
sales forecasting plays an even more important role
since the shelf life of products is very limited and re-
liable forecasts are fundamental to reduce and man-
age inefficiencies such as stock out and outdating. In
this paper, we address the problem of sales forecast-
ing for a set of fresh and highly perishable products
analyzing real data coming from a set of medium and
small size retailers operating in Apulia region, Italy.
Data was pre-processed to remove noise and identify
basic components, such as trends, cycles and season-
ality. The pre-processed data was used to design three
different forecasting models taking into account the
effect of exogenous variables, such as prices, on sales
behaviour. The first two models are based on ARIMA
multiplicative models (Box et al., 2008), while the
third is a more sophisticated transfer function model
(Makridakis et al., 2008). The three models were
identified and estimated by varying parameters in pre-
defined intervals. The best parameter setting was
selected based on a statistical analysis and a set of
performance indicators. A final step consists in em-
bedding these forecasting models within an algorith-
mic framework designed to be interactive for the user
and operating as a decision support system for supply
chain management.
The rest of the paper is organized as follows. In
Section 2 we describe the structure and characteristics
of our data set, and the adopted pre-processing tech-
niques. In Section 3 we provide theoretical insight
on multiplicative ARIMA models and present the first
419
Dellino G., Laudadio T., Mari R., Mastronardi N. and Meloni C..
Sales Forecasting Models in the Fresh Food Supply Chain.
DOI: 10.5220/0005293204190426
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 419-426
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

forecasting model. In Section 4 we describe the sta-
tistical analysis and performance indicators used for
model selection. In Section 5 we describe the second
and the third forecasting models designed to take the
impact of exogenous variables into account. Finally,
in Section 6 we provide some examples, while con-
clusions are given in Section 7.
2 DATA DESCRIPTION
The data set used for designing and setting the fore-
casting models comes from a real fresh food supply
chain. The available data is made of three year sales,
from 2011 to 2013, for a set of 19 retailers of small
and medium size operating in Apulia region in Italy.
We selected a subset of 156 fresh products belonging
to the category of best sellers for which the available
sales were characterized by large and reliable num-
bers.
Concerning the model implementation, we di-
vided the given data set into two different time sets: a
training set and a test set. The training set represents
the set of observations used to estimate the forecast-
ing model and its parameters. Once the model has
been estimated, we run it taking the test set as input
and deriving forecasts on this set. Then, we compare
forecasted sales with real sales over the test set. Thus,
the test set provides the forecasting horizon.
The training set is used to perform the so-called
in-sample analysis, while the test set is used to com-
pare forecast to observed data, assess the efficacy of
the forecasting model and perform the so-called out-
of-sample analysis. Both analyses rely on statistical
indicators which are described in the following sec-
tion.
2.1 Pre-processing
Data collected for model estimation needed to be pre-
processed for a two-fold reason: identify trends, cy-
cles and seasonality, and remove noise. A seasonality
of 7 days was observed, that is typical of food sold
on large scale distribution in which customers tend to
have well defined cyclical behaviour.
Once the training set is defined, sales are normal-
ized as follows. Let y
t
be the quantity of product P
sold in store V at time t. Then, the corresponding nor-
malized quantity z
t
is
z
t
=
y
t
− µ
σ
, (1)
where µ and σ are the sample mean, respectively, and
the standard deviation of time series y
t
over the train-
ing set.
Besides we attempted to filter data using more so-
phisticated approaches based on independent compo-
nent analysis (Hyv
¨
arinen and Oja, 2001), that are typ-
ically used in signal and image processing. However
it did not provide remarkable quality improvements
for our data set. The reader is referred to (Najarian
and Splinter, 2005) for a detailed description of ad-
vanced data processing techniques.
3 ARIMA MODELS
A time series can be considered as the realization of
a stochastic process that is observed sequentially over
time. Thus, once a time series of data is collected,
it is possible to identify a mathematical model to de-
scribe the stochastic process. The study of theoretical
properties of the defined model allows to perform a
statistical analysis of the time series and forecast fu-
ture values for the series.
A well known class of mathematical models for
time series forecasting is represented by the Autore-
gressive Integrated Moving Average (ARIMA) mod-
els (Box et al., 2008). ARIMA models are widely
used in statistics, econometrics and engineering for
several reasons: (i) they are considered as one of the
best performing models in terms of forecasting, (ii)
they are used as benchmark for more sophisticated
models, (iii) they are easily implementable and have
high flexibility due to their multiplicative structure.
Let z
t
be the realization of a stochastic process at
time t, that is an observation of time series at time
t, and let a
t
be a random variable with normal distri-
bution, having zero mean and variance equal to σ
2
a
.
Thus, the random variable a
t
represents the realiza-
tion at time t of a white noise process. An ARIMA
model with seasonality is defined as follows:
φ
p
(B)Φ
P
(B
s
)∇
d
∇
D
z
t
= θ
q
(B)Θ
Q
(B
s
)a
t
, (2)
where B is the backward shift operator which is de-
fined by Bz
t
= z
t−1
and
φ
p
(B) = 1 − φ
1
B − φ
2
B
2
.. . − φ
p
B
p
, (3)
Φ
P
(B
s
) = 1 − Φ
1
B
s
− Φ
2
B
2s
.. . − Φ
P
B
Ps
, (4)
θ
q
(B) = 1 − θ
1
B − θ
2
B
2
.. . − θ
q
B
q
, (5)
Θ
Q
(B
s
) = 1 − Θ
1
B
s
− Θ
2
B
2s
.. . − Θ
Q
B
Qs
, (6)
∇
d
= (1 − B)
d
, (7)
∇
D
= (1 − B
s
)
D
. (8)
The parameter p defines the order of the autoregres-
sive non-seasonal component AR, q defines the order
of the moving average non-seasonal component MA,
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
420

and the parameter d represents the order of non sea-
sonal integration necessary to obtain a stationary time
series. The parameters p, q and d are commonly used
for referring to non-seasonal models in a concise way.
For more complex models, in which similar pattern
at regular time intervals can be observed, it is more
realistic to take seasonality under consideration. A
data set comprised of food sales on large-scale stores
is typically affected by a weekly seasonality, which
reflects the customers’ habit to buy foods especially
in the weekend. The seasonal component is defined
by the parameters P, D and Q, where P defines the
order of the autoregressive non-seasonal component
SAR, Q defines the order of the moving average non-
seasonal component SMA, and D is the order of sea-
sonal differences. Finally, s defines the series’ sea-
sonality. A seasonal ARIMA model is synthetically
described as ARIMA(p,d,q) × (P,D,Q)
s
. The most
critical disadvantage of classical ARIMA models with
seasonality is that the effect of exogenous variables on
data is not taken into account. In the following sec-
tions we show how to cope with this issue, and to this
end we present two alternative forecasting models.
According to (Box et al., 2008), given a data set,
the best forecasting model can be identified according
to the following framework:
• model identification,
• model estimation,
• diagnostic check.
In the literature the model identification is imple-
mented through either an incremental approach or an
exhaustive one. In the first approach the value of
the parameters defining the ARIMA model are iter-
atively incremented and statistical significance tests
are performed for halting. The simplest way to im-
plement this approach is to define the parameter d as
follows: it starts setting d = 0 and testing the time se-
ries stationarity by statistical tests; based on the result
of the latter, either d is incremented or the process is
halted. For a complete application of the incremental
approach see, for instance, (Andrews et al., 2013). On
the contrary, in the exhaustive approach each param-
eter ranges in predefined intervals; see for instance
(H
¨
oglund and
¨
Ostermark, 1991). The main advantage
of this approach is that a larger set of combinations,
i.e., forecasting models, are compared and the result-
ing model is more accurate. However, the computa-
tional effort required may be larger, since for every
ARIMA model a set of statistical tests and analyses
have to be performed. In the proposed forecasting
models, we implemented the incremental approach
for parameters p, d, q, P, D and Q and we set sea-
sonality s = 7.
For each tuple (p,d,q) × (P,D, Q)
s
the maximum
likelihood principle is adopted for model parame-
ters’ estimation. Finally the diagnostic check of the
forecasting model is implemented by means of two
kinds of performance indicators, in-sample and out-
of-sample, that are used to determine the best model.
In the following section we analyze the diagnostic
check phase in more detail and provide a complete
description of the performance indicators used within
our forecasting models.
4 PERFORMANCE INDICATORS
In this section we describe a set of statistical indica-
tors used to assess the forecasting quality of the mod-
els. These indicators can be divided into two groups,
in-sample and out-of-sample indicators, according to
the set of data used for computing them. For the sake
of clearness, we describe the latter separately as their
meaning, as well as their use, is different within the
proposed forecasting models.
4.1 In-sample Indicators
This subset includes indicators that are computed on
the training set as defined in Section 2. These are
mostly used as lack of fit measures, based on the in-
formation entropy and parsimony of models. Thus,
in-sample analysis has the objective to measure the
matching between real data and simulated data ob-
tained by the mathematical model under analysis.
We computed two different indicators: the Ljiung-
Box test and the Hannan-Quinn Information Criterion
(HQC) (Box et al., 2008), (Burnham and Anderson,
2002). The Ljiung-Box test is a a portmanteau test in
which the null hypothesis is that the first m autocorre-
lations of the residuals r
h
are zero, i.e. they are like a
white process noise. The statistical test applied in this
study is
Q(m) = n(n + 2)
∑
m
h=1
r
2
h
n − h
, (9)
which follows a χ
2
(m − K) distribution with m − K
degrees of freedom, where K is the number of param-
eters estimated within the model and n is the num-
ber of observations in the test set. The Hannan-Quinn
Information Criterion (HQC) is a well known crite-
rion used to quantify the entropy of the information
and the information lost in the fitting process. Under
the assumption that the residuals are independent and
identically distributed,
HQC = n log(SSR/n) + 2K loglog(n), (10)
SalesForecastingModelsintheFreshFoodSupplyChain
421

holds, where SSR is the Sum of Squared Residu-
als. The HQC represents a compromise between the
Akaike Information Criterion (AIC) and the Bayesian
Information Criterion (BIC) and tends to penalize
lack of parsimony, that is a high value of the param-
eter K. The interested reader is referred to (Burn-
ham and Anderson, 2002) for a detailed description of
these in-sample indicators and others. For the sake of
implementation of our forecasting models, the latter
indicators are used as follows: it is performed a non
domination analysis with respect to variance, residu-
als and HQC for all the models obtained by chang-
ing the tuple (p, d, q) × (P,D,Q)
s
. The dominated
models, as well as models not satisfying the Ljung-
Box test, are excluded by the following diagnostic
check, while the remaining models undergo the out-
of-sample analysis.
4.2 Out-of-sample Indicators
The out-of-sample indicators are well known statisti-
cal indicators for quality and accuracy of forecasting
and they are computed on the test set. This implies
that they are used to compare forecast data and real
data within the test set and allow to make a quantita-
tive comparison among different models in terms of
quality of forecast. The first group of indicators in-
cludes absolute measures: they are scale dependent
and for this reason can only be used when different
indicators are computed on the same data set, but can
not be used to compare the behaviour of a forecast-
ing model on different data sets. Let us define f
t
as
the forecast of quantity of product P sold in store V
at time t and with test set {1,...,n}. We compute the
following indicators:
• Root Mean Squared Error (RMSE):
s
1
n
n
∑
t=1
(z
t
− f
t
)
2
,
• Mean Absolute Error (MAE):
1
n
n
∑
t=1
|z
t
− f
t
|,
• Maximum Absolute Error (MaxAE):
max
t=1,...,n
|z
t
− f
t
|.
The second set of indicators is comprised of relative
measures that are not scale dependent. On the one
hand, it is possible to compare the same model on
different scale data sets, but on the other hand these
measures are not defined for time t in which z
t
= 0.
Thus, it is preferable not to use them with either miss-
ing data or data too close to zero. We computed the
following indicators:
• Mean Absolute Percentage Error (MAPE):
100 ·
1
n
n
∑
t=1
z
t
− f
t
z
t
,
• Maximum Absolute Percentage Error (MaxAPE):
max
t=1,...,n
z
t
− f
t
z
t
,
• Coefficient of determination R
2
:
1 −
∑
n
t=1
(z
t
− f
t
)
2
∑
n
t=1
(z
t
− µ)
2
,
where µ is the average value of z
t
over the test set.
There are many works in the literature concerning
with statistical indicators. The reader is referred
to (Makridakis et al., 2008), (Makridakis and Hi-
bon, 2000) and (Armstrong, 2001) for a complete
overview. Among non-dominated models with re-
spect to in-sample indicators, we selected the model
with minimum MAE concluding the diagnostic check
and, hence, the model selection. Alternative (possi-
bly multi-objective) criteria could be chosen; how-
ever, our choice for the MAE was based on experts’
opinion, as retailers are mostly interested in minimiz-
ing the absolute deviation from actual sales.
5 EXOGENOUS VARIABLES
The main drawback of classical ARIMA models is
the lack of information about the impact of exoge-
nous variables on the time series. In many cases it
may be more realistic to take the impact of external
phenomena into account. In the case study under in-
vestigation, it is easy to understand that sales of fresh
goods are highly influenced by prices and the impact
of the latter on the forecasting process should be con-
sidered. In the literature several approaches can be
found to make forecasting more robust and reliable
including the effect of exogenous variables, in partic-
ular of prices. To this end, we designed two more
sophisticated forecasting models: the first is a gen-
eralization of the classical ARIMA model, while the
second follows a slightly different approach based on
transfer function theory. Both models are flexible and
can be used with any kind of exogenous variable.
5.1 ARIMAX Models
ARIMA model with exogenous variables, also re-
ferred to as ARIMAX, can be defined as follows:
φ
p
(B)Φ
P
(B
s
)∇
d
∇
D
z
t
= θ
q
(B)Θ
Q
(B
s
)a
t
+ βx
t
, (11)
where x
t
is the vector of exogenous variables and β
is the vector of regression coefficients. The latter has
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
422

to be estimated and its initial value is set equal to the
canonical correlation between z
t
(series of sales) and
x
t
(series of prices). According to (Makridakis et al.,
2008), the definition of β as regression coefficient is
not properly correct. Indeed, the ARIMAX can be
restated as
∇
d
∇
D
z
t
=
θ
q
(B)Θ
Q
(B
s
)
φ
p
(B)Φ
P
(B
s
)
a
t
+
β
φ
p
(B)Φ
P
(B
s
)
x
t
, (12)
which clearly points out that the relationship between
z
t
and x
t
is not linear. The authors propose a slight
modification of the previous ARIMAX model, that is
a regression model with ARIMA error in which there
is an explicit linear relation between z
t
and x
t
plus
an error component that is described by an ARIMA
model. More formally
z
t
= βx
t
+ n
t
, (13)
where n
t
is the error vector described by an ARIMA
model. (Makridakis et al., 2008) showed that the fore-
cast quality of a regression model with ARIMA er-
ror (13) is almost comparable with the quality of an
ARIMAX model (11) and the difference between the
two models is not remarkable. Therefore, we imple-
mented an ARIMAX forecast model as it is more sim-
ilar to classical ARIMA model and we believe that a
comparison between ARIMA and ARIMAX models
is more meaningful.
The general framework used to select the best
ARIMAX model reproduces the one described above,
and it is based on the same three phases of model
identification, model estimation and diagnostic check
(see Section 3).
5.2 Transfer Function Models
The third forecasting model we developed is based on
the assumption that the relation between time series
and exogenous variables can be modeled by a trans-
fer function (to be estimated) plus an error vector de-
scribed by an ARIMA model. More formally,
z
t
=
ω(B)B
b
δ(B)
x
t
+ n
t
, (14)
where the transfer function is defined by s poles, r
zeros and a delay b, with
ω(B) = 1 − ω
1
B − ω
2
B
2
.. . − ω
s
B
s
, (15)
δ(B) = 1 − δ
1
B − δ
2
B
2
.. . − δ
r
B
r
, (16)
and the vector of errors n
t
is described by the follow-
ing ARIMA model
φ
p
(B)Φ
P
(B
s
)∇
d
∇
D
n
t
= θ
q
(B)Θ
Q
(B
s
)a
t
. (17)
Unlike the previous two models, in this third one ad-
ditional parameters have to be estimated, namely pa-
rameters s, r and b. The exhaustive approach previ-
ously described for model identification is performed,
thus parameters s, r range in predefined intervals,
while parameter b is estimated according to the max-
imum likelihood principle. In order to perform an in-
sample analysis and choose the best value of unknown
parameters, for each pair (s, r) the simulated time se-
ries ˆz
t
is defined as
ˆz
t
=
ω(B)B
b
δ(B)
x
t
, (18)
The original time series z
t
is compared to ˆz
t
and the
following goodness of fit measure F is computed
F = 100 ·
1 − kz − ˆzk
kz − µk
, (19)
where µ is the average value of z
t
over the training set.
The pair (s,r) providing the best fitting F is selected
and the error vector is computed as n
t
= z
t
− ˆz
t
. The
algorithmic approach used to define the best ARIMA
model for n
t
is the same described in the previous sec-
tion.
Therefore, a transfer function model will be de-
scribed by a tuple (p, d, q) × (P, D,Q)
s
× (s,r,b),
whose values will be identified as discussed so far.
6 EXAMPLES
In this section we compare the three forecasting mod-
els previously described, testing them on a set of real
sales data. All forecasting models are implemented
in Matlab. The out-of-sample indicators are used to
assess the quality of the forecast provided. Note that,
in our implementation, the user is required to specify
store and item, retrieved by a database, along with the
time intervals defining training set and test set, and
what kind of exogenous variables has to be accounted
for.
The first example refers to a common fresh item,
1 liter of milk, considering a training set of 90 days
and a test set of 7 days. Recall that the test set also
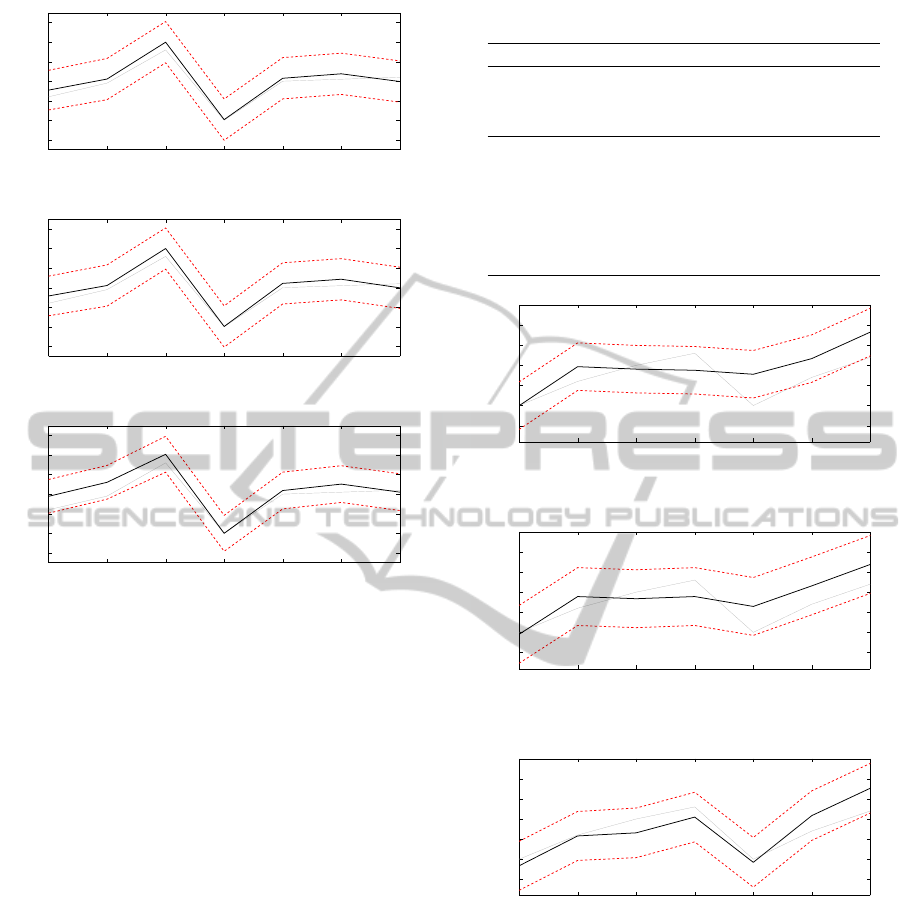
represents the forecasting horizon. In Figures 1, 2
and 3 observed data are depicted with a grey line,
forecasts with a black line and the red dashed lines
represent the 95% confidence interval for the fore-
cast. ARIMA and ARIMAX models provide similar
forecasts, while those based on the transfer function
model deviate more from the actual sales, especially
over the first half of the forecasting horizon.
SalesForecastingModelsintheFreshFoodSupplyChain
423
1075 1076 1077 1078 1079 1080 1081
−10
0
10
20
30
40
50
days
sales
Figure 1: Sales forecast based on ARIMA for milk.
1075 1076 1077 1078 1079 1080 1081
−10
0
10
20
30
40
50
days
sales
Figure 2: Sales forecast based on ARIMAX for milk.
1075 1076 1077 1078 1079 1080 1081
−10
0
10
20
30
40
50
days
sales
Figure 3: Sales forecast based on transfer function model
for milk.
Table 1 compares the performance of the three
forecasting models, the bold values denoting the best
value among the three.
The analysis based on out-of-sample indicators
confirms that ARIMA and ARIMAX models have a
quite similar performance, even though the ARIMA
model seems to be the best performing model accord-
ing to the adopted statistical indicators. Notice that,
for the ARIMA model, a MAPE of 13.48% corre-
sponds to a MAE of 2.31: this means that, on average,
we observe a forecast error of approximately 2 liters
of milk w.r.t. observed sales, with a worst case of less
than 4 liters (MaxAE = 3.94). The transfer function
model does not perform very well and the difference
is remarkable, especially for the MaxAPE.
In the second example we computed the forecast
for another very common fresh product, 250 grams of
mozzarella cheese, on the same training set of 90 days
and test set of 7 days. Comparison plots are reported
in Figures 4, 5 and 6 while Table 2 shows results for
the statistical indicators we computed.
In this case the transfer function model is the
best performing while the forecast quality of ARIMA
and ARIMAX models is almost the same, as already
emerged from the corresponding figures. Again we
notice that a MAPE of 31.92%, which might suggest
Table 1: Out-of-sample analysis for milk.
ARIMA ARIMAX TR FUN
(p, d,q) (0,0, 1) (0,0, 1) (2,0, 0)
(P,D, Q)
s
(1,1, 1)
7
(1,1, 1)
7
(1,1, 1)
7
(s,r,b) - - (2,2, 0)
RMSE 2.57 2.79 4.44
MAE 2.31 2.51 3.62
MaxAE 3.94 4.05 7.06
MAPE 13.48% 14.93% 23.34%
MaxAPE 28.44% 31.24% 57.32%
R
2
93.50% 92.32% 80.64%
840 841 842 843 844 845 846
−5
0
5
10
15
20
25
days
sales
Figure 4: Sales forecast based on ARIMA for mozzarella
cheese.
840 841 842 843 844 845 846
−5
0
5
10
15
20
25
days
sales
Figure 5: Sales forecast based on ARIMAX for mozzarella
cheese.
840 841 842 843 844 845 846
−5
0
5
10
15
20
25
days
sales
Figure 6: Sales forecast based on transfer function model
for mozzarella cheese.
a relatively inaccurate model, corresponds instead to
less than 3 units of products (MAE = 2.59).
Finally, the third example considers 200 grams of
salmon. Plots are showed in Figures 7, 8 and 9, while
the out-of-sample analysis is reported in Table 3.
The transfer function model seems to be the best
model in terms of RMSE, MAE, MaxAE and R
2
, even
though the ARIMAX model performs slightly better
as far as MAPE and MaxAPE are concerned. How-
ever, it is worth noting that, for the ARIMAX model,
smaller percentage errors (in terms of both MAPE
and MaxAPE) still implies higher absolute errors (in
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
424
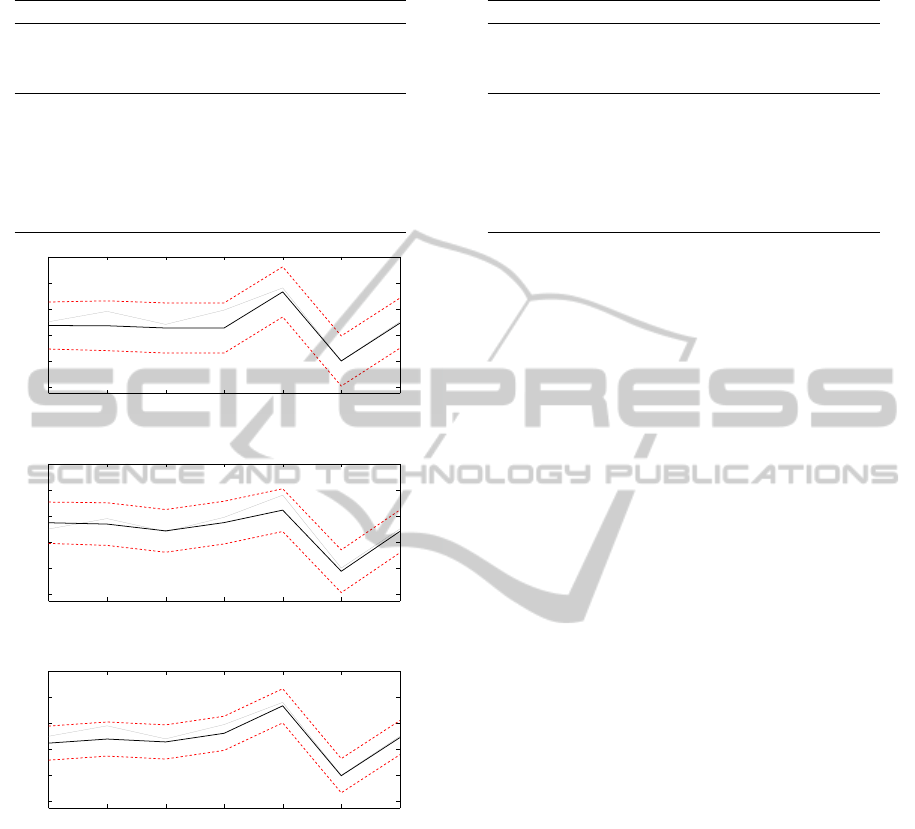
Table 2: Out-of-sample analysis for mozzarella cheese.
ARIMA ARIMAX TR FUN
(p, d,q) (1,1, 2) (0,0, 0) (2,0, 0)
(P,D, Q)
s
(1,1, 1)
7
(1,0, 0)
7
(1,1, 0)
7
(s,r,b) - - (3,2, 0)
RMSE 4.69 4.05 3.13
MAE 3.94 3.58 2.59
MaxAE 7.78 6.45 5.65
MAPE 44.45% 40.46% 31.92%
MaxAPE 66.79% 65.26% 54.90%
R
2
8.82% 32.17% 59.52%
610 611 612 613 614 615 616
−20
0
20
40
60
80
days
sales
Figure 7: Sales forecast of ARIMA for salmon.
610 611 612 613 614 615 616
−20
0
20
40
60
80
days
sales
Figure 8: Sales forecast of ARIMAX for salmon.
610 611 612 613 614 615 616
−20
0
20
40
60
80
days
sales
Figure 9: Sales forecast of transfer function model for
salmon.
terms of MAE and MaxAE). Instead, the opposite oc-
curs for the transfer function model, which suggests
that a single performance indicator may not suffice to
identify the best forecasting model. Nevertheless, in
this case, the ARIMA model is clearly outperformed
by the other two forecasting models.
Summing up these examples, it is evident that
there is no forecasting model clearly outperforming
the others, but the performance strictly depends on the
data set. ARIMAX models either dominate ARIMA
ones or they provide almost comparable results, while
the transfer function appears the most flexible model,
as it can be easily adapted to cope with different ex-
ogenous variables. By an overall analysis, the trans-
Table 3: Out-of-sample analysis for salmon.
ARIMA ARIMAX TR FUN
(p, d,q) (1,0, 0) (1,0, 0) (2,0, 2)
(P,D, Q)
s
(0,1, 1)
7
(1,0, 1)
7
(1,0, 1)
7
(s,r,b) - - (3,2, 0)
RMSE 6.94 5.34 5.21
MAE 4.96 4.21 4.08
MaxAE 13.74 11.51 10.15
MAPE 15.50% 11.05% 13.06%
MaxAPE 35.23% 20.56% 26.70%
R
2
80.24% 88.31% 88.87%
fer function model seems to be the model to prefer in
terms of forecasting accuracy and potentiality.
We now compare our forecasted sales with fore-
casts currently estimated by the management, based
on sales observed in the previous week. Comput-
ing out-of-sample indicators for management’s fore-
casted data for the selected sample products, we no-
tice that adopting rigorous forecasting methods usu-
ally pays off in terms of forecast accuracy. In fact, all
the three proposed forecasting models clearly domi-
nate the actual forecasting system, for both milk and
mozzarella cheese. More specifically, the actual man-
agement forecasting not only shows the worst MAE
(MAE
milk
= 4.14, MAE
mozzarella
= 5.57), but also
performs worse than the proposed models over all the
selected out-of-sample indicators. As for salmon, we
recall that the transfer function model and the ARI-
MAX model showed non-dominated performance in-
dicators; the management forecasts (MAE
salmon
=
4.57) appear worse than those provided by the afore-
mentioned models.
The final aim of this research is to design a deci-
sion support system in which the proposed forecast-
ing models are embedded. In fact, this forecasting
tool will be the basis for an order planning system.
Once real sales data becomes available, it is possible
to compare forecasted and real data, assess the quality
of forecasting and then either keep the current model
or estimate new model parameters. Then, based on
forecasted sales, management takes decisions on the
quantity to order for each item, and the correspond-
ing frequency. A detailed description of the decision
support system goes beyond the scope of this paper.
As a preliminary investigation, we depict poten-
tial implications of adopting our forecasting models
on the order policy, comparing the effects with those
related to the actual management. For instance, we
consider the case of mozzarella cheese, whose shelf
life is 18 days and minimum order quantity is of one
unit. We assume to place a single order at the begin-
ning of the planning horizon, aiming at covering all
the week demand. Sales in the previous week were
SalesForecastingModelsintheFreshFoodSupplyChain
425

67 units; thus, the actual policy would suggest to or-
der the same quantity. Instead, our best forecasting
model predicts sales for 49 units, which determines
the order quantity. The real sales are 48 units; there-
fore, our order proposal would imply a stock reduc-
tion of 18 units.
7 CONCLUSIONS
In this paper we described three different forecasting
models and compared their performances on a real
data set comprised of three year sales for fresh and
highly perishable foods. Due to the short shelf life of
products, accurate sales forecasting is a crucial issue
for supply chain management and optimization.
We developed an ARIMA model and two more
complex models, an ARIMAX model and a transfer
function model, in order to include the effect of ex-
ogenous variables, such as prices, and obtain more
realistic and reliable forecasts. All the models were
selected according to a standard algorithmic frame-
work comprised of three phases: model identification,
model estimation and diagnostic check. We made use
of classical statistical indicators to select the best fore-
casting model. We reported some examples to com-
pare the forecasting quality of the three models. Our
preliminary results show that it is not possible to iden-
tify a model that is clearly the best performing one,
since the forecasting quality strictly depends on the
data set. Nevertheless, the transfer function model
seems to be the most flexible and reliable one. Be-
sides, this model definitely dominates the actual man-
agement forecasting system: this result further sup-
ports the usefulness of adopting rigorous forecasting
methods, rather than relying on management experi-
ence, which might leave specific hidden trends unno-
ticed. Additional benefits are related to order policy
implications, as more accurate forecasts enable to re-
duce potential stock-outs and, even more important
for fresh products, outdating.
Future research may develop along two paths: on
the one side, it may focus on using more sophisticated
tools for model selection, improving forecast accu-
racy by means of non scale-dependent indicators and
considering the impact of other exogenous variables,
e.g. promotion and festivities. On the other side, it
may address the development of an automatic order
planning system, precisely aiming at managing stock-
out and outdating reduction.
ACKNOWLEDGEMENTS
This work was supported by the E-CEDI project,
funded by P.O. Puglia, Asse I FESR 2007-2013 Linea
1.2 – Azione 1.2.4.
REFERENCES
Andrews, B. H., Dean, M. D., Swain, R., and Cole, C.
(2013). Building arima and arimax models for pre-
dicting long-term disability benefit application rates
in the public/private sectors. Technical report, Society
of Actuaries and University of Southern Maine.
Armstrong, J. S. (2001). Principles of Forecasting: A Hand-
book for Researchers and Practitioners. Springer.
Box, G. E. P., Jenkins, G. M., and Reinsel, G. C. (2008).
Time Series Analysis: Forecasting and Control. Wiley,
4th edition.
Burnham, K. P. and Anderson, D. R. (2002). Model
Selection and Multimodel Inference: A Practical
Information-Theoretic Approach. Springer.
H
¨
oglund, R. and
¨
Ostermark, R. (1991). Automatic arima
modelling by the cartesian search algorithm. Journal
of Forecasting, 10(5):465–476.
Hyv
¨
arinen, A. and Oja, E. (2001). Independent Component
Analysis. Wiley.
Jacobs, F. and Chase, R. (2014). Operations and Supply
Chain Management. McGrawHill/Irwin, 14th edition.
Makridakis, S. and Hibon, M. (2000). The m3-competition:
results, conclusions and implications. International
Journal of Forecasting, 16(4):451–476.
Makridakis, S., Wheelwright, S. C., and Hyndman, R. J.
(2008). Forecasting Methods and Applications. Wiley
India Pvt. Limited, 3rd edition.
Najarian, K. and Splinter, R. (2005). Biomedical Signal and
Image Processing. Taylor & Francis.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
426
