
Autonomous Pareto Front Scanning using an Adaptive Multi-Agent
System for Multidisciplinary Optimization
Julien Martin
1
, Jean-Pierre Georg
´
e
1
, Marie-Pierre Gleizes
1
and Micka
¨
el Meunier
2
1
IRIT, University of Toulouse, 118 Route de Narbonne, Toulouse, France
2
SNECMA Villaroche, Rond Point Ren
´
e Ravaud - R
´
eau, 77550 Moissy-Cramayel, France
Keywords:
Pareto Front, Adaptive Multi-Agent System, Multi-Objective Optimization.
Abstract:
Multidisciplinary Design Optimization (MDO) problems can have a unique objective or be multi-objective. In
this paper, we are interested in MDO problems having at least two conflicting objectives. This characteristic
ensures the existence of a set of compromise solutions called Pareto front. We treat those MDO problems
like Multi-Objective Optimization (MOO) problems. Actual MOO methods suffer from certain limitations,
especially the necessity for their users to adjust various parameters. These adjustments can be challenging,
requiring both disciplinary and optimization knowledge. We propose the use of the Adaptive Multi-Agent
Systems technology in order to automatize the Pareto front obtention. ParetOMAS (Pareto Optimization
Multi-Agent System) is designed to scan Pareto fronts efficiently, autonomously or interactively. Evaluations
on several academic and industrial test cases are provided to validate our approach.
1 INTRODUCTION
MDO problems, as their name indicates, intricate sev-
eral disciplines in the same problem, each bringing
into it its own objectives and constraints. It can be, for
instance, the design of a car engine, where we want
to maximize the power (mechanics), while minimiz-
ing the noise (acoustics). Let us call this problem p1.
MDO problems that have at least two contradictory
objectives possibly admit an infinity of solutions, each
solution being a compromise in the objective search
space. This is the case of p1, illustrated in Figure 1.
A and C are extrema solutions. Solution point A rep-
resents the most silent engine possible but also the
least powerful. On the contrary, C represents the most
powerful but also the most noisy. The set of points be-
tween them are compromises of these two objectives,
such as point B.
A
B
C
Engine power
Engine noise
Pareto Front
D
Figure 1: Illustration of the p1 problem.
In general, obtaining the complete set of these so-
lutions is costly in MOO (Multi-Objective optimiza-
tion) (Dr
´
eo et al., 2006; Talbi, 2009) as it is neces-
sary to discover and filter, among a cloud of solutions,
those that are part of the Pareto front. There is a real
need in the industry for methods enabling to reduce
the cost of these calculations. Automatically obtain-
ing this set of solutions in an efficient way is the sci-
entific challenge of our study.
1.1 MOO Problem Formulation
A MOO problem is written under the following form:
Minimize f (x) = ( f
1
(x),... , f
p
(x))
Subject to g
i
(x) ≤ 0,i = 1, .. ., m
(1)
A MOO problem is constitued by variables, a
number p of objective functions f (p ≥ 2) and a num-
ber m of constraint functions g. Any of these func-
tions can be non linear, eventually everyone (Hwang
et al., 1979). The objectives can be dependent or in-
dependent, and are often difficult to compare (a cost
and a duration for instance).
263
Martin J., Georgé J., Gleizes M. and Meunier M..
Autonomous Pareto Front Scanning using an Adaptive Multi-Agent System for Multidisciplinary Optimization.
DOI: 10.5220/0005293302630271
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 263-271
ISBN: 978-989-758-073-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

1.2 Pareto Optimality
Pareto Dominance and Pareto Optimality are two
Pareto key concepts (Ben-Tal, 1980). We present
them in definition 1 and 2 below, using the same for-
mulation as in equation 1 :
Definition 1 (Pareto Dominance). Let us consider a
MOO problem with p minimization objectives. Let
u=(u
1
,. . . ,u
p
) and v=(v
1
,. . . ,v
p
) be two vectors of the
values of the objectives for two different solutions. It
is said that u dominates v in the sense of Pareto when
and only when
∀i ∈ {1,..., p}, u
i
≤ v
i
∧∃j ∈ {1,..., p} : u
j
< v
j
The solution point v is dominated by u as there
is no objective for which v is better. If we refer to
problem p1 illustrated in Figure 1, B dominated D.
The solution point D represents an engine both more
noisy and less powerful than the solution point B.
Definition 2 (Pareto Optimality). A solution x
u
is said
to be Pareto optimal if and only of there is no solution
x
v
for which
v = f (x
v
) = (v
1
,..., v
p
)
dominates u = f (x
u
) = (u
1
,..., u
p
)
As can be seen again in problem p1 in Figure 1,
D is not a Pareto optimal solution, as it is dominated
by B for instance. The set of Pareto optimal solutions
are the non dominated solutions (Horn, 1997). Graph-
ically, in the objective space, this set forms the Pareto
front.
The following section (2) discusses existing MOO
problem solving methods. The Adaptive Multi-Agent
System dedicated to the autonomous scanning of the
Pareto front is described in section 3 and the results in
section 4. Finally, section 5 presents ongoing work.
2 EXISTING METHODS
There is a huge diversity of methods for treating MOO
problems. In this part, we will present the two most
used groups of methods, namely the ”classical” meth-
ods and the ”intelligent” methods. After a rapid anal-
ysis of their strengths and weaknesses, we will justify
the use of an Adaptive Multi-Agent System to solve
these kind of problems.
2.1 Classical Methods
Classical methods concentrate on the transformation
of the MOO problem in a mono-objective problem,
so as to be able to use a mono-objective solver.
The Weighted Sum Method. The weighted sum
method transforms a MOO problem into an mono-
objective problem by attributing a weight w
j
for each
objective function, summing everything and mini-
mizing it with a mono-objective solver. The chosen
weights represent the relative importance for each ob-
jective f
j
in obtaining the solution (Tabucanon, 1988).
Minimize Z =
p
∑
j=1
w
j
f
j
(~x)
with w
j
≥ 0 and
p
∑
j=1
w
j
= 1
(2)
To find Pareto optimal solutions using this
method, the user needs to choose a set of weights,
find the first solution, modify the weights, relaunch
the mono-objective solving and so on. Without ex-
pert knowledge of the problem, the choice of these
weights w
j
can be quite hard. Moreover, if some ob-
jective functions are non linear, a modification of a
weights does not guarantee a different solution. It
is also impossible to find solution points in the con-
cave zones of the front with this method (Kim and
de Weck, 2005). Finally, it is hard to control the repar-
tition diversity of the solution points in the objective
space (Tabucanon, 1988; Coello, 1999). Work to en-
hance this method has been proposed (Jin et al., 2001;
Kim and de Weck, 2005). Nevertheless, specific pa-
rameters of these algorithms need to be correctly ini-
tialised to obtain satisfactory results.
There are others classical approaches such as the
ε-Constraint Method, the Benson method (Benson,
1978), goal-programming (Charnes and Cooper,
1977), interactive methods such as iMOODs (Tappeta
et al., 2002) and NIMBUS (Kaisa Miettinen, 2000). . .
These approaches show their limits as soon as the
user wants to extract the Pareto optimal solutions in
their entirety. The majority of them can at best find
a unique Pareto optimal solution point for each exe-
cution. To find several, the algorithm needs to be ex-
ecuted several times, without any guarantee concern-
ing the diversity of the points in regard to the objec-
tive space. Some of these approaches are incapable of
finding solutions in the zones where the Pareto front
is non convex, as is the case for the weighted sum
method. Some research was done to fix this (Kim
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
264

and de Weck, 2005), but only for problems with two
objectives, the scaling up still needs to be demon-
strated. All these approaches require user informa-
tions, on which depend the quality of the solutions.
The choice of these informations is generally difficult
and requires from the user expert knowledge on the
application domain or the algorithm, or even both.
The intelligent approaches appeared to tackle
these problems. They are part of the a posteriori ap-
proaches, for which the user intervenes afterwards the
solving to choose the solution point.
2.2 The Intelligent Methods
Contrary to the classical approaches, these methods
try to generate the Pareto front by considering each
objective as it is. One of the advantages over classical
methods is that they manage to evaluate several solu-
tions at each iteration. Moreover, they bring a greater
ease of use, particularly when no a priori knowledge
is available. The evolutionary methods are part of
the intelligent methods (Deb, 2001). They simulate
a biological process of evolution in a population
of candidate solutions so as to guide them towards
the Pareto front. These solutions are subjected to
mutation and crossing operations, producing a new
generation of solutions at each iteration, and only
a set of the best are kept during execution. The
difficulty is to manage to guide them towards the
front while guaranteeing the repartition diversity on
the whole front. The evolutionary methods regroup
genetic algorithms, evolutionary algorithms, as well
as evolution strategies. These three categories differ
on the way the solutions are evaluated as well as on
the mutation and crossing operators they use.
Non-Dominated Sorting Genetic Algorithm.
NSGA is a genetic algorithm based on the idea
proposed by Goldberg to sort the solutions by their
dominance ranking in the Pareto sense (Goldberg
et al., 1989). Srinivas and Deb used Goldberg’s work
and implemented NSGA (Srinivas and Deb, 1994)
so as to use the non dominance rank to evaluate the
quality of the solutions. The less there exists solu-
tions dominating s1 among the candidate population,
the more favourably s1 is evaluated.
In a second time, NSGA will diminish the score of
the solutions depending of the number of other solu-
tions in their neighborhood. This choice from Srini-
vas and Deb is related to the work of Goldberg and
Richardson (Goldberg and Richardson, 1987) who
proposed to degrade the score of similar solutions
rather than merge them, in order to ensure the reparti-
tion diversity of the solutions. The user has to choose
the parameters for calculating the neighborhood. It
has been shown that the performances of NSGA are
impacted by this choice (Srinivas and Deb, 1994).
These methods require, as with the classical meth-
ods, to fix specific parameters required for the func-
tioning (neighborhood, but also population size, se-
lection, mutation and crossover rates, etc.). More-
over, calculation costs increase enormously with the
increase in the number of objectives and population
size.
The aim of the use of an Adaptive Multi-Agent
System to obtain the Pareto front is to remove the
need for algorithm parameters, these systems being
able to learn during the solving. Moreover, the Adap-
tive Multi-Agent System, by cooperating with an un-
derlying solver having a set of specific characteristics,
is able to move along the Pareto front and scan for
new solutions in an autonomous and efficient way.
3 THE ParetOMAS SYSTEM
3.1 The Adaptive Multi-Agent System
Theory
The Adaptive Multi-Agent System theory (Capera
et al., 2003) addresses the problematic of complex
systems with a bottom-up approach where the con-
cept of cooperation is the core of selforganisation. A
general definition of cooperation could be the golden
mean between altruism and selfishness (Picard and
Glize, 2005). To stay in a cooperative state, three
mechanisms can be used (Capera et al., 2005):
• tuning: the agent adjusts its internal state to mod-
ify its behaviour,
• reorganisation: the agent modifies the way it in-
teracts with its neighborhood,
• evolution: the agent can create other agents or
selfsuppress when there is no other agent to pro-
duce a functionality or when a functionality is
useless.
The system will self-organise its activity to stay in
a cooperative state. From cooperative interactions be-
tween the system’s entities emerges a global function
that is more than the sum of the parts. This theory is
here applied to MOO to scan Pareto fronts.
3.2 ParetOMAS
The algorithm scanning the Pareto front is consti-
tuted by an Adaptive Multi-Agent System we call
AutonomousParetoFrontScanningusinganAdaptiveMulti-AgentSystemforMultidisciplinaryOptimization
265

ParetOMAS (Pareto Optimization Multi-Agent Sys-
tem). This system makes use of an underlying mono-
solution solver
1
and works with it so as to automat-
ically build the Pareto front of any given problem,
without the need of human intervention (but allowing
interaction if convenient).
Graphical tools have been developed so as to vi-
sualize the Pareto front building as it is occurring in
the objective space. ParetOMAS allows interaction:
the user can at any time request a search direction for
the following solutions. The user can also modify its
preferences concerning solution precision as well as
solution spacing. ParetOMAS is able to take into ac-
count these changes during execution.
As a result, the underlying solver needs to satisfy
specific criteria:
• being able to signal that it has converged under a
given precision,
• being able to bestow more or less importance to
objectives during the solving,
• being able to accept the modification of the de-
scription of a problem, for instance the transfor-
mation of a minimization in a maximization ob-
jective, during solving.
During the ID4CS
2
project, a mono-solution
Adaptive Multi-Agent System solver has been devel-
oped (Jorquera et al., 2013). It constitutes a solver
compatible with ParetOMAS and will be used to ob-
tain the results presented in section 4.
The role of ParetOMAS is to efficiently orient the
search of new solution points in the objective space,
so as to obtain a solution set constituting the Pareto
front, in accord with the preferences of the user con-
cerning precision, distribution, number of points, etc.
The solver finds a solution point, ParetOMAS detects
this and sends a new request to the solver so that
it can find a new solution point. The coupled sys-
tem {ParetOMAS, solver} constitutes a new adaptive
multi-solution solver. ParetOMAS is composed of
two types of agents: a ParetoGuide agent and Pare-
toSolutions agents. The user has access to a dedi-
cated interface to input its preferences (distance be-
tween solution points, choice of a search direction
. . . ). Their interactions are described in Figure 2. The
two following sub-sections present the roles of these
two agent types, and describe their behavior, interac-
tions and life-cycle.
1
Solver that provides a unique solution, in opposition to
a solver that provides a set of solutions
2
Integrative Design for Complex Systems - www.irit.fr/
id4cs
3.2.1 The ParetoGuide Agent
The ParetoGuide agent constitutes an interaction hub
between the user, the solver and the ParetoSolution
agent. There is only one ParetoGuide per instance of
ParetOMAS. Its role is to take into account the pref-
erences of the user and those of the ParetoSolution
agents during execution. Its nominal behaviour is de-
scribed by the algorithm 1. Each time a solution point
is found by the solver, ParetoGuide creates a Pare-
toSolution agent representing this new point.
The user and the ParetoSolutions agents can in-
form the ParetoGuide of a preferred direction for the
scanning of the front, in the objective search space. If
the user is making a choice, ParetoGuide ignores the
requests from the ParetoSolutions agents and takes
into account the one from the user. If this is the case
but there is an impossibility (boundaries of the pro-
blem for instance), ParetoGuide then defaults on the
preferences of the ParetoSolution agents while sig-
nalling to the user why it could not comply. In any
case, ParetoGuide then sends a corresponding request
to the solver so that it is able to find a new solution in
the chosen direction. This behaviour is illustrated in
Figure 2.
if Solver has found a solution then
Creation of a ParetoSolution agent;
if User is forcing a direction then
Send a request to the solver favouring
this direction;
else
Inquire of direction preferences from
the ParetoSolution agents;
Send a request to the solver favouring
this direction;
end
end
Algorithm 1: Nominal behaviour of the ParetoGuide
agent.
3.2.2 The ParetoSolution Agents
The role of the ParetoSolution agents is to orient the
ParetoGuide in the objective space so as to obtain
an efficient scanning and a relevant resulting front.
These agents are created dynamically by ParetoGuide
as described previously. Each ParetoSolution agent
possesses, in the objective space, a neighborhood of
other ParetoSolution agents. This neighborhood is
defined, for each ParetoSolution agent, by the set of
ParetoSolution agents being located at or under an eu-
clidean distance d, defined by the user (as it will rep-
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
266

Agent
Pareto Solution A
notifications
preferences
observation
interactions
User
Agent
Pareto Guide
Solver
preferences
ParetOMAS
A
B
C
Objective 1
Objective 2
direction
Agent
Pareto Solution B
Agent
Pareto Solution C
Figure 2: ParetOMAS during execution, three solutions points have been found.
resent the structure of the front at the end)
3
.
A ParetoSolution agent sends requests to Pare-
toGuide so as to obtain a neighborhood that satisfies
it. This is translated by ParetoGuide into a direction
in which to scan the objective space. The user, by
diminishing d, increases the sampling of the Pareto
front, and the other way round. d can be modified
any time during execution. A ParetoSolution agent
can also send a request to be ”shifted” in the objective
space so as to enhance the homogeneity of the sam-
pling (if the user wants a perfect ”grid” as a Pareto
plan for instance).
Informations given to a ParetoSolution agent
when it is created:
• its coordinates in the objective space,
• the state of the corresponding input variables,
• the objective values initially aimed,
• the calculation time needed to obtain this solution,
• its neighborhood of ParetoSolution agents,
• the calculation time of the neighborhood.
Each time a new ParetoSolution agent is created,
it notifies the agents situated in its neighborhood for
them to update their knowledge. It then adopts a nom-
inal behaviour as described in algorithm 2.
if Unsatisfactory neighborhood then
Send a request to ParetoGuide for a chosen
search direction;
else if Non homogeneous placement then
Send a request to ParetoGuide for a chosen
shift direction
end
Algorithm 2: Nominal behaviour of the ParetoSolution
agents.
3
It can be noted that contrary to the evolutionary meth-
ods, this distance has no direct impact on the solving, only
on the end result
4 IMPLEMENTATION AND
FEASIBILITY PROOF
ParetOMAS is currently in a prototype state. The user
is provided with a temporary graphical interface for
him to input its preferences, such as the distance be-
tween solution points and optional search direction
preferences. The Pareto front scanning is observable
in real time for problem with two or three objectives.
ParetOMAS has been tested on continuous and dis-
continuous Pareto fronts.
4.1 Continuous Pareto Front
TurboFan. This test case is provided by Snecma
4
as
a study case. The goal is to optimise output parame-
ters of a classic double flux turbo-reactor (civil plane
engine). The two output parameters to optimise are
the consumption s which needs to be minimized and
the thrust T dm0 which needs to be maximized, both
being contradictory. The two input variables are the
dilution rate bpr and the pressure ratio pi
c
. The dilu-
tion rate represents the ratio between the air volume
aspirated by the blower and the air volume reaching
the low pressure compressor. The pressure ratio is the
ration between the pressure produced by the compres-
sors and the initial pressure of the environment. bpr
and pi
c
each have their validity range and we want to
obtain all the couples of compromise solutions.
The results obtained by ParetOMAS are seen in
Figure 3. The space between the solution points can
be chosen by the user and an arbitrary value has been
used here. This problem is well known by Snecma
and the documentation indicates that all the Pareto
front points have in fact as a corresponding input
value the variable pi
c
at 40, and any value of bpr then
4
www.snecma.com
AutonomousParetoFrontScanningusinganAdaptiveMulti-AgentSystemforMultidisciplinaryOptimization
267

gives a Pareto optimal solution. This is verified by the
solution found by ParetOMAS. Figure 4 superposes
these solutions with a graphical representation of the
front obtained by exhaustive calculation (fixing pi
c
at
40 and adjusting bpr over its complete range).
Figure 3: The set of solutions proposed by ParetOMAS for
the TurboFan problem.
Figure 4: Superposition of the real Pareto front with the
points obtained by ParetOMAS on the TurboFan problem.
4.2 Discontinuous Pareto Front
The two following test cases present a discontinuous
Pareto front. This induces a risk that the solver used
by ParetOMAS stops in a local minimum. This situ-
ation requires a secondary behaviour for ParetoGuide
enabling it to guide the solver out of a local minima.
This exploration mechanism will be explained and re-
sults will be shown for a problem with two objectives
and one with three objectives.
4.2.1 A Problem with Two Objectives
This problem has been artificially generated to con-
front ParetOMAS to two contradictory objectives
with a discontinuous Pareto front. The problem is
constituted by a unique calculation model that de-
scribes the topology of the front. This model has two
input variables x and y, and two output variables X
and Y that require minimization:
X = x
Y =
1
x
+
30
50(x−.2)(x−.2)+1
+
20
40(x−.6)(x−.6)+1
+ y
2
The output Y is the sum of 4 functions:
• h(x) =
1
x
• k(x) =
30
50(x−.2)(x−.2)+1
• t(x) =
20
40(x−.6)(x−.6)+1
• w(x) = y
2
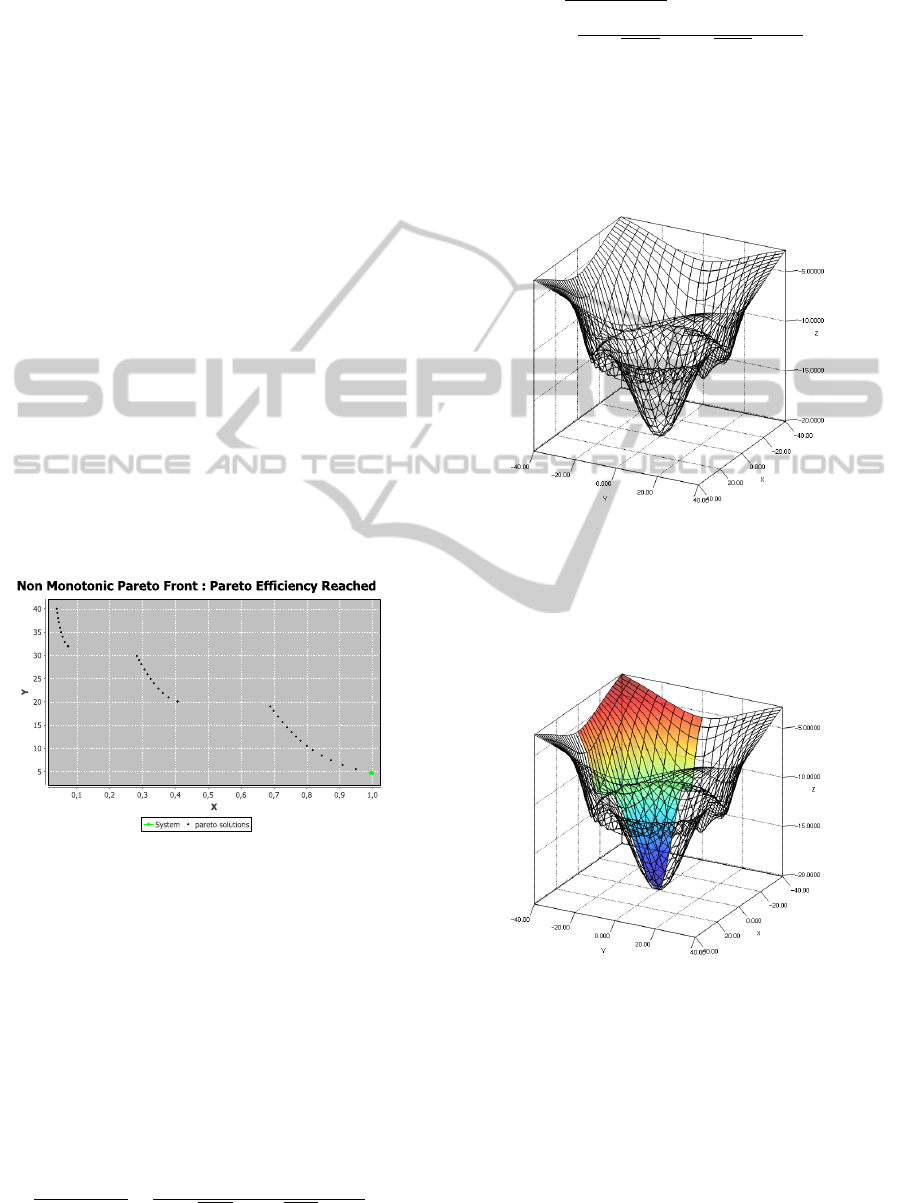
The sum of h, k and t results in a non-monotonous
function, illustrated Figure 5, which admits 2 local
minima, A and B. Finaly, function w is added to make
the search space above h(x) + k(x) + t(x) admissible.
The Pareto optimal solutions of this problem are situ-
ated on the curve described by h(x) + k(x) + t(x).
A
B
A'
B'
C
D
Figure 5: X = x and Y = h(x) + k(x) +t(x).
Figure 6 shows the solutions obtained by Pare-
tOMAS. Initial values of the input variables have been
chosen such that the first discovered solution point
is C on Figure 5. The objective Y is favoured com-
pared to objective X, thus the scanning direction goes
from left to right. ParetOMAS discovers the solutions
between points C and A. When it arrives at A, the
solver is blocked in a local minimum: it is not pos-
sible, locally, to improve Y by following the curve.
ParetOMAS, by a decision of ParetoGuide commutes
to an exploration mode to extract the system from the
local minimum. For this ParetoGuide temporarily re-
defines the problem:
• recording of the value of the objective that was
initially favoured,
• inversion of the nature of the other objective (mi-
nimization becomes maximization, and the other
way round),
• inversion of the favouring of objectives,
• surveillance of the evolution each new point cal-
culated by the solver so as to detect the moment
when the value of the objective that was initially
favoured becomes better than the value recorded
before exploration,
• reformulation back to the initial problem.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
268
This is how it is translated when the system ar-
rives at point A. The favoured objective is Y , Pare-
toGuide records its value (31.55). X and Y have both
minimization objectives. The objective on X becomes
a maximization objective and becomes the favoured
objective. The minimization objective on Y , while
not favoured compared to X, is still maintained so
that the solver, by taking it into account, tends to-
wards the curve. The problem is temporarily trans-
formed and has a unique solution at point D. Visu-
ally, we can see that the current working point moves
from A to A’ while staying stuck to the curve. When
this point oversteps A’, ParetoGuide detects that the
value of Y becomes better than when it was at point
A and switches back to the initial formulation of the
problem. The objective on X becomes a minimiza-
tion objective again and the objective on Y is favoured
again for the solving. ParetOMAS then discovers the
solutions between A’ and B, and is blocked again in
a local minimum. Commuting again in exploration
mode, it finds the solutions between B’ and D.
The solutions discovered by ParetOMAS are visi-
ble on Figure 6. For each point proposed, we can ver-
ify that input variable y is equal to zero, which shows
that the point is indeed on the front and by comparing
Y that it is a Pareto optimal solution.
Figure 6: Solutions obtained on the non-monotonous pro-
blem with two objectives.
4.2.2 A Problem with Three Objectives
This problem has been artificially generated in the
same spirit as the previous. But this time there are
three objectives, the front is a surface. The problem
has a unique calculation model responsible for the
topology of the front, takes three input variables x,
y and z, as well as three output variables X, Y and Z
requiring minimization:
X = x
Y = y
Z =
−20
0.002(x
2
+y
2
)+1
−
5
0.05(
√
x
2
+y
2
−30)(
√
x
2
+y
2
−30)+1
+ z
2
output Z is the sum of three functions:
• q(x, y) =
−20
0.002(x
2
+y
2
)+1
• r(x,y) = −
5
0.05
√
x
2
+y
2
−30)(
√
x
2
+y
2
−30)+1
• c(z) = z
2
q(x,y) + r(x,y) is visible on Figure 7. Those two
functions have been chosen so as to create a sort of
basin with an infinity of local minima, enabling the
testing of the exploration mode on a three objectives
problem.
Figure 7: q(x,y) + r(x, y).
Function c is added to make the search space
above q(x,y) + r(x, y) admissible. The Pareto optimal
solutions of this problem are illustrated Figure 8 : it
is the colored region of the surface.
Figure 8: Pareto optimal solutions.
The solutions discovered by ParetOMAS are visi-
ble on Figure 9. For each point proposed, we can ver-
ify that input variable z is equal to zero, which shows
that the point is indeed on the Pareto front.
4.3 Results Analysis
In this section, we are going to discuss the impact
of the input variables precision p and the distance d
AutonomousParetoFrontScanningusinganAdaptiveMulti-AgentSystemforMultidisciplinaryOptimization
269
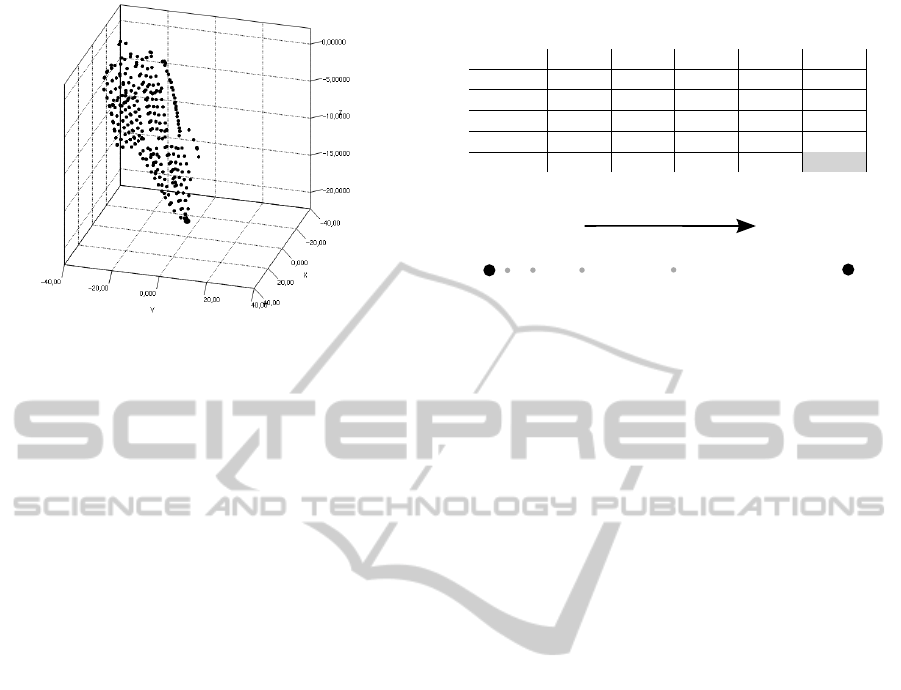
Figure 9: Solutions obtained on the three objectives pro-
blem.
between solution points on the functioning of Pare-
tOMAS.
The input variables precision p represents the
smallest value change that input variables can make.
Thus, dividing the precision by 10 induces a signif-
icant change, both in the optimization process and
the quality of the solutions. d is the distance in
the objective search space requiered by the user that
ParetOMAS needs to achieve between each adjacent
Pareto solution.
ParetOMAS sends requests to the ID4CS solver in
order to find Pareto solutions. Each of those requests
produce the calculation of an intermediate point by
ID4CS in the objective search space.
Table 1 shows, for different pairs of precision p
and distance d, the average number of intermediate
points that have been produced by the ID4CS solver
in order to get a new Pareto solution, satisfying the
distance and precision requierements. Those results
are from the TurboFan problem (section 4.1). For the
pair p=10
-3
and d=0.0625, the input variables preci-
sion is insufficient to obtain points this close in the
objective search space.
Distance Analysis: it can be seen that the average
number of intermediate points doesn’t change much
in regard with the distance d. This can be explained
by the fact that ID4CS use Adaptive Value Track-
ers (Yildirim and G
¨
urcan, 2014) for its input vari-
ables. This allows acceleration in the objective search
space, reducing evaluation cost. This acceleration is
illustrated on Figure 10. We can see that the interme-
diate calculated points are more and more spaced.
Precision Analysis: the average number of interme-
diate points increases when the precision parameter
p is small, which is normal. When the distance d is
reached, ParetOMAS asks ID4CS to stabilize on the
Pareto front. There is a decelaration in the objective
Table 1: Average number of intermediate points produced
by the solver to get a (p, d)-satisfying Pareto solution.
p=10
-7
p=10
-6
p=10
-5
p=10
-4
p=10
-3
d=16 31 28 23 20 14
d=4 29 24 21 17 12
d=1 27 22 18 14 9
d=0.25 24 20 16 12 6
d=0.0625 22 17 13 9 p ins.
Pareto
solution n
Pareto
solution n+1
search direction
intermediate calculated points
Figure 10: Acceleration in the objective search space.
search space, which is due to the functionnning of the
Adaptive Value Trackers. This deceleration is not im-
mediate : the smaller p, the bigger the average num-
ber of intermediate calcul points it takes to stabilize.
ID4CS is also an Adaptive Multi-Agent System,
and ParetOMAS doesn’t control it. Those two Adap-
tive Multi-Agent Systems cooperate in order to obtain
the Pareto front. Each point computed by ID4CS in-
duces an answer from ParetOMAS in order to find the
next Pareto solution located at a distance d from the
previous one.
5 ONGOING WORKS
ParetoGuide Behavior Refinement. The ParetoGu-
ide behavior is continuously updated in order to opti-
mize its operation with the ID4CS solver. The most
challenging part of this work is the translation of the
user and ParetoSolutions directions preferences into
something understandable by ID4CS.
ParetoSolution Agents. The behavior described in
subsection 3.2.2 is not totally implemented. Those
agents don’t use all the informations they have and
so are currently suboptimal. The precision toward
the prefered directions they send to ParetoGuide will
improve with their refinement, making ParetOMAS
more effective.
Problems Generator. In order to validate our ap-
proach, a problems generator is developed. The ob-
jective is to be able to automatically generate a great
number of problems having various topologies. A
metrics system allowing the automatic evaluation of
the obtained solutions is also developed.
Academic Benchmarks Comparison. We are re-
viewing academic benchmarks in order to compare
our approach with other optimization methods.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
270

Real-world Industrial Problems. ParetOMAS will
be tested on real-world industrial problems with
SNECMA problems. This will validate the scalabil-
ity of ParetOMAS with problems having 4 or more
objectives.
ACKNOWLEDGEMENTS
We want to thank Snecma and the french National
Association for Research and Technology for funding
this work.
REFERENCES
Ben-Tal, A. (1980). Characterization of pareto and lexi-
cographic optimal solutions. In Fandel, G. and Gal,
T., editors, Multiple Criteria Decision Making The-
ory and Application, volume 177 of Lecture Notes in
Economics and Mathematical Systems, pages 1–11.
Springer Berlin Heidelberg.
Benson, H. (1978). Existence of efficient solutions for vec-
tor maximization problems. Journal of Optimization
Theory and Applications, 26(4):569–580.
Capera, D., Fanchon, J., Georg
´
e, J.-P., and Camps, V.
(2005). A generic model based on automata for multi-
agent systems. In EUMAS, pages 79–90.
Capera, D., Georg
´
e, J., Gleizes, M.-P., and Glize, P. (2003).
The amas theory for complex problem solving based
on self-organizing cooperative agents. In Enabling
Technologies: Infrastructure for Collaborative Enter-
prises, 2003. WET ICE 2003. Proceedings. Twelfth
IEEE International Workshops on, pages 383–388.
Charnes, A. and Cooper, W. (1977). Goal programming and
multiple objective optimizations: Part 1. European
Journal of Operational Research, 1(1):39 – 54.
Coello, C. A. C. (1999). A comprehensive survey
of evolutionary-based multiobjective optimization
techniques. Knowledge and Information systems,
1(3):269–308.
Deb, K. (2001). Multi-objective optimization using evolu-
tionary algorithms, volume 16. John Wiley & Sons.
Dr
´
eo, J., P
´
etrowski, A., Siarry, P., and Taillard, E. (2006).
Metaheuristics for Hard Optimization: Methods and
Case Studies. Springer.
Goldberg, D. E. et al. (1989). Genetic algorithms in
search, optimization, and machine learning, volume
412. Addison-wesley Reading Menlo Park.
Goldberg, D. E. and Richardson, J. (1987). Genetic algo-
rithms with sharing for multimodal function optimiza-
tion. In Genetic algorithms and their applications:
Proceedings of the Second International Conference
on Genetic Algorithms, pages 41–49. Hillsdale, NJ:
Lawrence Erlbaum.
Horn, J. (1997). Multicriterion decision making. In Back,
T., Fogel, D. B., and Michalewicz, Z., editors, Hand-
book of Evolutionary Computation. IOP Publishing
Ltd., Bristol, UK, UK, 1st edition.
Hwang, C. L., Masud, A. S. M., et al. (1979). Multiple
objective decision making-methods and applications,
volume 164. Springer.
Jin, Y., Olhofer, M., and Sendhoff, B. (2001). Dynamic
weighted aggregation for evolutionary multi-objective
optimization: Why does it work and how?
Jorquera, T., Georg
´
e, J.-P., Gleizes, M.-P., and R
´
egis, C.
(2013). A Natural Formalism and a MultiAgent Al-
gorithm for Integrative Multidisciplinary Design Op-
timization (regular paper). In IEEE/WIC/ACM Inter-
national Conference on Intelligent Agent Technology
(IAT), Atlanta, USA, 17/11/2013-20/11/2013. IEEE
Computer Society.
Kaisa Miettinen, M. M. M. (2000). Interactive multiob-
jective optimization system www-nimbus on the in-
ternet. Computers and Operations Research, 27(7-
8):709–723.
Kim, I. and de Weck, O. (2005). Adaptive weighted-sum
method for bi-objective optimization: Pareto front
generation. Structural and Multidisciplinary Opti-
mization, 29(2):149–158.
Picard, G. and Glize, P. (2005). Model and experiments of
local decision based on cooperative self-organization.
In IICAI, pages 3009–3024.
Srinivas, N. and Deb, K. (1994). Multiobjective opti-
mization using nondominated sorting in genetic algo-
rithms. Evolutionary computation, 2(3):221–248.
Tabucanon, M. T. (1988). Multiple criteria decision making
in industry. Elsevier Amsterdam.
Talbi, E.-G. (2009). Metaheuristics - From Design to Im-
plementation. Wiley.
Tappeta, R., Renaud, J., and Rodr
´
ıguez, J. (2002). An inter-
active multiobjective optimization design strategy for
decision based multidisciplinary design. Engineering
Optimization, 34(5):523–544.
Yildirim, K. S. and G
¨
urcan,
¨
O. (2014). Adaptive synchro-
nization of robotic sensor networks. In International
Workshop on Robotic Sensor Networks, part of Cyber-
Physical Systems Week.
AutonomousParetoFrontScanningusinganAdaptiveMulti-AgentSystemforMultidisciplinaryOptimization
271
