Protecting Informative Messages over Burst Error Channels in

Chain-based Wireless Sensor Networks

Zahra Taghikhaki, Nirvana Meratnia and Paul Havinga

Pervasive System Group, University of Twente, Enschede, The Netherlands

Keywords: Wireless sensor networks, Reliability, Information-value, Adaptive error control, Information-aware, FEC.

Abstract: Regardless of the application, the way that data and information are disseminated is an important aspect in

Wireless Sensor Networks (WSNs). The wireless data dissemination protocol should often guarantee a

minimum reliability requirement. In this regard and to well-balance the energy and reliability, the more

important packets should be protected by more powerful error control codes than the less important ones.

This information-aware capability allows a system to deliver critical information with high reliability but

potentially at a higher resource cost. In this paper, we first find and evaluate the factors that may influence

the importance level of a packet and then design an error control approach by adaptively selecting codes for

each individual links which experience long-term-fading and for each individual packet at run-time instead

of applying network-wide settings prior to deployment. Moreover, we target the poor-explored chain-based

topology that is of interest for many applications (e.g. monitoring bridge, tunnel, etc.). Simulation results

validate the superiority of our approach compared with a number of Reed-Solomon-based error control

approaches.

1 INTRODUCTION

Adhering to the packet-level or data constraints

while designing a data disseminating protocol for

WSNs may improve the system performance.

Most telecommunication systems use a fixed

channel code to tolerate the expected worst-case

error rate, which implies that they fail to operate at

all if the error rate is worsened. The wireless channel

is typically time varying and can exhibit high error

rate over time. In order to improve the reliability of

the data which is transmitted in WSNs, the error

control approaches such as ARQ and FEC can be

applied. Putting their advantages aside, existing

error control techniques contribute to increase of the

energy consumption due to the redundant data to be

transmitted. Since energy is a scarce resource in

WSNs, the type and the strength of the error control

in use should be dependent on the type of the

application. Generally speaking, event detection

applications of WSNs need to execute more efficient

and powerful error control techniques compared

with periodic monitoring applications. However, the

distinction between different packet type as being

transmitted in these two classes of applications

(periodic data and alarm) is neither general enough

nor captures some important cases (e.g. the effect of

channel condition or aggregation function) in WSNs.

Therefore, even within a specific class of

application, it would not be a proper to use a single

error control code for all packets regardless of their

different channel conditions or importance of

information they carry. It is quite likely that even

two packets both of which carry periodic monitoring

data, not have the same amount of information and

importance. For example, in a chain-based WSN

data aggregation mechanisms are often used along

the path with the aim of reducing the number of

transmitted packets. Therefore, some packets may

contain the aggregated readings of many nodes.

These packets thus should be sent more reliably as

they carry more informational value. It would be

therefore a good idea to classify packets on the basis

of their information-value based on which a proper

error control scheme can be applied. By doing so,

more important packets that have relatively high

information-value are transmitted more reliably than

packets carrying less important information. This is

to well-balance the energy expenditure (caused by

data and parity packets) and reliability. It is worth

mentioning that by information-value we mean the

amount of information a packet may have for the

base station. Having dynamics of WSN into mind,

130

Taghikhaki Z., Meratnia N. and Havinga P..

Protecting Informative Messages over Burst Error Channels in Chain-based Wireless Sensor Networks.

DOI: 10.5220/0005294601300141

In Proceedings of the 4th International Conference on Sensor Networks (SENSORNETS-2015), pages 130-141

ISBN: 978-989-758-086-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

adopting an efficient and accurate network-wide

error control approach prior to network deployment

is almost impossible. A very weak error control

approach may not be able to correct many errors

while a too strong code results in waste of time and

energy resources. Dynamic error control schemes

which are allocating the correctional power in an on-

demand manner based on both the information-value

and channel state are viable alternatives to static

error control schemes, where the link conditions or

packets’ information-values are not taken into

account. In this way and for the sake of efficiency,

the information-value of a packet can be put into

perspective with the amount of effort (in terms of

energy expenditure) that is required to reliably

transmit the given packet. Furthermore, since the

wireless channel is inherently lossy and often

manifests itself with bursts errors correlated in time,

a reliable data dissemination should be capable of

counteracting a large number of consecutive or burst

errors. Since the application of run-time

information-aware adaptive error control

mechanisms for WSNs operating under timely and

spatially variable channel conditions has generally

been less-studied, in this paper we give emphasize to

this type of application. In this paper, first the factors

that may influence the information-value of a packet

will be investigated. Then we incorporate all these

obtained factors in order to estimate the information-

value of the packets. Finally, we exploit the

information-value as a means to properly adjust the

parameters of the adaptive error control code in use.

In this regards, we propose RAFEC*, which is a

Run-time Adaptive FEC-based data dissemination

protocol to enhance reliability, based on the amount

of information the packets carry over a long-term

error-bursty channel in a chain-based WSN. This

adaptation gives the possibility to vary the code

strength and complexity on-demand and on the fly.

One should not that the targeted topology in

RAFEC* is chain topology. Importantly, there is not

much work on reliable data dissemination in chain-

based wireless sensor networks and thus there are

some areas to which special attention should be paid.

Even though many reliable data disseminating

protocols have been designed for wireless sensor

networks (Al-Karaki and Kamal 2004), most of

them are usually designed for a general topology

such as mesh which work well in a multi-

dimensional deployment. For applications with

linear topology, in which nodes are usually lined up

in one-dimensional formation, however, a mesh

topology may not be appropriate or simply not

feasible due to the physical structure or measuring

point distribution, among others. Moreover, it is a

good idea to take the advantage of a linear topology

over a predetermined linear infrastructure (e.g.

bridge, tunnel, etc.), which may be quite different

than a randomly deployed network.

The Need for Packet-level FEC

Basically, FEC applied at the bit-level and byte-level

is appropriate for short-term errors and additive

white Gaussian noise when rapid fluctuation is

experienced over a short period of time. This is

because in this situation, only some bits or bytes of a

packet are influenced. FEC applied at bit- or byte-

level is less efficient in recovery from burst bit

errors caused by long-term fading and expanded

over several packets. In this regards, it is unable to

recover a completely lost or delayed packet.

Therefore, in these cases either ARQ or a packet-

level FEC should be employed. ARQ-based

approaches are effective only for a shorter time-scale

or short-term burst errors. In this respect, even

though ARQ could tolerate long-term fading to some

extent, but more persistent fluctuations make this

approach as inefficient as bit- and byte-level FEC.

To overcome the unreliability caused by more

persistent fluctuations or long-term burst errors,

application-level or packet-level FEC may be used.

The rest of this paper is organized as follows.

First we explain the assumption and model we used

in Section 2, which is followed by the related work

in Section 3. Then in Section 4, we describe the

problem statement and our contribution. We

elaborate on our proposed RAFEC* protocol in

Section 5. Then in section 6 we present the

simulation setup and performance evaluation results.

Finally in Section 7 we draw the conclusion.

2 ASSUMPTIONS AND MODELS

USED

We make the following assumptions regarding the

WSN:

• The WSN consists of N sensor nodes uniformly

and randomly deployed in a chain topology.

• The channel is considered to vary slowly with

respect to the data transmission rate, and thereby

the channels state transitions occur infrequently.

• A systematic code is preferred, as it less suffers

from delays imposed by the block code

mechanisms.

• Uncertainty parameters of the nodes and links

are fixed over transmitting a single code-word.

• The transmission errors are assumed to be local

ProtectingInformativeMessagesoverBurstErrorChannelsinChain-basedWirelessSensorNetworks

131

and spatially and temporally variable, which in

turn should be tackled on a per-link and not

network-wide basis.

Channel Model

In wireless networks, the cause of packet loss can

become more complex and dynamic so that the

frequency of the error bursts varies over time. We

use a Quasi-Stationary Gilbert-Elliot (QSGE) model,

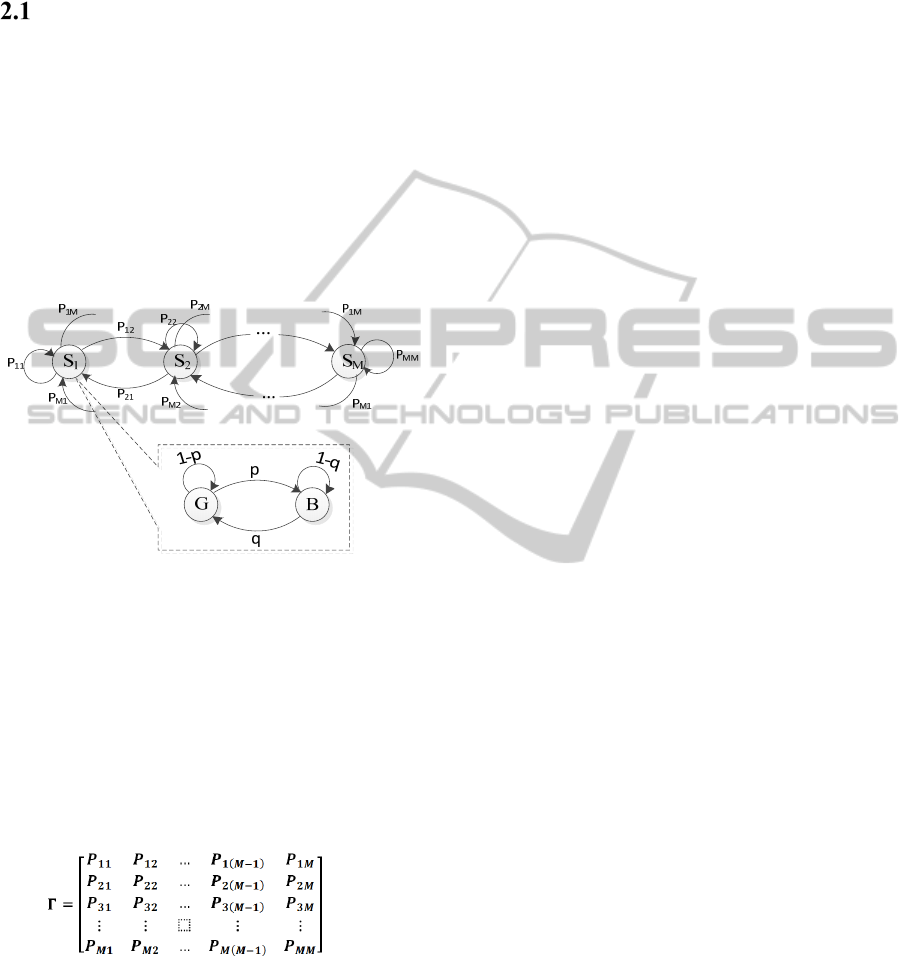
as shown in Figure 1, in order to model channel

states. Each state S

which corresponds to a specific

packet error rate 



follows a Gilbert-Elliot

model with some probabilities (p and q) associated

to it. The B (Bad) and G (Good) states are also a

series of Bernoulli trials.

Figure 1: Quasi-stationary Gilbert-Elliot model.

Each state S

represents the expected PER 





that 





<





<⋯<





, and the conditional one

step probabilities of going from channel state S

channel state S

is given by 



. The channel could

be described in form of a transition matrix with

entries as cross over probability over all combination

of states. The corresponding state transition matrix

Γ



 of the 0, that governs the process of how

the channel introduces different error rates, is

expressed as:

In order to simulate slowly varying channel the

following relationship among transition probabilities

should be presented:



,

≫

,

≫

,

≫⋯≫

,





,∀,



∈



1,





,

≫

,

≫

,

≫⋯≫

,





,∀,



∈



1,



3 RELATED WORK

Although numerous research have been published

related to error control in wireless networks,

especially in cellular networks, most of these are not

directly applicable to WSNs. The limited energy,

low complexity of the sensor node hardware, and

harsh/dynamic environment of the deployment area

necessitates an energy-efficient and more dynamic

or adaptive error control strategy to be used.

The adaptive reliable data dissemination

protocols typically fall in two main categories:

(i) Link-aware: This category of protocol including

(Comroe and Costello Jr 1984; Ahn, Hong et al.

2005; Charfi, Wakamiya et al. 2007; Liankuan,

Deqin et al. 2010; Eriksson, Bjornemo et al.

2011; Hurni and Braun 2011; Yu, Barac et al.

2012) (Yan-ming, Yong-jun et al. 2009;

Taghikhaki, Meratnia et al. 2012; Taghikhaki,

Meratnia et al. 2013) propose error control

schemes whose correction capability vary

according to the links quality.

(ii) Information-aware: The basic idea of this

category of protocols including (Deb, Bhatnagar

et al. 2003) (Deb, Bhatnagar et al. 2003)

(Bhatnagar, Deb et al. 2001; Karl, Löbbers et al.

2003) (Kopke, Karl et al. 2005) (Kleinschmidt,

Borelli et al. 2009; Kleinschmidt and da Cunha

Borelli 2009) is that not all ‘to be transferred’

packets require 100% reliable delivery. Instead,

the reliability is application-specific and

reliability requirements depend on the different

importance levels of packets or environmental

conditions. The advantage offered by this

category of protocols is that limited resources,

such as bandwidth and energy, will only be spent

on important information with high-reliability

requirements. These protocols basically rely on

information-awareness and consider diverse

priorities among different packets. The novelty

of these approaches is that they consider the need

for information-awareness and adaptability to the

link quality along with allocation of network

resources based on the criticality of data. Each

priority level is usually mapped to a desired

reliability for data delivery.

Most of these approaches assume a simple

independent loss channel, which is modeled by

Bernoulli distribution and therefore they usually fail

to be applied in error-bursty channels.

Basically, all packet transmissions in these

approaches have the same probability to fail and

each transmission error is independent from the

others. However, wireless channel is inherently

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

132

lossy and often manifests itself in the form of burst

errors correlated in time. Therefore, a reliable data

dissemination should be capable of counteracting

long-term fading possibly extending over several

packets because of high concentrations of errors. To

cope with this issue, a packet-level adaptive forward

error correction may be a good alternative.

Some approaches rely on the multiple path

transmission, which are highly dependent on the

network topology. In a chain-based topology where

the communication of a sensor node is often

restricted only to its immediate neighboring nodes

(i.e. successor and predecessor node), we cannot

well-benefit from the availability of multiple paths

to salvage data packets from node/link failures. In

case of using duplicate-sensitive aggregation

functions such as SUM or AVERAGE, these multi-

path approaches should employ some more resource

demanding methods to filter out the redundant data.

Moreover, these approaches require to some extent

ensure that only one of the upstream neighbors

forward the packet copies through multi-paths,

otherwise they will introduce large amount of

traffic, which leads to waste of resources in case all

upstream neighbors send multiple copies. To strictly

enforce that only one of the upstream nodes transmit

the packet copies, these approaches may either incur

extra overhead in the form of some control packets

or use some probabilistic methods to lower down the

probability of transmitting a packet by the upstream

nodes (Deb, Bhatnagar et al. 2003).

Majority of the information-aware protocols do

not evaluate the information-value of the packets

and assume that sensor nodes have a priori

knowledge to determine the importance level of the

packets. Using these approaches, when a source

node initiates a packet, it should set the importance

level (or information-value) of the packet. However,

asking sensor nodes to determine the importance

level of the sensory data introduces new challenges

which may require complex algorithms to perform

pattern matching or execute artificial intelligence

techniques. Moreover, in these approaches the

importance level of each packet is set once on the

source node and does not change along the path.

Therefore, if an important sensory data is modified

along the path in such a way that it cannot anymore

reflect the phenomena state, transmitting it leads to

wasting sensor/network resources. To cope with this

issue, the importance level of the packets should

vary along the path by considering the factors which

may influence the packet importance level.

Some approaches specially those which consider

the aggregation degree to determine the importance

level of the packets, poorly perform in case of being

applied in uniformly distributed deployments. Non-

uniform and unevenly distribution of sensor nodes

results in some areas to be monitored by many

sensors while other areas will be monitored only by

a few nodes. Therefore, considering just the

aggregation degree of the nodes may not well-reflect

the importance level of the data. In this regard, the

information-value of the packets should be

determined in such a way that could also be applied

for non-uniformly distributed deployments.

The above discussion highlights the need for an

adaptive reliable chain-based disseminating protocol

based on both packet information-value and link

quality. To this end and to address most of above

shortcomings, an adaptive energy-efficient reliable

disseminating protocol is needed which (i) can be

applied to non-uniform deployments with linear

topology (ii) tackles the long-term error bursts, (iii)

incorporates various factors that may influence the

information quality of the packets, and (iv) considers

packet delivery ratio as the link quality metric, rather

than considering immediate channel quality

indicators such as RSSI and SNR which are not

appropriate for long-term error burst.

4 PROBLEM STATEMENT AND

OUR CONTRIBUTION

Given an already deployed linear WSN, the problem

at hand is to design an adaptive, reliable, energy-

efficient, and Information-Link-aware data

dissemination protocol. We summarize our

contribution related to this paper as: (i) Investigating

and quantifying different factors which may

influence the information-value of packets and

incorporating the above identified factors in

evaluation of informational content and importance

of packets. (ii) proposing RAFEC*, i.e., an adaptive,

energy-efficient, reliable, information-link-aware

data dissemination approach, which is able to (a)

cope with periodic long-term loss process in a linear

chain-based WSNs and (b) switches among error

control codes with different powers to vary the code

strength and complexity in on demand.

5 RAFEC*

In this section we elaborate on RAFEC*, which is a

Run-time Adaptive FEC-based data dissemination

protocol that improves reliability of packet delivery

ProtectingInformativeMessagesoverBurstErrorChannelsinChain-basedWirelessSensorNetworks

133

based on the amount of information they carry over

a bursty channel in a chain-based WSN. To this end,

(i) the mechanism for associating the error control

codes to the states of QSGE model is described (ii)

packet information and link quality are estimated

and (iii) the strategy using which an appropriate

error control code is assigned to a specific packet is

explained.

Basically, the activities performed by every

sensor node i can be organized into sequences each

of which may correspond to processing one code-

word 





as shown in Figure 2

Assigning Error Control Codes to

the Channel States

As we stated before, in RAFEC* the channel is

modeled as a M-states QSGE model with a packet

error rate 



assigned to each state S

. Therefore,

at any moment of time the state of the channel

should fit one of the states specified by the channel

model.

Having the packet error rate PER

of each state

of the M-state QSGE model, an error control code

which can effectively counteract the available errors

may be designed. To this end, the error control codes

in RAFEC* are selected from a single family of FEC

block codes such as 



 which represented a

family block code for a Reed-Solomon code:



















,

|

2,0

where k represents number of original data and t

represents correction capability of the Reed-

Solomon code RS(n,k). Each member of family

block 









can correct up to a specific number

of error t. RAFEC* uses 









for the M-state

QSGE model. Therefore, each state S

of the M-state

channel, which exhibits a specific error rate 



can adopt one member of 









based on the

below Equation provided that |









|:

ECC



RS



n,











n,









∈













1





To this end, the most efficient error control code

denoted by ECC

which exhibits the “just enough”

correctional power for the channel state S

is RS (n,

). In this way, each channel state S

can be

described using two parameters 



and K

(



, K

). In short, a particular coding strategy

ECC

is associated with each channel state S

The

criteria by which this coding strategy is selected is

addressed in above Equation.

Assessing Packet Information and

Link Quality

Since the choice of error control code for each

packet in RAFEC* is based on the quality of service

parameters, the information-value and packet

importance as well as properties of error traces

which are captured from transmission history, the

following tasks need to be performed by the sensor

nodes:

• Estimation of packet’s information value

• Estimation of link quality

5.2.1 Estimation of Information-Value

The information-value could be influenced by

several factors which may have different priorities in

different applications. In what follows we express

these factors which we then take into consideration

to estimate information-value of a packet.

• Node functionality: Faulty sensor nodes could

influence network operation and pose a

challenging constraint in the design of a protocol

for WSNs. Most of reliable data dissemination

protocols usually concentrate on the link quality

and less effort has been put into the node’s

functionality. Having a reliable dissemination

protocol by itself is not useful if relay nodes

through which data is disseminated are faulty and

malfunctioning. Therefore, it is important that all

sensor units relevant to the accomplishing task

operate well-enough in order to ensure high

reliability. In this regard, the quality of sensing and

computing unit of relay nodes should be

considered when estimating packet information-

value. To estimate the quality of sensor units, we

use a trust-based approach as introduced in

(Taghikhaki, Meratnia et al. 2013).

• Node contribution degree: The relative position of

each node in the network may also impact the

information-value of a packet being disseminated

through the given node. Generally speaking, the

higher contribution degree  of a node, the higher

information-value. As can be seen from figure 3,

contribution degree of node S

is higher than S

it monitors three critical points (









3) while

only monitors one critical point (









1).

Node contribution degree is determined by the base

station which informs each node about its .

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

134

Figure 2: Activities performed by relay node i.

Figure 3: Illustrative example of node contribution degree.

• Node spatial density: If sensor nodes are not

evenly distributed, it is likely that some sensor

nodes simultaneously and so redundantly observe

a critical point while some nodes only and lonely

observe a critical point. In this case, relying only

on the coverage degree does not well reflect the

amount of information being sent by the sensor

nodes. As can be seen from Figure 4 although











<









, S

is the only node which can

observe critical point CP

while critical point CP

is being monitored by other three nodes in addition

to node S

. Therefore, a sensory data coming from

a region that is already covered (either fully or

partially) by other nodes has less informative

content. On the other hand, if a sensor node is

located in such a place where it covers one or some

critical points which are not been observed by any

otherwise node, its sensed data more likely carries

quite significant information. Node spatial density

can easily be determined by the base station in the

initialization phase and then the base station

informs each node about it.

Figure 4: Illustrative example of node spatial density.

• Strategic Area: The value of data collected from

different critical regions may not necessarily be

equal. A given application (either always or

sometime) may be more interested in data of some

specific cells/regions. Therefore, the information-

value of packets carrying this data is higher. As it

can be seen from 0 although node S

monitors two

critical points (i.e., CP

and CP

both having

importance of 1) and node S

monitors one critical

point CP

having importance of 4, information-

value of data coming from node S

is higher as it

covers a more strategic area. In the initialization

phase, the base station informs each node about the

strategic level (or criticalness) of an area in where

the given node is located.

Figure 5: Illustrative example of different strategic area.

• Traveled Distance Ratio: If a packet is lost at the

first hops, (i) lesser energy has been consumed for

its relay and (ii) lesser information (in case of

doing aggregation along the path) are lost,

compared to when it is lost at further hops.

Therefore, it makes sense to use stronger error

control codes for packets being relayed for longer

distance. This parameter can be determined by

increasing a counter (a packet’s field) whose value

is zero in the source node.

After identifying the aforementioned factors that

may impact the quality of data packets, we here

explain how to estimate the information-value and

importance of packets per hop.

In Equation (3) we combine all aforementioned

factors except Traveled Distance Ratio. The reason

to leave Traveled Distance Ratio out of this equation

is that all other factors are node-dependent while

Traveled Distance Ratio is both packet-dependent

and node-dependent.

ProtectingInformativeMessagesoverBurstErrorChannelsinChain-basedWirelessSensorNetworks

135

















,





CCo





∈



where CCovk represents the set of nodes that

cover the common/critical point k, SCovi states set

of common/critical points which have already been

covered by sensor node i, σ



denotes how critical

and strategic the data of common/critical point k is,

and γ

,



signifies node i functionality which is

obtained from (Taghikhaki, Meratnia et al. 2013).

for common/critical point k.

To also take Travelled Distance Ratio into

account, we utilize Equation (4), where SIDp

represents ID of the source node which initiates the

data packet p. The numerator evaluates the travelled

distance while the denominator represents the

distance between the base station (BS) and the

source node.

,

|



|



Exploiting Equation (3) and (4) further, information-

value denoted by χ



p,i



of packet p being sent by

sensor node i can be calculated using Equation (5).





,



















,1











,















̂













̂

 





where ̀ represents maximum information-value

that a data packet may have.

Weights (ϖ



,ϖ



) used in Equation (5)can be

adjusted according to the application specific

knowledge. For instance, if the application does not

perform aggregation on the intermediate nodes and

thus the relay nodes carry only the raw data, we may

set ϖ



1 and ϖ



0. For the sake of simplicity

and without loss of generality, we can map packet’s

information-value denoted by χ into d

discrete

values. Doing so, we will have d

different packet

types each of which contains a specific amount of

information and thus their required reliabilities are

different. Therefore, d

also shows the number of

required error control codes each of which is

assigned to a specific information-value. In this

thesis by using Equation (6), we map packet’s

information-value into discrete values 1, 2 and 3. By

doing so, three different packet types will be defined

in terms of information-value they may have.

However, depending on the available error control

codes which are implemented in the sensor nodes we

can have different values for d



1 0<0.3

2 0.3<0.6

3 0.6

5.2.2 Estimation of Link Quality

To estimate the link quality, RAFEC* employs a

passive link monitoring strategy, which exploits

existing traffic without incurring additional

communication overhead.

The link quality estimation process in RAFEC*

is performed first over a sequence of  packets (say

packet-level estimation) and then over a sequence of

 code-words (say code-word-level estimation).

Having statistics about a given link qualities over

the last sliding window, we calculate the average

error rate 



As will be stated later, dependent on amount of

information a packet carries, we change  in order

to capture the effective-error-rate on the links.

Adaptive Packet-link-Local Error

Control

Having both information-value of packets and

packet error rates captured from transmissions

history, strength and complexity of the error control

codes can be adapted on demand. Having higher

information-value or poorer link quality requires

utilization of a more powerful error control code. On

the contrary, having lower information-value or

higher quality link requires a weaker code.

It is noteworthy that we consider a multi-hop

FEC protection mechanism, in which intermediate

nodes need to perform encoding and decoding

functions individually and locally at each hop. This

way of locally protection helps our approach being

easily applied to large-scale networks.

In Section 5.1, we explained how Reed-Solomon

code is assigned to each channel state of QSGE

model based on the packet error rate 



of each

state S

. Basically, effective-error-rate  of a link

at any moment of time u should correspond to one of

the 



specified by the QSGE model.

Then according to Equation (7), the error control

code ECC

, which is associated to the state S

could

be decided as the code  that should be

utilized for the error rate .





Our strategy to estimate the effective error rate 

can be summarized as:

 First, we calculate the average error rate for three

different values (i.e. 1,2,3) assigned to . In this

regard, dependent on the value, three different

average error rates 









may obtain. According

to Equation() we put each of these three values to a

variable







SENSORNETS2015-4thInternationalConferenceonSensorNetworks

136























1







_









2







_









3

 Second, having Information-value of the packet we

estimate the effective error rate for each packet

as:

• If information-value of the packet is 1

then the effective error rate  will be



• If the packet has higher information-value

(2 then  will be Max(



,

• If the packet has the highest information-

value (3, the effective packet error rate

 will be Max





,





.

According to above, the effective packet error rate 

based on which the error control code is selected,

varies according to the information-value . In this

regard, a packet with high/low information-value

should be equipped with a strong/weak error control

code  presented in Equation (7).

6 PERFORMANCE EVALUATION

Performance Metrics

We consider the following metrics to evaluate the

performance of our approaches under different

circumstances.

• Information-aware Reliability Ratio (IRR):

This metric evaluates reliability ratio by taking

information-value of the packets into account

using Equation (9):



∑









1





∑







1





















∑



















where 





represents the number of sensor nodes.

Moreover, 











, 





and 





 are the

number of data packets with information-value

 transmitted by node i, received by node i

error-freely and correctly being recovered by

node i, respectively. According to Equation (9),

we will have three different IRRs each of which

representing the achieved reliability ratio for a

specific information-value .

• Code Rate: This metric represents the

proportion of the useful (non-parity) packets in a

code-word. By the means of this metric, we

express the code’s efficiency and the redundancy

introduced by the code.

• Information-aware System Efficiency: It is

generally accepted that additional parity packets

(or lowering the code rate) can be tolerated as

long as loss-resiliency at the receiver side is

increased. Therefore, the system efficiency

metric is introduced to express the tradeoff

between the energy expenditure and reliability.

To this end we make a relation between

information-value arriving at the destination with

the amount of redundancy (parity packets) and

define Equation(10) as:











∑









1





∑









1























∑

























∑



























where 



represents the number of redundant

(parity) packets sent by node i. and 

represents the amount of gain that an application

earns by receiving a packet with an information-

value . We assume that the gain of a packet with

3 is twice of that for 2 and four times of

that for 1. Therefore, 



3



2





2



41. By doing so,

receiving a packet with information-value 2

worth twice as much as receiving a packet with

information-value 1.

Simulation Setup and Scenario

We consider a chain consists of 20 nodes which are

linearly deployed in an area of

40025

and in

all simulations, the source or initiative node is the

leftmost node. The sensing range of nodes is to 35m.

Unless otherwise states, the simulation parameters

are as described here. The deployment area is

divided into some regions

(25)

half of which

are labeled as critical and the rest are labeled as

uncritical. It is worth mentioning that since RAFEC*

is a link-local error control approach, the number of

sensor nodes does not much influence the

performance of the application. We then send 5000

packets from one source node to the base station

with frequency of 1 pkt/s. The strategic level (or

criticalness) of the critical regions is selected from

the interval (Bhatnagar, Deb et al. 2001) while the

strategic-level of the uncritical regions are 1. At any

moment in time, 70% of all nodes and links work

almost properly with failure rate of 0.09. The failure

rate of other 30% of the nodes is set to 0.85. The

failure rate of other 30% of the links vary according

to a five-state QSGE model which will be state later.

The selection of failing nodes/links occur randomly

after every 1000 time unit in order to simulate

temporal correlation among failures of those 30%

nodes/links.

ProtectingInformativeMessagesoverBurstErrorChannelsinChain-basedWirelessSensorNetworks

137

Five-states QSGE erasure channel (as explained

in Section 22) is used. In order to simulate a slowly

varying channel, the following specifications are

used:

The probability of staying in one state, i.e. P

i,i

, is

extracted from (Rice and Wicker 1994) and the

remainder, i.e. 1- P

i,j

, is evenly allocated to

transitions from node i to all other nodes j (i≠j) so

that

∑



,

1

,

∀∈



1,9



,





.Each

state S

of the five-state QSGE model corresponds to

one PER

as: PER

=0.1, PER

=0.3, PER

=0.4,

PER

=0.5, PER

=0.7.

We model sending packets in each state of

QSGE model first according to a Gilbert-Elliot

model and then as a series of Bernoulli trials. The

Gilbert-Elliott channel model is defined by p and q

which change according to the N and N-K

parameters of the codes assigned to S

(0Table 1)

These two parameters are obtained as:

=0.07, p

=0.09, p

=0.11, p

=0.14, p

=0.2.

=0.5, q

=0.25, q

=0.166, q

=0.125, q

=0.1.

In our approach, a length-15 Reed-Solomon (RS)

code (i.e. N=15) is chosen over a five states channel

for packets with three different information-values.

The error control code ECC

which is assigned to

each state S

is presented in Table 1. The error codes

contained in this table are increasing in their

correctional power from the left to the right, and

similarly with respect to computational and parity

overhead.The information-value weights are set to





1,



1and 1231.Moreover,

the channel estimation windows size is





15while the sliding window size is



5.

Table 1: Error control codes of each state.

State S

ECC

RS(15,13) RS(15,11) RS(15,9) RS(15,7) RS(15,5)

Performance Evaluation

Figure 6 represents the IRR and each graph in this

figure belongs to one specific packet error rate

(PER) under which a packet that may carry different

amount of information is transmitted. One can see

that IRR of RAFEC* heavily depends on the

information-value of the packet. The more

informative packet (higher ), the less likely the

packet will be lost and so the higher contribution in

the overall RR. In Figure 6 the relationship among

the reliability ratio of different information-values in

RAFEC* is:





∗



3







∗



2







∗



1



Following this intuition, the IRR of the most

informative packets in RAFEC* are always

maximum and greater than 90%. Moreover, since

packets with 1 are less important for the

application, the RAFEC* does not use robust error

control for them and thereby the IRR for them is

relatively low. According to Figure 6, no fixed

relationship among reliability ratio of different

information-values for other approaches can be

inferred and they just exhibit a very random

behavior.

The average gained code rate for the received

packets which carry different informative content is

illustrated in Figure 7. The code rate of RAFEC* is

inversely proportional to the packet error rate as

RAFEC* needs to dynamically adjust the amount of

parity packets to be able to overcome the incurred

errors. Generally, the high error rate necessitates the

use of more parity packets, which in turn results in a

lower code rate. Since other approaches are all

static, changing the error rate does not have any

effect on the code rate. The code rates shown in

Figure 7 are averaged over three information-values.

To have a better insight about the obtained code rate

per different information-value, Figure

8 is

presented. The higher packet error rate necessitates

to equip data-words with a more powerful code,

which results in more parity packets and thereby

lower code rate. Obviously, packet with 3

produces low code rate which explains its superior

performance in terms of reliability.

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

138

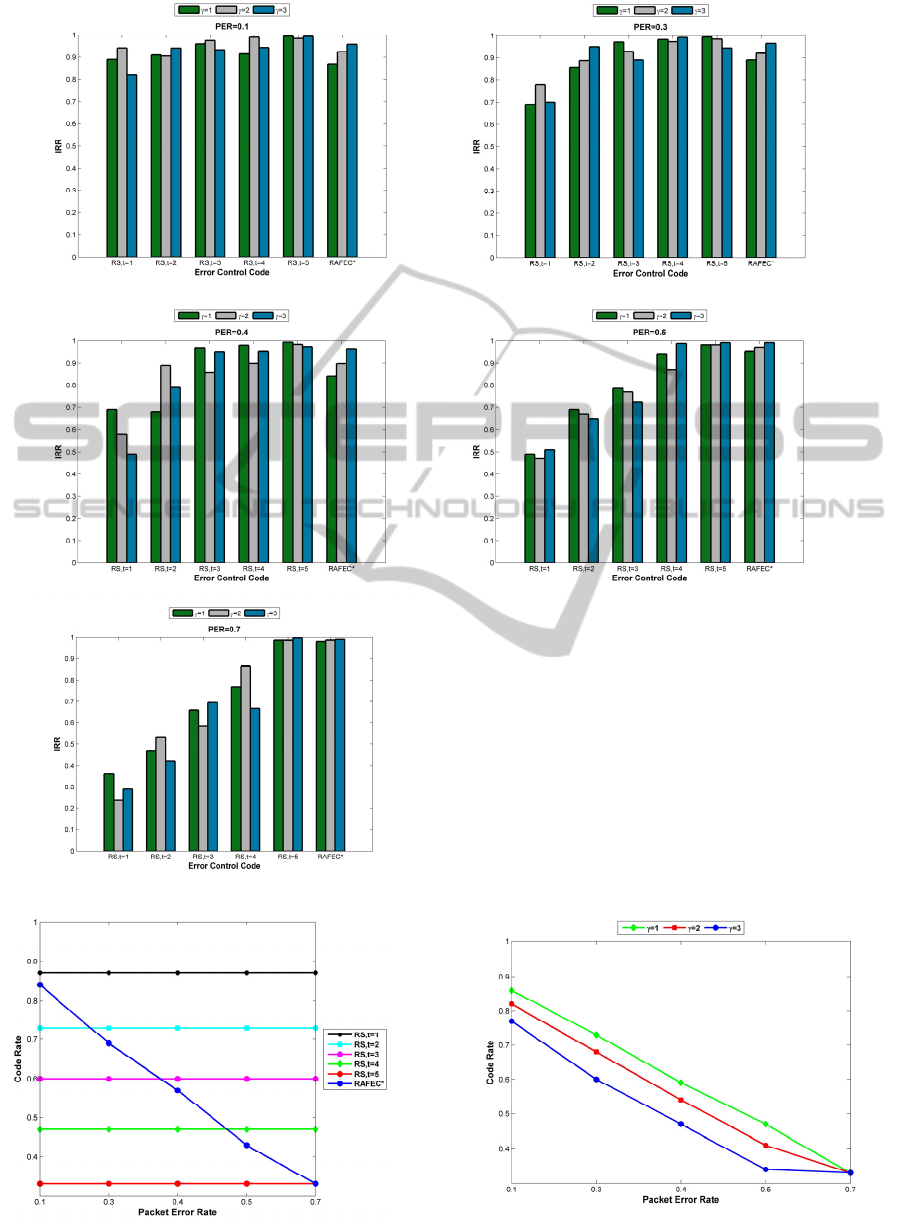
Figure 6: Information-aware reliability ratio for different packet error rate for RAFEC* and RSs.

Figure 7: Code rate comparison of RAFEC* and RSs.

Figure 8: Code rate comparison of RAFEC*.

ProtectingInformativeMessagesoverBurstErrorChannelsinChain-basedWirelessSensorNetworks

139

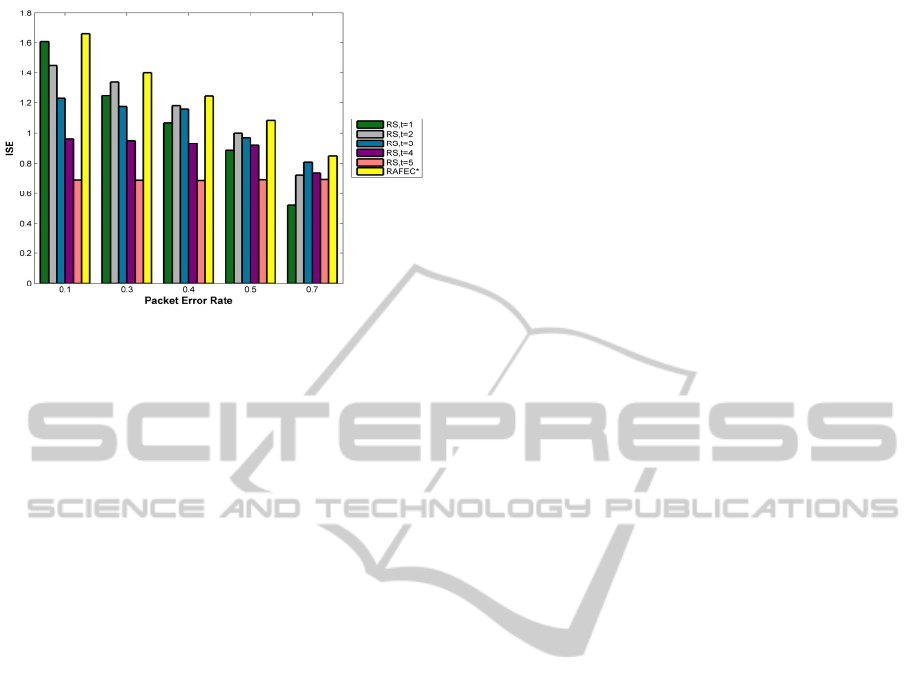
Figure 9: Information-aware system efficiency comparison

of RAFEC* and RSs.

Figure 9 illustrates Information-aware System

Efficiency of different codes, form which superiority

of RAFEC* over all other codes can be seen.

7 CONCLUSION

The purpose of WSNs is sensing and disseminating

information. Therefore, the loss of important

information at the perceived benefit of saving

energy, may inhibit the ability of a WSN to fulfil its

primary purpose.

In this paper, we propose RAFEC* a packet-

level reliable data dissemination protocol to support

information-awareness in a chain-based WSN.

Different from most of the proposed reliable

approaches that are proposed to work for the

topologies other than chain and so cannot efficiently

work for the chain topology, RAFEC* is customized

for this poor-explored topology. Using RAFEC*,

information can be delivered at desired levels of

reliability at proportional cost, in spite of the

presence of long-term fading in the channel.

RAFEC*, basically exploits the concept of dynamic

packet state and dynamic link state to control the

correction capability of the error control codes

exploiting only local knowledge of channel and

packets at each hop. Moreover, the history-based

evaluating link quality which RAFEC* utilizes,

provides a means to cope with longer-term

interferences, since the mechanism does not

immediately switch to a less/more powerful code

after one successful/failed transmission. Basically,

RAFEC* waits until a couple of transmission have

succeeded or failed and then change the error control

in-use.

In the simulation, we illustrate the superiority of

RAFEC* in terms of several metrics.

ACKNOWLEDGEMENT

This work is supported by IST FP7 STREP

GENESI: Green sEnsor NEtworks for Structural

monItoring project.

REFERENCE

Ahn, J.-S., S.-W. Hong, et al. (2005). "An adaptive FEC

code control algorithm for mobile wireless sensor

networks." Journal of Communications and Networks

7(4): 489-498.

Al-Karaki, J. N. and A. E. Kamal (2004). "Routing

techniques in wireless sensor networks: a survey."

Wireless communications, IEEE 11(6): 6-28.

Bhatnagar, S., B. Deb, et al. (2001). Service differentiation

in sensor networks. International Conference on

Wireless Personal Multimedia Communications.

Charfi, Y., N. Wakamiya, et al. (2007). Adaptive and

reliable multi-path transmission in wireless sensor

networks using forward error correction and feedback.

Wireless Communications and Networking

Conference.

Comroe, R. and D. J. Costello Jr (1984). "ARQ schemes

for data transmission in mobile radio systems."

Journal on Selected Areas in Communications 2(4):

472-481.

Deb, B., S. Bhatnagar, et al. (2003). Information assurance

in sensor networks. 2nd ACM international conference

on Wireless sensor networks and applications.

Deb, B., S. Bhatnagar, et al. (2003). ReInForM: Reliable

information forwarding using multiple paths in sensor

networks. 28th Annual IEEE International Conference

on Local Computer Networks.

Eriksson, O., E. Bjornemo, et al. (2011). On hybrid ARQ

adaptive forward error correction in wireless sensor

networks. 37th Annual Conference on Industrial

Electronics Society.

Hurni, P. and T. Braun (2011). "Link-quality aware run-

time adaptive forward error correction strategies in

wireless sensor networks." IAM, University of Bern,

IAM-11-003, Tech. Rep.

Karl, H., M. Löbbers, et al. (2003). A data aggregation

framework for wireless sensor networks. Dutch

Technology Foundation ProRISC Workshop on

Circuits, Systems and Signal Processing, Citeseer.

Kleinschmidt, J. H., W. C. Borelli, et al. (2009). "An

energy efficiency model for adaptive and custom error

control schemes in Bluetooth sensor networks." AEU-

International Journal of Electronics and

Communications 63(3): 188-199.

Kleinschmidt, J. H. and W. da Cunha Borelli (2009).

Adaptive error control using ARQ and BCH codes in

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

140

sensor networks using coverage area information. 20th

International Symposium on Personal, Indoor and

Mobile Radio Communications.

Kopke, A., H. Karl, et al. (2005). Using energy where it

counts: Protecting important messages in the link

layer. 2nd European Workshop on Wireless Sensor

Networks.

Liankuan, Z., X. Deqin, et al. (2010). Adaptive error

control in wireless sensor networks. IET International

Conference on Wireless Sensor Network

Rice, M. and S. B. Wicker (1994). "Adaptive error control

for slowly varying channels." IEEE Transactions on

Communications 42(234): 917-926.

Taghikhaki, Z., N. Meratnia, et al. (2012). An Error

Control Scheme for Delay Constrained Data

Communication in a Chain-Based Wireless Sensor

Network. The Seventh IEEE International Conference

on Broadband and Wireless Computing,

Communication and Applications (BWCCA).

Taghikhaki, Z., N. Meratnia, et al. (2013). "On QoS

guarantees of error control schemes for data

dissemination in a chain-based wireless sensor

networks." Sensors & Transducers Journal 18: 188-

202.

Taghikhaki, Z., N. Meratnia, et al. (2013). "A trust-based

probabilistic coverage algorithm for wireless sensor

networks." Procedia Computer Science 21: 455-464.

Yan-ming, C., X. Yong-jun, et al. (2009). An adaptive

fault-tolerant scheme for wireless sensor networks.

International Conference on Communications and

Mobile Computing.

Yu, K., F. Barac, et al. (2012). Adaptive forward error

correction for best effort Wireless Sensor Networks.

International Conference on Communications

ProtectingInformativeMessagesoverBurstErrorChannelsinChain-basedWirelessSensorNetworks

141