Multiphase Region-based Active Contours for Semi-automatic
Segmentation of Brain MRI Images
Farhan Akram
1
, Domenec Puig
1
, Miguel Angel Garcia
2
and Adel Saleh
1
1
Department of Computer Engineering and Mathematics, Rovira i Virgili University, 43007 Tarragona, Spain
2
Department of Electronic and Communications Technology, Autonomous University of Madrid, 28049 Madrid, Spain
Keywords:
Active Contours, Medical Image Analysis, Segmentation, Thresholding.
Abstract:
Segmenting brain magnetic resonance (MRI) images of the brain into white matter (WM), grey matter (GM)
and cerebrospinal fluid (CSF) is an important problem in medical image analysis. The study of these regions
can be useful for determining different brain disorders, assisting brain surgery, post-surgical analysis, saliency
detection and for studying regions of interest. This paper presents a segmentation method that partitions a
given brain MRI image into WM, GM and CSF regions through a multiphase region-based active contour
method followed by a pixel correction thresholding stage. The proposed region-based active contour method
is applied in order to partition the input image into four different regions. Three of those regions within the
brain area are then chosen by intersecting a hand-drawn binary mask with the computed contours. Finally, an
efficient thresholding-based pixel correction method is applied to the computed WM, GM and CSF regions to
increase their accuracy. The segmentation results are compared with ground truths to show the performance
of the proposed method.
1 INTRODUCTION
Image segmentation is a basic yet necessary task for
many medical applications, such as surgical planning,
post-surgical analysis, saliency detection and study of
regions of interest (Zhang et al., 2007). Segmenta-
tion of brain MRI images is a well-known problem
in medical image analysis. Its goal is to segment the
brain area into different disjoint regions: grey mat-
ter (GM), white matter (WM) and cerebrospinal fluid
(CSF). Due to the geometric complexity of the hu-
man brain cortex, manual slice-by-slice segmentation
is cumbersome and time consuming. The complexity
of intensity inhomogeneous regions makes brain MRI
images hard to segment with high accuracy (Balafar
et al., 2010). Numerous methods have been devised to
segment the brain into different non-overlapping re-
gions (Elnakib et al., 2011). In particular, the active
contour method introduced in (Kass et al., 1988) is
widely-used for image segmentation. In this method,
a curve evolves towards the boundaries of the object
of interest under a certain force field by minimizing
the curve’s intrinsic energy.
Active contour models can be classified into two
main categories: edge-based (Kass et al., 1988;
Caselles et al., 1997; Li et al., 2005) and region-based
(Mumford and Shah, 1989; Chan and Vese, 2001; Li
et al., 2007; Li et al., 2008; Zhang et al., 2010; Akram
et al., 2013; Akram et al., 2014) methods. Edge-
based active contour methods, which use an edge-
indicator function to drive the contour towards the ob-
ject boundaries, can hardly stop the evolution of the
contour with weak or blurred edges. Alternatively,
region-based active contour methods, which use im-
age statistical information, can properly segment the
image even with such weak or blurred edges. How-
ever, the traditional active contour method (Mumford
and Shah, 1989; Chan and Vese, 2001) is defined un-
der the assumption that the target image is homoge-
neous. Therefore, it cannot properly segment images
with intensity inhomogeneous regions. Although both
edge-based and region-based active contour methods
have their own pros and cons, region-based meth-
ods usually perform better than edge-based methods
(Zhang et al., 2010; Yang et al., 2010).
In (Vese and Chan, 2002), a multiphase level set
framework using n level sets was proposed to segment
a given image into 2
n
phases (regions). This method
is the extension to multiphase level sets of a previ-
ous work on active contours without edges (Chan and
Vese, 2001). It was developed under the assumption
that the input image must have homogeneous inten-
447
Akram F., Puig D., Garcia M. and Saleh A..
Multiphase Region-based Active Contours for Semi-automatic Segmentation of Brain MRI Images.
DOI: 10.5220/0005294804470454
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 447-454
ISBN: 978-989-758-089-5
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

sity regions. Therefore, it does not properly work on
images that contain inhomogeneous regions or with
small intensity differences among different regions.
In (Li et al., 2007; Li et al., 2008), a region-based
active contour method was proposed in the context
of intensity inhomogeneous regions. It computes the
image intensity mean over a local neighbourhood by
using a Gaussian kernel. Although that method can
successfully segment images with intensity inhomo-
geneity, it has a significantly high computational com-
plexity. Moreover, segmentation results of different
regions can overlap if the objects in the image have a
complex geometry.
In (Zhang et al., 2010), a region-based active con-
tour method was proposed based on a local fitted im-
age generated by using the local mean values pro-
posed in (Li et al., 2007; Li et al., 2008). This method
is also able to segment images with inhomogeneous
intensity regions, although it is less accurate than the
latter and also suffers from the region overlapping
problem in case of complex geometries such as brain
regions. Alternatively, a region-based active contour
method for brain MRI image segmentation was pro-
posed in (Akram et al., 2013; Akram et al., 2014).
That method applies a locally-computed active con-
tour method based on a signed pressure force (SPF)
function in order to segment the brain into WM and
GM regions. It has a lower computational complexity
and yields better segmentation results than the afore-
mentioned methods. However, since it is a two-phase
active contour method, it can only segment the input
images into two disjoint regions.
In the present paper, a four-phase region-based
active contour method is proposed. It applies two-
phase local and global fitted image models in order to
define a four-phase active contour energy functional.
The proposed method aims to segment the brain area
from a brain MRI image into three different non-
overlapping regions: WM, GM and CSF. This method
consists of three stages. In the first stage, a new four-
phase region-based active contour method is applied
to yield an initial segmentation of the given brain MRI
image. In the next stage, a hand-drawn binary mask
of the brain area is intersected with the final contours
obtained in the previous stage in order to constrain the
contour evolution to the brain area. In the last stage, a
thresholding-based pixel correction method is finally
applied in order to improve the segmentation results
of WM, GM and CSF regions. Experimental results
show that the proposed method yields segmentation
accuracies of around 91% for WM regions, 87% for
GM and 80% for CSF regions.
This paper is organized as follows. The three
stages of the proposed method are described in sec-
tion 2. Experimental results are shown in section
3. Finally, conclusions and further research lines are
given in section 4.
2 SEGMENTATION OF REGIONS
OF INTEREST IN MRI BRAIN
IMAGES
The proposed method to segment regions of interest in
MRI brain images consists of three stages described
below. The first stage segments the regions of interest
using a new region-based active contour method. The
second stage constrains the level set functions defined
in the previous stage by intersecting their contours
with a hand-drawn binary mask of the brain area. The
third stage performs a thresholding-based pixel cor-
rection of the computed WM, GM and CSF regions.
2.1 Multiphase Region-based Active
Contours
Since a piecewise active contour model based on a
two-phase level set function (Chan and Vese, 2001)
is able to segment a given image into two distinct re-
gions, it cannot be applied to the segmentation of the
three main regions of interest in the brain (WM, GM
and CSF). Therefore, it is necessary to apply a four-
phase level set method.
Active contours are dynamic curves that move to-
ward the object boundaries to partition an image into
distinct and non-overlapping regions. To segment a
brain image into three non-overlapping regions, an
energy functional is defined with both a region-based
area term and an edge-based length term. With piece-
wise multiphase active contour methods, two level
sets are necessary for segmenting an image into four
distinct regions (Vese and Chan, 2002). The proposed
energy functional utilizes the local and global mean
intensity values of two level sets (Chan and Vese,
2001; Li et al., 2007; Li et al., 2008). Let I : Ω → R
be an input image, Φ(φ
1
, φ
2
) be two level sets and
C(C
1
,C
2
) be the closed curves defined by the zero
level sets corresponding to Φ. An energy functional
E(Φ(φ
1
, φ
2
)) is defined as follows:
E(Φ(φ
1
, φ
2
)) = λ
1
F
local
(φ
1
) + λ
2
F
global
(φ
2
)
+ v
1
L
g
(φ
1
) + v
2
L
g
(φ
2
), (1)
where λ
1
> 0, λ
2
> 0, v
1
and v
2
are constants,
L
g
(φ
1
) and L
g
(φ
2
) are regularization terms that drive
the zero level curves C(C
1
,C
2
) into smooth curves by
taking into account image edges, and F
local
(φ
1
) and
F
global
(φ
2
) are force terms that use local and global
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
448

Figure 1: Brain MRI image segmentation comparison. The first column shows brain MRI images with initial contours. The
second column shows the final contours using the proposed method. The third column shows the final contours using the
multiphase level set framework proposed in (Vese and Chan, 2002).
fitted images defined by utilizing local and global in-
tensity mean values as proposed in (Li et al., 2007;
Li et al., 2008; Chan and Vese, 2001), respectively.
The local force term F
local
(φ
1
) is based on mean
values computed over a square neighbourhood and
drives the first level set to weak and blurred edges
by distinguishing inhomogeneous regions. In turn,
the global force term F
global
(φ
2
) extracts the bound-
aries of dark homogeneous regions. By substituting
F
local
(φ
1
), F
global
(φ
2
), L
g
(φ
1
) and L
g
(φ
2
) by their cor-
responding expressions (Li et al., 2005; Zhang et al.,
2010), the following formulation is obtained:
E(Φ(φ
1
, φ
2
)) = λ
1
Z
Ω
|I(x) − I
local
(x)|
2
dx
+ λ
2
Z
Ω
|I(x) − I
global
(x)|
2
dx
+ v
1
Z
Ω
g(I)δ
ε
(φ
1
)|∇φ
1
|dx
+ v
2
Z
Ω
g(I)δ
ε
(φ
2
)|∇φ
2
|dx, (2)
where δ
ε
(z) =
ε
π(z
2
+ε
2
)
is the regularized Dirac
function, H
ε
(z) =
1
2

1 + (
2
π
)arctan(
z
ε
)

is the regular-
ized Heaviside function, and g(I) =
1
1+|∇G
σ
1
∗I(x)|
2
is a
positive and strictly decreasing edge indicator func-
tion. In turn, functions I
local
and I
global
are local and
global fitted images respectively defined as:
I
local
= f
1
H
ε
(φ
1
) + f
2
(1 − H
ε
(φ
1
)) (3)
I
global
= c
1
H
ε
(φ
2
) − c
2
(1 − H
ε
(φ
2
)), (4)
In (3), f
1
and f
2
are the local mean values inside
and outside of the object boundaries in the image,
which are borrowed from (Li et al., 2007; Li et al.,
2008) and defined as:
f
1
=
K
σ
1
∗ [H
ε
(φ
1
)I(x)]
K
σ
1
∗ H
ε
(φ
1
)
(5)
f
2
=
K
σ
1
∗ [(1 − H
ε
(φ
1
))I(x)]
K
σ
1
∗ (1 − H
ε
(φ
1
))
, (6)
where σ
1
is the standard deviation of the truncated
Gaussian kernel, which is used to compute the local
MultiphaseRegion-basedActiveContoursforSemi-automaticSegmentationofBrainMRIImages
449

intensity means of the image. In (4), c
1
and c
2
are the
global mean values inside and outside of the object
boundaries in the image, which are borrowed from
(Chan and Vese, 2001) and defined as:
c
1
=
R
Ω
H
ε
(φ
2
)I(x)dx
R
Ω
H
ε
(φ
2
)dx
(7)
c
2
=
R
Ω
(1 − H
ε
(φ
2
))I(x)dx
R
Ω
(1 − H
ε
(φ
2
))dx
, (8)
By differentiating (2) using the calculus of vari-
ations (Aubert and Kornprobst, 2006), the partial
derivatives of functional E(Φ(φ
1
, φ
2
)) can be written
as:
∂φ
1
∂t
= λ
1
(I(x) − I
local
)( f
1
− f
2
)δ
ε
(φ
1
)
+ v
1
div

g(I)
∇φ
1
|∇φ
1
|

δ
ε
(φ
1
) (9)
∂φ
2
∂t
= λ
2
(I(x) − I
global
)(c
2
− c
1
)δ
ε
(φ
2
)
+ v
2
div

g(I)
∇φ
2
|∇φ
2
|

δ
ε
(φ
2
), (10)
The function Φ(φ
1
, φ
2
) that minimizes the energy
functional E(Φ(φ
1
, φ
2
)) in (2) satisfies the Euler La-
grange equation −
∂E(Φ)
∂φ
1
= 0 and −
∂E(Φ)
∂φ
2
= 0. In (9)
and (10), λ
1
( f
1
− f
2
)) and λ
2
(c
2
− c
1
)) can respec-
tively be replaced by constants γ
1
and γ
2
:
∂φ
1
∂t
= γ
1
(I(x) − I
local
)δ
ε
(φ
1
)
+ v
1
div

g(I)
∇φ
1
|∇φ
1
|

δ
ε
(φ
1
) (11)
∂φ
2
∂t
= γ
2
(I(x) − I
global
)δ
ε
(φ
2
)
+ v
2
div

g(I)
∇φ
2
|∇φ
2
|

δ
ε
(φ
2
), (12)
A signed distance function (SDF) defined below
is used for the initialization of the level set functions:
φ
i
(x,t) =



−ρ, x ∈ Ω − O
i
0, x ∈ ∂O
i
ρ, x ∈ O
i
,
(13)
where ρ > 0 is a constant (ρ = 1 in this work). In
(11), t = 0 and i = 1, 2 define the initial conditions
of both level set functions. After evolving the level
set functions using (9) and (10), they are regularized
by using φ
k
i
= G
σ
2
∗ φ
k
i
, where i = 1, 2 represents the
number of level sets and k is the iteration number dur-
ing the curve evolution. The regularization mentioned
above not only regularizes the level set functions but
also eliminates the need for re-initialization, which is
computationally very expensive. Here, σ
2
is the stan-
dard deviation of the Gaussian kernel used in the reg-
ularization process.
Figure 1 shows a visual comparison of the pro-
posed method against the multiphase level set method
proposed in (Vese and Chan, 2002). This result shows
that the latter cannot properly segment the given im-
ages, since the intensity average obtained in that four-
phase active contour method is computed globally
over the whole image. Therefore, it cannot distin-
guish between different intensity levels if the intensity
differences are too small.
However, the proposed method, which utilizes
intensity means computed both locally and glob-
ally over the image, can successfully segment non-
overlapping regions. Local intensity means are
used to distinguish small intensity differences and to
segment intensity inhomogeneous regions, whereas
global intensity means are used to segment dark ho-
mogeneous regions. By using local intensity means
for small intensity difference, which may refers to
weak edges and incorporating global means for sharp
edges, the proposed method also deals with the energy
leakage problem. For the local computation of inten-
sity means, the proposed method applies the Gaus-
sian kernel defined in (Li et al., 2007; Li et al., 2008),
which is able to distinguish small intensity differences
in a local neighbourhood. Therefore, it can properly
segment small regions in the image.
2.2 Extraction of WM, GM and CSF
Regions
In this stage, the brain region is first delimited by us-
ing a binary mask manually defined by drawing the
contour along the boundary of the brain area. After
generating that mask, the level sets corresponding to
the final contours inside the brain area are extracted
by intersecting each level set obtained in the previ-
ous stage with the new binary mask. The combina-
tion of these modified level sets is then used to de-
fine the WM, GM and CSF regions as follows. Let
φ
i
(x, y) be the level sets associated with a given brain
MRI image I(x, y), i = 1, 2, be the number of level set
and mask(x, y) be the hand-drawn binary mask of the
brain area. The modified level sets ζ
i
(x, y) restricted
to the brain area can be described as:
ζ
i
(x, y) = φ
i
(x, y) ∩ mask(x, y), (14)
The combination of modified level sets that yields
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
450

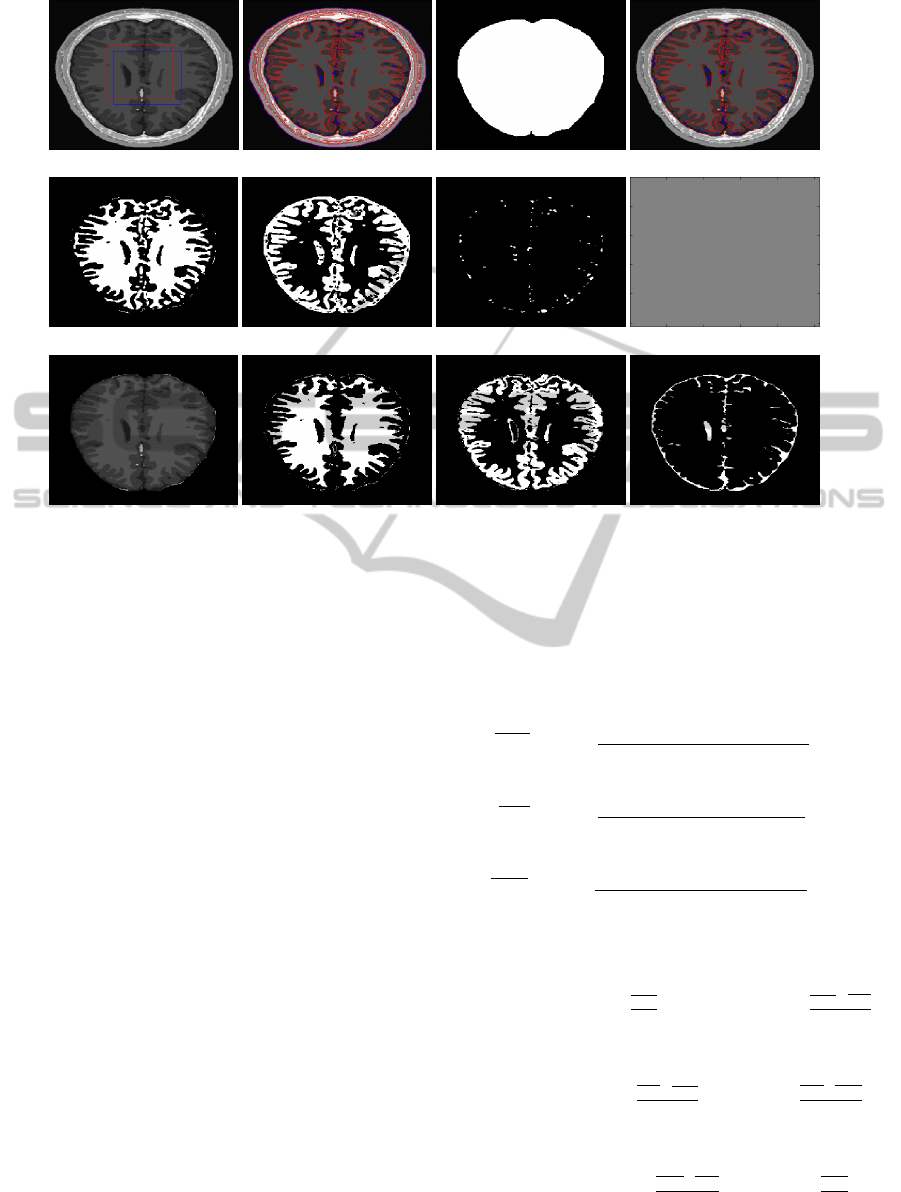
(a) (b) (c) (d)
(e) (f) (g) (h)
(i) (j) (k) (l)
Figure 2: Stages of the proposed algorithm. (a) Initial contour, (b) final contour, (c) binary mask of the brain region, (d) final
contour restricted to brain area, (e) ζ
1
> 0 and ζ
2
> 0 WM region, (f) ζ
1
< 0 and ζ
2
> 0 GM region, (g) ζ
1
< 0 and ζ
2
< 0
CSF region, (h) ζ
1
> 0 and ζ
2
< 0 region (empty or zero region, which is discarded), (i) extracted brain region with the binary
mask, (j) final WM region, (k) final GM region, (l) final CSF region.
the WM, GM and CSF binary regions is then defined
as:
W M(x, y) = (ζ
1
(x, y) > 0) ∩ (ζ
2
(x, y) > 0),
GM(x, y) = (ζ
1
(x, y) < 0) ∩ (ζ
2
(x, y) > 0),
CSF(x, y) = (ζ
1
(x, y) < 0) ∩ (ζ
2
(x, y) < 0),
Figures 2 (e), (f) and (g), respectively show an
example of the WM, GM and CSF regions com-
puted with the above combination of modified level
set functions.
2.3 Pixel Correction
In this last stage, the segmentation results obtained
after the previous stage are modified according to a
pixel correction algorithm based on simple threshold-
ing. The WM, GM and CSF binary regions computed
in previous stage are intersected with the input grey-
level image to compute the intensity average of their
non-zero pixels. These averages are then used to de-
fine a set of thresholds. If N is the number of rows and
columns (N = 256 in this work), the intensity means
corresponding to the three regions of interest are re-
spectively defined as:
W M(x, y) =
∑
N
x=1
∑
N
y=1
I(x, y)W M(x, y)
∑
N
x=1
∑
N
y=1
W M(x, y)
(15)
GM(x, y) =
∑
N
x=1
∑
N
y=1
I(x, y)GM(x, y)
∑
N
x=1
∑
N
y=1
GM(x, y)
(16)
CSF(x, y) =
∑
N
x=1
∑
N
y=1
I(x, y)CSF(x, y)
∑
N
x=1
∑
N
y=1
CSF(x, y)
, (17)
The binary images corresponding to the regions of
interest are finally defined as:
W M(x, y) =

1,
W M
2
+ 128 > I(x, y) >
W M+GM
2
0, otherwise
(18)
GM(x, y) =

1,
GM+W M
2
> I(x, y) >
GM+CSF
2
0, otherwise
(19)
CSF(x, y) =

1,
CSF +GM
2
> I(x, y) >
CSF
2
0, otherwise
(20)
MultiphaseRegion-basedActiveContoursforSemi-automaticSegmentationofBrainMRIImages
451

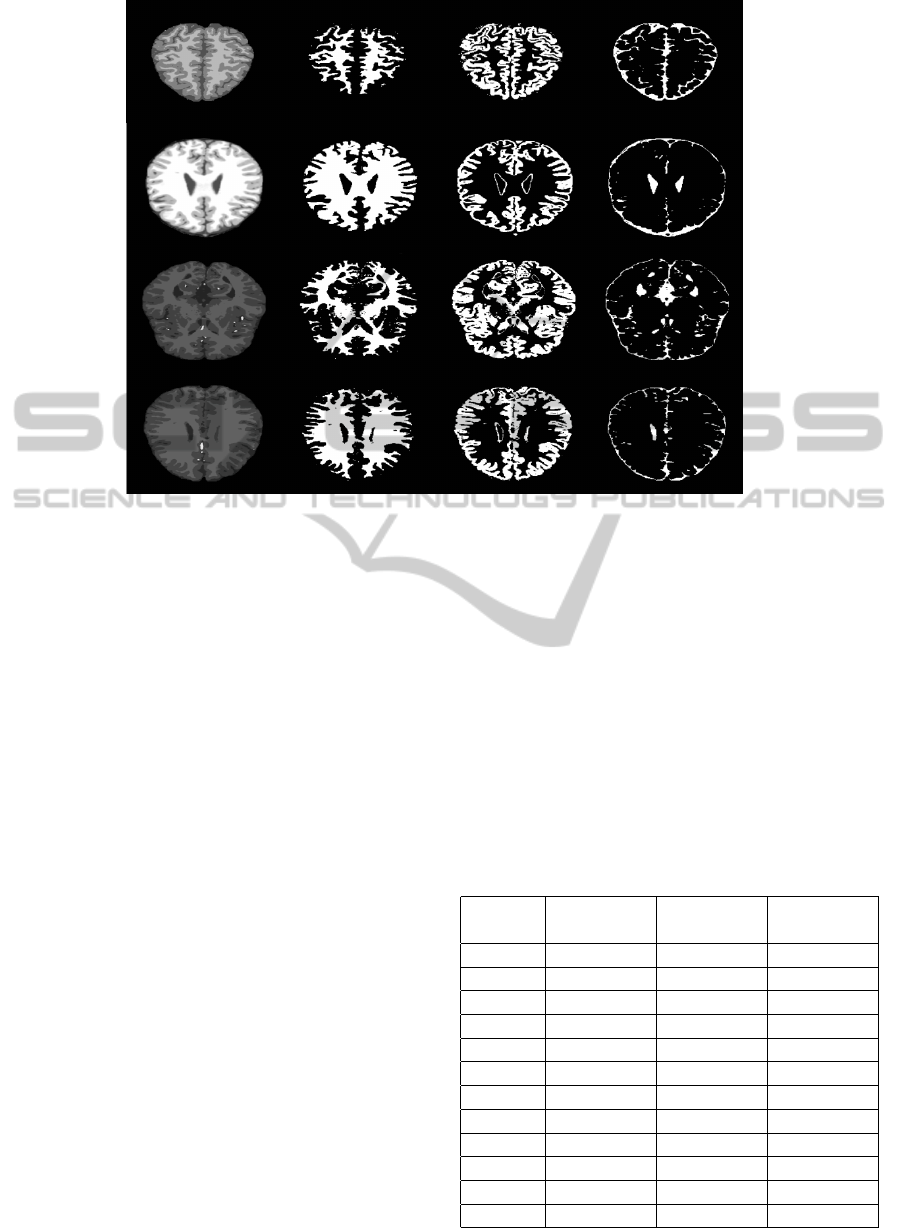
Figure 3: Segmentation of brain MRI image into distinct regions of interest. The first column shows the brain region after
applying the brain mask. The second column shows the segmented WM region after pixel correction. The third column shows
the segmented GM region after pixel correction. The fourth column shows the segmented CSF region after pixel correction.
3 EXPERIMENTAL RESULTS
The proposed method has been implemented using
MATLAB 7.12 on a 3.4 GHz Intel Core-i7 with 16GB
of RAM and tested on real brain MRI images of
256×256 pixels with 256 grey levels (8 bpp). These
images correspond to 20 brain anatomical models
(Brain, 2013). The following parameters have experi-
mentally been chosen: v
1
= 1, v
2
= 1, γ
1
= 1.5, γ
2
= 1,
ε = 1.5, ρ = 1, σ
1
= 3, σ
2
= 1, time step τ = 1, and
number of iterations n = 200.
Figure 2 shows results of the three stages of the
proposed method. Figure 2(a) shows a brain MRI im-
age with the initial contour. Figure 2(b) shows the fi-
nal contour using the proposed four-phase active con-
tour method. Figure 2(c) shows the hand-drawn bi-
nary mask of the brain area. Figure 2(d) displays
the final contour after restricting the growth of the
level set function to the brain area. Figure 2(e) shows
the extracted WM region from the modified level set
function with ζ
1
> 0 and ζ
2
> 0. Figure 2(f) shows
the extracted GM region obtained from the combina-
tion of the modified level set with ζ
1
< 0 and ζ
2
> 0.
Figure 2(g) shows the extracted CSF region obtained
from the modified level set function with ζ
1
< 0 and
ζ
2
< 0. Figure 2(h) shows the zero region obtained
from the modified level set function with ζ
1
> 0 and
ζ
2
< 0. Figure 2(i) shows the segmented brain region
by intersecting the given brain MRI image with the
binary mask of the brain region shown in Figure 2(c).
Figure 2(j) displays the final WM region after apply-
ing the pixel correction algorithm on the WM region
in Figure 2(e). Figure 2(k) displays the final GM re-
gion after applying the pixel correction algorithm on
the GM region in Figure 2(f). Finally, Figure 2(l) dis-
plays the final CSF region after applying the pixel cor-
rection algorithm on the CSF region in Figure 2(g).
Table 1: Percentage accuracy for test subject 035.
Slice WM GM CSF
number accuracy% accuracy% accuracy%
100 83.64 90.85 78.74
120 92.63 91.45 75.13
140 95.21 91.61 76.97
160 93.99 91.01 78.97
180 95.12 90.24 80.53
200 96.58 92.33 76.50
220 95.96 92.62 77.99
240 93.17 89.73 80.29
250 91.69 87.45 83.08
260 91.23 85.80 82.69
280 85.40 77.93 84.60
300 75.32 67.53 83.22
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
452

Table 2: Percentage accuracy of Vese-Chan multiphase and proposed method after stage 2 and stage 3 using slice number 210
in all of the test data (Brain, 2013).
Test
data
% Accuracy after stage 2 % Accuracy after stage 3
Vese-Chan method Proposed method Vese-Chan method Proposed method
CSF GM WM CSF GM WM CSF GM WM CSF GM WM
04 5.57 0.21 0.23 11.32 78.28 92.77 17.74 1.97 0.05 76.99 93.51 95.88
05 10.16 6.07 0.67 9.54 74.28 89.99 19.36 5.69 90.28 76.89 94.14 96.29
06 2.37 34.79 3.90 11.62 83.29 93.88 0.37 0 96.22 74.15 94.21 96.07
18 10.01 7.16 0.52 16.41 80.27 93.05 16.39 7.11 93.49 79.39 94.19 96.61
20 10.24 0 0 9.56 75.60 90.80 66.21 93.36 96.64 76.50 94.01 96.89
38 21.59 0.04 0.12 14.85 69.30 88.11 75.87 86.06 89.17 80.20 93.02 96.43
41 11.07 4.10 0.35 13.78 76.85 91.45 18.33 7.31 91.22 77.74 94.32 96.76
42 3.32 2.81 0.27 14.26 78.42 92.30 16.60 1.56 0.83 79.23 94.98 96.20
43 15.93 9.43 0.39 11.11 78.99 92.50 16.86 7.39 90.20 79.50 94.38 96.63
44 8.22 6.17 0.35 11.35 72.28 91.34 21.94 5.19 89.42 79.99 92.91 96.67
45 24.89 4.21 0.38 16.12 75.32 92.69 22.15 4.12 0.73 77.78 93.72 96.79
46 24.97 10.90 0.34 17.54 72.55 91 25.39 6.39 0.92 80.65 92.43 96.53
47 8.66 6.23 0.41 22.09 75.92 91.65 21.84 3.35 0 79.17 93.05 95.86
48 26.74 10.81 0.48 14.83 66.34 86.22 28.21 10.51 1.19 79.77 90.20 95.67
49 13.19 6.45 0.29 24.77 76.62 91.31 20.35 7.54 86.51 80.08 92.16 96.33
50 9.81 9.46 0.37 31.14 77.90 91.18 19.15 5.26 92.40 80.28 93.48 96.18
51 25.28 0 0 23.37 77.46 91.44 85.02 93.13 91.97 80.71 94.11 96.24
52 7.83 0 0 7.23 76.13 90.78 18.66 7.04 87.19 76.21 96.63 96.09
53 16.62 6.44 0.59 18.79 79.36 91.15 16.61 9.28 89.86 76.68 94.21 96.36
54 17.65 10.03 0.56 18.75 69.25 87.89 26.83 9.44 7.35 80.21 93.72 96.91
Table 1 shows the percentage accuracy of the
segmentation results of WM, GM and CSF regions
by comparing them with their respective ground
truths. It displays the segmentation accuracy for
different slices (2D images) of the test subject 04
from the 20 brain anatomical models (Brain, 2013).
The percentage accuracy of the proposed method is
computed by the following expression:
Accuracy =
|A ∩ B|
|A ∪ B|
× 100,
where |X | is the number of pixels equal to 1 (logical
true) in a given binary image X , A is the binary image
associated with the obtained region of interest (WM,
GM or CSF) and B is the ground truth corresponding
to that region.
Figure 3 shows the segmentation result of WM,
GM and CSF regions using the proposed method. The
first column in the figure displays the segmented brain
area after intersecting the given brain MRI image with
the hand-drawn binary mask of the brain region. The
second column displays the segmented WM region
after pixel correction. The third column displays the
segmented GM region after pixel correction. Finally,
the fourth column displays the segmented CSF region
after pixel correction.
Table 2 shows, accuracy comparison of segmen-
tation results between Vese-Chan and proposed meth-
ods with respect to given ground truth after stage 2
and stage 3. After stage 2, Vese-Chan method pro-
vides accuracy of 13.71%, 6.77% and 0.51% for CSF,
GM and WM, respectively. After stage 3, Vese-Chan
method provides accuracy of 27.69%, 18.59% and
59.78% for CSF, GM and WM, respectively. Af-
ter stage 2, proposed method provides accuracy of
15.92%, 75.72% and 91.08% for CSF, GM and WM,
respectively. After stage 3, proposed method provides
accuracy of 78.61%, 93.67% and 96.37% for CSF,
GM and WM, respectively.
Vese-Chan method that uses global intensity
means cannot properly segment images with intensity
inhomogeneity; therefore, it provides very less accu-
racy after stage 2. As we know that intensity inhomo-
geneous regions are not properly segmented by Vese-
Chan method, therefore, pixel correction method in
stage 3 cannot effectively improve its segmentation
results.
The proposed method provides quite acceptable
segmentation accuracy of GM and WM regions after
stage 2. But it provides very less segmentation accu-
racy of CSF region. After applying pixel correction
algorithm in stage 3 not only segmentation result of
CSF is improved but also segmentation result of GM
and WM are refined.
MultiphaseRegion-basedActiveContoursforSemi-automaticSegmentationofBrainMRIImages
453

4 CONCLUSIONS AND FUTURE
WORK
Segmentation of brain MRI images into distinct and
non-overlapping regions, such as WM, GM and CSF,
is a challenging problem due to the geometric com-
plexity of the regions to be segmented. The pres-
ence of noise and intensity inhomogeneity in the im-
age significantly increases the complexity of the prob-
lem. Since, there are three important regions (WM,
GM and CSF) in the brain area, a four-phase level
set method is necessary for segmenting the image into
three or four regions. This paper presents a four-phase
region based active contour method that segments an
MRI brain image into WM, GM and CSF regions with
a good accuracy. It uses both local and global inten-
sity averages in the definition of an energy functional,
such that local intensity mean values help the pro-
posed model to segment regions with intensity inho-
mogeneity, whereas global intensity mean values are
responsible for segmenting the homogeneous areas in
the image. In addition, a pixel correction method
based on simple thresholding is applied in order to
correct wrong pixels.
As a future work we aim at developing a new en-
ergy functional that will be able to segment noisy in-
tensity inhomogeneous images efficiently. This in-
volves the definition of a more efficient and robust
active contour method based on local texture regions.
Another research goal is the development of an auto-
matic technique to extract the brain area necessary for
intersecting the obtained level sets, thus avoiding the
hand-drawn binary mask utilized in the second stage
of the proposed technique.
ACKNOWLEDGEMENTS
This work was supported by the Spanish Government
through project TIN2012-37171-C02-02 and Cata-
lan Government Predoctoral grant AGAUR FI-DGR
2014.
REFERENCES
Akram, F., Kim, J. H., and Choi, K. N. (2013). Active
contour method with locally computed signed pres-
sure force function: An application to brain mr image
segmentation. In Seventh International Conference on
Image and Graphics (ICIG), pages 154–159. IEEE.
Akram, F., Kim, J. H., Lim, H. U., and Choi, K. N. (2014).
Segmentation of intensity inhomogeneous brain mr
images using active contours. Computational and
Mathematical Methods in Medicine, 2014:1–14.
Aubert, G. and Kornprobst, P. (2006). Mathematical Prob-
lems in Image Processing: Partial Differential Equa-
tions and the Calculus of Variations. Springer, New
York, 2nd edition.
Balafar, M. A., Ramli, A. R., Saripan, M. I., and Mashohor,
S. (2010). Review of brain mri image segmentation
methods. Artificial Intelligence Review, 33(3):261–
274.
Brain, A. M. (2013). Brain web: 20 anatomical models
of 20 normal brains, available at. http://brainweb.bic.
mni.mcgill.ca/brainweb/anatomic normal 20.html.
Caselles, V., Kimmel, R., and Sapiro, G. (1997). Geodesic
active contours. International Journal of Computer
Vision, 22(1):61–79.
Chan, T. F. and Vese, L. A. (2001). Active contours with-
out edges. IEEE Transactions on Image processing,
10(2):266–277.
Elnakib, A., Gimelfarb, G., Suri, J. S., and El-Baz, A.
(2011). Medical image segmentation: A brief sur-
vey. In Multi Modality State-of-the-Art Medical Image
Segmentation and Registration Methodologies, pages
1–39. Springer.
Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:
Active contour models. International Journal of Com-
puter Vision, 1(4):321–331.
Li, C., Kao, C.-Y., Gore, J. C., and Ding, Z. (2007). Implicit
active contours driven by local binary fitting energy.
In IEEE Conference on Computer Vision and Pattern
Recognition, CVPR’07., pages 1–7. IEEE.
Li, C., Kao, C.-Y., Gore, J. C., and Ding, Z. (2008). Min-
imization of region-scalable fitting energy for image
segmentation. IEEE Transactions on Image Process-
ing, 17(10):1940–1949.
Li, C., Xu, C., Gui, C., and Fox, M. D. (2005). Level set
evolution without re-initialization: a new variational
formulation. In IEEE Conference on Computer Vision
and Pattern Recognition, CVPR’05., pages 430–436.
IEEE.
Mumford, D. and Shah, J. (1989). Optimal approximations
by piecewise smooth functions and associated varia-
tional problems. Communications on Pure and Ap-
plied Mathematics, 42(5):577–685.
Vese, L. A. and Chan, T. F. (2002). A multiphase level set
framework for image segmentation using the mum-
ford and shah model. International Journal of Com-
puter Vision, 50(3):271–293.
Yang, Y., Li, C., Kao, C.-Y., and Osher, S. (2010). Split
bregman method for minimization of region-scalable
fitting energy for image segmentation. In Advances in
Visual Computing, pages 117–128. Springer.
Zhang, K., Song, H., and Zhang, L. (2010). Active contours
driven by local image fitting energy. Pattern Recogni-
tion, 43(4):1199–1206.
Zhang, Y., Matuszewski, B. J., Shark, L.-K., and Moore,
C. J. (2007). A novel medical image segmentation
method using dynamic programming. In International
Conference on Medical Information Visualisation-
BioMedical Visualisation, MediVis’07., pages 69–74.
IEEE.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
454