WaPT

Surface Normal Estimation for Improved Template Matching in Visual Tracking

Nagore Barrena

, Jairo R. S

anchez

and Alejandro Garc

ıa-Alonso

Interactive Computer Graphics, Vicomtech-Ik4, Donostia, San Sebasti

an, Spain

Industry and Advanced Manufacturing, Vicomtech-Ik4, Donostia, San Sebasti

an, Spain

Computer Science and Artiﬁcial Intelligent, University of the Basque Country, Donostia, San Sebasti

an, Spain

Keywords:

Surface Normal, Template Matching, Markerless Tracking.

Abstract:

This paper presents an algorithm which is an improvement of the template matching technique. The main goal

of the algorithm is to match 3D points with their corresponding 2D points in the images. In the presented

method, each 3D point is enriched with a normal vector that approximates the orientation of the surface where

the 3D point is lying. This normal improves the transfer process of patches providing more precise warped

patches, because perspective deformation is taken into account. The results obtained with the proposed transfer

method conﬁrm that matching is more accurate than traditional approaches.

1 INTRODUCTION

Nowadays, optical tracking methods are used in many

ﬁelds like robot navigation or augmented reality. In

essence they establish a relationship between an inter-

nal representation of the real scene (3D point cloud)

and the images which are captured by the camera.

In the case of markerless tracking methods the most

common solutions rely on matching some 3D points

with their corresponding 2D points in each image.

Among the most used techniques are matching us-

ing feature descriptors. These techniques are robust

against illumination, orientation and scale changes.

However, they present some efﬁciency problems. For

this reason while feature descriptors based methods

are kept for the initial matching, other techniques,

like optical ﬂow, are used to track the 2D correspon-

dences throughout video sequences. As optical ﬂow

estimates iteratively the displacement of each feature

from frame to frame, it is prone to drift. In order

to obtain more accuracy and palliate the drift in the

tracking process, methods like template matching are

normally used.

In these methods, for each 3D point of the point

cloud a patch around its projection from a reference

frame is saved as a reference template. Then template

matching techniques are applied during the tracking.

However, due to camera motion and the geometry of

the real scene, the matching with the reference tem-

plate can fail because of perspective deformations, as

can be seen in Figure 1. Nevertheless, in order to

solve the mentioned problems, the reference template

can be warped taking into account the camera position

and the geometry of the real scene.

Figure 1: Perspective deformations.

This paper presents an algorithm denominated

WaPT (Warped Template Patch Tracking). It im-

proves the patch transfer process and generates a more

accurate warped patch. Consequently, the template

matching process is more accurate.

WaPT extends the internal representation of the

real scene: each 3D point will have a normal vector

that approximates the orientation of the real surface

where it is placed on. In this way, the reconstruc-

tion process does not only ﬁnd 3D points, but it also

approximates their surface normals. WaPT uses this

orientation in order to improve the template matching

process.

The paper is structured as follows. Section 2 re-

views related publications in visual tracking. Section

496

Barrena N., Sánchez J. and García-Alonso A..

WaPT - Surface Normal Estimation for Improved Template Matching in Visual Tracking.

DOI: 10.5220/0005295104960503

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 496-503

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

3 describes in detail the WaPT method and the under-

lying template transfer and matching processes. Af-

terwards, Section 4 shows the experiments carried on

to evaluate this proposal, alongside a discussion. The

paper concludes in Section 5 with conclusions and

hints for future work.

2 RELATED WORK

Template matching techniques have been used by sev-

eral authors in order to match 2D features with 3D

points. Markerless tracking methods as visual SLAM

(Davison, 2003) match 3D points of the reconstructed

point cloud with their corresponding 2D points in the

images. In order to achieve this goal, the feature de-

tection and matching is one of the most used meth-

ods. In this way, SIFT (Lowe, 2004), FREAK (Alahi

et al., 2012) and SURF (Bay et al., 2006) are very

robust algorithms thanks to their invariance to illumi-

nation, scale and orientation changes. Consequently

the probability of a correct match is high. However,

the feature detection and matching process requires a

high computational cost.

Some authors like (Barron et al., 1994) use opti-

cal ﬂow techniques to estimate the image velocity, or

the shift of an speciﬁc point from frame to frame. Al-

though this method has lower computational cost, the

estimation of the feature displacement is not as accu-

rate as other methods and it is prone to drift.

On the other hand, relatively large image patches

can serve as features. Good examples are provided

by (Davison et al., 2007) and (Klein and Murray,

2007) who use patches as features. In order to match

correctly these patches, they use template matching

methods. The template matching processes use differ-

ent operators to estimate the similarity of the patches.

Sum of absolute difference (from now on SAD) (Wat-

man et al., 2004) is one of them. However, in order to

get better results against changes, for example bright-

ness, there are alternatives like the cross-correlation

coefﬁcient or the normalized cross-correlation coefﬁ-

cient operators (Szeliski, 2010).

Template matching methods may fail to obtain

the correspondences due to camera motion and per-

spective deformations. Surface orientation can be

used in order to take into account these deforma-

tions. (Molton et al., 2004) suggest a SLAM algo-

rithm which uses a probabilistic method to estimate

the most probable surface orientation in each mea-

surement. Later on, (Davison et al., 2007) make a

simpliﬁcation: they assume that 3D points always lie

on a planar surface oriented to the camera where they

were ﬁrst seen. They assume that the appearance of

the patch will not change at all.

However, (Furukawa and Ponce, 2010) obtain

very effective model reconstructions of statues and ar-

chitectural elements. The work emphasizes that the

use of surface orientation helped a lot to obtain such

good results.

For this reason WaPT extends the approach

proposing an analytic method to estimate the real ori-

entation of the 3D point in pre-process, in order to

warp the template patch better and to obtain more ac-

curacy in the matching process.

3 WaPT METHOD

Based on the work by (Davison et al., 2007), 3D

points are considered features that will be projected

into the query images to get the localisation of the

camera in real-time. In order to make this process ac-

curately WaPT follows two main stages:

3D Reconstruction Stage

A 3D reconstruction of the environment is done

and the estimation of a normal vector is calculated

for each 3D point. This normal deﬁnes the orien-

tation of the surface where the 3D point is placed

on. This process is run off-line and the main goal

is to get the point cloud of the environment and

the orientation of each 3D point to make the patch

transfer procedure more accurate in the next stage.

Tracking Stage

For each input frame the following steps are done

on-line:

1. Using the normal estimations calculated in the

3D Reconstruction stage the reference template

is warped, i.e a ﬁxed size patch is transferred

from the current image to the reference image

(where the point was ﬁrst seen during the 3D

reconstruction). Then, using a similarity mea-

surement the transferred patch is located in the

current image, and the center of this patch is

treated as a feature.

2. Then, the vector of features obtained in the pre-

vious step is used to calculate the pose of the

camera.

The following sections are devoted to describe in

detail the two stages of the WaPT algorithm.

3.1 3D Reconstruction Stage

The objective of the 3D Reconstruction Stage (pre-

process) is to generate a 3D representation of the en-

vironment. This representation should be the most

WaPT-SurfaceNormalEstimationforImprovedTemplateMatchinginVisualTracking

497

appropriate for the Tracking stage. The output of this

phase is a point cloud where a normal vector is as-

sociated to each 3D point. Each 3D point lies on a

surface of the environment and its associated vector

approximates the surface normal. To the best of our

knowledge previous work does not address the normal

estimation problem and only computes the 3D points.

The point cloud is obtained using the Structure

from Motion method (Dellaert et al., 2000), which

will be named from now on SfM. SfM combines

multi-view techniques with a Bundle Adjustment pro-

cess (Triggs et al., 2000). Its input is a sequence of

images of the environment. The images used in the

SfM process are denominated keyFrames. The goal

of our work in this paper is to estimate the normal for

each 3D point of the point cloud obtained by SfM.

To achieve this objective a minimization process has

been designed and implemented.

Consider the case shown in Figure 2. There are

two keyFrames where the same point is visible. The

keyFrame where the point was ﬁrst seen is denom-

inated Reference keyframe. A normal vector is as-

sociated to the 3D point deﬁning a plane. The ﬁg-

ure shows the projections of the 3D point on each

keyFrame. It also shows two patches around the pro-

jected 3D point and the plane deﬁned by the 3D point

and the normal.

Assume the following deﬁnitions:

Transferred Patch. A square patch deﬁned around

the projected 3D point in every keyFrame where the

3D point is visible, except the Reference keyFrame.

Reference Patch. The patch obtained when a given

Transferred patch is transferred to the Reference

keyFrame: the warped patch.

The process to obtain a Reference patch is the fol-

lowing one: given any 3D point, its projection onto

the keyFrame is used to deﬁne a Transferred patch.

Then, this Transferred patch is back-projected onto

the plane associated to the 3D point. This new poly-

gon is projected onto the Reference keyFrame gener-

ating the Reference patch (see Figure 2).

The objective of the minimization algorithm is to

ﬁnd the normal that minimizes the image difference

between the two image patches.

This work uses the Levenberg-Marquardt mini-

mization algorithm (Mor

e, 1978). This algorithm is

an iterative process, where a random normal is taken

as the initial guess. The plane deﬁned by the normal

is then used to transfer the Transferred patches to the

Reference keyFrame. Afterwards the algorithm eval-

uates the difference between the Transferred patch

and the Reference patch. The minimization algorithm

adjusts the normal so that the difference between all

the Transferred patches with the Reference patch is

the smallest. The algorithm exits when the difference

between the last iteration and the current one does not

exceed a ﬁxed threshold.

Let us explain in detail the enumerated steps:

3.1.1 Feature Plane

In the projective space a plane is deﬁned as shown

in equation (1) (Hartley and Zisserman, 2003). In

order to get it, three points (

) lying on the

plane are needed.

is used to represent the given

3D point. The other two points (

and

) are cal-

culated using the normal vector and the restriction

imposed by equation (2), where (a,b,c)

is the nor-

mal and (x, y, z)

the 3D point in the euclidean space.

Take into account that d is deﬁned by equation (3).

This equation presents singularities when the normal

is aligned with one of the main axis.

π =

(

−

) × (

−

)

−

(

)

(1)

ax + by +cz +d = 0 (2)

d = −(ax

+ by

+ cz

) (3)

3.1.2 Transfer the Patch

Each pixel of the Transferred patch is back-projected

onto the plane, i.e. each pixel of the Transferred patch

deﬁnes a point as the intersection of its back-projected

ray and the plane. Then, these points are projected to

the Reference keyFrame. The process can be seen in

Figure 2.

The back-projection of the point in the im-

age is deﬁned by equation (4), where P

is the

Moore-Penrose pseudo-inverse projection matrix of

the keyFrame and

C is the center of the camera in the

global reference system. In addition, a point which

lies in a plane must fulﬁl equation (5). Solving this

equation system the points are obtained. Then, the

projections of these points in the Reference keyFrame

are done, in order to obtain the Reference patch.

X = P

∗~x + λ ∗

C (4)

∗

X = 0 (5)

3.1.3 Evaluate Difference between Patches

In order to evaluate the difference between the im-

ages of the Transferred patch and Reference patch

the cross-correlation coefﬁcient is used. The cross-

correlation coefﬁcient is a measure of similarity of

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

498

Figure 2: Transfer process: back-projection of two points from the Transferred patch onto the Reference keyFrame using a

plane associated to a 3D point.

two images, where a perfect match will be 1 and

a perfect mismatch will be −1. WaPT algorithm

looks for the highest similarity between Reference

and Transferred patches. So, the value of the cross-

correlation coefﬁcient has to be as high as possible.

However, notice that this value is used in a minimiza-

tion process. For this reason the objective function

shown in equation (6) is used to evaluate the differ-

ence between patches, being crossCorrelation

the

normalized cross-correlation coefﬁcient of the patch

applied in frame i, and α,β the two angles used in the

parametrization of a normal.

min(α,β)

∑

(1 − crossCorrelation

(α,β)) (6)

3.2 Tracking Stage

As in all tracking processes the main goal of this one

is to obtain the camera extrinsic parameters for each

input frame. In this case the input data used for this

purpose is:

1. ReferenceImage set: A set of images and their

extrinsic parameters. They are the Reference

keyFrames. Recall that a Reference keyFrame is

where a 3D point was visible the ﬁrst time in the

3D Reconstruction stage.

2. PointCloud: a set with all the 3D points that build

a 3D reconstruction of the environment and their

normals. This set was obtained in the 3D Recon-

struction stage. Each 3D point stores the index

of its Reference keyFrame in the ReferenceImage

set.

The goal is to ﬁnd the projections of the 3D points

in the current image in order to localise the image.

With this purpose, n points from the PointCloud are

randomly chosen as features for the current image.

Through empiric processes, n = 50 has been chosen

for the experiments presented in this paper. These

points are projected onto the current frame. As it is

assumed that the shift between frames is small the ex-

trinsic parameters of the previous frame are used.

An adjustment has to be done in order to obtain the

position of the 3D points in the current image more

accurately. For each approximated projection of a 3D

point we deﬁne a patch. Then, two main steps are

performed to make the adjustment correctly:

1. Transfer the patch from the current image to the

Reference keyFrame of the 3D point. In this way,

a Reference patch is obtained.

2. A search process is performed, i.e. look for the

most similar patch to the Reference patch within

the current frame (similarity measurement).

3.2.1 Patch Transfer

The patch transfer is done using the same process as in

the 3D Reconstruction stage. Firstly, the projection of

the 3D point on the current image is used as the center

of the Transferred patch. Using the normal of the 3D

point the plane is obtained. Then, using this plane

the back-projection for each Transferred patch pixel is

done. The intensity of the pixel in the Reference patch

is obtained using bilinear intensity interpolation. In

this way, the image of the Reference patch is obtained.

WaPT-SurfaceNormalEstimationforImprovedTemplateMatchinginVisualTracking

499

3.2.2 Find Adjusted Projected Point

The goal of this step is to ﬁnd the patch in the cur-

rent image with the highest similarity to the Reference

patch. With this purpose the cross-correlation coefﬁ-

cient is applied into an established search area. The

search area is a ﬁxed size window W within the cur-

rent image. The projection of the 3D point is its cen-

ter. Experimentally we found that a 128 × 128 search

area gives good results in 720 ×480 images.

In order to achieve more accuracy in the search

process a three level pyramidal reduction is applied.

In this way:

• The three level reduction of W is calculated ob-

taining W

, W

and W

where W = W

• I is the original image, i.e the current image.

• In addition, a three level pyramidal reduction is

also calculated for the Reference patch R obtain-

ing R

, R

and R

where R = R

Notice that R

, R

and R

are the same im-

age with different resolutions. In order to get robust-

ness against noise the patches that will be used in the

search process are ﬁxed size regions placed in the cen-

ter of R

, R

and R

. Through empiric processes,

8 × 8 regions have been chosen for the experiments

presented in this paper.

Once the pyramidal levels are deﬁned an iter-

ative process is run. In this iterative process the

match uses ﬁrstly the lowest pyramidal levels (W

and R

).Then, the result is propagated to the higher

levels (seen Figure 3).

Figure 3: Iterative process where the similarity of the refer-

ence patches in different pyramidal levels is calculated. The

propagation of the adjusted feature from the lowest pyrami-

dal level to the current image can be seen as a result of the

process.

So, ﬁrstly R

is found in W

using the cross-

correlation coefﬁcient and the 8 × 8 region places in

the center of R

. The function returns a position in

of the region with the highest similarity to R

This position is propagated to the next level, i.e W

The search area of W

is redeﬁned taking into ac-

count the position calculated in the previous step, ob-

taining W

, which is smaller than W

. The pro-

cesses are repeated and R

is found in W

This iteration process is repeated until the position

is propagated to the ﬁnal level, W

, and ﬁnally to the

original image I. In Figure 3 the propagation of the

point from different levels can be seen.

This process is done for the n points, obtaining a

set with n features that will be used to ﬁnd the extrin-

sic parameters of the current camera.

4 EXPERIMENTAL RESULTS

This section evaluates the performance and precision

of the proposed algorithm. To measure the accuracy

of the algorithm, the similarity between the Reference

patch and the current patch is measured. The results

of our algorithm are compared to the approach em-

ployed by MonoSLAM (Davison et al., 2007), which

assumes that the orientation of the 3D points always

faces the camera.

With this purpose, an indoor video sequence was

recorded where a camera motion around the same

work place is visualized. The video sequence is built

by approximately 70 frames with 720 × 480 resolu-

tion.

As mentioned previously, in order to evaluate the

WaPT algorithm the similarity between patches is cal-

culated. The normalized cross-correlation coefﬁcient

is used for this purpose. The value ranges between

[−1,1], where 1 indicates that the patches are the

same and −1 perfect mismatch.

In the ﬁrst experiment, the similarity of the Ref-

erence patch and the current patch is calculated for

n = 50 points. The average of the normalized cross-

correlation coefﬁcient of all the points for each frame

is calculated. Figure 4 shows the evolution of these

averages during the video sequence: the WaPT al-

gorithm is represented with a red line whereas the

approach used by MonoSLAM is represented with a

blue line.

The average cross-correlation coefﬁcient value for

WaPT algorithm is 0.639 and in the case of the ap-

proach used by MonoSLAM algorithm is 0.574, i.e

the similarity of the patches is higher with the WaPT

algorithm.

On the other hand, for each frame the median and

the quartiles of the cross-correlation coefﬁcient val-

ues are calculated. These statistics are used to mea-

sure the stability of both algorithms. Figure 5 shows

the box-plots for the ﬁrst 10 frames for the WaPT

algorithm and Figure 6 depicts the same informa-

tion for the approach sued by MonoSLAM algorithm.

With the aim of making the comparison visually sim-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

500

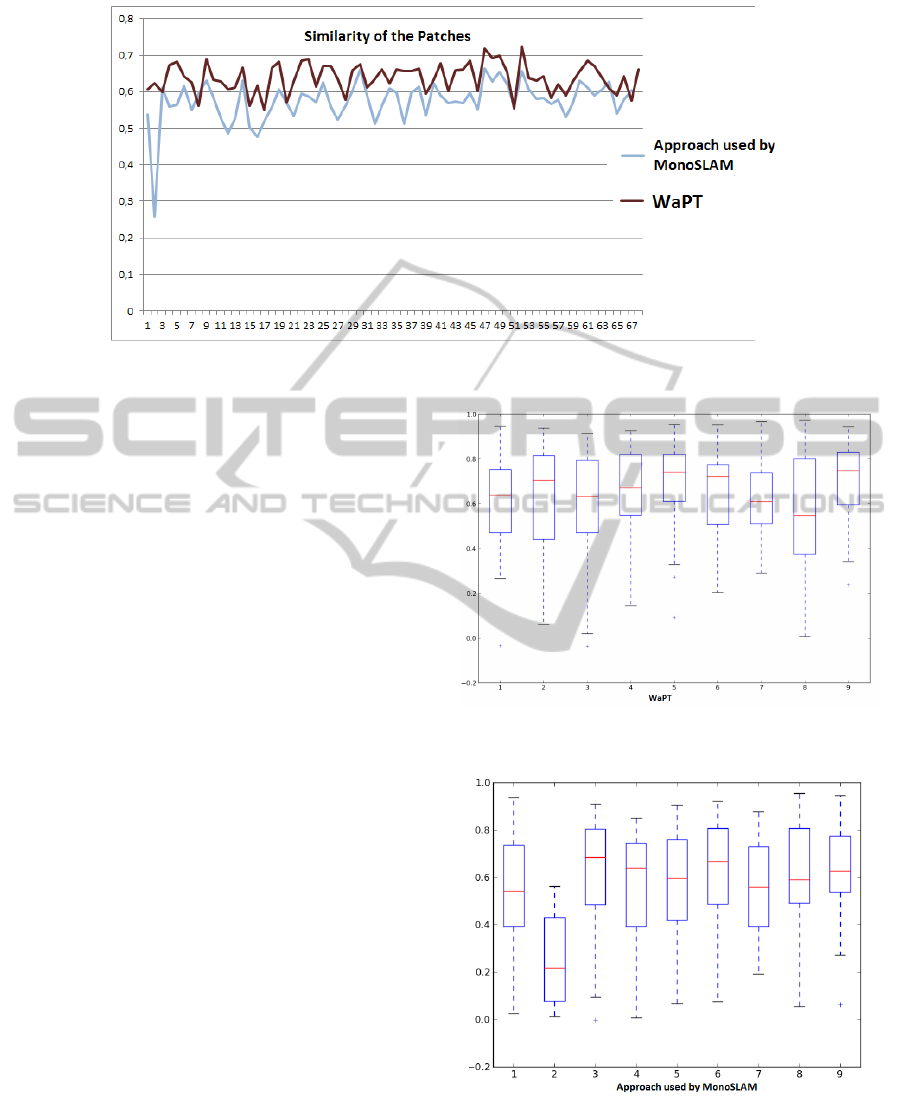
Figure 4: Evolution of the cross-correlation coefﬁcient average values.

pler, only the ﬁrst 10 frames are provided. These 10

frames are representative of the performance of the

algorithms.

4.1 Discussion

The ﬁrst discussion point is the difference between

the average normalized cross-correlation coefﬁcient

values appreciated in Figure 4. As it can be seen in

the ﬁgure, the WaPT algorithm obtains higher cross-

correlation coefﬁcient values during the video se-

quence. These values deﬁne the similarity between

images, and have to be as close as possible to 1.

Therefore, applying WaPT algorithm the template

matching process is more accurate due to the similar-

ity of the patches, i.e. WaPT algorithm obtains more

similar patches than approach used by MonoSLAM.

Furthermore, the average of cross-correlation co-

efﬁcient values in both algorithms conﬁrms that state-

ment. The average value for WaPT algorithm (0.639)

is 11% higher than the value obtained for the ap-

proach used by MonoSLAM (0.574). It means that

taking into account that similarity is measured in

range [−1, 1], WaPT lacks a 18% to achieve a perfect

match while approach used by MonoSLAM lacks a

29%.

The graphics shown in Figures 5 and 6 repre-

sent the distribution of a continuous variable (cross-

correlation coefﬁcient) for both algorithms respec-

tively. The 3rd quartiles in the WaPT algorithm

are higher than in the case of approach used by

MonoSLAM.

Regarding the median values, the same trend is

observed. The median values in WaPT algorithm are

higher than in approach used by MonoSLAM. As a

general trend, it is appreciated that the WaPT algo-

rithm gets more similar patches than the approach

Figure 5: Box-plots of the cross-correlation coefﬁcient val-

ues in the ﬁrst 10 frames. WaPT algorithm.

Figure 6: Box-plots of the cross-correlation coefﬁcient val-

ues in the ﬁrst 10 frames. Approach used by MonoSLAM

algorithm.

used by MonoSLAM.

The box-plots graphics demonstrate it; the 3rd

quartiles, the median values and even the minimum

WaPT-SurfaceNormalEstimationforImprovedTemplateMatchinginVisualTracking

501

values are higher in the case of WaPT.

All exposed data conﬁrms that, in this test, the

WaPT algorithm improves the accuracy in the tem-

plate matching process, getting consequently more

accurate feature positions. In autonomous navigation

systems the tracking process has to be done in large

environments where the data from sensors help to im-

prove the tracking process. So, matching improve-

ments are not critical.

Nevertheless, in augmented reality applications,

the accuracy is very important to visualize the vir-

tual elements correctly, that is, drift and jitter must

be reduced as much as possible. In augmented reality

applications this contribution might provide a valu-

able improvement. It is more accurately than template

matching algorithms used in traditional methods.

5 CONCLUSIONS AND FUTURE

WORK

The work presented in this paper proposes a new in-

ternal representation of the environment for marker-

less tracking. Besides the point cloud, a normal vector

for each point is also stored.

In the 3D reconstruction process, not only the 3D

points of the environment are calculated. A minimiza-

tion process is also run in order to estimate the best

normal for each point.

In the tracking process these normals are used to

obtain an improved warped template in order to obtain

a more precise matching.

Perspective deformations are reduced when tem-

plate matching techniques and patches as features are

used.

The results obtained in Section 4 are a ﬁrst vali-

dation. In this validation, the similarity of the patches

are calculated in order to know the matching process

precision. The results have been favourable to WaPT,

proving its higher accuracy. This approach provides

more precision than traditional methods, which as-

sume that the points are facing the camera.

When more experiments conﬁrm the results pro-

vided by this paper, new research should be done in

order to ﬁnd methods that accelerate the reconstruc-

tion process for surface normals. One possible ap-

proach could be to start assuming that all surfaces

face the camera as (Davison et al., 2007) and, on-line,

perform a progressive improvement. These normals

might be also useful for surface illumination com-

pensation when comparing images taken in different

lighting conditions.

As future work more validations are planed. Se-

quences with different perspectives, where points do

not face the camera, will be used. In this kind of se-

quences, the traditional methods should be even more

compromised.

In WaPT, the Reference patch is located in the

Reference keyFrame, which is the keyFrame where

the point was ﬁrst seen. In order to improve more the

precision and the patch similarities, it is planed to use

as the Reference keyframe the one where the point is

visible and it is more similar to the current image.

ACKNOWLEDGEMENTS

Work partially funded by the Spanish Ministry of

Economy and Competitiveness. Project ELAS-

TRACK (TIN2012-33879).

REFERENCES

Alahi, A., Ortiz, R., and Vandergheynst, P. (2012). Freak:

Fast retina keypoint. In Computer Vision and Pat-

tern Recognition (CVPR), 2012 IEEE Conference on,

pages 510–517. Ieee.

Barron, J. L., Fleet, D. J., and Beauchemin, S. S. (1994).

Performance of optical ﬂow techniques. 12:43–77.

Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:

Speeded up robust features. In Computer Vision–

ECCV 2006, pages 404–417. Springer.

Davison, A. J. (2003). Real-time simultaneous localisa-

tion and mapping with a single camera. In Computer

Vision, 2003. Proceedings. Ninth IEEE International

Conference on, pages 1403–1410. IEEE.

Davison, A. J., Reid, I. D., Molton, N. D., and Stasse, O.

(2007). Monoslam: Real-time single camera slam.

In Pattern Analysis and Machine Intelligence, IEEE

Transactions on, volume 29, pages 1052–1067. IEEE.

Dellaert, F., Seitz, S. M., Thorpe, C. E., and Thrun, S.

(2000). Structure from motion without correspon-

dence. In Computer Vision and Pattern Recognition,

2000. Proceedings. IEEE Conference on, volume 2,

pages 557–564. IEEE.

Furukawa, Y. and Ponce, J. (2010). Accurate, dense, and

robust multiview stereopsis. 32(8):1362–1376.

Hartley, R. and Zisserman, A. (2003). Multiple view geom-

etry in computer vision. Cambridge university press.

Klein, G. and Murray, D. (2007). Parallel tracking and map-

ping for small ar workspaces. In Mixed and Aug-

mented Reality, 2007. ISMAR 2007. 6th IEEE and

ACM International Symposium on, pages 225–234.

IEEE.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. 60:91–110.

Molton, N., Davison, A. J., and Reid, I. (2004). Locally pla-

nar patch features for real-time structure from motion.

In BMVC, pages 1–10.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

502

Mor

e, J. J. (1978). The levenberg-marquardt algorithm: im-

plementation and theory. In Numerical analysis, pages

105–116. Springer.

Szeliski, R. (2010). Computer vision: algorithms and ap-

plications. Springer.

Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgibbon,

A. W. (2000). Bundle adjustmenta modern synthesis.

In Vision algorithms: theory and practice, pages 298–

372. Springer.

Watman, C., Austin, D., Barnes, N., Overett, G., and

Thompson, S. (2004). Fast sum of absolute differ-

ences visual landmark detector. In Robotics and Au-

tomation, 2004. Proceedings. ICRA’04. 2004 IEEE

International Conference on, volume 5, pages 4827–

4832. IEEE.

WaPT-SurfaceNormalEstimationforImprovedTemplateMatchinginVisualTracking

503