
Simultaneous Frame-rate Up-conversion of Image and Optical Flow
Sequences
Shun Inagaki
1
, Hayato Itoh
1
and Atsushi Imiya
2
1
School of Advanced Integration Science, Chiba University, Yayoi-cho 1-33, Inage-ku, 263-8522, Chiba, Japan
2
Institute of Management and Information Technologies, Chiba University, Yayoi-cho 1-33, Inage-ku, 263-8522, Chiba,
Japan
Keywords:
Up-conversion, Optical Flow, Long Time Image-sequence, Variational Image Analysis.
Abstract:
We develop a variational method for the frame-rate up-conversion of optical flow fields, in which we combine
motion coherency in an image sequence and the smoothness of the temporal flow field. Since optical flow
vectors define the motion of each point in an image, we can construct interframe images from low frame-rate
image sequences using flow field vectors. The algorithm produces both interframe images and optical flow
fields from a set of successive images in a sequence.
1 INTRODUCTION
In this paper, we develop a variational method for
the frame-rate up-conversion of optical flow fields
and video sequences. We combine image registra-
tion and optical flow computation for frame-rate up-
conversion. Therefore, our algorithm produces both
interframe images and optical flow fields from a set
of successive images in a sequence.
For the application of well-established image
analysis algorithms to low-frame-rate image se-
quences, which are common in bio-imaging and long-
distance extrapolation, we are required to up-convert
the frame rate of image sequences. In this conversion,
the generation of interframe images is a fundamen-
tal requirement. Our proposed method generates the
interframe images of a sequence to analyse motions
in the sequence. The frame rate of images by long-
distance extrapolation using a vehicle-mounted imag-
ing system is low. To understand environment using
optical flow field (Vardy and Moller, 2005) from such
a low frame-rate image sequence, we are required to
generate a temporally dense optical flow field, since
well-established algorithms used to decipher images
assume to use a high-frame-rate image sequence. To
resolve this problem on the application of traditional
method to use low-frame-rate image sequences, we
are required to up-convert the optical flow field.
An optical flow field is a deformation field be-
tween two temporally successive frames. Therefore,
the frame rate of an optical flow sequence depends on
the frame rate of the input image sequence. The frame
rate of a video sequence interpolated by interframe
images is twice as high as that of the input video se-
quence. Therefore, increasing the frame rate of an
optical-flow field sequence is required to up-convert
the frame rate of the input image sequence by inter-
polating frames.
The methods of frame interpolation use optical-
flow fields to generate inter-frame images. Several
methods of frame-rate up-conversion for an image se-
quence using the optical flow field have been pro-
posed (Werlberger et al., 2011; Lee et al., 2010). In
this conversion, although for the generation of sub-
frame images, the frame-rate up-conversion of an im-
age sequence is a fundamental requirement, our ob-
jective is the up-conversion of the optical flow field
sequence. However, our method generates subframe
images of a sequence as intermediate information.
Superresolution recovers high-resolution images
and/or image sequences from a low-resolution im-
ages and/or image sequences. There are some meth-
ods based on temporal coherence (Volz et al., 2011;
Mobahi et al., 2012; Zimmer et al., 2011), which is
based on the idea that successive frames have simi-
lar contents and small transformations (Sadek et al.,
2009). Therefore, temporal coherence is effective for
sequences of successive images. These method sup-
pose a tube through frames in this assumption. In ref.
(Volz et al., 2011; Zimmer et al., 2011), the authors
proposed a method to calculate optical-flow fields by
modelling the motion fields as being smooth along
their trajectories. Furthermore, in ref. (Mobahi et al.,
2012), the authors developed an interpolation method
between two input images based on temporal coher-
ence. Therefore, we introduce the assumption of tem-
68
Inagaki S., Itoh H. and Imiya A..
Simultaneous Frame-rate Up-conversion of Image and Optical Flow Sequences.
DOI: 10.5220/0005296800680075
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 68-75
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

poral coherence into optical flow temporal superreso-
lution method. This implies we assume that the image
sequences we calculate are temporally coherent.
Warping and morphing are fundamental tech-
niques in computer graphics to interpolate and gener-
ate shapes and objects. In medical applications, mor-
phing is used for the description of the deformation
process of biological organs. This process predicts the
deformable motion of biological organs in the human
torso such as the beating heart, and the deformation
of lungs the during breathing. Shape retrieval cate-
gorises and classifies shapes, and finds shapes from
portions of shapes. In shape retrieval, the matching of
shapes based on the diffeomorphism of shapes (Ar-
rate et al., 2010) is used. In the matching process of
images, the variational registration strategy (Moder-
sitzki, 2004) is a typical tool.
In computer vision, a well-established evaluation
method is the computation of least mean error be-
tween the ground truth and computed results. In up-
conversion, there is, however, no ground truth for the
evaluation of the up-converted results Therefore, we
cannot evaluate results using tradition method in com-
puter vision. For the evaluation of the up-converted
optical flow field and images, we compute the tempo-
ral continuity of the field and image sequences. In this
paper, we also prove the convergence condition for
the simultaneous up-conversion of the optical-flow-
field and image sequences. This condition conforms
the uniqueness of the up-converted sequences.
2 INTER-FRAME
OPTICAL-FLOW FIELD
Setting f(x
x
x,t) to be a spatiotemporal image, we de-
velop an algorithm to compute the optical-flow field
u
u
u
1
2
(x
x
x,t) of f(x
x
x,t +
1
2
). For the convenience of analy-
sis, we set
f
+
(x
x
x) = f(x
x
x,t + 1), f
−
(x
x
x,t) = f(x
x
x,t), (1)
g(x
x
x) = f(x
x
x,t +
1
2
), (2)
v
v
v = u
u
u
1
2
(x
x
x,t), w
w
w = u
u
u
1
2
(x
x
x,t +
1
2
). (3)
Furthermore, stting
g(x
x
x) = f
+
(x
x
x−w
w
w), g(x
x
x) = f
−
(x
x
x+v
v
v), u
u
u = v
v
v+w
w
w, (4)
we can have the interframe image g and the up-
converted optical flow fields, v
v
v and w
w
w as the minimis-
ers of
J(g,v
v
v,w
w
w) = I
+
+ I
−
+ αG+ βU + γV, (5)
for
1
I
+
=
Z
Ω
Ω
Ω
(g(x
x
x) − f
+
(x
x
x−w
w
w))
2
dx
x
x, (6)
I
−
=
Z
Ω
Ω
Ω
(g(x
x
x) − f
−
(x
x
x+ v
v
v))
2
dx
x
x, (7)
G =
Z
Ω
Ω
Ω
|∇g|
2
dx
x
x, (8)
U =
Z
Ω
Ω
Ω
(|∇v
v
v|
2
+ |∇w
w
w|
2
)dx
x
x, (9)
V = |v
v
v+ w
w
w−u
u
u|
2
, (10)
where |x
x
x| is the l
2
-norm of the vector x
x
x. Figure 1 (a)
shows the relationships of eq. (4). We extend eq. (5)
v
w
u
f
- f
+
g
x
y
T
t t+1/2 t+1
(a)
flame tg
1
f
1
f
2
g
2
f
3
v
1
w
1
v
2
w
2
(b)
Figure 1: Interframe optical flow. (a) g, f
−
, f
+
, u
u
u, v
v
v and
w
w
w. (b) Input images f
1
, f
2
and f
3
, output images g
k
and
g
k+1
, and output optical flow v
v
v
k
, w
w
w
k
, v
v
v
k+1
and w
w
w
k+1
. The
constant-intensity timeline tube is smooth along with the
trajectories of optical-flow fields.
to an image sequence. Let the interframe image g
k
be
the image between two given frames
f
k
:= f(x,y,k), f
k+1
:= f(x,y,k + 1). (11)
Setting the vectors v
v
v
k
and w
w
w
k
to be the flow vector
fields between f
k
and g
k
and between g
k
and f
k+1
,
respectively, we assume that each v
v
v
k
and w
w
w
k
satisfy
the optical flow constraint. Then, we have the energy
functional
J({g
k
,v
v
v
k
,w
w
w
k
}
n−1
k=1
) =
Z
Ω
(J
d
+ αJ
g
+ βJ
s
+ γJ
t
)dx
x
x,
(12)
where
J
d
=
n−1
∑
k=1
((g
k
(x
x
x) − f
k
(x
x
x+ v
v
v
k
))
2
+( f
k+1
(x
x
x−w
w
w
k
) −g
k
(x
x
x))
2
), (13)
J
g
=
n−1
∑
k=1
|∇g
k
|
2
dx
x
x (14)
J
s
=
n−1
∑
k=1
(|∇v
v
v
k
|
2
+ |∇w
w
w
k
|
2
), (15)
J
t
= J
1st
t
+ J
2nd
t
, (16)
1
For vector-valued function f
f
f from R
2
to R
2
, the vector
gradient ∇f
f
f is a 2×2 matrix. The norm |∇ f
f
f| is the Frobe-
nius norm of ∇ f
f
f which is defined as
q
tr∇ f
f
f∇f
f
f
⊤
, where
trF
F
F is the trace of the matrix F
F
F.
SimultaneousFrame-rateUp-conversionofImageandOpticalFlowSequences
69

for
J
1st
t
=
n−1
∑
k=1
(|w
w
w
k
−v
v
v
k
|
2
)
+
n−2
∑
k=1
(|v
v
v
k+1
−w
w
w
k
|
2
) (17)
J
2nd
t
=
n−2
∑
k=1
(|v
v
v
k+1
−2w
w
w
k
+ v
v
v
k
|
2
+|w
w
w
k+1
−2v
v
v
k
+ w
w
w
k
|
2
). (18)
Here, J
d
is the data term for image registration. J
s
,
J
t
and J
g
are regularisation terms for the computa-
tion of smooth flow fields. The constraints J
1st
t
and
J
2nd
t
require that the flow field is temporally piece-
wise smooth and temporally piecewise linear, respec-
tively. As the minimisers of the variational problem,
we obtain vector fields v
v
v
k
and w
w
w
k
and generate g
k
si-
multaneously for the estimation of higher-frame-rate
optical-flow fields and images.
3 NUMERICAL METHOD
3.1 Discretisation
To minimise the energy functional of eq. (12), setting
V
k
= (g
k
(x
x
x) − f
k
(x
x
x+ v
v
v
k
))∇f
k
(x
x
x+ v
v
v
k
)
+γ
1
(2v
v
v
k
−w
w
w
k
−w
w
w
k−1
)
+γ
2
(v
v
v
k+1
−4w
w
w
k
+ 6v
v
v
k
−4w
w
w
k−1
+ v
v
v
k−1
),
(19)
W
k
= (g
k
(x
x
x) − f
k+1
(x
x
x−w
w
w
k
))∇f
k+1
(x
x
x−w
w
w
k
)
+γ
1
(2w
w
w
k
−v
v
v
k
−v
v
v
k+1
)
+γ
2
(w
w
w
k+1
−4v
v
v
k+1
+ 6w
w
w
k
−4v
v
v
k
+ w
w
w
k−1
),
(20)
G
k
= (2g
k
(x
x
x) −( f
k
(x
x
x+ v
v
v
k
) + f
k+1
(x
x
x−w
w
w
k
))),
(21)
the Euler-Lagrange equations of eq. (12) are
∆v
v
v
k
−
V
k
β
= 0,
∆w
w
w
k
−
W
k
β
= 0, (22)
∆g
k
−
G
k
α
= 0.
For the associate diffusion equations of the Euler-
Lagrange equations of eq. (22),
∂v
v
v
k
∂t
= ∆v
v
v
k
−
1
β
V
k
,
∂w
w
w
k
∂t
= ∆w
w
w
k
−
1
β
W
k
, (23)
∂g
k
∂t
= ∆g
k
(x
x
x) −
1
α
G
k
using semi-implicit discretisation, we obtain the iter-
ation form
(I
I
I −τL
L
L)v
v
v
(m+1)
k
= v
v
v
(m)
k
−
τ
β
V
(m)
k
,
(I
I
I −τL
L
L)w
w
w
(m+1)
k
= w
w
w
(m)
k
−
τ
β
W
(m)
k
, (24)
(I
I
I −τL
L
L)g
(m+1)
k
= g
(m)
k
−
τ
α
G
(m)
k
,
where L
L
L and I
I
I are the discrete Laplacian matrix and
the identity matrix whose degree depends on the size
of the discrete images.
In each step of the iteration, the results are ex-
pressed on the Euler frame. Image samples obtained
by the Lagrange frame do not guarantee correspon-
dence between points. Therefore, we resample the
results using the Lagrange frame
2
. In the Lagrange-
frame-sampled images, we use Delaunay-triangle-
based interpolation (Hjelle and Daehlen, 2006), since
the method satisfies the minimum gradient property.
The iteration forms (Varga, 2000) derived in the
previous sections are described in the form
(I
I
I −τL
L
L)a
a
a
(m+1)
= a
a
a
(m)
− f(a
a
a
(m)
). (25)
The Laplacian matrix L
L
L is described as
L
L
L = D
D
D⊗I
I
I + I
I
I ⊗D
D
D, (26)
D
D
D =
−1 1 0 ··· 0 0 0
1 −2 1 ··· 0 0 0
0 1 −2 ··· 0 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 ··· 1 −2 1
0 0 0 ··· 0 1 −1
,
where A
A
A ⊗ B
B
B is the Kronecker product of matrices
A
A
A and B
B
B, assuming the Newmann condition on the
boundary.
The eigenvalues of D
D
D are λ
k
= 4sin
2
πk
2M
for the
M ×M matrix (Demmel, 1997), and the eigenmatrix
(Strang and Nguyen, 1996) of D
D
D is
Φ
Φ
Φ =
εcos
(2j + 1)i
2π
πM
, (27)
ε =
1 if j = 0
1
√
2
otherwise.
2
There are two reference frames, which are called
the Euler frame and Lagrange frame (Modersitzki, 2004).
When we have an image B and an invertible transform ϕ,
the frames are described as B
Lagrange
(ϕ(i, j)) := B(i, j) and
B
Euler
(i, j) := B(ϕ
−1
(i, j)).
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
70

Φ
Φ
Φ is the matrix of the DCT-II transform. Therefore,
the matrix L
L
L is decomposed as
L
L
L = (Φ
Φ
Φ⊗Φ
Φ
Φ)(Λ
Λ
Λ⊗I
I
I + I
I
I ⊗Λ
Λ
Λ)(Φ
Φ
Φ
⊤
⊗Φ
Φ
Φ
⊤
) = U
U
UΣ
Σ
ΣU
U
U
⊤
(28)
and the eigenvalues of L
L
L are λ
i
+ λ
j
. Then, since eq.
(25) is redescribed as
a
a
a
(m+1)
= U
U
U
⊤
(I
I
I −τΣ
Σ
Σ)
−1
U
U
U(a
a
a
(m)
− f(a
a
a
(m)
)), (29)
where
(I
I
I −τΣ
Σ
Σ)
−1
= Diag
1
1−τ(λ
i
+ λ
j
)
, (30)
that is, a
a
a
(m+1)
is numerically computed from a
a
a
(m)
us-
ing DCT-II (Strang and Nguyen, 1996) and a filtering
operation for the Neumann boundary condition.
3.2 Convergence Conditions
3.2.1 Double Frame Method
For the case n = 2, the interframe images g is com-
puted from a pair of frames f(·,t) and f(·,t + 1).
From the third equation of (23), we have the iteration
form
g
g
g
(m+1)
= U
U
U(I
I
I −τΣ
Σ
Σ)
−1
U
U
U
⊤
(1−
2τ
α
)g
g
g
(m)
+ c
c
c
(m)
, (31)
For a large m, we can assume that c
c
c
(m)
is a constant
vector. The iteration form
g
g
g
(m+1)
= U
U
U(I
I
I −τΣ
Σ
Σ)
−1
U
U
U
⊤
(1−
2τ
α
)g
g
g
(m)
+ c
c
c, (32)
converges to a unique solution, if the relation
max(|(1−
2τ
α
)|) ≤ 1, (33)
is satisfied. This condition derived from spectral ra-
dius of the matrix (I
I
I −τΣ
Σ
Σ)
−1
leads to the conclusion
that the iteration form of eq. (32) produces a sequence
g
g
g
(m)
for m ≥ 1 which converges a unique solution, if
τ ≤ α.
For the up-conversion of the optical flow field,
setting c
c
c =
γτ
β
(w
w
w − u
u
u) and κ
κ
κ ≥
γτ
β
( f
f
f
−
(x
x
x + v
v
v) −
g
g
g(x
x
x))∇
v
f
f
f
−
(x
x
x+ v
v
v) we define the iteration form
v
v
v
(m+1)
= U
U
U(I
I
I −τΣ
Σ
Σ)
−1
U
U
U
⊤
(1−
γτ
β
)v
v
v
(m)
+c
c
c+ κ
κ
κ. (34)
for the copulation of v
v
v.
Assuming |f
f
f
−
(x
x
x + v
v
v) −g
g
g(x
x
x)| ≪ 1 for a large m,
and
γτ
β
1−
γτ
β
≪ 1, (35)
for τ ≪
β
2γ
and τ ≤
2β
γ
the iteration form converges.
These conditions derives the conclusion that τ ≪
β
2γ
and τ ≤
2β
γ
for convergence of the iteration form. The
convergence of the computation of w
w
w is evaluated us-
ing the same iteration form with eq. (34).
3.2.2 Multiple Frame Method
Setting ξ = −
τ
α
( f
k
(x
x
x + v
v
v
k
) + f
k+1
(x
x
x −w
w
w
k
)) we have
the iteration form
g
g
g
(m+1)
= U
U
U(I
I
I −τΣ
Σ
Σ)
−1
U
U
U
⊤
(1−
2τ
α
)g
g
g
(m)
+ ξ, (36)
Using the same methodology to evaluate the conver-
gence condition for 5, we have the condition τ ≤ α.
Setting X
X
X = (v
v
v
1
,w
w
w
1
,v
v
v
2
,.. .,v
v
v
n
,w
w
w
n
) we have the it-
eration form
X
X
X
(m+1)
= U
U
U(I
I
I −τΣ
Σ
Σ)
−1
U
U
U
⊤
X
X
X
(m)
Φ
Φ
Φ
⊤
(I
I
I −
τ
β
((−Λ
Λ
Λ) + (−Λ
Λ
Λ)
2
))Φ
Φ
Φ+ κ
κ
κ,
(37)
where
κ
κ
κ =
τ
β
(g
k
(x
x
x) − f
k
(x
x
x+ v
v
v
k
))∇f
k
(x
x
x+ v
v
v
k
)
τ
β
(g
k
(x
x
x) − f
k+1
(x
x
x−w
w
w
k
))∇f
k+1
(x
x
x−w
w
w
k
)
!
⊤
.
(38)
Therefore, the spectral radius of matrix
M
M
M = (I
I
I −
τ
β
((−Λ) + (−Λ)
2
))Φ
Φ
Φ+ κ
κ
κ), (39)
decides the convergence condition. The maximum
value of the matrix M
M
M is established for λ =
1
2
. Fur-
thermore, the relation
max(|1−
τ
β
((−λ) + (−λ)
2
)|) = 1 ≤ 1. (40)
is satisfied. These condition implies that the iteration
form for flow computation yields a unique solution.
3.3 Multiresolution Method
For the up-conversion of the optical flow field, we
are required to establish point correspondences from
a large-displacement image sequence. Therefore, for
the initial estimation of point correspondences we
adopt the coarse-to-fine strategy using the pyramid
transform. By establishing point correspondences
in the higher level of the pyramid, we compute up-
converted optical flow fields and the interframe im-
age. as shown in Figure 2. Then, we estimate the
point correspondences in the lower level in the pyra-
mid by using the coarse-to-fine grid expansion.
Figure 2 illustrates a frame-rate up-conversion
method with Gaussian pyramid transform. In this
pipeline, By establishing point correspondencesin the
higher level of the pyramid, this pipeline first up-
converts the optical flow fields and the interframe im-
age. The recursively the algorithm estimates point
correspondences on the lower level in the pyramid
by using the coarse-to-fine grid expansion. In this al-
gorithm, the number frameNumber
once
is selected as
three for the method.
SimultaneousFrame-rateUp-conversionofImageandOpticalFlowSequences
71

Algorithm 1: Coarse-to-fine inter-frame optical flow com-
putation.
for k = 1 to frameNumber
all
− f rameNumber
once
do
if k = 1 then
for j = 0 to frameNumber
once
−1 do
v
v
v
k+ j
,w
w
w
k+ j
,g
k+ j
←
/
0
end for
end if
for i = 0 to maxPyramidLevel do
Downsizing of f
k
s to 2
−i
× Original Size
Solve eq. (23)
Upsizing of v
v
v
k
, w
w
w
k
and g
k
and setting as initial
value
end for
output v
v
v
k
,w
w
w
k
,g
k
for j = 0 to frameNumber
once
−1 do
v
v
v
k+ j
← v
v
v
k+ j+1
as initial value.
w
w
w
k+ j
←w
w
w
k+ j+1
as initial value.
g
k+ j
← g
k+ j+1
as initial value.
end for
end for
Figure 2: Multiframe image and optical flow up-conversion
with the coarse-to-fine strategy. By establishing point corre-
spondences in the higher level of the pyramid, the pipeline
computes the up-covered optical flow fields and the inter-
frame image. Then, the algorithm estimates point corre-
spondences on the lower level in the pyramid by using the
coarse-to-fine grid expansion.
4 NUMERICAL EXAMPLES
Figure 3 shows, from top to bottom, the images used,
the flow fields obtained by our algorithm, and the
ground-truth flow fields. In these examples, f(x,y,t)
and f(x,y,t + 2) are used as inputs. The sequences
are, from left to right, Yosemite, Grove2 and Rubber-
Whale. These results lead to the conclusion that the
semicircular part and checkered part in RubberWhale
are not calculated correctly. Since, in this example,
there are no specific features, optical-flow field is dif-
fused around.
Table 1 shows the errors between the computed
flow fields and ground-truth flow fields according to
(a) Yosemite (b) Grove2 (c) Rubber
(d) Yosemite (e) Grove2 (f) Rubber
(g) Yosemite (h) Grove2 (i) Rubber
Figure 3: Results of the two-frame method. (a) An im-
age from the Yosemite sequence. (b) An image from the
Grove2 sequence. (c) An image from the RubberWhale se-
quence. (d) The subframe optical flow field of the Yosemite
sequence. (e) The subframe optical flow field of the Grove2
sequence. (f) The subdrame optical flow field of the Rub-
berWhale sequence. (g) The ground-truth optical flow field
of the Yosemite sequence. (h) The ground-truth optical flow
field of the Grove2 sequence. (i) The ground-truth optical
flow field of the RubberWhale sequence.
the Middlebury evaluation page. Our method has two
to three times the error of well-established methods.
However, taking account of the fact that two flow
fields and one image between two frames are calcu-
lated, our scores are in an acceptable range.
Figure 4 (a) shows five sucessive images from the
Metronome sequence. Form this sequence, f(x,y,t)
and f(x, y,t + 2) are used as inputs for the evaluation
of our algorithm. Furthermore, f(x,y,t + 1) is used as
the ground truths. Smoothness and coherency of the
subframe images and optical-flow fields are evaluated
by the warp image error (WIE) and EMD such that
WIE
2
=
Z
R
2
|f(x
x
x−w
w
w
k
,t +1)− f(x
x
x+v
v
v
k
,t)|
2
dx
x
x. (41)
For the Metronom sequence, Fig. 4(b) shows,
from top to bottom row, three frames from the input
image sequence, the optical flow fields computed by
the large-displacement optical flow computation, the
subframe image sequence and its optical flow fields
computed by the two-frame method and the subframe
image sequence and its optical flow fields by the mul-
tiframe method using three frames.
Figure 5 shows histograms of the square norm of
the optical flow vectors of three methods; the linear
method (a), the two-frame method (b) and the three-
frame method (c). For linear interpolation, we set
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
72

Table 1: Angular errors and endpoint errors in Grove2CRubberWhale and Yosemite sequences. These values are averages in
one frame.
EndpointError(pixel) AngularError(degree)
mean std mean std
Grove2(v
v
v) 1.08 1.03 16.62 17.76
Grove2(w
w
w) 1.05 1.02 16.03 17.76
RubberWhale(v
v
v) 0.61 0.73 20.05 22.92
RubberWhale(w
w
w) 0.59 0.73 19.48 22.92
Yosemite(v
v
v) 0.46 0.81 8.59 12.60
Yosemite(w
w
w) 0.47 0.86 9.17 14.32
v
v
v = w
w
w = u
u
u/2. Figure 5(d) shows the average warp
image errors. Figure 5 shows the three-frame method
derives smooth high frame-rate optical flow fields by
computing interframe images.
Figure 6 shows the original image for the beat-
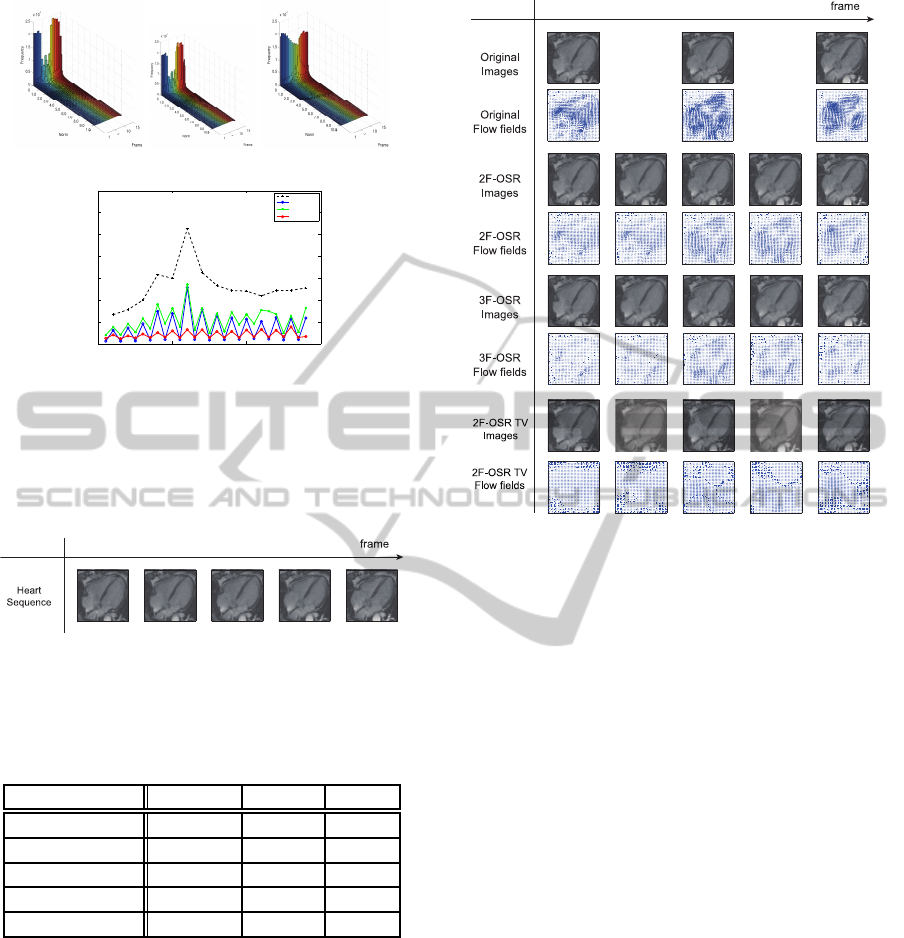
ing heart sequence. Fig. 7 shows, from top to bot-
tom row, shows three frames from the input image se-
quence, the optical flow fields computed by the large-
displacement optical flow computation, the subframe
image sequence and its optical flow fields computed
by the two-frame method and the subframe image se-
quence and and its optical flow fields by the multi-
frame method using three frames and the the sub-
frame image sequence and its optical flow fields by
2 frame TV method
3
. Figure 8 shows comparison of
the three-frame method and two-frame TV method.
Top and bottom rows are results for the three-frame
method and the two-frame TV method, respectively.
From left to right interframe images, v
v
v and w
w
w.
For the beating heart sequence, Fig. 9 shows his-
tograms of the square norm of the optical flow vec-
tors of four methods; the linear method (a), the two-
frame method (b) and the three-frame method (c) and
the two-frame method with TV constrain (d). Figures
9(e) is the average warp image errors for the beating
heart sequence.
Figures 4 and 6 show that the interframe images
are clearly generated. Furthermore, the smoothness
and coherence of time trajectory of optical flow fields
is evaluated by the earth movers’ distance between
histograms of norms of the optical flow vectors. Fig-
ures 5 and 9 show that the three-frame method pro-
duces smooth optical flow fields and smooth inter-
frame images. Figure 8 implies that, for the beating
heart sequence, the interframe optical flow fields com-
puted using smoothness constrain produces are clear
3
The functional derivative of the total variation (TV)
R
R
2
|∇f|dx
x
x of f is ∇
⊤
∇f
|∇f|
Numerically, ∇
⊤
∇f
√
|∇f|
2
+ε
2
,
where ε is a small positive number, is achieved for the com-
putation ∇
⊤
∇f
|∇f|
By replacing
R
R
2
|∇g|
2
dx
x
x and
R
R
2
|∇u
u
u|
2
dx
x
x
in eq.(5) to
R
R
2
|∇g|dx
x
x and
R
R
2
|∇u
u
u|
2
dx
x
x, we define the two-
frame TV method.
and accurate comparing the optical flow fields com-
puted by using TV constrain.
Tables 2 and 3 list the parameters for numeri-
cal experiments. Furthermore, for the 2 frame TV
method, we set ε = 10
−5
.
Table 2: Parameters for the 2 frame method.
α β γ
Card 8×10
−2
10
3
10
3
Metronome 8×10
−2
10
3
10
3
(a)
(b)
Figure 4: Up-conversion of the optical flow fields and in-
terframe images. (a) is the original image sequence of the
Metronome. (b) From the top to the bottom row, shows
three frames from the input image sequence, the optical
flow fields computed by the large-displacement optical flow
computation, the subframe image sequence and its opti-
cal flow fields computed by the two-frame method and the
subframe image sequence and its optical flow fields by the
multi-frame method using three frames.
SimultaneousFrame-rateUp-conversionofImageandOpticalFlowSequences
73
(a) Linear (b) 2frame (c) 3frame
0 5 10 15
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Frame
Temporal Gradient
Original
Linear
2 Frames(L
2
)
3 Frames(L
2
)
(d) Warp image error of Metronome
Figure 5: Statistical comparisons of methods I. (a), (b)
and (c) are histograms of least square norm of the optical
flow field for the linear method, the two-frame method and
the three-frame method, respectively, for the Metronome
sequence. (d) is the average warp image errors for the
Metronome, respectively.
(a)
Figure 6: Up-conversion of the optical flow fields and inter-
frame images for the beating heart sequence. The original
image sequence of the beating heart sequence.
Table 3: 3 Parameters for 3 frame method.
α β γ
Card 8×10
−2
3×10
2
3×10
Metronome 8×10
−2
10
3
10
2
Rubber Whale 7×10
−2
2×10
2
2×10
Grove 2 7×10
−2
2×10
2
2×10
Yosemite 7×10
−2
4×10
2
4×10
5 CONCLUSIONS
We developed a variational method for the frame-rate
up-conversion of the optical-flow field-sequence in
which we combine motion coherence in an image se-
quence and the smoothness of the temporal flow field.
For the evaluation of the accuracy of up-converted
sequences, we proposed a results evaluation method
without the ground truth. Furthermore, we have
proved the convergence condition for the numerical
method to up-convertthe optical-flow-field and image
(a)
Figure 7: Up-conversion of the optical flow fields and in-
terframe images for the beating heart sequence. From the
top to the bottom row, shows three frames from the input
image sequence, the optical flow fields computed by the
large-displacement optical flow computation, the subframe
image sequence and its optical flow fields computed by the
two-frame method and the subframe image sequence and
and its optical flow fields by the multi-frame method using
three frames and the subframe image sequence and its opti-
cal flow fields by 2 frame TV method.
sequences to conform the uniqueness of the solutions.
Since optical flow vectors define the motion of each
point in an image, we can construct interframe images
from low frame-rate image sequences using optical-
flow field vectors. This implies that our method can
be used to estimate ego-motion from a low frame-rate
image sequence obtained by remote exploration.
ACKNOWLEDGEMENTS
This research was supported by the “Computational
Anatomy for Computer-Aided Diagnosis and Ther-
apy: Frontiers of Medical Image Sciences” and “Mul-
tidisciplinary Computational Anatomy and Its Appli-
cation to Highly Intelligent Diagnosis and Therapy”
projects funded by a Grant-in-Aid for Scientific Re-
search on Innovative Areas from MEXT, Japan, and
by Grants-in-Aid for Scientific Research funded by
the Japan Society for the Promotion of Science.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
74

(a) Intrfram image (b) 3frame v
v
v (c) 3frame w
w
w
(d) Interframe im-
age
(e) 2frame TV v
v
v (f) 2frame TV w
w
w
Figure 8: Comparison of the three-frame and two-frame TV
methods. Top and bottom rows are results for the three-
frame method and the two-frame TV method, respectively.
From left to right interframe images, v
v
v and w
w
w.
1
2
3
4
5
6
7
8
9
10
0
1.0
2.0
3.0
4.0
5.0
+
0
0.5
1
1.5
2
2.5
3
3.5
x 10
4
Frame
Norm
Frequency
(a) Linear
1
2
3
4
5
6
7
8
9
10
0
1.0
2.0
3.0
4.0
5.0
+
0
0.5
1
1.5
2
2.5
3
3.5
x 10
4
Frame
Norm
Frequency
(b) 2frame
1
2
3
4
5
6
7
8
9
10
0
1.0
2.0
3.0
4.0
5.0
+
0
0.5
1
1.5
2
2.5
3
3.5
x 10
4
Frame
Norm
Frequency
(c) 3frame
1
2
3
4
5
6
7
8
9
10
0
1.0
2.0
3.0
4.0
5.0
+
0
0.5
1
1.5
2
2.5
3
3.5
x 10
4
Frame
Norm
Frequency
(d) 2fram-
eTV
1 2 3 4 5 6 7 8 9
0.03
0.035
0.04
0.045
0.05
0.055
0.06
0.065
0.07
0.075
Frame
Error
Linear
2 Frames(L
2
)
3 Frames(L
2
)
2 Frames(TV)
(e) Warp image error
Figure 9: Statistical comparisons of methods II. (a), (b), (c)
and (d) are histograms of least square norm of the optical
flow field for the linear method, the two-frame method, the
three-frame method, the two-frame method with TV con-
strain, respectively, for the Metronome sequence. (e) is the
average warp image errors for the beating heart sequence.
REFERENCES
Arrate, F., Ratnanather, J. T., and Younes, L. (2010). Diffeo-
morphic active contours. In SIAM J. Imaging Science,
volume 3, pages 176–198.
Demmel, J. W. (1997). Applied Numerical Linear Algebra.
SIAM, Philadelphia.
Hjelle, O. and Daehlen, M. (2006). Triangulations and Ap-
plications. Springer, Heidelberg.
Lee, W. H., Choi, Y., Choi, K., and Ra, J. B. (2010). Frame
rate up conversion via image fusion based on varia-
tional approach,. In Prceedings of 17th IEEE ICIP,
pages 335–888. IEEE.
Mobahi, H., Collobert, R., and Weston, J. (2012). Deep
learning from temporal coherence in video. In Proced-
dings of VISAPP2012, pages 367–372. SCITEPRESS.
Modersitzki, J. (2004). Numerical Methods for Image Reg-
istration. OUP, Oxford.
Sadek, R., Ballester, C., Garrido, L., Meinhardt, E., and
Caselles, V. (2009). Deep learning from temporal co-
herence in video,. In Proceddings of ICML09, pages
733–744. ACM.
Strang, G. and Nguyen, T. (1996). Wavelets and Filter
Banks. Wellesley-Cambridge Pres, Cambridge, MA.
Vardy, A. and Moller, R. (2005). Biologically plausible
visual homing methods based on optical flow tech-
niques. In Connection Science, volume 17, pages 47–
89.
Varga, R. S. (2000). Matrix Iterative Analysis. Springer,
Heidelberg, 2nd edition.
Volz, S., Bruhn, A., Valgaerts, L., and Zimmer, H. (2011).
Modeling temporal coherence for optical flow,. In
13th ICCV, pages 1116–1123. IEEE.
Werlberger, M., Pock, T., Unger, M., and Bischof, H.
(2011). Optical flow guided tv-l1 video interpolation
and restoration. In LNCS, volume 6819, pages 273–
286.
Zimmer, H., Bruhn, A., and Weickert, J. (2011). Optic flow
in harmony. In IJCV, volume 93, pages 368–388.
SimultaneousFrame-rateUp-conversionofImageandOpticalFlowSequences
75
