
A Comparison between Multi-Layer Perceptrons and Convolutional
Neural Networks for Text Image Super-Resolution
Cl
´
ement Peyrard
1,2
, Franck Mamalet
1
and Christophe Garcia
2
1
Orange Labs, 4 rue du Clos Courtel, 35512 Cesson-S
´
evign
´
e, France
2
LIRIS, INSA Lyon, 20 avenue Albert Einstein, Villeurbanne, France
Keywords:
Super-Resolution, Text Image, Multi-Layer Perceptron, Convolutional Neural Network, OCR.
Abstract:
We compare the performances of several Multi-Layer Perceptrons (MLPs) and Convolutional Neural Net-
works (ConvNets) for single text image Super-Resolution. We propose an example-based framework for both
MLP and ConvNet, where a non-linear mapping between pairs of patches and high-frequency pixel values is
learned. We then demonstrate that for equivalent complexity, ConvNets are better than MLPs at predicting
missing details in upsampled text images. To evaluate the performances, we make use of a recent database
(ULR-textSISR-2013a) along with different quality measures. We show that the proposed methods outper-
forms sparse coding-based methods for this database.
1 INTRODUCTION
Super-Resolution (SR) methods aim to provide a
high-definition image from one or several low resolu-
tion (LR) images. With the increasing quantity of vi-
sual data due to advances in information technologies
and portable devices, these methods have been exten-
sively studied in the last decades. SR can ensure a
better visual experience for HD displays or visual ap-
peal in videos or photographs, but also improve the re-
sults of automated resolution-dependent vision tasks
such as face recognition/detection or optical character
recognition (OCR), if used as a pre-processing step.
SR techniques can be divided into several cate-
gories. (Nasrollahi and Moeslund, 2014) provides a
complete overview of the existing methods, according
to the available single or multiple LR images. Mul-
tiple image Super-Resolution takes advantage of the
redundancy of the information in the different image
representing the same scene to merge this low res-
olution information into a high resolution (HR) im-
age after an alignment process. Several techniques
have been introduced such as Iterative Back Projec-
tions (Irani and Peleg, 1991), Projection Onto Convex
Sets (Stark and Oskoui, 1989), Maximum Likelihood
and Maximum A Posteriori (Cheeseman et al., 1996).
For Single Image Super-Resolution (SISR), the task
is of another nature as we only have one representa-
tion of the original scene. The recovery of the original
high-resolution is a drastically ill-posed inverse prob-
lem, and the details lost during the down-sampling
process might only be refined either by processing
an up-sampled version of the LR image (interpolation
or reconstruction based methods, such as (Sun et al.,
2011)), or by training a system on some external data
(Freeman et al., 2002) to hallucinate high-resolution
information from a LR one (learning-based methods).
More specifically, Text Image SR – also referred
to as Text Document SR – has been handle in dif-
ferent ways. Several methods have been proposed
or applied for multiple images (Donaldson and My-
ers, 2005; Mancas-Thillou et al., 2005; Protter et al.,
2009). For the task of Single Images, (Thouin and
Chang, 2000) used an iterative method to minimize
a Bimodal-Smoothness-Average score, (Dalley et al.,
2004) adopted a bayesian approach for SR of binary
text images. (Luong and Philips, 2007) proposed a
non-local search to take advantage of characters re-
dundancies in documents. (Zheng et al., 2014) pro-
posed a fast matting technique that consists in ex-
tracting and interpolate foreground, background and
a matte (proportion of foreground/background), and
enhance the matte layer with a Teager Filter before
using it to mix the foreground and background layers
back together.
Most recent and successful text image are learn-
ing based ones, and this paper will start with a short
survey in 2. We then express the SR problem in 3
and depict our proposal in 4. We describe our ex-
perimentations in 5 and present the obtained results.
84
Peyrard C., Mamalet F. and Garcia C..
A Comparison between Multi-Layer Perceptrons and Convolutional Neural Networks for Text Image Super-Resolution.
DOI: 10.5220/0005297200840091
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 84-91
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Conclusion and perspectives are finally given in 6.
2 LEARNING-BASED METHODS
FOR SUPER-RESOLUTION
We provide a quick review of some learning-based
methods for SISR.
2.1 Dictionnary Training and Sparse
Coding
Different learning framework have already been pro-
posed in the literature. Authors successively proposed
to learn dictionaries of LR/HR patch pairs called D
L
and D
H
, and reconstruct a SR image from a mixture
of the HR versions of the closest LR patches. (Free-
man et al., 2002) first proposed to look up for the 16
nearest neighbours in a dictionary and keep the high
patches showing a good spatial compatibility on over-
lapping region. A similar method have been applied
by(Fan et al., 2012) on text images. (Glasner et al.,
2009) set up a intra-image dictionary to take advan-
tage of the redundant structures inside an image at
different positions and scales. These methods exhibits
very good results given an image with redundancy
and a known Point Spread Function for the decima-
tion process.
Later, in (Yang et al., 2010; Walha et al., 2012),
authors proposed to find the best sparse representa-
tion of a feature vector y in D
L
(called
b
α) for the min-
imization problem:
b
α = argmin
α
k
y − D
L
α
k
2
2
+ λ
k
α
k
1
(1)
so that one can reconstruct the HR version of the cur-
rent patch with the same sparse
b
α, but using D
H
. To
ensure sparsity on
b
α, a regularization parameter is
added, here using `
1
norm. Note that in (Yang et al.,
2012) and (Peleg and Elad, 2014), Neural Networks
are used to speed up the choice of the sparse vector
α. In (Timofte et al., 2013), this speed-up is done by
pre-computing a neighbourhood for each atom in the
dictionary.
2.2 Autoencoders
With the recent work on autoencoding architectures,
two different approaches were proposed to take ad-
vantage of autoencoders for SR. The first one (Gao
et al., 2013) is strongly related to sparse coding meth-
ods. It encodes a dictionary of LR/HR patch pairs in a
Restricted Boltzmann Machine and take advantage of
the RBM framework to iteratively reconstruct an HR
image as a sparse mixture of the embedded patches,
via a sparse activation of hidden neurons. The second
(Nakashika et al., 2013) makes use of a Deep Belief
Network to learn the autoencoding of the DCT coef-
ficients of HR images. Then, from the low-frequency
coefficient of a scaled-up LR image, the network iter-
atively recovers high-frequency as it is the only kind
of image it has learned to produce. (Peleg and Elad,
2014) also use a RBM to encode a relationship be-
tween sparse representations in overcomplete dictio-
naries.
2.3 Artificial Neural-networks Based
Methods
ANN are architectures inspired from the human brain.
They interconnect cells that perform a non-linear
mapping between their weighted inputs (”dendrites”)
and their output (”axone”). The Perceptron model
was first introduced by (Rosenblatt, 1958) to model
human neurons. It applies a non-linear function Φ
(such as tanh) to the weighted sum of its inputs (see
1).
y = Φ
w
bias
+
N
∑
i=1
w
i
x
i
!
(2)
…
Figure 1: Perceptron Model.
ANN for SR were introduced in (Ahmed et al.,
1995; Plaziac, 1999), where they proposed to take ad-
vantage of a neural networks to handle interpolation
problems: how to choose the best missing pixel be-
tween existing pixels. Later, (Pan and Zhang, 2003)
successfully applied a neural network design to es-
timate residual errors in an HR estimate from the
ones in LR on natural and text images. The first
model presented in this paper is related to their as we
want to automatically learn how to infer missing de-
tails. (Panagiotopoulou and Anastassopoulos, 2007)
trained a network successively using examples at dif-
ferent scales for scanned document SR. (Carcenac,
2007) proposed a Neural Network architecture for
face image super-resolution. Recently, (Dong et al.,
2014) proposed a Deep Convolutional Neural Net-
work, that maps an interpolated image to its HR coun-
terpart. A first layer is employed to extract features
AComparisonbetweenMulti-LayerPerceptronsandConvolutionalNeuralNetworksforTextImageSuper-Resolution
85

maps, which are non-linearly mapped onto a second
layer of feature maps of the same size. Finally, a fu-
sion of the maps is performed by a single fully con-
nected convolution.
In the present work, we compare two neural based
approaches and favour a high frequency restoration
scheme rather than an intensity based one.
3 PROBLEM FORMULATION
We model the SR problem by a reconstruction pro-
cess. Given an HR image x and its LR counterpart
y, we want to infer the missing details in an upscaled
version of the LR image. Therefore, we choose a sim-
ple interpolation method (e.g. bicubic) that produces
an estimate
b
x
bic
of the SR image. This estimate is
often smooth, blurry, and may also present ringing ar-
tifacts.
At each position (k,l) of an image, the estimate
b
x
bic
(k, l) differs from the original (or ideal HR) image
x(k, l) by an error e(k, l), defined as:
e(k, l) = x (k, l)−
b
x
bic
(k, l) (3)
the estimate
b
x
bic
being the upscaled version of the
original LR image:
b
x
bic
= f
I
(y) (4)
with an interpolation function f
I
. Therefore, we want
a SR system to be able to provide an estimate
b
e(k, l)
of this difference. This difference can be considered
as high spatial frequency information, as the interpo-
lated image gives a smooth version of the desired HR
image. The reconstruction process is then:
b
x
SR
=
b
x
bic
+
b
e (5)
In the next section, we present the set up of two
neural-based architectures able to provide this esti-
mate.
4 PROPOSED METHODS
In this paper, we aim to compare two neural networks
models for the SR problem. For both, the framework
is the same: a network takes as input a LR patch ex-
tracted from y, and targets, for a given scale factor
s, s
2
output values that correspond to the estimate
b
e for each s
2
central pixel in the corresponding SR
patch (see 2). We also wish to limit the complexity
of the networks, i.e. restrict the number of weights
to be learned to differentiate from deep learning ap-
proaches.
Figure 2: Representation of a LR patch (left) and the
s
2
= 4 central pixels (for a scale factor of two).
To train these networks, we start with collecting
pairs of LR patch and corresponding s
2
reconstruc-
tion errors (see 3). The weights of the neural networks
are classically trained using a backpropagagtion algo-
rithm with momentum to lower the mean square error
E =
1
N
∑
(
b
e − e)
2
.
A simple normalization is applied to the input
patches by subtracting the central pixel value of the
LR patch, and dividing by a constant K
in
. The s
2
out-
puts correspond to the missing details between the s
2
ground truth pixel and the s
2
upsampled pixels ob-
tained by the interpolation method. They are normal-
ized by a pre-determined constant K
out
as well.
HR
Image
LR
Image
Bicubic
Image
-
Input Patch
Target Upsampling
Residual Error
Pair
Extraction
Normalization
Normalization
Figure 3: Training dataset construction
(for 5×5 input patch and a scale factor s = 2).
At reconstruction (4), overlapping patches are ex-
tracted, and the estimated high-frequency details are
added to the interpolated image
b
x
bic
.
LR
Image
Bicubic
Image
Normalization
Normalization
+
Trained Neural
Network
HR
Image
Figure 4: Reconstruction scheme for a SR image
(represented for 5 × 5 input patch, s = 2 scale factor).
A classical alternative for input patches is to use
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
86

an upscaled version of the patches (extracted from
b
x
bic
for instance) to spread the information onto a wider
input area. The problem would get closer to a deblur-
ring one, but is still part of a SR approach as we origi-
nally rely on an interpolation method, which only de-
pends on some LR data and cannot be properly mod-
elled with a blurring kernel or a degradation model.
Here, we decided to keep the original LR information,
as it holds all the available information while keeping
reasonable dimensions for the input data.
4.1 Multi-Layer Perceptron
As stated in the previous paragraph, this method is
quite similar to the one described in (Pan and Zhang,
2003), but the direct use of pixel intensity to predict
details has not been exploited to the best of our knowl-
edge. We design a MLP with N
2
neurons for the in-
put layer and s
2
linear neurons for the output layer.
The N
2
inputs correspond to a N × N patch. Most
…
Input Layer
Hidden
Layer
Output
Layer
…
Hidden
Layer
Figure 5: Proposed MLP architecture for SR.
approaches in the literature only make use of one
hidden-layer for SR with MLP. We noted that two hid-
den layers, with respectively N
N1
and N
N2
neurons per
layer with tanh activation function, were more likely
able to capture the non linearity of the input-target
mapping. However, this increases the complexity of
the network.
4.2 Convolutional Neural Network
ConvNets (LeCun and Bengio, 1995) are biologically
inspired neural architectures that include several con-
volutional layers in the network. They can be consid-
ered as feature detectors that keep track of the spatial
position of those features, producing a set of feature
maps at each layer. The strength of this architecture
is that convolution kernels are learnt using backprop-
agation, leading to an optimal solution compared with
hand-crafted filters.
In classification, one can add pooling layers (orig-
inally called downsampling layers), when the precise
position of features is not crucial. For the SR prob-
lem, however, the spatial location of a feature in the
image is very important, and pooling, if used, should
be handled with care. Our experiments in this pa-
per do not involve any pooling layer, as simple test
demonstrated that the result do not benefit from such
layers.
…
…
Input Layer
(patch)
C1
Output
Layer
C2
Hidden
Layer
…
Figure 6: Proposed ConvNet architecture for SR.
We propose to use the following architecture: the
LR patch at the input layer is convolved with N
C1
ker-
nels, producing N
C1
maps for the first layer C1. Each
of these maps are then convolved with a second set of
N
C2
kernels following the same connection scheme as
the one presented in (Garcia and Delakis, 2004). Each
map in C1 is convolved by two dedicated kernels to
foster specialization, giving a first subset of 2 × N
C1
kernels for C2. In parallel, fusion is also performed
convolving each possible pair of maps of C1 by a ker-
nel, which gives another
N
C1
2
kernels. Therefore we
have:
N
C2
= (2 × N
C1
) +
N
C1
!
(N
C1
− 2)!2!
= N
C1
(N
C1
+ 3)
2
(6)
We add a hidden layer of N
C2
neurons, each of which
is connected to a single map, non-linearly merging
the information of the last maps into a single output
value that is presented to the output layer. The out-
put layer consists in s
2
fully connected linear neurons.
Note that all the previous layers include tanh activa-
tion function. We train this network with our set of
patch and target pairs, using backpropagation to si-
multaneously learn the weights of the neurons and the
kernels of the convolutions.
5 EXPERIMENTAL RESULTS
To compare the performances of our proposed ap-
proaches, we use the text image database ULR-
textSISR-2013a released by (Nayef et al., 2014). The
AComparisonbetweenMulti-LayerPerceptronsandConvolutionalNeuralNetworksforTextImageSuper-Resolution
87

test set contained in this database consists in 30
grayscale images of black text over a white back-
ground: 5 different texts, each rendered with 3 differ-
ent fonts (Arial, Times, Courier) and 2 different sizes
(10 and 12 pt, at 150dpi), using anti-aliasing filters
during Portable Document Format (PDF) file genera-
tion. They contain bold and italic characters.
5.1 Evaluation Procedure: Measures
We use the same measure as (Nayef et al., 2014) to
evaluate the performances of the different proposed
methods: Mean Squared Error (MSE), Peak Signal to
Noise Ration (PSNR), OCR accuracy.
1. MSE reflects the squared difference in gray lev-
els between two images. Its square root (RMSE)
gives the standard error (in graylevel), indicating
the average error obtained in our reconstruction.
2. Employed in signal processing, PNSR give a more
absolute meaning to the reconstruction, given the
maximum value the signal can reach. It is still
closely related to the MSE.
PSNR = 10 × log
255
2
MSE
3. When processing text images we can produce a
joint evaluation of both standard measures and
classification, recognition or detection scores.
Optical Character Recognition systems allow
to produce an accuracy measure for evaluation
(which is the Levenstein distance between recog-
nized characters and ground truth transcription,
divided by the total number of characters). Fol-
lowing the proposal of (Nayef et al., 2014), we
evaluate our performances of our using the same
tools (Tesseract OCR 3.02 and UNLV-ISRI accu-
racy tool). The results do not take into account
ground truth spacing characters, although includ-
ing the related errors.
5.2 Settings
5.2.1 Framework Global Settings
Normalization. We set K
in
= 256 to normalize the
input patch from which we subtract the central value.
This way, we ensure that values range from −1 to 1.
For output detail pixels, we choose K
out
= 100 for im-
ages of black text over a white background, which is
K
out
' ν with ν being the variance of the histogram of
target values in the training dataset.
Patch Size. In order to provide an equivalent evalu-
ation of the two methods, we try to use an equivalent
amount of information at the entrance of both sys-
tems. For ConvNets, we use 9×9 LR patches. Tak-
ing into account the border effect of convolutions in
the first layers, we consider that presenting only 7×7
patches to the MLP is equivalent in terms of informa-
tion. Experiments show that the MLP does not benefit
from larger patches.
Scale. In this study, we only consider ×2 SR since
the database (Nayef et al., 2014) was provided for this
upsampling factor, although our implementation can
handle higher scale factors (the output layers would
be 3×3 for ×3 SR, 4×4 for ×4 SR, etc.)
Training Database. For training, we use text im-
ages generated with the process employed to build the
database (Nayef et al., 2014): Times and Arial fonts
(10 and 12pt at 150dpi), bold, italic and normal em-
phasis; FreeType generation and Matlab downsam-
pling. An interesting aspect of this database is that it
includes three different fonts (Arial, Times, Courier)
in the test data while only two of them are present in
the training data. This allows to evaluate if the SR
method generalizes to text of different nature.
We extract 120,000 pairs for training as described
in 3. We simply reject strictly uniform input patches
(typically, white patches).
5.2.2 Performance Evaluation of the MLP
We evaluated with different numbers of neurons per
hidden layer and tried to outline a global trend (see
1). For each configuration, we run 100 epochs over
the whole set of pairs, with a constant learning rate
λ = 10
−3
and a momentum of 0.2. Generally, the re-
sults get better with an increasing number of neurons,
but it also depends on the repartition of the weights
and how N
N1
is related to N
N2
. However, the con-
figuration seems to reach its limits and at a certain
point and increasing the complexity of the network
does not improve the performances. The best perfor-
mances are obtained for a network with 100 neurons
in N1, and 150 neurons in N2 layers (configuration 6,
20,754 weights).
5.2.3 Performance Evaluation of the ConvNet
To choose the most interesting network dimensions
for our purpose, and given the chosen architecture
(4.2), we tested several ConvNet sizes as reported in
2. For each configuration, we use 5×5 kernels for
C1 and 3×3 kernels for C2. We can notice that small
networks with N
C1
as small as configurations 2 or 3
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
88

Table 1: Performances of different MLP configurations.
Config. 1 2 3 4 5 6 7
N1-N2 10-10 10-50 50-50 50-100 50-150 100-150 100-200
Complex. 654 1,254 5,254 8,004 10,754 20,754 26,004
PSNR 22.01 22.67 23.05 23.25 23.63 24.15 24.05
MSE 20.52 19.03 18.20 17.80 17.05 16.03 16.23
OCR 91.97 93.28 92.85 93.73 93.82 94.69 94.44
Table 2: Performances of different ConvNet configurations.
Config. 1 2 3 4 5 6 7 8 9 10
C1 2 4 8 12 16 20 24 28 32 40
Complex. 185 498 1,520 3,070 5,148 7,754 10,888 14,550 18,740 28,704
PSNR (dB) 20.49 21.59 22.89 23.25 23.88 23.79 24.18 24.16 24.55 24.48
MSE 24.36 21.51 18.48 17.74 16.47 16.67 15.91 15.95 15.27 15.39
OCR (%) 90.35 90.70 93.35 95.08 95.23 95.10 95.49 96.09 96.42 96.13
perform well with less than 2,000 weights. The ar-
chitecture reaches its limits for N
C1
= 32 which has
18,740 weights.
As mentioned before, we tried to limit the size
of the network. We also explored larger networks
where the hidden layer was fully connected, increas-
ing drastically the complexity up to 481,784 weights.
They allow to reach higher scores (25.69 dB / 13.58
/ 96.67%) but are out of the scope of the desired low
complexity.
5.3 Results
For the selected architectures, we can observe in 1 and
2 the advantage of ConvNets compared with MLP.
For an equivalent complexity (e.g. around 20, 000
weights), ConvNets produces a better version of miss-
ing high-frequencies, improving both pixel-wise mea-
sures (PSNR from 24.15 to 24.55 dB) and OCR score
(94.69 to 96.44%). Some results are shown in figures
7(b) and 7(c).
The bicubic image (7(a)) exhibits serious blur ar-
tifacts, and the gain of the proposed Neural-based
methods is clear. Moreover, we can note a better
reconstruction of some sensitive details for the Con-
vNets: holes in the ”e” letters are more visible, ”s”
letters are better shaped, and some fine edges such as
”n”, ”k” or ”g” curves are more nicely reconstructed.
We report in 3 the state of the art results published
on this database, and compare them with our best re-
sults. We can see the benefit of our method over the
sparse coding methods for both pixel-wise measures
and OCR accuracy score. We observe a gain for MLP
and ConvNet, of respectively +4.46 dB and +4.86
dB for PSNR, and +1.10% and +2.85% for OCR ac-
curacy.
(a) Bicubic interpolation
(b) MLP result
(c) ConvNet result
Figure 7: Bicubic and Super-resolved test image.
Table 3: Proposed methods performances compared with
State-of-the-Art ones.
Method RMSE PSNR (dB) OCR (%)
Bicubic 34.92 17.32 88.57
Yang 26.75 19.69 93.59
Walha 29.45 18.82 93.16
MLPTextSR 16.03 24.15 94.69
CNNTextSR 15.27 24.55 96.44
Original HR - - 97.86
Supplementary Experiments
The proposed database is very specific as it only con-
tains text images with black font over a white back-
AComparisonbetweenMulti-LayerPerceptronsandConvolutionalNeuralNetworksforTextImageSuper-Resolution
89
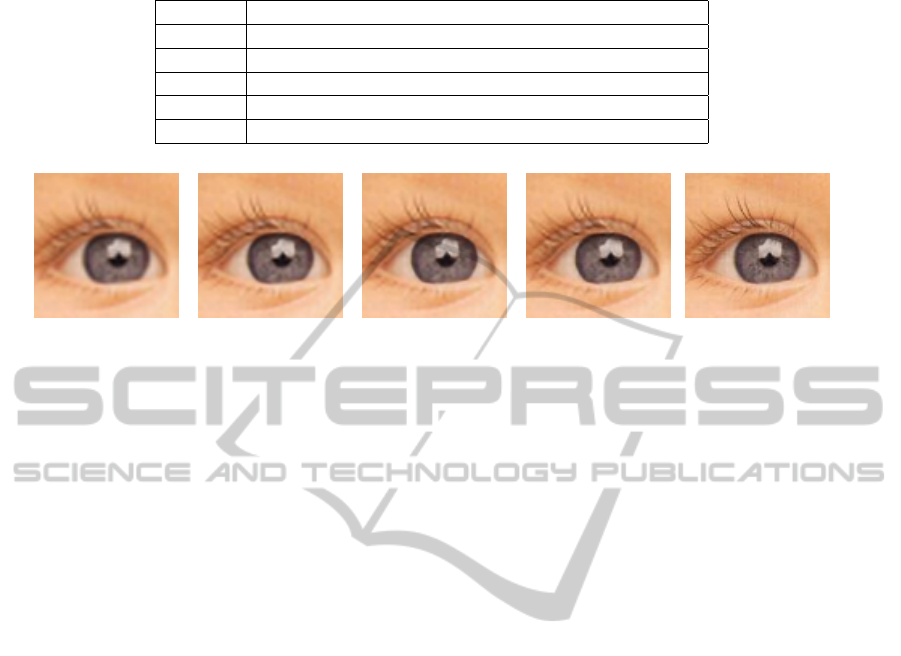
Table 4: PSNR scores for ”Set5”.
Bicubic ANR SRCNN Our (7×7) Our (9×9)
baby 37.07 38.44 38.3 37.92 37.96
bird 36.81 40.04 40.64 40.23 40.32
butterfly 27.43 30.48 32.2 31.63 31.66
head 34.86 35.66 35.64 35.47 35.48
woman 32.14 34.55 34.94 34.64 34.63
(a) Bicubic (b) ANR (c) SRCNN (d) Our method 9×9 (e) Groundtruth
Figure 8: Results for natural images (×2).
ground. Thus, for the sake of generalization, we tried
our system on natural images. We use the same data
as (Dong et al., 2014) or (Yang et al., 2010) for train-
ing, and images extracted from BSD100 segmentation
database for validation. The test dataset is ”Set5”. We
tried to preserve fairness with the other methods. As
(Dong et al., 2014) use 24,800 32×32 subimages for
training their system while we use patches (7×7 or
9×9 for this last experiment), we consider that we can
randomly extract 2,000 patches from each of the 92
training images without turning into a deeper learn-
ing process than they do. In terms of complexity, their
system contains W = 8, 032 weights. Using N
C1
= 20
for both 7×7 and 9×9 patch sizes, we end up with re-
spectively W
7×7
= 7, 434 and W
9×9
= 7, 754. We use
the same setting as 5.2.3, except for 3×3 convolutions
for all convolutions in the 7×7 input patches case.
Our results (4 and 8) are competitive with the recent
methods applied on this dataset: Anchored Neighbour
Regression (Timofte et al., 2013) and SRCNN (Dong
et al., 2014).
6 CONCLUSIONS AND
PERSPECTIVES
We compared two neural network based methods
and demonstrated the efficiency of reasonably sim-
ple Convolutional Networks to provide super resolved
single text images via a good estimate of missing de-
tails from overlapping patches of their low resolution
version. Furthermore, we observed better results than
the proposed state-of-the-art sparse coding methods.
The experiments on natural images demonstrated that
the proposed ConvNet architecture can be generalized
to other types of images.
These results motivate further research: take
advantage of recent proposed architectures for
ConvNets in SR to enhance our model, confront our
system to noisy contexts where patch-based method
usually perform well at denoising and adapt it to dif-
ferent kinds of images such as overlaid text in TV
streams.
REFERENCES
Ahmed, F., Gustafson, S., and Karim, M. (1995). High-
fidelity image interpolation using radial basis function
neural networks. In Proceedings of the IEEE 1995
National Aerospace and Electronics Conference, vol-
ume 2, pages 588–592.
Carcenac, M. (2007). A modular neural network for
super-resolution of human faces. Applied Intelligence,
30(2):168–186.
Cheeseman, P., Kanefsky, B., Kraft, R., Stutz, J., and Han-
son, R. (1996). Super-resolved surface reconstruc-
tion from multiple images. In Maximum Entropy and
Bayesian Methods, pages 293–308. Springer.
Dalley, G., Freeman, B., and Marks, J. (2004). Single-frame
text super-resolution: a bayesian approach. In Inter-
national Conference on Image Processing, volume 5,
pages 3295–3298 Vol. 5.
Donaldson, K. and Myers, G. (2005). Bayesian Super-
Resolution of Text in Video with a Text-Specific Bi-
modal Prior. IEEE Computer Society Conference on
Computer Vision and Pattern Recognition, 1:1188–
1195.
Dong, C., Loy, C. C., He, K., and Tang, X. (2014). Learn-
ing a deep convolutional network for image super-
resolution. In Computer Vision–ECCV 2014, pages
184–199. Springer.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
90

Fan, W., Sun, J., Naoi, S., Minagawa, A., and Hotta,
Y. (2012). Local Consistency Constrained Adap-
tive Neighbor Embedding for Text Image Super-
Resolution. 10th IAPR International Workshop on
Document Analysis Systems, pages 90–94.
Freeman, W., Jones, T., and Pasztor, E. (2002). Example-
based super-resolution. Computer Graphics and Ap-
plications, IEEE, 22(2):56–65.
Gao, J., Guo, Y., and Yin, M. (2013). Restricted boltzmann
machine approach to couple dictionary training for
image super-resolution. In IEEE International Con-
ference on Image Processing, pages 499–503.
Garcia, C. and Delakis, M. (2004). Convolutional face
finder: A neural architecture for fast and robust face
detection. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 26(11):1408–1423.
Glasner, D., Bagon, S., and Irani, M. (2009). Super-
resolution from a single image. IEEE 12th Interna-
tional Conference on Computer Vision, pages 349–
356.
Irani, M. and Peleg, S. (1991). Improving resolution by im-
age registration. CVGIP: Graph. Models Image Pro-
cess., 53(3):231–239.
LeCun, Y. and Bengio, Y. (1995). Convolutional networks
for images, speech, and time series. The handbook of
brain theory and neural networks, 3361.
Luong, H. Q. and Philips, W. (2007). Non-local text image
reconstruction. In Ninth International Conference on
Document Analysis and Recognition, volume 1, pages
546–550.
Mancas-Thillou, C., Mirmehdi, M., and Copernic, A.
(2005). Super-resolution text using the teager filter.
First International Workshop on Camera-Based Doc-
ument Analysis and Recognition, pages 10–16.
Nakashika, T., Takiguchi, T., and Ariki, Y. (2013). High-
Frequency Restoration Using Deep Belief Nets for
Super-resolution. International Conference on Signal-
Image Technology & Internet-Based Systems, pages
38–42.
Nasrollahi, K. and Moeslund, T. (2014). Super-resolution:
a comprehensive survey. Machine Vision and Appli-
cations, 25(6):1423–1468.
Nayef, N., Chazalon, J., Gomez-Kr
¨
amer, P., and Ogier, J.
(2014). Efficient example-based super-resolution of
single text images based on s elective patch process-
ing. In 11th International Workshop on Document
Analysis Systems, pages 227–231.
Pan, F. and Zhang, L. (2003). New image super-resolution
scheme based on residual error restoration by neural
networks. Optical Engineering, 42(10):3038–3046.
Panagiotopoulou, A. and Anastassopoulos, V. (2007).
Scanned images resolution improvement using neu-
ral networks. Neural Computing and Applications,
17(1):39–47.
Peleg, T. and Elad, M. (2014). A Statistical Prediction
Model Based on Sparse Representations for Single
Image Super-Resolution. IEEE Transactions on Im-
age Processing, 7149(c):1–1.
Plaziac, N. (1999). Image interpolation using neural net-
works. Trans. Img. Proc., 8(11):1647–1651.
Protter, M., Elad, M., Takeda, H., and Milanfar, P. (2009).
Generalizing the nonlocal-means to super-resolution
reconstruction. Image Processing, IEEE Transactions
on, 18(1):36–51.
Rosenblatt, F. (1958). The perceptron: a probabilistic model
for information storage and organization in the brain.
Psychological review, 65(6):386.
Stark, H. and Oskoui, P. (1989). High-resolution image re-
covery from image-plane arrays, using convex projec-
tions. J. Opt. Soc. Am. A, 6(11):1715–1726.
Sun, J., Xu, Z., and Shum, H.-Y. (2011). Gradient pro-
file prior and its applications in image super-resolution
and enhancement. IEEE Transactions on Image Pro-
cessing, 20(6):1529–1542.
Thouin, P. D. and Chang, C.-I. (2000). A method for
restoration of low-resolution document images. Inter-
national Journal on Document Analysis and Recogni-
tion, 2(4):200–210.
Timofte, R., De, V., and Gool, L. V. (2013). Anchored
Neighborhood Regression for Fast Example-Based
Super-Resolution. IEEE International Conference on
Computer Vision, pages 1920–1927.
Walha, R., Drira, F., Lebourgeois, F., and Alimi, A. M.
(2012). Super-resolution of single text image by
sparse representation. In Proceeding of the workshop
on Document Analysis and Recognition, pages 22–29.
ACM.
Yang, J., Wang, Z., Lin, Z., Cohen, S., and Huang, T.
(2012). Coupled dictionary training for image super-
resolution. IEEE Transactions on Image Processing,
21(8):3467–3478.
Yang, J., Wright, J., Huang, T. S., and Ma, Y. (2010). Im-
age super-resolution via sparse representation. IEEE
Transactions on Image Processing, 19(11):2861–
2873.
Zheng, Y., Kang, X., Li, S., He, Y., and Sun, J. (2014). Real-
time document image super-resolution by fast mat-
ting. In 11th IAPR International Workshop on Doc-
ument Analysis Systems, pages 232–236.
AComparisonbetweenMulti-LayerPerceptronsandConvolutionalNeuralNetworksforTextImageSuper-Resolution
91
