
Estimating the Best Reference Homography for Planar Mosaics From
Videos
Fabio Bellavia and Carlo Colombo
Computational Vision Group, University of Florence, Florence, Italy
Keywords:
Hierarchical Mosaicing, Viewpoint Computation, Underwater Vision.
Abstract:
This paper proposes a novel strategy to find the best reference homography in mosaics from video sequences.
The reference homography globally minimizes the distortions induced on each image frame by the mosaic ho-
mography itself. This method is designed for planar mosaics on which a bad choice of the first reference image
frame can lead to severe distortions after concatenating several successive homographies. This often happens
in the case of underwater mosaics with non-flat seabed and no georeferential information available. Given
a video sequence of an almost planar surface, sub-mosaics with low distortions of temporally close image
frames are computed and successively merged according to a hierarchical clustering procedure. A robust and
effective feature tracker using an approximated global position map between image frames allows us to build
the mosaic also between locally close but not temporally consecutive frames. Sub-mosaics are successively
merged by concatenating their relative homographies with another reference homography which minimizes
the distortion on each frame of the fused image. Experimental results on challenging real underwater videos
show the validity of the proposed method.
1 INTRODUCTION
Over the last decade, image mosaicing has received
a considerable attention for its wide range of prac-
tical applications (Brown and Lowe, 2007). How-
ever, despite the recent progress in the field, obtain-
ing good mosaics still remains a challenging and not
fully solved task. This is mostly due to the assump-
tion of input data with sufficiently scene distance or
image acquired by camera rotations only (Hartley and
Zisserman, 2003). These requisites cannot be effec-
tively met in practice, causing image misalignments
and ghosting artefacts. In order to avoid or alle-
viate these issues, several image stitching and post
processing techniques have been developed in recent
years (Lin et al., 2011; Zaragoza et al., 2014; Zhang
and Liu, 2014).
Furthermore, video mosaicing has become quite
popular in underwater vision (Pizarro and Singh,
2003; Bellavia et al., 2007; Prados et al., 2012), due to
its applications to in situ exploration and autonomous
navigation. While common panoramic mosaics as-
sume spherical or cylindrical models, in the case of
underwater environments planar surface models are
assumed. A problem commonly ignored, yet often
present in practice, is the selection of a reference ho-
mography reprojection frame on which to attach the
various mosaic images. The most common and trivial
choice is to use the first frame image or, often sup-
ported by geo-referential camera positions, a user pre-
defined one. A bad choice for the reference frame can
lead to very distorted mosaics (see Fig. 1 (left)). This
can also result after some sequential frame concate-
nations into degenerate and incorrect configurations.
This problem is accentuated in underwater videos due
to the unstable trajectory of the acquisition vehicle
with roll and pitch shakes and the non-flat truly na-
ture of the seabed in most cases. To the best of our
knowledge, methods to solve this issue exist in the
literature solely for the case of planar mosaics from
rotation-only frames (Capel, 2001).
This paper presents in Sect. 2 a novel multi-step
method to estimate the mosaic reference homography
in the case of planar mosaics from video sequences.
An output example is shown in Fig. 1 (right). This
general approach is sided with a robust full mosaic
pipeline particularly designed for underwater envi-
ronments, where the non-planar nature of the scenes
make it difficult to match and track the keypoints re-
quired to compute inter-frame homographies. Some
selected results on real underwater video sequences
from different oceanographic campaigns are given in
512
Bellavia F. and Colombo C..
Estimating the Best Reference Homography for Planar Mosaics From Videos.
DOI: 10.5220/0005297305120519
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 512-519
ISBN: 978-989-758-091-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: A distorted mosaic due to a wrong reference ho-
mography selection (left). Note that in the former case more
than half of the frames accumulate on the bottom with large
scale variations and distortions. This is not present in the
output given by the proposed method (right). In both cases
no post-processing color correction or blending have been
applied.
Sect. 3, showing the good performance of the overall
algorithm. Finally, conclusions and future work are
draw out in Sect. 4.
2 METHOD DESCRIPTION
2.1 Overview
The overall pipeline of the method is schematically
described in Fig. 2. The approach starts by dividing
the video sequence into successive piecewise planar
sub-mosaics with low geometric distortions with re-
spect to the original image frames, as described in
Sect. 2.2.
Sequential concatenation of temporally consecu-
tive frames is sufficient to produce the piecewise pla-
nar sub-mosaics. However, a global strategy is re-
quired to match frames locally close but temporally
non-consecutive. This is required in order to reduce
the propagation of homography estimation errors due
to the non-planar real nature of the scene.
An approximated 2D map of the video frame po-
sitions is then computed, by considering the average
translation between successive frames, which is up-
dated when two close frames are discovered. The
best paths on the map are used to robustly track fea-
tures in spatially close but non-consecutive frames
and compute the homography between them. De-
tails of this step are given in Sect. 2.3. Finally, as
Sub-mosaic generation:
- consecutive image matching and
homography computation
- sequential greedy homography
concatenation
Feature track map building:
- frame location map generation
- best path computation
- keypoint track across sub-mosaics
Hierachical sub-mosaic merging
- sub-mosaic alignment
- reference homography estimation
- post-processing
Figure 2: A schematic view of the mosaic pipeline.
described in Sect. 2.4, sub-mosaics are merged us-
ing the tracked keypoints one at a time according to
a hierarchical clustering, preferring sub-mosaics with
high overlap. When two sub-mosaics are merged, the
best reference homography between them is found in
order to minimize the distortion of the image frames.
This is achieved by exploring the search space of the
“average” homographies between the two sub-mosaic
images. Common blending and photometric post-
processing steps are eventually applied to refine the
results (Uyttendaele et al., 2001; Kwatra et al., 2003;
Brown and Lowe, 2007; Prados et al., 2012).
2.2 Sub-mosaic Generation
Given the video sequence of n +1 consecutive frames
I
0
, I
1
, . . . , I
n
, the first step is to extract the image
keypoints to obtain the matches between overlapping
frames and their associated homography. For this pur-
pose, the HarrisZ detector (Bellavia et al., 2011) is
used, providing robust and reliable corner features.
In the following step, homographies between con-
secutive image frame pairs (I
k
, I
k+1
) are computed.
In particular, feature matches are computed using
the sGOr matching selection strategy (Bellavia et al.,
2014) under the further assumption that the optical
flow between successive frames is bounded. That is,
given a generic keypoint pair (x
k
, x
k+1
) with x
i
∈ I
i
, it
must hold
k x
k
− x
k+1
k< ε
r
(1)
EstimatingtheBestReferenceHomographyforPlanarMosaicsFromVideos
513

where the threshold ε
r
is set to a third of the diago-
nal of the rectangular video frame. The homography
H
k,k+1
∈ R
3×3
that maps points from I
k
to I
k
+
1
is com-
puted on the obtained matches using the noRANSAC
method (Bellavia and Tegolo, 2011), a robust exten-
sion of the RANSAC 7-point algorithm (Hartley and
Zisserman, 2003) using normalized errors.
Finally, a piecewise planar sub-mosaic S
i, j
going
from frame i to frame j (see Fig. 3) is constructed
from its keyframe sequence K
i, j
K
i, j
= I
k
1
, I
k
2
, . . . ,I
k
m
(2)
with i = k
1
< k
2
< . . . < k
m
= j, as explained here-
after. The first image frame and keyframe I
i
of the
subsequence is used as reference, so that the ho-
mography map H
i, j
w
relating the sub-mosaic to any
keyframe I
k
w
, is simply obtained by concatenating the
sequential homographies from H
i,i+1
to H
k
w−1
,k
w
:
H
i, j
w
= H
k
w−1
,k
w
H
k
w−1
,k
w−2
. . . H
i,i+1
(3)
The sub-mosaic is then built according to a greedy
strategy by sequentially looking for next keyframe in
I
i+1
, I
i+2
, . . .. The frame I
j
is added as keyframe if the
overlap between the current sub-mosaic and the pro-
jection of frame I
j
onto the sub-mosaic is less than a
threshold. The sub-mosaic generation process stops
when the projection of frame I
j+1
is too distorted to
be included in K
i j
. In this case I
j
is added as the fi-
nal keyframe with the sub-mosaic S
i, j
as output and
starting from I
j+1
a new sub-mosaic is grown.
The distortion criterion is defined as follows. As-
suming rectangular video frames, their projections
into quadrilaterals in the mosaic are considered dis-
torted if one of the following conditions is met: (1) the
ratio between the original and projected frames is out-
side a user-defined range, (2) the area of the bounding
box including all common keypoints in the projected
mosaic is below a threshold, (3) the ratio between the
minimum and maximum semi-axis lengths of the pro-
jected quadrilateral exceeds a given value.
2.3 Feature Track Map Building
Sequential sub-mosaics can be merged using only the
homography between boundary keyframes, for exam-
ple using the homography H
j, j+1
between the sub-
mosaics S
i, j
and S
j+1,w
, with i < j < w. However,
this solution is not robust, due to inevitable inaccura-
cies in the homography which may propagate across
the sequence, especially when coming back to an al-
ready seen location of the mosaic. According to this
observation, adding more robust matches and recog-
nizing loop-closures (Konolige and Agrawal, 2008)
may improve the result thanks to a suitable keypoint
tracking strategy, implemented as follows.
Figure 3: From left to right, two consecutive sub-mosaics
from the mosaic of Fig. 1(right). The reference image
frames I
k
1
on which successive frames are concatenated (see
text) are highlighted by boxes. No color correction or blend-
ing have been applied.
Given a threshold ε
t
= 1.5 px the enriched set of
matches M
k−1,k
is computed, considering all the key-
point matching pairs and not only the filtered subset
given in input to the RANSAC (see Sect. 2.2). With
an abuse of notation for indicating homogeneous nor-
malized coordinates, we have
M
k−1,k
= {(x
k−1
, x
k
) : x
k−1
∈ I
k−1
,
x
k
∈ I
k
, k x
k
− H
k−1,k
x
k−1
k< ε
t
}
(4)
where matches are selected according to the nearest
neighbour approach (Lowe, 2004) on the homogra-
phy reprojection error. This allows to track more
keypoints across non-consecutive frames since longer
tracks can be built.
In order to handle loop-closure, a robust global
keypoint tracking map is also implemented, see
Fig. 4. Under the assumption of an almost planar sur-
face, an initial frame location map T
0
: {I
k
} → R
2
for
each frame I
k
in the video sequence is computed us-
ing the average displacement between corresponding
matches
T
0
(I
k
) = T
0
(I
k−1
) +
1
N
∑
M
k−1,k
(x
k
− x
k−1
) (5)
The process is started from T
0
(I
0
) = 0, where the
summation is on the match pairs (x
k−1
, x
k
) ∈ M
k−1,k
and N = |M
k−1,k
| (blue line on Fig. 4(a)). Further it-
erations i are introduced to progressively update the
map T
i
, as in the case of the Self-Organizing Map
learning method (Haykin, 1998). In detail, given the
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
514

(a) (b)
Figure 4: The frame location map (a) corresponding to the
mosaic in (b). The first and last iterations T
0
and T are
plotted as blue and red lines, respectively, and no blending
and color correction have been applied to the mosaic. The
zoomed region in (a) shows the minimum path A
a,b
and the
best path B
a,b
between two frames I
a
and I
b
. The maximum
allowable edge distance is ε
r
. (Best viewed in color.)
set of frames I
w
in a radius ε
r
from I
k
J
i
k
= {I
w
: k T
i
(I
k
) − T
i
(I
w
) k≤ ε
r
} (6)
where ε
r
is set as for Eq. 1, T
i
is updated to T
i+1
as
follows
T
i+1
(I
k
) = T
i
(I
k
) +
d
i
L
∑
J
i
k
g
k,w
N
∑
M
k,w
(x
k
− x
w
) (7)
where the outer summation is on the frames I
w
∈ J
i
k
,
L = |J
i
k
|, the inner summation as for Eq. 5 and M
k,w
is defined analogously to M
k−1,k
(see Eq. 4). The
value 0 < d < 1 is an exponential decay going with
the iteration i to limit the iterations and g
k,w
is a
Gaussian weight on the distance k T
i
(I
k
) − T
i
(I
w
) k.
When d
i
' 0 no further updates are needed, and the
final map T is obtained (from blue to red lines as it-
erations proceed in Fig. 4(a)). Note that the planar
displacement approximation of the map cannot han-
dle scale variations, so that there is no perfect cor-
respondence between Fig. 4(a) and Fig. 4(b). Nev-
ertheless, this does not interfere with the final key-
point tracking. The graph G = (V, E) is associated
to the map T , where the set of nodes is V = {I
k
},
i.e. the frames of the sequence, and an edge E
k,z
be-
tween vertexes I
k
and I
z
with an associated weight
k T (I
k
) − T (I
z
) k exists only if ∃ i such that I
z
∈ J
i
k
.
A keypoint x
w
on frame I
w
is tracked to the key-
point x
z
in the frame I
z
following the chain of matches
(x
w
, x
k
1
), (x
k
1
, x
k
2
), . . . , (x
k
m
, x
z
) according to the best
path B between the frame I
w
and I
z
on the graph G.
For any match pair in the chain it must hold that
(x
k
i
, x
k
j
) ∈ M
k
i
,k
j
. The best path E
w,k
1
, E
k
1
,k
2
, . . . E
k
m
,z
must concatenates short weight edges, since matches
from distant frames are more unstable and error
prone. Furthermore, the best path length must be
short because very long paths accumulate errors.
We computed the best path B from a frame I
k
to a frame I
w
by an extended version of the Floyd-
Warshall all-shortest-paths algorithm (Cormen et al.,
2009). Hereafter, both a path and its length with be
referred with the same symbol. In the first step we
compute the minimum path length A between all the
frames in G, using the standard algorithm updating
rule at each iteration 0 ≤ i ≤ |V |, i.e.
A
i
a,b
=
(
A
i−1
a,c
+ A
i−1
c,b
if A
i−1
a,c
+ A
i−1
c,b
< A
i−1
a,b
A
i−1
a,b
otherwise
(8)
where A
i
a,b
is the shortest path length at iteration i be-
tween frames I
a
and I
b
, and A
0
a,b
= E
a,b
. Denoting the
shortest path length at the last iteration by A
a,b
= A
|V |
a,b
,
this is used as follows to bound the length of the best
path B
i
a,b
using a factor f = 2. Defining the auxiliary
values C
i
a,b
representing the maximum edge weight in
the path between I
a
and I
b
, the update rule for the last
step are
B
i
a,b
=
B
i−1
a,c
+ B
i−1
c,b
if B
i−1
a,c
+ B
i−1
c,b
< f A
a,b
and
max(C
i−1
a,c
,C
i−1
c,b
) < C
i−1
a,b
B
i−1
a,b
otherwise
(9)
and
C
i
a,b
=
max(C
i−1
a,c
,C
i−1
c,b
) if B
i−1
a,c
+ B
i−1
c,b
< f A
a,b
and
max(C
i−1
a,c
,C
i−1
c,b
) < C
i−1
a,b
C
i−1
a,b
otherwise
(10)
initialized as for the previous step as B
0
a,b
= C
0
a,b
=
E
a,b
, the edge in the best path are updated accordingly.
An example of the best path between two frames is
given in Fig. 4(a).
Denoting the best path at the last iteration with
B
a,b
= B
|V |
a,b
, referring to Sect. 2.2, the robust matches
between two sub-mosaics S
i, j
and S
w,z
are obtained
by trying to track on the best path B
s,t
each of the
keypoints x
i, j
of any keyframe I
s
∈ K
i, j
to a keypoint
x
z,w
of any keyframe I
t
∈ K
w,z
. The obtained robust
matches M
z,w
i, j
= {(x
i, j
, x
z,w
)} across the sub-mosaics
are used to compute the homography H
z,w
i, j
and finally
merge the sub-mosaics as explained in the next sec-
tion.
EstimatingtheBestReferenceHomographyforPlanarMosaicsFromVideos
515
Note that for computing the RANSAC given in-
lier set M
z,w
i, j
an error threshold 5 times greater than
that used in the other RANSAC inlier set M
k,w
is em-
ployed. This is done to partially relax the planar sur-
face assumption, which is unreal in concrete cases,
and allow larger surface deformations.
2.4 Hierarchical Sub-mosaic Merging
Sub-mosaics are merged incrementally according to
their overlap, following a hierarchical clustering al-
gorithm. In particular, defining by S
0
= {S
i, j
} the
initial cluster partition, at each step 0 ≤ i < |S
0
|, we
try to merge all the possible pairs (S
i, j
, S
w,z
), with
S
i, j
, S
w,z
∈ S
i
, using the robust homography H
z,w
i, j
com-
puted as in Sect. 2.3, to which the reference homog-
raphy
˜
H
z,w
i, j
described next is applied. Denoting by S
∗
i, j
the area of the sub-mosaic S
i, j
according to the ref-
erence homography
˜
H
z,w
i, j
and in similar way for S
∗
w,z
,
only the sub-mosaic pair with the minimal overlap er-
ror R
w,z
i, j
R
w,z
i, j
= 1 −
S
∗
i, j
∩ S
∗
w,z
S
∗
i, j
∪ S
∗
w,z
(11)
is effectively merged in the next cluster partition S
i+1
,
until no more merges can be done. The reference ho-
mography
˜
H
z,w
i, j
between two sub-mosaics is computed
by trying to minimize the distortion of all the frames
in K
i, j
and K
w,z
in the merged mosaic. In particular,
considering the pair (S
i, j
, S
w,z
), we define the auxil-
iary merged mosaics S
1
and S
2
obtained respectively
using the first frames I
i
∈ K
i, j
and I
w
∈ K
w,z
as ref-
erences (see Fig. 5 (top and middle rows)). In the
first case the homography H
z,w
i, j
is used to map points
of S
z,w
onto the reference frame I
i
, while in the other
case the inverse (H
z,w
i, j
)
−1
maps points of S
i, j
onto I
w
.
Both S
1
and S
2
are aligned according to the robust
matches (x
i, j
, x
z,w
) ∈ M
z,w
i, j
(see Sect. 2.3). In partic-
ular, S
1
and S
2
are translated so that the new origins
are in their centroids and rotated according to the ro-
tation R of the best similarity transform obtained by
the least-square solution (Zhang and Liu, 2014), i.e.
˜
x
1
= x
1
−
∑
M
w,z
i, j
x
i, j
(12)
˜
x
2
= C
x
2
−
∑
M
w,z
i, j
x
w,z
(13)
C =
1
a
2
+ b
2
a b
b a
(14)
where
˜
x
1
and
˜
x
2
are the aligned new point coordinates
for points x
1
∈ S
1
and x
2
∈ S
2
respectively. The values
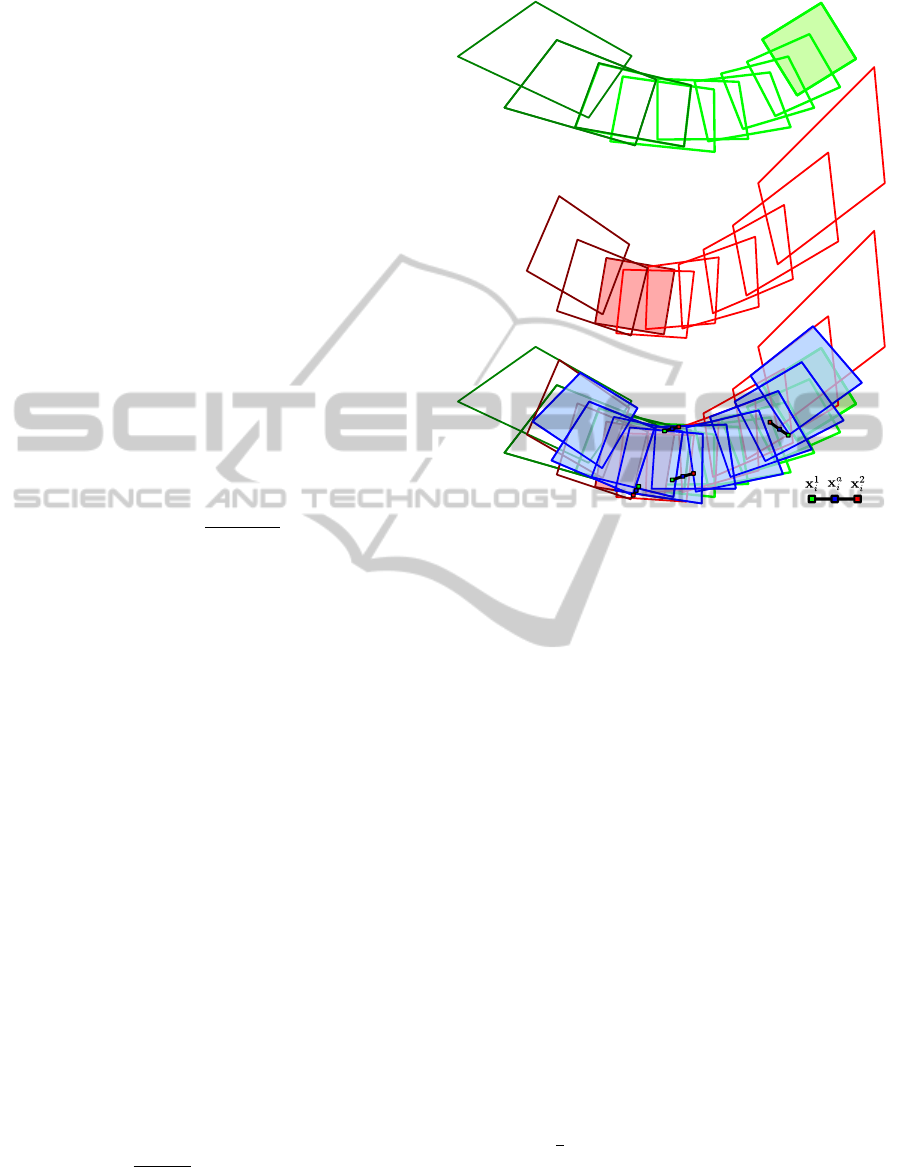
Figure 5: The auxiliary mosaics S
1
(green frames, top row)
and S
2
(red frames, middle row) obtained using respec-
tively as reference frames I
i
∈ K
i, j
(green filled frame) and
I
w
∈ K
w,z
(red filled frame) from S
i, j
(lighter color) and
S
w,z
(darker color) are aligned to find the best reference ho-
mography (bottom row). Four pairs of corresponding ran-
dom sampled points (x
1
i
, x
2
i
) are used to generate the mid-
points x
a
i
on which computing the reference homography
˜
H
z,w
i, j
(bottom row, blue frames). The error P is given by
accounting for the distortion of each resulting (blue) frame.
(Best viewed in color).
a and b are computed on lest-squares according to the
similarity transform
x
i, j
=
a b c
1
b a c
2
0 0 1
x
w,z
(15)
with an abuse of notation for homogeneous coordi-
nates and a, b, c
1
, c
2
∈ R (see Fig. 5 (bottom row,
green and red frames) for an example).
The reference homography
˜
H
z,w
i, j
is chosen by
RANSAC, looking for the “average” homography
which minimizes the error P (see Fig. 5 (bottom row,
blue frames)). Given four corresponding randomly
sampled non-collinear points x
i
1
and x
i
2
on S
1
and
S
2
respectively, 1 ≤ i ≤ 4, and the associated mid-
points x
i
a
=
1
2
(x
i
1
+ x
i
2
), the “average” homography is
given by the homography H
1
a
mapping x
1
i
to x
a
i
. Un-
der the assumption of n × m rectangular frames, for
each frame I
k
∈ K
i, j
∪ K
w,z
, we compute a distortion
error P on the quadrilateral
˜
I
k
, obtained by applying
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
516

H
1
a
to the image of I
k
on S
1
P = max
I
k
∈K
i, j
∪K
w,z
(P
O
+ P
N
+ P
A
+ P
α
) (16)
Figure 6: Configuration for computing the error P when
projecting the image frame I
k
to
˜
I
k
through the mosaic ho-
mography H (see text). Corresponding vertex pairs are
(v
i
,
˜
v
i
) for 1 ≤ i ≤ 4.
Considering the four quadrilateral sides of length
l
i
of
˜
I
k
in consecutive order, under the assumption that
n > m with l
1
, l
3
corresponding to the side of length
n on I
k
and in similar way l
2
, l
4
to m (see Fig. 6), we
define the different errors composing P. In particular,
P
O
measures the error on the ratio between the oppo-
site sides of
˜
I
k
:
P
O
= 2 −
1
2
min(l
1
, l
3
)
max(l
1
, l
3
)
+
min(l
2
, l
4
)
max(l
2
, l
4
)
(17)
while P
N
measures the error on the ratio between con-
secutive sides of
˜
I
k
:
P
N
= 1 −
min(r,
m
n
)
max(r,
m
n
)
(18)
where
r = min
l
1
l
2
,
l
2
l
3
,
l
3
l
4
,
l
4
l
1
(19)
The error P
A
gives the error ratio between the frame
area nm and the area of its image A
˜
I
k
P
A
= 1 −
min(A
˜
I
k
, nm)
max(A
˜
I
k
, nm)
(20)
while P
α
measures the angular error
P
α
= (max(cos
12
, cos
23
, cos
34
, cos
41
))
5
(21)
cos
ab
being the absolute value of the cosine between
the two sides l
a
and l
b
. An example of resulting mo-
saic obtained by merging sub-mosaics according to
the best reference homography
˜
H
z,w
i, j
of Fig. 5 is shown
in Fig. 7. Finally, as post-processing step on the fi-
nal merged mosaic, multi-band blending (Brown and
Lowe, 2007) and color correction using an extension
of the Reinhard’s method (Reinhard et al., 2001) are
applied.
Figure 7: The initial sub-mosaics S
i, j
, S
w,z
(top) and the re-
sulting mosaic (bottom) according to the computed refer-
ence homography
˜
H
z,w
i, j
of Fig. 5. In both cases no post-
processing color correction or blending have been applied.
(a) (b)
Figure 8: Snapshots of the two test video sequences. In the
case the video sequence (a) the shaded area containing a
fixed robot arm has been cropped. (Best viewed in color.)
3 EXPERIMENTAL RESULTS
We tested the proposed pipeline on two underwa-
ter video sequences which together with the software
code are freely available online
1
. Snapshots of video
frames are shown in Fig. 8, in the case of the first
video, the image area of the frame including the robot
arm was cropped. To remove redundant data, the orig-
inal 25 fps videos were downsampled to 5 fps. The
corresponding output mosaics are shown in Fig. 9.
As it can be noted, the resulting mosaics are good,
with no evident misalignment glitches or strong frame
deformations. Underwater scenes are very challeng-
ing, due to their high intensity changes and repeated
patterns, which make the feature tracking difficult, so
1
http://www.math.unipa.it/fbellavia/dl/mosaic.zip
EstimatingtheBestReferenceHomographyforPlanarMosaicsFromVideos
517

(a) (b)
Figure 9: Output mosaics corresponding respectively to the video sequences of Fig. 8(a)-(b). (Best viewed in color).
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
518

that the quality of the results strengthen the validity of
the feature track map computation of Sect. 2.3.
As it can be seen from the output mosaics, the pro-
posed method is effective in choosing the reference
mosaic homography (see Sect. 2.4). Note that, us-
ing the first image frame as reference, in the case of
Fig. 8(a) would lead to very distorted images, as can
be observed even from corresponding initial merged
sub-mosaics (see Fig. 5 (top and middle rows, green
and red frames)). Indeed, the proposed method al-
lowed us to get in a completely automatic way as
good-looking mosaics as those obtained with strong
expert user intervention.
4 CONCLUSIONS
This paper proposes a new approach to compute the
best reference mosaic homography that minimizes the
frame distortions in the case of planar mosaics. For
this purpose, a full hierarchical mosaicing pipeline
was designed, with particular attention to underwa-
ter mosaicing applications that, due to the scene com-
plexity, require robust feature tracking schemes as the
one proposed in this paper. Experimental results show
the validity of our method, yielding to high quality
unsupervised mosaics.
Future work will include more evaluation tests as
well incorporating in the pipeline new stitching algo-
rithms (Zaragoza et al., 2014; Zhang and Liu, 2014)
to replace the standard 7-point homography compu-
tation, with the aim to improve results in the case of
strong 3D content.
ACKNOWLEDGEMENT
Thanks to Pamela Gambogi of the “Soprintendenza
per i Beni Archeologici della Toscana”, Italian Min-
istry of Culture, for providing the input video se-
quences.
This work has been carried out during the AR-
ROWS project, supported by the European Commis-
sion under the Environment Theme of the “7th Frame-
work Programme for Research and Technological De-
velopment”.
REFERENCES
Bellavia, F., Gagliano, G., Tegolo, D., and Valenti, C.
(2007). Global archaeological mosaicing for under-
water scenes. WSEAS Transactions on Signal Process-
ing, 2(7):997–1003.
Bellavia, F. and Tegolo, D. (2011). noRANSAC for funda-
mental matrix estimation. In British Machine Vision
Conference, pages 1–11.
Bellavia, F., Tegolo, D., and Valenti, C. (2011). Improving
Harris corner selection strategy. IET Computer Vision,
5(2):87–96.
Bellavia, F., Tegolo, D., and Valenti, C. (2014). Keypoint
descriptor matching with context-based orientation es-
timation. Image and Vision Computing, 32(9):559 –
567.
Brown, M. and Lowe, D. G. (2007). Automatic panoramic
image stitching using invariant features. International
Journal of Computer Vision, 74(1):59–73.
Capel, D. P. (2001). Image Mosaicing and Super-resolution.
PhD thesis, University of Oxford.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,
C. (2009). Introduction to Algorithms (3. ed.). MIT
Press.
Hartley, R. and Zisserman, A. (2003). Multiple View Geom-
etry in Computer Vision. Cambridge University Press,
2 edition.
Haykin, S. (1998). Neural Networks: A Comprehensive
Foundation. Prentice Hall, 2 edition.
Konolige, K. and Agrawal, M. (2008). Frameslam: From
bundle adjustment to real-time visual mapping. IEEE
Transactions on Robotics, 24(5):1066–1077.
Kwatra, V., Sch
¨
odl, A., Essa, I. A., Turk, G., and Bobick,
A. F. (2003). Graphcut textures: image and video syn-
thesis using graph cuts. 22(3):277–286.
Lin, W. Y., Liu, S., Matsushita, Y., Ng, T. T., and Cheong,
L. F. (2011). Smoothly varying affine stitching. In
IEEE Conference on Computer Vision and Pattern
Recognition, pages 345–352.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
Pizarro, O. and Singh, H. (2003). Toward large-area mo-
saicing for underwater scientific applications. IEEE
Journal of Oceanic Engineering, 28(4):651–672.
Prados, R., Garcia, R., Gracias, N., Escartin, J., and Neu-
mann, L. (2012). A novel blending technique for un-
derwater giga-mosaicing. IEEE Journal of Oceanic
Engineering, 37(4):626–644.
Reinhard, E., Ashikhmin, M., Gooch, B., and Shirley, P.
(2001). Color transfer between images. IEEE Com-
puter Graphics and Applications, 21(5):34–41.
Uyttendaele, M., Eden, A., and Szeliski, R. (2001). Elim-
inating ghosting and exposure artifacts in image mo-
saics. In Computer Vision and Pattern Recognition,
pages 509–516.
Zaragoza, J., Chin, T. J., Tran, Q. H., Brown, M., and Suter,
D. (2014). As-Projective-As-Possible image stitching
with moving DLT. IEEE Transaction on Pattern Anal-
ysis and Machine Intelligence, 36(7):1285–1298.
Zhang, F. and Liu, F. (2014). Parallax-tolerant image stitch-
ing. In IEEE Conference on Computer Vision and Pat-
tern Recognition, pages 3262–3269.
EstimatingtheBestReferenceHomographyforPlanarMosaicsFromVideos
519
