Linear Discriminant Analysis for Zero-shot Learning Image Retrieval

Sovann En

, Fr

eric Jurie

, St

ephane Nicolas

, Caroline Petitjean

and Laurent Heutte

LITIS, University of Rouen, Rouen, France

GREYC, University of Caen Basse-Normandie, Caen, France

Keywords:

Image Retrieval, Linear Discriminant Analysis, Zero Shot Learning.

Abstract:

This paper introduces a new distance function for comparing images in the context of content-based image

retrieval. Given a query and a large dataset to be searched, the system has to provide the user – as efﬁciently

as possible – with a list of images ranked according to their distance to the query. Because of computational

issues, traditional image search systems are generally based on conventional distance function such as the

Euclidian distance or the dot product, avoiding the use of any training data nor expensive online metric learning

algorithms. The drawback is that, in this case, the system can hardly cope with the variability of image

contents. This paper proposes a simple yet efﬁcient zero-shot learning algorithm that can learn a query-adapted

distance function from a single image (the query) or from a few images (e.g. some user-selected images in a

relevance feedback iteration), hence improving the quality of the retrieved images. This allows our system to

work with any object categories without requiring any training data, and is hence more applicable in real world

use cases. More interestingly, our system can learn the metric on the ﬂy, at almost no cost, and the cost of the

ranking function is as low as the dot product distance. By allowing the system to learn to rank the images,

signiﬁcantly and consistently improved results (over the conventional approaches) have been observed on the

Oxford5k, Paris6k and Holiday1k datasets.

1 INTRODUCTION

Content-based image retrieval (CBIR) consists in

ﬁnding the visually closest images with regards to the

content of an input query. State-of-the art CBIR sys-

tems have been dominated for a while by the bag of

visual words (BoVW) representation (Sivic and Zis-

serman, 2003; Philbin et al., 2007) and its deriva-

tives (Perronnin et al., 2010; J

egou et al., 2012). The

BoVW approach involves quantizing local descriptors

(usually SIFT) into visual words and representing im-

ages by the frequencies of visual words. Approaches

based on BoVW derivatives differ from the BoVW

approach in that they replace the frequency of visual

words with the aggregated version of the difference

between image local descriptors and their closest vi-

sual words. This aggregation can be done using either

Fisher Vector (Perronnin et al., 2010) or Vector of

Local Aggregated Descriptor (VLAD) (J

egou et al.,

2012). These recent works have been shown to per-

form signiﬁcantly better than BoVW approaches.

Recently, researchers have been trying to scale

such systems up to large scale datasets, e.g. datasets

including a hundred of millions of images (J

egou

et al., 2012). In this latest trend, the efﬁciency be-

comes more and more important. The ranking must

be able to retrieve the images from hundreds of mil-

lions of images, almost in real time. An effective re-

trieval system must be able to obtain high recall us-

ing relatively low number of candidates (high pre-

cision). Thus, the ranking function plays an im-

portant role in effective and efﬁcient retrieval algo-

rithms. Ranking functions used in image retrieval sys-

tems can be broadly grouped into two categories: (i)

those based on conventional distance measures, and

(ii) those based on machine learning algorithms. Con-

ventional ranking, such as dot product, is very of-

ten the ﬁrst choice of many researchers in the ﬁeld,

owing to its simplicity, straightforward interpretation

and low computational cost. The second category is

employed to better capture the variability in the im-

ages and to retrieve semantically related images. A

typical scenario of this approach can be: retrieve all

the sunset images from the image database by feed-

ing into the system a ”sunset” query. This approach

is typically more robust when dealing with, seman-

tically related, largely-varying visual content. How-

ever, this second approach may need hundreds (or

even thousands) of training samples to produce mean-

ingful models. More importantly, they are limited to

EN S., Jurie F., Nicolas S., Petitjean C. and Heutte L..

Linear Discriminant Analysis for Zero-shot Learning Image Retrieval.

DOI: 10.5220/0005300200700077

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 70-77

ISBN: 978-989-758-090-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

a few object categories due to the needed resources.

In this paper, we aim at bridging these two ap-

proaches together by means of the zero-shot learn-

ing paradigm, in which no training images are avail-

able for test categories. We assume indeed no an-

notation data nor predeﬁned classes are available for

learning a classiﬁer/manifold. Given a query image

and without any prior knowledge of the data/classes

the system should be able to learn a ranking function,

adapted to the query, that costs as less as possible and

rank the images on a visual-similarity basis. The pro-

posed system, based on Linear Discriminant Analy-

sis (LDA), needs as low as one single sample (the

query) to learn a new model for every single query.

The cost of learning new query-adapted model is neg-

ligible and the ranking is as fast as the dot product dis-

tance. This allows us to achieve the highest efﬁciency

comparing to other supervised learning, yet the results

can be signiﬁcantly and consistently improved.

Linear Discriminant Analysis has been a rich

source of inspiration in the literature, giving birth to

many different variations of the original LDA. For

instance, (You et al., 2011) proposed a kernel based

LDA algorithm. Differently, (Zhu and Martinez,

2006) extended the original LDA framework by the

use of subclasses in compelling complex within-class

variations. We claim that those variations of LDA

might produce better results over the original ver-

sion, but would need much more samples to train the

model and would require doing a lot of online com-

putations. This would limit the system to work only

on those annotation-available objects. In contrast, we

show that the original LDA, albeit its simplicity, al-

lows to learn a model without using any annotation

data and yet produces meaningful improvement over

traditional distance measure.

The remaining of the paper is organized as fol-

lows. In section 2, we begin by presenting some re-

lated work of LDA in the context of image retrieval

system. Then we go gently to various variations of

LDA in literature and zero shot learning in general.

In Section 3, we present our retrieval approach in the

framework of zero-shot learning approach. In section

4, we describe the experimentation protocol followed

by our experimental results and discussion. Finally,

we conclude the paper in Section 5.

2 RELATED WORKS

LDA has been long used in the context of image re-

trieval but are targeted for different tasks. For in-

stance, (Tao et al., 2006) used LDA in relevance feed-

back step to select a subset of image features to con-

struct a suitable dissimilarity measure. (Lu and He,

2005), instead of learning subspace of the image fea-

ture, use LDA to obtain the semantic subspace by

learning on a large number of user’s feedback infor-

mation. (Swets and Weng, 1996) used LDA for di-

mensionality reduction to select the most discrimi-

nant features then performed image similarity mea-

sure based on euclidean distance. We are interested,

in this paper, in using LDA as a query-adapted func-

tion for similarity measure (as we will detail in the

next section).

LDA has been widely used in literature for clas-

siﬁcation problems. A number of variations of LDA

has been largely studied (Kim et al., 2007; Zhao et al.,

2014; You et al., 2011). In (Zhao et al., 2014) a new

way to combine the unlabelled data and labelled data

together is proposed to enhance the performance of

LDA. (Kim et al., 2007) suggested an incremental

LDA which is accurate as well as efﬁcient in both time

and memory, and could be targeted for online learn-

ing tasks. (You et al., 2011) suggested an approach

to map the original class (or subclass) distributions

into a kernel space where they are best separated by

a hyperplane. Experimental results in a large vari-

ety of datasets have demonstrated that this approach

achieves higher recognition rates than most of other

methods based on LDA. In the latest work related to

LDA (Deng et al., 2014), the idea is to extend the

classical LDA technique to linear ranking analysis,

by considering the ranking order of class centroids on

the projected subspace. This technique, even if tar-

geted for zero-shot learning, would require annotation

data to optimize two criteria: (1) the minimization of

the classiﬁcation errors with the assumption that each

class is gaussianly distributed; (2) the maximization

of the sum (average) of the k minimum distances of

all neighbouring-class (centroids) pairs.

However, these improved versions of LDA con-

trast with our motivation where we assume no anno-

tation data is available and the system should be able

to retrieve any object without prior knowledge of it.

To the best of our knowledge, we are the ﬁrst to pro-

pose this ranking strategy based on one-shot learning

approach for image retrieval.

Unlike LDA, zero-shot learning is relatively new

in the domain. Zero-shot learning is useful to predict

a new class label whose training data is not available

for learning. For example, (Larochelle et al., 2008)

experimented and reported to be able to uncover the

novel classes of digits that were not presented in the

training set. The motivation comes from the fact that

no training data can cover all the possible objects

in real world, but only some sort of description is

available for that object category. Zero-shot learning

LinearDiscriminantAnalysisforZero-shotLearningImageRetrieval

makes use of those descriptions to uncover the hidden

category. In (Palatucci et al., 2009), the authors pro-

posed a semantic knowledge (concept) to extrapolate

to novel classes. The observation x is ﬁrst described in

the feature space, then the model will map x in the fea-

ture space to a semantic space of p dimensions, then

map this semantic encoding to a class label. (Lam-

pert et al., 2009), however, introduced a binary at-

tribute layer to describe various object instances and

detect unseen object classes based on these attributes.

(Parikh and Grauman, 2011) worked on the same

”attribute based” principle, but in a relative way via

a trained ranking function. Interestingly, (Hoo and

Chan, 2013) used probabilistic latent semantic anal-

ysis to discover attributes (topic) in an unsupervised

manner and use it in zero-shot learning approach.

3 OUR APPROACH

Let q be a query image and q = {q

,...q

} ∈ R

a set of visual features representing the image. We

address the question of how to represent images by

D-dimensional features later in this section.

On the other hand, we assume having a large

collection of images, denoted as X = {x

,...x

∈ R

,∀j ∈ [1 ···n]. These images are represented

using the same type of visual features as the query.

The retrieval system has to be able to retrieve, as efﬁ-

ciently as possible, the set of the most similar images,

based on their distance to the query. This is to say that

we have to rank the images of the dataset according

to their distance to the query, i.e. we have to com-

pute X

= {x

r(1)

r(2)

,...x

r(n)

} such that S(q,x

r(i)

) <

S(q,x

r( j)

) ⇐⇒ i < j, where i, j ∈ [1···n]. S is a

function measuring the visual similarity between two

images.

As said in the introduction, the most commonly

used similarity function is the dot product, i.e.

S(q,x

) = q

·x

(1)

because of its simplicity and efﬁciency (Sivic and Zis-

serman, 2003; J

egou et al., 2012; Perronnin et al.,

2010)). However, as the dataset becomes larger, hav-

ing a better similarity function becomes crucial to

avoid overwhelming the user with irrelevant images.

The conventional ranking function is very fast but

does not cope well with variations of the images. Met-

ric learning is efﬁcient and better captures the varia-

tions, but requires too much training data and can only

be applied to those data-available object categories

(implying that some categories must be pre-deﬁned,

which is not the case in general).

Our approach consists in deﬁning the similarity

function based on Linear Discriminant Analysis in the

context of zero-shot learning to overcome this limita-

tion. The goal of zero-shot learning is to map the ob-

servations to an object class even if the direct mapping

function is not available (the model of this class could

not be trained). A general paradigm to achieve this

is ﬁrst by mapping the observation into another space

(e.g. semantic space or attribute space). Next, an-

other mapper will map the observation from the mid-

level feature to the class label. Unlike other zero-shot

learning systems that mostly operate on mid-level fea-

tures (attribute or semantic layer) and for which there

are some available training data (on the seen category)

to derive unseen objects, our approach works on al-

most no seen object category. The only knowledge

we have to know lies in the two matrices µ and Σ,

which are the mean and covariance of the distribution

of X . The interesting point is that these matrices can

be pre-computed once for all and do not depend on

the query.

Let us start by assuming that the images of X can

either be relevant or non relevant to the query q. The

distributions of these two classes can be approximated

by multivariate normal distributions characterized by

their means and the covariance matrices (µ

y=1

, Σ

y=1

)

and (µ

y=0

, Σ

y=0

LDA based Similarity Function. In LDA, an ob-

servation is labeled as relevant if P(y = 1|x) > P(y =

0|x) where P(y = k|x) is represented by a multivariate

normal distribution f :

P(y = k|x) =

f (x;µ

y=k

,Σ

y=k

)P(y = k)

∑

l∈0,1

f (x;µ

y=l

,Σ

y=l

)P(y = l)

(2)

where

∑

l∈0,1

P(y = l) = 1 and P(y = l) is the prior

probability of the class l. Using the log of the likeli-

hood ratios, the previous equation becomes:

log



P(y = 1|x)

P(y = 0|x)



= log



f (x;µ

y=1

,Σ

y=1

)

f (x;µ

y=0

,Σ

y=0

)



log



P(y = 1)

P(y = 0)



> 0

(3)

However, we do not assume having any train-

ing image at all to explicitly deﬁne the two classes.

The idea is hence to approximate the value of (µ

y=1

) and (µ

y=0

, Σ

y=0

). The dataset X where the

non-relevant images are generally dominant is a good

distribution to approximate the non-relevant class.

Hence, let µ

y=0

and Σ

y=0

denote the mean and co-

variance of the distribution of X. Even if this assump-

tion does not hold because it might contain some rel-

evant images, we will show that the achieved results

are signiﬁcantly improved in the experimentation sec-

tion. To approximate the relevant class, we employed

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

Figure 1: The black and the red circles represent µ

(mean

of the non relevant distribution) and µ

(mean of the relevant

distribution) respectively. x

and x

represent two particu-

lar instances in the dataset. At each iteration, LDA is not

only looking for the direct similarity between the query to

the observation, but also take into account the non relevant

instance and make a comparison whether the observation is

closer to the query or to the non relevant distribution.

the query image q as a single known vector. The query

image will be used as the center of the distribution

(µ

y=1

= q). As we do not have enough images to ap-

proximate the value of Σ

y=1

, we make the assumption

that the two classes share the same covariance matri-

ces (Σ

y=0

= Σ

y=1

= Σ). Hence, the equation (3) can

be rewritten as:

log



P(y = 1|x)

P(y = 0|x)



= log



P(y = 1)

P(y = 0)



−

(q −µ

y=0

)

−1

(q −µ

y=0

)

−1

(q −µ

y=0

) > 0

(4)

The ranking of the images can be obtain by simply

using w

.x > C where w = Σ

−1

(q −µ

y=0

) and C is a

constant based on prior probability, mean and covari-

ance. As we are interested by ranking the dataset and

not detecting relevant/non relevant images, C can be

ignored as it does not depend on x. By replacing this

new similarity function in the Eq. (1), we obtain:

S(q,x

) = w

·x

(5)

where w = Σ

−1

(q −µ

y=0

). This is particularly useful

because the w can be obtained at almost no cost (sim-

ple products/sums) for each iteration and the value of

(µ

y=0

,Σ) can be calculated ofﬂine.

The dot product in Eq. (5) between the hyperplan

w and the observation x

can thus be seen as the dif-

ference between two mahalanobis distances, with the

same covariance matrix, of x

to the centers of the two

normal distributions. This can be illustrated by the toy

example shown in Fig.1. Unlike the conventional sim-

ilarity measures that compute the distance between

the observation x

and the query only, our LDA-based

similarity function allows one step further by consid-

ering also the distance between the observation x

and

the non relevant distribution (d(x

,µ

)).

Figure 2: Example of an original query (ﬁrst left image)

and its associated positive samples generated by extracting

sub-windows on the original query (from Oxford Dataset).

Computation of the Mean(µ

y=1

) using Sub-

queries. In practice, it is generally better to insert

more input images to produce a statistically stable

mean of the relevant class, so that the model can be

more robust to image variations. We introduce here,

some additional relevant images by computing sub-

windows on the original query (shown in Fig. 2). The

additional images are generated with at least 70% of

the original size to guarantee that the system is not in-

troducing noise into the model. The mean query ˆq is

then calculated on this small set of generated images.

ˆq is then used in Eq. (5) in replacement of q. Hence,

we obtain:

S(q,x

) = w

·x

,w = Σ

−1

( ˆq −µ

y=0

). (6)

Image Representation. To better assess the be-

haviour of our zero-shot learning approach, we em-

ployed two image representations namely Fisher Vec-

tor (S

anchez et al., 2013) and VLAD (J

egou et al.,

2012). The image is ﬁrst described by a dense SIFT

descriptor of 128 dimension which is later reduced to

a 64 dimensional vector, thanks to a PCA and whiten-

ing, following (J

egou and Chum, 2012). Now, Let

P = {p

,t = 1...T } denotes the set of d dimensional

local descriptors extracted from the image (d = 64).

A codebook of size K is built with a kmeans on these

descriptors. We will next calculate the VLAD and

Fisher Vector representations as follows:

VLAD. The VLAD descriptor associates each lo-

cal descriptor to the nearest neighbour visual words

(cluster) c

. Then the differences between each local

descriptor p

and its nearest visual words are accumu-

lated:

∑

p:NN(p

)=i

−c

for all i = 1..K (7)

LinearDiscriminantAnalysisforZero-shotLearningImageRetrieval

The VLAD vector is the aggregated version of all

. Thus it contains Kd dimensions where d is the

dimension of the local SIFT-based descriptor.

Fisher Vectors. Let us assume that the samples

are independent and can be modeled as a mixture of

K Gaussian distributions.

Let Λ = {ω

,µ

,Σ

,k = 1...K} be the parameters

of the mixture of K Gaussians, where ω

,µ

,Σ

are

respectively the mixture weight, mean vector and co-

variance matrix. Each vector p

is associated to the

Gaussian k with a soft assignment γ

(k) also known

as the posterior probability, and deﬁned as:

(k) =

)

∑

j=1

)

(8)

where u

(p) denotes the k-th Gaussian and is deﬁned

as:

(p) =

(2π)

d/2

|Σ

1/2

−

(p−µ

)

−1

(p−µ

)

(9)

The Fisher Vector of P can be expressed as the

concatenation of the three main components:

√

∑

t=1

(γ

(k) −w

) (10)

√

∑

t=1

(k)(

−µ

)

) (11)

√

∑

t=1

(k)

√

[

−µ

)

−1] (12)

where the division and exponentiation of vec-

tors should be understood as term-by-term operations.

The ﬁnal dimension after aggregation is (2d + 1)K

where K is the number of Gaussians and d is the di-

mension of the local descriptors. To simplify the pro-

cess, we will follow the same direction as in (J

egou

et al., 2012), where it is suggested to keep only the

mean component (Eq. 10) and ignore other compo-

nents. In this case, the Fisher Vector will have only

Kd dimensions as in the case of VLAD.

4 EXPERIMENTAL RESULTS

In this section, we ﬁrst introduce our experimenta-

tion protocol. Then, we present the experimental re-

sults with various settings to show how LDA performs

comparing to dot product. Finally, we present the ex-

perimental results based on LDA with product quanti-

zation and asymmetric distance computation in larger

scale retrieval system.

Table 1: Datasets used in our experimentation. Flickr1M is

used as distractor only.

Dataset #Queries #Images

Oxford5k 55 5064

Paris6k 55 6512

Holiday1k 500 1492

Flickr1M - 1M

4.1 Experimentation Protocol

Parameters. The dense SIFT extractor is set to ex-

tract 128 features from 24 ×24 patches, every 8 pix-

els. The 128D vectors are reduced to 64D using PCA

whitening, which has been reported to improve the

performance (J

egou and Chum, 2012). Regarding the

size of the codebook, we follow the same protocol as

in (J

egou et al., 2012) where K is between 16 and

64. A second PCA is used to reduce the number of

features of the VLAD/Fisher Vector; the reduced di-

mension is in the range 16 to 1024.

Baseline System. As baseline system, we choose

to employ dot product as similarity measure, all other

things being equal. The image representation is the

same as the one used in our retrieval system.

Datasets. To test the proposed technique, we em-

ployed three public datasets (see Table 1): Oxford5k,

Paris6k and Holiday1k. Since LDA needs more sam-

ples to produce a good covariance matrix, we em-

ployed also Flickr1M

dataset as a distractor to form

Oxford1M, Paris1M and Holiday1M. The retrieval

result is measured by the Mean Average Precision

(mAP) as in (Philbin et al., 2007).

4.2 Results

In this section, we ﬁrst investigate our approximation

of the mean and covariance matrices. We ﬁrst

identify a good trade-off between the number of

sub-queries to be used and the computational time

to generate them. Then we present the effect of the

approximation of the shared covariance matrices.

Finally, we present the comparison results between

our zero-shot ranking system and the baseline.

Approximation of the Mean of the Relevant

Class. As shown in Section 3, our motivation is to

approximate the two distributions on the ﬂy and to

allow the system to learn a new ranking function

(Eq. 12). Let us recall that the mean of the relevant

class can be approximated by one (the query) or

a small set of sub-queries. Fig. 3 shows the mAP

vs an increasing size of sub-queries from 1 to 100

http://press.liacs.nl/mirﬂickr/dlform.php

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

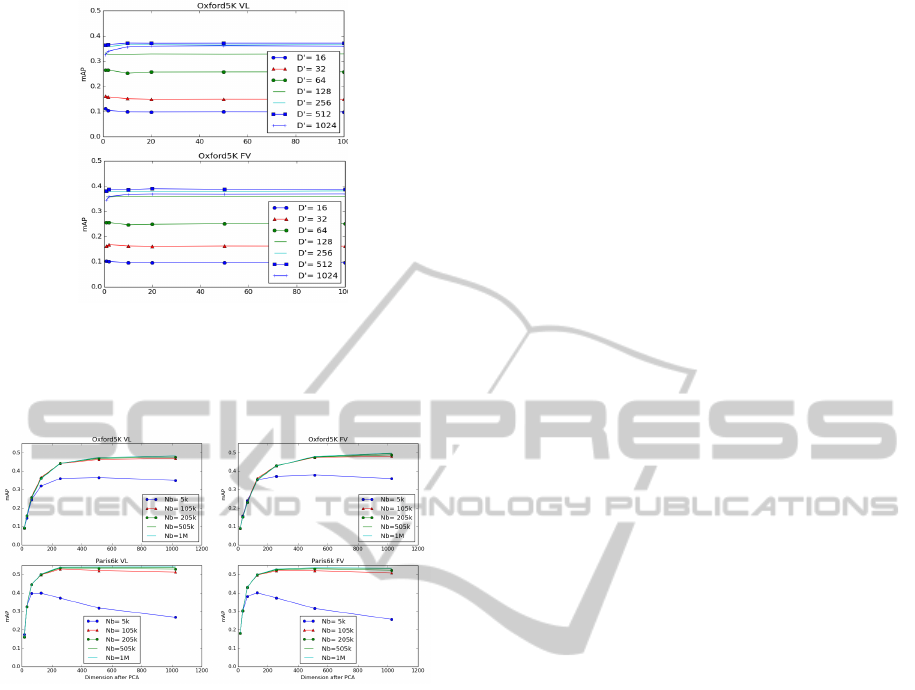
Figure 3: Approximation of the mean of the relevant class

using the query or with additional sub-queries from 1 to 100

(abscissa). The ordinate shows the retrieval results measure

in mAP learnt with k=64 Oxford dataset. D

refers to the

dimension after PCA of Vlad and Fisher vector.

Figure 4: Inﬂuence of the approximation of the shared co-

variance matrix for LDA-based retrieval system. The tested

datasets are Oxford5k and Paris6k with different covariance

matrices approximated with the images in the dataset itself

with ﬂickr1M.

(abscissa), with K = 64 and the dimension after PCA

∈ {16,32,64,128,256,512,1024}. The slope

of the curves appears to be null when the number

of positive samples is superior to 10. The same

behaviour is also observed with different codebook

sizes (K = 16) and other datasets (Holiday and Paris).

Interestingly, this suggests that we need only 10

samples to approximate a stable value of the mean.

This number is negligible comparing to the size of

the dataset. For the rest of the paper, we will ﬁx the

number of positive samples to 10.

Approximation of the Covariance Matrices.

Because the data set might contain some relevant

instances and thus it might affect the covariance

matrices, we are interested in this section in the size

of the image used to approximate the covariance

matrices. We present in Fig. 4, the retrieval results

on Oxford5k and Paris6k by employing different

numbers of additional sub-queries to generate the

covariance matrices ranging from 5k (the original

size) to 1M by using the images from Flickr1M.

When using approximately 5k to calculate the

covariance matrices, we observed some unexpected

behaviour when the dimension of the vector becomes

larger. This effect might be the problem of having

no enough observations to produce statistically

stable covariance matrices. As shown in Fig. 4, our

approximation technique, even if simple yet achieves

signiﬁcant improvement over the results provided by

the baseline system. In the following experiment, we

will used the covariance matrices calculated from 1M

vectors.

Comparison between LDA and Dot Product. Fig.

5 shows that the results based on LDA are signiﬁ-

cantly higher than the ones from the dot product. The

three left and the three right columns show the re-

trieval results on (Paris6k, Oxford5k, Holiday1k) and

(Paris1M, Oxford1M, Holiday1M). The abscissa rep-

resents the dimension of the vector after PCA and

the ordinate represent the retrieval results measured in

mAP. At almost every dimension and for each dataset,

the mAP of LDA is signiﬁcantly higher than the re-

sults based on dot product. In addition, when inject-

ing more images (ﬂickr1M) into the system, the dot

product distance seems not to capture well the differ-

ent variations in the image and thus results in decreas-

ing a lot of mAP while LDA-based retrieval seems to

better maintain the retrieval results. The average time

for retrieving a single query on a dataset of 1M images

based on dot product is around 3.9 seconds while with

LDA, it takes around 3.95 seconds.

4.3 Product Quantization

Product Quantization (PQ) and Asymetric Distance

Computation (ADC) have been proven to be an ef-

fective compression and approximation technique for

image retrieval (J

egou et al., 2012). We are interested

in this section on how Product Quantization (PQ) and

Asymetric Distance Computation (ADC) perform by

adapting them to our similarity ranking function. Let

∈ R

be the query vector and X = {x

,...x

∈ R

,∀j ∈ [1 ···n], a set of vectors representing

the images in the data set. The ADC approximates

the distance between the query q

with x

∈ X by:

d(q

) = d(q

,q(x

)) (13)

where q(x

) is the quantized version (closest cluster

vector) of x

learnt prior to the search. In practice,

the size of the cluster should be large enough to bet-

ter approximate the distance. However, making the

LinearDiscriminantAnalysisforZero-shotLearningImageRetrieval

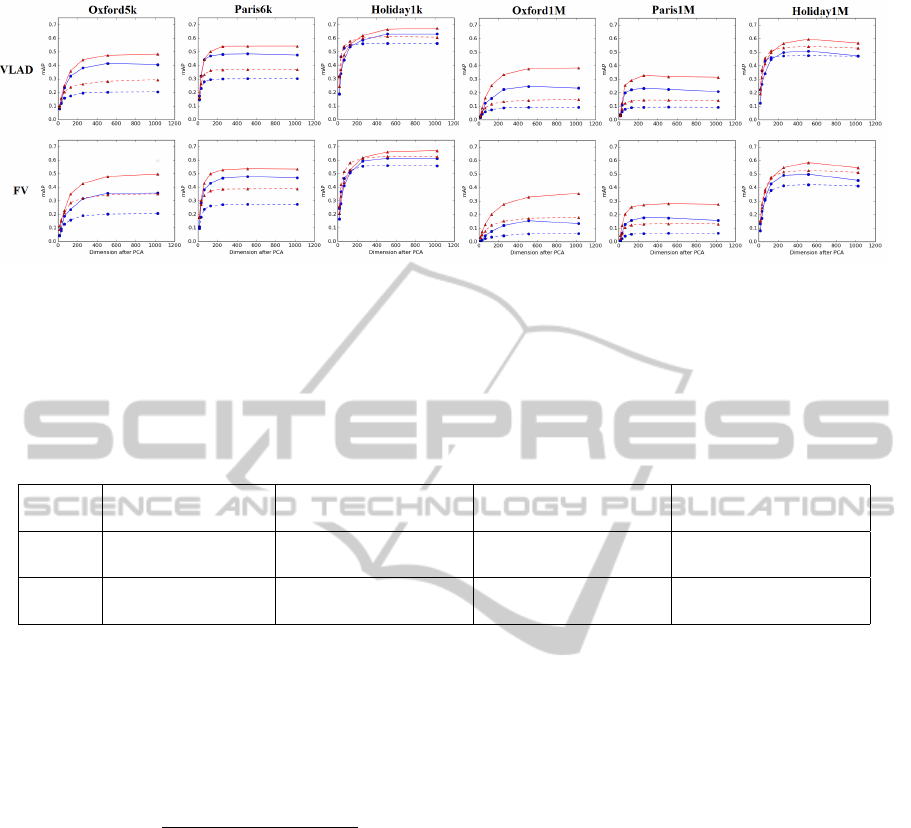
Figure 5: Retrieval results measured in mAP: comparison of LDA (plain line) and dot product (dash line). The abscissa

represents the dimension of the vector after PCA. The three left and the three right columns show the retrieval results on

(Paris6k, Oxford5k, Holiday1k) and (Paris1M, Oxford1M, Holiday1M). The ﬁrst and the second row show the retrieval

results based on VLAD and Fisher Vector respectively. The codebook sizes are K = 16 (blue line) and K = 64 (red line). One

can see that the retrieval results based on LDA (plain line) are signiﬁcantly higher than the dot product (dash line) distance

for almost all dimensions and datasets.

Table 2: Results on Oxford, Paris and Holiday with Flickr1M as distractor with and without PQ measured in mAP. The

codebook size is 64 and each segment has 16D. The tested dimensions after PCA are 128 and 1024 which corresponds to PQ

codes of 16 and 64 bytes.

Feature Method Oxford Paris Holiday

D’=128 D’=1024 D’=128 D’=1024 D’=128 D’=1024

VLAD LDA/Dot 0.25/0.11 0.38/0.15 0.29/0.14 0.31/0.14 0.49/0.41 0.57/0.53

LDA+PQ/Dot+PQ 0.18/0.06 0.33/0.09 0.23/0.09 0.26/0.09 0.44/0.40 0.53/0.43

Fisher LDA/Dot 0.20/0.15 0.35/0.18 0.26/0.12 0.28/0.13 0.46/0.47 0.55/0.51

LDA+PQ/Dot+pQ 0.17/0.08 0.32/0.14 0.21/0.09 0.24/0.10 0.41/0.36 0.44/0.44

codebook size higher is not favourable due to the cost

of complexity at approximation time. Another simple

solution is to construct a large set of sub-centroids by

splitting the feature vector into m segments and each

segment is encoded in the same manner with a cluster

Id number. Hence, the approximate distance can be

rewritten as:

d(q

,q(x

)) =

∑

d(u

),q

)))

(14)

where j = 1..m and u

) ∈R

D/m

corresponds to the

segment of the vector q

. Supposing the vector q

has 128 dimensions and m is set to be 16, each quan-

tizer q

(.) has 256 clusters (and thus can be coded

with 1 byte), the total number of approximation vector

is 255

. During the processing phase, the calculation

can be accelerated by using a look-up table.

Although, this technique has been applied on Eu-

clidean distance (see Eq. 14), we aim at adapting this

technique with our ranking function where the dis-

tance is a simple dot product distance. Recalling our

similarity function (Eq. 5), and by splitting the vector

into m segments:

S(q,x

) = w

·x

∑

S(w

i, j

) (15)

Note that, in the previous ADC calculation, the

approximation introduced two errors. One by replac-

ing the actual vector with the cluster center, another

one occurs when calculating the distance by the sum

of distances between each segment. In our dot prod-

uct, however, the second approximation error is elim-

inated thanks to the nature of the dot product distance.

We present in Table. 2, the results of PQ + ADC

adapted to our ranking function. The experimentation

is again running on the three dataset with Flickr1M.

The dimension after PCA used are 128 and 1024

coded with 16 and and 64 bytes respectively for each

image. At every dimension D

, the retrieval results

based on LDA are higher than the one provided by the

Dot product ranking. Furthermore, even with PQ, our

LDA-based ranking still achieves higher result com-

paring to the dot product approach. This make our

system more robust even if used with high compres-

sion technique.

5 CONCLUSION

We have introduced linear discriminant analysis as a

ranking approach for image search system in the con-

text of zero-shot learning. By allowing the system

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

to learn to rank the image, signiﬁcant and consistent

improvement has been validated on several datasets.

More interestingly, our approach is able to learn a new

query-adapted ranking function at almost no cost and

rank the images at the minimum cost as conventional

ranking functions. Furthermore, our query-adapted

function can be transformed into a single dot prod-

uct distance and is thus suitable for the state of the art

techniques for compression and fast distance calcula-

tion. This makes our ranking system suitable even for

the context of large-scale retrieval.

ACKNOWLEDGEMENT

The authors would like to thank Conseil Rgional de

Haute-Normandie , France, for sponsoring this work

in the context of PlaIR2.0 project.

REFERENCES

Deng, W., Hu, J., and Guo, J. (2014). Linear ranking anal-

ysis. In IEEE Conference on Computer Vision and

Pattern Recognition, pages 3638–3645.

Hoo, W. L. and Chan, C. S. (2013). Plsa-based zero-shot

learning. In IEEE International Conference on Image

Processing, pages 4297–4301.

egou, H. and Chum, O. (2012). Negative evidences and

co-occurences in image retrieval: The beneﬁt of pca

and whitening. In European Conference on Computer

Vision, pages 774–787.

egou, H., Perronnin, F., Douze, M., S

anchez, J., P

erez, P.,

and Schmid, C. (2012). Aggregating local image de-

scriptors into compact codes. Transactions on Pattern

Analysis and Machine Intelligence, 34(9):1704–1716.

Kim, T.-K., Wong, K.-Y. K., Stenger, B., Kittler, J., and

Cipolla, R. (2007). Incremental linear discriminant

analysis using sufﬁcient spanning set approximations.

IEEE Conference on Computer Vision and Pattern

Recognition, pages 1–8.

Lampert, C. H., Nickisch, H., and Harmeling, S. (2009).

Learning to detect unseen object classes by between-

class attribute transfer. In IEEE Conference on Com-

puter Vision and Pattern Recognition, pages 951–958.

Larochelle, H., Erhan, D., and Bengio, Y. (2008). Zero-

data learning of new tasks. In AAAI, volume 1, pages

646–651.

Lu, K. and He, X. (2005). Image retrieval based on in-

cremental subspace learning. Pattern Recognition,

38(11):2047–2054.

Palatucci, M., Pomerleau, D., Hinton, G. E., and Mitchell,

T. M. (2009). Zero-shot learning with semantic output

codes. In Advances in neural information processing

systems, pages 1410–1418.

Parikh, D. and Grauman, K. (2011). Relative attributes. In

IEEE International Conference on Computer Vision,

pages 503–510.

Perronnin, F., Liu, Y., S

anchez, J., and Poirier, H. (2010).

Large-scale image retrieval with compressed ﬁsher

vectors. In Computer Vision and Pattern Recognition,

pages 3384–3391.

Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman, A.

(2007). Object retrieval with large vocabularies and

fast spatial matching. In Conference on Computer Vi-

sion and Pattern Recognition, pages 1–8.

anchez, J., Perronnin, F., Mensink, T., and Verbeek, J.

(2013). Image classiﬁcation with the ﬁsher vector:

Theory and practice. International journal of com-

puter vision, 105(3):222–245.

Sivic, J. and Zisserman, A. (2003). Video google: A text

retrieval approach to object matching in videos. In

International Conference on Computer Vision, pages

1470–1477.

Swets, D. L. and Weng, J. J. (1996). Using discrimi-

nant eigenfeatures for image retrieval. IEEE Trans-

actions on pattern analysis and machine intelligence,

18(8):831–836.

Tao, D., Tang, X., Li, X., and Rui, Y. (2006). Direct ker-

nel biased discriminant analysis: a new content-based

image retrieval relevance feedback algorithm. IEEE

Transactions on Multimedia, 8(4):716–727.

You, D., Hamsici, O. C., and Martinez, A. M. (2011). Ker-

nel optimization in discriminant analysis. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

33(3):631–638.

Zhao, M., Zhang, Z., Chow, T. W., and Li, B. (2014).

Soft label based linear discriminant analysis for im-

age recognition and retrieval. Computer Vision and

Image Understanding, 121:86–99.

Zhu, M. and Martinez, A. M. (2006). Subclass discriminant

analysis. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 28(8):1274–1286.

LinearDiscriminantAnalysisforZero-shotLearningImageRetrieval