Selective Encryption of Medical Images

Aissa Belmeguenai, Lakhdar Grouche and Raﬁk Djemili

Laboratoire de Recherche en Electronique de Skikda, Universit´e 20 Aoˆut 1955- Skikda,

BP 26 Route d’El-hadaeik, Skikda, Algeria

Keywords:

Encryption by Region, Grain-128, Medical Images.

Abstract:

The transfer of image in the digital world plays a very important role, their security is an important issue,

and encryption is one of the ways to ensure security. Few applications like medical image security needs to

secure only selected region of the image. This work proposes a selective encryption approach for medical

images. The approach based on Grain-128 which provides the facilities of implementation of selective image

encryption and decryption. Several tests are done in order to prove the approach performance including visual

tests, key sensitivity, entropy analysis and correlation coefﬁcient analysis.

1 INTRODUCTION

Sometimes the secure information is isolated in a one

region or few regions of the image then encrypt only

these regions, this allows us to gain considerabletime.

In this way, the encryption does not delay the pro-

cess; instead it can be inserted as an integral part of

the processing chain. In an application, when the se-

lective encryption is adopted, the choice of regions to

encrypt can be done in three ways which are: Man-

ual: The regions are deﬁned using the mouse as an

electronic pen. Semi-automatic: In this case the re-

gions are determinedby programand always leave the

user the possibility of a manual correction (Malet and

al, 1988). For example, edge detection followed by a

correction or improperly closed contours that overlap.

Automatic: When data parts are in the same co-

ordinates location of the regions, these are prede-

ﬁned and the choice is made consistently. Sometimes

the determinations of regions are programmed in ﬁrst

then the result of processing will be used to encrypt

pilot regions. For example, for the following interest

area that carries a particularity in the image. During

an operation of Prenatal chromosome analysis and if

the presence of a chromosomal abnormality of num-

ber, this is in the form of a trisomy 13 or trisomy 21

(Geneix and al, 1988), (Malet and al, 1989). How-

ever, when establishing the caryotype of the patient,

the interest area (trisomy 13 or trisomy 21) from se-

cret information and that they should be within the

specialist doctor who has the sole authority to access

and pronounce these results to the patient.

To keep this information secret, this paper de-

scribes an implementation of Grain-128 for selective

encryption medical images. Several tests are done

for proving the system performance including visual

tests, correlation coefﬁcient analysis, entropy analysis

and key sensitivity.

2 GRAIN-128

In this section we give a brief description of Grain-

128. The Grain-128 Keystream Generator was pro-

posed by Hell, Johansson, Maximov, and Meier

(M.Hell and W.Meier, 2006) as a variant of Grain-

v1 (Canniere and Preneel, 2005), (C. Cid and Kuri-

hara, 2009). The cipher consists of two 128-bit shift

registers, one linear feedback (LFSR), one nonlinear

feedback (NLFSR) and nonlinear Boolean functions

The feedback polynomial of the NLFSR has alge-

braic degree of two, and h has degree of three. The

content of the LFSR is denoted by u

, u

i+1

, ...u

i+127

and the content of the NLFSR is denoted by

, v

i+1

, ...v

i+127

The LFSR is governed by the linear recurrence:

i+128

= u

⊕ u

i+7

⊕ u

i+38

⊕u

i+70

⊕ u

i+81

⊕ u

i+96

. (1)

The NLFSR is governed by the nonlinear recurrence:

Belmeguenai A., Grouche L. and Djemili R..

Selective Encryption of Medical Images.

DOI: 10.5220/0005301200930099

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 93-99

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

i+128

= u

⊕ v

i+26

⊕ v

i+56

⊕ v

i+91

⊕ v

i+96

⊕

i+3

i+67

⊕ v

i+11

i+13

⊕ v

i+17

i+18

oplusv

i+27

i+59

(2)

⊕v

i+40

i+48

⊕ v

i+61

i+65

⊕ v

i+68

i+84

The contents of the LFSR and NLFSR represent the

state of the Grain-128.

The combining function h of Grain-128 produces

its output value based of the selected bits from the

NLFSR and the LFSR as:

h(i) = u

i+8

i+1

⊕ u

i+13

i+20

⊕v

i+95

i+42

⊕ u

i+60

i+79

(3)

⊕v

i+12

i+95

The output stream of the Grain-128 generates

from the selected bits from the LFSR and NLFSR

states and the output of h. it is computed as:

y(i) = ⊕

j∈A

i+ j

⊕ h(i) ⊕ u

i+93

. (4)

Where A = {2, 15, 36, 45, 64, 73, 89}.

3 SELECTIVE IMAGE

ENCRYPTION

In this section, one is interested in the selective im-

age encryption. In the selective image encryption,

the encryption is not applied to entire data but it is

applied to selected data only. Here the encryption

process is applied only to the selected regions of in-

terest leading to reduce the time for encryption see

(N. S. Kulkarni and Gupta, 2008), (Z. Brahimi, 2008)

and (Panduranga and al, 2013). Selection of interest-

ing regions are done manually or automatically based

on the application. To do this, we apply at the input

of cryptosystem both informations (encrypted image

and keystream generator) except that the keystream

generator is controlled by encrypted areas.

Let f be the original image and g be binary image

representing the regions to be encrypted, such that

g(i, j) =



1 if f(i, j) = to encrypt

0 if otherwise

(5)

At the reception the reverse operation is applied

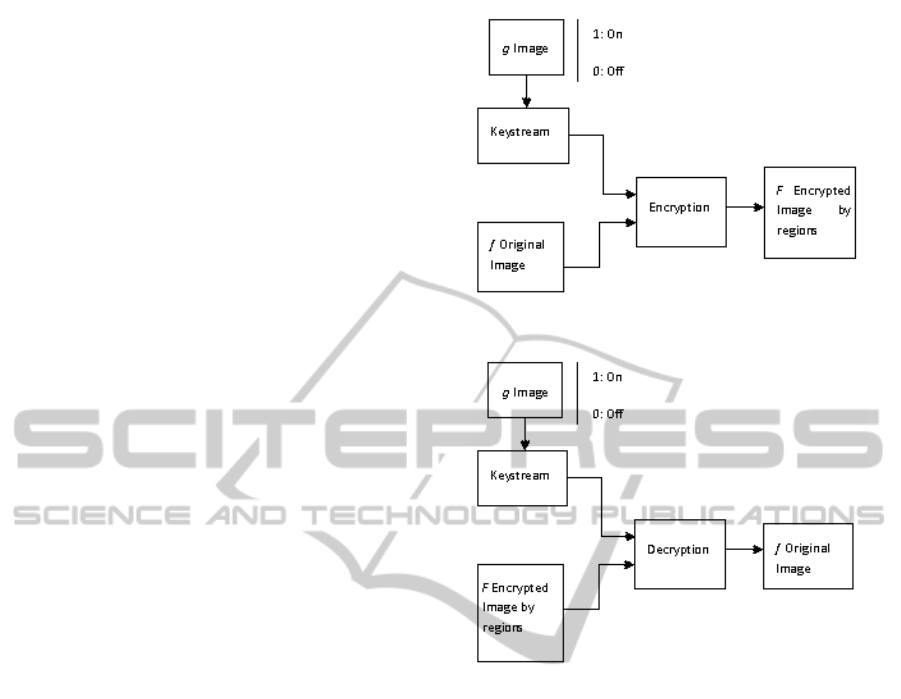
to extract the hidden information. Figure 1 shows the

block diagram of selective image encryption process

and ﬁgure 2 shows the block diagram of selective im-

age decryption process.

Figure 1: Block diagram of selective image encryption pro-

cess.

Figure 2: Block diagram of selective image decryption pro-

cess.

4 PROPOSED SELECTIVE

IMAGE ALGORITHM

The proposed selective image algorithm is using the

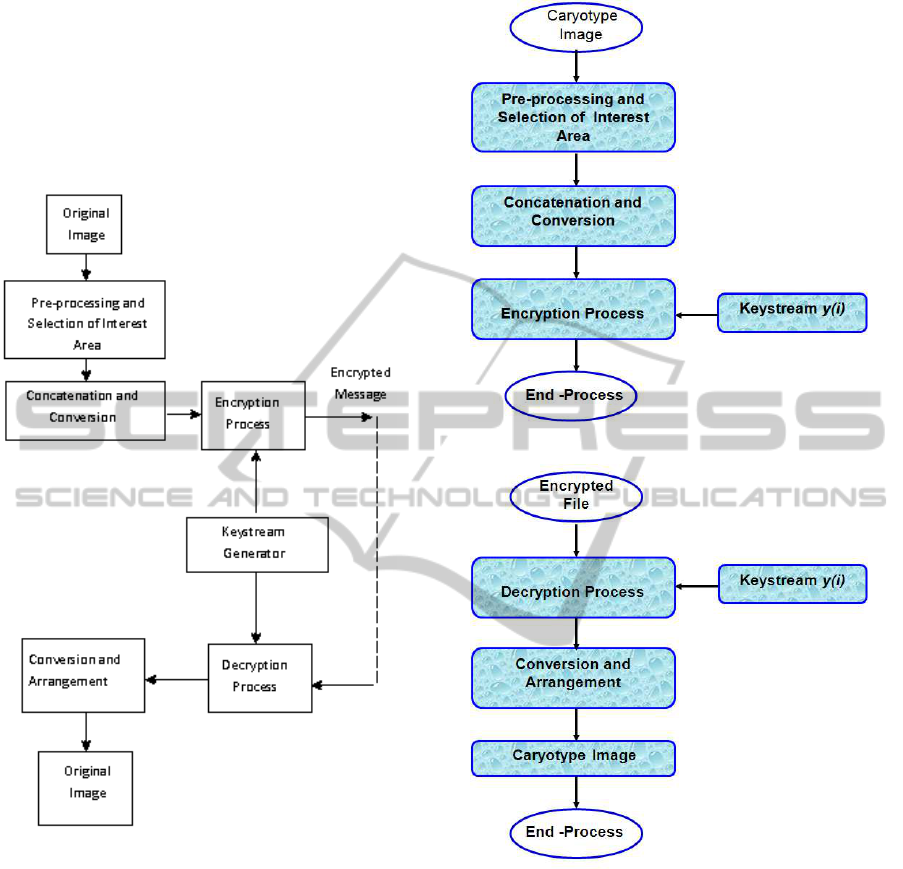
Grain-128 keystream generator. Figure 3 depict the

block diagram of the proposed approach. The ﬂow

charts of the encryption and decryption process are

presented respectively in ﬁgures 4 and 5.

In a human Caryotype, the numbers of defects are

usually trisomy 13 and trisomy 21 thereforeobserving

three chromosomes in these boxes means that there is

an anomaly of number, which means that the contents

of these boxes must be within reach only of the doctor

in charge. In addition, the doctor in charge wrote his

ﬁnal diagnosis in the observation part.

Since these three areas, boxes 13, 21 and the ob-

servation text constitute a conﬁdential medical re-

port then they are automatically hidden and accessible

only by the doctor in charge. Thus, medical conﬁden-

tiality is respected.

The individual steps of encryption and decryption

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

process are discussed in the following sub-sections.

Let Caryotype (i.e. original image) of 391 × 300 pix-

els. Let R

, R

and R

three regions of interest in

Caryotype, respectively corresponding to boxes 13,

21 and the observation text. We denote by ⊕ the sum

modulo 2. By p, q and y we note respectively the dig-

ital selected regions, cipher digital selected regions

and digital keystream.

Figure 3: Block diagram of the proposed approach.

4.1 Pre-processing and Selection of

Interest Area

At ﬁrst, the Caryotype gray scale image is converted

into a matrix of pixel values. Second, select R

, R

and R

regions.

4.2 Concatenation and Conversion

Convert the region R

, R

and R

into a one dimen-

sional of decimal pixel values. This is then converted

into a one dimensional binary sequence and stored it

in p used for encryption process.

Figure 4: Flow chart of the encryption process.

Figure 5: Flow chart of the decryption process.

4.3 Encryption Process

The encryption process work as follow:

• Load the digital selected regions p;

• N ← the length of p ;

• for i = 1 to N to make :

Generate the digital keystream y

as it shows

the keystream algorithm in section 4.6;

• End to make;

• for i = 1 to N to make:

Encrypt the digital selected regions p using

relation

SelectiveEncryptionofMedicalImages

q(i) = p(i) ⊕ y(i) ,

• End to make ;

• Sent the cipher digital selected regions q.

4.4 Decryption Process

The decryption process work as follow:

• Load the cipher digital selected regions q

• N ← the length of q ;

• for i = 1 to N to make :

Generate the digital keystream y

as it shows

the keystream algorithm in section 4.6;

• End to make ;

• for i = 1 to N to make :

Decrypt the cipher digital selected regions

using relation

p(i) = q(i) ⊕ y(i)

• End to make ;

4.5 Conversion and Arrangement

Convert the decrypted digital selected regions p into

a one dimensional of decimal pixel values, then put

each pixel in its place in the Caryotype image.

4.6 Keystream Algorithm

• Read N, length of the digital selected regions p ;

• Introduce the values of initialization of LFSR and

NLFSR ;

• for i = 1 to N + 127 to make:

Generate binary sequences u(i) and v(i) re-

spectively produced by LFSR and NLFSR as

shown the equations 1 and 2;

• End to make.

• for i = 1 to N to make:

Generate the binary sequence h(i) produced

by the combining function h ;

Generate the output of keystream using the

relation:

y(i) = ⊕

j∈A

i+ j

⊕ h(i) ⊕ u

i+93

• End to make.

5 SIMULATION AND RESULTS

In the simulation, three selected regions automatically

, R

and R

indicated in ﬁgures 6, 7 and 8 are used

to validate the approach. Simulation was carried out

using MATLAB V 7.5. By comparing the original

regions and their corresponding encrypted regions in

ﬁgures 6, 7 and 8, there is no visual information ob-

served in the encrypted regions. Figure 9 show the

visual testing of encryption and decryption for Cary-

otype.

In the experiments, the original regions and their

corresponding encrypted regions and their histograms

are shown in ﬁgures 6, 7 and 8. It is clear that the en-

crypted regions histograms are nearly uniformly dis-

tributed, and signiﬁcantly different from the original

regions histograms. So, the encrypted regions do not

provide any clue to employ any statistical attack on

Figure 6: Experimental results for selected region R

: show

the original region R

and its corresponding encrypted re-

gion and their histograms.

Figure 7: Experimental results for selected region R

: show

the original region R

and its corresponding encrypted re-

gion and their histograms.

Figure 8: Experimental results for selected region R

: show

the original region R

and its corresponding encrypted re-

gion and their histograms.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

Figure 9: Visual testing of encryption and decryption for

caryotype.

the proposed design, which makes statistical attacks

difﬁcult.

5.1 Correlation Coefﬁcient Analysis

Table 1 and Table 2 show the correlation coefﬁcient

results. By Cor

, Cor

, and Cor

we denote

respectively correlation coefﬁcient between original

image and encrypted image, correlation coefﬁcient

between original image and decrypted image, corre-

lation coefﬁcient between encrypted image and de-

crypted image with wrong key and correlation coef-

ﬁcient between original image and decrypted image

with wrong key.

It is observed that the values of Cor

, Cor

, and

Cor

shown in the table 1 and table 2 are quite close to

the value of zero, which implies that the original im-

ages and their encrypted images are totally different

i.e. the encrypted image has no features and highly

independent on the original image. It is also clear that

the values of Cor

shown in the table 1 are equal to

the value 1, which implies the encrypted images are

the same as the original images.

Table 1: Correlation Coefﬁcients Analysis.

Cases Cor

Cor

Region 1 0.0100438 1.0000000

Region 2 0.0554183 1.0000000

Region 3 -0.0062774 1.0000000

Caryotype 0.0059980 1.0000000

Table 2: Correlation Coefﬁcients Analysis.

Cases Cor

Cor

Region 1 -0.0305526 0.0159771

Region 2 0.0688412 0.0102282

Region 3 -0.0058162 -0.0093714

Caryotype -0.0024934 -0.0018975

5.2 Entropy Analysis

It is well known that the entropy E(M) of a message

source M can be calculated as:

E(M) =

T−1

∑

i=0

P(M

)log2

P(M

)

. (6)

Where T Gray value of an input image (0-255), P(M

)

represents the probability of symbol M

and the en-

tropy is expressed in bits. Let us suppose that the

source emits 2

symbols with equal probability, i.e.,

M = {M

, M

, ..., M

}. Truly random source entropy

is equal to 8.

Table 3 and table 4 show the entropy results. By

, E

, and E

we denote respectivelyentropy val-

ues: of original image, encrypted image, decrypted

image and decrypted image with wrong key. The val-

ues of E

and E

presented in the table 3 and table

4 are very close to the theoretical value of 8. This

means that information leakage in the encryption pro-

cess is negligible and the encryption system is secure

upon the entropy attack.

5.3 Key Sensitivity

A good cryptosystem should be sensitive to the secret

SelectiveEncryptionofMedicalImages

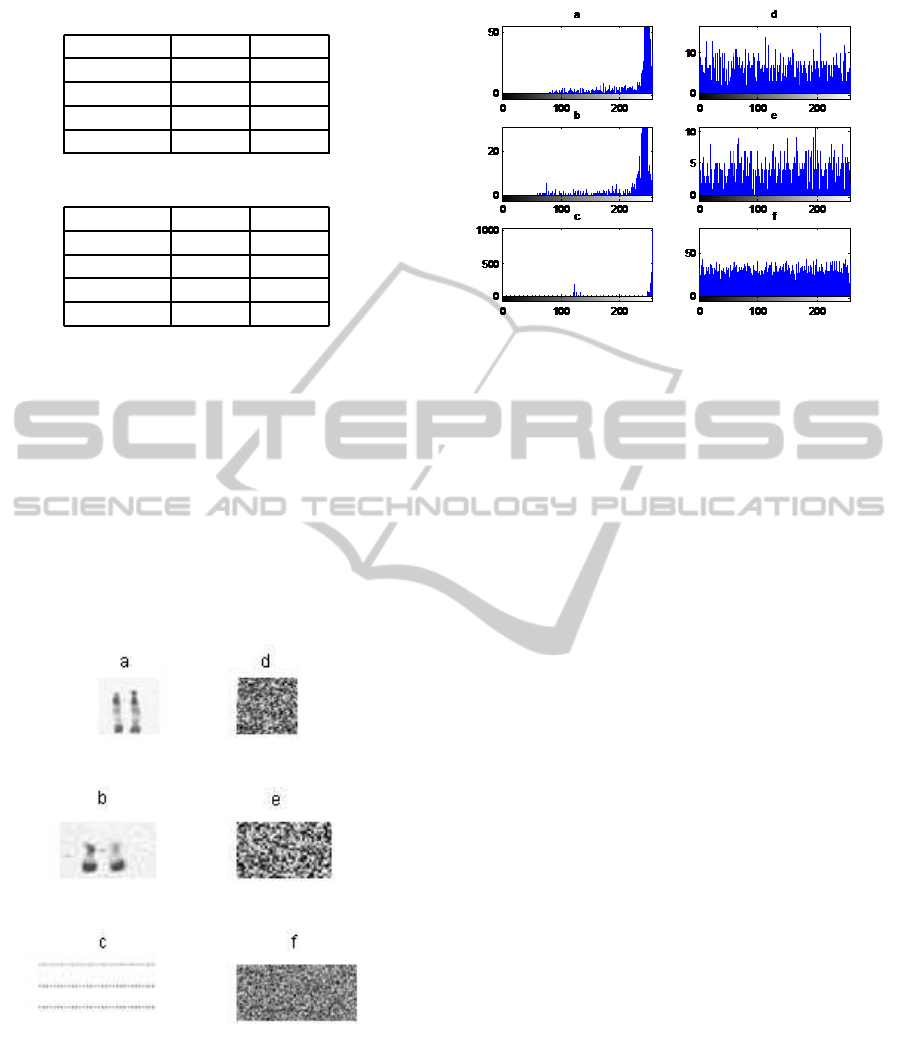
Table 3: Image Entropy.

Cases E

Region 1 5.3746 7.8923

Region 2 5.3398 7.8101

Region 3 1.2416 7.9755

Caryotype 2.9176 7.9812

Table 4: Image Entropy.

Cases E

Region 1 5.3746 7.8668

Region 2 5.3398 7.8128

Region 3 1.2416 7.9790

Caryotype 2.9176 7.9847

keys, which means change of a single bit in the secret

key should produce a completely different encrypted

image. The Grain-128 was tested to the keys sensi-

tivity, we decrypt the encrypted regions illustrated by

ﬁgures 6,7 and 8 with true key and, we decrypt the

encrypted regions illustrated by ﬁgures 6,7 and 8 with

wrong key (slightly different key). The results are

given by ﬁgures 10 and 11. The values of Cor

and

Cor

given in the table 2 are quite close to the value

of zero, and the values of E

given in the table 4 are

very close to the theoretical value of 8, which implies

that the proposed cryptosystem is highly sensitive to

the key.

Figure 10: Sensitivity analysis: Frame (a), (b) and (c) re-

spectively, show the decrypted regions with true key of the

encrypted regions shown in ﬁgures 6,7 and 8. Frame (d), (e)

and (f) respectively; show the decrypted regions with wrong

key of the encrypted regions shown in ﬁgures 6,7 and 8.

6 CONCLUSIONS

In this Work, a selective image encryption algorithm

Figure 11: Sensitivity analysis: Frame (a), (b) and (c) re-

spectively, show the histograms of decrypted selected re-

gions with true key of the encrypted regions shown in ﬁg-

ures 6,7 and 8. Frame (d), (e) and (f) respectively; show

the histograms of decrypted regions with wrong key of the

encrypted regions shown in ﬁgures 6,7 and 8.

for medical image using Grain-128 keystream genera-

tor was introduced. Simulations were carried out with

three different selected regions. The visual test indi-

cates that the encryptedregions was very different and

no visual information can be deduced about the orig-

inal region for all tested regions. This method is very

simple, fast and easy to implement, as encryption and

decryption selective image algorithm.

REFERENCES

C. Cid, S. K. and Kurihara, J. (2009). The rakaposhi stream

cipher. In in Proceedings of the 11th international

conference on Information and Communications Se-

curity, ICICS’09, Berlin, Heidelberg. Springer-Verlag,

pp. 32-46.

Canniere, C. D. and Preneel, B. (2005). Trivium a

stream cipher construction inspired by block ci-

pher design principles. In eSTREAM, ECRYPT

Stream Cipher Project, Report 2005/030 (2005-04-

29). http://www.ecrypt.eu.org/stream.

Geneix, A. and al (1988). Image processing in human cy-

togenetics new steps toward quantiﬁcation. In Karyo-

gram (U.S.A.). vol 14, p45-49,1988.

Malet, P. and al (1988). New cytogenetic techniques and

medical applications. In Sem Hop Paris. 64, n23,

1576-1586,1988.

Malet, P. and al (1989). L’analyse chromosomique par

traitement d’images aspects r´ecents et perspectives. In

Annales de G´en´etiques. vol 32, n3, p.164-16,1989.

M.Hell, T. and W.Meier (2006). A stream cipher proposal:

Grain-128. In In IEEE International Symposium on

Information Theory. ISIT 2006.

N. S. Kulkarni, B. R. and Gupta, I. (2008). Selective encryp-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

tion of multimedia images. In NSC 2008. December

17-19.

Panduranga, H. T. and al (2013). Selective image encryp-

tion for medical and satellite images. In International

Journal of Engineering and Technology (IJET). vol 5

No 1, 2013.

Z. Brahimi, H. Bessalah, A. T. M. K. K. (2008). Selec-

tive encryption techniques of jpeg2000 codestream for

medical images transmission. In WSEAS Transactions

on Circuits and Systems. vol 7, July 2008.

SelectiveEncryptionofMedicalImages