
Adaptive Segmentation by Combinatorial Optimization
Lakhdar Grouche and Aissa Belmeguenai
Laboratoire de Recherche en Electronique de Skikda LRES, 20 aoˆut University, BP 26 Route El Hadaeik, Skikda, Algeria
Keywords:
Iterative Segmentation, Kangaroo Method, Non-oriented Graph, Entire Number Formulation, Combinatorial
Optimization.
Abstract:
In this paper we present an iterative segmentation. At the beginning it is using a stochastic method called
Kangaroo in order to speed up the regions construction. Later the problem will be presented as non-oriented
graph then reconstructed by linear software as entire number. Next, we use the combinatorial optimization to
solve the system into entire number.
Finally, the impact of this solution became apparent by segmentation, in which the edges are marked with
special manner; hence the results are very encouraging.
1 INTRODUCTION
The techniques of images segmentation have seen
considerable development these last years, because
we have passed the split-and-merge (H.Yang, 1997),
to the use of watersheds, to active edges mini-
mization, and finally to multi-agents segmentation
(S.Mazouzi, 2007).
The segmentation methods by increasing regions
based to measurement relatedto gray level,or to prob-
ability measurement, bring a good initial identifica-
tion for regions of interest, but suffer from the ma-
jor inconvenient of non precise localization of regions
edges. The approach of segmentation by the active
edges presents good results concerning the localiza-
tion of regions edges of interest, providing that the
initialization of these edges will not be far from the
final edges. The hybrid approaches can combine in-
formation coming from several methods looking very
promising.
These diversitiesof methods have made that we do
not have a universal method of segmentation, but we
have an algorithm of segmentation to be used for each
application and its evaluation depends on the obtained
results. This complexity is related to the principle of
segmentation, because we are looking for a compro-
mise between an over segmentation in which there are
so much details and an under segmentation in which
there are a lack of details (W.Eziddin, 2012).
Finally, as a conclusion of the image method seg-
mentation, we can underline that the iterative method
of segmentation lead, in general, to the best results
than the non-iterative methods.
In the present work we have developed an iterative
method of segmentation, which treat directly the com-
promise of segmentation, it is intended performance
by the following strengths:
1. Self adaptive: it does adapt automatically with the
sample in order to avoid huge number of iteration.
This self-adaptive sentence will be constituted of
two other sentences:
(a) One first sentence in which we have used a
heuristic to estimate the step used during the
constitution of regions, in order to reduce the
number of iteration and consequently the exe-
cution time of this sentence.
(b) A second sentence which is of practical use,
this heuristic will be applied on images of dif-
ferent nature, in which the gray level inside
each region is almost constant, more or less
constant and completely variable.
2. Optimal: the problem formulation as entire then
the use of the graphs theory and the combina-
torial optimization enable the fine segmentation
and avoid the oversegmentation or the under-
segmentation.
Its application on diversity of samples, contain at the
same time regions of close levels, and regions of too
far levels, givinggood results. By this fact our method
turns effective, and it is valid for a large variety of
applications.
92
Grouche L. and Belmeguenai A..
Adaptive Segmentation by Combinatorial Optimization.
DOI: 10.5220/0005301300920097
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 92-97
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 THEORETICAL TOOLS
2.1 Definitions
The segmentation of an image A, regarding the ho-
mogenous criteria H (gray level, texture,..) , is a par-
tition of A on homogenous regions r
1
, r
2
, . . . , r
n
.
H have an argument for one or several regions close
to the initial image A to return a decision of its homo-
geneity, H((r
i
, r
j
, ...) ∈ Z
2
) → {true, false}. In our
work, we introduce several parameters on the region
that we would like to study, these latter will be devel-
oped in the section 2.3.
n
[
i=1
(r
i
) = A (1)
∀i ∈ {1, 2, . . . , n} r
i
is related (2)
∀i ∈ {1, 2, . . . , n} H(r
i
) is true (3)
∀r
i
, r
j
voisines H(r
i
, r
j
) is false. (4)
Regarding this definition, the segmentation depends
on the criteria H used. The choice of this criterion is
really primordial.
2.2 Regions Training
Let A the image to make segmentation with a(i, j),
the gray level of pixels and C the image label (the im-
age of labeled regions) with c(i, j), the gray level of
pixels, the pixels of each region have the same level
noted code. To go from A to C, we proceed with dou-
ble scan as follow. Each pixel c(i, j) ∈ C is computed
by the Algorithm Code.
Algorithm Code
Initialization: we initialize the code = 1, the gap ε =
0, we start with the pixel high-left of the image
c(1, 1) = code.
Horizontal: for two horizontal pixels close:
If |a(i, j) − a(i, j + 1)| ≤ ε
then c(i, j + 1) = c(i, j)
else code = code+ 1 , c(i, j + 1) = code;
EndIf
If (end of line)
then code = code+ 1
EndIf
Vertical: for two vertical pixels close:
If (|a(i, j) − a(i+ 1, j)| ≤ ε) then
c(i, j) = min(c(i, j), c(i+ 1, j))
c(i+ 1, j) = min(c(i, j), c(i+ 1, j));
EndIf
Equality: Iterate the vertical scan untill not equality
of image C.
Let B the vector of codes used in the Algorithm Code
so lentgh(B) = n.
A propagation with equality levels ε = 0 give
regions only for perfect images, but in the general
case the levels of the same region are variables,
they vary from one sample to the other. So we
have to make compromise between one ε weak giv-
ing over-segmentation and another big giving under-
segmentation. To this stage two approaches are pos-
sible:
1. The first approach consists of starting from the
equality ε = 0, then increment it gradually, till the
regions training, but this procedure is boring in
time, because the propagation process is repeated
each iteration. This drawback is appearing usually
for far regions levels.
2. A second approach consists of starting from the
equality ε = 0, then find an estimation function
which adapt the increment step according to the
sample. This self adaption increase the quickly
the step ε, decrease the number of iteration and
speed up the convergenceprocess to regions train-
ing. A detailed method of speed up will be pre-
sented in section 3.1 .
Finally the two approaches require a stop condition;
this latter is fixed according to the classification rate
of pixels in regions.
2.3 Connection Graph
Having A, C and B, we proceed to the regions extrac-
tion one by one. For each region, we determine the
following parameters (A.Herbulot, 2007); for exam-
ple for one region r
i
coded by B(i),
• s
r
i
the surface of r
i
,
• µ
r
i
the average level,
• h
r
i
the histogram,
• ρ
r
i
= {x : h
r
i
(x) = max(h
r
i
)} the mode,
• I
r
i
= [a, b] such as Σ
b
x=a
h
r
i
(x) > 0.8 ∗ Σ
255
x=0
h
r
i
(x)
the confidence interval .
The coded image C leads to non oriented graph G =
(V, E) (E.Fleury, 2009; F.Khadar, 2009).
AdaptiveSegmentationbyCombinatorialOptimization
93

- The set of nodes V present the regions r
i
with i ∈
V (1) in which each node is characterized by its
parameters (s
r
i
, µ
r
i
, h
r
i
, ρ
r
i
, I
r
i
) and kVk = n.
- A link between i and j, e = (i, j) ∈ E such as i, j ∈
V show the regions r
i
and r
j
are close. This link
does not exist unless the parameters of regions are
distinct (3) and (4).
3 PROBLEM FORMULATION
3.1 The Kangaroo Method to Speed up
the Convergence
The stochastic method of Kangaroo (G.Fleury, 1993)
, is metaheuristic used in the NP-difficult problems,
that we have adopted to our problem to accelerate the
process of regions constitutions. As indicated by its
name, it has a variable step, thus we have experimen-
tally used an empiric formula to update the step of
each iteration (5, 6). Following the step of propaga-
tion, the trained regions of some pixels form an over-
segmentation and their pixels are not classified.
Let ψ the pixel number non classified and S = size,
the ratio of non classification τ is expressed as:
τ =
ψ
S
(5)
Since this ratio is expressing the number of non-
classified pixels, so it does show good sign of the in-
crement step of Kangaroo and consequently the esti-
mation function ε. Because a high τ means that the
majority of pixels are not classified, which means that
we are far from the convergence, so we have to in-
crement the step ε and inversely for low τ means that
the process of propagation is close to the convergence,
consequently we have to reduce the step ε. In practice
several estimation functions of this step of increment
ε have been tested we have kept the one given by (6).
ε = ε+ 10.τ (6)
The regions construction is estimated achieved when
τ < 10%, the non-classified left pixels are assigned to
the close region.
3.2 Individual Regions Processing
Now as the regions are marked, each region is ex-
tracted separately, and their parameters µ
r
i
, ρ
r
i
and
I
r
i
they are calculated. Then the two next logical vari-
ables are deduced:
y
i
=
n
1 if |µ
r
i
−ρ
r
i
|<s1
0 otherwise
(7)
z
i
=
n
1 if I
r
i
<s2
0 otherwise
(8)
Practically we have fixed the parameters, s1 = 9, in
order that the statistical average and the region mode
are close, so significant and s2 = 30, so that the pixels
of the same region will have a uniform visual aspect,
because beyond the human eye can make differences.
The edge e = (i, j) ∈ E will be presented by a log-
ical variable x
ij
= x
ji
this latter at the time of segmen-
tation optimization.
x
ij
=
n
1 if r
i
6=r
j
0 otherwise
(9)
3.3 Formulation of the Problem into
Entire Number
Following the regions construction, according to
(G.L.Nemhauser and L.A.Wolsey, 1988; M.Baiou
and F.Barahona, 2011), we have the following con-
straint :
Region: each region i give two logical variables, y
i
and z
i
such as:
y
i
+ z
i
≥ 0 (10)
The region i is not effective unless y
i
+ z
i
= 2.
Edge: e = (i, j) ∈ E between the regions i and j pre-
sented by the variable x
ij
= x
ji
is not effective un-
less the regions i and j are also so. Therefore it
should verify the following constraints:
x
ij
≥ 0 (false)
x
ij
≤ 1 (true)
2x
ij
≤ y
i
+ y
j
(modes)
2x
ij
≤ z
i
+ z
j
(distributions)
Estimation: to have effective differences,
Maximize Σ
kVk
i=1
(y
i
+ z
i
) (11)
Relaxation: each region i having y
i
+ z
i
< 2, it is
decomposed into two regions u and v such as
y
u
+ z
u
≥ 1 and y
v
+ z
v
≥ 1, then we refresh the
parameters of the graph G = (V, E) and finally
we rewrite the corresponding constraints to the re-
cently created or modified regions.
4 SEGMENTATION ALGORITHM
Our algorithm of segmentation uses the principle of
top-down iterative cutting. Having the image to be
segmented A, we proceed as follow:
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
94
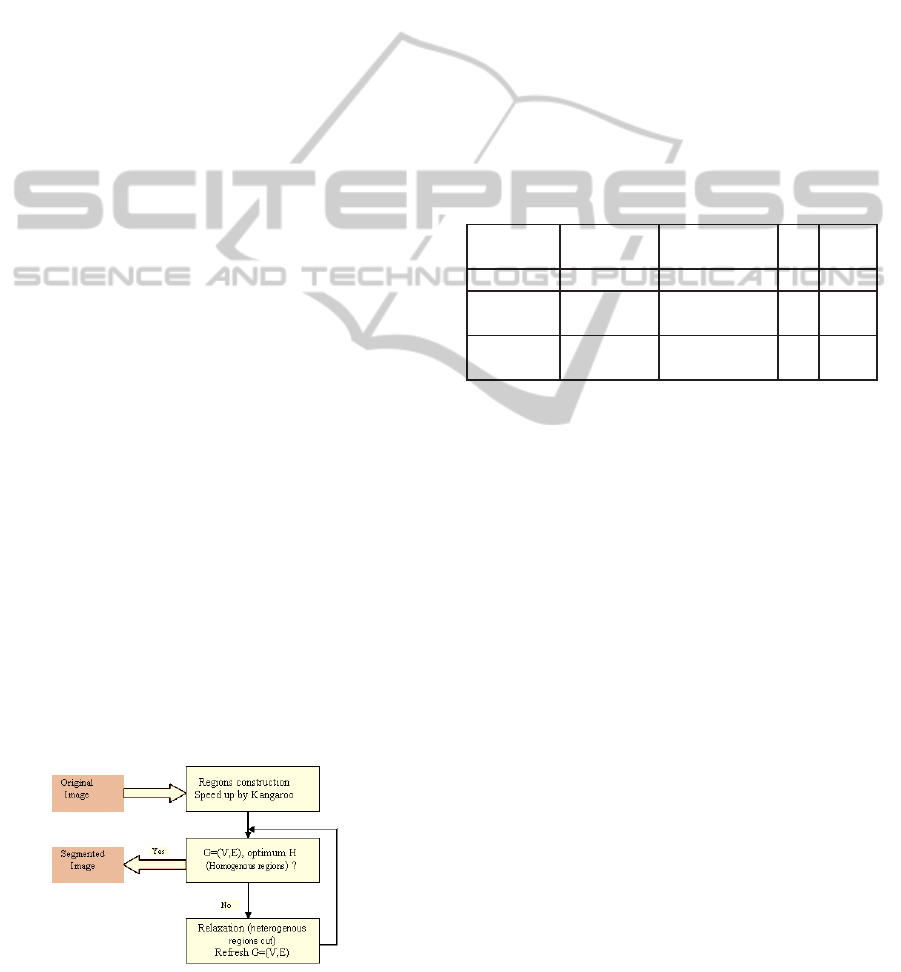
i- Regions construction:
Let A the image to be segmented and C the
image of the coded regions. We denote C =
SPPpropag(A, ε) the routine enabling this code
with an error gap ε within the gray levels of the
same regions, we have used the Kangaroo method
as follow:
1 - Initialization ε = 1
2 - C = SPPpropag(A, ε)
3 - Calculation of τ then ε = ε+ Round(10.τ)
4 - If τ > 0.1
then back to the step 2
Endif
The use of this stochastic algorithm, has allowed
us to reduce with considerable manner the num-
ber of iteration of the propagation regardless the
image sample.
ii - The graph calculation :
Starting from the image of the regions code C, the
one of the departure A, a graph G = (V, E) is being
calculated. The logical variables y
i
, z
i
of each re-
gion are calculated as well as the variables edges
x
ij
with a number of regions kVk.
iii - Estimation :
calculation of the combinatorial optimization
function H = Σ
kVk
i=1
(y
i
+ z
i
).
If H is maximum
then end of process
else following the step of relaxation
Endif
iv - Relaxation :
for each region i having y
i
+ z
i
< 2, an optimum
cutting (K.Chehdi, 1991) is applied to decompose
this region into two sub-regions r
i
= r
u
+ r
v
then
back to the step ii−.
The synoptic of figure 1 summarize the steps of
our algorithm of segmentation.
Figure 1: the principle of the algorithm of segmentation.
5 EXPERIMENTAL RESULTS
5.1 Speed up the Regions Construction
By applying our method upon several images sam-
ples, we recorded the following results:
We proposed in this paper, the acceleration results
of regions which are constituted by three images in
which, the gray levels by region are homogenous
in the first ones (Gap ≤ 4), more or less variables
(6 ≤ Gap ≤ 9) in the second and completely hetero-
geneous (25 ≤ Gap ≤ 40) in the third one.
The algorithm starts the first iteration with a gap ε = 1
and τ is evaluated at the end of iteration according to
(5) , if the stop condition 3.1 is not reached then ε is
calculated according to (6) to start the following iter-
ation.
Table 1: Result of speed up convergence.
images Gap in Iteration of ε τ
the region SPPpropag in %
circles ≤ 4 1st iteration 1 6.6
alumgrns 6, 9 1st iteration 1 12.9
2nd iteartion 2 8.6
rice 25, 40 1st iteration 1 98
2nd iteartion 11 7.5
The results gathered in (Table 1) confirm the fol-
lowing:
• The first is indeed concerning the Kangoroo
method, because the regions constitution is al-
ways achieved in about two or three iteration,
which reduce and minimize greatly the time of
this stage.
• The second shows that our empiric formula of
Kangaroo step of evaluation ε is valid for large
range of images samples.
• The column of step ε shows that this latter varies
with respect to gray level variation inside the re-
gions, and it adapts automatically for each situa-
tion.
The gaps in gray level inside the same image, they are
variable from one region to the other. Sometimes the
regions construction which the gap is high, they will
be followed with fusion of close regions. This phe-
nomenon is totally normal because it is the Kangaroo
principle but it will be solved in the relaxation stage
which will be discussed in section 5.2 in page 5.
AdaptiveSegmentationbyCombinatorialOptimization
95
5.2 Relaxation and Correction of
Segmentation
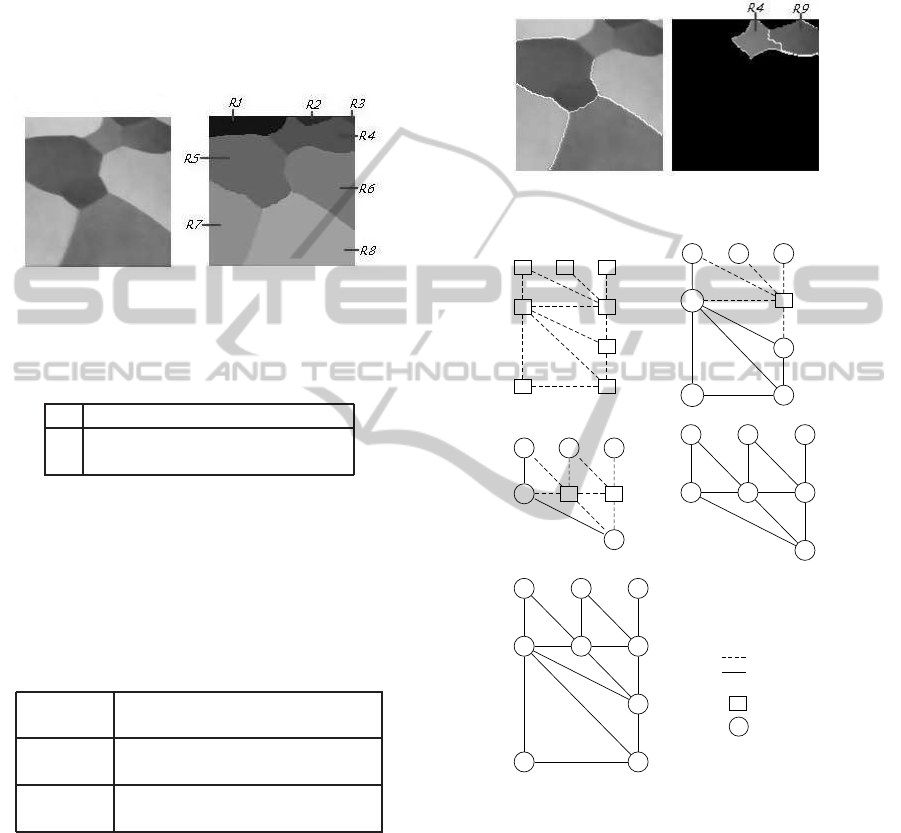
In the image of figure 2 in the left, the steps i− and
ii− of the algorithm has given the images of figure 2
in the right, presented by the graph of figure 4, high
left. This latter contain 8 regions and 11 edges, so we
have a graph G = (E,V) with kVk = 8 and kEk = 11,
having the data as follow:
Figure 2: original (left) regions (right).
The step iii− of the Algorithm has given:
Table 2: Result of the 1st iteration.
V 1 2 3 4 5 6 7 8
y
i
1 1 1 0 1 1 1 1
z
i
1 1 1 0 1 1 1 1
Thus the Table 2 illustrates the results of the first it-
eration and as we can notice, the region r
4
does not
satisfy the H criteria.
a- An estimation function H = 14, whereas it’s max-
imum have to be 16, therefore it is not optimum.
b- Edges vector E, such as:
Table 3: Link vector E after the 1st estimation.
(i, j) ∈ E (1, 4) (2, 4) (3, 4) (1, 5)
x
ij
0 0 0 1
(i, j) ∈ E (4, 5) (4, 6) (5, 6) (5, 7)
x
ij
0 0 1 1
(i, j) ∈ E (5, 8) (6, 8) (7, 8)
x
ij
1 1 1
The compounds to 0 in E correspond to missing
edges in the graph and this means that the separa-
tion between regions in these positions is not ef-
fective. Whereas the compounds to 1 correspond
to available edges in the graph and they are pre-
sented in the image by white line separating the
regions in these positions as shown by figure 3 in
left.
According to ( 9), the Table 3 shows that all the
binary variables x
ij
connected to r
4
are 0 (∀(i = 4
or j = 4) ⇒ x
ij
= 0).
c- The results of this first iteration of estimation are
presented by the graph of figure 4 high right.
The algorithm then follows the step iv−. Regarding
the data, the relaxation acts on the region r
4
, because
it is the less homogenous.
Figure 3: Before the relaxation (left) after the relaxation
(right).
R
1
R
2
R
3
R
5
R
4
R
6
R
7
R
8
x
15
x
14
x
24
x
34
x
45
x
56
x
46
x
57
x
58
x
68
x
78
R
1
R
2
R
3
R
5
R
4
R
6
R
7
R
8
x
15
x
14
x
24
x
34
x
45
x
56
x
46
x
57
x
58
x
68
x
78
R
1
R
2
R
3
R
5
R
4
R
9
R
6
x
15
x
14
x
24
x
29
x
39
x
45
x
56
x
49
x
46
x
69
R
1
R
2
R
3
R
5
R
4
R
9
R
6
x
15
x
14
x
24
x
29
x
39
x
45
x
56
x
49
x
46
x
69
R
1
R
2
R
3
R
5
R
4
R
9
R
6
R
7
R
8
x
15
x
14
x
24
x
29
x
39
x
45
x
56
x
57
x
58
x
49
x
46
x
69
x
68
x
78
R
i
R
j
x
i j
= 0
R
i
R
j
x
i j
= 1
y
i
+ z
i
≺ 2
R
i
y
i
+ z
i
= 2
ÄÒ
R
i
½
Figure 4: Algorithm in graphs.
As we can notice, the region r
4
is treated sepa-
rately; the result is illustrated by figure 3 left. This
step of relaxation is illustrated by the graph of figure
4 down left. It has lead to two new regions rated 4 and
9, having the parameters y
4
= z
4
= 1, and y
9
= z
9
= 1.
Following this stage, the second iteration of es-
timation gives new graph G = (E,V), presented by
figure 4 down right, such as kVk = 9 is a set of
edges kEk = 14, therefore an estimation function
H = H
Max
= 18, then all the variables x
ij
are set to
1.
The immediate consequence, it is an optimum es-
timation, therefore the algorithm is coming to the end,
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
96

Figure 5: Final segmentation.
and the final segmentation is given by the 5.
Hence the merged regions by mistake in the Kan-
garoo stage are separated again in this stage of relax-
ation.
6 CONCLUSIONS
We have expanded in this paper, an iterative segmen-
tation method based upon the process of segmentation
by a set of regions significantly different, then to re-
alize an iterative adjustment to converge to the exact
regions.
The use of stochastic method of Kangaroo, al-
lowed us not only to speed up the initialization phase
of the process but also self-adaptation of our method
with the sample image to be segmented.
Next, the representation of the problem as none ori-
ented graph G = (E,V) then its formulation by a en-
tire linear program (PLE) which have make easy the
problem study under several constraints. Further the
theory of the combinatorial optimization was a con-
siderable support in branching of segmentation.
The performance evaluation of our method was
applied on a diverse set of images (small to large vari-
ations gray levels within the same regions). In these
different situations,
- The initialization stage, by its self adaptation, is ac-
celerated and it converges to the maximum after tree
3 iterations,
- The stage of the optimization refines the processing
by giving precise edges and regions more homoge-
neous.
By this encouraging results, our segmentation method
can be a new way to use other segmentation ap-
proaches involving highest semantic level of knowl-
edge.
Now, this work is extended into two axes:
• The first one consists to refine and confirm the es-
timator (6) by experimentation upon a set of var-
ied of images of great size.
• The second consists of increasing the prob-
lem complexity by inserting the color parameter
among the decision parameters
REFERENCES
A.Herbulot (2007). Mesures statistiques non param´etriques
pour la segmentation d’images et de vid´eos et min-
imisation par contours actifs. Doctorat, universit´e de
Nice-Sophia Antipolis, Nice.
E.Fleury (2009). R´eseaux de capteurs, Th´eorie et
mod´elisation. Lavoisier.
F.Khadar (2009). Contrˆole de topologie dans les r´eseaux
de capteurs : de la th´eorie ´a la pratique. Doctorat,
universit´e, Lille 1.
G.Fleury (1993). M´ethodes stochastiques et d´eterministes
pour les probl´emes NP-difficiles. Doctorat Blaise Pas-
cal,, Clermont Ferrand.
G.L.Nemhauser and L.A.Wolsey (1988). Integer and Com-
binatorial Optimization. John Wiley and Sons, New
York.
H.Yang, L. (1997). Split and merge segmentation employ-
ing thresholding technique. volume 1.
K.Chehdi, D. (1991). Binarisation d’images par seuillage
local optimal maximisant un crit´ere d’homog´en´eit´e.
volume p.1069-1072.
M.Baiou and F.Barahona (2011). On the linear relaxation
of the p-median problem, volume 8.
S.Mazouzi, F. (2007). A multi agent approach for range
image segmentation. volume 4696.
W.Eziddin (2012). Segmentation it´erative d”images par
propagation de connaissances dans le domaine pos-
sibilit´e: Application ´a la d´etection de tumeurs en im-
agerie mammographique. Doctorat T´el´ecom, Bre-
tagne.
AdaptiveSegmentationbyCombinatorialOptimization
97
