
Self-collision Detection using Sphere Chains
Francisco A. Madera, Enrique Ayala, Francisco Moo-Mena
Facultad de Matematicas, Universidad Autonoma de Yucatan, Merida, Yucatan, Mexico
Keywords:
Collision Detection, Human Animation, Approximation with Spheres.
Abstract:
An algorithm to detect self-collisions in a human object is presented. We proposed to approximate the human
object by spheres, which are placed inside the object mesh to fill the correspondent volume. We introduce the
concept of sphere chain, a set of joined spheres which contains some regions of the human mesh. The object
is approximated by several chains in the preprocessing stage to be prepared for the running stage to perform
the collision detection.
1 INTRODUCTION
Self-collision refers to the collision of the primitives
in the same object and it happens during the anima-
tion, when some regions of the object mesh are over-
lapped. To detect this kind of overlap helps to obtain
an efficient animation cycle: animation, collision de-
tection, collision response. Common collision detec-
tion methods involve two stages: the mesh prepara-
tion in a preprocessing stage, and the collision detec-
tion in the animation stage.
Objects can be approximated with basic primi-
tives such as spheres, boxes, OBB (Oriented Bound-
ing Box), among others. The construction of a hierar-
chy with Bounding Volumes (BV) can be performed
using a top-down or a bottom-up approaches. The
bottom-up approach has shown better results in the
accuracy (Ericson, 2005). Rather than start with a tri-
angle, we decided to start from a set of triangles that
form a tubular shape and that can be bounded with a
sphere.
Human movement is one of the most labor inten-
sive tasks in computer graphics and animation appli-
cations: games, simulations, medicine, etc. We divide
the human in five regions and bound each one with
spheres. Regions have tubular (limbs) or non-tubular
(torso) shapes. By joining the set of spheres of each
region we can form a chain of spheres that covers part
of the human mesh. As a result, we can perform the
collision detection between the spheres of the chains
independently of the other chains.
We pursuit to balance the throughput of the col-
lision detection process, grouping the whole set of
spheres of the mesh in smaller sets of spheres called
chains. The division of the work of the collision de-
tection makes to handle the process with less number
of primitives in every part, the chains, independently
of each other. We suggested to partition the mesh in
tubular regions to form chains, taking advantage of
the articulated object.
We can exploit the fact that the chain’s collision
detection are independent of the other chains to im-
prove the time of the running stage in a parallel im-
plementation. The sphere chains can be grouped in a
hierarchy and have a BVH (Bounding Volume Hier-
archy) constructed, but we decided to leave the sphere
chains as they are, since there are few spheres. This
implementation is created for the whole mesh with
sphere chains (M
1
) and without sphere chains (M
2
)
to compare their efficiency in sequential and in paral-
lel implementations.
The contributions are as follows:
• The extension of a tubular sphere approximation
to non-tubular regions to fill the human torso.
• The decomposition of a human object by chains
of spheres.
• The comparison of the performance of the self-
collision detection algorithm with and without
chains.
• The parallel implementation of the collision de-
tection algorithm.
The remain of the paper is organized as follows:
In Section 2 previous work is presented, Section 3 de-
tails the sphere approximation for tubular and for non-
tubular regions, in Section 4 the chain construction is
described. The running stage is detailed in Section 5,
and involves two processes: the sphere update, and
325
A. Madera F., Ayala E. and Moo-Mena F..
Self-collision Detection using Sphere Chains.
DOI: 10.5220/0005301603250331
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 325-331
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

the overlapping test. Experimental results are per-
formed in Section 6, and finally conclusion and fur-
ther work are presented in Section 7.
2 PREVIOUS WORK
Collision detection in articulated objects have been
investigated for years. Some methods focus on the
segments of bones to build a rigid body geometry such
as (Zhang et al., 2007) where an algorithm to perform
self-collisions is proposed. It consists of one pre-
processing step and two run-time steps: (1) prepro-
cessed link-level bounding volume hierarchy (BVH)
construction, (2) link-level spatial culling using Tay-
lor models and a dynamic BVH and (3) exact contact
determination using conservative advancement and
temporal culling. This method requires the skeleton,
the motion bound calculation, and the OBB hierarchy
construction. Moreover, they construct Taylor models
to improve the accuracy of the OBBs. Another work
based on the same motion that considers rigid seg-
ments in articulated objects is found in (Kim et al.,
2014). This method employs SSV (swept sphere vol-
umes) to detect collisions and returns the first time of
impact between the rigid bodies.
Even when rigid bodies can speed up the self-
collision detection in articulated bodies, the informa-
tion returned is the first contact point, so that for a
mesh representation, a set of polygons is required.
This manner, (Kavan et al., 2006) describe how to
perform collision detection for models skinned with
a spherical method. They suggested a procedure for
refitting of bounding spheres for spherical blend skin-
ning with sub-linear time complexity. The collision
depends on the motion, the joint transformation ma-
trices which requires the skeleton of the human. Our
spheres are tighter than the ones used in this method,
moreover our updating process is faster since it de-
pends on the pivot polygons motion.
Spheres and ellipses are also utilized in (M
¨
uller
and Chentanez, 2011), where a simulation particles
are placed on a given visual mesh, which are con-
nected to form a simulation mesh. The particles are
driven by the simulation while the vertex positions
are computed from the particle positions via skinning.
Animated particles are used to attach the simulation
mesh or as collision primitives. Similar to the method
proposed in this work, they create spheres tangent to
the surface particles (ellipsoids), so that ellipsoids are
replaced by their circumspheres in the collision re-
sponse process. We propose to create a sphere ap-
proximation filling the volume of the tubular shapes
rather than bounding the polygons of the mesh.
The study of spheres aligned in a sequential order
was suggested by Guibas et al (Guibas et al., 2002)
and Ayala (Enrique Ayala, 2014). Guibas proposed to
study deformable necklaces flexible chains of balls,
called beads, in which only adjacent balls may inter-
sect. Ayala et al. study the self-collision detection of
a sequence of spheres with strong deformations us-
ing binary trees. These two last methods work with
spheres disregarding the object mesh, so that consid-
erations of the mesh must be done by using techniques
of volume filling such as (Shier and Bourke, 2013)
where a solid can be filled with basic primitives. In
particular sphere packing has been investigated as a
theoretical foundation and implemented in several ap-
plications such as radio surgical treatment planning
(Teuber et al., 2013).
Another work of inspiration is the method pro-
posed in (Weller and Zachmann, 2009), where data
structure called the Inner Sphere Trees to fill the inte-
rior of the object with a set of non-overlapping vol-
umes that approximate the object’s volume is per-
formed. Our work disregard the non-overlapping fea-
ture due to we pursuit the collision detection process-
ing. Unlike that work, we do not test the penetration
volume, but we handle less number of spheres. Ev-
ery sphere is attached to its closed triangle similar to
ours. However, this method is prepared for rigid bod-
ies only.
Li et al. (Li et al., 2011) used a disk filled with
rays to construct cages in the human body. Cages are
utilized to deform the human during the skinning de-
formation. While we employ a disk, they employed
several disks to form the cages with more memory
usage. Zhu et al. (Zhu et al., 2013), define a torso
cross-section to extract the geometric characteristics
of human models for clothing design. The applica-
tion is just for modeling, so that they did not regard
the issues for animation and collisions.
3 SPHERE APPROXIMATION
A region R
i
of the mesh consists of a set of polygons
∆ = {∆
0
,∆
1
,...,∆
n−1
}. A human mesh is divided in
five regions as suggested in (Wang et al., 2014) and
illustrated in Figure 1. The regions are as follows: the
left arm R
0
, the right arm R
1
, the left leg R
2
, the right
leg R
3
, and the torso R
4
.
3.1 Tubular Regions
R
0
, R
1
, R
2
, and R
3
are tubular regions that can be
approximated by a set of spheres. Spheres created
along the surface of the tubular object (represented
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
326

Figure 1: The human mesh is partitioned in five regions
(left) and approximated with spheres (right).
by triangular meshes) are located in the center of the
diameter of their corresponding region and they have
the exact size as they collide with the surface. Thus,
there are four approximated tubular regions: ϕ(R
0
),
ϕ(R
1
), ϕ(R
2
), ϕ(R
3
).
We utilised the method proposed in (Madera et al.,
2013) where the algorithm finds the shape defined by
the base curve of the input object. A circumference
is positioned in one of the ends of the tubular mesh,
then, the circumference starts moving along the mesh
looking for the best way to construct a sphere over its
center. After a sphere is created, the circumference
continues moving along the surface looking for the
best places to create spheres.
3.2 Non-tubular Regions
The torso is approximated with spheres ϕ(R
4
); in
fact, we extent the method used for tubular objects
explained above to non-tubular objects. We employ
a disk filled with rays, which comes from the center
of the disk and points outwards. The disk is placed
on the bottom part of the torso and starts moving up
along the torso with a displacement of δ units. During
this motion, the ray-triangle intersection test is per-
formed with the rays of the disk and the polygons of
the object’s mesh. The number of rays N
r
is 80 and
the disk traces the torso and determines the conve-
nient locations to construct spheres. The information
recorded is utilized to create spheres.
Figure 2: Two sequences of spheres vertically aligned to the
y-axis due to the stand up pose is aligned to the y-axis.
A human torso is not a tubular-shaped object. This
means that only one sphere is not a good approx-
imation, two spheres per level (disk position) were
employed instead, N
s
= 2 (Figure 2). We partition
the volumetric object in two sets, specifically the sur-
rounding region obtained from the disk translation
is divided in two parts (Figure 3). The surround-
ing region is formed by a set of polygons that col-
lide with the rays of the disk. To calculate the ac-
curacy of the sphere approximation, we tested the
difference between the mesh bounded and the cor-
respondent sphere. We call this measure F and it is
computed for each vertex v
i
of the surrounding region
and indicates the difference between the radius of the
sphere and the distance of its center and such a vertex:
F
i
=
J
.r −
k
J
.c −v
i
k
.
Figure 3: The surrounding region is divided in two parts and
approximated with a sphere each.
Even when two or more spheres can have a bet-
ter approximation than using only a sphere, spheres
can be adjusted to improve their accuracy. The mo-
tion of the circumferences takes place in the plane
formed by
~
γ
0
~
γ
1
towards the disk center direction (Fig-
ure 4). Doing this translation, the overlapping among
the spheres is unavoidable, but this does not affect the
accuracy. This is called the sphere adjustment pro-
cess.
Figure 4: Spheres can be moved along the plane
~
γ
0
~
γ
1
to-
wards the disk center direction.
We observe in Figure 4 that the set of vertices in
green are partitioned in two parts, having bounded by
a sphere each. Spheres are scaled down and moved
towards each other in order to obtain more accurate
approximation as depicted in Figure 5. This way, F is
minimized and spheres become more accurate.
Figure 5: The left sphere can be scaled down to the size of
the blue sphere.
Since the torso has an elliptical shape, we decided
to use two vertical sequences of spheres to fill it. As
Self-collisionDetectionusingSphereChains
327

the spheres of the torso are arranged in two vertical
sequences, we label the different sides as following:
the left side spheres ϕ(R
4
)
L
, the right side spheres
ϕ(R
4
)
R
, the top side spheres ϕ(R
4
)
T
, and the down
side spheres ϕ(R
4
)
D
as illustrated in Figure 6.
Figure 6: The left ϕ(R
4
)
L
, right ϕ(R
4
)
R
, top ϕ(R
4
)
T
, and
down ϕ(R
4
)
D
spheres of the torso.
We compare the accuracy of our spheres approxi-
mation method (ϕ
1
) against the accuracy of the mini-
mum enclosing ball algorithm (ϕ
2
) proposed by Welz
(Welzl, 1991). This comparison is performed with
the F value. We first obtain a sphere from a set of
vertices, and then we apply the adjustment process to
increase the accuracy (ϕ
0
1
).
4 CHAIN CONSTRUCTION
Tubular regions are approximated by a set of joined
spheres that contains only a limb of the human. We
proceeded to group the set of joined spheres for two
limbs and therefore to create a chain of spheres. As
we have four limbs, we take them in pairs, forming
6 chains. Note that the union of the spheres of two
limbs includes some spheres of the torso.
Let ζ
i
be the chain i formed by the union of the
spheres of some regions, then we have the chains con-
structed in Table 1 and depicted in Figures 7 and 8.
Table 1: The six chains of the human mesh.
ζ
0
= ϕ(R
0
) ∪ϕ(R
4
)
L
∪ ϕ(R
2
)
ζ
1
= ϕ(R
1
) ∪ϕ(R
4
)
R
∪ ϕ(R
3
)
ζ
2
= ϕ(R
0
) ∪ϕ(R
4
)
T
∪ ϕ(R
1
)
ζ
3
= ϕ(R
2
) ∪ϕ(R
4
)
D
∪ ϕ(R
3
)
ζ
4
= ϕ(R
0
) ∪ϕ(R
4
)
T
∪ ϕ(R
4
)
R
+ ϕ(R
3
)
ζ
5
= ϕ(R
1
) ∪ϕ(R
4
)
T
∪ ϕ(R
4
)
L
+ ϕ(R
2
)
Figure 7: Spheres of chains 0,1,2 in purple.
Figure 8: Spheres of chains 3,4,5 in purple.
Some spheres belong to more than one chain, due
to a limb is connected to the other three limbs. We
based our collision detection algorithm in the sphere
overlap test using a brute force rather than using a
BVH. In the future, when creating the Narrow Phase,
finer approximation can be done by taking the spheres
as root nodes and creating their child nodes to bound
the polygons of the surrounding region.
5 THE RUNNING STAGE
In the running stage, the human is animated, the self-
collision detection is called in every frame and the
spheres are refitted.
5.1 Sphere Update
Sphere contains a set of polygons, that is, a polygon is
assigned to the sphere closest to it. This way, ∆
i
∈
J
j
if and only if k
J
j
.c − ∆
i
k ≤ k
J
k
.c − ∆
i
k, ∀k 6= j.
We call this set of polygons the surrounding region of
sphere j (Figure 9).
Figure 9: Surrounding regions of three spheres (left) and
the four pivot polygons of a surrounding region(right).
We implemented an animation using the morphing
method. Some poses are taken as basis of the frames
and a quadric B
´
ezier interpolation is applied between
such poses to obtain smooth deformations.
During the human motion, spheres are updated
to follow the mesh deformation. We use four poly-
gons for each surrounding region which indicates
the motion to be followed (Figure 9, right). In ev-
ery frame, polygons of the mesh are moved, so that
J
j
.c+ =
1
4
(∆
r
+∆
s
+∆
t
+∆
u
), where ∆
r
,∆
s
,∆
t
,∆
u
∈
J
∆
j
. Thus, the new position of
J
j
is the average of
the new positions of its pivot polygons (Figure 10).
The radius is also re-calculated taking the average of
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
328
the distances from the center of the sphere to the pivot
polygons.
Figure 10: Sphere center is updated with the centroid of
its four pivot polygons. Sphere marked with dotted lines is
deformed to the sphere marked with solid lines.
An improvement would be to have more pivot
polygons to refit the sphere size, but more expensive
operations are demanded.
5.2 Overlapping Test
An application to use the approximation is presented:
the collision detection algorithm. In this work we
only implemented the brute force approach in sequen-
tial and parallel versions. The construction of the
BVH demands parent and children nodes, that obvi-
ously increase the number of spheres and therefore a
benefit to a parallel implementation.
Self-collision is performed by checking an overlap
between spheres in each chain. This is a broad phase
collision detection which returns the pairs of spheres
colliding and therefore the surrounding regions in-
volved. An overlap between spheres
J
A
and
J
B
occurs if (k
J
A
.c −
J
B
.c k
2
)
2
< (
J
A
.r +
J
B
.r)
2
.
This inequality verifies the squared distance between
two spheres, using the 3-vector Euclidean norm, k
. k
2
, and requires 11 basic operations.
The overlap test can be applied using the brute
force or the BVH strategies. In the brute force
strategy, every sphere is compared against the other
spheres, and in the BVH strategy, a k-ary BVH is re-
quired to be constructed in the preprocessing stage to
be traversed in this running stage. We proceeded to
implement the former strategy due to the number of
spheres handled is small.
Let ζ
j
= {
J
0
,
J
1
,...,
J
n−1
} be the set of spheres
in chain j, n be the number of spheres per chain, and
n
c
be the number of chains. We can perform the colli-
sion detection process computing the overlap among
all the spheres of the mesh. The collision detection
can be computed in every chain independently of the
other chains.
In the M
2
approach (without chains) we consider
the total number of spheres in the mesh m, thus m
2
comparisons for all the spheres are required. In the
M
1
approach (with chains),
J
i
is compared against
the other spheres. The algorithm requires O(n) time
for a sphere, that is O(n
2
) for a chain, and O(n
c
n
2
) for
all the chains, being n the number of spheres in each
chain and n
c
the number of chains.
The overlap test is considered for all the spheres of
the torso. Left side spheres are considered in chains
ζ
0
and ζ
5
, right side spheres are considered in chains
ζ
1
and ζ
4
. Two spheres collide when they are not ad-
jacent.
The parallelization of the methods M
1
, and M
2
gives a change in the performance and exploits the
features of each method. In the second method M
2
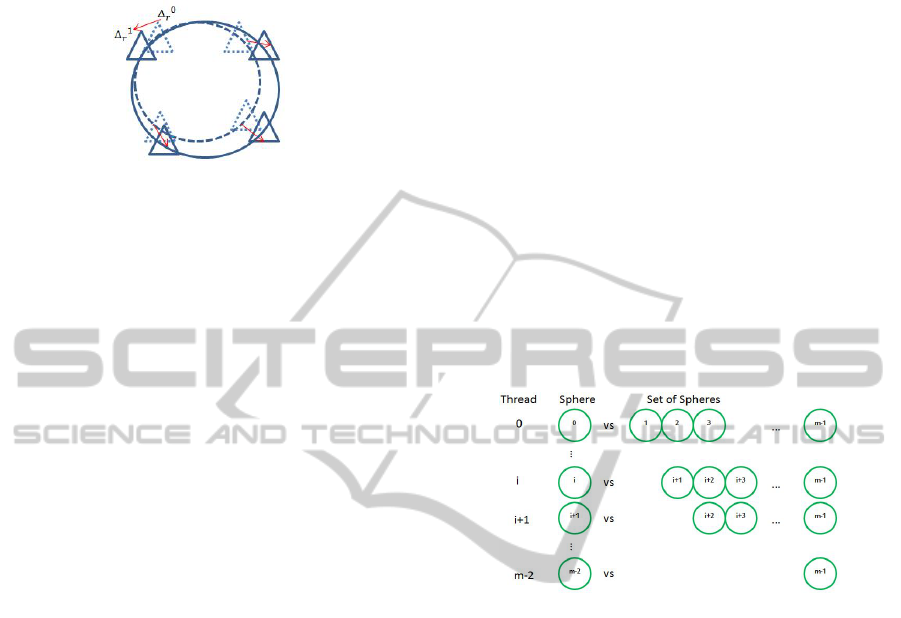
,
we can have a thread per sphere, then we would have
a O(m) time (Figure 11). In the method M
1
, using
chains, we can have n
c
threads and the time expected
is O(n
2
). On the other hand, increasing the number
of threads by n
2
, the time is reduced to O(n) since the
overlap test is performed per sphere in each chain.
Figure 11: m threads are launched to perform the overlap
test for each sphere.
6 EXPERIMENTS
Our experiments were run on a PC with a 2.40GHz
Xeon processor, 12 GB main memory with Windows
7 operating system. The algorithm was coded in C++
with OpenGL API. We employed a human mesh. The
human was constructed using the MakeHuman tool
and has 26,292 polygons. Two kinds of experiments
were carried on, firstly the sphere approximation of
the pre-processing stage, and secondly the collision
detection of the running stage.
The first experiment is based on the accuracy of
the spheres created, comparing the method ϕ
1
with
the minimum enclosing ball method ϕ
2
. The accu-
racy of the spheres created can be tested by the dis-
tance measure F among the vertices of the surround-
ing region and the spheres that cover such region. The
parameters considered are as follows: number of rays
in the disk (N
r
), number of spheres per level (N
s
), dis-
placement of the disk δ, and penetration depth PD.
We take N
r
= 80 and δ = 0.25. Penetration depth
Self-collisionDetectionusingSphereChains
329

(a) Sphere 0 (b) Sphere 1 (c) Sphere 2 (d) Sphere 3
(e) Sphere 4 (f) Sphere 5 (g) Sphere 6 (h) Sphere 7
Figure 13: Approximation of the human with 2 spheres per level, using ϕ
1
(blue), ϕ
2
(red) and ϕ
0
1
(green).
refers to the overlapping spheres, that is PD = 0 if
non-overlap exists, and 0.50 if the half of the two
spheres involved are overlapped.
Our experiments were conducted to measure the
accuracy of the spheres created. We employed N
s
= 2,
and PD = 30%. We perform the calculus of the
spheres by the first (ϕ
1
) and the second (ϕ
2
) methods,
then we adjusted ϕ
1
to enhance the accuracy (ϕ
0
1
) us-
ing the Sphere Adjustment routine. Spheres are la-
beled in a bottom-up manner, from left to right as
shown in Figure 12. We name the rays of the disc
as r
0
,r
1
,...,r
79
and compare the rays length of the
spheres for both methods ϕ
0
1
and ϕ
2
.
In sphere 0, ϕ
2
is better in the first half of the set
of the colliding points. On the contrary, in sphere 1,
ϕ
0
1
is better in the first half of the set of the colliding
points. In spheres 2 and 3 the behavior is the same
as in spheres 0 and 1, respectively; this means that
the torso shape remains equal. In sphere 4, ϕ
2
is bet-
ter from r
8
and in sphere 5, ϕ
2
is better in r
0
-r
25
. In
spheres 6 and 7, ϕ
2
= ϕ
0
1
in the middle of the collid-
ing points, and ϕ
0
1
is better before r
16
for sphere 6 and
after r
16
for sphere 7 (Figure 13).
ϕ
0
1
has a better approximation than ϕ
2
in regions
with non circular shape, otherwise ϕ
2
has a better ap-
proximation.
The second experiment consists of the collision
detection in the running stage. The human is animated
using 40 frames (Figure 14). The number of overlaps
is bigger in M
1
since the spheres are repeated in some
chains. The average number of spheres in each chain
is 23, then the 6 chains contain 138 spheres, more than
the total number of spheres in the mesh: 80.
(a) ϕ
1
(b) ϕ
2
(c) ϕ
0
1
Figure 12: Approximation of spheres 0, 1, 2, 3, 4 and 5
using 2 spheres per level.
Figure 14: The human animation.
Figure 15: The time in milliseconds of the the running stage
of methods M
1
and M
2
using CPU.
Figure 16: The time in milliseconds of the the running stage
of methods M
1
and M
2
using GPU.
Figure 15 shows the time in milliseconds for evey
frame, comparing the methods M
1
(chains) and M
2
(no chains) in CPU. M
2
is faster than M
1
as the num-
ber of tests is smaller. In the GPU, M
1
takes less time
than M
2
as illustrated in Figure 16. This is because
the parallel run when using threads. In both cases
CPU and GPU, the number of overlaps is bigger in
M
1
than in M
2
. CUDA was employed to parallelize
the algorithm.
Since we are handling few spheres, the parallelism
is not exploiting, we require much more spheres as
indicated in (Enrique Ayala, 2014) about 10,000 or
more. To overcome this problem a hierarchy should
be done, creating children and parent nodes from
the current spheres. Additionally, we could consider
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
330

more humans moving around, and then perform both,
the self-collision detection in each human, and the
collision detection between pairs of humans.
Observe that the number of spheres per chain in-
dicates the number of overlapping tests, independent
of the animation employed. This occurs because of
the self-collision process in a chain. We proved this
statement by running a second animation, obtaining
similar times.
7 CONCLUSIONS
A collision detection algorithm is detailed that em-
ploys sphere chains as a preprocessing stage. Our
method is performed for the broad phase collision de-
tection and can be used in articulated objects where
tubular regions are presented. We take into account
the surrounding regions which can be returned when
spheres are colliding. For more accuracy, a narrow
phase algorithm should be employed.
Our limitations are as follows: more chains are
required to exploit the parallel implementation, head,
hands, and feet are not considered.
The work can be extended by computing the col-
lision detection in several humans, using of a BVH
(binary, quadtree, octree, hybrid), using other types
of BVs, utilizing other objects: human hand, snakes,
animals with several legs such as octopus, spider,
quadrupeds. The sphere refitting can achieve more
accuracy by considering more pivot polygons.
We could extent our approach to Continuous Col-
lision Detection by implementing an interpolation be-
tween the human motion trying to avoid the tunneling
problem and other parallel techniques can be applied.
ACKNOWLEDGEMENTS
I want to thank to CONACYT and the University of
Yucatan for their financial support.
REFERENCES
Enrique Ayala, Francisco A. Madera, F. M.-M. (2014). Self-
collision detection in tubular objects approximated by
spheres. IJCSI International Journal of Computer Sci-
ence Issues, 11(5):14–21.
Ericson, C. (2005). Real-Time Collision Detection. Morgan
Kaufmann publishers.
Guibas, L., Nguyen, A., Zhang, L., and Russel, D. (2002).
Collision detection for deforming necklaces. In In
Symposium on Computational Geometry, pages 33–
42.
Kavan, L., O’Sullivan, C., and
ˇ
Z
´
ara, J. (2006). Efficient col-
lision detection for spherical blend skinning. In Pro-
ceedings of the 4th International Conference on Com-
puter Graphics and Interactive Techniques in Aus-
tralasia and Southeast Asia, GRAPHITE ’06, pages
147–156, New York, NY, USA. ACM.
Kim, Y. J., Manocha, D., and Tang, M. (2014). Hierarchi-
cal and controlled advancement for continuous colli-
sion detection of rigid and articulated models. IEEE
Transactions on Visualization and Computer Graph-
ics, 20(5):755–766.
Li, J., Lu, G., and Ye, J. (2011). Automatic skinning and
animation of skeletal models. Vis. Comput., 27(6-
8):585–594.
Madera, F. A., Laycock, S. D., and Herrera, C. G. (2013).
Ray-triangle collision detection to approximate ob-
jects with spheres. In Proceedings of the IASTED
International Conference on Computer Graphics and
Imaging, CGIM 2013, pages 70–76.
M
¨
uller, M. and Chentanez, N. (2011). Adding physics to
animated characters with oriented particles. In Ben-
der, J., Erleben, K., and Galin, E., editors, VRIPHYS,
pages 83–91. Eurographics Association.
Shier, J. and Bourke, P. (2013). An algorithm for random
fractal filling of space. Computer Graphics Forum,
32(8):89–97.
Teuber, J., Weller, R., Zachmann, G., and Guthe, S. (2013).
Fast sphere packing with adaptive grids on the gpu. In
Brunnett, G., Coquillart, S., and Welch, G., editors, In
GI AR VRWorkshop, pages 181–201, W
¨
urzburg, Ger-
many. Springer Vienna.
Wang, P., Lau, R. W., Pan, Z., Wang, J., and Song, H.
(2014). An eigen-based motion retrieval method
for real-time animation. Computers & Graphics,
38(0):255 – 267.
Weller, R. and Zachmann, G. (2009). Technical Report lfl-
09-09, Department of Informatics, Clausthal Univer-
sity of Technology, Clausthal-Zellerfeld, Germany.
Welzl, E. (1991). Smallest enclosing disks (balls and ellip-
soids). In Results and New Trends in Computer Sci-
ence, pages 359–370. Springer-Verlag.
Zhang, X., Redon, S., Lee, M., and Kim, Y. J. (2007). Con-
tinuous collision detection for articulated models us-
ing taylor models and temporal culling. ACM Trans.
Graph., 26(3).
Zhu, S., Mok, P. Y., and Kwok, Y. L. (2013). An effi-
cient human model customization method based on
orthogonal-view monocular photos. Comput. Aided
Des., 45(11):1314–1332.
Self-collisionDetectionusingSphereChains
331
