SPHERA

A Unifying Structure from Motion Framework for Central Projection Cameras

Christiano Couto Gava

1,2

and Didier Stricker

1,2

Department Augmented Vision, German Research Center for Artiﬁcial Intelligence, Kaiserslautern, Germany

Department of Informatics, Technical University of Kaiserslautern, Kaiserslautern, Germany

Keywords:

Spherical Images, Structure from Motion, Central Projection Cameras, 3D Reconstruction.

Abstract:

As multi-view reconstruction techniques evolve, they accomplish to reconstruct larger environments. This is

possible due to the availability of vast image collections of the target scenes. Within the next years it will

be necessary to account for all available sources of visual information to supply future 3D reconstruction

approaches. Accordingly, Structure from Motion (SfM) algorithms will need to handle such variety of image

sources, i.e. perspective, wide-angle or spherical images. Although SfM for perspective and spherical images

as well as catadioptric systems have already been studied, state of the art algorithms are not able to deal with

these images simultaneously. To close this gap, we developed SPHERA, a unifying SfM framework designed

for central projection cameras. It uses a sphere as underlying model, allowing single effective viewpoint vision

systems to be treated in a uniﬁed way. We validate our framework with quantitative evaluations on synthetic

spherical as well as real perspective, spherical and hybrid image datasets. Results show that SPHERA is a

powerful framework to support upcoming algorithms and applications on large scale 3D reconstruction.

1 INTRODUCTION

The popularity of full panoramic images has signif-

icantly increased during the past few years. This

is conﬁrmed by the variety of spherical image ac-

quisition hardware and software packages available

nowadays (Civetta, 2009), (LizardQ, 2014), (Seitz-

Roundshot, 2014), (PTgui-Pro, 2014). Another rea-

son for the increased popularity of such images is the

possibility to create immersive environments where

the user experiences a ﬁrst-person view, such as

Google Street View (Anguelov et al., 2010). Full

spherical images are specially attractive for this kind

of visualization as well as 3D reconstruction of large

scenes. These applications ﬁnd appliance in doc-

umentation, education, preservation of cultural her-

itage, gaming, city planing, etc. Applications based

on multi-view reconstruction usually require the ac-

quisition of several images to produce a 3D model

of the target scene. Hence, they implicitly demand

Structure from Motion (SfM) to recover the cameras’

poses before the 3D model can be computed.

Spherical images are also more suitable for SfM

than standard perspective images. Due to their wide

ﬁeld of view, scene features are observed in more im-

ages, thus increasing the number of constraints on

cameras’ poses. Consequently, methods have been

derived to perform SfM on wide ﬁeld of view cam-

eras. More speciﬁcally, (Chang and Hebert, 2000),

(Micusik and Pajdla, 2006), (Bagnato et al., 2011) ad-

dress SfM on omnidirectional images, while (Kangni

and Laganiere, 2007), (Pagani and Stricker, 2011),

(Aly and Bouguet, 2012) deal with full spherical im-

ages. Not surprisingly, perspective SfM has been ex-

tensively studied e.g. by (Snavely et al., 2006), (Hart-

ley and Zisserman, 2004), (Ma et al., 2003). Although

these approacheshave shown to work well for the spe-

ciﬁc image type they were designed for, up to the au-

thors knowledge they are unable to handle images of

any other type.

Given the current effort to reconstruct ever grow-

ing environments (Agarwal et al., 2009), (Furukawa

et al., 2010) every source of visual information shall

be taken into account, regardless of the shape of im-

age surface. This is an issue that has not yet being

addressed. Apart from performance and accuracy, an-

other highly desirable feature of 3D reconstruction al-

gorithms is to update and improve the scene model

whenever new images are available. Here again, the

ability to deal with different camera types is essential.

Therefore, we present SPHERA, a novel Structure

from Motion framework to bridge the gap between

285

Gava C. and Stricker D..

SPHERA - A Unifying Structure from Motion Framework for Central Projection Cameras.

DOI: 10.5220/0005301702850293

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 285-293

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

current SfM methods for central projection cameras.

We build on the model proposed in (Geyer and Dani-

ilidis, 2001) and adopt the unit sphere to represent im-

ages and to treat heterogeneous camera types in an

uniﬁed way. Our approach dynamically selects the

best information available to recover camera poses

and scene structure. Experiments on synthetic and

real image sequences validate our framework as a

valuable contribution to support large scale 3D recon-

struction algorithms.

Related Work

The work presented in (Chang and Hebert, 2000) uses

epipolar geometry to compute scene structure from

an omnidirectional vision system mounted on a robot

platform. However, the camera pose problem is not

addressed. In (Micusik and Pajdla, 2006), the au-

thors focus on omnidirectional images with a ﬁeld of

view larger than 180

and devise a camera model spe-

ciﬁc for that type of image. Although scene struc-

ture can be recovered, the technique is limited to the

two-view geometry problem. Consequently, the pro-

posed camera model can hardly be used in a more

generic SfM approach. In (Bagnato et al., 2011), the

authors present a variational approach to achieve ego-

motion estimation and 3D reconstruction from om-

nidirectional image sequences. Nonetheless, the en-

vironment must be densely sampled so that the re-

lationship between image derivatives and 3D motion

parameters is still valid. Thus, this approach can not

be used in a more general, sparse SfM.

A method to recover camera poses from a set of

spherical images on a sparsely sampled environment

is presented in (Kangni and Laganiere, 2007). How-

ever, SfM is performed based on panoramic cubes

computed for each spherical image. That is, the cam-

era poses are recovered by casting the spherical prob-

lem back to the standard perspective problem. In

(Aly and Bouguet, 2012), spherical images are used

to estimate the relative camera poses and to build a

map of the environment. To simplify the problem,

Aly and Bouguet assume planar motion, i.e. all cam-

era frames lie on the same plane. This assumption

strongly limits the applicability of the proposed tech-

nique. Finally, our approach is closely related to (Pa-

gani and Stricker, 2011), as both exploit full spherical

images to deliver a sparse representation of the scene

along with recovered camera poses. Nevertheless, the

method presented in (Pagani and Stricker, 2011) was

designed exclusively for spherical cameras, whereas

our framework naturally handles any kind of central

projection camera.

2 BACKGROUND

2.1 Spherical Images

A spherical image is a 180

×360

environment map-

ping that allows an entire scene to be captured from

a single point in space. Consequently, every visible

3D point P

given in world coordinate system can be

mapped onto the image surface. This is done by a

two-step process. First, analogue to the perspective

case, P

is represented in the camera coordinate sys-

tem as P

= RP

+ t, with R and t representing the

camera rotation matrix and translation vector. Sec-

ond, and different from the perspective projection, P

is projected onto the image surface by scaling its coor-

dinates, as shown in Fig. 1-(a). Without loss of gen-

erality, we assume a unit sphere. Thus, the scaling

becomes a normalization and p = P

/kP

Spherical images are stored as a 2D pixel-map as

depicted in Fig. 1-(b). This map is obtained using a

latitude-longitude transformation, with 0 ≤ φ ≤ π and

0 ≤ θ ≤ 2π.

(a) (b)

Figure 1: (a) Spherical coordinates and illustration of the

spherical projection. (b) Pixel-map of a spherical image.

2.2 Sphere as Unifying Model

Our approach is grounded on the seminal work de-

veloped in (Geyer and Daniilidis, 2001), where the

authors proposed a unifying model for the projective

geometry of vision systems having a single effective

viewpoint. These vision systems are commonly re-

ferred to as central projection cameras and include

catadioptric sensors featuring conic mirrors of differ-

ent shapes, such as parabolic, hyperbolic or elliptic.

Geyer and Daniilidis showed that any central cata-

dioptric projection is equivalent to a two-step map-

ping via the sphere. It is well known from the pin-

hole model that standard perspective imaging charac-

terizes a single viewpoint system. Nonetheless, per-

spective images are also central catadioptric systems

with a virtual planar mirror and are, therefore, covered

by the aforementioned model. In practice, that means

it is possible to treat these central projection systems

as spherical cameras, provided the mapping from the

original image surface to the sphere is known. This

mapping may be seen as a warping transformation

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

286

from the original image to the unit sphere. As an ex-

ample, Fig. 2 shows the result of warping a perspec-

tive image onto the sphere.

(a) (b)

Figure 2: Example of (a) an original perspective im-

age (Strecha et al., 2008) and (b) its warped version. The

warped image appears mirrored due to the viewpoint (“out-

side” the unit sphere).

2.3 Spherical Camera Pose Estimation

2.3.1 Epipolar Geometry

The epipolar geometry for full spherical cameras has

already been presented in (Torii et al., 2005). Thus,

here we provide a short overview. Consider a pair

of spherical cameras C

and C

. Let R and t be the

associated rotation matrix and translation vector. A

point p

on the surface ofC

, along with the centers of

the cameras, deﬁne a plane Π that may be expressed

by its normal vector n

= Rp

× t = [t]

, where

[t]

is the skew-symmetric matrix representing the

cross-product. For any point p

on C

belonging to

Π the condition p

= 0 holds, which is equivalent

to p

[t]

= 0, where E = [t]

R is the essential

matrix (Hartley and Zisserman, 2004). The condition

= 0 is known as the epipolar constraint and is

the same result obtained in the perspective case. This

shows that the epipolar constraint is independent of

the shape of the image surface.

Figure 3: Epipolar geometry for two spherical images.

2.3.2 Pose Estimation

There are mainly two techniques for computing cam-

era poses. The ﬁrst is useful for relative pairwise

pose estimation, typically when only 2D image cor-

respondences (2D-2D correspondences)are available.

Without loss of generality, one of the cameras is as-

sumed as reference and R and t represent the pose of

the second camera. In this case, R and t may be de-

termined with e.g. the 5-point algorithm (Stew´enius

et al., 2006). The second technique is normally used

when a number of 3D scene points and their respec-

tive projections onto an image are known, i.e. a set of

2D-3D correspondences is available. This conﬁgures

a Perspective-n-point (PnP) problem, which can be

solved with a minimum of 6 correspondences (Quan

and Lan, 1999).

3 THE PROPOSED APPROACH

Given a set of images of a scene, our goal is to ac-

curately estimate the pose of all cameras as well as

to recover a sparse 3D point cloud of the underlying

scene representing its geometry. The set of central

projection cameras is then deﬁned as

C =







∈ SO(3),

∈ R



, (1)

where j = 0,..,M − 1, M is the total number of cam-

eras and

and

are the rotation matrix and trans-

lation vector representing the estimated pose of cam-

era C

. To aid the non-linear optmization, we adopt

an axis-angle parameterization for the rotation matrix

and C

is then parameterized by a vector ρ

∈ R

. All

together, the cameras are parameterized by a vector

ρ ∈ R

, with m = 6M.

Likewise, we denote the set of sparse 3D points

reconstructed along with the camera poses as

P =



∈ R



, (2)

where i = 0, ..,N − 1, N is the number of points and

holds the estimated coordinates of a scene point P

We then formulate the problem of recovering all

cameras’ poses along with a sparse point representa-

tion of the scene as a non-linear optimization prob-

lem. More precisely, the parameter vector ρ is opti-

mized in order to minimize

min

N−1

∑

i=0

M− 1

∑

j=0

(ρ), (3)

where f

(ρ) is a cost function for each point

and

camera C

. The parameters ρ

that minimize Eq. 3

are the sought camera poses. Then, ρ

is used to up-

date the points

to obtain the sparse scene represen-

tation.

3.1 Reprojection Error

The reprojection error of a point

on camera C

computed as

(ρ) = cos

−1

ˆp

), (4)

where p

ˆp

is the scalar product between the ex-

pected projection p

and the measured projection ˆp

SPHERA-AUnifyingStructurefromMotionFrameworkforCentralProjectionCameras

287

obtained with

and

. The expected projec-

tion p

is determined by the keypoint location corre-

sponding to P

. Note that as −1≤ p

ˆp

≤ 1, we have

0 ≤ e

(ρ) ≤ π and it is not necessary to take the ab-

solute value in Eq. 4. Furthermore, we do not use any

approximation of the reprojection error as in (Pagani

and Stricker, 2011). As we aim at high accuracy, the

error deﬁned in Eq. 4 is the exact geodesic distance,

i.e. the exact angular deviation, between p

and ˆp

Together, all reprojection errors of a given

∈ P may

be expressed as a vector e

(ρ) ∈ R

. Additionally, to

each point P

we associate a visibility map



, p

) | C

∈ C , p

∈ S



, (5)

where S

represents the unit sphere. We denote the

pair (C

, p

) as the observation of a scene point P

camera C

. The existence of (C

, p

) implies that P

is visible on camera C

. Taking the visibility map into

account allows to reduce the dimensionality of e

(ρ)

from M to |V

|, where |V

| is the number of observa-

tions of P

. Consequently, the dimensionality of e

(ρ)

is no longer ﬁxed. Instead, it is adapted to the visibil-

ity of the corresponding point P

3.2 Minimizing the Reprojection Error

Finding the camera poses and scene structure as de-

scribed above can be achieved by solving a bundle

adjustment problem (Triggs et al., 1999), i.e. by min-

imizing the reprojection error with respect to all ex-

isting 3D points. This allows us to rewrite Eq. 3 in

the form shown in Eq. 6. However, different from

the classical bundle adjustment, we do not consider

the 3D point coordinates as parameters to optmize.

Instead, only the camera parameters are used. This

leads to two important advantages. First, the dimen-

sion of the parameter search space is strongly re-

duced, simplifying and speeding up non-linear reﬁne-

ment. Second, the set of 3D points used to solve Eq. 6

may be dynamically changed, allowing to use only the

best, consistent, points.

min

N−1

∑

i=0

M− 1

∑

j=0

(ρ), γ



1, if C

∈ V

0, otherwise

(6)

In practice, we use (Agarwal et al., 2010) as the

core non-linear solver upon which SPHERA is built.

In addition, we solve a modiﬁed version of Eq. 6,

where only the most reliable points are used. These

points are deﬁned as

∗



∈ P | e

(ρ) < τ, ∀(C

, ˆp

) ∈ V



, (7)

where τ is a threshold imposed to all individual repro-

jection errors e

(ρ).

4 EVALUATION

4.1 Preliminaries

Keypoints are detected and matched using the method

proposed in (Gava et al., 2013), where a multi-scale

keypoint detector and matcher was developed for

high resolution spherical images. Nonetheless, it is

worth mentioning that SPHERA is completely inde-

pendent of how keypoints are detected, described and

matched. Consequently, any other keypoint detector

and matcher may be adopted (see Section 4.3).

We validate our framework using synthetic spher-

ical as well as real perspective and spherical images.

The resolution of all spherical images presented be-

low is 14142× 7071 (100 Mega-pixels). Experiments

are divided into four categories: The ﬁrst category

consists of a set of synthetic spherical cameras where

the goal is to validate our framework on spherical im-

ages using groundtruth. The second is composed ex-

clusively of real perspective images. Here, the idea

is to show that our framework is suitable for standard

SfM, i.e. it may be used even when no spherical im-

age is available. The third category consists of spheri-

cal images only, where we compared SPHERA to the

work presented in (Pagani and Stricker, 2011) in two

different real world scenarios. The fourth and last cat-

egory is a hybrid dataset, i.e. real perspective and

spherical images are used simultaneously. The aim

is to demonstrate SPHERA’s ability to improve scene

geometry estimation whenevermore images are avail-

able, independent of their types

. Whenever avail-

able, groundtruth data is used for evaluation. Oth-

erwise, we rely on the global mean reprojection er-

ror computed taking all images and all reconstructed

points into account.

4.2 Synthetic Dataset

An artiﬁcial room with ﬂat walls and dimensions

4x4x3 meters was created using (Blender, 2014) and

9 spherical images were rendered (see Fig. 4-(a)).

The poses of these artiﬁcially generated cameras were

used as groundtruth. Additionally, the depth map

shown in Fig. 4-(b) was stored and serves to measure

the accuracy of the recovered scene geometry.

After detecting and matching keypoints with

Gava’s approach, camera poses and scene structure

were recovered with SPHERA. Residual errors were

computed in the following way. The position error is

the Euclidean distance between the groundtruth and

estimated camera positions. To measure the orienta-

tion error, we chose a function presented in (Huynh,

Assuming central projection cameras.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

288

(a) (b)

Figure 4: (a) Sample image of the synthetic dataset. (b) Groundtruth depth map used to evaluate the accuracy of scene

geometry estimation (contrast enhanced to improve visualization).

2009) and deﬁned as klog





k, with R the desired

rotation and

R the estimated rotation matrix. This is a

metric in SO(3) and can be efﬁciently computed with

quaternions. For details we refer to (Huynh, 2009).

Table 1 summarizes the errors in camera pose estima-

tion for . Although very small, these values are not

zero mainly due to the precision of detected keypoint

locations.

Table 1: Errors in camera pose estimation for the synthetic

dataset. Mean and standard deviation are identiﬁed by µ and

σ, respectively.

orient. error [degree] pos. error [cm]

µ 6.72× 10

−5

1.92× 10

−3

σ 1.73× 10

−4

3.2× 10

−3

Here, we also evaluated the inﬂuence of the ac-

cepted reprojection error τ (see Eq. 7) on the re-

covered camera poses and scene structure. We re-

peated the experiment varying τ within the interval

[τ

min

,τ

max

]. Although τ is an angular deviation, for

convenience values are converted and presented in

pixels. We chose τ

min

and τ

max

to be equivalent to

1 and 5 pixels, respectively.

We noticed that the impact of varying τ on cam-

era pose estimation was neglectable, i.e. the values

presented in Table 1 remained constant in practice.

This happens due to the fact that, although τ varies

by a factor of 5, the global mean reprojection er-

ror remains in the interval [0.365, 0.406] pixels (see

Fig. 5). However, the same does not hold for the re-

covered scene structure and deserves attention. We

compute the residual error of a reconstructed point

as k

− P

k, where the coordinates of P

are obtained

as follows. A virtual spherical camera is located at

the origin of the global coordinate system. The pro-

jection of

onto this virtual camera delivers p

′

. Then

= I



′



′

, where I



′



is the groundtruth

depth retrieved from the stored depth map. Not sur-

prisingly, the accuracy of the recovered scene geome-

try correlates with the mean reprojection error, as de-

picted in Fig. 5.

Figure 5: Inﬂuence of the mean reprojection error on the

accuracy of recovered scene geometry. Vertical bars show

the respective standard deviations scaled down by a factor

of 10. Values were computed using all reconstructed points

(over 30 thousand).

4.3 Perspective Datasets

To validate our approach on perspective images, we

compared it to Bundler (Snavely et al., 2006), a pop-

ular software developed for SfM on standard perspec-

tive images. Bundler is the camera calibration tool

currently used in (Furukawaand Ponce, 2008), (Agar-

wal et al., 2009), (Furukawa et al., 2010) and is pub-

licly available.

The experiments presented in this section were

carried out on the datasets published in (Strecha et al.,

2008). For each dataset, we ran Bundler on the

original images and SPHERA on the corresponding

warped images as shown in Fig. 2. To ensure a fair

comparison, we ran our pipeline using the same key-

points detected by Bundler (Lowe, 2004) after warp-

ing their coordinates to the unit sphere. This elimi-

nates the inﬂuence of image feature location on the

evaluation. Moreover, it shows SPHERA’s indepen-

dence of keypoint detectors as pointed out in Sec-

tion 4.1. Results on camera pose estimation are

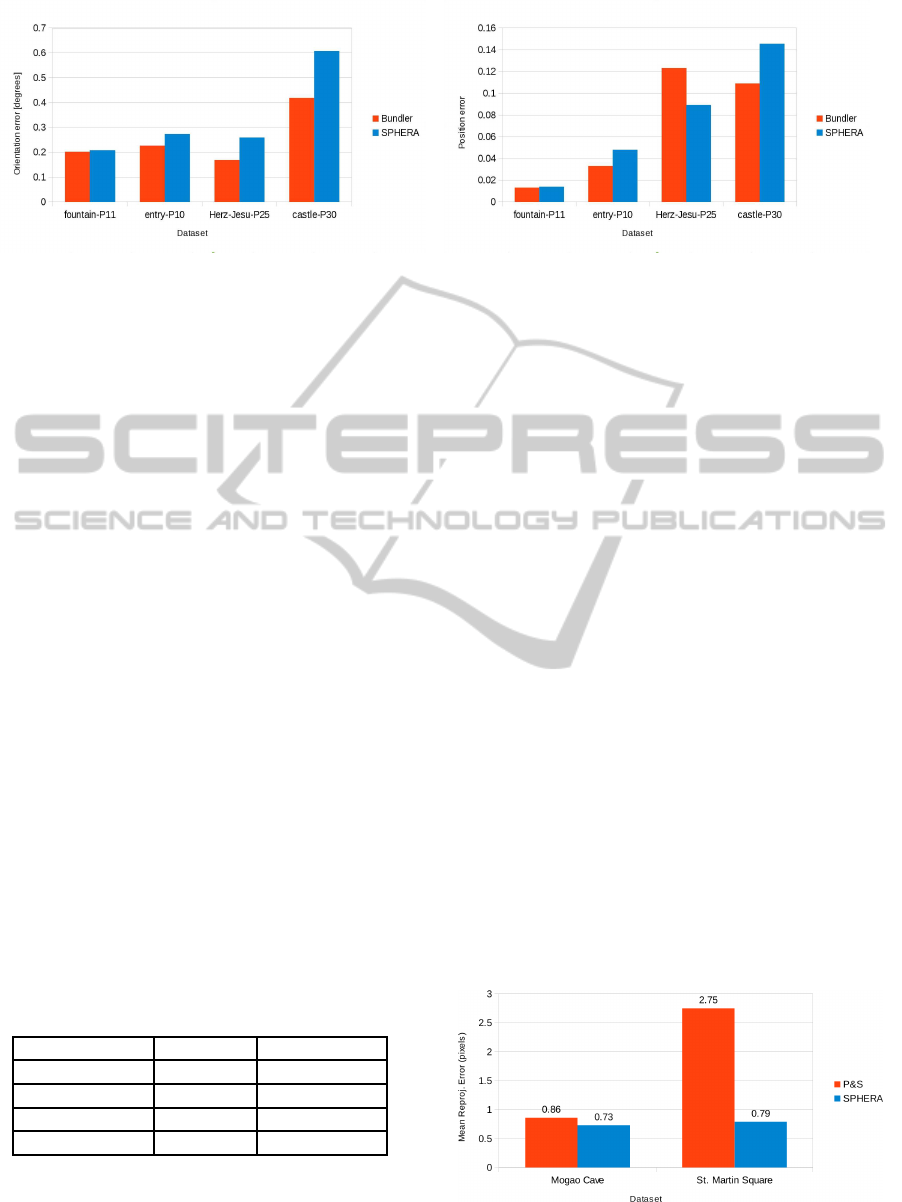
summarized in Fig. 6. Orientation errors were ob-

SPHERA-AUnifyingStructurefromMotionFrameworkforCentralProjectionCameras

289

(a) (b)

Figure 6: (a) Orientation error and (b) position error on perspective image datasets obtained with Bundler and SPHERA. See

text for details.

tained as in the previous section. Position errors,

however, were computed after preprocessing the es-

timated camera positions. To account for the differ-

ences in scale, the baseline between the closest cam-

era pair was normalized and the remaining camera po-

sitions were scaled accordingly. After that, the Eu-

clidean distance was measured as in Section 4.2.

As can be seen, Bundler performs slightly better

and the reason is as follows. Bundler works exclu-

sively on perspective images and optimizes the cam-

era poses along with their individual intrinsic param-

eters such as focal length and lens distortion. In

contrast, SPHERA has been designed to operate on

any kind of central projection camera, but the opti-

mization of intrinsic parameters has not been inte-

grated yet. Therefore, for the experiments presented

in this section, we used a constant focal length in

our pipeline and a variable focal length for Bundler.

In fact, the differences observed in Fig. 6 are pro-

portional to the variance of the focal length within

each dataset, see Table 2. The exception is Herz-Jesu-

P25, where Bundler delivers smaller orientation error

whereas SPHERA provides better camera positions.

Table 2: Variation of focal lengths estimated with Bundler.

The second column shows the standard deviation and the

third column the difference between maximum and min-

imum values. Note that, except for the Herz-Jesu-P25

dataset, the differences in Fig. 6 are proportional to the vari-

ation of the focal length.

dataset σ

[pixel] range [pixel]

fountain-P11 8.49 23.02

entry-P10 10.97 28.41

Herz-Jesu-P25 4.01 16.15

castle-P30 20.44 118.86

4.4 Spherical Datasets

In this section we compare SPHERA and the ap-

proach presented in (Pagani and Stricker, 2011). We

ran both pipelines on two datasets. The ﬁrst dataset

consists of 9 spherical images captured inside one

of the Mogao Caves, in China. The second dataset

contains 35 spherical images taken at the Saint Mar-

tin Square in Kaiserslautern, Germany, and represents

outdoors, more challenging, environments. Due to the

lack of groundtruth data for these datasets, we based

our evaluation on the global mean reprojection er-

ror. The assumption is that the correlation observed

in Section 4.2 can be used to infer the relative accu-

racy of the estimated scene geometry.

As can be seen in Fig. 7, SPHERA improves the

reprojection error on both datasets, specially on the

St. Martin Square. In the case of the Mogao Cave, due

to its simple geometry and rich texture (Fig. 8-(a)),

only few points are discarded based on Eq. 7, what

explains the small difference in the reprojection error

for this dataset. The St. Martin Square dataset is more

challenging (Fig. 8-(b)). It contains many low tex-

tured regions, depth discontinuites, occlusions as well

as repetitive patterns. Therefore, several points are in-

consistent and discarding them from the camera pose

estimation leads to the difference observed in Fig. 7.

These results suggest that SPHERA delivers more ac-

curate scene structures. Figure 8 displays the sparse

point clouds yielded by our framework, where details

of the surroundings are accurately reconstructed.

Figure 7: Global mean reprojection error on spherical im-

age datasets obtained with (Pagani and Stricker, 2011) and

SPHERA. See text for details.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

290

(a) (b)

(e) (f)

Figure 8: First row: Sample images of the Mogao Cave and St. Martin Square datasets. Second and third rows: reconstructed

point clouds delivered by SPHERA, containing approximately 106000 and 197000 3D points for the Mogao Cave and St.

Martin Square, respectively.

4.5 Hybrid Dataset

In this section we evaluate the SPHERA framework

on a hybrid dataset composed of perspective and

spherical images. The idea is to show that our frame-

work naturally handles different central projection

cameras simultaneously. This dataset is composed

of the same 35 spherical images used in the previ-

ous experiment and additional 11 perspective images

of resolution 3888× 2592 pixels. As shown in Fig. 9,

the reprojection error obtained with spherical images

(same as previous experiment) is better than the error

for perspective images.

The main reason spherical camera pose estima-

tion is better than its perspective counterpart is due to

their wide ﬁeld of view. As can be seen in Fig. 10,

matches between spherical images cover the entire

scene and thus impose more constraints on cameras’

poses. As expected, the reprojection error decreases

when perspective and spherical images are used si-

multaneously.

5 CONCLUSIONS

This paper presents SPHERA, a novel unifying Struc-

ture from Motion framework designed for central pro-

jection cameras. The goal is to cover the gaps be-

SPHERA-AUnifyingStructurefromMotionFrameworkforCentralProjectionCameras

291

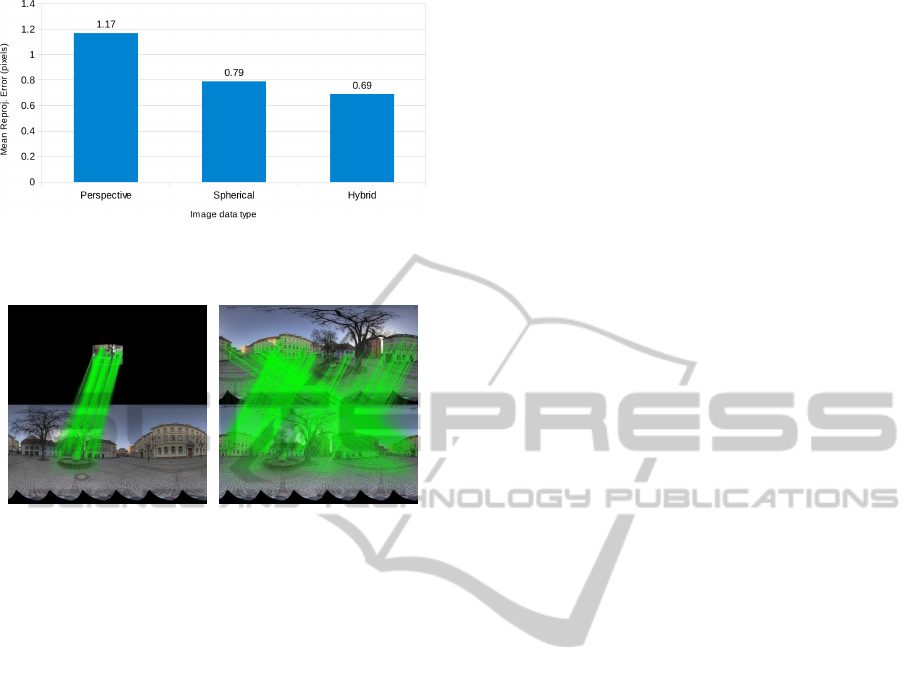
Figure 9: Global mean reprojection error for the hybrid St.

Martin Square experiment. Note how it decreases when per-

spective and spherical images are used together.

(a) (b)

Figure 10: (a) Symmetric matches between a warped per-

spective image and a spherical image. Matches are drawn

on their corresponding pixel maps to ease visualization. (b)

Symmetric matches between two full spherical images.

tween algorithms developed for perspective,spherical

and catadioptric images. Through extensive quantita-

tive evaluation on synthetic and real image sequences,

we showed that our approach delivers high quality

camera pose as well as scene geometry estimations

when compared to state of the art approaches opti-

mized for speciﬁc camera types.

Future work aims at integrating the optimization

of intrinsic parameters to increase the accuracy of

perspective cameras pose estimation. Additionally,

we plan to validate our framework on larger, hybrid

image datasets, supported by groundtruth data. Fi-

nally, SPHERA will be the underlying SfM mecha-

nism in our upcoming dense multi-view reconstruc-

tion approach.

ACKNOWLEDGEMENTS

This work was funded by the project DENSITY

(01IW12001). The authors would like to thank

Richard Schulz for the creation of the synthetic

dataset.

REFERENCES

Agarwal, S., Mierle, K., and Others (2010). Ceres solver.

https://code.google.com/p/ceres-solver/.

Agarwal, S., Snavely, N., Simon, I., Seitz, S. M., and

Szeliski, R. (2009). Building rome in a day. In ICCV,

pages 72–79, Kyoto, Japan.

Aly, M. and Bouguet, J.-Y. (2012). Street view goes in-

doors: Automatic pose estimation from uncalibrated

unordered spherical panoramas. In WACV, pages 1–8.

IEEE.

Anguelov, D., Dulong, C., Filip, D., Frueh, C., Lafon,

S., Lyon, R., Ogale, A., Vincent, L., and Weaver, J.

(2010). Google street view: Capturing the world at

street level. Computer, 43.

Bagnato, L., Frossard, P., and Vandergheynst, P. (2011). A

Variational Framework for Structure from Motion in-

Omnidirectional Image Sequences. Journal of Math-

ematical Imaging and Vision, 41(3):182–193.

Blender (2014). http://www.blender.org/. Retrieved Octo-

ber 19, 2014.

Chang, P. and Hebert, M. (2000). Omni-directional struc-

ture from motion. In OMNIVIS, Washington, DC,

USA. IEEE Computer Society.

Civetta (2009). http://www.weiss-ag.org/solutions/civetta/.

Retrieved October 16, 2014.

Furukawa, Y., Curless, B., Seitz, S. M., and Szeliski, R.

(2010). Towards internet-scale multi-view stereo. In

CVPR.

Furukawa, Y. and Ponce, J. (2008). Accurate, dense, and

robust multi-view stereopsis. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 01(01):1–

14.

Gava, C. C., Hengen, J.-M., Taetz, B., and Stricker, D.

(2013). Keypoint detection and matching on high res-

olution spherical images. In ISVC, pages 363–372,

Rethymnon, Crete, Greece.

Geyer, C. and Daniilidis, K. (2001). Catadioptric projective

geometry. Int. Journal of Computer Vision, 43:223–

243.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521540518, second edition.

Huynh, D. Q. (2009). Metrics for 3d rotations: Comparison

and analysis. Journal of Mathematical Imaging and

Vision, 35(2):155–164.

Kangni, F. and Laganiere, R. (2007). Orientation and pose

recovery from spherical panoramas. ICCV, 0:1–8.

LizardQ (2014). http://www.lizardq.com. Retrieved Octo-

ber 16, 2014.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. Int. Journal of Computer Vision,

60:91–110.

Ma, Y., Soatto, S., Kosecka, J., and Sastry, S. (2003). An in-

vitation to 3D vision, from images to models. Springer

Verlag.

Micusik, B. and Pajdla, T. (2006). Structure from motion

with wide circular ﬁeld of view cameras. IEEE Trans.

Pattern Anal. Mach. Intell., 28(7):1135–1149.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

292

Pagani, A. and Stricker, D. (2011). Structure from motion

using full spherical panoramic cameras. In OMNIVIS.

PTgui-Pro (2014). New house internet services b.v.

http://www.ptgui.com. Retrieved October 16, 2014.

Quan, L. and Lan, Z. (1999). Linear n-point camera pose

determination. IEEE Trans. Pattern Anal. Mach. In-

tell., 21(8):774–780.

Seitz-Roundshot (2014). http://www.roundshot.ch. Re-

trieved October 16, 2014.

Snavely, N., Seitz, S. M., and Szeliski, R. (2006). Photo

tourism: exploring photo collections in 3D. In ACM

SIGGRAPH 2006 Papers, SIGGRAPH, pages 835–

846, New York, NY, USA. ACM.

Stew´enius, H., Engels, C., and Nist´er, D. (2006). Recent

developments on direct relative orientation. Journal

of Photogrammetry and Remote Sensing, 60:284–294.

Strecha, C., von Hansen, W., Van Gool, L., Fua, P., and

Thoennessen, U. (2008). On Benchmarking Camera

Calibration and Multi-View Stereo for High Resolu-

tion Imagery. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition.

Torii, A., Imiya, A., and Ohnishi, N. (2005). Two- and

Three- View Geometry for Spherical Cameras. In

OMNIVIS.

Triggs, B., Mclauchlan, P. F., Hartley, R. I., and Fitzgibbon,

A. W. (1999). Bundle adjustment: A modern synthe-

sis. In Proc. of the International Workshop on Vision

Algorithms: Theory and Practice, pages 298–372.

SPHERA-AUnifyingStructurefromMotionFrameworkforCentralProjectionCameras

293