TVL

Shape Approximation from Scattered 3D Data

E. Funk

1,2

, L. S. Dooley

and A. Boerner

Department of Computing and Communications, The Open University, Milton Keynes, U.K.

Department of Information Processing for Optical Systems, Institute of Optical Sensor Systems,

German Aerospace Center, Berlin, Germany

Keywords:

Shape Reconstruction, Radial Basis Function Interpolation, L

Total Variation Minimization, Iterative Large

Scale Optimization.

Abstract:

With the emergence in 3D sensors such as laser scanners and 3D reconstruction from cameras, large 3D point

clouds can now be sampled from physical objects within a scene. The raw 3D samples delivered by these

sensors however, contain only a limite d degree of information about the environment the objects exist in,

which means that further geometrical high-level modelling is essential. In addition, issues like sparse data

measurements, noise, missing samples due to occlusion, and the inherently huge datasets involved in such

representations makes this task extremely challenging. This paper addresses these issues by presenting a new

3D shape modelling framework for samples acquired from 3D sensor. Motivated by the success of nonlinear

kernel-based approximation techniques in the statistics domain, existing methods using radial basis functions

are applied to 3D object shape approximation. The task is framed as an optimization problem and is extended

using non-smooth L

total variation regularization. Appropriate convex energy functionals are constructed and

solved by applying the Alternating Direction Method of Multipliers approach, which is then extended using

Gauss-Seidel iterations. This signiﬁcantly lowers the computational complexity involved in generating 3D

shape from 3D samples, while both numerical and qualitative analysis conﬁrms the superior shape modelling

performance of this new framework compared with existing 3D shape reconstruction techniques.

1 INTRODUCTION

The analysis and perception of environments from

static or mobile 3D sensors is widely envisioned as

a major technological breakthrough and is expected

to herald a signiﬁcant impact upon both society and

the economy in the future. As identiﬁed by the

German Federal Ministry of Education and Research

agele, 2011), spatial perception plays a pivotal role

in robotics, having an impact in many vital technolo-

gies in the ﬁelds of navigation, automotive, safety, se-

curity and human-robot-interaction. The key task in

spatial perception is the reconstruction of the shape

of the observed environment. Improvements in shape

reconstruction have direct impact on three fundamen-

tal research disciplines: self localization from cam-

era images (Canelhas et al., 2013), inspection in re-

mote sensing (Hirschm

uller, 2011) and object recog-

nition (Canelhas, 2012). Applying 3D sensors in un-

controlled practical environments, however, leads to

strong noise and many data outliers. Homogeneous

surface colours and variable illumination conditions

lead to outliers and make it a difﬁcult task to obtain

3D samples from over-exposed areas. Figure 1 shows

an example 3D point cloud obtained from a stereo

camera traversing a building. Many 3D points such as

marked by 1 suffer from strong noise. Occlusions

frequently occur in realistic scenes 2 and make

automated shape reconstruction even more challeng-

ing.

a) b)

Figure 1: a) The acquired 3D samples shown as a point

cloud. b) The scanned staircase as a photograph.

Dealing with noise and outliers inevitably in-

volves applying statistical techniques. In the last

decade, so-called kernel-based methods have become

well-accepted in statistical processing. Successful

294

Funk E., Dooley L. and Boerner A..

TVL1 Shape Approximation from Scattered 3D Data.

DOI: 10.5220/0005301802940304

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 294-304

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

techniques like deep learning or support vector ma-

chines exploit kernel-based methods in the ﬁelds of

machine learning and robotics for interpolation and

extrapolation (Sch

olkopf and Smola, 2001). Since in-

terpolation and extrapolation are required when deal-

ing with error-prone 3D samples, the application of

kernel-based approximation techniques for shape ap-

proximation is especially relevant to this domain. The

initial aim was the investigation and development of a

suitable kernel for geometrical shape modelling from

noisy 3D samples.

Many indoor and urban outdoor environments

contain a rather small set of large planar shapes. This

information can be exploited to help reduce the noise

sensitivity leading to higher approximation accuracy.

Integrating piecewise smoothness into the approxima-

tion task has attracted a lot of interest in the image

processing community. A regularization technique,

also known as Total Variation (TV) minimization, is

applied to penalize strong variations in the colour val-

ues (Rudin et al., 1992; Getreuer, 2012). Pock et al.

(2011) extended the traditional TV approach to se-

cond derivatives of the ﬁltered image pixels. Figure

2 shows the comparison of the TVL

approach with

state of the art statistical ﬁltering techniques. The ex-

tension of the TV technique to 3D shapes, is still a

fertile area of research which is considered as the se-

cond aim in this paper.

(a) Ground truth (b) Input image

(d) Median (e) Huber (f) TV

Figure 2: Comparing the total variation minimization with

common statistical techniques for height maps ﬁltering. Im-

age courtesy: Bredies et al., (2011).

A further challenge in automated shape approxi-

mation is the processing of large datasets. A realistic

dataset usually contains several millions of 3D points.

However, kernel-based and total variation techniques

suffer from high computational complexity prohibit-

ing their application to datasets which contain more

than a few thousand points (Bach et al., 2012). Such

methods normally require a set of linear equations

to be solved, which incurs O(N

) complexity. Even

if such a method could feasibly process N = 1,000

points in 10 ms, it would still take 115 days to process

1,000,000 points. This major complexity issue moti-

vated the third aim of this paper which is to develop

efﬁcient strategies for handling non-smooth (L

) total

variation regularization on large datasets.

The remainder of this paper is organised as fol-

lows: A short overview of 3D shape reconstruction

approaches is provided in Section 2, including issues

such as approximation quality and stability. Section 3

discusses the three contributions of this work: i) ap-

plication of RBFs for implicit 3D shape modelling,

ii) integration of non-smooth TVL

regularization for

noise suppression, and iii) efﬁcient optimization re-

ducing the computation complexity from O (N

) to

O(N). A critical quantitative analysis is then pre-

sented in Section 4, and concluding comments are

provided in Section 5.

2 LITERATURE REVIEW

The problem of reconstructing a surface of an object

from a set of scattered 3D points attracted a lot of at-

tention in the literature (Alexa et al., 2001; Ohtake

et al., 2003; Gomes et al., 2009) thus this section will

review existing techniques relating to the aims of this

paper, namely: shape representation using radial ba-

sis functions, statistical regularization model for noise

suppression, and efﬁcient optimization.

2.1 Shape Reconstruction

Two general shape representation approaches for 3D

data currently exist: explicit and implicit representa-

tions.

Explicit Models are polygon meshes, non uni-

form B-Splines (NURBS) or Bezier curves (Hughes

et al., 2014). The research in computer graphics

lead to large number of software frameworks such

as OpenGL (Wolff, 2013) enabling the visualization

of parametric polygon meshes with the help of paral-

lel graphics hardware. For this reason initial research

on automated shape reconstruction from 3D scattered

points focused on the direct construction of triangle

meshes, also known as Delaunay-Triangulation. Me-

thods such as α shapes (Edelsbrunner and M

ucke,

1994; Bernardini et al., 1999; Bodenm

uller, 2009)

aim at create a polygonal mesh by connecting the in-

put samples by triangle edges. This however, leads to

inaccurate results when error-prone samples are pro-

vided. Other family of parametric shapes are NURBS

(Piegl and Tiller, 1997; Rogers, 2001) and Bezier

curves (Agoston, 2005), which are commonly used

in 3D modelling. These methods are able to create

smooth surfaces for non-uniform control point sets.

In order to apply these methods to automated shape

reconstruction from scattered 3D points, the surface is

TVL1ShapeApproximationfromScattered3DData

295

Figure 3: Smooth shape representation from scattered

points and surface orientations (arrows) via an implicit

function f (x).

deﬁned as a graph in the parameter space. This makes

the problem non polynomial (NP) hard so its applica-

tion to larger datasets is prohibited (Zhao et al., 2001).

Implicit Models: Several state of the art tech-

niques represent a shape implicitly by an indicator

function f (x) to indicate inside f (x) < 0 or outside

f (x) > 0 of the object with x ∈ R

as the location in

the 3D space. The surface of the object is the set of all

x, where f gives zero. Figure 3 illustrates an implicit

shape where the dots indicate the samples on the sur-

face ( f (x) = 0) and the point orientations the normal

of the shape (∇ f (x

) = n

). This representation allows

to extract smooth surfaces from irregularly sampled,

noisy and incomplete datasets (Gomes et al., 2009).

Facing the noise sensibility issues of Delaunay-

Triangulation techniques, Alexa et al. proposed to

apply moving least squares (MLS) for smoothing (av-

eraging) the point samples prior to reconstructing a

mesh via a Delaunay-Triangulation technique (Alexa

et al., 2001). A simple implicit shape is for instance

a plane, deﬁned by its four parameters n

x + d = 0

with n ∈ R

as the plane normal vector and d as off-

set to the origin along n. Deﬁning a shape function as

f (x) = b(x)

u with b(x) = (x

,1) and u as the

plane coefﬁcients u = (n

,d) enables to ﬁnd u

via a regression task (Alexa et al., 2003). Similarly,

Guennebaud extended the shape model to spheres

and proposed the popular Algebraic Point Set Sur-

faces (APSS) method (Guennebaud and Gross, 2007).

Ohtake et al. and Oztireli et al. addressed the over

smoothing issues by applying non linear regression

for shape approximation (Ohtake et al., 2003; Oztireli

et al., 2009). The MLS techniques are well capable of

ﬁltering data sets with moderate or small noise. How-

ever, it is still not feasible for realistic datasets, as in-

troduced in Figure 1.

Implicit Models with Basis Functions: Moti-

vated by the drawbacks of MLS approaches, Calakli

and Taubin proposed to apply a global optimization

process (Calakli and Taubin, 2011). Acquired 3D

samples are structured with an octree and the implicit

values of f (x) are distributed on the corners of the oc-

tree nodes (voxels). This approach enables large holes

to be closed and allows to handle sparse spatial sam-

ples which lead to isolated fragments when MLS is

applied. A similar approach is proposed by Kazhdan

and Hoppe, where the voxel corners are the B-Splines

control points (Kazhdan and Hoppe, 2013). Both ap-

proaches suffer from the fundamental drawback that

a priori information is required from an expert user to

deﬁne the depth of the octree structure, which makes

using it in automated applications very difﬁcult.

Another family of implicit surface reconstruction

algorithms uses smooth radial basis functions (RBF).

The main difference between RBF based approxima-

tion and discrete octree models (Calakli and Taubin,

2011; Kazhdan and Hoppe, 2013) is that RBFs are

not necessarily centred on the octree leaves but di-

rectly on the samples. This reduces the risk of ap-

plying inappropriate discretisation and to lose shape

details (Gomes et al., 2009; Carr et al., 2001).

Novel approaches (Zach et al., 2007) propose to

create a dense grid of a user speciﬁed resolution and

to use the L

norm to penalize the changes between

the implicit grid corner values. Accurate results are

achieved when a ﬁne grid is applied, although the ap-

proach does not consider the smoothness of the se-

cond derivative of the shape leading to non smooth

reconstruction. Another drawback of the method is

that it is restricted to small and compact objects since

the computation time and memory consumption for

the dense grid quickly become prohibitive.

Bredies et al. proposed to apply so-called gene-

ralized total variation minimization on depth images

to penalize the variance in the second derivatives lead-

ing to piecewise smooth shapes (Figure 2). The ac-

curacy of the method motivates its extension to 3D

shapes, which has not been reported in the literature.

Bredies et al. state that the stability of the approach

heavily depends on the smoothness of the data, which

is feasible when smooth RBFs are applied (Bredies

et al., 2010). Thus, when developing an RBF based

approximation model with a TV regularization, the

choice of an appropriate RBFs type is crucial.

With a popular RBF example being Gaussian,

which is of inﬁnite differential degree, but tends to

smooth out ﬁne detail, Wahba studied the application

of Duchon’s Thin Plate Splines (Duchon, 1977) that

facilitate control of the smoothness degree (Wahba,

1990). Due to its global deﬁnition domain, Thin Plate

Splines do not result in sparse systems and lead to

complex computations. Even more adverse, a change

of a single RBF centre affects the complete shape

model in the full approximation domain, which is not

the case for RBF using compact support such as Gaus-

sians. Later, Wendland proposed several RBF types

with compact support of minimal smoothness degree

(Wendland, 1995). Wendland’s RBFs also control

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

296

the smoothness of the approximated function and still

lead to sparse and efﬁcient linear regression systems.

Moreover, as presented in Section 3, the smaller the

smoothness degree the more stable is the regression

process. The Thin Plate RBFs, however, have been

shown to achieve superior approximation quality in

the presence of noise (Tennakoon et al., 2013). Impor-

tant aspects when selecting an appropriate RBF type

are presented in Section 3.1.

2.2 Efﬁcient L

Optimization

Extending the shape approximation with a L

penalty

requires more advanced techniques to solve the opti-

mization task. This issue has been discussed for some

time in the statistics and numerical optimization com-

munity. However, efﬁcient techniques being capable

of dealing with thousands or millions of data samples

are in the current research focus.

Tibshirani proposed the Least Absolute Shrink-

age and Selection (Lasso) technique to minimize cost

functions such as

k y − Kα k

+ k α k

(1)

with k α k

∑

|α

| enabling its application on

images with several hundreds of thousands entries in

α (Tibshirani, 1994). This form is common for regres-

sion problems, where the signal y is approximated lin-

early by the model matrix K. The additional k · k

penalty term enforces only a small amount of non ze-

ros entries in α. This behaviour is suitable for prob-

lems where the vector α is expected to have many zero

entries. A common application is for example signal

approximation by only a small set of frequencies rep-

resented by α.

When representing a shape with N RBFs

f (x) =

∑

ϕ(x,x

)α

= k

α (2)

with k

= ϕ(x,x

) its second derivatives are penalized

by k Dα k

with D

j,i

= ∂

ϕ(x

). This way k Dα k

penalizes the amount of non smooth regions in the

extracted model. However, since the entries in Dα

are not separated as it is the case in (1), such prob-

lems are more difﬁcult to solve and using the Lasso

technique is not possible. Initially, interior active sets

methods have been applied to solve the TVL

objec-

tive (Alizadeh et al., 2003). Chen et al. additionally

demonstrated that the efﬁciency of primal-dual me-

thods is of magnitudes higher than of the interior me-

thods (Chen et al., 2010). Also Goldstein et al. pro-

posed a primal-dual approach known as the Bregman

Split (Bregman, 1967) to separate the smooth data

term f

=k y−Kα k

from the non smooth regulariza-

tion term f

=k Dα k

and to optimize each of them

independently (Goldstein and Osher, 2009). Boyd et

al. extended the Bregman Split approach by Dykstra’s

alternating projections technique (Dykstra, 1982) and

proposed the Alternating Direction Method of Mul-

tipliers (ADMM) (Boyd et al., 2011), which further

improves the convergence. Discussions related to ap-

plications of ADMM are reported by Parikh and Boyd

(2014).

The bottleneck of ADMM is the minimization

of the smooth part f

=k y − Kα k

. Solving this

for α with efﬁcient Cholesky factorization suffers

from a complexity of O(N

). However, an iterative

linear solver such as Jacobian or Gauss-Seidel may

reduce the complexity to O(N) as discussed by Saad

or Friedman et al. relating to L

regularization (Saad,

2003; Friedman et al., 2010). Nevertheless, further

investigations on the applicability of iterative linear

solvers and ADMM on 3D shape modelling do not

exist.

2.3 Summary

The presented state of the art in robust shape approxi-

mation and optimization methods covers several ap-

propriate options for investigation. Table 1 shows

the seminal methods summarizing the beneﬁts and

drawbacks of each technique. The TVL

approach

(Bredies et al., 2010) delivers high quality with arte-

facts such as missing data, noise, outliers, or sharp

edges in the image domain. This technique, how-

ever, suffers from high computational complexity and

needs to be extended to 3D shape approximation.

Section 2.2 states that the ADMM technique is ex-

pected to outperform the efﬁciency of existing TVL

algorithms when extended with an iterative solver.

The next Section investigates the impact of dif-

ferent RBFs applied for signal and shape approxima-

tion from scattered 3D points before the new ADMM

technique for TVL

optimization on large datasets is

presented.

3 THE METHOD

The ﬁrst part of this section pursues the ﬁrst research

objective and discusses the fundamentals of RBF

based approximation and compares different types of

RBFs with respect to quality and stability when least

squares optimization is performed. Section 3.2 ap-

plies the proposed RBFs and deﬁnes the convex opti-

mization task to perform shape reconstruction from

scattered 3D samples augmented with a TV regular-

ization term. The last part of this section presents the

TVL1ShapeApproximationfromScattered3DData

297

Table 1: Shape approximation comparison. Here + indicates that a method is moderately successful in a particular aspect,

and ++ indicates that a method is very successful.

Method Missing Data Noise Outliers Comput. Speed Sharp Edges

α shapes (Edelsbrunner and M

ucke, 1994) ++ +

Adaptive α shapes (Bernardini et al.,

1999)

+ ++ +

APSS (Guennebaud and Gross, 2007) + + + +

Smooth Signed Distance (Calakli and

Taubin, 2011)

++ + + +

Poisson (Kazhdan and Hoppe, 2013)

++ + + +

TVL

Depth Fusion (Bredies et al., 2010)

++ ++ ++ ++

developed optimization technique that allows to re-

duce the computational complexity while still being

able to solve TVL

regularized approximation tasks.

3.1 Interpolation with Radial Basis

Functions

When approximating any signal from a set of mea-

surements, the general aim is to determine a function

f : R

7→ R from a set of N sample values at x

∈ R

The core idea of RBF based approximation is that the

function f (x) may be represented by a linear combi-

nation of M weighted functions such as

f (x) =

∑

ϕ(x,x

)α

. (3)

Each of the basis functions ϕ(x,x

) is centered

at each measurement x

, and basically computes the

similarity between x and x

∈ R

. One possible form

for ϕ is a Gaussian ϕ(x,x

) = e

−kx−x

k/σ

with σ inﬂu-

encing the width of the support.

The underlying idea of RBF approximation is il-

lustrated for a one-dimensional signal in Figure 4,

where f is deﬁned as a sum of all given Gaussians

with their weights α

respectively. Usually it is as-

sumed that the widths σ of the basis functions are

known a priori so only the weighting factors α

are

to be found, leading to f (x).

The task is therefore to perform regression over N

samples and to ﬁnd M weights via minimization of

Figure 4: Illustrative example of a function f (red line) con-

structed by a weighted linear combination of Gaussian ra-

dial basis functions.

min

∑

−

∑

ϕ(x

))

where y

is the i-th measured sample at position x

This can also be rewritten in matrix-vector form as:

min

k y − Kα k

. (4)

where K is often referred to as the design matrix or

the kernel matrix with K

i, j

= ϕ(x

). The solution is

obtained via

α = A

−1

y (5)

with A = (K

K). This is the well known linear least

squares regression. Note that the function f (x) itself

is not restricted to be linear.

In the last two decades several types of RBFs have

been proposed for different applications. For the ap-

plication on shape approximation three RBF types are

investigated. i) The Gaussian which is the state of

the art, ii) Thin-Plate splines (Duchon, 1977) with

global smooth properties and the iii) compactly sup-

ported RBFs (CSRBFS) (Wendland, 1995) which en-

able sparse regression systems to be created and to

control the smoothness of the solution. Table 2 shows

the three types of the investigated RBFs with the cor-

responding explicit forms for data dimension d = 3.

Note that the scaling of each RBF type is achieved by

scaling the argument

(r) = ϕ(

) with r =k x

− x

. (6)

In order to make a systematic decision which RBF

type is best suited for the underlying application,

Table 2: Investigated radial basis functions for data dimen-

sion d = 3.

Type ϕ

(

r) Cont. m

Gaussian e

−r

∞

CSRBF (1 − r)

(1 − r)

(4r + 1) C

(1 − r)

(35r

+ 18r + 1) C

Thin-Plate r

2m−3

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

298

the stability and the approximation quality is consid-

ered. When solving for α in (5), the condition of K

cond K = |

max

min

| plays an important role. λ

min

and

max

are the minimal and maximal eigenvalues of K

respectively. In practice, it is not feasible to evalu-

ate the condition number on large systems since the

computation of the eigenvalues has a complexity of

O(N

). Therefore, a generalized approach to assess

the stability a priori is proposed.

Considering the minimal distance between two

samples as q

min

j6=i

k x

− x

and interpret-

ing f (x) =

∑

ϕ(x)α

as a transfer function, it is

proposed to analyse the system behaviour in the fre-

quency domain. The key to this is the Fourier-Bessel

transform of ϕ(r) (Wendland, 2004). Interpreting the

frequency ω as the minimal distance q

between the

approximated samples provides the best-case stabil-

ity of the regression model without having to perform

experiments on data. More practically, the boundaries

for the lowest eigenvalue are discussed and put in re-

lation to the expected sample radius q

. This enables

qualitative assessment of a basis function without per-

forming any numerical experiments. Regarding the

stability evaluation presented in Figure 5, the Thin-

Plate RBF is the only type, which remains stable for

all q

. Depending on the smoothness, CSRBF with C

and C

follow. The Gaussian RBF is the least stable

basis function with λ

min

slightly below zero.

Another important aspect when selecting an RBF

type is the approximation quality. Similarly to the

case of stability assessment, numerical experiments

often only indicate the behaviour of the RBFs re-

stricted to the given dataset. Thus, it is proposed to

appraise the theoretical error bounds in a similar way,

as has been shown with the generalized stability. The

diagram in Figure 6 presents the best achievable error

up to a positive scale factor for each RBF type given

the sampling density q

. It is clear that the higher the

sampling density, the better the approximation qual-

ity. Notably, the CSRBF-C

achieves higher quality

than other compact RBFs with lower sampling den-

sity q

and is very similar (overlays) with the global

Thin-Plate RBF.

This evaluation indicates the superior perfor-

mance of the Thin-Plate RBF, though this is not ap-

plicable in most realistic applications because the sup-

port is not restricted to the neighbouring domain. Fur-

thermore, the presented evaluations claim that ap-

plying the compactly supported RBFs with C

achieves comparable properties. Table 3 shows

the summarized investigation results, where a higher

number of plus signs reﬂect better performance. Ac-

cording to the evaluation it is clear that CSRBF is

more stable and more accurate than the Gaussian

Figure 5: The lower bounds for λ

min

(higher is better) of dif-

ferent RBFs depending on the normalized sampling radius

, d = 3 and different continuities C

Figure 6: The lower bounds (lower is better) for the approx-

imation error of each RBF type.

RBFs and provides comparable performance to the

Thin-Plate splines without requiring global support.

These key observations imply that using CSRBF for

3D data approximation is an attractive option which

will now be examined in the next Section.

Table 3: Comparative overview of the RBF models.

Gaussian Thin Plate CS-RBF

Stability + + + + + +

Approximation + + ++ + + + +

Smoothness + + + + + + + (+)

Efﬁciency + + +

3.2 Shape Reconstruction from

Scattered Points

The principal idea of shape modelling with RBF is

to extract an implicit function which represents the

shape by its zero value as introduced in Figure 3.

More formally, an algebraic function f (x), f : R

7→ R

needs to be constructed by regression. Given a set of

measured 3D points, the task is further to ﬁnd a func-

tion f (x) which returns zero on every i-th sample x

and interpolates well between the samples. Since the

zero level alone does not provide information about

TVL1ShapeApproximationfromScattered3DData

299

Figure 7: Example sparse matrices K

∇

and K for (10) when

CSRBF is applied.

the orientation of the surface, the surface normals n

at every sample are used as constraints for the gradi-

ent ∇ f (x) wrt. x. The task is now to ﬁnd f (x

) = 0

giving zero at every sample position and ∇ f (x

) = n

Integrating all this information, a convex cost func-

tional is deﬁned.

min

∑

k f (x

) k

+ k n

− ∇ f (x

) k

(7)

To simplify the optimization problem the normaliza-

tion term k ∇ f (x

) k

= 1 is omitted. In order to obtain

the gradient ∇ f , only the gradient of ϕ needs to be

computed, which is precomputed analytically. Putting

(7) into matrix notation leads to the short form of the

cost function

min

k Kα

α k

+ k n − K

∇

α k

. (8)

The matrix K contains the values of the RBFs K

n,m

ϕ(x

) ∈ R and K

∇n,m

= ∇ϕ(x

) ∈ R

repre-

sents the derivatives of ϕ wrt. x

. The matrices are of

sizes K ∈ R

N×M

and K

∇

∈ R

3N×M

. At this point it be-

comes clear that radial basis functions with local sup-

port return for distant points x

zeros which leads

to sparse matrices K and K

∇

improving the storage

and the computation efﬁciency. Figure 7 shows ex-

ample matrices K and K

∇

when a RBF with compact

support is applied. Black dots illustrate the non-zero

matrix values.

Figure 8 shows an example of applying CSRBF-

on a synthetic point set. The red line in Figure 8a)

indicates the cut-plane at which the Figure 8b) has

been rendered, while Figure 8c) shows the 3D shape

reconstruction.

Next, it is proposed to extend the cost term with

an additional total variation regularization term en-

forcing piecewise smoothness. In computer vision it

is accepted practise (Getreuer, 2012) to measure the

total variation by computing the Frobenius norm of

a Hessian matrix. In contrast, it is proposed to com-

pute the second derivatives with respect to the radius

r of the RBF ϕ(r). Comparing the single computa-

tion ∂

ϕ(r) to the evaluation of the 3 × 3 Hessian

matrix with nine elements, this reduces the computa-

tional cost by a factor of nine and is easier to compute

analytically. Similar to the case when computing the

gradients of f , the second derivative is also a sum of

derived RBFs

TV (x) =

∑

∂

ϕ(r)α

(9)

with r =k x

− x k

. Applying the TV regularization,

the cost function becomes

min

k Kα k

+ k n − K

∇

α k

+λ k Dα k

(10)

with D

n,m

= ∂

ϕ(x

) and λ as the weighting of

the regularization term. The factors α

corresponding

to the largest eigenvalue of D are attenuated the most

while weights lying in the kernel of D, are not affected

at all. Figure 9 shows an example when the input sam-

ples have been perturbed by noise (Figure 10a) and

the shape is reconstructed via a) simple least squares

(LSQ) and b) TV L

. In both images the red colour

corresponds to the TV cost intensity (9). Clearly,

when applying TV minimization the shape accuracy

of the reconstruction is improved and the red TV in-

tensity is reduced signiﬁcantly.

Increasing the normally distributed sample noise

up to σ ≈ 30% of the bounding box, the effect of the

regularization is demonstrated in Figure 10. While the

simple LSQ model does not achieve a smooth shape

(Figure 10b) the new regularized approach in Figure

10c) shows considerable perceptual improvement in

terms of the quality of the shape reconstruction.

In the next section, the proposed numerical tech-

nique to efﬁciently solve the TVL

task is presented.

3.3 TVL

Solver

To minimize the task (10) it is proposed to apply the

Lagrangian approach from the Alternating Direction

Method of Multipliers (ADMM) (Boyd et al., 2011).

Formally, (10) is restated to

a) b) c)

Figure 8: a) Synthetic input points, b) the cut plane visu-

alizing f (x) as red ( f < 0) green ( f > 0), c) reconstructed

shape from a).

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

300

a) b) c)

Figure 10: a) Noisy 3D samples of the step function. b) Direct LSQ. c) TV L

regularized approximation.

a) b)

Figure 9: a) The TV cost (red) overlaid with the unregular-

ized shape obtained via LSQ. b) The reduced TV cost (less

red colour) after performing regularized approximation fol-

lowing (10).

min

α,z

L(α,z) = f

(α) + f

(z)+

(Dα − z) +

k Dα − z k

(11)

where f

(α) is the data part from (10) depending on

α, and f

(z) = λ k z k

is the non-smooth regular-

ization part weighted by λ. The basic approach is

to minimize for α, then for z iteratively. The terms

(Dα − z) and k Dα − z k

make sure that Dα is

close to z after an iteration ﬁnishes reducing the du-

ality gap. This restriction is controlled by ρ which is

usually a large scalar. The iterative optimization pro-

cess between α and z is summarized in Algorithm 1.

The minimization for z involves a sub gradient over

k · k

and its solution is known as the shrinkage oper-

ator (Efron et al., 2004) being applied on each element

independently:

= shrink(a, b)

= a − b · sign(b − a)

where a =

+ (Dα)

, b =

(12)

with (Dα)

as the i-th element of the vector Dα and

sign(b − a)

gives 1 if b > a and zero otherwise.

Algorithm 1: ADMM for L

approximation

1. Solve for α:

∇

+ K

K + ρD

D)α = K

∇

n + D

(ρz − b).

2. Evaluate: z

k+1

= shrink(

+ (Dα)

,λ/ρ)

3. Evaluate: b

k+1

:= b

+ (Dα

k+1

− z

k+1

)ρ

While steps 2 and 3 are direct evaluations and can be

performed in parallel after Dα

k+1

has been precom-

puted, step 1 incurs high computational complexity.

It is proposed to solve α

k+1

via Gauss-Seidel itera-

tions well known from large scale linear system opti-

mization (Saad, 2003). However, the standard Gauss-

Seidel process suffers from difﬁcult convergence con-

ditions. Thus, successive over relaxation (SOR) is ap-

plied with a weight factor ω. By applying SOR in step

1 Algorithm 1 is solved via:

k+1

= α

+ ω

− (K

∇i

∇

+ K

K + ρD

D)α

∇i

+ K

+ ρD

(13)

with y

= K

∇i

n + D

(zρ − b) and ith columns of a

matrix respectively. Considering that K

∇

, K and D

are sparse when CSRBF is applied, the computation

is reduced to Algorithm 2.

Algorithm 2: Matrix free TVL

1. For each RBF centre α

compute:

(a) Find all neighbouring centres and all neighbou-

ring samples located in the support of α

(b) Compute the equation (13) using only the

collected neighbours.

k+1

2. Evaluate: z

k+1

= shrink(

+ (Dα)

,λ/ρ)

3. Evaluate: b

k+1

:= b

+ (Dα

k+1

− z

k+1

)ρ

The optimization is controlled by two important

parameters: ω for the successive over relaxation and

the RBF scaling s, as introduced in table 2 and (6).

Figure 11 shows the effect of these parameters on the

approximation quality and the achieved convergence

rates. The experiments have been performed on the

synthetic dataset from Figure 8. Figure 11a) illus-

trates the approximation quality over the scaling s, the

quality attains its optimum when s = 10 is reached.

This observation corresponds to the generalized in-

vestigations from Figure 6, where s = 10 is q

= 0.1.

Furthermore, the empirical impact analysis of the over

TVL1ShapeApproximationfromScattered3DData

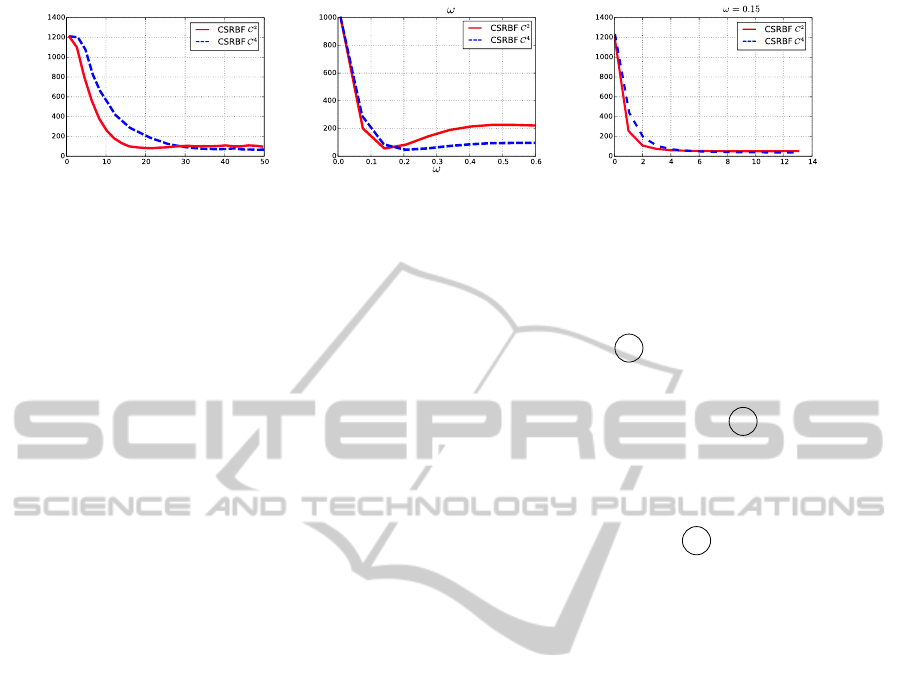
301

Minimal points within RBF support

Residuum

Eﬀect of

Iteration

Residuum

Convergence

a) b) c)

Figure 11: a) The impact of the scaling parameter s, b) the over relaxation weighting ω, c) convergence behavior for ω = 0.15

when CSRBF-C

or CSRBF-C

are applied.

relaxation parameter ω on the convergence concludes,

that ω ≤ 0.15 enables to remove the instability issues

for CSRBF-C

and CSRBF-C

when SOR is applied.

Note that when applying the Gaussian RBF, ω is re-

quired to be very small (ω ≈ 1e − 3), leading to an

impractically high number of iterations. This fact is

a consequence of the stability properties of the Gaus-

sian, investigated in Section 3.1.

The next section evaluates the proposed TVL

shape approximation framework with respect to ex-

isting methods by applying the algorithms on a large

dataset with an existing ground truth.

4 EVALUATION

This Section evaluates the proposed shape recon-

struction framework on different datasets and com-

pares it with two successful surface reconstruction

techniques: The Poisson approximation (Kazhdan

and Hoppe, 2013), and the Smooth-Signed-Distance

(SSD) algorithm (Calakli and Taubin, 2011). The

selected methods have been identiﬁed as success-

ful techniques for shape reconstruction under strong

noise. Both use the implicit model to represent the

shapes, however, in contrast to the presented work the

compared methods structure the data via an octree of

predeﬁned depth and apply discrete optimization via

ﬁnite differences to extract the zero level of the sur-

face.

The analysis uses a 3D point cloud as the input,

and since 3D samples with a ground truth were not

available, a virtual camera ﬂight was simulated in or-

der to generate error prone data with an established

ground truth. The simulation of the moving camera

and noisy 3D measurements were achieved by extend-

ing the CAD software Blender (Open Source Com-

munity, 2014). This enabled different noise levels

on the measurements to be applied and provided an

accurate model of the observed environment. Figure

12a) shows the ground truth model used for the simu-

lated measurements in assessing the quality of recon-

structed 3D shapes in Figure 12e). An outdoor scene

was selected since similar environments are used in

many robotic applications. The facade consisted of

large planar areas with a number of sharp edges as

identiﬁed in point 1 . The proposed TVL

tech-

nique performs signiﬁcantly better than the Poisson

approach and similarly well compared to SSD. Dur-

ing the simulation several areas 2 have been oc-

cluded by the railing, thus have not been sampled.

This increases the difﬁculty of the reconstruction task.

Here, TVL

interpolates a shape, which corresponds

more to the ground truth than the two compared tech-

niques. The area marked by 3 is the balcony, where

only a small part of the ﬂoor has been sampled. In

such areas, both TVL

and SSD perform well, sig-

niﬁcantly outperforming the Poisson approach. The

diagram in Figure 12f) shows the error distribution

of the reconstructed shapes. It is produced by re-

sampling the ground truth model and the approxi-

mated shapes with 5M points and by measuring the

minimal distance between each reconstructed sample

and a ground truth sample. The point-to-point (ptp)

distance is shown on the horizontal axis. The his-

togram height is normalized resulting in a fraction of

samples being inside a histogram bin. The further the

peak moves to the left of the diagram, the better is

the reconstruction accuracy. As also illustrated by the

Figures 12 a)-d), TVL

slightly outperforms SSD and

is signiﬁcantly more accurate than Poisson.

5 CONCLUSION

This paper has presented a new 3D shape modelling

strategy for noisy error prone 3D data samples. Mod-

elling 3D shapes with radial basis functions has been

proposed with the choice of the most appropriate RBF

corroborated using generalized stability and approx-

imation quality assessments. The shape regression

model has been extended by non-smooth L

regu-

larization assuming planar areas to improve the ac-

curacy of the reconstructed shape in indoor and ur-

ban environments. Since the TVL

optimization task

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

302

a) Ground truth

0.1

b) TVL1-C

c) SSD

d) Poisson

e) Shape results

ptp-distance

fraction of samples

TVL1-

Poisson

SSD

f) Error histogram

Figure 12: Evaluation results for the proposed TVL

and

the compared techniques.

is computationally expensive, a low complexity opti-

mization technique has been developed. The opti-

mization process exploits the Lagrangian form of

the optimization task with an iterative over relax-

ation technique. This enables realistic datasets con-

taining several millions points to be effectively pro-

cessed. Quantitative analysis conﬁrms that the pro-

posed method achieves superior accuracy on the syn-

thetic objects.

For future research, the presented solution will be

adapted and extended to recursive, real-time 3D map-

ping applications where environment measurements

are received as a data stream. The corresponding 3D

shape approximation model will be then able to recur-

sively modify its shape as new measurements become

available.

REFERENCES

Agoston, M. (2005). Computer Graphics and Geometric

Modelling: Implementation & Algorithms. Computer

Graphics and Geometric Modeling. Springer.

Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin,

D., and Silva, C. T. (2001). Point set surfaces. In

Proceedings of the Conference on Visualization ’01,

VIS ’01, pages 21–28, Washington, DC, USA. IEEE

Computer Society.

Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin,

D., and Silva, C. T. (2003). Computing and render-

ing point set surfaces. Visualization and Computer

Graphics, IEEE Transactions on, 9(1):3–15.

Alizadeh, F., Alizadeh, F., Goldfarb, D., and Goldfarb, D.

(2003). Second-order cone programming. Mathemat-

ical Programming, 95:3–51.

Bach, F. R., Jenatton, R., Mairal, J., and Obozinski, G.

(2012). Optimization with sparsity-inducing penal-

ties. Foundations and Trends in Machine Learning,

4(1):1–106.

Bernardini, F., Mittleman, J., Rushmeier, H., Silva, C., and

Taubin, G. (1999). The ball-pivoting algorithm for

surface reconstruction. IEEE Transactions on Visual-

ization and Computer Graphics, 5(4):349–359.

Bodenm

uller, T. (2009). Streaming surface reconstruction

from real time 3D-measurements. PhD thesis, Techni-

cal University Munich.

Boyd, S., Parikh, N., Chu, E., Peleato, B., and Eckstein, J.

(2011). Distributed optimization and statistical learn-

ing via the alternating direction method of multipliers.

Found. Trends Mach. Learn., 3(1):1–122.

Bredies, K., Kunisch, K., and Pock, T. (2010). Total gene-

ralized variation. SIAM J. Img. Sci., 3(3):492–526.

Bregman, L. (1967). The relaxation method of ﬁnding

the common point of convex sets and its application

to the solution of problems in convex programming.

{USSR} Computational Mathematics and Mathemat-

ical Physics, 7(3):200 – 217.

Calakli, F. and Taubin, G. (2011). SSD: Smooth signed

TVL1ShapeApproximationfromScattered3DData

303

distance surface reconstruction. Computer Graphics

Forum, 30(7):1993–2002.

Canelhas, D. R. (2012). Scene Representation, Registration

and Object Detection in a Truncated Signed Distance

Function Representation of 3D Space. PhD thesis,

Orebro University.

Canelhas, D. R., Stoyanov, T., and Lilienthal, A. J.

(2013). Sdf tracker: A parallel algorithm for on-line

pose estimation and scene reconstruction from depth

images. In Intelligent Robots and Systems (IROS),

2013 IEEE/RSJ International Conference on, pages

3671–3676. IEEE.

Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J.,

Fright, W. R., McCallum, B. C., and Evans, T. R.

(2001). Reconstruction and representation of 3d ob-

jects with radial basis functions. In Proceedings of the

28th Annual Conference on Computer Graphics and

Interactive Techniques, SIGGRAPH ’01, pages 67–

76, New York, NY, USA. ACM.

Chen, X., Lin, Q., Kim, S., Pe

na, J., Carbonell, J. G.,

and Xing, E. P. (2010). An efﬁcient proximal-

gradient method for single and multi-task regression

with structured sparsity. CoRR, abs/1005.4717.

Duchon, J. (1977). Splines minimizing rotation-invariant

semi-norms in sobolev spaces. In Schempp, W. and

Zeller, K., editors, Constructive Theory of Functions

of Several Variables, volume 571 of Lecture Notes in

Mathematics, pages 85–100. Springer Berlin Heidel-

berg.

Dykstra, R. (1982). An Algorithm for Restricted Least

Squares Regression. Technical report, mathematical

sciences. University of Missouri-Columbia, Depart-

ment of Statistics.

Edelsbrunner, H. and M

ucke, E. P. (1994). Three-

dimensional alpha shapes. ACM Trans. Graph.,

13(1):43–72.

Efron, B., Hastie, T., Johnstone, I., and Tibshirani, R.

(2004). Least angle regression. Annals of Statistics,

32:407–499.

Friedman, J. H., Hastie, T., and Tibshirani, R. (2010). Reg-

ularization paths for generalized linear models via

coordinate descent. Journal of Statistical Software,

33(1):1–22.

Getreuer, P. (2012). Rudin-Osher-Fatemi Total Variation

Denoising using Split Bregman. Image Processing On

Line, 2:74–95.

Goldstein, T. and Osher, S. (2009). The split bregman

method for l1-regularized problems. SIAM J. Img.

Sci., 2(2):323–343.

Gomes, A., Voiculescu, I., Jorge, J., Wyvill, B., and

Galbraith, C. (2009). Implicit Curves and Sur-

faces: Mathematics, Data Structures and Algorithms.

Springer Publishing Company, Incorporated, 1st edi-

tion.

Guennebaud, G. and Gross, M. (2007). Algebraic point set

surfaces. ACM Trans. Graph., 26(3).

agele, M. (2011). Wirtschaftlichkeitsanalysen neuartiger

Servicerobotik-Anwendungen und ihre Bedeutung f

die Robotik-Entwicklung.

Hirschm

uller, H. (2011). Semi-global matching - motiva-

tion, developments and applications. In Fritsch, D.,

editor, Photogrammetric Week, pages 173–184. Wich-

mann.

Hughes, J., Foley, J., van Dam, A., and Feiner, S. (2014).

Computer Graphics: Principles and Practice. The

systems programming series. Addison-Wesley.

Kazhdan, M. and Hoppe, H. (2013). Screened poisson sur-

face reconstruction. ACM Trans. Graph., 32(3):29:1–

29:13.

Ohtake, Y., Belyaev, A., Alexa, M., Turk, G., and Seidel,

H.-P. (2003). Multi-level partition of unity implicits.

ACM Trans. Graph., 22(3):463–470.

Open Source Community (2014). Blender, open source

ﬁlm production software. http://blender.org. Ac-

cessed: 2014-06-6.

Oztireli, C., Guennebaud, G., and Gross, M. (2009). Fea-

ture Preserving Point Set Surfaces based on Non-

Linear Kernel Regression. Computer Graphics Fo-

rum, 28(2):493–501.

Piegl, L. and Tiller, W. (1997). The NURBS Book. Mono-

graphs in Visual Communication. U.S. Government

Printing Ofﬁce.

Rogers, D. F. (2001). Preface. In Rogers, D. F., editor,

An Introduction to NURBS, The Morgan Kaufmann

Series in Computer Graphics, pages xv – xvii. Morgan

Kaufmann, San Francisco.

Rudin, L. I., Osher, S., and Fatemi, E. (1992). Nonlinear

total variation based noise removal algorithms. Phys.

D, 60(1-4):259–268.

Saad, Y. (2003). Iterative Methods for Sparse Linear Sys-

tems. Society for Industrial and Applied Mathematics,

Philadelphia, PA, USA, 2nd edition.

Sch

olkopf, B. and Smola, A. J. (2001). Learning with Ker-

nels: Support Vector Machines, Regularization, Opti-

mization, and Beyond. MIT Press, Cambridge, MA,

USA.

Tennakoon, R., Bab-Hadiashar, A., Suter, D., and Cao,

Z. (2013). Robust data modelling using thin plate

splines. In Digital Image Computing: Techniques and

Applications (DICTA), 2013 International Conference

on, pages 1–8.

Tibshirani, R. (1994). Regression shrinkage and selection

via the lasso. Journal of the Royal Statistical Society,

Series B, 58:267–288.

Wahba, G. (1990). Spline models for observational data,

volume 59 of CBMS-NSF Regional Conference Series

in Applied Mathematics. Society for Industrial and

Applied Mathematics (SIAM), Philadelphia, PA.

Wendland, H. (1995). Piecewise polynomial, positive deﬁ-

nite and compactly supported radial functions of mini-

mal degree. Advances in Computational Mathematics,

4(1):389–396.

Wendland, H. (2004). Scattered Data Approximation. Cam-

bridge University Press.

Wolff, D. (2013). OpenGL 4 Shading Language Cookbook,

Second Edition. EBL-Schweitzer. Packt Publishing.

Zach, C., Pock, T., and Bischof, H. (2007). A globally opti-

mal algorithm for robust tv-l1 range image integration.

In Computer Vision, 2007. ICCV 2007. IEEE 11th In-

ternational Conference on, pages 1–8.

Zhao, H., Oshery, S., and Fedkiwz, R. (2001). Fast surface

reconstruction using the level set method. In In VLSM

01: Proceedings of the IEEE Workshop on Variational

and Level Set Methods.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

304