
A Homotopy Surface Cutting using Paths Crossing in Geodesic Distance
Anuwat Dechvijankit
1
, Hiroshi Nagahashi
2
and Kota Aoki
2
1
Department of Computational Intelligence and Systems Science, Tokyo Institute of Technology, Yokohama, Japan
2
Imaging Science and Engineering Laboratory, Tokyo Institute of Technology, Yokohama, Japan
Keywords:
Geodesic Distance, Graph Cut, Homotopy, Surface Parameterization, Topology.
Abstract:
Topology is a property of surfaces that plays a major role in computer graphics. Processing or analysis between
two surfaces generally requires both of them to be in same topology. There are many tools or applications
such as parameterization or remeshing that require disk topology surfaces as input. Therefore, it is important
to convert any surfaces to be same as a topological disk. The common procedure is to define a graph of edges
inside the surface that should be split into two edges and to turn the surface into topological disk. We call it
as homotopy cutting. Problems become more difficult when dealing with high genus surfaces such as a torus.
Based on a novel method, we present an enhancement method to generate a cut graph in high-genus surface
for homotopy cutting. By using geodesic properties of each edge, we can generate equally or more suitable
edge-graph than original method while keeping similar performance and stability as original one.
1 INTRODUCTION
Geometry processing is an important research in 3D
computer graphics field. Without efficient algorithms,
it is very difficult to develop any kinds of advanced
applications for end-users. Some of important appli-
cations in 3D computer graphics, such as texture map-
ping (Bennis et al., 1991), normal mapping (Cohen
et al., 1998), remeshing (Hormann and Greiner, 2000)
and parameterization (Tutte, 1963; Floater, 1997) re-
quire a specific topology of input mesh. There are
many cases where topological disk surface is speci-
fied for further processing. Such topological require-
ment in input mesh has significant impact on several
researches. There are many properties in each mesh
such as closed/open, holes and genus which require
different approach on them.
When processing a mesh that requires disk topol-
ogy input, all kinds of meshes have different mea-
sures. An open surface has originally the same topol-
ogy as a disk which can pass directly, but may need
to be taken care in case of containing holes. Some
problems arise when dealing with a closed surface
since it has different topology from the disk. The
process of surface cutting into a disk is required. In
case of sphere topology, it does not require much pro-
cesses; only short graph edge is necessary. However,
there need some processes to ensure the quality of
graph edges in homotopy cutting. The problem be-
comes more complex and more interesting when deal-
ing with high genus surfaces.
This paper presents a homotopy cutting on high
genus surfaces. Our approach is an enhancement of a
novel method (Gu et al., 2002) in homotopy cutting;
cutting surfaces into disks. A benefit of this method
is to be able to handle any kinds of 2-manifold sur-
faces, regardless of specific topology. We present an
algorithm that creates a cut graph on the area where
geodesic path comes from different directions in ex-
act geodesic distance (Mitchell et al., 1987; Surazh-
sky et al., 2005) (see example in figure 1). With some
extra calculation, we can define equally or more ap-
propriate cut graph from original method while keep-
ing performance and stability.
Figure 1: Geodesic distance radius from a starting point on
genus 1 rocket arm model. At the hole (tunnel), we can see
some sharp pattern which can be recognize as geodesic path
came from different directions.
130
Dechvijankit A., Nagahashi H. and Aoki K..
A Homotopy Surface Cutting using Paths Crossing in Geodesic Distance.
DOI: 10.5220/0005302601300137
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 130-137
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Notations
Before explaining various algorithms of homotopy, let
us define basic notations. We represent a 2-manifold
triangular surface or mesh by M := (V,F), where
V := {v
i
∈ R
3
| i = 1,...,n
v
} is a set of n
v
vertices
and F := { f
i
(a,b,c) | i = 1, ..., n
f
: a,b, c = 1,...,n
v
:
a 6= b 6= c} is a set of n
f
faces. We also define
E := {e
i
(a,b) | i = 1,...,n
e
: a, b = 1,...,n
v
: a 6= b}
as a set of n
e
edges found in the surface M . We as-
sume that the mesh has genus g topology.
2 RELATED WORKS
As for a topic of topological converting in the past
years, there was a novel work by (Erickson and Har-
Peled, 2002) that studied the problem of cutting a
topological surface into a disk efficiently. They pro-
posed a cutting method that gave some elegant the-
oretical guarantees. However, the algorithm is very
complex to be implemented. It finds the shortest loop
path connecting vertices to the vertex itself by using a
front propagation technique, and then tests if the con-
sidering loop path reduces the surface genus or simply
cuts the surface into two pieces. It has topologically-
sufficient cut as 2g loops. The generation of minimal
length cut that converts a high genus surface into a
topological disk is a NP-hard problem. One method
is a brute force approach which consumes a lot of
time. However, it is an approximation of the shortest
cut graph calculated in O(g
2
nlogn) where n denotes
complexity of the surface. (Erickson and Whittlesey,
2005) studied about a greedy homotopy basis and im-
proved its calculation speed in O(n log n) by using a
straightforward application of Dijkstra’s shortest path
algorithm (Dijkstra, 1959).
From the efficiency point of view, it is impor-
tant to compute non-trivial cycles on orientable sur-
faces. Non-trivial cycles mean non-contractible and
non-separating cycles which guarantee the topologi-
cal surface cutting into disk. Recently, (Kutz, 2006)
presents an algorithm that computes a shortest non-
trivial cycle in O(n log n) on an orientable combinato-
rial surface of bounded genus. The algorithm is based
on universal-cover constructions to find short cycles.
There are several studies that try to define a cut
graph by surface properties. A study by (Patan
`
e et al.,
2007) presents an algorithm that builds up the cut
graph on the iso-contours from Reeb graph which
codes the topology of a given surface M in a combi-
natorial structure and generates loops together. There
are deep studies by (Dey et al., 2008; Dey et al., 2013)
that show how to recognize short handle and tunnel
loops in a surface by using Reeb graph. Another study
by (Jin et al., 2013) presents an algorithm to compute
the shortest homotopic loop with negative Euler char-
acteristic based on the surface hyperbolic uniformiza-
tion metric. They also demonstrated two applications:
constructing extremal quasi-conformal mappings be-
tween same topology surfaces, and detecting homo-
topy between two paths or cycles on a surface.
There is an iterative method called “geometry im-
ages” by (Gu et al., 2002), which is similar to that of
(Dey, 1994). This method presents a remeshing ap-
proach using square surface parameterization to cre-
ate a mapping between irregular surface M in R
3
do-
main, and square plane in R
2
domain. To get low er-
ror on the remeshing, they present how to create a cut
graph from any kinds of surfaces M regardless from
the pre-analysis of topology and boundary edges.
(a) Geometry of surface (b) Geometry image
Figure 2: A geometry image.
Since our approach is based on (Gu et al., 2002)
approach, we explain in section 3 how it creates a cut
graph for homotopy cutting on an irregular surface M
with genus g.
3 PREVIOUS ALGORITHM
The algorithm of (Gu et al., 2002) is divided into
two parts, i.e., homotopy cutting and its augmenta-
tion. The augmentation aims to improve its subse-
quent square planar domain parameterization. We ex-
plain the first part that involves the definition of a cut
graph and a converting surface M into disk.
At the beginning, when the mesh M has bound-
aries, let B be the set of original boundary edges that
remain unchanged in the whole process and will be in-
cluded in final cut graph ρ. It first starts by removing
a single seed triangle from the mesh. At this moment,
each edge of the seed triangle is adjacent to only one
triangle respectively (see figure 3(b)). After removing
the seed triangle from the mesh, there are two pro-
cessing phases.
In the first phase, it repeatedly detects an edge ad-
jacent exactly to one triangle that is not in B, and
AHomotopySurfaceCuttingusingPathsCrossinginGeodesicDistance
131
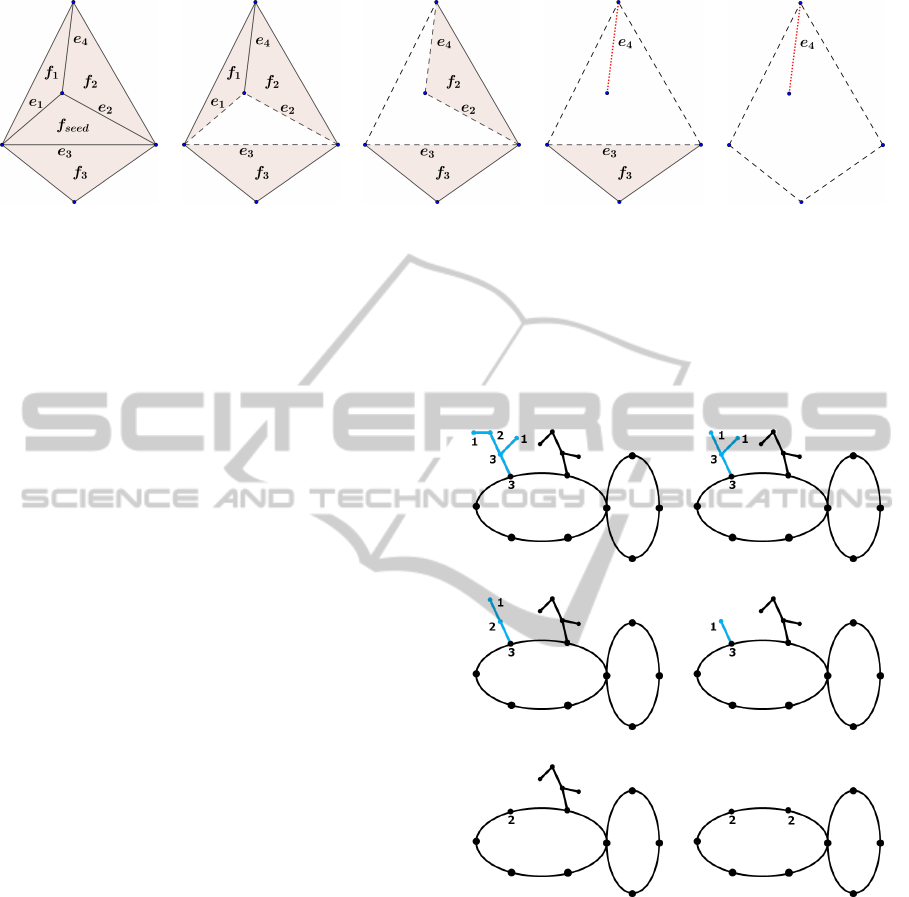
(a) (b) (c) (d) (e)
Figure 3: Processes from removing a seed triangle from a mesh. Dash lines mean edges that are adjacent to only one triangle
at the moment. (a) shows before removing stage. (b) shows after removing the seed triangle; that is, edges e
1
,e
2
and e
3
are
adjacent to only one triangle. Assume that geodesic distance from f
seed
to e
1
is the smallest. (c) shows the result of removing
edge e
1
and face f
1
. The edge e
4
become the one that adjacent to only one triangle. Let e
2
is next smallest geodesic distance.
(d) shows the result of removing e
2
and f
2
. The edge e
4
becomes a candidate of cut graph edge (red dot line). (e) shows the
result of next step that removing e
3
and f
3
.
removes both the edge and the triangle from the mesh
structure. The rest two edges are left (see figure 3(c)).
If the rest edges of the removing triangle are not ad-
jacent to any triangle, then the edges will become one
of candidates of cut graph (see figure 3(d)). Gener-
ally, removing one edge and one triangle triggers ad-
ditional two edges to be adjacent to only one triangle
further. Because of the above condition, the removing
propagation will keep spreading out from the seed tri-
angle according to geodesic distance in order to get
minimum radius result. Since a 2-manifold triangle
mesh is being processed, every triangle will be re-
moved eventually. Therefore, this phase ends when
there is no triangle left and there remain only edges
and their vertices as candidate cut graph edges. At
this point, the cut ρ consists of a set of connecting 2g
loops.
In the second phase, we again iteratively detect a
valence-1 vertex and its corresponding edge, and re-
move both the vertex and the edge (see figure 4). The
purpose of this phase is to remove unnecessary dan-
gling edges remained in the first phase. The dangling
edges will be repeatedly trimmed away until there is
no valence-1 vertex left in the cut ρ. There are only
edges that form connected loops as a cut graph in the
cut ρ. At last, all loops in ρ are straightened by com-
puting a local shortest path in each loop. Finally, the
connected 2g loop cut graph in ρ is homotopy basis:
a cut graph that converts the surface into a topological
disk patch.
For the case of closed surface of genus g = 0, the
overall processes from this part will generate the cut
ρ that consists of only one vertex. To enable the map-
ping into planar domain, we add two adjacent edges
of the vertex into the cut graph ρ. On the other hand,
for the case of a mesh having one or more holes, it will
result in connected graphs between any holes’ edges
and homotopy basis.
(a) (b)
(c) (d)
(e) (f)
Figure 4: Process on removing dangling edges. The num-
bers on vertices indicate present valence number. We focus
on the removing of blue dangling edges. (a) shows initial
state where there are two valence-1 edges. (b) - (d) show
the following steps that remove valence-1 edge along with
its vertex. (e) shows that all blue dangling edges have been
removed. (f) shows the process of removing other dangling
edges until valence-1 edge has not been found in graph.
4 GEODESIC DISTANCE
The algorithm by (Gu et al., 2002) creates front prop-
agation on geodesic distance. We consider an exact
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
132

geodesic distance proposed by (Mitchell et al., 1987)
as knows as MMP algorithm. It computes exact short-
est paths on a triangular mesh. These paths typically
cut across faces in the mesh, which is different from
typical Dijkstra shortest paths (Dijkstra, 1959) that
run across edges in the mesh.
MMP algorithm creates a geodesic path for “sin-
gle source and all destinations” scheme. The algo-
rithm computes a set of intervals of each edge. An
interval represents an accessible pencil of lines from
its pseudo-source. Each interval also acts as a pseudo-
source to propagate across faces of the rest of mesh.
The algorithm propagates the distance information
out from the source in a Dijkstra-like fashion which
can traceback any positions on mesh to the source.
Figure 5 shows the concept of propagation of the al-
gorithm where intervals i
β
and i
γ
can be traceback to
v
source
through i
α
.
Figure 5: Propagation scheme of MMP algorithm: interval
i
α
on edge e
a
propagates distance pencil paths across an
adjacent face to adjacent edges e
b
and e
c
.
The performance of MMP algorithm : they prove
a worst case running time of O(n
2
logn) when n is the
number of mesh edges. However in practical calcula-
tion, it can achieve on 100K triangles mesh within a
few seconds. Also, there is an approximate version of
MMP algorithm proposed by (Surazhsky et al., 2005)
that can speed up the calculation by trying to merge
an interval with adjacent intervals on the same edge
before starting the propagation.
Notations
After calculating the exact geodesic distance from
a vertex v
s
, each edge e
i
that is not a boundary
one, has a set of m intervals I
e
i
:= {i
e
i, j
( f
p
,e
p
,D) |
i = 1,...,n
v
, j = 1, ...,m}, where f
p
represents the
face where propagation of interval’s pseudo-source
across and e
p
represents the edge that has interval’s
pseudo-source. D represents another information
about geodesic distance of considering interval.
5 OUR APPROACH
Given a triangular 2-manifold mesh M without any
topological information about genus g, we adopt a ge-
ometry image method (Gu et al., 2002) to define 2g
cut loop graph for homotopy basis. Instead of hav-
ing a cut graph along the propagation by geodesic
distance criteria, we try to have a cut graph in the
area where it has the same geodesic distance but its
pseudo-sources come from different edges and faces.
To define such area, we calculate the exact
geodesic distance from a source vertex v
s
by MMP
algorithm (Mitchell et al., 1987) and then analyze the
set of intervals in each edge e
i
. First, we define edges
whose intervals have pseudo-sources laid on both side
of adjacent faces. However, this case typically can
detect few edges and cannot cover all areas where the
cut graph should exist. Second, we define remaining
edges whose intervals cannot be a pseudo-source of
adjacent edges. We define these two specific charac-
teristic edges as a set of edges
˜
E. At this point,
˜
E
contains a lot of unnecessary dangling edges. There-
fore, we eliminate them from
˜
E by the same approach
in the original method.
We ensure that the cut graph has non-separating
cycles by considering neighbor edges of
˜
E. We de-
fine a set of neighbor edges as
ˆ
E, then the candidate
cut graph edges can be given by ρ ≡ (
˜
E ∪
ˆ
E), and
the rest edges
´
E are given as
´
E ≡ (E − ρ). How-
ever, ρ may contain contractible cycles too. There-
fore, we again need to define non-separating and non-
contractible cycles from ρ. We follow similar basis
from the original method by removing an edge exactly
adjacent to one triangle. However, we create priority
of removing edges in a queue according to
´
E,
ˆ
E and
˜
E. From this point, we follow the remaining origi-
nal processes: removing dangling edges and shorten
loop.
We explain in details how to define the set
˜
E and
how to ensure the generation of non-separating and
non-contractible cut graph.
5.1 Pseudo-sources of Intervals from
Both Sides
The main idea of our approach is to detect areas where
geodesic distance’s paths are crossing together, like
wave occlusion. Since we generate a cut graph, we
define such areas as a set of edges.
First, we detect an edge e
i
whose intervals I
e
i
sat-
isfy the condition: if there is an interval that f
p
is not
same as other intervals then we consider e
i
∈
˜
E. From
figure 6(a), we can see clearly that e
a
has two inter-
vals i
e
a,1
and i
e
a,2
, where first one has a pseudo-source
AHomotopySurfaceCuttingusingPathsCrossinginGeodesicDistance
133
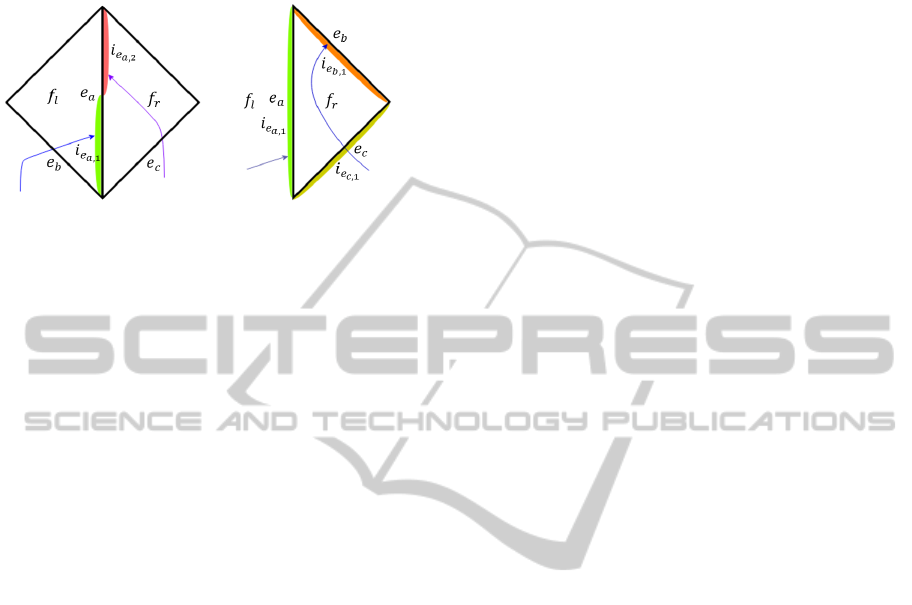
from f
l
while second one has another pseudo-source
from f
r
. Typically, this kind of edges can be found a
few in mesh (green edges in figure 7(a)).
(a) from both sides type (b) non-propagation type
Figure 6: Two types of edges that are considered as area of
crossing geodesic distance’s path.
5.2 Non-propagation Edge Intervals
Along with the edge type described in section 5.1, we
need to define another edge type in cut graph. That
is, this type of edges are nearby crossing of geodesic
distance’s paths.
We detect an edge e
i
whose intervals I
e
i
satisfy
the condition: all intervals have pseudo-sources from
same face f
p
(pseudo-source edge e
p
can be differ-
ent). Let opposite face be f
¯p
and other two adjacent
edges of f
¯p
be e
¯
i
1
and e
¯
i
2
. We consider both e
¯
i
1
and
e
¯
i
2
edges by the following conditions.
• Edge intervals have pseudo-sources from both
sides (section 5.1).
• Edge intervals have e
p
6= e
i
.
If both e
¯
i
1
and e
¯
i
2
match one of above conditions,
then we consider e
i
∈
˜
E.
Considering an edge e
a
in figure 6(b), we can
clearly see that edges e
b
and e
c
of opposite face f
r
(e
¯
i
1
and e
¯
i
2
) have all intervals where their pseudo-sources
are not on e
a
, so we include e
a
into
˜
E. Vise-versa,
when we are considering edge e
c
; we can clearly see
that edge e
b
has an interval where its pseudo-source
is on e
c
so we exclude e
c
from
˜
E.
Typically, this kind of edges can be found a lot in
mesh and cover all areas of mesh (blue edges in fig-
ure 7(a)). Therefore, we need to eliminate unneces-
sary edges in
˜
E. Present state of cut graph looks sim-
ilar to dangling edges in original one so we run the
same iterative process to remove the valance-1 ver-
tices in the graph.
5.3 Ensure for Non-separating Cycles
After detecting the edges in
˜
E whose geodesic dis-
tance’s paths are crossing, we aim to create a ho-
motopy cut graph which requires non-separating and
non-contractible cycles from
˜
E.
At this stage,
˜
E may typically contains separating
or contractible cycles (see figure 7(b)). For separating
cycles issue, we define all edges in
ˆ
E to be neighbors
of each edge in
˜
E. We consider that a set of edges
ρ ≡ (
˜
E ∪
ˆ
E) contains 2g loops inside it.
5.4 Prioritize Removing-edge Queues
After making sure that ρ contains 2g loops, we try to
create a valid cut graph along them. From this condi-
tion, we must eliminate edges that cause contractible
cycles from ρ and maintain non-separating property.
Also, there are non-considered edges
´
E ≡ (E − ρ)
which will be excluded from the cut graph.
One advantage of the original method is to guar-
antee a valid cut graph when the propagation finished.
Because of that, we used the original propagation
scheme. However, we also want the cut graph to be
around
˜
E as first priority and around
ˆ
E as second pri-
ority. Therefore, we altered the orders of removing
edge in the original propagation scheme. We created
three removing-edge queues rather than single queue
in the original one. Each queue contains edges based
on:
´
E,
ˆ
E and
˜
E. And we mark each of them for low-
to-high priority in the order of
´
E,
ˆ
E and
˜
E.
First, we remove faces around v
s
as seed triangles.
Next, we iteratively analyze edges (adjacent only one
triangle) in a non-empty queue under the conditions
that the edge and its adjacent face on low priority
queue are removed first and the edge with shortest
geodesic distance in the queue will be removed first.
After the propagation terminates and all queues
become empty, the remaining edges contain 2g loops
with non-separating and non-contractible properties.
Again, we might shorten each loop for better quality
in some further applications. At last, we generate a
cut graph that enables to convert the mesh with genus
g into topological disk patch.
6 EXPERIMENTAL RESULTS
We tested the algorithms on a workstation PC (Intel
Xeon
TM
10 cores running at 2.50GHz) by using pa-
rameterization results from both original (Gu et al.,
2002) and our approach methods. We also recorded
time consumed for generating cut graphs. We man-
ually selected a vertex in the input mesh as v
s
then
generated a cut graph. To create cut graphs from both
methods with similar conditions, we want the both
propagations to be spread out from a same location.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
134
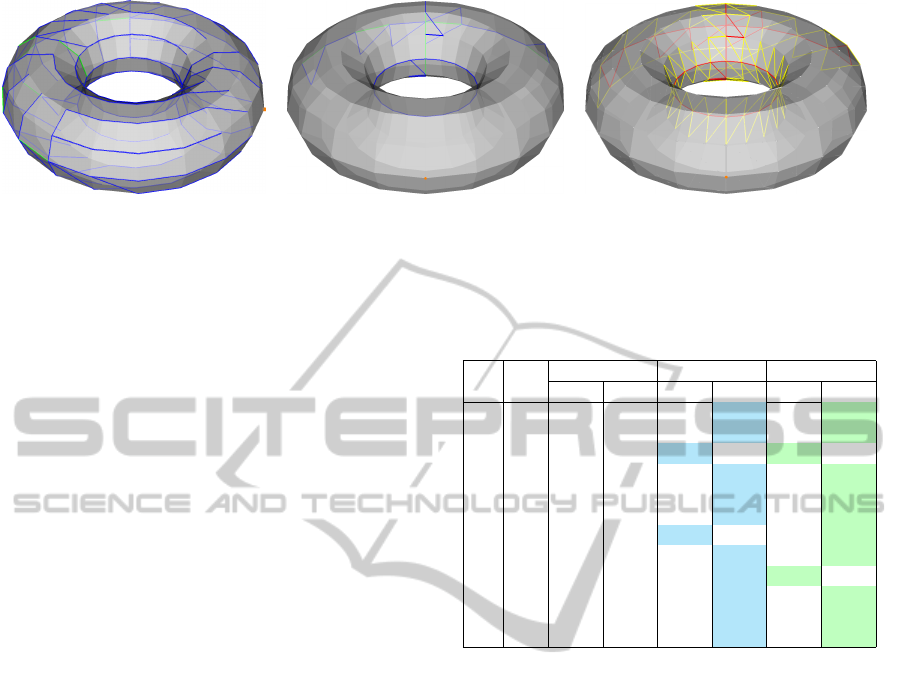
(a) (b) (c)
Figure 7: Processes to define
˜
E and
ˆ
E on a torus model. (a) shows green colored edges that their intervals’ pseudo-sources are
from both sides, and blue colored edges that their intervals have not propagated. (b) shows the graph after removing dangling
edges. (c) shows
˜
E in red color and
ˆ
E in yellow color.
Although the original algorithm removes single seed
triangle, our approach removes seed triangles around
v
s
. Therefore, we altered how to remove a seed trian-
gle in original one to be same as our approach. With
this alternation, it should not affect to overall perfor-
mance in original one. Also, we applied shorten loops
process after the propagation terminated.
After converting the input mesh into disk topo-
logical patch, we applied stretch-minimizing param-
eterization by (Yoshizawa et al., 2004). We evalu-
ated the parameterization results from both methods
by using L
2
error (the root-mean-square stretch over
all direction in planar domain) proposed by (Sander
et al., 2001; Sander et al., 2002). See more details in
appendix.
After evaluating several meshes whose genuses
are greater than or equal 1 (g ≥ 1), we noticed that
original method and our approach can generate very
similar or same cut graphs on asymmetry lookalike
meshes in most cases. However, on some symmetri-
cal shapes, cut graphs can be different from each oth-
ers. Therefore, we selected some results which have
noticeable difference on cut graphs between original
and our approaches, and do parameterizations.
As shown in table 1, our approach can deliver
lower L
2
error than the original one in most cases.
There are some cases that the original one has a large
error value while our approach can deliver a small er-
ror. Although, our approach might double calcula-
tion time but it can deliver results very fast even on
high-details meshes. Also, we did the experiment us-
ing single-thread runtime which can be speeded up by
parallel computation when defining edges
˜
E.
We show some visual results obtained from our
experiments in figure 8. Note that all meshes do not
contain any holes and case 02-03, 04-05, 06-07 and
08-09 are same models with different v
s
location.
Table 1: Experimental results. Blue and green cells indicate
lower errors in comparison.
case genus
time (sec) square circular
original our original our original our
01 1 0.006 0.009 1.351 1.335 1.493 1.446
02 1 0.014 0.030 1.492 1.468 1.687 1.663
03 1 0.014 0.029 1.562 1.636 1.800 2.102
04 1 0.040 0.106 1.551 1.417 2.011 1.635
05 1 0.040 0.106 1.561 1.362 1.924 1.538
06 2 0.028 0.051 1.667 1.466 2.246 1.701
07 2 0.028 0.052 1.390 1.442 1.603 1.554
08 3 0.489 1.217 1.457 1.452 1.688 1.679
09 3 0.527 1.228 2.041 2.025 9.279 9.827
10 3 0.263 0.574 471.2 1.509 4.068 1.978
11 3 0.497 1.163 939.2 1.625 6.348 4.115
12 3 0.110 0.142 221.3K 79.9K 383.2K 203.4K
7 CONCLUSIONS
We presented an enhancement method to generate a
cut graph in high-genus surface for homotopy cutting.
Cut graph is generated based on an exact geodesic dis-
tance theory, by detecting areas where geodesic dis-
tance’s paths are crossing together. We showed how
to detect these areas into a set of edges by analyz-
ing edges’ intervals. Then, we also showed how to
ensure non-separating and non-contractible cycles by
including neighbor edges into the set and applying
original approach with minor adjustments in propa-
gation queues. We can generate equally or more suit-
able edge-graph than the original method while keep-
ing similar performance and stability as original one.
An open topic of this propagation scheme is, it
still requires manual starting location of propagation
(seed triangle or v
s
in our approach). The quality of
cut graph depends on user specific positions. To gen-
erate an optimal cut graph on a high genus surface,
it is better to have shortest cut loop where it passes
through on each surface’s tunnel. Therefore, it is in-
teresting to consider how to define starting location v
s
for generating optimal cut graph.
AHomotopySurfaceCuttingusingPathsCrossinginGeodesicDistance
135

ACKNOWLEDGEMENTS
The images in figures 2 are from (Gu et al., 2002) pa-
per and presentation file. Models are courtesy of the
AIM@SHAPE repository. Special thanks are given
to Danil Kirsanov for exact geodesic distance code,
to Shin Yoshizawa for parameterization code and to
the anonymous reviewers for comments and sugges-
tions. This study is supported by JSPS KAKENHI
(Grant Number 24300035).
REFERENCES
Bennis, C., V
´
ezien, J.-M., and Igl
´
esias, G. (1991). Piece-
wise surface flattening for non-distorted texture map-
ping. SIGGRAPH Comput. Graph., 25(4):237–246.
Cohen, J., Olano, M., and Manocha, D. (1998).
Appearance-preserving simplification. In Proceedings
of the 25th Annual Conference on Computer Graphics
and Interactive Techniques, SIGGRAPH ’98, pages
115–122, New York, NY, USA. ACM.
Dey, T. K. (1994). A new technique to compute polygo-
nal schema for 2-manifolds with application to null-
homotopy detection. In Proceedings of the Tenth An-
nual Symposium on Computational Geometry, SCG
’94, pages 277–284, New York, NY, USA. ACM.
Dey, T. K., Fan, F., and Wang, Y. (2013). An efficient com-
putation of handle and tunnel loops via reeb graphs.
ACM Trans. Graph., 32(4):32:1–32:10.
Dey, T. K., Li, K., Sun, J., and Cohen-Steiner, D. (2008).
Computing geometry-aware handle and tunnel loops
in 3d models. ACM Trans. Graph., 27(3):45:1–45:9.
Dijkstra, E. W. (1959). A note on two problems in con-
nexion with graphs. NUMERISCHE MATHEMATIK,
1(1):269–271.
Erickson, J. and Har-Peled, S. (2002). Optimally cutting a
surface into a disk. In Proceedings of the eighteenth
annual symposium on Computational geometry, SCG
’02, pages 244–253, New York, NY, USA. ACM.
Erickson, J. and Whittlesey, K. (2005). Greedy optimal
homotopy and homology generators. In Proceedings
of the Sixteenth Annual ACM-SIAM Symposium on
Discrete Algorithms, SODA ’05, pages 1038–1046,
Philadelphia, PA, USA. Society for Industrial and Ap-
plied Mathematics.
Floater, M. S. (1997). Parametrization and smooth ap-
proximation of surface triangulations. Comput. Aided
Geom. Des., 14:231–250.
Gu, X., Gortler, S. J., and Hoppe, H. (2002). Geometry
images. ACM Trans. Graph., 21(3):355–361.
Hormann, K. and Greiner, G. (2000). Quadrilateral remesh-
ing. In Proceedings of Vision, Modeling and Vizual-
ization, 2000, pages 153–162.
Jin, M., Ding, N., and Yang, Y. (2013). Computing short-
est homotopic cycles on polyhedral surfaces with hy-
perbolic uniformization metric. Comput. Aided Des.,
45(2):113–123.
Kutz, M. (2006). Computing shortest non-trivial cycles on
orientable surfaces of bounded genus in almost lin-
ear time. In Proceedings of the Twenty-second An-
nual Symposium on Computational Geometry, SCG
’06, pages 430–438, New York, NY, USA. ACM.
Mitchell, J. S. B., Mount, D. M., and Papadimitriou, C. H.
(1987). The discrete geodesic problem. SIAM J. Com-
put., 16(4):647–668.
Patan
`
e, G., Spagnuolo, M., and Falcidieno, B. (2007). Fam-
ilies of cut-graphs for bordered meshes with arbitrary
genus. Graph. Models, 69(2):119–138.
Sander, P. V., Gortler, S. J., Snyder, J., and Hoppe,
H. (2002). Signal-specialized parametrization. In
Proceedings of the 13th Eurographics Workshop on
Rendering, EGRW ’02, pages 87–98, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
Sander, P. V., Snyder, J., Gortler, S. J., and Hoppe, H.
(2001). Texture mapping progressive meshes. In Pro-
ceedings of the 28th Annual Conference on Computer
Graphics and Interactive Techniques, SIGGRAPH
’01, pages 409–416, New York, NY, USA. ACM.
Surazhsky, V., Surazhsky, T., Kirsanov, D., Gortler, S. J.,
and Hoppe, H. (2005). Fast exact and approximate
geodesics on meshes. ACM Trans. Graph., 24(3):553–
560.
Tutte, W. T. (1963). How to draw a graph. Proceedings of
The London Mathematical Society, s3-13:743–767.
Yoshizawa, S., Belyaev, A., and Seidel, H.-P. (2004). A
fast and simple stretch-minimizing mesh parameteri-
zation. In SMI ’04: Proceedings of the Shape Model-
ing International 2004, pages 200–208, Washington,
DC, USA. IEEE Computer Society.
APPENDIX
Given a triangle T with 2D planar coordinates
p
1
, p
2
, p
3
where p
i
= (s
i
,t
i
) and corresponding 3D co-
ordinates q
1
,q
2
,q
3
. Since the mapping is affine, its
partial derivatives are constant over s and t directions
and given by:
S
s
= ∂S/∂s = (q
1
(t
2
−t
3
) + q
2
(t
3
−t
1
) + q
3
(t
1
−t
2
))/2A
P
S
t
= ∂S/∂t = (q
1
(t
2
−t
3
) + q
2
(t
3
−t
1
) + q
3
(t
1
−t
2
))/2A
P
where A
P
denotes area of triangle (p
1
, p
2
, p
3
) in pla-
nar domain.
Let denote Γ(T) and γ(T ) are maximum and min-
imum lengths eigenvalues of Jacobian [S
s
,S
t
], repre-
sent the largest and smallest length obtained when
mapping unit vectors from planar domain to the sur-
face. The local stretch norms over a triangle T is
given by:
L
2
(T ) =
q
(Γ
2
+ γ
2
)/2 =
q
(S
2
s
+ S
2
t
)/2
We define norms over the entire mesh M = {T
i
}:
L
2
(M ) =
s
∑
T
i
∈M
(L
2
(T
i
)
2
A
T
i
)/
∑
T
i
∈M
A
T
i
where A
T
i
denotes area of triangle T
i
in 3D domain.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
136
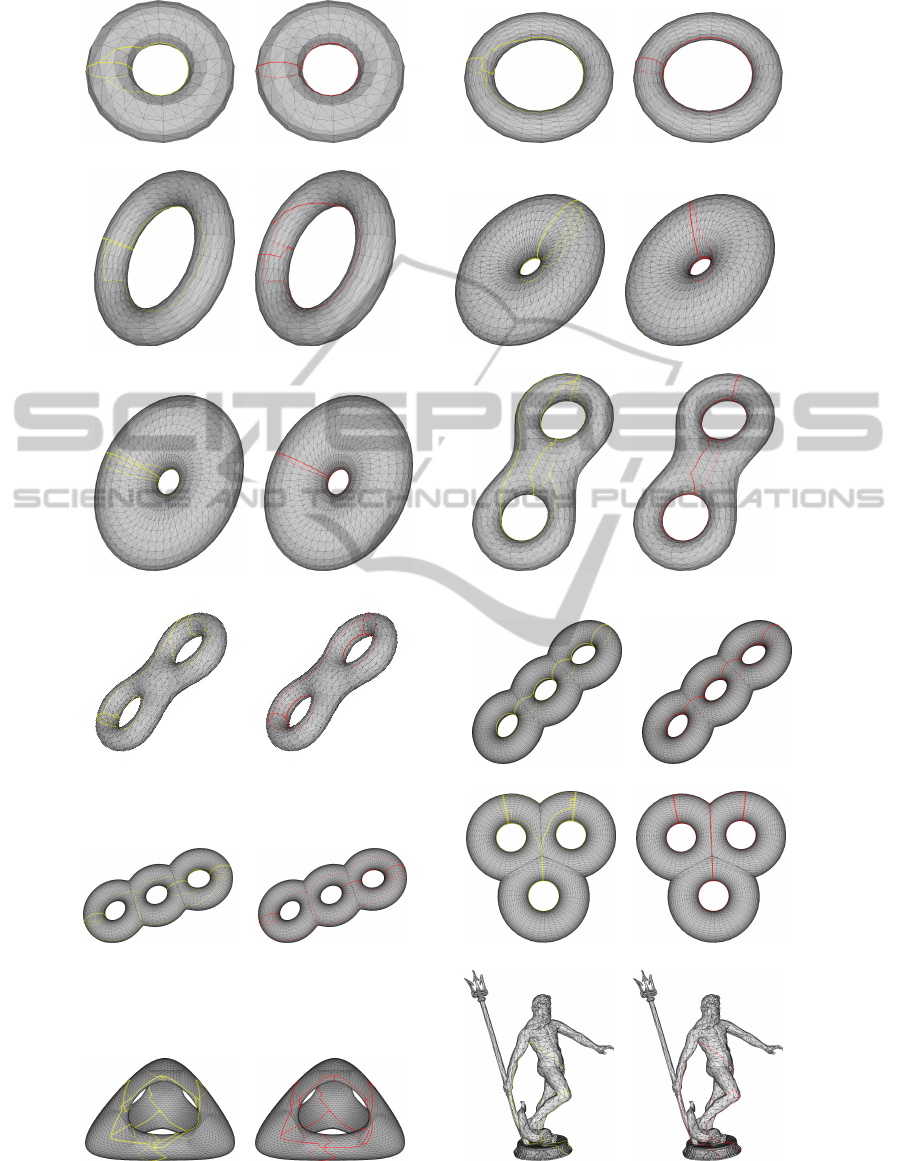
(a) case 01 (vertices 200, faces 400) (b) case 02 (vertices 500, faces 1000)
(c) case 03 (vertices 500, faces 1000) (d) case 04 (vertices 1152, faces 2304)
(e) case 05 (vertices 1152, faces 2304) (f) case 06 (vertices 766, faces 1536)
(g) case 07 (vertices 766, faces 1536) (h) case 08 (vertices 6568, faces 13144)
(i) case 09 (vertices 6568, faces 13144) (j) case 10 (vertices 4192, faces 8392)
(k) case 11 (vertices 6652, faces 13312) (l) case 12 (vertices 2496, faces 5000)
Figure 8: Results of homotopy cutting from original (Gu et al., 2002) and our approach methods. The meshes having yellow
line are results obtained by original approach. The meshes having red line are our results.
AHomotopySurfaceCuttingusingPathsCrossinginGeodesicDistance
137
