
Second Degree of Freedom of Elastic Objects
Adjustable Poisson’s Ratio for Mass Spring Models
Maciej Kot and Hiroshi Nagahashi
Imaging Science and Engineering Laboratory, Information Processing Department,
Tokyo Institute of Technology, Tokyo, Japan
Keywords:
Mass Spring Models, Deformable Objects.
Abstract:
In this paper, we show how to construct mass spring models for the representation of homogeneous isotropic
elastic materials with adjustable Poisson’s ratio. Classical formulation of elasticity on mass spring models
leads to the result, that while materials with any value of Young’s modulus can be modeled reliably, only
fixed value of Poisson’s ratio is possible. We show how to extend the conventional model to overcome this
limitation.
1 INTRODUCTION
Computer graphics community has been using mass
spring models (MSMs) for the representation of de-
formable objects since the earliest attempts to accom-
modate elastic solids in computer generated anima-
tions. While MSMs were popular because of their
low implantation complexity, the link between their
physical properties and spring-network parameters
has never been properly established. This led to be-
lief that MSMs cannot represent elastic objects accu-
rately and that the models do not converge to certain
solutions upon mesh refinement (Van Gelder, 1998;
Nealen et al., 2006). Consequently more physically
accurate techniques such as finite element method
(FEM) gained popularity.
The accuracy of the description of an elastic object
is, however, not a problem in MSM representations.
The standard lattice based models used in physics,
mechanical engineering and other related fields of-
fer a description of elastic solids, which is as accu-
rate as the limitations of linear elasticity theory allow
it to be (Ladd and Kinney, 1997; Ostoja-Starzewski,
2002; Kot et al., 2014). There is however a limitation
to what can be modeled with MSMs. The classical
models allow to obtain any value of Young’s modu-
lus E, however Poisson’s ratio ν is limited to 1/4 for
volumetric objects and 1/3 for 2D meshes. This al-
lows to freely adjust the stiffness of an object, but is
not sufficient to replicate all types of materials. In this
work we show how to efficiently extend conventional
MSM to overcomethis limitation and obtain a reliable
model of any homogeneous isotropic solid.
2 MASS SPRING MODELS
If we consider a homogeneous isotropic solid, its
elastic properties are defined by exactly two param-
eters (elastic moduli). Classically Young’s modulus
E and Poisson’s ratio ν are the popular pair. The
Young’s modulus is the ratio of stress to strain mea-
sured along the same axis under an uniaxial stress
condition, that is, it gives the resistance to directional
stretching/compression. The Poisson’s ratio is the ra-
tio of transverse to axial strain (denotes to what de-
gree material expands in one direction when com-
pressed in another). Depending on the application,
besides E and ν, other moduli are often used such as
bulk modulus K, or Lam´e parameters λ and µ. In any
description only two of them are independentand pro-
viding a link between spring-network parameters, and
a chosen pair of the elastic moduli is sufficient to de-
scribe elastic properties of the MSM.
In case of 2D MSM, an isotropic homogeneous
structure can be obtained with hexagonal lattice
(Fig. 1) (Ostoja-Starzewski, 2002). All the springs
have the same spring coefficient k and the relation be-
tween the spring coefficient and the Lam´e constants
for a such network are given by
λ = µ =
3
4
√
3
k, (1)
from which it follows that E =
2
√
3
k and ν =
1
3
.
Springs are assumed to be of a unit length.
Similarly a volumetric isotropic solid can be con-
structed with cubic lattice MSM (Ladd and Kinney,
138
Kot M. and Nagahashi H..
Second Degree of Freedom of Elastic Objects - Adjustable Poisson’s Ratio for Mass Spring Models.
DOI: 10.5220/0005303601380142
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 138-142
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

k
k
k
k
k
k
k
Figure 1: Hexagonal lattice.
C B C
B A B
C B C
B A B
A A
B A B
C B C
B A B
C B C
Figure 2: Cubic lattice. The nearest neighbors of a node are
classified in three groups A, B and C. They correspond to
the potential connections along cube edges, face diagonals
and cube diagonals.
1997). The spring connections are present between
nearest neighbors (A) and second nearest neigh-
bors (B) (Fig. 2) and all have the same spring co-
efficient k. The elastic moduli for such network are
given by
E = 2.5
k
a
ν = 1/4, (2)
where a is the length of an edge of an elemental
cube.
The models discussed above have a limitation on
the value of Poisson’s ratio, which comes from a well-
established result of the continuum mechanics. If
the constituents of a material interact with the cen-
tral forces dependent upon distance alone the Pois-
son’s ratio of a homogeneous and isotropic material is
identically 1/4 (or 1/3 for a 2D system) (Love, 1906;
Lakes, 1991). Other values of the Poisson’s ratio can
be obtained by incorporating non-central forces into
the model, e.g. the angular terms, or forces that do not
depend on distance alone or by introducinganisotropy
(Lakes, 1991).
β
k
Figure 3: Hexagonal lattice with normal as well as angular
springs.
An example of such extension is the Kirkwood
model of an isotropic 2D material (Ostoja-Starzewski,
2002). It is based on a hexagonal lattice and intro-
duces additional angular springs, which provide a re-
sisting force when an angle between two coinciding
springs changes from its neutral value of 60
◦
(Fig. 3).
The Poisson’s ratio is given by
ν
2D
=
1−
3β
2ka
2
.
3+
3β
2ka
2
, (3)
where a is a length of an edge of a triangle, k is a
spring stiffness coefficient of regular springs and β of
angular ones.
Similar modifications are possible in case of 3D
materials and the problem of constructing MSM-like
models capable of representing isotropic materials
with arbitrary values of Poisson’s ratio have been ex-
plored before by a number of researchers (Baudet
et al., 2007; Lakes, 1991; Zhao et al., 2011). An
overview of well established techniques can be found
in (Sahimi, 2003). Typically additional degrees of
freedom are added to the model by incorporating
beams, angular springs and other custom three or
four node connections which react not only to stretch-
ing, but shearing or applying toque as well. Intro-
ducing such elements allows to obtain wide range of
materials, however as volumetric objects are inher-
ently more complex than two dimensional structures,
the description of their properties tends to be more
complex as well. Analytical solutions are in most
cases too difficult to derive and obtaining desirable
properties of such models often involves a numerical
minimization and parameter fitting, which tunes the
model to the particular problem at hand. This fact,
together with increased computational and memory
costs, makes such models less suitable for practical
applications.
In contrast in this work we will explore an ap-
SecondDegreeofFreedomofElasticObjects-AdjustablePoisson'sRatioforMassSpringModels
139
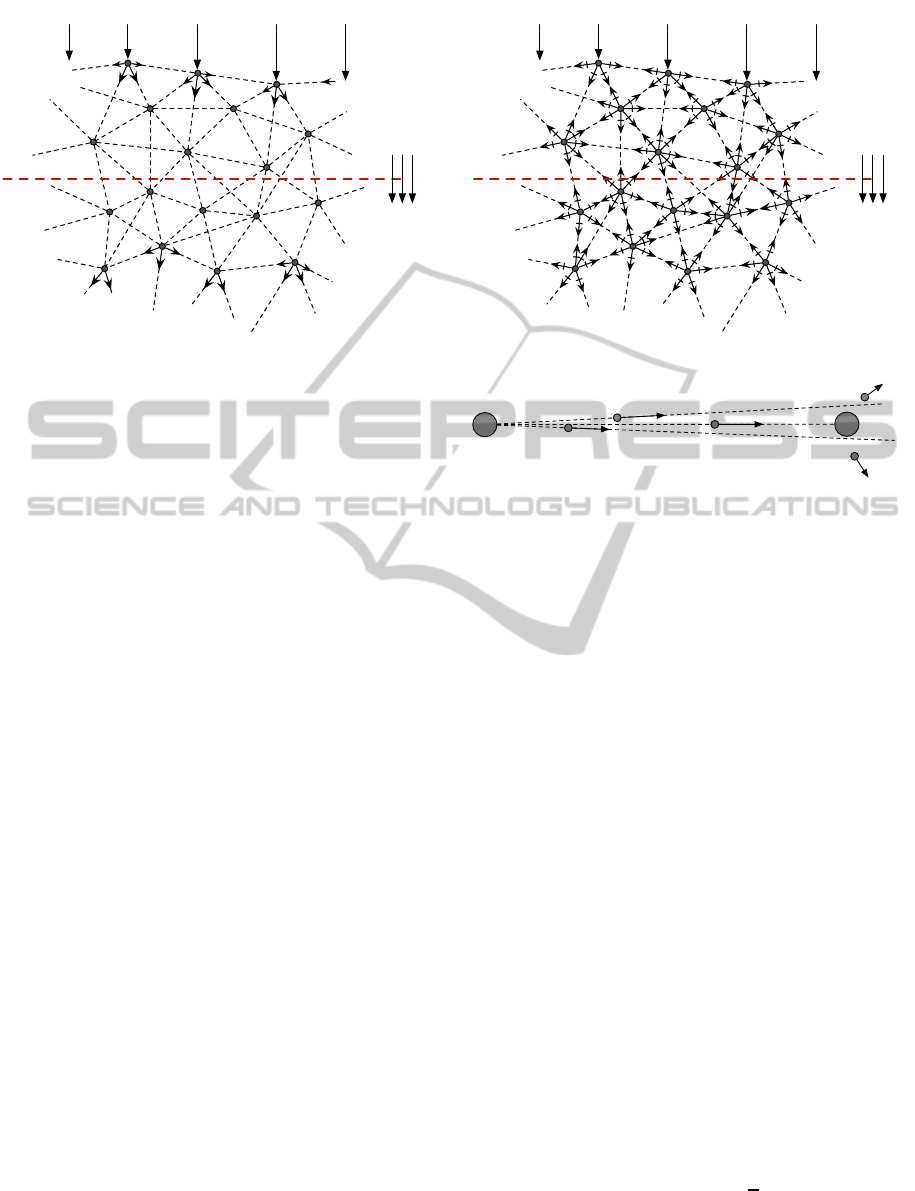
F
Figure 4: Momentum flow through a simple MSM.
proach of constructing MSM which allows to achieve
arbitrary values of ν, without introducing additional
structures into the model. Our approach will in fact
make use only of nodes and their relative pairwise dis-
tances.
3 EXTENDED MASS SPRING
MODELS
Simple MSMs described in Section 2 can be viewed
as a network in the Fig. 4. Forces in such networks
act along straight lines between particles, and as we
know, this leads to ν = 1/4, which may be considered
a geometric property of the space (the way distance
to neighboring nodes changes, when we change the
position of a node).
We generalize this model by introducing addi-
tional phenomenon. When two nodes approach, they
start repelling each other as usual, and additionally
each of them starts radiating momentum in ”random”
directions.
To visualize how we can justify such behavior,
let us consider a particle-carrier interaction model in
which we assume, that constituents of the matter (par-
ticles) interact with each other by means of exchang-
ing carriers (which in turn can be considered a small
particles). Carriers interact with particles (and with
each other) by means of central forces (elastic colli-
sions), therefore this model still uses central forces
as most basic means of interaction. Carriers how-
ever have a finite velocity so the transfer of momen-
tum does not happen instantaneously; the big particles
move as well. Having this in mind, we may assume
that a carrier shot form one particle, may not hit the
other particle with a sniper’s precision. In such case
it will disperse in a ”random” direction and will not
F
Figure 5: Dispersive momentum flow.
Figure 6: Momentum dispersion.
come back to the first particle (Fig. 6). If a particle
is bombarded from all directions uniformly, the dis-
persed carriers will also appear to be radiating from
the particle uniformly (even if the actual distribution
of dispersion angles is not trivial).
Figure 5 illustrates the dissipative part of the inter-
action, where each node absorbs the incoming carri-
ers and radiates them uniformly in all directions. Such
network will behave like a gas or fluid with no viscos-
ity.
We will model this phenomenon using MSMs in
the following way. When two nodes approach each
other causing increase of momentum flow between
them, only a fraction of the flow will participate in
the direct exchange of momentum between these two
nodes and appear as a regular force of the spring
F
µ
= −κ
µ
∆L. The rest of the flow will be distributed
uniformly to all springs connected to a node (scaled
to the length of a spring), causing dissipation of mo-
mentum F
∗
= −qκ
µ
∆L. Parameter q denotes the ratio
between dissipative momentum flow, and the direct
one.
Material modeled in such way is now character-
ized by two parameters – µ gives the strength of direct
interactions, and q[µ] of the dispersive ones.
The standard expression for a stress in an elastic
body
σ
ij
= Kδ
ij
ε
kk
+ 2µ(ε
ij
−
1
3
δ
ij
ε
kk
), (4)
can be rewritten, by treating our material as a su-
perposition of Cauchy’s isotropic structure, in which
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
140

λ = µ with a fluid in which σ
ij
= Bε
kk
δ
ij
, where Bε
kk
corresponds to pressure.
σ
ij
= µδ
ij
ε
kk
+ 2µε
ij
+ Bδ
ij
ε
kk
, B = λ−µ (5)
σ
ij
=
5
3
µδ
ij
ε
kk
+ 2µ(ε
ij
−
1
3
δ
ij
ε
kk
) + Bδ
ij
ε
kk
(6)
The direct interactions will correspond to µ pa-
rameter, dispersive ones to B. Both can be controlled,
which allows to achieve other values of Poisson’s ra-
tio:
ν =
B+ µ
2(B+ 2µ)
, (7)
ν =
1+
5
3
Q
2(2+
5
3
Q)
, Q =
B
5
3
µ
, (8)
where in a perfect structure Q = 2q, and it denotes
the ratio between dispersed and not dispersed carriers.
The multiplication by the factor of 2 is introduced for
convenience (one spring connects two nodes).
4 TESTS
We have applied our technique to Ladd’s cubic lat-
tice models and verified that we are able to obtain any
value of Poisson’s ratio with their use.
In order to estimate numerically the values of E
and ν in an MSM, the following numerical experi-
ment has been performed: a block of an elastic mate-
rial was compressed by applying static displacement
to its opposite ends along x direction, and the resulting
deformation was measured both for random and cubic
MSMs. The Young’s modulus and Poisson’s ratio are
related to the elastic response of such a system by
E =
F/A
∆x/L
x
ν =
∆y
∆x
where F is the reaction force, A the cross-sectional
area of the block (in YZ plane), and ∆x and ∆y are
the deformations of the block along x and y direc-
tions respectively. The initial block dimensions were
70a
0
×15a
0
×15a
0
(where a
0
is an arbitrary unit of
length) and the base spring constant has been set to k
0
.
The static displacement in x direction was imposed on
all the nodes on the boundary of the block.
The results are presented in Fig. 7 and they con-
firm that any value of Poisson’s ratio can be achieved
with a very high accuracy. Figure 8 shows visual ex-
amples of a few chosen materials with different ν. Al-
though the presented shapes are very simple, the tests
-1.2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
-1 -0.5 0 0.5 1 1.5 2 2.5 3
Poisson’s ratio
q
Figure 7: Poisson’s ratio in Cubic lattice MSM. Red curve
represents a theoretical prediction. Blue points are the re-
sults of measurements.
show that our extended MSM is capable of modeling
bulk materials accurately. Given sufficiently high res-
olution any complex shape can be modeled reliably.
5 CONCLUSIONS
In this article we showed an approach of construct-
ing MSM which allows to achieve arbitrary values
of ν, without introducing additional structures into
the MSM. We demonstrated that by incorporating the
concept of momentum dispersion additional degree of
freedom can be added to the classical MSM, allowing
it to freely represent homogeneous isotropic materials
characterized by two different constants (in contrast
to one constant description given by classical MSM).
Because our method does not introduce additional el-
ements to the MSM itself, the memory costs remain
unchanged and the computational costs rise by much
lower degree when compared with methods which do
introduce additional elements to the MSM.
This makes our method useful for real time ap-
plications involving deformable elastic objects of any
kind (e.g. in computer games), and especially attrac-
tive for simulating fracture or crack propagation(peri-
dynamics) – the application for which MSMs are gen-
erally considered to be better suited than FEM based
approaches, but suffer from the fact that they cannot
represent all types of materials.
The simplest implementation of our model, when
used with explicit time integrator, requires additional
iteration through all the springs in the system, effec-
tively doubling the computational time when com-
pared to the simple MSM. Some improvements are
however possible; for instance the value of momen-
tum dispersed on the nodes in the ’previous’ frame
could be used to approximate the value in the current
frame, which eliminates the need of additional itera-
tion through the springs, but may influence the stabil-
ity of the simulation. However, in case of quasi-static
SecondDegreeofFreedomofElasticObjects-AdjustablePoisson'sRatioforMassSpringModels
141

Figure 8: A block of material with dimensions 2×3 ×2 compressed in y direction to 75% of its natural length. Different
values of Poisson’s ratio, from the left: -1, 0, 0.25, 0.47.
simulation (such as point based integration techniques
(Bender et al., 2013)), it should not affect the stability.
Additionally the accuracy of our models is ex-
pected to be higher than that of techniques involving
parameter fitting and the analytical description of our
model is provided. This makes our MSM an attractive
starting point for developing more advanced models
(e.g. for anisotropic materials). In our model we have
assumed that the dispersion of the force happens uni-
formly in all directions. In MSMs it will translate into
equal redistribution of the incoming force to all the
springs connected with a node (scaled by the length).
Because redistribution is isotropic, so will be the elas-
tic properties of the material. However by introduc-
ing non uniform dispersion mechanisms it should be
possible to achieve non isotropic behaviors without
extensive modifications of the current model. Such
modifications may be a good direction for the future
work, as they would allow to efficiently model or-
ganic tissues e.g. for surgical simulations, the applica-
tion for which MSMs are still actively used, but once
again suffer from the lack of a mathematical model
that would allow to express their elastic properties.
ACKNOWLEDGEMENTS
Authors acknowledge the support of JSPS KAKENHI
(Grant Number 24300035).
REFERENCES
Baudet, V., Beuve, M., Jaillet, F., Shariat, B., and
Zara, F. (2007). Integrating Tensile Parameters in
3D Mass-Spring System. Technical Report RR-
LIRIS-2007-004, LIRIS UMR 5205 CNRS/INSA de
Lyon/Universit´e Claude Bernard Lyon 1/Universit´e
Lumi´ere Lyon 2/
´
Ecole Centrale de Lyon.
Bender, J., M¨uller, M., Otaduy, M. A., and Teschner, M.
(2013). Position-based methods for the simulation of
solid objects in computer graphics. In EUROGRAPH-
ICS 2013 State of the Art Reports. Eurographics As-
sociation.
Kot, M., Nagahashi, H., and Szymczak, P. (2014). Elas-
tic moduli of simple mass spring models. The Visual
Computer.
Ladd, A. J. C. and Kinney, J. H. (1997). Elastic constants
of cellular structures. Physica A: Statistical and The-
oretical Physics, 240(1-2):349–360.
Lakes, R. S. (1991). Deformation mechanisms in negative
Poisson’s ratio materials: structural aspects. Journal
of Materials Science, 26:2287–2292.
Love, A. E. H. (1906). A treatise on the mathematical the-
ory of elasticity. Cambridge University Press.
Nealen, A., M¨uller, M., Keiser, R., Boxerman, E., Carl-
son, M., and Ageia, N. (2006). Physically based
deformable models in computer graphics. Comput.
Graph. Forum, 25(4):809–836.
Ostoja-Starzewski, M. (2002). Lattice models in microme-
chanics. Applied Mechanics Reviews, 55(1):35–60.
Sahimi, M. (2003). Rigidity and Elastic Properties: The
Discrete Approach. Heterogeneous Materials: Linear
Transport and Optical Properties. Interdisciplinary
Applied Mathematics v 1, (Chapter 8). Springer-
Verlag New York.
Van Gelder, A. (1998). Approximate simulation of elastic
membranes by triangulated spring meshes. J. Graph.
Tools, 3(2):21–42.
Zhao, G.-F., Fang, J., and Zhao, J. (2011). A 3d distinct
lattice spring model for elasticity and dynamic fail-
ure. International Journal for Numerical and Analyt-
ical Methods in Geomechanics, 35(8):859–885.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
142
