
Accelerated Ray Tracing using R-Trees
Dirk Feldmann
Department Scene Analysis, Fraunhofer IOSB, Ettlingen, Germany
Keywords:
Ray Tracing, R-Tree, Acceleration, Spatial Index, GPU, CUDA, Stackless Algorithm.
Abstract:
Efficient ray tracing for rendering needs to minimize the number of redundant intersection tests between
rays and geometric primitives. Hence, ray tracers usually employ spatial indexes to organize the scene to be
rendered. The most popular ones for this purpose are currently kd-trees and bounding volume hierarchies,
for they have been found to yield best performances and can be adapted to contemporary GPU architectures.
These adaptations usually come along with costs for additional memory or preprocessing and comprise the
employment of stackless traversal algorithms.
R-trees are height-balanced spatial indexes with a fixed maximum number of children per node and were
designed to reduce access to secondary memory. Although these properties make them compelling for GPU
ray tracing, they have not been used in this context so far.
In this article, we demonstrate how R-trees can accelerate ray tracing and their competitiveness for this task.
Our method is based on two traversal schemes that exploit the regularity of R-trees and forgo preprocessing or
alterations of the data structure, with the first algorithm being moreover stackless. We evaluate our approach
in implementations for CPUs and GPUs and compare its performance to results we obtained by means of
kd-trees.
1 INTRODUCTION
Efficient ray tracing needs to organize the objects of
a scene in such a way that there are as few as possi-
ble redundant intersection tests between rays and the
geometric primitives those objects consist of. This
is usually accomplished by employing spatial indexes
such as kd-trees, octrees, bounding volume hierar-
chies (BVHs) or various types of grids. Among these
data structures, kd-trees and BVHs have received
much attention in recent years, because they can be
implemented on contemporary GPUs in order to har-
ness their parallel computing capabilities.
R-trees (Guttman, 1984) were designed to index
spatial data in large databases and aim for reduc-
ing access to secondary memory. They are height-
balanced trees with arity usually > 2 and are used, for
instance, in modern database management systems,
like MySQL or Oracle Spatial (Oracle Corp., 2014a;
Oracle Corp., 2014b). Their regularity makes R-trees
well-suited for accelerating ray tracing, because it en-
ables efficient stackless traversal schemes without ad-
ditional costs for extra pointers or extensive prepro-
cessing. Furthermore, the accompanying and poten-
tially high memory locality of the contained data ben-
efits the architectures of today’s GPUs, whose perfor-
mances are sensitive to cache misses. But to the best
of our knowledge, R-trees have not yet been used as
acceleration data structures in ray tracing.
In this work we describe how R-trees can be em-
ployed to accelerate ray tracing of static scenes and
demonstrate their suitability for this task by means of
a CPU-based ray tracer and a CUDA-based one. We
present two different algorithms for ray traversal that
exploit the regularity of R-trees: The first one is stack-
less, requires neither additional memory nor pointers
and is superior to a conventional stack-based traversal
scheme. Our second algorithm uses a small amount
of additional memory and improves the performance
of parallel ray tracing on GPUs in certain situations,
compared to our stackless method. We furthermore
compare the performance of our R-tree-based CPU
implementation with results we obtain by means of
kd-trees constructed using the popular surface area
heuristic. The results indicate that R-trees can be
competitive alternatives to kd-trees, but the traversal
of R-trees is additionally more convenient than those
of kd-trees or BVHs.
The remainder of this article is structured as fol-
lows: Section 2 summarizes the most important work
related to ours and gives a description of R-trees, for
these data structures appear to be less well known.
247
Feldmann D..
Accelerated Ray Tracing using R-Trees.
DOI: 10.5220/0005304802470257
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 247-257
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

(a) Bunny (b) Cathedral (c) Fairy (d) Conference
Figure 1: We employed the depicted test scenes and camera poses to evaluate the methods presented throughout this work: (a)
Standford Bunny, 69 632 triangles, (b) Sibenik Cathedral, 75 284 triangles, (c) a frame from the Utah Fairy Forest animation,
173 579 triangles, (d) Conference Room, 331 135 triangles.
In Section 3, we enter on aspects that need consider-
ation in order to use R-trees for accelerating ray trac-
ing. The two different algorithms for determining in-
tersections between rays and the geometric primitives
indexed by R-trees are presented in Section 4. In Sec-
tion 5, we evaluate the performance of our approach
and discuss the results. Additionally, we compare the
performance of our R-tree-based method for CPU ray
tracing to results we obtain when using kd-trees in-
stead. We conclude our work with a discussion and
prospects of future research in Section 6. The test
scenes we employed throughout this work are shown
in Figure 1.
2 BACKGROUND AND RELATED
WORK
By employing appropriate spatial indexes to keep the
number of redundant intersection tests of rays with
objects within a scene as small as possible, ray tracing
implementations on modern GPUs can achieve inter-
active frame rates and beyond for static scenes (Horn
et al., 2007). From the wide field of spatial indexes,
which is covered in detail in (Samet, 2006), popu-
lar choices for organizing scenes have been various
kinds of grids, octrees, kd-trees, general BSP-trees
and bounding volume hierarchies (BVHs) (Suffern,
2007, p. 443). In the context of GPU ray tracing,
many researchers found kd-trees and BVHs to be the
most appropriate spatial indexes, because they yield
good performances (Wächter and Keller, 2006; Stich
et al., 2009) and can be adapted to processor architec-
tures of GPUs (Hachisuka, 2009; Hapala et al., 2011;
Hapala and Havran, 2011). The main difference be-
tween these two data structures is that BVHs partition
scenes with respect to the objects, whereas kd-trees
partition the underlying space.
R-trees (see Section 2.2) are spatial indexes that
share properties with BVHs as well as with kd-trees,
but have unique features of their own: Like BVHs,
R-trees organize objects based on their minimal axis-
aligned bounding boxes, but like in kd-trees, nodes
are split with respect to locations in space determined
by some heuristic (see Section 2.2.1). The resulting
splits, however, are not necessarily strictly binary par-
titions of the underlying space, but rather resemble
divisions in BVHs. In contrast to the latter ones, R-
trees are balanced in height and are designed analo-
gously to B-trees for reducing accesses to secondary
memory by increasing the locality of data in memory.
Furthermore, R-trees can be either constructed incre-
mentally by successive insertion of data or by using
methods for bulk loading all data at once (see (Sellis
et al., 1987; Arge et al., 2008), for instance).
Although the features of R-trees indicate a good
suitability for their application in ray tracing, which
has been pointed out in (Sylvan, 2010), these data
structures apparently have not been further examined
in this context so far. Surprisingly, they are not even
mentioned in recent surveys on ray tracing (Wald
et al., 2007; Hachisuka, 2009) or articles on splitting
BVHs (Stich et al., 2009).
2.1 KD-Trees and BVHs
Kd-trees have been reported to perform particularly
well in ray tracing when being constructed by means
of surface area heuristic (SAH) (MacDonald and
Booth, 1990), but their most severe disadvantage has
been for long time their high construction times. This
limitation has been alleviated by algorithms for more
efficient construction (Wald and Havran, 2006). Al-
though the overall performance of kd-trees is fre-
quently superior to those of BVHs, because kd-trees
adapt better to the complexity of scenes, BVHs are
often preferred due to their simplicity (Wächter and
Keller, 2006; Stich et al., 2009). Other studies in-
dicate that BVHs perform better for tracing coherent
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
248
rays, whereas kd-trees are superior in case of incoher-
ent rays (Zlatuska and Havran, 2010).
When implementing kd-trees or BVHs on GPUs,
it is necessary to account for certain aspects of the
underlying processor architecture: The local memory
available to a GPU thread is significantly less than to
programs running on CPUs. This impairs or even pre-
vents the allocation large amounts of local memory
and thus the employment of traversal algorithms that
rely on stacks or queues, for instance. Hence, vari-
ous methods for stackless kd-tree and BVH traversal
have been developed (Hapala et al., 2011; Hapala and
Havran, 2011), but they require additional processing
steps or extra storage for pointers or traversal states.
Furthermore, the performance of GPU kernels
strongly depends on the locality of data in memory
and the number of cache misses, because the latter
will delay the execution of a large number of threads
at once. Presenting data in a coherent way by means
of cache-friendly data structures and access patterns
is thus an important issue.
More details on the employment of kd-trees and
BVHs in ray tracing can be found in (Wächter and
Keller, 2006),(Hachisuka, 2009) and (Wald et al.,
2007), for example, where the latter article focuses
on ray tracing of dynamic scenes.
2.2 R-Trees
R-trees (Guttman, 1984) are height-balanced spatial
indexes related to B-trees (Bayer and McCreight,
1972). Data are stored based on their n-dimensional
minimal axis-aligned bounding boxes (AABBs),
which serve as keys and are commonly used to
support point-location and window queries (Samet,
2006). Like with B-trees, only the leaf nodes at the
lowest level l = 0 hold actual data. The entries of in-
termediate nodes at levels l > 0 point to nodes at the
next lower level l − 1. Except for the root located at
the topmost level L, each node contains at least m > 0
(usually m ≥ 2) and at most M > m entries. The root
may hold less than m entries, especially if the tree is
empty, but cannot contain more than M entries. Each
node maintains an n-dimensional AABB that encloses
the bounding boxes of the entries contained in that
node. The structure of a 2D R-tree is illustrated in
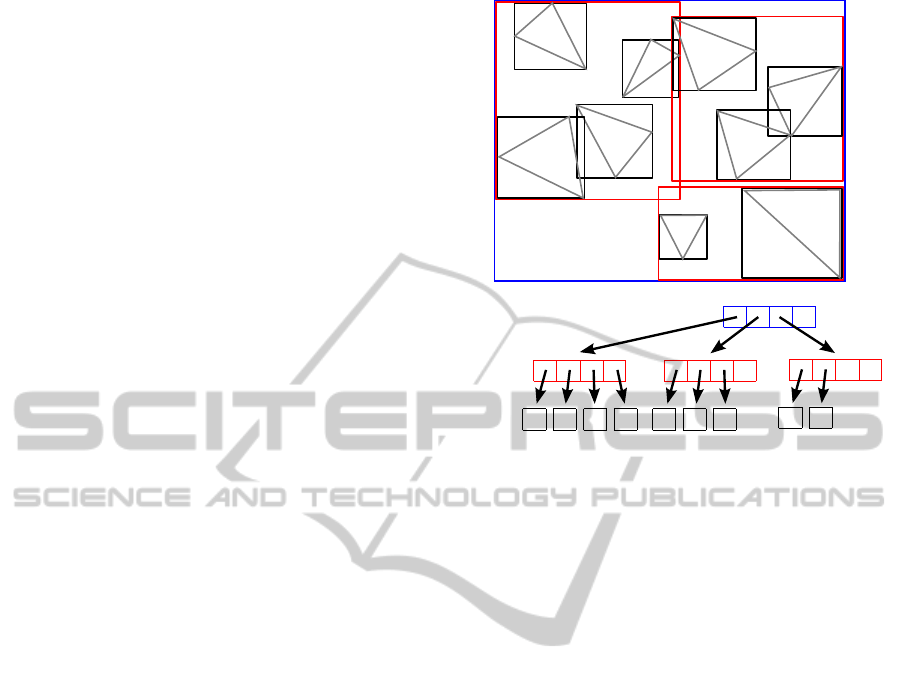
Figure 2.
When data are inserted into an R-tree, leaf nodes
may overflow if they had to contain more than M en-
tries and hence must be split into two. The result-
ing extra leaf is inserted at the original leaf’s parent,
which in turn may overflow as well. This can trigger
cascades of node splits up to the root. If the root has
to be split, the tree grows by adding a new level L + 1
R
4
R
1
A
D
C
G
R
2
E
F
B
R
3
I
H
A C D G
R
1
B E F
R
2
H
I
R
3
R
4
l = 0
l = 1
l = 2
Figure 2: The data (triangles) A – I are stored in the leaf
nodes of a 2D R-tree with m = 2 and M = 4 at level l = 0
based on their AABBs. Entries of nodes at levels l > 0
point to nodes at the next lower level. Each node maintains
an AABB enclosing its entries (rectangles R
1
- R
4
).
and a new root, which receives the former root and its
new sibling become as the only children. Likewise,
if data are removed, nodes may underflow and must
hence be merged in order to satisfy the constraint of
holding at least m entries. Whenever an entry is added
or removed from a node, that node’s AABB must be
adjusted in such a way that it remains the minimal
AABB for all of the node’s entries. Except for the
increased complexity that comes along with splitting
nodes, the proceedings for adding data to or deleting
data from R-trees is the same as with B-trees.
In order to split nodes, there are various strategies
that directly influence the structure of an R-Tree and
thus its performance in subsequent find operations.
These strategies usually try to minimize properties of
the AABBs of the resulting nodes, such as their vol-
ume, mutual overlap or surface, and are employed dif-
ferently or mixed in R-Tree variants.
2.2.1 R-Tree Construction
As illustrated in Figure 2, objects and their AABBs
stored in R-trees may overlap. Hence, the nodes,
which we identify with their maintained AABBs, may
also overlap each other at the same level. This im-
pedes ray traversal, because all paths in the tree start-
ing at locations where nodes overlap may lead to ge-
ometric primitives that may be intersected. In addi-
tion, nodes that include large amounts of dead space,
i.e., space only occupied by AABBs, but not by actual
AcceleratedRayTracingusingR-Trees
249

geometric primitives, must be tested for intersections
with rays, although the contained primitives may not
be intersected at all. Therefore, it is desirable to avoid
such situations by minimizing overlap and dead space
during the construction of R-trees. Since optimizing
for both these parameters at reasonable costs is in-
feasible in non-trivial situations, we have to rely on
heuristics to yield well-structured R-trees.
In the following, we briefly present two existing
approaches on building R-trees by successive inser-
tion of data. At the level of leaf nodes, data are the
geometric primitives to be stored in the R-tree. At the
level of intermediate nodes, data are pointers to nodes
at the next lower level. In any case, data must always
be provided with their associated AABB.
For more details on the construction and split al-
gorithms, we refer to the original articles (Guttman,
1984; Beckmann et al., 1990).
The approach for constructing R-trees
in (Guttman, 1984) is formulated for AABBs in
2D and relies on selecting the node that requires the
least area enlargement when data are inserted. Ties
are resolved by selecting the node of least area. When
nodes need to be split due to overflow, the entries are
distributed in such a way that the total area occupied
by the two resulting nodes (and thus dead space) is
minimized.
The R
∗
-tree (Beckmann et al., 1990), a variant of
the R-tree, uses different strategies for choosing nodes
when inserting data at the levels of intermediate and
leaf nodes. In the former case, entries (i.e., other
nodes) are inserted at the node whose box needs least
area enlargement; ties are resolved by selecting the
node of least area. In case of leaf nodes, data are as-
signed to the node whose box will overlap least with
those of its siblings afterwards; ties are resolved by
using the node that requires least area enlargement.
Node splits in R
∗
-trees are performed by sorting
the entries of a node according to the minimum and
maximum values of their AABBs in each dimension
d. For each of the 2d sorts, a series of partitions into
two sets is constructed: The first i entries in the sort,
where m ≤ i ≤ M +1 −m, are assigned to the first set
of the i-th partition and the remaining M + 1 − i ones
to the second set. Each of these partitions along one
of the d axes represents a possible redistribution of
the entries from the overflowing node into two nodes.
The perimeters of all these candidates are summed up,
and the overflowing node is split along the axis where
the sum is minimal. Once the split axis has been de-
termined, the entries are distributed according to the
associated partition in which the two candidates have
least area overlap.
In addition, the R
∗
-tree extends the original R-
tree by using a technique called forced reinsert: As
a node ν overflows, instead of immediately splitting
it, its entries are sorted with respect to the distances
of their boxes’ centers from the center of ν’s box.
Depending on choice, the k entries with greatest or
least distance are removed (ejected) from ν. Starting
at the tree’s root, the ejected entries are then tried to
be reinserted at their respective levels. As a result,
they may become assigned to different parents at the
level of ν, because these new parents may have be-
come better choices with respect to the tree’s structure
and the criterion for selecting nodes. In this way, the
node occupancy is increased and potentially expen-
sive split operations are delayed. If the ejected entries
cannot be reinserted or if reinsertion would assign all
of them again to their original parent, a split must be
performed anyway.
In more recent work in (Beckmann and Seeger,
2009), the authors present the revised R
∗
-tree (RR
∗
-
tree). This variant employs modified strategies for
splitting and selecting nodes that supersede the need
for forced reinserts.
3 RAY TRACING USING
R-TREES
For the purpose of ray tracing, spatial indexes are
usually traversed to determine the object that is in-
tersected by the ray at least distance from the ori-
gin of that ray. R-trees have similarities to BVHs,
as they hold AABBs at every node, and ray traver-
sal is analog: Starting at the root, the maintained box
is checked for intersection with a given ray. If the
ray intersects the box, each of the n ∈ [m, M] chil-
dren’s boxes is tested for intersection with the ray, and
the process is recursively repeated for each positively
tested child node. In case the ray does not intersect
a box, the entries contained within that node do not
need to be considered any further, since they are not
intersected the ray either. The process terminates as
soon as all candidate objects at level l = 0 have been
tested.
Due to their structure, R-trees have certain proper-
ties that make them particularly interesting for accel-
erating ray tracing: In contrast to common BVHs or
kd-trees, R-trees are always balanced in height, i.e.,
all leaf nodes storing geometric primitives are located
at the same level (depth). Hence, paths from the root
towards leaves have constant lengths. Furthermore,
the number of nodes per level is limited by the value
chosen for M. This regularity allows to traverse R-
trees without maintaining an auxiliary stack and to
keep the memory consumption during traversal con-
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
250
stant, which is of special importance for parallel ray
tracing on GPUs, where the tree is traversed by mul-
tiple rays simultaneously.
3.1 Considerations for Ray Tracing
The equivalents of area and perimeter of 2D boxes
in 3D are volume and surface, respectively, and over-
lap is the common volume occupied by two or more
boxes. As pointed out in Section 2.2.1, the amounts of
dead space and overlap between nodes influences the
performance of R-trees. The amount of dead space
depends on the quality of approximations of the geo-
metric primitives by AABBs (and thus on the geom-
etry of the scene), on the choice of data assignment
to nodes and on the strategy for splitting nodes. The
latter two aspects also influence the amount of mutual
overlap.
Furthermore, R-tree nodes must be split if they ex-
ceed their limit of M entries, but the resulting nodes
must not contain less than m entries. Since m and M
determine how many entries must be checked if a ray
intersects the containing node, these two parameters
will influence the performance of R-trees as well.
Another aspect that influences ray tracing perfor-
mance is the order in which the n child nodes (entries)
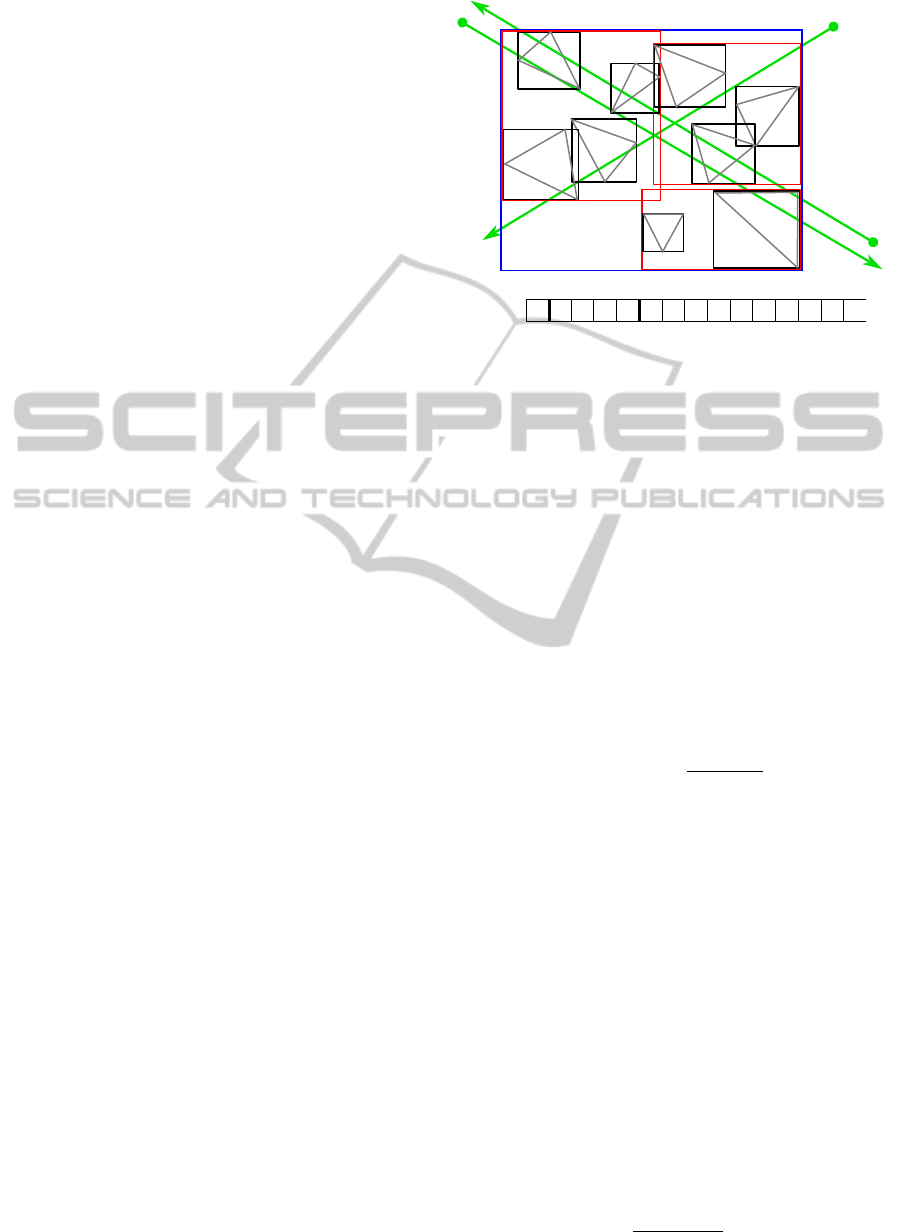
are visited and is illustrated in Figure 3: Preferably,
the entries of R-tree nodes are stored in a coherent
block of memory, e.g., in an array, but visiting them
in their order in memory is not necessarily optimal.
Hence, the R-tree’s ray tracing performance changes
with the direction of rays. For the purpose of early
ray termination, the best sequence for visiting entries
would be the one obtained by sorting the contained
geometric primitives according to their distances from
a ray’s origin in increasing order. This order, however,
is usually not known in advance.
In summary, when using R-trees for ray tracing,
their performance is influenced by the following fac-
tors:
• the underlying geometry of the scene
• the strategy for assigning entries to nodes
• the strategy for splitting nodes
• the number of entries per node, i.e., m and M
• the order in which children of nodes are tested for
intersections with rays
4 RAY TRAVERSAL
Ray traversal in R-trees and its variants is similar to
the proceeding employed with BVHs (see Section 3).
ray
1
ray
2
ray
3
R
4
R
1
A
D
C
G
R
2
E
F
B
R
3
I
H
memory
R
4
R
1
-
A C
D
G
E F H IB
-
R
2
R
3
Figure 3: If the R-tree in Figure 2 is intersected by rays,
the order in which nodes are tested for intersection influ-
ences the data structure’s performance. In case of vis-
iting nodes in the depicted memory order, the intersec-
tion at triangle I is closest to ray
1
, but is found only after
R
1
, A,C, D, G, R
2
, B, E, F, R
3
and H have been tested. The
intersection at A is closest to ray
2
and is found first by
chance. Thus, testing the entries of R
2
and R
3
is needless.
ray
3
intersects C, but R
2
and its children need to be tested
for intersection as well, because these boxes are closer to
that ray’s origin.
In contrast to most trees and BVHs, R-trees are bal-
anced in height, which allows us to derive the follow-
ing relations:
The total number of nodes N in an R-tree of height
L + 1 holding at most M entries per node is given by
N =
L
∑
i=0
M
i
=
M
L+1
− 1
M − 1
where N, L, M ∈ N. Starting at the root, we may num-
ber all nodes in level order from left to right, including
empty nodes (see Figure 4), and store the whole tree
sequentially in an array.
Since there are M
L−l
nodes at level l ≤ L, the first
node at l is located at position ∆
L
(l) within the array,
where
∆
L
(l) =
0 l = L
L−(l+1)
∑
i=0
M
i
l < L
Given an intermediate node’s index n and level l > 0,
the index n
e
of its first child/entry is
n
e
= n
e
(n) = (n − ∆
L
(l)) · M + ∆
L
(l − 1)
Likewise, if l < L, the index n
p
of a node’s parent is
n
p
= n
p
(n) =
(n − ∆
L
(l))
M
+ ∆
L
(l + 1)
AcceleratedRayTracingusingR-Trees
251

5 6
7
8
20
19
18
17
...
9
0
2
3
1 4
level
L
L-1
L-2
...
0
Figure 4: Level-order numbering of nodes in an R-tree with
M = 4. Empty nodes (dashed gray line style) must be num-
bered as well. Nodes from levels below L − 2 are omitted
for the sake of clarity.
The position k, 0 ≤ k < M, of n within its parent n
p
is
computed by
k = χ(n) = (n − ∆
L
(l)) mod M
Based on these relations, we devise the follow-
ing two algorithms for traversing R-trees and comput-
ing the closest intersection of the contained geometric
primitives with a given ray, if any such intersection
exists. The algorithm presented in Section 4.1 is a
straightforward implementation of depth-first traver-
sal, but forgoes any additional stack. In Section 4.2,
we present a second traversal scheme that visits nodes
in the order of their distances from a ray’s origin.
Hereinafter, we assume that the primitives stored in
the R-trees are triangles, for they are very common in
rendering. A comparison of the performance of the
two algorithms is presented in Section 5.2.
4.1 Stackless Ray Traversal
Our algorithm for stackless depth-first traversal of R-
trees is given in the pseudo code in Listing 1.
If the given ray intersects a box or a triangle, func-
tion intersects() returns the distance t from that
ray’s origin to the location of its first intersection with
the object. Otherwise, the function returns ∞. The
result t
min
of the algorithm is the minimum of all dis-
tances obtained from intersections of a given ray with
triangles. If there are no intersections, t
min
= ∞.
The loop starting at line 21 locates the next sibling
of the current node n by examining whether n is the
last entry within its parent, i.e., χ(n) = M − 1. If so,
the process is repeated for the parent of n until either
an ancestor n
0
of n with χ(n
0
) < M −1 has been found
or the root node has been reached again. Otherwise,
if χ(n) < M − 1, n
0
is set to n. The algorithm then
continues with the next node n
0
+ 1. In this way, all
relevant nodes will be visited, and the algorithm is
guaranteed to terminate as soon as it has processed
the last entry of the root.
1 t
min
= ∞;
2 for (n = 0, l = L; n < N ; ) {
3 p roc e edW i thC h ild ? = false;
4 if ( ! isE mpt y Nod e (n) ) {
5 t = i nte rse cts ( ray , get Box (n)) ;
6 if ((t < ∞)∧ (t < t
min
)) {
7 if (l > 0) // vi sit ing int erm e dia te node
8 pro c eed W ith C hil d ? = true;
9 else { / / vis iti ng le af node
10 foreach ( tr ian gle o f n as tri ) {
11 t
tri
= i n ter sec ts ( ray , tri ) ;
12 if ((t
tri
< ∞) ∧ (t
tri
< t
min
))
13 t
min
= t
tri
;
14 } } } }
15 if ( pro c eed Wit h Chi l d ?) {
16 n = n
e
(n); // p roc ee d w it h fir st ch ild .. .
17 --l ; // ... at the next lo wer l eve l
18 } else {
19 n
0
= n;
20 // If n is las t entry wi thi n it s
pa re nt , .. .
21 while ((l < L)∧ (χ(n
0
) == M − 1)) {
(* @ \ l abe l { l bl : l ine - lo op }@*)
22 n
0
= n
p
(n); // ... try p are nt of n .. .
23 ++l; // ... at th e next hi ghe r lev el
24 }
25 if (l < L)
26 n = n
0
+ 1; // p roc eed w it h next sib lin g
27 else // or , if s till a t t he ro ot ,...
28 n = N; // . .. exit l oop at n ex t i ter ati on
29 }
30 }
31 return t
min
;
Listing 1: Pseudo code for our algorithm for stackless ray
traversal in R-trees. The syntax is borrowed from the pro-
gramming languages C/C++.
4.2 Ordered Ray Traversal
The algorithm in Listing 1 suffers from the problem
described in Section 3.1: Its performance depends on
the directions of rays and on the order in which child
entries are stored in memory. In case of primary rays,
for instance, the effect becomes apparent by differ-
ences in frame rates as the virtual camera is placed at
opposite locations of the scene, but looks at the same
point. However, if the mutual overlap between nodes
at the same level is low, there is a good chance that
an AABB located closer to a ray’s origin contains a
geometric primitive that is also intersected by that ray
at less distance than a primitive in an AABB further
away.
Based on this consideration, we devised another
algorithm for ray traversal in R-trees that relies on
sorting node entries and requires a small amount of
additional memory per ray: For each level l, we al-
locate a small stack and a pointer to its top and start
ray traversal at the root of the R-tree. Each entry of
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
252

a node at l > 0 that is intersected by a given ray is
pushed onto the stack of level l. We then sort the en-
tries on the stack according to the distances of their
first intersection with that ray in decreasing order. The
entry with least distance is thus located at the top of
the stack, and the one with largest distance at the bot-
tom. We repeat the process with the first node pointed
to by the stack pointer at level l. Note that this node
is located at l − 1. If we arrive at a leaf, we test the
contained triangles for intersection with the ray and
update the overall minimal distance t
min
, if necessary.
If a node turns out to be empty or is missed by the
ray, we proceed with the next node on the stack of
level l. When a stack runs empty, we ascend in the
tree by increasing the level and continue with nodes
from the corresponding stack. The algorithm termi-
nates as soon as the stack of the topmost level runs
empty.
Since each stack has to hold at most M entries at a
time, it can be implemented by an array of fixed size.
Provided that the node entries and stack pointer are
numbers of the same data type, the amount of extra
memory required per ray is thus proportional to L ·
(M + 1) (at level l = 0, no stack is needed, though it
is convenient to provide one).
Pseudo code for this algorithm is presented in
Listing 2.
5 IMPLEMENTATION AND
EVALUATION
Our approach relies on R
∗
-trees (Beckmann et al.,
1990) in 3D, and we only use triangles as geometric
primitives for ray tracing static scenes. The numbers
for minimum and maximum entries per node are set to
m = 2 and M = 4, respectively, because this configu-
ration yielded best results in our experiments. The R-
trees are constructed on the CPU using pointers and
are packed according to the proceeding described in
Section 4 into a linear memory layout in a subsequent
step. Rays are not packeted (Wald et al., 2001), but
traced individually.
We implemented a simple CPU ray tracer de-
signed for execution on common desktop computers
using C++. The code relies in large parts on C++ tem-
plates, including some STL containers, and is mainly
optimized by the compiler alone. The ray tracer
merely allows basic parallel ray tracing by utilizing
the compiler’s OpenMP support in order to trace rays
from C different rows of the resulting image concur-
rently, where C is number of CPU cores.
Our CUDA ray tracer accesses R-trees via a set of
1D textures. Positions of the first nodes ∆
L
(l) at each
1 t
min
= ∞;
2 sta cks [L + 1][M ] ; // e ntr ies at c urr ent l eve l
3 d ist anc es [L + 1]; // L + 1 is m or e c onv eni ent
4 sp [L + 1]; // s tac k p oi n te r s
5 for (n = 0, l = L; n < N ; ) {
6 if ( ! isE mpt y Nod e (n) ) {
7 if (l > 0) { // v i si t in g in t erm edi a te no de
8 sp [l ] = 0;
9 for (i = 0; i < M; ++i) {
10 n
0
= n
e
+ i;
11 if ( ! isE mpt y Nod e (n
0
)) {
12 t = i nte rse cts ( ray , get Box (n
0
));
13 if ((t < ∞)∧ (t < t
min
)) {
14 sta ck s [l ][ sp [l]] = n
0
;
15 dis tan ces [ sp [l]] = t ;
16 ++ sp[l ];
17 } }
18 }
19 sort ( s ta ck [l] , d is ta nces , sp [l ]) ;
20 } else { // v i si t in g l ea f node
21 foreach ( tr ian gle o f n as tri ) {
22 t
tri
= i n ter sec ts ( ray , tri ) ;
23 if ((t
tri
< ∞) ∧ (t
tri
< t
min
))
24 t
min
= t
tri
;
25 }
26 ++l; // d on e with th is le vel
27 } }
28 while ((l ≤ L)∧ (sp[l ] < 1) )
29 ++l ;
30 if ((l ≤ L)∧ (sp[l ] > 0) {
31 n = sta cks [l ][-- sp [l ]];
32 --l ; // n is now fro m th e ne xt lo wer l evel
33 } else
34 n = N ; // e xi t loop
35 }
36 return t
min
;
Listing 2: Pseudo code for our algorithm for ordered ray
traversal in R-trees. The algorithm requires additional
memory to maintain a small stack per level (arrays stacks
and sp). Function sort() performs in-place sorting of the
stack according to the distances of the intersections from
the ray’s origin.
each level l are precomputed and stored together with
the number of an R-tree’s maximum level L in the
constant memory area of the ray tracer’s kernel. In
all cases, we achieved best performance results when
running CUDA ray tracing kernels in a configuration
of h blocks with 128 threads each, where h is the num-
ber of rows in the rendered image.
All measurements in the following were obtained
on a desktop computer with an Intel i7-4820K CPU at
3.7 GHz, 32 GB RAM and an NVIDIA GeForce GTX
780 graphics adapter with 3 GB memory (NVIDIA
Corp., 2014). Images were rendered at resolutions of
1024 × 1024 pixels, so that h = 1024 for all CUDA
kernel executions. The CPU ray tracer was executed
using all C = 8 processor cores available.
AcceleratedRayTracingusingR-Trees
253

5.1 Comparison of R-Tree Construction
Schemes
We constructed R
∗
-trees by successive insertion of tri-
angles and investigated the following strategies for se-
lecting nodes (cf. Section 2.2.1):
1. minVolume: minimize the volume enlargement
of nodes, regardless of their level. This is
the same strategy employed by the original R-
tree (Guttman, 1984).
2. minSurface: minimize the surface area enlarge-
ment of nodes. This corresponds to the sur-
face area heuristic (SAH) (MacDonald and Booth,
1990).
3. minOverlap: minimize the mutual overlap of
nodes, resolve ties by selecting the node that
needs least volume enlargement
4. R*-tree: minimize the volume enlargement at
intermediate nodes and the overlap at leaf nodes
5. R*-treeSrfc: similar to R*-tree, but minimize
the surface enlargement at intermediate nodes and
the overlap at leaf nodes
Alterations of the method for splitting nodes pre-
sented in (Beckmann et al., 1990), like using vol-
ume as measurements for determining split axes or re-
distributing entries, only impaired ray tracing perfor-
mance, and we thus relied on the original approach.
The influence of the node selection strategies on ray
tracing performance is summarized in Table 1. The
values were obtained by rendering our test scenes
from the fixed camera poses shown in Figure 1 using
primary and shadow rays. For ray traversal by means
of our CPU implementation, we employed the stack-
less algorithm presented in Section 4.1, whereas our
GPU tracer relied on the method for ordered traversal
described in Section 4.2.
The results in Table 1 show that the two strate-
gies based on minimizing surfaces of AABBs, i.e.,
R*-treeSrfc and minSurface, are best for con-
structing R
∗
-trees for the purpose of ray trac-
ing. Minimizing the mutual overlap by means of
minOverlap diminished the performance consider-
ably, especially in case of the Bunny test scene
where CPU ray tracing performance was degraded by
≈ 2690% and our CUDA ray tracer even failed to
launch.
Furthermore, the results indicate a correlation be-
tween the insertion strategy and the geometry of a
scene and can be explained as follows:
Strategy minSurface favors the formation of boxes
of cubic shape, whereas minVolume prefers flat boxes
that may have zero extension along one axis and thus
Table 1: The strategies for selecting nodes where trian-
gles are inserted into R-trees directly influence their struc-
ture and thus their performance in ray tracing. Values
were obtained by tracing primary and shadow rays. Using
minOverlap and the Bunny test scene, our CUDA kernels
failed to launch and we were unable to obtain results.
scene
minVolume
minSurface
minOverlap
R*-tree
R*-treeSrfc
CPU
Bunny 1.95 s 1.59 s 53.0 s 1.90 s 1.57 s
Cath. 6.40 s 4.95 s 13.6 s 5.39 s 3.54 s
Fairy 5.92 s 3.31 s 8.50 s 5.65 s 3.41 s
Conf. 3.99 s 3.30 s 5.79 s 3.94 s 3.01 s
GPU
Bunny 67 ms 63 ms – 71 ms 59 ms
Cath. 221 ms 162 ms 478 ms 201 ms 138 ms
Fairy 169 ms 98 ms 263 ms 158 ms 104 ms
Conf. 134 ms 113 ms 199 ms 134 ms 98 ms
zero volume, but which may have large surfaces. Both
strategies can reduce dead space, but minSurface
outperforms minVolume for the same reason that
makes SAH the preferred method for building kd-
trees: Provided the origins and directions of rays are
uniformly distributed in space, the conditional prob-
ability of a ray intersecting a box B
1
to intersect a
completely contained box B
2
is approximately pro-
portional to the ratio
S (B
2
)
S (B
1
)
of their surfaces S (B
i
), i ∈
{
1, 2
}
(see (MacDonald and Booth, 1990; Wald and
Havran, 2006)). Strategy minSurface chooses the
node where this probability is highest, and the inter-
section test between a ray and the outer box is thus
less likely to be redundant.
Strategy minOverlap assigns entries to nodes re-
gardless of dead space. This behavior is particularly
problematic at upper R-tree levels, where AABBs oc-
cupy potentially large volumes that may have to over-
lap due to the scene geometry. In case of the Bunny
scene, the virtual camera is moreover not located as
deep “inside” the R-tree as in the other scenes, but
is surrounded by only few AABBs from levels close
to L. Hence, much more tests for intersection with
rays and AABBs of large volume are needed, which
explains the poor performance of this method.
The strategies R*-tree and R*-treeSrfc are
composed of minOverlap and minVolume or
minSurface, respectively. However, only leaf nodes
are subject to minOverlap, and triangles are “di-
rected” already towards their respective parents based
on spatial locality and on (local) minimization of dead
space at higher levels. Optimizing for mutual over-
lap of leaf nodes results in a reduction of the num-
ber of paths that need to be followed during traver-
sal in R-trees. In this way, better performances are
yielded than in cases of minVolume and minSurface.
This proceeding has been reported to be a means
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
254

Table 2: Ray tracing performance of R-trees when omit-
ting forced reinserts during construction by means of
R*-treeSrfc strategy.
Bunny Cathedral Fairy Conference
CPU
1.92 s 4.42 s 3.81 s 3.01 s
(−23%) (−25%) (−12%) (±0%)
GPU 69 ms 154 ms 115 ms 105 ms
(−17%) (−12%) (−11%) (−7%)
of improving the performance of R
∗
-trees over R-
trees (Beckmann et al., 1990) and is confirmed by our
results.
In addition, we found that forced reinserts used
with R
∗
-trees improve their structure and ray trac-
ing performance in most cases. The results we ob-
tained when sparing forced reinserts during construc-
tion of R-trees by means R*-treeSrfc strategy are
given in Table 2.
5.2 Comparison of Ray Traversal
Algorithms
We evaluated the two algorithms for tracing rays in R-
trees presented in Section 4 by means of our CPU and
GPU ray tracer, respectively. Performance was mea-
sured in the same way as described in Section 5.1 with
R-trees being constructed using the R*-treeSrfc
strategy and forced reinserts. In case of ordered ray
traversal, the auxiliary stacks were sorted using in-
sertion sort, because this sorting algorithm is easy
to implement, in-place and efficient for small data
sets (Sedgewick, 2002). We also acquired timings by
using a conventional stack-based traversal algorithm
in our CPU implementation for comparison. The re-
sults are given in Table 3.
Table 3: Ray tracing performances of R-trees using the
traversal algorithms presented in Section 4 and a common
stack-based method (CPU ray tracer only).
scene stackless ordered stack
CPU
Bunny 1.57 s 1.82 s 2.09 s
Cathedral 3.54 s 4.23 s 5.94 s
Fairy 3.41 s 3.77 s 4.41 s
Conference 3.01 s 3.37 s 3.81 s
GPU
Bunny 65 ms 59 ms –
Cathedral 120 ms 138 ms –
Fairy 102 ms 104 ms –
Conference 98 ms 98 ms –
In most cases, best performance was achieved by
means of the stackless algorithm for ray traversal.
The ordered algorithm proved to be somewhat bet-
ter in case of the Bunny scene, in which the virtual
camera was placed at a location contained only by
few AABBs at higher levels of the R-tree. In the
remaining scenes, the camera was located deeper in-
side the R-trees. Hence, sorting nodes based on their
distances from the origins of the rays was needles
in most situations, and the accompanying overhead
diminished the ray tracing performance. However,
if we placed the virtual camera outside the AABBs
of R-trees, our ordered ray traversal outperformed
the stackless method. For instance, rendering the
Cathedral scene by means of our GPU ray tracer
from a virtual viewpoint outside the R-tree took 51
ms using the ordered traversal method, compared to
68 ms using the stackless algorithm. We therefore
propose to employ the presented traversal algorithms
for R-trees with respect to the position of the virtual
camera.
5.3 Comparison with KD-Trees
We compared the performance of R-trees in our CPU
ray tracer to timings we obtained from ray tracing by
means of kd-trees. The kd-trees were constructed us-
ing the local greedy surface area heuristic (SAH) and
the O
nlog
2
(n)
algorithm described in (Wald and
Havran, 2006). The method we employed to traverse
kd-trees is the stack-based algorithm given in (Hapala
and Havran, 2011). For the sake of better compara-
bility, we compare kd-tree traversal to a more simi-
lar stack-based algorithm for traversing R-trees. The
R-trees were again constructed using R*-treeSrfc
strategy and forced reinserts. Both traversal algo-
rithms are merely optimized to the effect that they
skip AABBs/half spaces which are further away from
a ray’s origin than any intersection with a triangle al-
ready encountered. The results are listed in Table 4
and were obtained by rendering our test scenes twice
from the fixed camera poses shown in Figure 1: one
time by tracing primary rays only, and another time
using primary and shadow rays.
With the exception of the Bunny scene, the perfor-
Table 4: Timings in seconds from our comparison of R-trees
and kd-trees for ray tracing. Kd-trees were traversed using
a stack-based algorithm, and the results given for R-trees
apply to the stack-based traversal scheme also employed
in Section 5.2. The corresponding results for primary and
shadow rays are hence identical to those given in Table 3.
scene R
∗
-tree kd-tree
primary rays
Bunny 1.38 s 1.59 s
Cathedral 3.30 s 2.04 s
Fairy 2.59 s 2.23 s
Conference 2.43 s 2.14 s
primary and
shadow rays
Bunny 2.09 s 2.96 s
Cathedral 5.94 s 4.01 s
Fairy 4.41 s 3.96 s
Conference 3.81 s 3.46 s
AcceleratedRayTracingusingR-Trees
255

mance of kd-trees for ray tracing was superior to those
of R-trees. In case of Bunny, the better performance
of R-trees results from the small number of triangles
in that scene instead of from the position of the vir-
tual camera. In similar scenes consisting of less than
≈ 100000 triangles, but not presented in this work,
we found ray tracing by means of R-trees always to
be faster.
If we compared the results of stackless R-tree
traversal on CPUs in Table 3 to the corresponding
timings of stack-based kd-tree traversal in Table 4,
ray tracing using R-trees would be the faster method.
Since we did not consider alternatives for stackless
kd-tree traversal, we deem such a comparison be-
tween two fundamentally different algorithms and
any conclusions drawn from it inappropriate.
5.4 Construction Times
Although this work is not focused on the times
needed for constructing R
∗
-trees, it is worth mention-
ing that they are significantly lower than the times
required for constructing SAH kd-trees by means of
the O
nlog
2
(n)
algorithm presented in (Wald and
Havran, 2006). We list the times from our implemen-
tation in Table 5 primarily to provide indications for
other researchers and potential future work.
Table 5: Timings in seconds required for constructing spa-
tial indexes containing our test scenes shown in Figure 1.
R-trees were constructed using forced reinserts.
scene R
∗
-tree kd-tree
Bunny 0.61 s 7.03 s
Cathedral 0.62 s 4.37 s
Fairy 1.63 s 20.02 s
Conference 2.91 s 27.59 s
In case of our test scenes Bunny and Conference,
the timings we obtained for kd-trees are remarkably
similar to those reported in (Wald and Havran, 2006)
(6.7 s and 30.5 s, respectively), although we have dif-
ferent hardware and an independent implementation.
The build times of the O (nlog(n)) algorithm the au-
thors presented in that work (3.2 s and 15.0 s, respec-
tively), are also much higher than the times required
for building R
∗
-trees. The latter in turn, are yet sig-
nificantly higher than the times for building BVHs of
scenes corresponding to Bunny and Conference by
the sophisticated methods presented in (Wald, 2007).
6 CONCLUSIONS AND FUTURE
WORK
In this article, we gave a first demonstration of the
suitability of R-trees for accelerating ray tracing. We
presented two algorithms for traversing R-trees that
exploit the regularity of these data structures in order
to compute intersections between the geometric prim-
itives stored within and rays. The method for stack-
less traversal requires neither to restructure the trees
nor extra memory for internal pointers or other. Al-
though our algorithm for ordered traversal may per-
form better with certain camera poses, the stackless
variant is particularly interesting due to its simplicity
and suitability for implementation on modern GPUs.
Ray traversal on GPUs might be further improved by
exploiting the fixed path lengths of R-trees and care-
ful optimization. In addition, we have only traced in-
dividual rays and neglected the influence of ray coher-
ence so far, but packeting rays as presented in (Wald
et al., 2001; Günther et al., 2007) is likely to increase
ray tracing performance of R-trees.
Moreover, we investigated construction schemes
for R-trees and their influence on ray tracing perfor-
mance. We showed that altering the measure from
volume to surface in the original strategy of R
∗
-trees
for selecting nodes for data insertion results in a con-
siderable improvement. More sophisticated methods
for constructing R-trees, like the ones used with RR
∗
-
trees (Beckmann and Seeger, 2009), for example, or
bulk-loading data (Sellis et al., 1987; Arge et al.,
2008) might yield even better results. These methods
could probably benefit from ideas designed for opti-
mizing BVHs, such as the ones presented in (Wächter
and Keller, 2006; Wald, 2007).
Our direct comparison with kd-trees showed that
these yield better performance results in most situ-
ations yet, but the employment of stackless meth-
ods for R-tree traversal appears preferable over stack-
based kd-tree traversal.
Major points for optimizing the performance of R-
trees in ray tracing might also be revealed by thor-
oughly investigations of the caching behavior of R-
trees on GPUs.
Considering the simplicity of ray traversal and the
potentially high data locality that result from their
regular structure, R-trees may become a competitive
choice for accelerating GPU ray tracing as more re-
search is done on this subject.
ACKNOWLEDGMENTS
We thank all persons who created the models we used
throughout this work and made them publicly avail-
able. Additionally, we give thanks to M. Pohl for her
helpful comments on this article.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
256

REFERENCES
Arge, L., Berg, M. D., Haverkort, H., and Yi, K. (2008). The
Priority R-tree: A Practically Efficient and Worst-case
Optimal R-tree. ACM Trans. Algorithms, 4(1):9:1–
9:30.
Bayer, R. and McCreight, E. (1972). Organization and
Maintenance of Large Ordered Indexes. Acta Infor-
matica, 1(3):173 – 189.
Beckmann, N., Kriegel, H.-P., Schneider, R., and Seeger, B.
(1990). The R*-tree: An Efficient and Robust Access
Method for Points and Rectangles. In SIGMOD ’90:
Proceedings of the ACM SIGMOD International Con-
ference on Management of Data, volume 19(2), pages
322–331. ACM.
Beckmann, N. and Seeger, B. (2009). A Revised R*-tree in
Comparison with Related Index Structures. In Pro-
ceedings of the 2009 ACM SIGMOD International
Conference on Management of Data, SIGMOD ’09,
pages 799–812. ACM.
Günther, J., Popov, S., Seidel, H.-P., and Slusallek, P.
(2007). Realtime Ray Tracing on GPU with BVH-
based Packet Traversal.
Guttman, A. (1984). R-trees: A Dynamic Index Structure
for Spatial Searching. In SIGMOD ’84: Proceed-
ings of the ACM SIGMOD International Conference
on Management of Data, pages 47–57. ACM.
Hachisuka, T. (2009). Ray Tracing on Graphics Hard-
ware. Technical report, University of California at San
Diego.
Hapala, M., Davidovi
ˇ
c, T., Wald, I., Havran, V., and
Slusallek, P. (2011). Efficient Stack-less BVH Traver-
sal for Ray Tracing. In Proceedings of the 27th Spring
Conference on Computer Graphics, SCCG ’11, pages
7–12, New York, NY, USA. ACM.
Hapala, M. and Havran, V. (2011). Review: Kd-tree Traver-
sal Algorithms for Ray Tracing. Computer Graphics
Forum, 30(1):199–213.
Horn, D. R., Sugerman, J., Houston, M., and Hanrahan,
P. (2007). Interactive K-d Tree GPU Raytracing. In
Proceedings of the 2007 Symposium on Interactive 3D
Graphics and Games, I3D ’07, pages 167–174, New
York, NY, USA. ACM.
MacDonald, D. J. and Booth, K. S. (1990). Heuristics for
Ray Tracing Using Space Subdivision. The Visual
Computer, 6(3):153–166.
NVIDIA Corp. (2014). GeForce GTX 780 Specifications.
http://www.geforce.com/hardware/desktop-gpus/
geforce-gtx-780/specifications.
Oracle Corp. (2014a). MySQL 5.6 Reference
Manual. http://downloads.mysql.com/docs/
refman-5.6-en.a4.pdf.
Oracle Corp. (2014b). Oracle Spatial and Graph Devel-
oper’s Guide. http://docs.oracle.com/database/121/
SPATL/E49172-03.pdf.
Samet, H. (2006). Foundations of Multidimensional and
Metric Data Structures. Morgan Kaufmann, 1st edi-
tion.
Sedgewick, R. (2002). Algorithms in Java Parts I – IV.
Addison Wesley, 3rd edition.
Sellis, T. K., Roussopoulos, N., and Faloutsos, C.
(1987). The R+-Tree: A Dynamic Index for Multi-
Dimensional Objects. In Proceedings of the 13th In-
ternational Conference on Very Large Data Bases,
VLDB ’87, pages 507–518, San Francisco, CA, USA.
Morgan Kaufmann Publishers Inc.
Stich, M., Friedrich, H., and Dietrich, A. (2009). Spatial
Splits in Bounding Volume Hierarchies. In Proceed-
ings of the Conference on High Performance Graph-
ics 2009, HPG ’09, pages 7–13, New York, NY, USA.
ACM.
Suffern, K. (2007). Ray Tracing from the Ground Up. A. K.
Peters, Ltd., 1st edition.
Sylvan, S. (2010). R-trees: Adapting Out-Of-Core Tech-
niques to Modern Memory Architectures. Talk at
Game Developers Conference, http://gdcvault.com/
play/1012452/R-Trees-Adapting-out-of.
Wächter, C. and Keller, A. (2006). Instant Ray Tracing:
The Bounding Interval Hierarchy. In Proceedings
of the 17th Eurographics Conference on Rendering
Techniques, EGSR’06, pages 139–149, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
Wald, I. (2007). On Fast Construction of SAH-based
Bounding Volume Hierarchies. In Proceedings of the
2007 IEEE Symposium on Interactive Ray Tracing,
RT ’07, pages 33–40, Washington, DC, USA. IEEE
Computer Society.
Wald, I. and Havran, V. (2006). On Building Fast kd-Trees
for Ray Tracing, and on Doing That in O(N log N). In
Proceedings of the 2006 IEEE Symposium on Interac-
tive Ray Tracing, pages 61–70.
Wald, I., Mark, W. R., Günther, J., Boulos, S., Ize, T., Hunt,
W., Parker, S. G., and Shirley, P. (2007). State of the
Art in Ray Tracing Animated Scenes. In STAR Pro-
ceedings of Eurographics 2007, pages 89–116. The
Eurographics Association.
Wald, I., Slusallek, P., Benthin, C., and Wagner, M. (2001).
Interactive Rendering with Coherent Ray Tracing. In
Computer Graphics Forum, pages 153–164.
Zlatuska, M. and Havran, V. (2010). Ray Tracing on a
GPU with CUDA – Comparative Study of Three Al-
gorithms. In Proceedings of WSCG’2010, communi-
cation papers, pages 69–76.
AcceleratedRayTracingusingR-Trees
257
