Hierarchical SNR Scalable Video Coding with Adaptive Quantization for

Reduced Drift Error

Roya Choupani

, Stephan Wong

and Mehmet Tolun

Computer Engineering Department, Delft University of Technology, Delft, The Netherlands

Computer Engineering Department, C¸ankaya University, Ankara, Turkey

Electrical Engineering Department, Aksaray University, Aksaray, Turkey

Keywords:

Scalable Video Coding, Rate Distortion Optimization, Drift Error.

Abstract:

In video coding, dependencies between frames are being exploited to achieve compression by only coding the

differences. This dependency can potentially lead to decoding inaccuracies when there is a communication

error, or a deliberate quality reduction due to reduced network or receiver capabilities. The dependency can

start at the reference frame and progress through a chain of dependent frames within a group of pictures

(GOP) resulting in the so-called drift error. Scalable video coding schemes should deal with such drift errors

while maximizing the delivered video quality. In this paper, we present a multi-layer hierarchical structure for

scalable video coding capable of reducing the drift error. Moreover, we propose an optimization to adaptively

determine the quantization step size for the base and enhancement layers. In addition, we address the trade-off

between the drift error and the coding efﬁciency. The improvements in terms of average PSNR values when

one frame in a GOP is lost are 3.70(dB) when only the base layer is delivered, and 4.78(dB) when both the

base and the enhancement layers are delivered. The improvements in presence of burst errors are 3.52(dB)

when only the base layer is delivered, and 4.50(dB) when both base and enhancement layers are delivered.

1 INTRODUCTION

The scalability property of video coding provides the

possibility of changing the video quality if it is re-

quired by network conditions or display device ca-

pabilities of the receiver. The scalability property of

video is provided by multi-layer video coding through

decomposition of the video into smaller units or lay-

ers (Adami et al., 2007). The ﬁrst layer which in-

cludes the video content in its lowest quality (in terms

of resolution, frame rate, or bits-per-pixel) is called

the base layer. All other layers add to the quality of

the video, and are called enhancement layers (Segall

and Sullivan, 2007),(Schwarz et al., 2006). The or-

der of including the layers in multi-layer video coding

is important and a higher level layer cannot be uti-

lized when the lower level layers are not present (Lan

et al., 2007). A signiﬁcant number of video coding

methods using scalable video coding (SVC) schemes

have been reported in literature (Segall, 2007),(Ohm,

2005),(Schwarz et al., 2007a),(Abanoz and Tekalp,

2009) and a comprehensive overview paper on SVC

methods is presented in (Adami et al., 2007) and

(Wien et al., 2007). State-of-the-art video coding

methods however, utilize motion-compensated tem-

poral ﬁltering (MCTF), where each inter-coded video

frame is encoded by predicting the motion of every

macro-block with respect to a reference frame and en-

coding the differences or residues. When an MCTF-

based SVC method delivers only some of the encoded

video layers, the reconstructed frames will be dif-

ferent than the encoded frames. The difference ∆I

′

between the encoded frame I and the reconstructed

frame I

′

increases at the subsequent decodings based

on imperfectly reconstructed reference frames. This

error which accumulates until an intra-coded frame

is reached, is called the drift error. The drift error is

the result of selective transmission where some of the

DCT coefﬁcients are eliminated, and/or re-quantized

which changes the original quantized DCT coefﬁ-

cients (Yin et al., 2002). The drift error can occur

in multi-layer scalable video coding methods if the

decoder does not receive all enhancement layer data

(Lee et al., 2004). Improving the robustness of SVC

methods against packet loss through data redundancy

(Abanoz and Tekalp, 2009) or selective protection

of layers (Xiang et al., 2009),(LOPEZ-FUENTES,

2011) reduces the bit rate performance of the encoder

117

Choupani R., Wong S. and Tolun M..

Hierarchical SNR Scalable Video Coding with Adaptive Quantization for Reduced Drift Error.

DOI: 10.5220/0005306001170123

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 117-123

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

(Wien et al., 2007). For instance, the enhancement

layer(s) information can be used in the motion predic-

tion loop of the encoder to improve the coding per-

formance (Ohm, 2005). Consequently, the absence

of the enhancement layer(s) at the decoder can con-

tribute to the drift error.

Some video coding standards such as H.263 and

MPEG4 prefer drift-free solutions where the encoder

performs motion prediction using only the base layer

information. This means that the reconstruction will

be error free if only the base layer is delivered. How-

ever, these solutions are provided with a reduction

in performance. Other approaches that attempt to

optimize the coding efﬁciency while minimizing the

drift error have been proposed in literature (Reibman

et al., 2001),(Regunathan et al., 2001). In (Seran

and Kondi, 2007), the authors report a coding method

which maintains two frame buffers in the encoder and

decoder. These buffers are based on the base layer,

and the base and enhancement layers. They initially

use the base and enhancement layer buffer for encod-

ing and decoding. Their method measures the drift

error based on the channel information. When the

drift error exceeds a predeﬁned threshold, the method

switches to the base layer buffer, assuming that the

base layer is always available to the receiver. A sim-

ilar method reported in (Reibman et al., 2003) bal-

ances the tradeoff between compression efﬁciency

and the drift error. The authors assume two cod-

ing parameters, namely the quantizer and the predic-

tion strategy. By selecting the appropriate parame-

ter based on the network conditions, they try to op-

timize the video coding process. In (Yang et al.,

2002), a method is proposed to minimize the rate dis-

tortion by utilizing the distortion feedback from the

receiver. The authors assume the base and the en-

hancement layer macro-blocks can be encoded in dif-

ferent modes. They optimize the coding by choosing

the quantization step and the coding mode for each

macro-block.

The main problem with these methods is that the

decision about optimizing the encoder parameters is

made by considering the average value of drift er-

ror. As a result, the same parameter values are ap-

plied to all frames of a group of picture (GOP). How-

ever, since the drift error cannot propagate beyond a

GOP, each frame contributes to the accumulation of

error with a different rate. For instance, the last frame

in a GOP has no impact on error accumulation while

the error happening in the ﬁrst frame propagates until

the end of the current GOP. In this paper, we address

the video quality degradation due to the drift error in

SVC. We consider adjusting the coding parameters

according to the network conditions and the frame po-

sition in the GOP. We propose a method to improve

the coding efﬁciency in terms of the R-D ratio, while

reducing the drift error whenever the reconstruction

is performed using the base layer only. Moreover, we

consider measurements to make the encodedvideo ro-

bust against single and multiple frame losses.

2 OPTIMIZING VIDEO

ENCODER PERFORMANCE BY

MINIMIZING THE DRIFT

ERROR

Video coding optimization and visual quality preser-

vation have conﬂicting requirements. Motion-

compensation techniques for instance are not robust

against frame losses and apt to quality loss due to the

drift error. Our proposed method for reducing the drift

error while preserving the coding efﬁciency is based

on the following observations:

• The dependency of a frame to its preceding frame

creates a chain of frames that are dependent on

each other (dependency chain). The drift error

has a direct correlation with the number of video

frames in a dependency chain. On the other

hand, a longer GOP provides a better I-frames to

P/B-frame ratio and hence a smaller bit-per-pixel

rate. In (Goldmann et al., 2010) the video quality

degradation due to the drift error is analyzed sub-

jectively. Although the quality degradation varies

with the spatial details and the amounts of local

motion, the quality of video drops below fair for

GOP lengths greater than 5. The result of this

analysis is compatible with our observation.

• The drift error also has direct correlation with the

mismatch between the original frames and the re-

constructed frames. When some part(s) of a frame

data is lost or corrupted, the other parts are used

for the frame reconstruction. In multi-layer SVC,

the receiver may reconstruct the video using the

base layer, or the base layer and some of the en-

hancement layers. Hence, the size of the enhance-

ment layer(s) should be adjusted with the maxi-

mum tolerable distortion rate of the video.

Based on the above observations, the proposed

method reduces the number of dependent frames by

introducing a dyadic hierarchical structure. Besides,

the amount of data in the base and enhancement lay-

ers is adjusted adaptively as a function of the location

of the frame in the dependency chain. An optimum

GOP length is sought after to minimize the drift er-

ror while preserving the performance of the encoder.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

118

The amount of data transmitted in the enhancement

layer(s) and the quality degradation due to the drift er-

ror are inversely proportional and hence, an optimum

balance should be found for the best performance and

the least distortion. In this paper we consider only one

enhancement layer.

2.1 R-D Optimization in Hierarchical

Coding of Video Frames

In the proposed multi-layer SVC, different quanti-

zation parameters are used in the base and the en-

hancement layers. The motion compensated blocks,

which we refer to as residues, are transformed us-

ing DCT and quantized using two different quantiza-

tion step-sizes. A ﬁne quantization which produces

larger quantized coefﬁcients (considering the abso-

lute values), and a coarse quantization which results

in smaller quantized coefﬁcients. We use the coarse

quantization results as the base layer. The difference

between the ﬁne quantized coefﬁcients and the coarse

quantized coefﬁcients are considered as the enhance-

ment layer. The encoding and decoding processes can

be expressed as shown in Equations 1 and 2 where BL

and EL represent the base layer and the enhancement

layer bitstreams, respectively.

BL = VLC(Q(DCT(Residues), QP

))

EL = VLC(Q(DCT(Residues), QP

)−

Q(DCT(Residues), QP

))

(1)

Reconstruction using only the base layer (BL

′

), and

the base and the enhancement layers (BEL

′

) are

shown in Equation 2.

′

(Residues) = IDCT(IQ(IVLC(BL), QP

))

BEL

′

(Residues) = IDCT(IQ(IVLC(BL)+

IVLC(EL), QP

))

(2)

where QP

and QP

are the base layer and the

enhancement layer quantization parameters, respec-

tively, and IVLC is the inverse of the variable length

coding process. As it is shown in Equation 2, the re-

constructed frame is obtained from inverse discrete

transform of the base and the enhancement layers

quantized residues. Whenever the enhancement layer

is not delivered, the reconstructed frame is deviated

from the encoded frame. This deviation is a function

of the amount of data in the base and the enhance-

ment layers, which are determined by the quantiza-

tion parameters of these layers namely QP

and QP

and the number of the frames in a dependency chain

which indicates the propagation extent of the drift er-

ror. On the other hand, the bit rate of the base layer

is a function of QP

. Hence, for a given bit rate, the

optimized coding efﬁciency and lowest rate distortion

depend on the QP

, QP

, and GOP length parame-

ters. The drift error can be largely reduced by utiliz-

ing a hierarchical dyadic organization of the frames in

a group of pictures which restricts the maximum er-

ror propagation range to ⌈log

GOP⌉ (Schwarz et al.,

2007b). Clearly, not all frames are used as a refer-

ence frame while some frames are used as reference

for many frames. These observations lead us to adapt

the quantization parameters QP

and QP

with the po-

sition of the frame in a GOP for each bit rate. This

adaptation results in different distortion levels in the

frames of a GOP while the average distortion is min-

imized. The rate distortion optimization in a GOP

given the base layer and the enhancement layer quan-

tization step-sizes is shown in Equation 3. We as-

sumed the video contains only one enhancement layer

however, it is readily extendable to include several en-

hancement layers.

J(QP

, QP

, GOPlen, ρ) =

∑

GOPlen

i=1

...

(QP

(i), QP

(i)) + λ

(QP

(i), QP

(i), ρ)

(3)

where J is an auxiliary function denoting the opti-

mization process, GOPlen is the number of frames in

a GOP, λ is the Lagrange multiplier. D

is the distor-

tion and R

is the bit rate of frame i when quantiza-

tion parameters QP

(i) and QP

(i) are used, respec-

tively. The optimization is carried out for a given bit

rate, ρ, and over a GOP. The summation in Equation

3 therefore, minimizes the total distortion of frames

in a GOP, when their total bit rate is limited to ρ. The

length of the dependency chain is a determining factor

in the total distortion of the video due to the drift er-

ror. Therefore, the rate distortion problem depends on

the quantization parameters of each frame in a GOP,

and the GOP length. Since we arrange the frames of

a GOP in a dyadic hierarchical structure, each GOP

contains many dependency chains which should be

considered in optimization process.

2.2 The Scalability Features of the

Proposed Method

Signal-to-noise (SNR) scalability in the proposed

method is provided as a multi-layer coding of the

frames where the number of layers determines the

granularity of the video with the main feature of hav-

ing a different approach for handling the drift er-

ror. For instance, the ﬁne granularity quality scal-

able (FGS) coding in MPEG-4 was chosen so that the

drift error is completely omitted by using base layer

frames as reference frames in motion compensation.

It is obvious that the drift free coding of MPEG-4

comes with a reduction in coding efﬁciency. How-

ever, our approach is based on balancing the bit rate

HierarchicalSNRScalableVideoCodingwithAdaptiveQuantizationforReducedDriftError

119

with the distortion caused by the drift error. The quan-

tization parameters after decomposing the frames into

the base and the enhancement layers is adapted in a

way that in the frames which serve as reference for

a larger number of frames, the enhancement layer

is smaller and hence the inaccuracy with the origi-

nal frame when the enhancement layer is missing be-

comes smaller.

Temporal scalability in the traditional video

coding methods is achieved through placing some

of the frames in the base layer and the rest in the

enhancement layer(s). An important restriction in

the temporal scalability feature of the traditional

methods is that the number of layers determine the

achievable temporal scalability rate(s). This means

that a continuous temporal scalability is not feasible

in these methods whereas, this feature is provided

in the proposed method as described below. In the

proposed method, the hierarchical organization of

the frames provide several dependency chains. Since

eliminating a frame from end of a dependency chain

does not cause any drift-free, we perform temporal

down-sampling by removing these frames in each

GOP. For instance, assuming a GOP of 16 frames

(Figure 1) the dependency chains and order of the

frames for elimination for temporal down-sampling

is as below:

1 → 2

1 → 3 → 4

1 → 5 → 6

1 → 5 → 7 → 8

1 → 9 → 10

1 → 9 → 11 → 12

1 → 9 → 13 → 14

1 → 9 → 13 → 15 → 16

Frame elimination order :

2, 4, 6, 8, 10, 12, 14, 16, 3, 7, 11, 15, 5, 13, 9, 1

It is worth to note that the temporal scalability prop-

erty of the proposed method is drift error free.

Figure 1: The Dependency Chains in the Dyadic Hierarchi-

cal Structure for Multi-layer SNR Scalable Video Coding.

3 EXPERIMENTAL RESULTS

The proposed method is experimentally veriﬁed us-

ing some video sequences. In order to verify the per-

formance of our method, we need to determine the

optimization parameters. Optimized quantization pa-

rameters for each frame is computed iteratively. As

explained in Section 2.1 the QP for the base and the

enhancement layer(s) are optimized to minimize the

distortion due to the drift error for a given bit rate.

The optimization variables are the quantization step

size of each frame which is dependent on the posi-

tion of the given frame in the frame dependency chain

and the GOP length. Considering that the maximum

length of a frame dependency chain in a dyadic hier-

archical organization of the frames is log

(GOP), we

express the QP for each frame as shown in Equation

StepE

(i) = QP

StepE

(i)+ ∆

StepB

(i) = QP

StepE

(i)+ (log

(GOP) − Pos

)

×∆

+ τ

(4)

where QP

StepB

is the quantization step size used at

the base layer (lowest quality), QP

StepE

is the quan-

tization step size used for the highest quality quanti-

zation (base + enhancement), i refers to the current

frame in the GOP, Pos

is the number of frames de-

pendent on the current frame (frame i) in the longest

frame dependency chain, ∆

is the QP step size in-

crement, and τ

is a constant used as the step size

bias value. QP

StepE

step size is incremented by adding

the QP step size increment and then QP

StepB

is opti-

mized. Quantization matrices QP

and QP

are related

to QP

StepB

and QP

StepB

as shown in Equation 5.

= Q× QP

StepB

= Q× QP

StepE

(5)

where Q is the default quantization table used by

MPEG-4. To determine the optimum value for the

step sizes, we iteratively tried different values of ∆

for GOP lengths of 8, 16, 32, and 64. The highest to-

tal quality in a GOP (minimum distortion) for a given

bit rate is sought as the optimized quantization param-

eters which depend on the content of the frame in that

GOP.

The proposed method is experimentally evaluated

by comparing its performance against the following

methods:

• Drift-free implementation where the base layer of

the reference layer is used for motion prediction.

Drift-free methods have the advantage of experi-

encing no distortion in terms of error accumula-

tion when the enhancement layer is not delivered

however, they suffer from coding performance.

• Hierarchical organizing the frames with a ﬁxed

quantization parameter optimized for the whole

GOP. This experiment shows the gain we obtain

by adaptively optimizing the quantization param-

eter which is the main contribution of the pro-

posed method.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

120

• The method proposed in (Yang et al., 2002) opti-

mizes the rate distortion of SNR SVC video coder

by determining the coding mode for each MB.

Their assumption of using enhancementlayer data

of the reference frame for motion prediction of the

current frame, and transmitting each frame in one

packet are similar to our assumptions and hence

makes a more realistic comparison possible.

• Verifying burst error effect. This experiment ver-

iﬁes the impact of single and burst errors when

only base layer, and when both base and enhance-

ment layers are delivered.

We measured the performance of the proposed

method when the videos are scaled down and only

the based layer is delivered. In this experiment, the

videos are encoded using the proposed method with

hierarchical frame organizations and adaptive quanti-

zation step size, and the sequentialcoding of the video

with a ﬁxed quantization step size. The proposed

method outperforms the sequential video encoding

by an average PSNR improvement of 2.86(dB). The

PSNR values of the reconstructed frames for both

methods have been depicted in Figure 2. The second

0 25 50 75 100 125 150 175 200 225 250 275 300 325 350 375 400

Frame

PSNR (dB)

Sequential Coding

Figure 2: PSNR values of the reconstructed frames by the

proposed method and the sequential coding method using

base layer only.

set of experiments measures the performance of the

proposed method compared to the drift-free method

suggested in MPEG-4 (144962, 1998)(Peng et al.,

2005), and the adaptiveallocation method proposed in

(Yang et al., 2002). The authors of (Yang et al., 2002)

assume no data loss happens in the base layer. There-

fore, the distortions feedback from the receiver are

the result of losses at the enhancement layer and the

drift error. Since our proposed method does not rely

on the feedback from the receiver, we modiﬁed the

method proposed in (Yang et al., 2002) to optimize for

a given bit rate. We implemented their proposed low

complexity sequential optimization method where the

base layer and the enhancement layer are optimized

sequentially, considering no error concealment and

frame re-transmission in the network. We assume the

videos are encoded for different bit-rates. Besides, a

10% frame loss is imposed in the transmissions where

the position of the lost frames are randomly selected

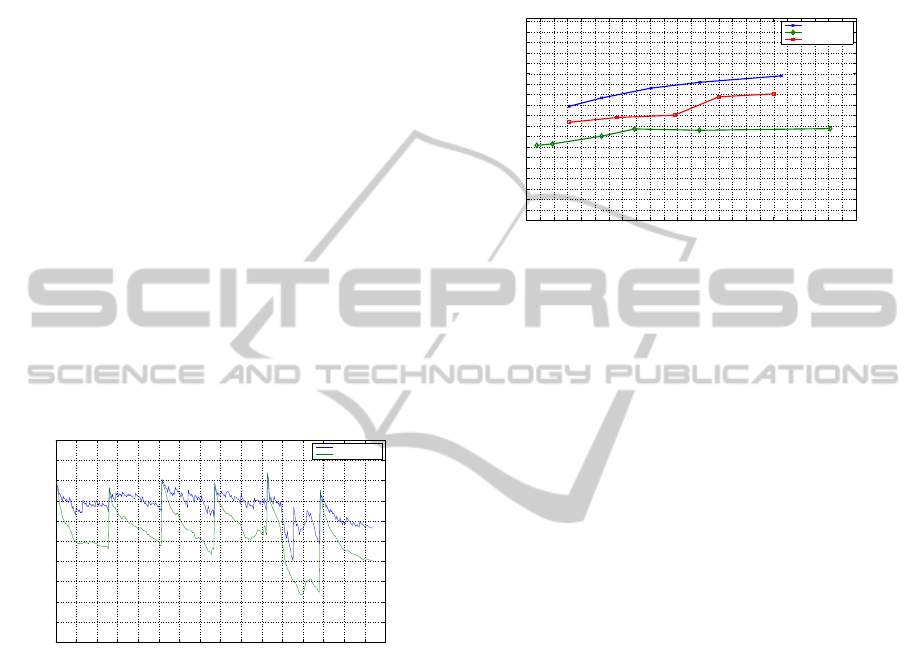
but are the same in all three methods. Figure 3 de-

picts the results of the comparison. The proposed

100 125 150 175 200 225 250 275 300 325 350 375 400 425 450 475 500 525 550 575 600 625 650 675 700

24.5

25.2

25.9

26.6

27.3

28.7

29.4

30.1

30.8

31.5

32.2

32.9

33.6

34.3

35.7

36.4

37.1

37.8

Kbits/sec

PSNR (dB)

Proposed Method

Drift−free Coding

Adaptive Allocation

Figure 3: PSNR at different bit rates with 10% frame loss.

method provides better performance than the drift-

free sequential coding with ﬁxed quantization, and

adaptive bit-rate allocation proposed in (Yang et al.,

2002). The main reason for the better performance of

the proposed method is the shorter dependency chains

in the GOPs. Since the drift error results in more seri-

ous quality degradation when the lost frame is farther

from the end of the dependency chain, the proposed

method experiences alower level of performance loss.

Our ﬁnal experiment evaluates the robustness of

the proposed method in presence of the frame loss.

The experiment includes two cases. In case one sev-

eral frames at random positions of a GOP are lost.

The reconstructed videos when some frames are miss-

ing are evaluated by measuring the PSNR values of:

• the base layer of the delivered frames only where

we assume the videos are scaled down,

• and the base and the enhancement layers, in which

case we assume the videos are transmitted without

scaling down.

The comparative results are illustrated in Figures 4

and 5. The second case for robustness evaluation is

considered to measure the video quality degradation

in presence of burst errors. A burst error is deﬁned

as a sequence of missing frames with a length of 5

to 10 frames. Figures 6 and 7 depict the results of

the burst error experiments. The results of the ex-

periments indicate that the proposed method outper-

forms the traditional video coding methods in pres-

ence of frame losses. The average PSNR values when

both the base and the enhancement layers are deliv-

ered are 31.36(dB) and 27.66(dB) in the proposed

method and the standard video coding respectively.

The average PSNR values when only the base layer

is delivered are 30.58(dB) and 25.80(dB) at the pro-

HierarchicalSNRScalableVideoCodingwithAdaptiveQuantizationforReducedDriftError

121

0 25 50 75 100 125 150 175 200 225 250 275 300 325 350 375 400

2.5

7.5

12.5

17.5

22.5

27.5

32.5

37.5

Frame

PSNR (dB)

Proposed Method

Sequential Coding

Figure 4: PSNR of the reconstructed frames using only the

base layer in presence of single frame losses.

0 25 50 75 100 125 150 175 200 225 250 275 300 325 350 375 400

2.5

7.5

12.5

17.5

22.5

27.5

32.5

37.5

Frame

PSNR (dB)

Proposed Method

Sequential Coding

Figure 5: PSNR of the reconstructed frames using the base

and the enhancement layers in presence of single frame

losses.

posed method and the sequential coding respectively.

This improvement can be associated with two effec-

tive factors. The ﬁrst factor is the hierarchical struc-

ture of arranging the frames which makes the frame

dependency chains shorter in the proposed method.

The second factor which is valid when only the base

layer is delivered is the adaptive quantization of the

frames. We reconstruct the missing frames with a pre-

ceding intact frame having a higher level of accuracy

in the reference frame. The effect of this factor is ev-

ident from the average PSNR values of the delivered

frames where the difference in average PSNR value

when both layers are delivered is 4.78(dB) while it is

3.70(dB) when only the base layer is delivered. The

improvements in the robustness of the video in pres-

ence of burst errors are 3.52(dB) for the base layer

only delivered videos where the average PSNR values

are 22.32(dB) and 18.8(dB) for the proposed method

and the sequential coding respectively, and 4.50(dB)

when the base and the enhancement layers are deliv-

ered with the average PSNR values are 24.01(dB) and

19.51(dB) for the proposed method and the sequential

coding respectively.

It is important to note that the optimization by the

proposed method is carried out after motion estima-

tion and the DCT steps of video coding and hence

quite efﬁcient in terms of processing time.

0 25 50 75 100 125 150 175 200 225 250 275 300 325 350 375 400

2.5

7.5

12.5

17.5

22.5

27.5

32.5

37.5

Frame

PSND (dB)

Proposed Method

Sequential Coding

Figure 6: PSNR of the reconstructed frames using only the

base layer in presence of multiple frame losses.

0 25 50 75 100 125 150 175 200 225 250 275 300 325 350 375 400

2.5

7.5

12.5

17.5

22.5

27.5

32.5

37.5

42.5

Frame

PSNR (dB)

Proposed Method

Sequential Coding

Figure 7: PSNR of the reconstructed frames using the base

and the enhancement layers in presence of multiple frame

losses.

4 CONCLUSIONS

A new scalable video coding method for reducing

drift error has been proposed. The proposed method

utilizes the hierarchical organization of the video

frames, and optimizes coding by adapting quantiza-

tion step size of each frame according to its position

in a GOP. The method is used for SNR, and tempo-

ral video scaling in presence of frame loss in noisy

communication networks. The proposed method im-

proves the performance of the SVC coder by relying

on the observation that elimination of the drift error

reduces the coding performance. Therefore, an opti-

mization should be sought to reduce the distortion due

to the drift error while preserving the quality of the

transmitted video. The optimized video has a multi-

layer SVC format where the enhancement layer size

is adaptively changed according to the network con-

ditions and the frame position in GOP for minimum

distortion. The improvement attained by the proposed

method is at least 3.52(dB) in terms of PSNR values.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

122

REFERENCES

144962, I. (1998). Coding of audio-visual objects.

Abanoz, T. B. and Tekalp, A. M. (2009). Svc-based scal-

able multiple description video coding and optimiza-

tion of encoding conﬁguration. Signal Processing:

Image Communication, 24:691–701.

Adami, N., Signoroni, A., and Leonardi, R. (2007).

State-of-the-art and trends in scalable video compres-

sion with wavelet-based approaches. IEEE Transac-

tions on Circuits and Systems for Video Technology,

17(9):1238–1255.

Goldmann, L., Simone, F. D., Dufaux, F., Ebrahimi, T., Tan-

ner, R., and Lattuada, M. (2010). Impact of video

transcoding artifacts on the subjective quality. Inter-

national Workshop on the Quality of Multimedia Ex-

perience (QoMEX), Second, pages 52–57.

Lan, X., Zheng, N., Xue, J., Gao, B., and Wu, X. (2007).

Adaptive vod architecture for heterogeneous networks

based on scalable wavelet video coding. IEEE Trans-

actions on Consumer Electronics, 53(4):1401–1409.

Lee, Y.-C., Altunbasak, Y., and Mersereau, R. M. (2004).

An enhanced two-stage multiple description video

coder with drift reduction. IEEE Transaction on Cir-

cuits and Systems for Video Technology, 14(1):122–

127.

LOPEZ-FUENTES, F. A. (2011). P2p video streaming

combining svc and mdc. International Journal of Ap-

plied Mathematics and Computer Science, 21(2):295–

306.

Ohm, J. (2005). Advances in scalable video coding. Pro-

ceedings of the IEEE, 93(1):42–56.

Peng, W.-H., Tsai, C.-Y., Chiang, T., and Hang, H.-M.

(2005). Advances of mpeg scalable video coding stan-

dard. Knowledge-Based Intelligent Information and

Engineering Systems, 3684:889–895.

Regunathan, S., Zhang, R., and Rose, K. (2001). Scalable

video coding with robust mode selection. Signal Pro-

cessing: Image Communication, 16(8):725–732.

Reibman, A., Bottou, L., and Basso, A. (2003). Scal-

able video coding with managed drift. IEEE Transac-

tions on Circuits and Systems for Video Technology,

13(2):131–140.

Reibman, A., Bottou, U., and Basso, A. (2001). Dct-based

scalable video coding with drift. IEEE International

Conference on Image Processing (ICIP2001), 2:989–

992.

Schwarz, H., Marpe, D., and Wiegand, T. (2006). Analy-

sis of hierarchical b-pictures and mctf. IEEE Interna-

tional Conference on Multimedia and Expo (ICME),

pages 1929–1932.

Schwarz, H., Marpe, D., and Wiegand, T. (2007a).

Overview of the scalable video coding extension of

the h.264/avc standard. IEEE Transaction on Circuits

and Systems for Video, 17(9):1103–1120.

Schwarz, H., Marpe, D., and Wiegand, T. (2007b).

Overview of the scalable video coding extension of

the h.264/avc standard. IEEE Trans. on Circuits and

Systems for Video Technology, 17(9):1103–1120.

Segall, A. (2007). Ce 8: Svc-to-avc bit-stream rewriting

for coarse grain scalability. Joint Video Team, Doc.

JVT-V035.

Segall, A. and Sullivan, G. J. (2007). Spatial scalability.

IEEE Transaction on Circuits Systems for Video Tech-

nology, 17(9):1121–1135.

Seran, V. and Kondi, L. (2007). Drift controlled scalable

wavelet based video coding in the overcomplete dis-

crete wavelet transform domain. Journal of Image

Communication, 22(4):389–402.

Wien, M., Schwarz, H., and Oelbaum, T. (2007). Perfor-

mance analysis of svc. IEEE Transactions on Circuits

and Systems for Video Technology, 17(9):1194–1203.

Xiang, W., Zhu, C., Siew, C. K., Xu, Y., and Liu, M. (2009).

Forward error correction-based 2-d layered multiple

description coding for error-resilient h.264 svc video

transmission. IEEE Transaction on Circuits and Sys-

tems for Video Technology, 19(12):1730–1738.

Yang, H., Zhang, R., and Rose, K. (2002). Drift manage-

ment and adaptive bit rate allocation in scalable video

coding. IEEE International Conference on Image Pro-

cessing, 2:49–52.

Yin, P., Vetro, A., Lui, B., and Sun, H. (2002). Drift com-

pensation for reduced spatial resolution transcoding.

IEEE Transaction on Circuits and Systems for Video

Technology, 12:1009–1020.

HierarchicalSNRScalableVideoCodingwithAdaptiveQuantizationforReducedDriftError

123