A Haar Wavelet-based Multi-resolution Representation Method of

Time Series Data

Muhammad Marwan Muhammad Fuad

Forskningsparken 3, Institutt for kjemi, NorStruct, The University of Tromsø - The Arctic University of Norway,

NO-9037 Tromsø, Norway

Keywords: Dimensionality Reduction Techniques, Haar Wavelets, Multi-resolution, Similarity Search, Time Series

Data Mining.

Abstract: Similarity search of time series can be efficiently handled through a multi-resolution representation scheme

which offers the possibility to use pre-computed distances that are calculated and stored at indexing time

and then utilized at query time together with filters in the form of exclusion conditions which speed up the

search. In this paper we introduce a new multi-resolution representation and search framework of time

series. Compared with our previous multi-resolution methods which use first degree polynomials to reduce

the dimensionality of the time series at different resolution levels, the novelty of this work is that it applies

Haar wavelets to represent the time series. This representation is particularly adapted to our multi-resolution

approach as discrete wavelet transforms have the ability of reflecting the local and global information

content at every resolution level thus enhancing the performance of the similarity search algorithm, which is

what we have shown in this paper through extensive experiments on different datasets.

1 INTRODUCTION

A time series is an ordered collection of

observations over a period of time. Time series data

arises in many applications including medical,

financial, and engineering. For this reason, time

series data mining has received attention over the

last years.

Time series data mining handles several tasks,

the most important of which are query-by-content,

clustering, and classification. Executing these tasks

requires performing another fundamental task in

data mining which is the similarity search.

A similarity search problem consists of a

database D, a query or a pattern q, which does not

necessarily belong to D, and a constraint that

determines the extent of proximity that the data

objects should satisfy to qualify as answers to that

query.

The time series similarity search problem has

many applications in computer science. Similarity

between two time series can be depicted using a

similarity measure, which is usually a costly

operation compared with other tasks such as CPU

time or even I/O time.

Direct sequential scanning compares every

single time series in D against q to answer this

query. Obviously this is not an efficient approach

given that modern time series databases are usually

very large.

The main framework for reducing the

computational cost of the similarity search problem

is the Generic Multimedia Indexing (GEMINI)

algorithm (Faloutsos et al, 1994). GEMINI reduces

the dimensionality of the time series by converting

them from a point in an n-dimensional space into a

point in an N-dimensional space, where N<<n. If the

similarity measure defined on the reduced space is a

lower bound of the original similarity measure then

the similarity search returns no false dismissals in

this case. A post-processing sequential scan on the

candidate response set is performed to filter out all

the false alarms and return the final response set.

Figure 1 illustrates the GEMINI algorithm.

Dimensionality Reduction Techniques, also

known as Representation Methods, follow the

GEMININ framework to find a faster solution to the

similarity search problem in time series databases.

This is achieved by mapping the time series to

lower dimensional spaces, thus reducing their

dimensionality, and then processing the query in

620

Muhammad Fuad M..

A Haar Wavelet-based Multi-resolution Representation Method of Time Series Data.

DOI: 10.5220/0005307006200626

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 620-626

ISBN: 978-989-758-074-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

those reduced spaces. The main objective of

dimensionality reduction is to reveal data structure

which is hard to obtain from a high-dimensional

space (Yang, 2010).

Figure 1: The GEMINI algorithm for range queries.

Several dimensionality reduction techniques

have been suggested in the literature, of those we

mention: Piecewise Aggregate Approximation

(PAA) (Keogh et al., 2000) and (Yi and Faloutsos,

2000), Piecewise Linear Approximation (PLA)

(Morinaka et al., 2001), and Adaptive Piecewise

Constant Approximation (APCA) (Keogh et al.,

2001).

The problem with all these dimensionality

reduction techniques is that they use a “one-

resolution” approach. The dimension of the reduced

space is decided at indexing time and the

performance at query time depends completely on

the choice made at indexing time. But in practice we

do not necessarily know a priori the optimal

dimension of the reduced space.

This was the motivation behind our multi-

resolution approach which offers more control on

the parameters that determine the effectiveness and

efficiency of the dimensionality reduction methods.

The basis of these multi-resolution methods is to

map the time series to multiple spaces instead of

one. In (Muhammad Fuad and Marteau, 2010b) we

presented Weak-MIR: a multi-resolution indexing

and retrieval method of time series. Weak-MIR is a

standalone method that uses two filters to exclude

non-qualifying time series. Later in (Muhammad

Fuad and Marteau, 2010c) we introduced MIR-X

which associates the multi-resolution approach with

another dimensionality reduction technique. Our last

multi-resolution method Tight-MIR was presented in

(Muhammad Fuad and Marteau, 2010a). Tight-MIR

has the advantages of the two previously mentioned

methods. All these versions were validated through

extensive experiments.

In this paper we introduce a new multi-resolution

method of time series data which uses the Discrete

Wavelet Transform (DWT), namely the Haar

Wavelets, in conjunction with the multi-resolution

approach. This combination boosts the performance

of the multi-resolution approach.

In the following we first present the related

background in Section 2. In Section 3, we introduce

the new method which we validate in Section 4.

Finally, the concluding discussion is presented in

Section 5.

2 BACKGROUND

Multi-representation approaches store data at

different scales called resolution levels. The

principle of this representation is that a

representation of a higher resolution contains all the

data of the lower resolutions (Sun and Zhou, 2005).

Multi-resolution methods are widely used in

multimedia databases. In (Figueras et al., 2002) a

multi-resolution Matching Pursuit is used to

decompose images. Multi-resolution is also used for

a color reduction algorithm in (Ramella and Sanniti

di Baja, 2010). In (Vogiatzis and Tsapatsoulis, 2006)

the authors use multi-resolution schemes to estimate

missing values for DNA micro-arrays.

Multi-resolution methods have also been

exploited in time series information retrieval and

data mining. In (Bergeron and Foulks, 2006) a

visualization application for very large

multidimensional time series datasets is developed.

The proposed data model supports multiple

integrated spatial and temporal resolutions of the

original data. Using multi-resolution techniques to

effectively visualize large time series is also applied

in (Hao et al., 2007) where the proposed framework

uses multiple resolution levels. In (Castro and

Azevedo, 2010) the authors propose a method based

on the multi-resolution property of iSAX (Shieh and

Keogh, 2008), (Shieh and Keogh, 2009) to derive

AHaarWavelet-basedMulti-resolutionRepresentationMethodofTimeSeriesData

621

motifs at different resolutions. In (Lin et al., 2005)

the authors propose a multi-resolution PAA (Keogh

et al, 2000), (Yi and Faloutsos, 2000); a well-known

time series dimensionality reduction technique, to

achieve an algorithm for iterative clustering. This

clustering process is sped up by examining the time

series at increasingly higher resolution levels of the

PAA.

In (Vlachos et al., 2003) and (Lin et al., 2007)

the authors propose a time series k-means clustering

algorithm based on the multi-resolution property of

wavelets. In (Megalooikonomou et al, 2005) and

(Wang et al, 2010) a method of multi resolution

representation of time series is presented.

In (Muhammad Fuad and Marteau, 2010b) we

presented the Multi-resolution Indexing and

Retrieval Algorithm (Weak-MIR). Weak-MIR

involves a multi-resolution representation of time

series. The indexing system stores different numbers

of pre-computed distances, corresponding to the

number of resolution levels. Lower resolution levels

have lower dimensions, so distance computations at

these levels are less costly than higher resolution

levels where dimensions are higher, so distance

evaluations are more expensive. But the

computational complexity at any level is always less

than that of sequential scanning because even at the

highest level the dimension is still lower than that of

the original space which is used in sequential

scanning. The search algorithm of Weak-MIR starts

at the lowest resolution level and tries to exclude the

time series, which are not answers to the query, at

that level where the distances are not costly to

calculate, and the algorithm does not access a higher

level until all the pre-computed distances of the

lower level have been exploited.

Later in (Muhammad Fuad and Marteau, 2010c)

we introduced another version of the multi-

resolution method called MIR-X. MIR-X combines

a representation method with a multi-resolution one,

so we have two representations of each segment of

the time series. We showed in (Muhammad Fuad

and Marteau, 2010c) how MIR-X can boost the

performance of Weak-MIR. MIR-X uses one of the

two filters that Weak-MIR uses together with the

lower-dimensional distance of a time series

dimensionality reduction technique.

In (Muhammad Fuad and Marteau, 2010a) we

presented Tight-MIR which is an improved multi-

resolution indexing and retrieval algorithm. The

principle of Tight-MIR is based on the remark that

the two filters used in Weak-MIR can be applied

separately, so the second filter in Tight-MIR is

applied by directly accessing the raw data in the

original space using a number of points that

corresponds to the dimension of the reduced space at

that resolution level. Tight-MIR has the advantages

of both Weak-MIR and MIR-X in that it is a

standalone method, like Weak-MIR, yet it has the

same competitive performance of MIR-X. This fact

has been shown through extensive experiments.

3 THE HAAR WAVELET-BASED

MULTI-RESOLUTION

METHOD (H-MIR)

Despite the improvement that Weak-MIR, MIR-X

and Tight-MIR offer, they all share a drawback that

hinders their performance; the dimensionality

reduction technique they use, which is first degree

polynomials linking the two end points of each

segment of the time series, is too basic. A more

sophisticated dimensionality reduction technique

that better reflects the local and global information

content of the whole time series at every resolution

level will give better results.

Of all the dimensionality reduction techniques

known in the literature one is particularly adapted

for this purpose. It is Discrete Wavelet Transform

3.1 Discrete Wavelet Transform

(DWT)

Wavelets are mathematical tools for hierarchically

decomposing functions. Regardless of whether the

function of interest is an image, a curve, or a surface,

wavelets offer an elegant technique for representing

the levels of details present (Stollnitz et al., 1995).

Wavelets have successfully been used in many fields

of computer science such as image compression

(DeVore et al., 1992), image querying and many

others. DWT has also been used in time series

information retrieval as a dimensionality reduction

technique (Chan and Wai-chee Fu, 1999),

(Popivanov and Miller, 2002), (Wu et al., 2000). The

advantage that DWT has over other methods in

indexing time series data is that DWT is a multi-

resolution representation method and it can represent

local information in addition to global information.

Table 1: Example of the Haar wavelet decomposition.

Resolution Averages DTW Coefficients

4 [8,4,3,5]

2 [6,4] [2,-1]

1 [5] [1]

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

622

0 20 40 60 80 100 120

-2.5

-2

-1.5

-1

-0.5

0.5

1.5

2.5

Figure 2: DWT representation of a time series.

Haar wavelets are the simplest form of wavelets.

Haar wavelet transform is a series of averaging and

differentiating operations. To get an idea of how 1-

dimensional Haar wavelets work, let us consider the

following 4-dimensional time series:



5,3,4,8s

. By taking the average of each two

successive values we get the following 2-

dimenisonal time series:



4,6



. Recursively

repeating this process we get the full decomposition

s as shown in the Table 1.

So the wavelet transform of

s is



1,2,1,5  .

The principal idea behind using DWT as a

dimensionality reduction technique is that a time

series can uniquely be represented by a wavelet

transform, but by keeping only the

first

N coefficients we can reduce the dimensionality

and keep much of the information that is in the

original time series. For instance, Figure 2 shows the

DWT decomposition at level 7 of a 128-dimension

time series.

A lower bounding distance to the Euclidean

distance was presented in (Chan and Wai-chee Fu,

1999) and it was proven that this lower bound

guarantees no false alarms. It is important to

mention that DWT requires that the length of the

time series be a power of 2.

3.2 The Proposed H-MIR Algorithm

The basis of our new H-MIR representation method

is as follows: let

be the original

n -dimensional

space where the time series are embedded. At each

resolution level k each time series is represented by

DWT (Haar wavelets) keeping the first

coefficients. We refer to this reduced space



The distance between this DWT

representation and the time series is minimal thus

this representation is the best approximation at level

k. The image of all the points of the time series on

DWT is an

n -dimensional vector which we call the

image vector and denote by



s . The DWT

representation at every resolution level is denoted





. We define two distances, the first is

d :

an n-dimensional distance metric (so it is the

distance between two time series in

, or the

distance between a time series and its image vector).

The second distance denoted by

)( kR

d is the

distance between two DWT representations of two

time series at level k. As mentioned in Section 3.1,

this distance is proven to lower bound the Euclidean

distance.

The principle of H-MIR is to speed up the search

by establishing exclusion conditions that filter out

non-qualifying time series using pre-computed

distances.

Given a query

),(



, let

)(k

s ,

)( k

be the

image vectors of

s ,

, respectively, on their DTW

representation at level k. Given that

is metric

and by applying the triangle inequality we get:













Ssqqdsqdsqd

knnkn



)()(

,,,

(1)

The range query can thus be expressed as:









)()(

knkn

qqdsqd 



(2)

Since the distance between

)(k

and s at level

minimal we get:









)()(

knkn

ssdsqd 

(3)

So equation (2) can be written as:









)()(

knkn

qqdssd 



(4)

So all the time series that satisfy:









)()(

knkn

qqdssd 



(5)

are non-qualifying and can be safely excluded.

In a similar manner, and by applying the triangle

inequality again, we get:









)()(

knkn

ssdqqd 



(6)

Equation (6) implies that all the time series that

satisfy:









)()(

knkn

ssdqqd 



(7)

are non-qualifying and can also be excluded.

From equations (5) and (7) we get the first filter

of H-MIR which is:













)()(

knkn

ssdqqd

(8)

In addition to the above filter H-MIR, and at

AHaarWavelet-basedMulti-resolutionRepresentationMethodofTimeSeriesData

623

4 6 8 10 12 14 16 18 20

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

x 10



Latency Time

Foetal ecg

Tight-MIR

H-MIR

1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6

x 10



Latency Time

Yoga

Tight-MIR

H-MIR

1 2 3 4 5 6 7 8

0.5

1.5

2.5

x 10



Latency Time

CBF

Tight-MIR

H-MIR

1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6

x 10



Latency Time

Wafer

Tight-MIR

H-MIR

1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2

x 10



Latency Time

Gun Point

Tight-MIR

H-MIR

1 2 3 4 5 6 7 8 9

0.5

1.5

2.5

3.5

x 10



Latency Time

FaceAll

Tight-MIR

H-MIR

Figure 3: Comparison of the latency time between MIR-Tight and H-MIR on datasets (Foetal ecg), (CBF), (Yoga), (Wafer),

(GunPoint) and (FaceAll).

each resolution level k, uses the following exclusion

condition:









)()()(

kRkRkR

sqd

(9)

Equation (9) is the second filter of H-MIR.

Indexing Time: At each resolution level k the time

series are mapped to a

–dimension space using a

DWT transform and keeping the first

coefficients.

We compute and store all the distances





Ssssd

,,

)(

Query Time: The query is also mapped to a

–

dimension space using a DWT transform and

keeping the first

coefficients.

The first filter has a much lower computational cost

than the second filter as it does not include any

online distance evaluation. The computational cost

of the second filter also increases as the resolution

level gets higher.

After applying the first filter to all time series at

all resolution levels, we apply the second filter.

This filter is applied starting the lowest level first

before moving to the higher level because this filter

requires computing

whose computational cost

increases as the resolution level gets higher, but the

pruning power of the second filter also rises as we

move to higher resolution levels.

4 EXPERIMENTS

In order to evaluate the performance of our new

method H-MIR we conducted several similarity

search experiments on different time series datasets

from different time series repositories (Povinelli),

(SISTA's Identification Database), (StatLib -

Datasets Archive), (Keogh et al., 2011) using

different threshold values. In our experiments we

compared H-MIR against Tight-MIR since it was

shown in (Muhammad Fuad and Marteau, 2010a)

that Tight-MIR outperforms both Weak-MIR and

MIR-X.

As mentioned in Section 3.1 DWT is applicable

to time series whose lengths are of the power of 2,

so when this was not the case for the dataset tested

we truncated the time series.

As in (Muhammad Fuad and Marteau, 2010a),

the comparison criteria was based on the latency

time concept presented in (Schulte et al., 2005)

which calculates the number of cycles the processor

takes to perform different arithmetic operations (>,+

- ,*,abs, sqrt) to execute the similarity search. This

number for each operation is multiplied by the

latency time of that operation to get the total latency

time of the similarity search. The latency time is 5

cycles for (>, + -), 1 cycle for (abs), 24 cycles for

(*), and 209 cycles for (sqrt) (Schulte et al., 2005).

In the first set of experiments we compared H-

MIR against Tight-MIR on different datasets of

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

624

10 15 20 25 30 35 40

x 10



Latency Time

motorCurrent

Tight-MIR

H-MIR

Sequential Scan

1 1.2 1.4 1.6 1. 8 2 2.2 2.4 2.6 2.8 3

x 10



Latency Time

Wind

Tight-MIR

H-MIR

Sequential Scan

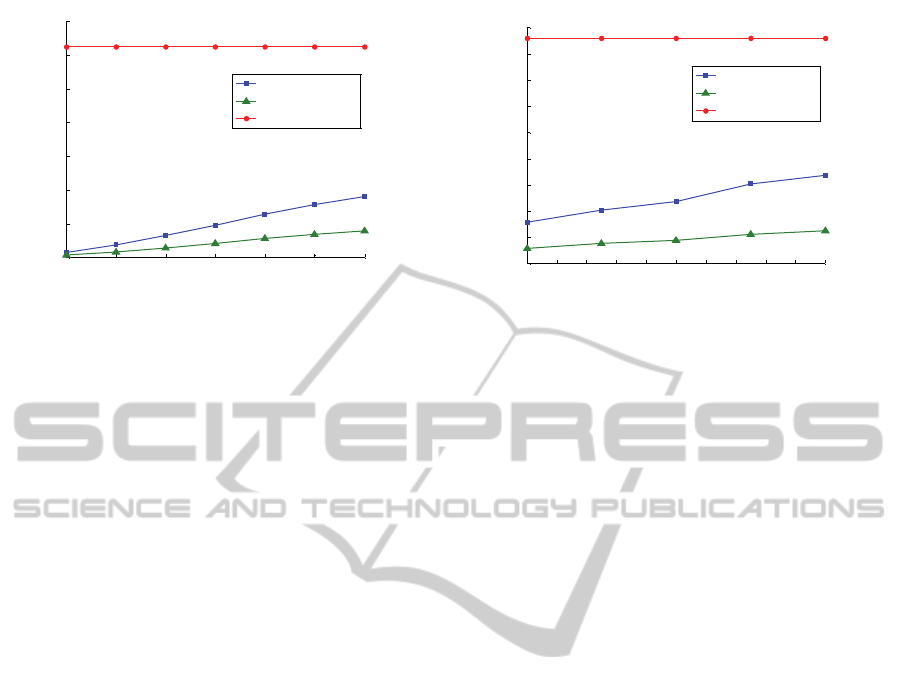
Figure 4: The latency time of H-MIR, Tight-MIR, and sequential scanning on datasets (motoCurrent) and (Wind).

different dimensionalities and sizes and for different

threshold values. In Figure 3 we present some of the

results obtained.

The results obtained show that H-MIR

outperforms Tight-MIR on all these datasets and for

all values of the threshold ε.

As in (Muhammad Fuad and Marteau, 2010a),

we also tested the stability of H-MIR on a wide

range of time series dimension. We report in Figure

4 the results of the similarity search on two time

series with very different dimensions, the first is

(Wind) whose dimension is 12, and the second is

(motoCurrent) whose dimension is 1500. These

experiments were conducted for different values of

the threshold ε. For comparison, we also report the

results obtained by using Tight-MIR and sequential

scanning. This latter method represents the baseline

performance.

As we can see, H-MIR has a stable performance

on time series of different dimensions, which is the

same advantage that Tight-MIR has.

5 CONCLUSIONS

We presented in this paper a new representation

method of time series data which, in contrast to

other time series representation methods, uses

multiple spaces to represent the data. We also

proposed a framework for performing the similarity

search using the new method. This framework

reduces the number of online distance evaluations by

using pre-computed distances and exclusion

conditions. The particularity of the new method over

other multi-resolution representation methods is that

the new method uses a dimensionality reduction

technique, DWT, which is especially adapted for our

method owing to its multi-resolution nature. We

validated our new method through experiments on

datasets from different time series archives.

We believe our new method can be extended to

handle other data types, especially to process image

querying where the concept of multi-resolution

levels is pertinent and where DWT is widely used.

REFERENCES

Bergeron, R. D., and Foulks, A., 2006: Interactive out-of-

core visualization of multiresolution time series data,

numerical modeling of space plasma flows:

ASTRONUM-2006. Proceedings of the 1st IGPP-

CalSpace International Conference, Palm Springs,

California.

Castro, N., and Azevedo, P., 2010: Multiresolution motif

discovery in time series. Proceedings of the SIAM

International Conference on Data Mining, SDM 2010,

, Columbus, Ohio, USA. SIAM.

Chan, K., and Wai-chee Fu, A., 1999: Efficient time series

matching by wavelets. In Proc. 15th. Int. Conf. on

Data Engineering.

DeVore, R., Jawerth, B. and Lucier, B., 1992: Image

compression through wavelet transform coding. IEEE

Transactions on Information Theory.

Faloutsos, C., Ranganathan, M., and Manolopoulos, Y.,

1994: Fast subsequence matching in time-series

databases. In Proc. ACM SIGMOD Conf.,

Minneapolis.

Figueras i Ventura R. M., Frossard P., and Vandergheynst

P., 2002: Evolutionary multiresolution matching

pursuit and its relations with the human visual system.

In Proceedings of the European Signal Processing

Conference, Toulouse, France.

Hao, M., Dayal, U., Keim, D. A., Schreck, T., 2007:

Multi-resolution techniques for visual exploration of

large time-series data. Proc. of Eurographics/IEEE-

VGTC Symposium on Visualization.

Jacobs, C. E., Finkelstein, A., and Salesin, D. H., 1995:

Fast multiresolution image querying. In Proceedings

of SIGGRAPH 95, ACM, New York.

Keogh, E., Chakrabarti, K., Pazzani, M., and Mehrotra,

AHaarWavelet-basedMulti-resolutionRepresentationMethodofTimeSeriesData

625

2000. Dimensionality reduction for fast similarity

search in large time series databases. J. of Know. and

Inform. Sys.

Keogh, E., Chakrabarti, K,. Pazzani, M., and Mehrotra, S.,

2001: locally adaptive dimensionality reduction for

similarity search in large time series databases.

SIGMOD.

Keogh, E., Zhu, Q., Hu, B., Hao. Y., Xi, X., Wei, L. &

Ratanamahatana, C.A., 2011. The UCR Time Series

Classification/Clustering Homepage: www.cs.ucr.edu/

~eamonn/time_series_data/

Lin, J., Vlachos, M., Gunopulos, D., Keogh, E., 2007:

Multi-Resolution Time Series Clustering and

Application to Images. Multimedia Data Mining and

Knowledge Discovery, Springer.

Lin, J., Vlachos, M., Keogh, E., and Gunopulos, D., 2005:

A MPAA-based iterative clustering algorithm

augmented by nearest neighbors search for time-series

data streams. Proceedings of the 9th Pacic-Asia

Conference on Knowledge Discovery and Data

Mining (PAKDD'05), Springer.

Megalooikonomou, C., 2005: Multiresolution symbolic

representation of time series. In Proceedings of the

21st IEEE International Conference on Data

Engineering (ICDE). Tokyo, Japan.

Morinaka, Y., Yoshikawa, M., Amagasa, T., and Uemura,

S., 2001: The L-index: An indexing structure for

efficient subsequence matching in time sequence

databases. In Proc. 5th Pacific Asia Conf. on

Knowledge Discovery and Data Mining.

Muhammad Fuad, M. M., Marteau, P. F., 2010a: Fast

retrieval of time series by combining a multiresolution

filter with a representation technique. The

International Conference on Advanced Data Mining

and Applications–ADMA2010, ChongQing, China.

Muhammad Fuad, M. M., Marteau P. F., 2010b: Multi-

resolution approach to time series retrieval. Fourteenth

International Database Engineering & Applications

Symposium– IDEAS 2010, Montreal, QC, Canada.

Muhammad Fuad, M. M., Marteau P. F., 2010c: Speeding-

up the similarity search in time series databases by

coupling dimensionality reduction techniques with a

fast-and-dirty filter. Fourth IEEE International

Conference on Semantic Computing– ICSC 2010,

Carnegie Mellon University, Pittsburgh, PA, USA.

Popivanov, I., and Miller, R. J., 2002: Similarity search

over time series data using wavelets. ICDE.

Povinelli, R., http://povinelli.eece.mu.edu/

Ramella, G., Sanniti di Baja, G., 2010: Multiresolution

histogram analysis for color reduction, Progress in

Pattern Recognition, Image Analysis, Computer

Vision, and Applications - 15th Iberoamerican

Congress on Pattern Recognition, CIARP 2010, Sao

Paulo, Brazil.

Schulte, M. J., Lindberg, M. and Laxminarain, A., 2005:

Performance evaluation of decimal floating-point

arithmetic In IBM Austin Center for Advanced Studies

Conference.

Shieh, J., and Keogh, E., 2009: iSAX: Disk-aware mining

and indexing of massive time series datasets. Data

Mining and Knowledge Discovery.

Shieh, J., and Keogh, E., 2008: iSAX: Indexing and

mining terabyte sized time series. In Proceeding of the

14th ACM SIGKDD international Conference on

Knowledge Discovery and Data Mining, Las Vegas,

Nevada, USA.

SISTA's Identification Database. http://www.esat.

kuleuven.ac.be/~tokka/daisydata.html.

StatLib - Datasets Archive. http://lib.stat.cmu.edu/

datasets/.

Stollnitz, E., DeRose, T., and Salesin, D., 1995: Wavelets

for computer graphics: a primer, part 1. IEEE

Computer Graphics and Applications.

Sun, S., and Zhou, X., 2005: Semantic caching for web-

based spatial applications. In Proceeding of APWeb

2005, Shanghai, China.

Vlachos, M., Lin, J., Keogh, E., Gunopulos, D., 2003:

Multi-resolution k-means clustering of time series and

applications to images. Workshop on Multimedia Data

Mining (MDM), SIGKDD.

Vogiatzis, D., Tsapatsoulis, N., 2006: Missing value

estimation for DNA microarrays with mutliresolution

schemes. Lecture Notes in Computer Science,

Springer Berlin / Heidelberg. Artificial Neural

Networks - ICANN.

Wang, Q., Megalooikonomou, V., and Faloutsos, C.,

2010: Time series analysis with multiple resolutions.

Inf. Syst. 35, 1.

Wu, Y. L., Agrawal, D., and Abbadi, A. E., 2000: A

comparison of DFT and DWT based similarity search

in time-series databases. In Proc. 9th Int. Conf. on

Information and Knowledge Management.

Yang, Z., 2010: Machine learning approaches to

bioinformatics. 1st. World Scientific Printers;

Singapore.

Yi, B. K., and Faloutsos, C., 2000: Fast time sequence

indexing for arbitrary Lp norms. Proceedings of the

26th International Conference on Very Large

Databases, Cairo, Egypt.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

626