
A Perceptual Measure of Illumination Estimation Error
Nikola Bani
´
c and Sven Lon
ˇ
cari
´
c
Image Processing Group, Department of Electronic Systems and Information Processing, Faculty of Electrical Engineering
and Computing, University of Zagreb, 10000 Zagreb, Croatia
Keywords:
Color Constancy, Illumination Estimation, Image Enhancement, Perception, White Balancing.
Abstract:
The goal of color constancy is to keep colors invariant to illumination. An important group of color constancy
methods are the global illumination estimation methods. Numerous such methods have been proposed and
their accuracy is usually described by using statistical descriptors of illumination estimation angular error. In
order to demonstrate some of their fallacies and shortages, a very simple learning-based global illumination
estimation dummy method is designed for which the values of statistical descriptors of illumination estima-
tion error can be interpreted in contradictory ways. To resolve the paradox, a new performance measures is
proposed that focuses on perceptual difference between different illumination estimation errors. The effect of
ground-truth illumination distribution of the benchmark datasets on method evaluation is also demonstrated.
1 INTRODUCTION
Achieving color constancy means keeping image col-
ors invariant to scene illumination (Ebner, 2007) that
often alters them as shown in Fig. 1. This is impor-
tant before further image processing processing and it
is done in two steps: illumination estimation, which
is the crucial step, and chromatic adaptation i.e. re-
moving the illumination cast. In most cases for color
constancy the following image f formation process
with Lambertian assumption included is used:
f
c
(x) =
Z
ω
I(λ, x)R(x, λ)ρ
c
(λ)dλ (1)
where c is a color channel, x is a given image pixel,
λ is the wavelength of the light, ω is the visible spec-
trum, I(λ, x) is the spectral distribution of the light
source, R(x, λ) is the surface reflectance, and ρ
c
(λ) is
the camera sensitivity of the c-th color channel. Uni-
form illumination is often assumed and this leads to
removing x from I(λ, x). Then the observed color of
the light source e is:
e =
e
R
e
G
e
B
=
Z
ω
I(λ)ρ(λ)dλ. (2)
Only the direction of e is needed to perform
chromatic adaptation. Because the values of I(λ)
and ρ
c
(λ) are often unknown, calculating e is
an ill-posed problem. It is solved by making as-
sumptions, which has resulted in numerous color
(a) (b)
Figure 1: The same scene (a) with and (b) without illumi-
nation color cast.
constancy methods that can be split in at least two
groups. In the first group are low-level statistics-
based methods like White-patch (WP) (Land, 1977)
and its improved version (Bani
´
c and Lon
ˇ
cari
´
c,
2014b), Gray-world (GW) (Buchsbaum, 1980),
Shades-of-Gray (SoG) (Finlayson and Trezzi,
2004), Grey-Edge (1st and 2nd order (GE1 and
GE2)) (Van De Weijer et al., 2007a), Weighted
Gray-Edge (Gijsenij et al., 2012), Color Spar-
row (CS) (Bani
´
c and Lon
ˇ
cari
´
c, 2013), Color
Rabbit (CR) (Bani
´
c and Lon
ˇ
cari
´
c, 2014a), using
color distribution (CD) (Cheng et al., 2014b). The
second group is composed of learning-based methods
like gamut mapping (pixel, edge, and intersection
based - PG, EG, and IG) (Finlayson et al., 2006),
using high-level visual information (HLVI) (Van
De Weijer et al., 2007b), natural image statis-
tics (NIS) (Gijsenij and Gevers, 2007), Bayesian
learning (BL) (Gehler et al., 2008), spatio-spectral
learning (maximum likelihood estimate (SL) and
136
Bani
´
c N. and Lon
ˇ
cari
´
c S..
A Perceptual Measure of Illumination Estimation Error.
DOI: 10.5220/0005307501360143
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 136-143
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

with gen. prior (GP)) (Chakrabarti et al., 2012),
exemplar-based learning (EB) (Joze and Drew,
2012), Color Cat (CC) (Bani
´
c and Lon
ˇ
cari
´
c, 2015).
Most digital cameras have color constancy im-
plemented at the beginning of their image pipeline
so it operates on raw linear images (Gijsenij et al.,
2011). The implemented illumination estimation
method should be as precise and as fast as possible
because of the digital cameras’ limited computational
power. To determine which of the methods that are
fast enough should be used, accuracy comparison is
conducted by comparing statistical descriptors of il-
lumination estimation error. In this paper it is shown
that the mostly used descriptors may be misleading in
showing the methods’ practical performance.
For the sake of demonstration, a learning-based
global illumination estimation dummy method is de-
signed in a way to make two of the mostly used error
statistical descriptors give contradictory accounts on
the method’s accuracy. The contradiction is resolved
through discussion and by proposing a new illumina-
tion estimation performance measure. It combines the
good properties of some of the mostly used statisti-
cal descriptors and it takes the perceptual error into
account. Additionally, the negative effect of faulty
design of the benchmark datasets on comparison be-
tween different methods is also shown.
The paper is structured as follows: In Section II
the illumination estimation evaluation for global il-
lumination estimation methods is explained, in Sec-
tion III the dummy method intended to show the eval-
uation shortages is described and tested, in Section
IV the results are discussed, and in Section V a new
illumination estimation performance measure is pro-
posed.
2 ESTIMATION EVALUATION
2.1 Benchmark Datasets
The first thing required to conduct a global illumina-
tion estimation method testing is a benchmark dataset.
Such dataset contains images and their ground-truth
illumination. The ground-truth illumination is usually
extracted by placing a calibration object into the scene
of each dataset image. The color of the achromatic
surface of the calibration object e.g. gray patches or
gray ball is then used as ground-truth illumination,
which is provided together with the images. Some of
the color constancy datasets are the GreyBall (Ciurea
and Funt, 2003), the ColorChecker (Gehler et al.,
2008) and its re-processed linear version (L. Shi,
2014), the NUS datasets (Cheng et al., 2014b). The
GreyBall dataset contains 11346 non-linear images,
which were taken from a video sequence. Very often
its linear version is used and it is obtained by perform-
ing an approximate inverse gamma correction of the
original images.
2.2 Error Description
Before a color constancy method is applied to an im-
age, first the calibration object has to be masked out.
When the illumination estimation is performed, the
angle between it and the ground-truth illumination is
calculated and it serves as the angular error. After this
procedure is performed for all images of the dataset,
all of the per image angular errors are described by
means of statistical descriptors. Since the distribution
of the angular errors is not symmetrical, the most used
descriptor is the median of the angular error (Hordley
and Finlayson, 2004). Some other useful descriptors
include the mean and the trimean of the angular error.
In many cases a method having a lower median angu-
lar error is considered to be better than some other
method having a higher median angular error. Al-
though other illumination estimation error measures
exist e.g. different mathematical and perceptual dis-
tances, angular error is the most widely used error
measure and it has a high correlation with the sub-
jective measures (Gijsenij et al., 2009). However, ev-
ery objective error measure including angular error is
only an approximation of the perceived error because
the human vision color constancy is incomplete and
scene dependent.
3 THE DUMMY METHOD
3.1 Motivation
The reason for introducing a dummy method for
global illumination estimation is to show the fallacies
and shortages of the mostly used angular error statis-
tical descriptors. Since assumptions are needed for il-
lumination estimation methods, let’s consider several
facts and assumptions to show how foundations of the
dummy method might hypothetically be reasoned.
The first one is that most common illuminations
are daylight, sunlight, or some kind of incandes-
cence. It has been shown that all of these have a
spectrum that can be modelled by the black-body ra-
diation (Judd et al., 1964) (Finlayson and Schaefer,
2001). Since assumptions are needed for the process
of illumination estimation, the next step is to assume
that some of the illuminations occur more often than
the other. This assumption can be confirmed to some
APerceptualMeasureofIlluminationEstimationError
137
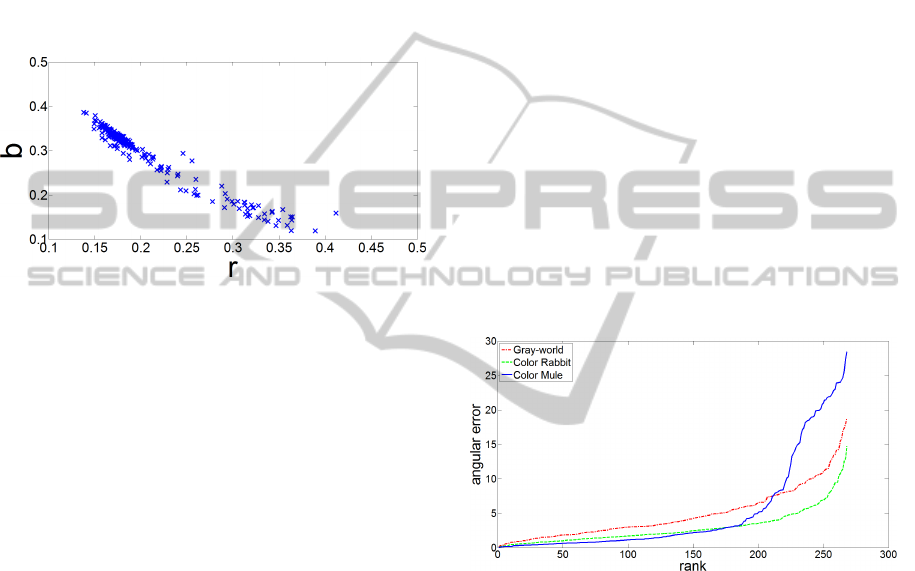
degree by looking at the distribution of real-life illu-
minations by taking the ground-truth illuminations of
illumination estimation benchmark datasets. Fig. 2
shows the chromaticites of ground-truth illumination
of the Sony dataset (Cheng et al., 2014b). It can be
seen that some regions of the chromaticity space are
filled denser than the some other ones. This also holds
for the remaining NUS datasets (Cheng et al., 2014b)
and other datasets as well. Because it is evident that
some illuminations are more probable to occur, this
fact should be somehow used to obtain a better illu-
mination estimation.
Figure 2: The rb-chromaticities of the Sony dataset (Cheng
et al., 2014b) ground-truth illuminations.
3.2 Realization
Beside accuracy, computation speed is also consid-
ered in illumination estimation method design. In or-
der to assure that the dummy method is fast, it is de-
signed to assume that some illuminations occur more
often and therefore to simply select one fixed illumi-
nation value, which is returned as illumination es-
timation for every given image. This value is ob-
tained in the learning process in which for each of
the ground-truth illuminations from the learning set
the angles between it and the rest of the learning set
ground-truth illuminations are calculated. The illumi-
nation that results in angles with the lowest median
angle is then selected to be the fixed value. If the as-
sumption holds, then in the testing phase this value
should produce a relatively good illumination for the
majority of the images whose scenes are lit by the
most often illuminations.
Since this dummy method always stubbornly
gives the same illumination estimation, it is named
Color Mule (CM) for the purpose of a simpler nota-
tion in the rest of the paper.
3.3 Experimental Results
Illumination estimation is widely applied in digital
cameras at the beginning of the image processing
pipeline on raw images (Gijsenij et al., 2011) and
the image formation model used in Eq. (1) is lin-
ear. Therefore the NUS datasets with linear images
were used. Each of these datasets contains images
taken with a different camera. The well-known re-
processed linear version (L. Shi, 2014) of the original
ColorChecker dataset (Gehler et al., 2008) was not
used because in the majority of papers the black level
was erroneously not subtracted from the images be-
fore the testing procedure (Lynch et al., 2013), which
may lead to confusion when comparing the results of
methods from different publications.
Since the dummy CM method is a learning-based
one, it was tested by conducting a three-fold cross-
validation on the benchmark datasets. Table 1 shows
the angular error statistics for CM and other methods.
The results for other methods were taken from (Cheng
et al., 2014b) and (Cheng et al., 2014a). In terms of
median angular error, which is the most important,
CM outperforms all other methods on most of the
datasets. However, its trimean and especially mean
angular errors are far from being the best. Such dis-
agreement between the most important angular error
statistical descriptors opens the questions how to in-
terpret these results.
Figure 3: Comparison of sorted angular errors on the Sony
dataset (Cheng et al., 2014b) for the Gray-world, Color
Rabbit, and Color Mule.
4 DISCUSSION
4.1 Angular Error Distribution
When CM is excluded, then for 90% of all pairs com-
posed of methods from Table 1 it holds that if the
mean angular error of the pair’s first method is greater
than the mean angular error of the second method,
then so is the median angular error and vice versa.
On the other hand, when considering only pairs where
one of the methods is CM, this holds for only 33% of
them indicating a discrepancy between the mean and
median.
The first step to resolve the paradox of contradict-
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
138

Table 1: Angular error of selected low-level statistics-based methods, the proposed dummy method, and selected learning-
based methods on nine NUS benchmark image databases (lower is better).
Low-level statistics-based methods Learning-based methods
Method CR CD GW WP GGW GE1 GE2 CM PG EG IG ML GP NIS
Dataset Mean angular error (
◦
)
Canon1 3.09 2.93 5.16 7.99 3.16 3.45 3.47 5.43 6.13 6.07 6.37 3.58 3.21 4.18
Canon2 2.81 2.81 3.89 10.96 3.24 3.22 3.21 5.46 14.51 15.36 14.46 2.80 2.67 3.43
Fuji 2.94 3.15 4.16 10.20 3.42 3.13 3.12 5.79 8.59 7.76 6.80 3.12 2.99 4.05
Nikon1 3.06 2.90 4.38 11.64 3.26 3.37 3.47 6.26 10.14 13.00 9.67 3.22 3.15 4.10
Oly 2.65 2.76 3.44 9.78 3.08 3.02 2.84 5.29 6.52 13.20 6.21 2.92 2.86 3.22
Pan 2.89 2.96 3.82 13.41 3.12 2.99 2.99 5.70 6.00 5.78 5.28 2.93 2.85 3.70
Sam 2.94 2.91 3.90 11.97 3.22 3.09 3.18 5.72 7.74 8.06 6.80 3.11 2.94 3.66
Sony 2.88 2.93 4.59 9.91 3.20 3.35 3.36 5.07 5.27 4.40 5.32 3.24 3.06 3.45
Nikon2 3.57 3.81 4.60 12.75 4.04 3.94 3.95 7.66 11.27 12.17 11.27 3.80 3.59 4.36
Dataset Median angular error (
◦
)
Canon1 2.08 2.01 4.15 6.19 2.35 2.48 2.44 1.88 4.30 4.68 4.72 2.80 2.67 3.04
Canon2 1.86 1.89 2.88 12.44 2.28 2.07 2.29 1.87 14.83 15.92 14.72 2.32 2.03 2.46
Fuji 1.84 2.15 3.30 10.59 2.60 1.99 2.00 2.15 8.87 8.02 5.90 2.70 2.45 2.95
Nikon1 1.91 2.08 3.39 11.67 2.31 2.22 2.19 1.89 10.32 12.24 9.24 2.43 2.26 2.40
Oly 1.79 1.87 2.58 9.50 2.15 2.11 2.18 1.71 4.39 8.55 4.11 2.24 2.21 2.17
Pan 1.70 2.02 3.06 18.00 2.23 2.16 2.04 1.59 4.74 4.85 4.23 2.28 2.22 2.28
Sam 1.88 2.03 3.00 12.99 2.57 2.23 2.32 1.99 7.91 6.12 6.37 2.51 2.29 2.77
Sony 2.10 2.33 3.46 7.44 2.56 2.58 2.70 1.81 4.26 3.30 3.81 2.70 2.58 2.88
Nikon2 2.42 2.72 3.44 15.32 2.92 2.99 2.95 2.38 10.99 11.64 11.32 2.99 2.89 3.51
Dataset Trimean angular error (
◦
)
Canon1 2.56 2.22 4.46 6.98 2.50 2.74 2.70 2.47 4.81 4.87 5.13 2.97 2.79 3.30
Canon2 2.17 2.12 3.07 11.40 2.41 2.36 2.37 2.71 14.78 15.73 14.80 2.37 2.18 2.72
Fuji 2.13 2.41 3.40 10.25 2.72 2.26 2.27 2.97 8.64 7.70 6.19 2.69 2.55 3.06
Nikon1 2.23 2.19 3.59 11.53 2.49 2.52 2.58 2.87 10.25 11.75 9.35 2.59 2.49 2.77
Oly 2.01 2.05 2.73 9.54 2.35 2.26 2.20 2.60 4.79 10.88 4.63 2.34 2.28 2.42
Pan 2.12 2.31 3.15 14.98 2.45 2.25 2.26 2.64 4.98 5.09 4.49 2.44 2.37 2.67
Sam 2.18 2.22 3.15 12.45 2.66 2.32 2.41 2.79 7.70 6.56 6.40 2.63 2.44 2.94
Sony 2.26 2.42 3.81 8.78 2.68 2.76 2.80 2.40 4.45 3.45 4.13 2.82 2.74 2.95
Nikon2 2.67 3.10 3.69 13.80 3.22 3.21 3.38 4.96 11.11 12.01 11.30 3.11 2.96 3.84
ing statistical descriptor values is to look at the actual
angular errors. Fig. 3 shows the sorted angular er-
rors on the Sony (Cheng et al., 2014b) dataset for the
well-known Gray-World method, the accurate Color
Rabbit method, and the dummy Color Mule method.
It can be seen that for about slightly more than half
of the images CM results in a relatively low angular
error, which in turn results in a low median. How-
ever, the tail of CM’s angular error distribution con-
tains significantly higher values than the tails of other
methods’ angular error distributions. Since the me-
dian does not consider this, it is automatically ren-
dered not to be informative enough to provide a good
description of CM’s performance.
4.2 Perceptual Significance of the
Angular Error
It might seem that for CM a better descriptor would
be the mean angular error. But before drawing con-
clusions like this one, first the perceptual significance
of the angular error should be considered. Under We-
ber’s law (Weber, 1846) the just noticeable difference
increases linearly with the absolute error as was con-
firmed in (Gijsenij et al., 2009). In the same paper
a simple example is given to clarify this: while the
difference between the results of algorithms with er-
rors of 3
◦
and 4
◦
is noticeable to most people, this is
hardly the case if these errors are 15
◦
and 16
◦
. This
is explained even further by obtained experimental re-
sults. If ε
min
and ε
max
are two illumination estimation
angular errors with ε
max
being the greater one, then
the difference ∆ε = ε
max
− ε
min
between them is no-
ticeable if it is at least 0.06 · ε
max
. This means that for
an noticeable improvement an error ε has to be low-
ered to
ε
0
= (1 − 0.06) · ε = 0.94 · ε. (3)
For a noticeable decline the error ε has to be raised to
ε
∗
=
1
1 − 0.06
· ε =
1
0.94
· ε. (4)
This shows the weakness of the mean angular er-
ror, which does not take into account the percep-
APerceptualMeasureofIlluminationEstimationError
139

tual difference as can be demonstrated by choosing a
method and creating its degraded version. The degra-
dation process is done by increasing the all of the ini-
tial method’s angular errors by 5%, which is less then
needed for a noticeable difference. By degrading the
Color Rabbit method on the Sony dataset, its mean
angular error raises from 2.88
◦
to 3.02
◦
even though
there is no noticeable difference between the results
of the initial and degraded method on individual im-
ages. If the degradation is performed in another way
by choosing five errors that are less than 1
◦
and in-
creasing them by 5
◦
, the Color Rabbit’s mean raises
to 3.01
◦
, which is less than 3.02
◦
in the first case, but
it nevertheless results in five noticeable and serious il-
lumination estimation accuracy deteriorations in con-
trast to the first degradation way.
Since both the mean and the median angular errors
have shortages with respect to describing a method’s
performance, a better measure containing the best of
these two statistical descriptors and taking into ac-
count the perceptual difference should be devised.
5 PROPOSED MEASURE
5.1 Definition
To resolve the paradox caused by describing the Color
Mule’s performance using the mean and median an-
gular errors, we propose a new error measure based
on the angular errors and two facts about their percep-
tion. The first one is that an angular error below 1
◦
is
not noticeable (Finlayson et al., 2005) (Fredembach
and Finlayson, 2008). The errors ε ∈ [0
◦
, 1
◦
] should
therefore not be penalized. The second fact is the al-
ready mentioned linear increase of the just noticeable
difference with the absolute error as stated by Weber’s
law and described by Eq. (3) and Eq. (4). Based on
these equations an error ε > 1 can be described by us-
ing the number of just noticeable differences n that
have led to its distancing from the 1
◦
:
ε =
1
0.94
n
. (5)
Since n takes into account the actual linear percep-
tual difference caused by the angular error, we pro-
pose it to be the basis for describing the perceptual
error of the illumination estimation. It is calculated as
follows:
n = log
1
0.94
ε =
lnε
ln
1
0.94
. (6)
Since
1
ln
1
0.94
is a constant, it has no impact on errors
comparison. Therefore a slightly modified difference
description m can be used:
m = nln
1
0.94
= lnε. (7)
The expression in Eq. (7) can be additionally inter-
preted by looking at its derivative:
dm =
dε
ε
. (8)
As expected from the previous discussion, the in-
crease of the perceptual difference is directly pro-
portional to the increase of the angular error and in-
versely proportional to the angular error that is in-
creased. Like in Weber’s law, this means that in order
to achieve the same perceptual difference, for higher
angular errors the angular increase has to be larger
then for the lower angular errors.
For the general case where ε > 0 the measure m
from Eq. (7) is given as follows:
m =
(
0 if 0 ≤ ε ≤ 1
lnε if ε > 1
. (9)
The simplest way to use this measure to describe a
methods performance on an image dataset is to calcu-
late its mean value for all angular errors. The advan-
tage of this mean over the mean angular error is that
it considers the perceptual differences between differ-
ent angular errors and its advantage over the median
angular error is that is considers all angular errors.
5.2 Experimental Results
Table 2 shows the value of the proposed measure
for the dummy Color Mule and some of the selected
methods. The ranking between other methods ex-
cluding Color Mule remained the same as the rank-
ing based on the median angular error. Color Mule
is now ranked lower than the Color Rabbit and Color
Distribution methods, but higher than the Gray-world
and White-patch methods. The exception is only the
Olympus dataset where the Gray-world method out-
performs Color Mule. It can be seen that the proposed
measure penalizes the angular error distribution tail
of the proposed method, but not as strict as the mean
angular error. On the other hand it does not simply
disregard it as the median angular error thus avoiding
confusion. The sorted proposed measure values on
the Sony dataset for several chosen methods can be
seen in Fig. 4.
5.3 Dataset Illumination Distribution
The proposed measure mostly resolves the paradox
that resulted from the proposed method. However,
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
140

Table 2: Proposed measure for several selected methods on
nine NUS benchmark image databases (lower is better).
Selected methods
Method CR CD GW WP CM
Dataset Proposed measure
Canon1 0.8875 0.8233 1.2945 1.7062 1.0165
Canon2 0.7823 0.8003 1.0950 2.0899 1.0361
Fuji 0.8058 0.8419 1.1384 2.0114 1.0748
Nikon1 0.8418 0.8785 1.1658 2.0879 1.1010
Oly 0.7442 0.7667 0.9843 1.9116 0.9980
Pan 0.7878 0.8409 1.0887 2.3174 0.9959
Sam 0.8223 0.8256 1.1042 2.2348 1.0723
Sony 0.8345 0.8485 1.3177 1.8817 0.9565
Nikon2 1.0194 1.0708 1.2258 2.3318 1.2780
Figure 4: Comparison of sorted proposed measure values on
the Sony dataset (Cheng et al., 2014b) for the Gray-world,
Color Rabbit, and the proposed method.
there is still the question how such a simple method
could have outperformed much more sophisticated
methods in terms of median angular error and even
some of the methods in terms of the proposed mea-
sure. The reason for this may be found in the
dataset ground-truth illumination as can be demon-
strated with the Sony dataset. In Fig. 2 it can be
seen that for the Sony dataset most of the of ground-
truth illumination chromaticities lay in the left part of
the chromaticity space region. This can be demon-
strated even further quantitatively by looking at the
histogram of the red chromaticity component values
of the ground-truth illumination in Fig. 5. Now the
density of certain regions becomes even more clear:
e.g. over 86% of the values are less than 0.27. Such
density in a relatively small region can hardly be
found in other benchmark datasets.
The proposed method simply (ab)uses this de-
sign fault that happened in image selection during
the dataset creation and by choosing a good illumina-
tion value, it successfully covers most of the ground-
truth illuminations in the testing process. This is
also the reason why the median angular error could
have been so low when compared to the one of other
methods. At the same time the number of images
whose ground-truth illuminations were distanced fur-
ther from the majority of other ground-truth illumi-
nations was small, but the errors was big enough to
cause a very high mean angular error regardless of
the low median.
Figure 5: Histogram of the red chromaticity component val-
ues for the Sony (Cheng et al., 2014b)dataset ground-truth
illumination chromaticities.
When using non-linear images of the GreyBall
dataset (Ciurea and Funt, 2003), which has evenly
spread ground-truth illuminations as shown in Fig. 6,
the dummy Color Mule method performs very poor
in terms of all performance measures including the
proposed one as shown in Table 3. For the GreyBall
dataset the proposed measure is consistent with the
existing ones.
Figure 6: The rb-chromaticities of the GreyBall
dataset (Ciurea and Funt, 2003) ground-truth illumi-
nations.
6 CONCLUSIONS AND FUTURE
RESEARCH
A new illumination estimation accuracy measure has
been proposed. In contrast to the most widely
used angular error statistical descriptors, the proposed
measure takes into account the perceptual difference
between various errors. The good properties of mean
and median are used by using all angular errors and
penalizing them based on perceptual difference. Ad-
ditionally, a method has been proposed that shows the
importance of the representativity of the real-world
scene illuminations in the benchmark datasets.
APerceptualMeasureofIlluminationEstimationError
141

Table 3: Different performance measures for different color
constancy methods on the original GreyBall dataset (Ciurea
and Funt, 2003) (lower is better).
method mean (
◦
) median (
◦
) proposed
do nothing 8.28 6.70 1.6209
Low-level statistics-based methods
GW 7.87 6.97 1.8017
WP 6.80 5.30 1.5385
SoG 6.14 5.33 1.5732
general GW 6.14 5.33 1.5732
GE1 5.88 4.65 1.5013
GE2 6.10 4.85 1.5343
Learning based methods
PG 7.07 5.81 1.6478
EG 6.81 5.81 1.6616
IG 6.93 5.80 1.6510
NIS 5.19 3.93 1.3369
EB 4.38 3.43 1.1924
CM 9.78 8.65 1.9069
ACKNOWLEDGEMENTS
This research has been partially supported by the Eu-
ropean Union from the European Regional Develop-
ment Fund by the project IPA2007/HR/16IPO/001-
040514 ”VISTA - Computer Vision Innovations for
Safe Traffic.”
REFERENCES
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2013). Using the Random
Sprays Retinex Algorithm for Global Illumination Es-
timation. In Proceedings of The Second Croatian
Computer Vision Workshop (CCVW 2013), pages 3–7.
University of Zagreb Faculty of Electrical Engineer-
ing and Computing.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2014a). Color Rabbit: Guid-
ing the Distance of Local Maximums in Illumina-
tion Estimation. In Digital Signal Processing (DSP),
2014 19th International Conference on, pages 345–
350. IEEE.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2014b). Improving the White
patch method by subsampling. In Image Processing
(ICIP), 2014 21st IEEE International Conference on,
pages 605–609. IEEE.
Bani
´
c, N. and Lon
ˇ
cari
´
c, S. (2015). Color Cat: Remember-
ing Colors for Illumination Estimation. Signal Pro-
cessing Letters, IEEE, 22(6):651–655.
Buchsbaum, G. (1980). A spatial processor model for object
colour perception. Journal of The Franklin Institute,
310(1):1–26.
Chakrabarti, A., Hirakawa, K., and Zickler, T. (2012). Color
constancy with spatio-spectral statistics. Pattern Anal-
ysis and Machine Intelligence, IEEE Transactions on,
34(8):1509–1519.
Cheng, D., Prasad, D., and Brown, M. S. (2014a). On Illu-
minant Detection.
Cheng, D., Prasad, D. K., and Brown, M. S. (2014b). Il-
luminant estimation for color constancy: why spatial-
domain methods work and the role of the color distri-
bution. Journal of the Optical Society of America A,
31(5):1049–1058.
Ciurea, F. and Funt, B. (2003). A large image database
for color constancy research. In Color and Imaging
Conference, volume 2003, pages 160–164. Society for
Imaging Science and Technology.
Ebner, M. (2007). Color Constancy. The Wiley-IS&T Se-
ries in Imaging Science and Technology. Wiley.
Finlayson, G. D., Hordley, S. D., and Morovic, P. (2005).
Colour constancy using the chromagenic constraint.
In Computer Vision and Pattern Recognition, 2005.
CVPR 2005. IEEE Computer Society Conference on,
volume 1, pages 1079–1086. IEEE.
Finlayson, G. D., Hordley, S. D., and Tastl, I. (2006). Gamut
constrained illuminant estimation. International Jour-
nal of Computer Vision, 67(1):93–109.
Finlayson, G. D. and Schaefer, G. (2001). Solving for
colour constancy using a constrained dichromatic re-
flection model. International Journal of Computer Vi-
sion, 42(3):127–144.
Finlayson, G. D. and Trezzi, E. (2004). Shades of gray and
colour constancy. In Color and Imaging Conference,
volume 2004, pages 37–41. Society for Imaging Sci-
ence and Technology.
Fredembach, C. and Finlayson, G. (2008). Bright chroma-
genic algorithm for illuminant estimation. Journal of
Imaging Science and Technology, 52(4):40906–1.
Gehler, P. V., Rother, C., Blake, A., Minka, T., and Sharp, T.
(2008). Bayesian color constancy revisited. In Com-
puter Vision and Pattern Recognition, 2008. CVPR
2008. IEEE Conference on, pages 1–8. IEEE.
Gijsenij, A. and Gevers, T. (2007). Color Constancy us-
ing Natural Image Statistics. In Computer Vision and
Pattern Recognition, 2008. CVPR 2008. IEEE Confer-
ence on, pages 1–8.
Gijsenij, A., Gevers, T., and Lucassen, M. P. (2009). Per-
ceptual analysis of distance measures for color con-
stancy algorithms. JOSA A, 26(10):2243–2256.
Gijsenij, A., Gevers, T., and Van De Weijer, J. (2011).
Computational color constancy: Survey and exper-
iments. Image Processing, IEEE Transactions on,
20(9):2475–2489.
Gijsenij, A., Gevers, T., and Van De Weijer, J. (2012). Im-
proving color constancy by photometric edge weight-
ing. Pattern Analysis and Machine Intelligence, IEEE
Transactions on, 34(5):918–929.
Hordley, S. D. and Finlayson, G. D. (2004). Re-evaluating
colour constancy algorithms. In Pattern Recognition,
2004. ICPR 2004. Proceedings of the 17th Interna-
tional Conference on, volume 1, pages 76–79. IEEE.
Joze, H. R. V. and Drew, M. S. (2012). Exemplar-Based
Colour Constancy. In British Machine Vision Confer-
ence, pages 1–12.
Judd, D. B., MacAdam, D. L., Wyszecki, G., Budde, H.,
Condit, H., Henderson, S., and Simonds, J. (1964).
Spectral distribution of typical daylight as a function
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
142

of correlated color temperature. JOSA, 54(8):1031–
1040.
L. Shi, B. F. (2014). Re-processed Version of the Gehler
Color Constancy Dataset of 568 Images.
Land, E. H. (1977). The retinex theory of color vision. Sci-
entific America.
Lynch, S. E., Drew, M. S., and Finlayson, k. G. D. (2013).
Colour Constancy from Both Sides of the Shadow
Edge. In Color and Photometry in Computer Vision
Workshop at the International Conference on Com-
puter Vision. IEEE.
Van De Weijer, J., Gevers, T., and Gijsenij, A. (2007a).
Edge-based color constancy. Image Processing, IEEE
Transactions on, 16(9):2207–2214.
Van De Weijer, J., Schmid, C., and Verbeek, J. (2007b). Us-
ing high-level visual information for color constancy.
In Computer Vision, 2007. ICCV 2007. IEEE 11th In-
ternational Conference on, pages 1–8. IEEE.
Weber, E. (1846). Der Tastsinn und das Gemeingef
¨
uhl.
Handw
¨
orterbuch der Physiologie, 3(2):481–588.
APerceptualMeasureofIlluminationEstimationError
143
