
Local Changes in Marching Cubes to Generate Less Degenerated
Triangles
Thiago F. Leal
1,2
, Aruquia B. M. Peixoto
3
, Cassia I. G. Silva
1,4
,
Marcelo de A. Dreux
5
and Carlos A. de Moura
6
1
Department of Mathematics, Rio de Janeiro Federal Institute, IFRJ, Paracambi, Rio de Janeiro, Brazil
2
Mechanical Engineering Doctorate Program, Rio de Janeiro State University, UERJ, Rio de Janeiro, Brazil
3
Department of Basic Disciplines, CEFET/RJ, Nova Iguaçu, Rio de Janeiro, Brazil
4
Computer Science Doctorate Program, Fluminense Federal University, UFF, Niteroi, Rio de Janeiro, Brazil
5
Mechanical Engineering Department, Rio de Janeiro Pontifical Catholic University, PUC-Rio, Rio de Janeiro, Brazil
6
Mathematics and Statistics Institute, Rio de Janeiro State University, UERJ, Rio de Janeiro, Brazil
Keywords: Implicit Surface, Marching Cubes, Computational Geometry.
Abstract: The Marching Cubes algorithm is widely used to generate surfaces from implicit functions. It builds a mesh
of triangles but many degenerated ones happen to appear among them, which can make the mesh thus built
unfit for many applications, like the Finite Element Method. To overcome this undesired behavior our work
proposes changes on the triangle generation that are automatically generated by Marching Cubes inside each
voxel. We first generate the polygon border inside each voxel that intersects the surface. Each polygon is
tested so as to guarantee the need to insert a new vertex inside itself, the triangles being then generated
according to each polygon properties in order to guarantee the best ratio between their sides and angles. The
resulting triangles inside each voxel exhibit the best possible ratio between their dimensions, thus leading to
a better mesh.
1 INTRODUCTION
Implicit functions are widely used to modeling
surfaces. They arise in the form of an algebraic
function or as a sampling in a grid, like functional
magnetic resonance imaging (FMRI), in medical
images.
In this work data remain in the space R
3
and the
implicit surface is defined as an isovalue set for the
implicit function. To define the isovalue as zero
means that all points for which f(x,y,z)=0 belong to
the surface. We will make a sampling of these points
in order to build a mesh that approximates the
surface thus defined.
There are many methods to generate an implicit
surface from an implicit function, like Marching
Cubes (Lorensen and Cline, 1987), Surface Nets
(Gibson, 1998), Extended Marching Cubes (Kobbelt
2001), Dual Marching Cubes (Nielson, 2004) and
Dual Contouring (Ju et al., 2002).
These methods start with a sampling of the the
implicit function values on a grid, which can be
either a uniform or an adaptive grid. Given that
sampling, every voxel from this grid is traversed to
find the voxels that intersect the surface, and one or
more vertex of the mesh are positioned in these
voxels, in order to be connected and generate the
mesh.
There are many different approaches to analyze a
mesh, but the most relevant are: topology, geometry
or quality of the mesh. Some works deal with the
topological characteristics of a surface in its
generation and/or simplification (Peixoto and
Moura, 2014), (Zomorodian, 2005), (Schaefer,
2007) and (Nielson and Hamann, 1991). If we look
towards geometrical characteristics, like curvature or
geodesics, some interesting works are (Martinez,
2005), (Velho et al., 2002) and (Wenger, 2005).
In this work we deal with the quality of
polygons, namely triangles, that generate an
unstructured mesh. The quality of the triangles in
this mesh is essential to many applications in
Engineering, like Finite Element Methods. Some
works deal with this characteristic (Dietrich 2009)
and (Gibson, 1998).
We propose a change in the Marching Cubes
143
F. Leal T., B. M. Peixoto A., I. G. Silva C., de A. Dreux M. and A. de Moura C..
Local Changes in Marching Cubes to Generate Less Degenerated Triangles.
DOI: 10.5220/0005309201430149
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 143-149
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

algorithm in order to generate a mesh of triangles
with better ratio between their sides and angles.
2 MARCHING CUBES AND
THEIR MODIFICATIONS
Marching Cubes (Lorensen and Cline, 1987) is an
algorithm that generates a tridimensional
representation of the border of a volume. The
surface is polygonized, with the values of an implicit
function being used to positioning the vertex points
of the mesh that generates the triangles of the
approximating surface.
Its first application was carried on for medical
images, where a series of bi-dimensional images
slices makes it possible to computationally
reconstruct a model for the patient anatomy. This
turns much easier the generation and visualization of
medical images for traumas and broken bones.
Nowadays Marching Cubes is widely employed
in many other areas that need to generate a surface
from an implicit function, from animation to
different engineering applications.
2.1 Marching Cubes
Marching Cubes starts with a cube that contains the
surface. Each axis of this cube is subdivided, thus
generating a grid with new small cubes, the voxels.
Each voxel is transverse and if it intersects the
surface, the vertex of the mesh is generated, being
positioned in the border of each voxel. These
vertices are automatically connected to generate the
triangles inside this voxel. The algorithm moves to
the next voxel so as to generate the next triangles.
Figure 1: Marching Cubes: The original 15 configurations.
The original MC uses a table with 15 possible
configurations, except rotation, to decide how to
automatically generate the triangles, as shown in
figure 1.
2.2 Topological Ambiguities
After the original configurations presented in
Marching Cubes, some cases with topological
ambiguity arise. In these cases, we can have two
options to connect the vertex of the mesh inside a
voxel. These options can generate two completely
distinct topological configurations, e.g. one with a
connected surface and another one with two or more
disconnected surfaces.
Some techniques were created to deal with these
flaws (Lorensen and Cline, 1987), (Chernyaev,
1995). These works take the original 15
configurations and expand them to 33 final
configurations, without ambiguity of the resulting
surface topology.
Even with these new configurations, the structure
inside each voxel remains the same, with the
algorithm automatically generating the mesh
triangles. After the voxel traverse the whole grid, the
mesh is generated with all triangles, as shown in
figure 2, right.
2.3 Degenerated Triangles
The Marching Cubes algorithm can lead to some
difficulties, due to the limitation in the use of an
automated triangle generation. It is common to get
hold of degenerated triangles, by which it is meant
the existence of a very small edge or angle, as
compared to the two others. For numerical
applications, such triangles can lead to unstability,
so that the solution fails to be reached by the
numerical method.
Figure 2 shows a detail of a sphere polygonised
with the Marching Cubes algorithm. We can see
some degenerated triangles, mainly in the sphere
center.
Figure 2: Polygonization of a sphere, with the details of
triangles on the mesh center.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
144

3 LOCAL CHANGE
The changes in Marching Cubes algorithm herein
proposed are performed only inside each voxel
during the polygonization. In short, in this work we
do not look at the neighbors of this voxel. That is the
reason why we call this change a “Local Change”.
In the cases where isolated triangles appear
inside a voxel, nothing is done with these triangles.
For example, figure 3 shows some cases where the
voxel generates isolated triangles. Only the
configurations 7 and 11 can have changes in the
triangles connections, because they have polygons
with four and five edges, respectively.
Figure 3: Some Marching Cubes configurations that
contain isolated triangles.
The algorithm proposed in this work is composed by
four steps:
Generate the border of each polygon
Separate the vertex with a bad angle
Insert a new vertex, if necessary
Connect the vertex.
3.1 Generate the Border of Each
Polygon
The first step is to change the Marching Cubes table.
The original table automatically generates the
triangles. For every possible configuration and
positioning, Marching Cubes choses a vector with
the voxel edges that intersect the surface. For each
of these edges the positioning of the vertex that
generates the triangles of the mesh is calculated.
Each sequence of the vector three elements
corresponds to a triangle.
In our algorithm, we change this vector with the
first entries being the isolated triangles, if they exist.
After this step, if there is a polygon with four or
more sides, a flag-2 is used to indicate that the next
entries are the border of this polygon, and not a
triangle.
Figure 4 shows, in the left, the triangles
automatically generated by Marching Cubes. This
case gives the vector {2, 10, 5, 3, 2, 5, 3, 5, 4, 3, 4,
8, -1, -1, -1, -1}, where we have four triangles
generated by the edges of the voxel (2, 10, 5), (3, 2,
5), (3, 5, 4) and (3, 4, 8). In the right, we have the
vector {-2, 2, 10, 5, 4, 8, 3, -1, -1, -1, -1, -1, -1, -1, -
1, -1}. Since we do not have isolated triangles, only
a polygon with five edges, then the vector starts with
the flag “-2”, to indicate that we have only the
border of a polygon, and we have the five edges of
the voxel that defines this polygon (2, 10, 5, 4, 8, 3).
Figure 4: Marching Cubes triangles and configurations. a)
The original Marching Cubes triangles {2, 10, 5, 3, 2, 5, 3,
5, 4, 3, 4, 8, -1, -1, -1, -1}, b) Modified Marching Cubes
table {-2, 2, 10, 5, 4, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1}.
3.2 Separate the Vertex with a Bad
Angle
This work deals with the local changes that are done
inside a single voxel. For this reason we fail to have
information about the neighbours of a voxel. If a
vertex of the polygon inside a voxel has a too small
angle, no information about their neighbours is
available to produce any change for this angle.
This case of too small angles will be treated in
another work, where we have access to the entire
mesh. To prevent that this small angle makes the
mesh still worst, we will not split it.
We create an edge connecting the two vertexes
that are connected to this vertex, thus getting a new
triangle. If in this case we cannot make a better
angle, at least we do not create triangles with worst
angles, and let this small angle be isolated so as to
be treated in a global change.
Figure 5 shows a polygon with a vertex, on the
top, with a small angle. At the left it shows the
triangles automatically generated by Marching
Cubes: three new triangles with worse angles. Our
algorithm is shown at the right, where we take the
small angle and connect their neighbours, creating
one triangle with a bad angle. With the local
changes, we cannot make this angle better, but we
do not create triangles with angles worse than the
ones of the polygon original border.
LocalChangesinMarchingCubestoGenerateLessDegeneratedTriangles
145

Figure 5: Polygon with a bad angle on his top. a)
Automatic triangulation due to Marching Cubes. b) Our
algorithm, that prevents to split the bad angle.
3.3 Insert a New Vertex
After each vertex with a bad angle is marked, to
prevent its splitting, we analyse the remaining
polygon to check up whether it is necessary to
position a new vertex inside it. This new vertex is
used to generate triangles with better angles, but
note: it is positioned only in four or more edge
polygons.
In the case of a four edge polygon, the ratio of
the bigger and the smaller edges are analysed, and if
they remain bellow a threshold, indicating that there
is a significant difference between these edges, then
a new vertex is positioned inside this polygon. For
all polygons with five or more edges, a new vertex is
inserted. This new vertex is placed closer to the
smaller one. It may be thought that an attraction
force pulls this new vertex closer to the smaller
edges.
Every vertex of the polygon is connected to two
edges. To every vertex we calculate the length of the
smallest edge (LSE), and we associate this
information to the edge. We make a sum of all the
lengths associated to these vertices (SLME).
With these information we create an attraction
factor √(1 + SLME/LSE) to every vertex. The final
position of the new vertex is the sum of every
position of the vertices of the polygon multiplied by
this attraction factor.
In this work, we only use the vertex that
generates the border to positioning the new vertex,
because it is a local change, where we do not have
access to the voxel neighbours. We do not position
the new vertex close to the surface, using the
implicit function, because we can generate structures
like pyramids inside a voxel, even in smooth
surfaces, what to applications in numerical methods
can generate unstable results.
With this positioning, this new edge is closer to
the smaller edges, generating new triangles with
better ration between their sides. Figure 6 shows two
possible positions for a new vertex inside a polygon.
At the left, the new vertex is positioned on the
polygon center, and at the right, the positioning of
the new vertex is closer to the smaller edge. In this
figure, we can see that the triangles generated at the
left show better quality between their sides and
angles.
Figure 6: Positioning a new vertex inside a polygon. a)
Positioning in the center. b) Positioning closer to the
smallest edge.
3.4 Connect the Vertex
There are two cases to connect the vertex of a
polygon: if there is a new inserted vertex inside the
polygon, or if there is only the original border
vertex.
If there is a new vertex inserted inside the
remaining polygon, then all polygon vertices are
connected to them, as shown in Figure 6.
When there is no vertex inside the polygon, we
choose the vertex with biggest angle. It will be
connected to the border vertex that is at a distance of
two edges, and that has a bigger angle. With this
procedure, the bigger angles are split, thus
generating triangles with better angles.
Figure 7 right shows an automatic triangulation
made by Marching Cubes, where a big angle on the
top left remains as a big angle in the triangle. In the
left, we split this angle, generating two triangles
with better angle in this vertex.
Figure 7: Generating triangles from the border of a
polygon. a) Automatic triangulation, due to Marching
Cubes. b) Our algorithm, that splits the bigger angle.
4 RESULTS
To analyse the results, we use a histogram to see the
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
146
angles distribution. The axis x corresponds to the
angles, where each interval has a size of five angles,
and the axis y shows the number of vertices that
have angles in this interval.
The algorithm presented in this work can
introduce one vertex inside some voxels. With this,
the total numbers of triangles, and vertices, can be
different for a surface polygonised with Marching
Cubes and with our algorithm.
In order to see the difference between the
meshes generated with Marching Cubes and our
algorithm, we draw the borders of the triangles in
the mesh. To have a better analysis of the
distribution of the angles, we show the histogram of
every surface. We analyse three surfaces: a sphere, a
hyperboloid and a grid with many holes.
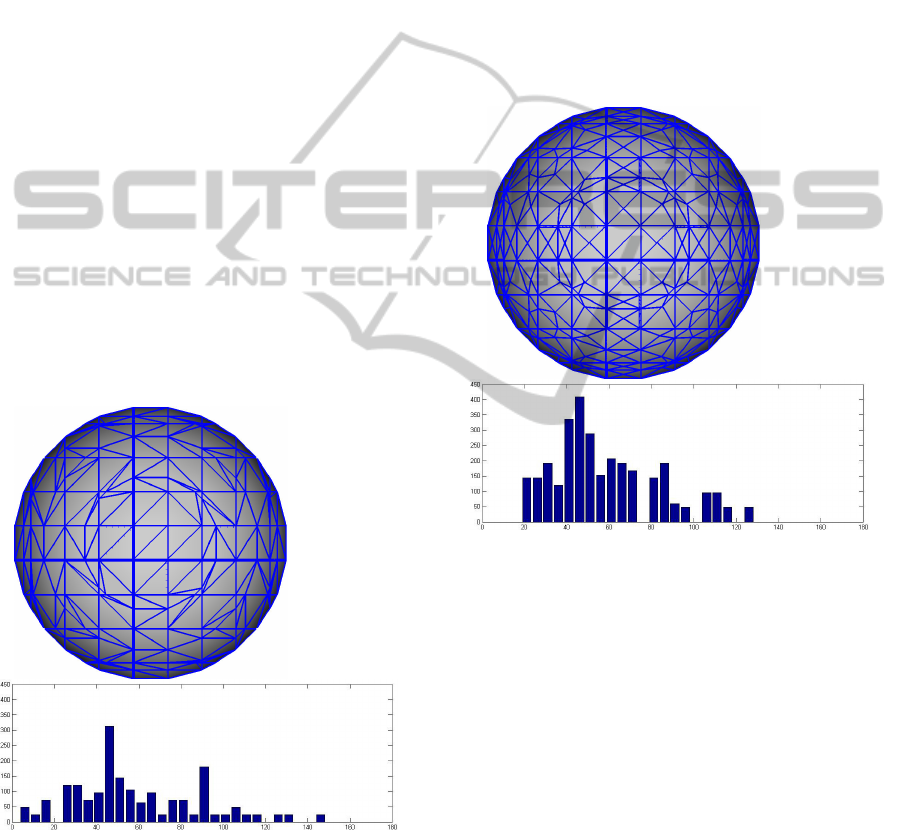
4.1 Sphere
We start with a sphere that is polygonized using a
grid with ten subdivisions in each axis, generating
10
3
voxels. With this very coarse grid, we can see
the mesh with more details, with the triangles that
generate the mesh.
The figure 8 shows a polygonization done with
Marching Cubes. In this case we can see many
degenerated triangles around the sphere center.
Figure 8: Sphere polygonized with Marching Cubes, and
the histogram with the distribution of the angles. There are
524 triangles in this mesh.
On the histogram of this distribution we can see
a peak in the interval 45-50, and another smaller
peak in the interval 90-95. The remaining angles
show a distribution much more dispersed, like a
statistical uniform distribution. In this surface, there
is a significant number of vertices with angles
between 5 to 20 degrees, and the angles of the
triangles are in the interval 5 to 145 degrees.
Figure 9 shows the polygonization of the same
sphere, with the same grid, using the algorithm
presented in this work. We can see that the triangles
around the sphere center have better angles, and the
ratio between their sides are better too.
The histogram shows that the angles are more
concentrated around the interval 45-50, with less
dispersion, and the smallest angle starts with 20
degrees. In this case, the angles of the triangles are
in the interval 20 to 130 degrees.
Figure 9: Sphere polygonized with the algorithm presented
in this work, and the histogram with the distribution of the
angles. There are 852 triangles in this mesh.
4.2 Hyperboloid
The surfaces presented in this section, and in the
next, are polygonised with a less coarse grid, each
axis has forty subdivisions, generating 40
3
voxels.
This makes it easier to analyse the distribution of the
angles of the triangles, but a little more difficult to
see the triangles that generate the mesh.
The hyperboloid generated by Marching Cubes is
shown in figure 10. Even with a grid with many
subdivisions, that generates many triangles, we can
see that there are many triangles with small angles.
The histogram has a peak on the interval 50-55,
and there is a significant amount of angles in the
interval 0-5. The angles of the triangles are in the
interval 0 to 170 degrees, with a big dispersion.
LocalChangesinMarchingCubestoGenerateLessDegeneratedTriangles
147

Figure 10: Hyperboloid polygonized with Marching
Cubes, and the histogram with the distribution of the
angles. There are 15308 triangles in this mesh.
Figure 11: Hyperboloid polygonized with the algorithm
presented in this work, and the histogram with the
distribution of the angles. There are 25179 triangles in this
mesh.
Figure 11 shows the polygonization of the
samehyperboloid, with the same grid, using the
algorithm presented in this work.
The mesh on the surface shows that the triangles
have better angles, and some new vertex was
introduced to generate this mesh.
The histogram shows that the angles are more
concentrated around the interval 50-55, with less
dispersion. The amount of angles in the interval 0-5
decrease, even with more triangles in this mesh.
4.3 The Grid
The Grid is a surface generated with cosines that is a
tube involving a grid, generating many holes.
Figures 12 and 13 show a front view of this surface.
In figure 12 we can see the surface polygonized
with Marching Cubes. We can see that there are
many triangles with small angles.
The histogram shows a peak in the interval 50-
55, a significant amount of angles in the interval 0-5,
and the angles are more dispersed.
Figure 12: The Grid polygonized with Marching Cubes,
and the histogram with the distribution of the angles.
There are 10457 triangles in this mesh.
Figure 13 shows the same Grid, but polygonized
with our algorithm. In this figure, there are less
triangles with small angles. The histogram shows a
peak in the interval 50-55, but in this case, the
angles are less dispersed, being concentrated around
this peak.
5 CONCLUSIONS AND FUTURE
WORKS
This work deals with the local changes in Marching
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
148
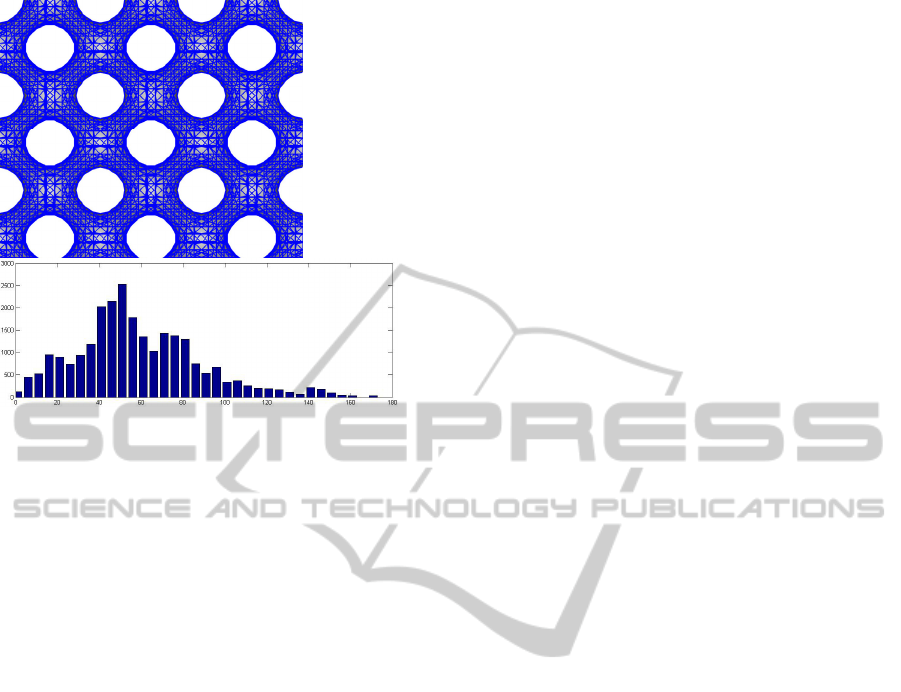
Figure 13: The Grid polygonized with the algorithm
presented in this work, and the histogram with the
distribution of the angles. There are 25077 triangles in this
mesh.
Cubes algorithm. These changes are performed only
inside a voxel, with no information about the
neighbours, this is the reason why these changes are
called local changes.
We can see, analyzing the triangles of the mesh
that are drawn on the surface, that the mesh resulting
from these changes has better triangles, with better
angles and better ratio between their sides.
The histograms of the surfaces polygonized with
Marching Cubes have some peaks, but the angles are
more dispersed, closer to a uniform distribution. All
histograms of the surfaces polygonized with the
algorithm presented in this work show an angles
concentration around the interval 40-60, and less
angles dispersion.
In future works we can use information from the
entire mesh, repositioning the vertex with small
angles, which are in the border of the polygon, thus
generating a mesh with better angles triangles.
Another approach is to deal not just with a surface,
but with an entire volume.
REFERENCES
Dietrich C. A., Scheidegger C., Comba J. L. D., Nedel
L.P., Silva C. T., 2009, Marching cubes without skinny
triangles, Computing In Science & Engineering, Vol.
11, No. 2. pp 82-87.
Chernyaev, E. V., 1995. Marching Cubes 33:
Construction of Topologically Correct Isosurfaces,
Technical Report CERN CN 95–17, CERN.
Gibson, S. F. F., 1998, Constrained Elastic Surface Nets:
Generating Smooth Surfaces from Binary Segmented
Data, Proceedings of the First International
Conference on Medical Image Computing and
Computer-Assisted Intervention, MICCAI, pp. 888-
898.
Ju, T., Losasso, F., Schaefer, S., Warren, J., 2002, Dual
Contouring of Hermite Data, Proceedings of the 29th
Annual Conference on Computer Graphics and
Interactive Techniques, SIGGRAPH 2002. Pp. 339-
346.
Kobbelt, L. P., Botsch, M., Schwanecke, U., Seidel, H-P.,
2001, Feature Sensitive Surface Extraction from
Volume Data, Proceedings of the 28th Annual
Conference on Computer Graphics and Interactive
Techniques, SIGGRAPH 2001. pp 57-66.
Lorensen, W. E., Cline, H. E., 1987. Marching cubes: A
high resolution 3D surface construction algorithm,
Proceedings of the 14th annual conference on
Computer graphics and interactive techniques, pp.163-
169.
Martinez, D., Velho, L., Carvalho, P. C., 2005, Computing
Geodesics on Triangular Meshes. Computers &
Graphics v. 29, n.5, p. 667-675.
Nielson, G. M., Hamann, B., 1991. The Asymptotic
Decider: Resolving the Ambiguity in Marching Cubes,
Proceedings of the 2
0
Conference on Visualization '91,
VIS 91, pp. 83-91, IEEE Computer Society Press.
Nielson, G. M., 2004, Dual Marching Cubes, Proceedings
of the Conference on Visualization 2004, VIS 2004.
Pp. 489-496.
Peixoto, A. B. M., Moura, C. de, 2014, Topology
Preserving Algorithms for Implicit Surfaces
Simplifying and Sewing, Proceedings of 14th
International Computational Science and Its
Applications – ICCSA. pp. 352-367.
Schaefer, S., Ju, T., Warren, J., 2007, Manifold Dual
Contouring, IEEE Transactions on Visualization and
Computer Graphics. Pp. 610-619.
Shewchuk, J. R., 2002, What Is a Good Linear Finite
Element? - Interpolation, Conditioning, Anisotropy,
and Quality Measures. In Proc. of the 11th
International Meshing Roundtable, p. 115-126.
Velho, L, Figueiredo, L. H., Gomes, J, 2002, Implicit
Objects in Computer Graphics, Springer.
Wenger, A., 2005, Isosurfaces: Geometry, Topology, and
Algorithms, Taylor & Francis.
Zomorodian, R., 2005, Topology for Computing,
Cambridge: Cambridge University Press.
LocalChangesinMarchingCubestoGenerateLessDegeneratedTriangles
149
