
An Optimum-Rounding 5/3 IWT based on 2-Level Decomposition for
Lossless/Lossy Image Compression
Somchart Chokchaitam
Department of Electrical Engineering, Faculty of Engineering, Thammasat University, Patoom-Thani 12120, Thailand
Keywords: 5/3 IWT, 2-Level Decomposition, Rounding Effect, Image Compression.
Abstract: Lifting structures and rounding operations are main tools to construct integer wavelet transforms (IWT) that
are well applied in lossless/lossy compression. However, the rounding operation generates its non-linear
noise that makes its performance worse. In this report, we propose a new optimum-rounding 5/3 IWT based
on 2-level decomposition for lossless/lossy image compression. Our proposed 5/3 IWT is designed to
reduce rounding operation as much as possible. Filter characteristics of our proposed 5/3 IWT are the same
as the conventional 2-level 2D 5/3 IWT excluded rounding effect. Coding performances of the proposed 5/3
IWT are better than those of conventional 5/3 IWT in lossy performance, because of reduction of rounding
effects. Especially, its performance in near lossless compression is much better than the conventional one.
However, they have almost the same lossless performance. Simulation results confirm effectiveness of our
proposed 5/3 IWT.
1 INTRODUCTION
Many researchers have been paying attention to the
standardization of new image compression system
JPEG 2000 (Christopoulos, C., 2000). The Integer
Wavelet Transform (IWT) (Calderbank, A.R., 1998)
is one of the famous lossless algorithms because the
IWT-based coding system can provide not only
lossy coding but also lossless coding thanks to
lifting structures (LS) (Daubechies, I., 1998) and
rounding operations. However, the error generated
from rounding operation causes PSNR degradation
in lossy coding (Reichel, J., 2001) when
quantization is applied. The conventional IWT is a
one-dimensional (1D) filter bank (FB)
(Vaidyanathan, P.P., 1993) constructed from double
LS. To perform 2D FB for image application, the 1D
LWT is applied twice in horizontal and vertical
dimension, successively. Namely, it is a separable
2D IWT.
Recently, many researchers proposed a
nonseparable 2D IWT. The number of rounding
operations of those IWT is less than that of
conventional 2D IWT, whereas filter characteristics
of a nonseparable 2D IWT (Chokchaitam, S., 2002)
are the same as those of conventional 2D IWT when
error generated by the rounding operation is
negligible. Therefore, coding performance of
nonseparable 2D IWT is better than that of the
conventional 2D IWT in lossy coding, especially at
high bit rate when quantization errors are relatively
small compared to the rounding errors. However, if
nonseparable 2D IWT is applied for multi-stage, the
rounding operations are not optimized.
In this report, a new optimum-rounding 5/3 IWT
based on 2-level decomposition is proposed for
lossless/lossy compression. The proposed optimum-
rounding 5/3 IWT is mainly reduced rounding
operations based on two methods: 1) Reducing
rounding from nonseparable 2D IWT and 2)
Reducing rounding from redundancy of 2-level
decomposition. In simulation results, lossy coding
performances of the proposed 5/3 IWT confirm its
effectiveness comparing to the conventional IWT.
Coding performance of our new proposed 2D 5/3
IWT is better than those of both the conventional 2-
level 2D IWT and the existing 2-level nonseparable
2D IWT. However, their performance in lossless
coding are almost the same results.
This report is organized as follows. In section 2,
we review signal processing of the conventional 2-
level 2D 5/3 IWT based on applying the
conventional 1D 5/3 IWT in horizontal and vertical
direction independently twice. Then, we review a
signal processing of the conventional 2-level
nonseparable 2D 5/3 IWT for image compression in
13
Chokchaitam S..
An Optimum-Rounding 5/3 IWT based on 2-Level Decomposition for Lossless/Lossy Image Compression.
DOI: 10.5220/0005309700130019
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 13-19
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

section 3. In section 4, we propose the 2-level
optimum-rounding 5/3 IWT. Simulation results
confirm effectiveness of our proposed IWT in both
lossless coding and lossy coding in section 5.
Finally, we summarize our proposed IWT in section
6.
2 THE CONVENTIONAL 2D 5/3
IWT
2.1 The Conventional 2D 5/3 IWT for
1-Level Decoposition
The conventional 2D 5/3 IWT is reconstructed by
applying the conventional 1D 5/3 IWT in horizontal
and vertical direction independently as illustrated in
figure 1. Input signal (X) is decomposed into 4
subbands (Y
LL
, Y
LH
, Y
HL
, Y
HH
). For example, Y
LH
indicates horizontally low-passed and vertically
high-passed subband. The z
1
and z
2
denotes
horizontal and vertical dimension, respectively. The
Q
LL
, Q
LH
, Q
HL
, Q
HH
denote quantization in subband
LL, LH, HL, and HH, respectively. The LS denotes
lifting structure. The ® and “↓2” denote the
rounding operation and the down-sampler by two.
As shown in Fig. 1, six rounding operations are
required to perform the conventional 2D 5/3 IWT
where parameter P
1
(z) and P
2
(z) are the following
=−
1+
2
(1)
=−
1+
4
(2)
1
1
−
z
2(z
1
)
2(z
1
)
R
R
1
2
−
z
2
(z
2
)
2
(z
2
)
R
R
1
2
−
z
2(z
2
)
2(z
2
)
R
R
Q
LL
Y
LL
Q
LH
Y
LH
Q
HL
Y
HL
Q
HH
Y
HH
X
}
LS 6
}
LS 1
}
LS 2
}
L
S 3
}
LS 4
}
LS 5
P
1
(z
1
)
P
1
(z
2
)
P
1
(z
2
)
P
2
(z
2
)
P
2
(z
2
)
P
2
(z
1
)
Figure 1: Analysis part of the conventional 2D 5/3 IWT.
2.2 The Conventional 2D 5/3 IWT for
2-Level Decomposition
The conventional 2-level 2D 5/3 IWT is
reconstructed by applying the conventional 2D 5/3
IWT in previous section to decompose subband Y
LL
again. Therefore, subband Y
LL
is decomposed into 4
subbands (Y
LL2
, Y
LH2
, Y
HL2
, Y
HH2
). As shown in
figure 2, twelve rounding operations are required to
perform the conventional 2-level 2D 5/3 IWT.
1
1
−
z
2(z
1
)
2(z
1
)
R
R
1
2
−
z
2(z
2
)
2(z
2
)
R
R
1
2
−
z
2(z
2
)
2(z
2
)
R
R
Y
LL2
Y
LH2
Y
HL2
Y
HH2
}
LS 12
}
LS 7
}
LS 8
}
LS 9
}
LS 10
}
LS 11
P
1
(z
1
)
P
1
(z
2
)
P
1
(z
2
)
P
2
(z
2
)
P
2
(z
2
)
P
2
(z
1
)
1
1
−
z
2(z
1
)
2(z
1
)
R
R
1
2
−
z
2(z
2
)
2(z
2
)
R
R
1
2
−
z
2(z
2
)
2(z
2
)
R
R
Q
HH2
X
}
LS 6
}
LS 1
}
LS 2
}
LS 3
}
LS 4
}
LS 5
P
1
(z
1
)
P
1
(z
2
)
P
1
(z
2
)
P
2
(z
2
)
P
2
(z
2
)
P
2
(z
1
)
Q
HL2
Q
LH2
Q
LL2
Y
LH1
Y
HL1
Y
HH1
Q
HH1
Q
HL1
Q
LH1
Figure 2: Analysis part of the conventional 2D 5/3 IWT for 2-level decomposition.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
14

3 THE CONVENTIONAL
NON-SEPARABLE 2D 5/3 IWT
3.1 The Conventional Nonseparable 2D
5/3 IWT for 1-Level Decomposition
The signal processing of the conventional
nonseparable 2D 5/3 IWT is designed to reduce
rounding operation for 1 level. As shown in figure 3,
analysis part of the conventional nonseparable 2D
5/3 IWT requires only four rounding operations;
whereas, its filter characteristics are same as those of
conventional 2D 5/3 IWT. Because of advantages of
the nonseparable 2D FB, parameters in different LS
of conventional 2D 5/3 IWT can be combined. For
example, parameters of LS 1 and LS 5 in figure 1
are combine into those of LS 1’ in figure 3.
Therefore, the number of rounding operations
required to perform the conventional nonseparable
2D 5/3 IWT is reduced to four rounding operations.
3.2 The Conventional Nonseparable 2D
5/3 IWT for 2-Level Decomposition
Similar to the conventional 5/3 IWT, the
conventional 2-level nonseparable 2D 5/3 IWT is
reconstructed by applying the conventional
nonseparable 2D 5/3 IWT to decompose subband
Y
LL
into 4 subbands (Y
LL2
, Y
LH2
, Y
HL2
, Y
HH2
). As
shown in figure 4, eight rounding operations are
required to perform the conventional 2-level 2D 5/3
IWT.
2(z
1
,z
2
)
1
2
−
z
2
(z
1
,z
2
)
1
1
−
z
1
2
−
z
2(z
1
,z
2
)
2(z
1
,z
2
)
R
R
R
R
Q
LL
Y
LL
Q
LH
Y
LH
Q
HL
Y
HL
Q
HH
Y
HH
X
}
LS 1’
}
LS 4’
}
LS 3’
}
LS 2’
P
1
(z
2
)
P
1
(z
1
)
P
1
(z
1
)
P
1
(z
2
) P
1
(z
1
)P
1
(z
2
)
P
2
(z
2
)
P
2
(z
2
)
P
2
(z
1
)
P
2
(z
1
)
-P
2
(z
1
)P
2
(z
2
)
Figure 3: Analysis part of the conventional nonseparable
2D 5/3 IWT.
4 THE OPTIMUM-ROUNDING
5/3 IWT FOR 2-LEVEL
DECOMPOSITION
4.1 Rounding-optimization Concept
In this section, we illustrate concept how to optimize
number of rounding operations. First, we simplify
2(z
1
,z
2
)
1
2
−
z
2(z
1
,z
2
)
1
1
−
z
1
2
−
z
2(z
1
,z
2
)
2(z
1
,z
2
)
R
R
R
R
X
}
LS 1’
}
LS 4’
}
LS 3’
}
LS 2’
P
1
(z
2
)
P
1
(z
1
)
P
1
(z
1
)
P
1
(z
2
) P
1
(z
1
)P
1
(z
2
)
P
2
(z
2
)
P
2
(z
2
)
P
2
(z
1
)
P
2
(z
1
)
-P
2
(z
1
)P
2
(z
2
)
2(z
1
,z
2
)
1
2
−
z
2(z
1
,z
2
)
1
1
−
z
1
2
−
z
2(z
1
,z
2
)
2(z
1
,z
2
)
R
R
R
X
}
LS 5’
}
LS 6’
P
1
(z
2
)
P
1
(z
1
)
P
1
(z
1
)
P
1
(z
2
) P
1
(z
1
)P
1
(z
2
)
P
2
(z
2
) P
2
(z
1
)
R
Q
LL2
Y
LL2
Y
LH2
Y
HL2
Y
HH2
}
LS 8’
}
LS 7’
P
2
(z
2
)
P
2
(z
1
)
-P
2
(z
1
)P
2
(z
2
)
Q
LH2
Q
HH2
Q
HL2
Y
LH1
Y
HL1
Y
HH1
Q
LH1
Q
HH1
Q
HL1
Figure 4: Analysis part of the conventional nonseparable 2D 5/3 IWT for 2-level decomposition.
AnOptimum-Rounding5/3IWTbasedon2-LevelDecompositionforLossless/LossyImageCompression
15

the interested part before optimizing as shown in
figure 5(a). Then, the lifting structure 1 in figure
5(a) is expanded into the lifting structure 1’ and 1”
in figure 5(b). Finally, the lifting structure 1 in figure
5(a) can be combined with the lifting structure 2 and
3 in figure 5(a) to the lifting structure 2’ and 3’ in
figure 5(c), respectively.
2(z)
2(z)
R
2(z)
2(z)
R
R
X
}
LS 1
}
LS 2
}
LS 3
P’
2
(z)
P’
3
(z)
P’
1
(z)
Figure 5(a): The interested part before optimizing.
2(z)
2(z)
R
2(z)
2(z)
R
R
X
}
LS 1’
}
LS 2
}
LS 3
P’
2
(z)
P’
3
(z)
P’
1
(z)
LS 1”
}
2(z)
2(z)
R
Figure 5(b): The expanded part of LS1.
2(z)
2(z)
2(z)
2(z)
R
R
X
}
LS 2’
}
LS 3’
P’
4
(z)
P’
6
(z)
P’
5
(z)
P’
7
(z)
2(z)
2(z)
Figure 5(c): The Optimization result.
The coefficients in figure 5(c) are the following
′
=
′
+′
′
(3)
′
=′
(4)
′
=′
(5)
′
=
1 + ′
′
+
′
(6)
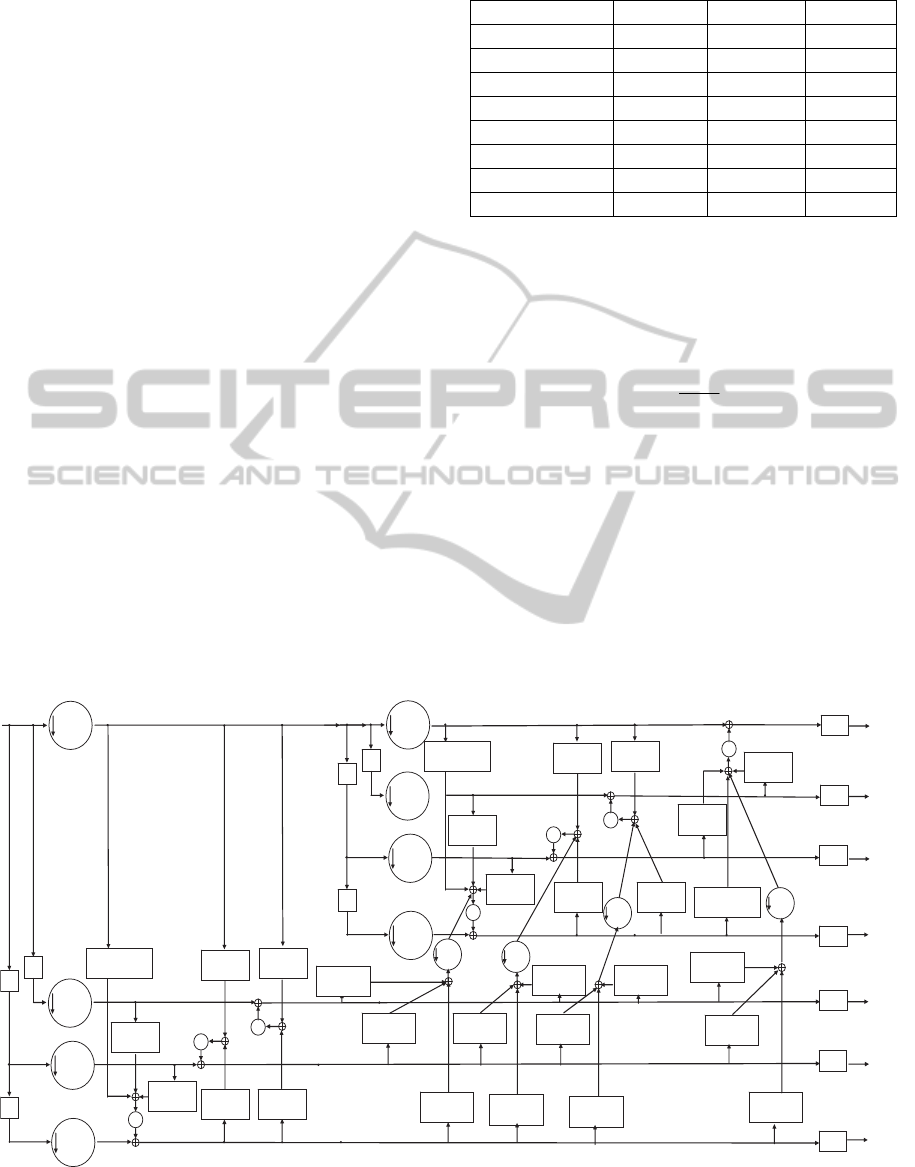
4.2 The Optimum-rounding 5/3 IWT
for 2-Level Decomposition
The proposed optimum-rounding 5/3 IWT for 2-
level decomposition subbands Y
LL
into 4 subbands
(Y
LL2
, Y
LH2
, Y
HL2
, Y
HH2
), similar to the other.
However, the proposed optimum-rounding 5/3 IWT
is designed to reduce rounding operation in LS4’ (in
figure 4) by expanding all coefficients of LS4’ into
LS5”, LS6”, LS7” and LS8” (in figure 6) Therefore,
the proposed 5/3 IWT requires only seven rounding
operations. The expanded coefficients in LS5” are
following:
,
=
1 +
4
,
(7)
,
=
1 +
4
,
(8)
,
=−
1 +
1 +
16
,
(9)
where
,
=
(10)
The expanded coeffiecients in LS6” are following:
,
=
1 +
4
,
(11)
,
=
1 +
4
,
(12)
,
=−
1 +
1 +
16
,
(13)
where
,
=
−
(
14
)
The expanded coeffiecients in LS7” are following:
,
=
1 +
4
,
(15)
,
=
1 +
4
,
(16)
,
=−
1 +
1 +
16
,
(17)
where
,
=
−
(18)
The expanded coefficients in LS8” are following:
,
=
1 +
4
(19)
,
=
1 +
4
(20)
,
=−
1 +
1 +
16
(21)
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
16
5 SIMULATION RESULTS
In this section, we apply some 8-bit gray-level
images as input signals to illustrate effectiveness of
our proposed method comparing those of the
conventional 5/3 IWT. Lossless-coding performance
is tested in section 5.1. Effectiveness of the proposed
method is illustrated as the results from lossy-coding
performance in section 5.2.
5.1 Lossless-coding Performance
Table 1 illustrate lossless coding performance of all
IWT in term of the entropy rate calculated by
HPP
ss
s
=−
log
2
(22)
where P
s
indicates probability of a symbol “s”. The
“Conv.”, “Nonsep.” and “Prop.” indicate “the
conventional separable 2D 5/3 IWT for 2-level
decomposition”, “the conventional nonseparable 2D
5/3 IWT for 2-level decomposition” and “the
proposed optimum-rounding 5/3 2D IWT for 2-level
decomposition”, respectively. The best entropy rate
of each category is highlighted. Lossless
performance of the proposed IWT almost the same
as those of all 5/3 IWT. The optimized rounding
operation doesn’t directly affect entropy rate of
output.
Table 1: Entropy rate in lossless coding of all 5/3 IWT.
Image Name Conv. Nonsep. Prop.
Couple 4.43
4.41
4.42
Aerial
5.80
5.81 5.82
Girl
4.72 4.72
4.74
Chest 6.28
6.24
6.26
Mobile 5.10
5.09
5.10
Barbara
5.19 5.19
5.20
Flower
5.42 5.42
5.45
Lena
5.06 5.06
5.08
5.2 Lossy-coding Performance
Table 2-3 illustrate lossy coding performance of
both methods in term of PSNR (Peak Signal to
Noise Ratio) defined as
][)
σ
255
(log10
2
E
2
10
dBPSNR =
(23)
where
2
E
σ
denotes variance of error signal between
original signal and decoded signal. The “∞” denotes
infinity because of no error. The best PSNR of each
category is highlighted. From the results in table 2-3,
lossy coding performances of the proposed IWT are
the best in many images at 5 bpp. because number of
rounding operation is less. However, lossy coding
performances of the proposed IWT and those of
nonseparable 2D 5/3 IWT are best at 4 bpp.
Therefore, our proposed method is the best for lossy
coding especially in high bit rate. Figure 7-9
2(z
1
,z
2
)
1
2
−
z
2(z
1
,z
2
)
1
1
−
z
1
2
−
z
2(z
1
,z
2
)
2(z
1
,z
2
)
R
R
R
X
}
LS 1”
}
LS 3”
}
LS 2”
P
1
(z
2
)
P
1
(z
1
)
P
1
(z
1
)
P
1
(z
2
) P
1
(z
1
)P
1
(z
2
)
P
2
(z
2
)
P
3
(z
1
,z
2
)
P
2
(z
1
)
2(z
1
,z
2
)
1
2
−
z
2(z
1
,z
2
)
1
1
−
z
1
2
−
z
2(z
1
,z
2
)
2(z
1
,z
2
)
R
R
X
}
LS 5”
}
LS 6”
P
1
(z
2
)
P
1
(z
1
)
P
1
(z
1
)
P
1
(z
1
)P
1
(z
2
)
P
2
(z
2
)
2
(
z
1
,
z
2
)
P
4
(z
1
,z
2
)
P
5
(z
1
,z
2
)
2
(
z
1
,
z
2
)
P
6
(z
1
,z
2
)
P
7
(z
1
,z
2
)
P
5
(z
1
,z
2
)
P
10
(z
1
,z
2
)
P
11
(z
1
,z
2
)
R
P
1
(z
2
)
P
2
(z
1
)
}
LS 7”
2
(
z
1
,
z
2
)
P
9
(z
1
,z
2
)
R
Q
LL2
Y
LL2
Y
LH2
Y
HL2
Y
HH2
}
LS 8”
P
2
(z
2
)
P
2
(z
1
)
-P
2
(z
1
)P
2
(z
2
)
Q
LH2
Q
HH2
Q
HL2
Y
LH1
Y
HL1
Y
HH1
Q
LH1
Q
HH1
Q
HL1
2
(
z
1
,
z
2
)
P
12
(z
1
,z
2
)
P
13
(z
1
,z
2
)
P
14
(z
1
,z
2
)
Figure 6: Analysis part of the proposed optimum-rounding 5/3 IWT for 2-level decomposition.
AnOptimum-Rounding5/3IWTbasedon2-LevelDecompositionforLossless/LossyImageCompression
17

illustrate a part of image “Barbara” based on an
original image, a nonseparable 2D 5/3 IWT at 5 bpp.
and our proposed optimum-rounding 5/3 IWT at 5
bpp., respectively.
Table 2: PSNR of decoded image at 5 bpp.
Image Name Conv. Nonsep. Prop.
Couple ∞ ∞ ∞
Aerial 46.1 47.3
47.6
Girl ∞ ∞ ∞
Chest 44.4
45.9 45.9
Mobile 47.1 47.7
47.8
Barbara 47.9 48.3
48.9
Flower 46.5 47.6
47.9
Lena 47.9
48.2 48.2
Table 3: PSNR of decoded image at 4 bpp.
Image Name Conv. Nonsep. Prop.
Couple 46.8 48.1
48.2
Aerial 43.0
44.0
43.9
Girl 46.3
47.9 47.9
Chest 41.5
42.2 42.2
Mobile 45.8
47.6 47.6
Barbara 46.0
47.5 47.5
Flower 44.6
45.8
45.7
Lena 46.1
47.7 47.7
Figure 7: A part of original image “Barbara”.
6 CONCLUSIONS
In this report, we proposed an optimum-rounding
5/3 IWT for 2-level decomposition. The lossy-
coding performance of our proposed IWT is better
than those of the conventional IWT because the
Figure 8: A part of decoded image “Barbara” based on
nonseparable 2D 5/3 IWT at 5 bpp.
Figure 9: A part of decoded image “Barbara” based on our
proposed optimum-rounding 5/3 IWT at 5 bpp.
proposed IWT has less number of rounding
operations; whereas, filter characteristics of all
methods are exactly same if rounding effects are
neglected. Simulation results confirm effectiveness
of our proposed method in lossy coding especially at
high bit rate.
REFERENCES
Christopoulos, C., 2000. The JPEG 2000 Still Image
Coding System: an overview, IEEE Transaction on
consumer Electronics, 46(4), pp. 1103-1127.
Calderbank, A.R., Daubechies, I., Sweldens, W., Yeo, B.-
L., 1998. Wavelet Transforms that Map Integers to
Integers, Applied and Computational Harmonic
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
18

Analysis, 5(3), pp. 332-369.
Daubechies, I., Sweldens, W., 1998. Factoring Wavelet
Transform into Lifting Steps, Journal of Fourier
Analysis and Applications, 4(3), pp. x1-268.
Reichel, J., Menegaz, G., Nadenau, M.J., Kunt, M., 2001.
Integer Wavelet Transform for Embedded Lossy to
Lossless Image Compression, IEEE Trans. On Image
Processing, vol. 10, no. 3, pp. 383-392.
Vaidyanathan, P.P., 1993. Multirate Systems and Filter
Banks, Prentice Hall Signal Processing Series.
Chokchaitam, S., Iwahashi, M., 2002. Lossless/Lossy
Image Compression based on Nonseparable Two-
Dimensional L-SSKF, ISCAS 2002.
Komatsu, K., Sezaki, K., Yasuda, Y., 1995. Reversible
Subband Coding Images, IEICE Transaction, vol. J78-
D-II, no. 3, pp. 429-436.
AnOptimum-Rounding5/3IWTbasedon2-LevelDecompositionforLossless/LossyImageCompression
19
