Computing Corpus Callosum as Biomarker for Degenerative Disorders

Thomas Kovac, Sammy Rogmans and Frank Van Reeth

Expertise Centre for Digital Media, Hasselt University - tUL - iMinds, Wetenschapspark 2, 3590 Diepenbeek, Belgium

Keywords:

Biomarker, Corpus Callosum, Image Registration, GPGPU, CUDA.

Abstract:

The developed framework can automatically extract a plane with minimal corpus callosum area while simul-

taneously segmenting it. The method used, introduced by Ishaq, treats the corpus callosum area as a function

of the plane extraction parameters and it uses deformable registration to generate a displacement ﬁeld that

can be used for the calculation of the corpus callosum area. Our registration framework is accelerated using

CUDA, which enables researchers to benchmark huge amounts of data (patients) to test the hypothesis of the

corpus callosum evolution as a biomarker for multiple degenerative disorders like e.g. Alzheimer disease and

multiple sclerosis (MS).

1 INTRODUCTION

Multiple Sclerosis (MS) is an inﬂammatory disorder

of the brain and spinal cord and it has been known

to cause atrophy and deformation in the corpus cal-

losum. Longitudinal studies try to quantify these

changes by using medical image analysis techniques

for measuring and analyzing the size and shape of the

corpus callosum. These medical techniques mostly

analyze and track changes in the corpus callosum by

measuring the cross-sectional area by selecting a 2-

D measuring plane, typically the midsagittal plane.

If this identiﬁcation is done incorrectly, the measure-

ment of the corpus callosum area will also be faulty.

Therefore, an automation of ﬁnding a plane with min-

imal corpus callosum area is implemented to ensure

that the measurement of the cross-sectional area is

done correctly with high accuracy.

The employed method of ﬁnding a plane with

minimal corpus callosum area depends heavily on de-

formable image registration. As the image registra-

tion process must be performed multiple times, it is

important that the registration is performed as quickly,

and correctly, as possible. The use of a GPU greatly

improves computation time, so this framework is built

out of algorithms and data structures that exploit its

parallel computation capabilities and hardware. The

implemented framework is algorithmically inspired

by the work of various research groups and combines

the advantageous approaches into one method.

2 RELATED WORK

There is a vast amount of literature devoted to image

registration. In this section, we mention several domi-

nant image registration approaches. We also consider

related research in ﬁnding a plane with minimal cor-

pus callosum area.

2.1 Image Registration

To date, there are multiple deformable registration

algorithms proposed and validated. This includes

thin-plate splines (Bookstein and Green, 1993), vis-

cous ﬂuid registration (Christensen et al., 1996), sur-

face matching (Thompson and Toga, 1996), ﬁnite-

element models (Metaxas, 1997), spline-based regis-

tration (Szeliski and Coughlan, 1997), demons reg-

istration (Thirion, 1998), and B-spline registration

(Rueckert et al., 1999).

Spline-based registration methods are currently

very popular. Their ﬂexibility and robustness pro-

vide the ability to perform mono-modal and multi-

modal registration. The appealing characteristics of

both free-form deformation and spline-based methods

are the most important reason why many studies have

been conducted involving these techniques. Rueckert

et al. present a method, using cubic B-splines curves

to deﬁne a displacement ﬁeld, which maps voxels in a

moving image to those in a reference image (Rueck-

ert et al., 1999). Each individual voxel movement be-

tween reference and moving image, is parameterized

in terms of uniformly spaced control points that are

138

Kovac T., Rogmans S. and Van Reeth F..

Computing Corpus Callosum as Biomarker for Degenerative Disorders.

DOI: 10.5220/0005310201380149

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 138-149

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Corpus callosum cross-section.

aligned with the voxel grid. The displacement vectors

are obtained via interpolation of the control point co-

efﬁcients, using piecewise, continuous B-spline basis

functions.

Besides the popularity of spline-based registration

methods and their potential to greatly improve the ge-

ometric precision for a variety of medical procedures,

they are usually computationally intensive (Shackle-

ford et al., 2010). Shackleford points to reports of

algorithms requiring hours to compute for demand-

ing image resolutions (Rohde et al., 2003; Aylward

et al., 2007), depending on the speciﬁc algorithm im-

plementation. To remedy these shortcomings, Shack-

leford has proposed a GPU-based image registration

design to accelerate both the B-spline interpolation

problem as well as the cost-function gradient com-

putation that makes use of coalesced accesses to the

GPU global memory and an efﬁcient use of shared

memory.

2.2 Minimal Corpus Callosum Area

The corpus callosum joins the two cerebral hemi-

spheres. It acts as a bridge existing out of nerve ﬁbers

and it provides the exchange of information across the

two hemispheres. Neurological diseases have been

known to affect the shape and size of the anatomical

structures in the brain. Measurement of this change

and its correlation with disease progression has been

one of the goals of clinical research (Hubel, 1995; Si-

mon, 2006; Compston and Coles, 2008). See Figure

1 for a graphical representation of the cross-section of

a corpus callosum.

MS often affects the brain ventricles width, overall

brain width and specially the corpus callosum whose

area loss has been documented in longitudinal studies

(Simon et al., 2006; Simon, 2006). These effects on

the corpus callosum size have generally been quanti-

ﬁed by measuring the cross-sectional area of the cor-

pus callosum. This was done through selecting a 2-D

measuring plane from a MRI volume, typically the

midsagittal plane, and measuring the area of the cor-

pus callosum cross-section in this plane. This method

is highly dependent on the accurate selection of the

measuring plane, as it inﬂuences the measurement of

the area. As longitudinal studies require patients to

undergo several scans over a long period of time, fac-

tors such as the error in positioning of the human head

in the MRI scanner between two scans can potentially

be a source of error in the selection of the midsagittal

plane and consequently the measurement of the cor-

pus callosum area.

Another popular brain morphometry measure is

the brain volume. However, work by Duning et al.

has challenged the use of the whole brain volume as

a measure of brain atrophy due to its susceptibility

to dehydration and rehydration effects (Duning and

Kloska, 2005), whereas the corpus callosum, being a

dense ﬁbrous structure, is hypothesized to be less sen-

sitive to hydration effects and its area is potentially a

more reliable measure of neuro-degeneration and at-

rophy (Ishaq, 2008).

3 MOTIVATION

In the previously mentioned studies, the changes in

the corpus callosum size have been quantiﬁed by

measuring the corpus callosum cross-sectional area

imbedded in a measurement plane. Therefore, it

is paramount that the accurate measurement of this

change in corpus callosum area is dependent on the

repeatable identiﬁcation of the same corpus callo-

sum cross-section in different scans. Typically, the

midsagittal plane (MSP) serves as this measurement

plane.

Ishaq emphasizes on two major disadvantages of

using MSP as the plane for measurement of the cor-

pus callosum area (Ishaq, 2008). First, accurate and

repeatable identiﬁcation of the same corpus callosum

cross-section is difﬁcult due to potential changes in

brain anatomy over time, which can potentially affect

the interhemispheric symmetry and the shape of the

interhemispheric ﬁssure. Even small errors in the se-

lection of the MSP have been found to mystify the

interpretation of the actual changes in the corpus cal-

losum area due to pathology. Second, these extraction

methods only incorporate the information regarding

the brain hemispheric symmetry and the interhemi-

spheric ﬁssure, but completely ignore the characteris-

tics of the corpus callosum itself. However, the rate

of corpus callosum atrophy and deformation can be

independent of the rate of the hemispheric degenera-

tion, therefore the repeatable extraction of the same

corpus callosum cross-section becomes difﬁcult even

ComputingCorpusCallosumasBiomarkerforDegenerativeDisorders

139

for those cases where the brain hemispheres undergo

minimal or no change between scans. These issues

cast doubt on the reliability of employing the MSP as

the measurement plane for measuring the corpus cal-

losum area.

To this end, Ishaq proposed a novel and clinically

meaningful criterion for deﬁning an ideal measure-

ment plane for the corpus callosum area measure-

ment. It differs from symmetry and feature-based

methods because it is based on ﬁnding the plane

which optimizes certain physical properties of the

corpus callosum itself. This is clinically more mean-

ingful and speciﬁcally tailored for the task at hand,

that is, the measurement of corpus callosum area

changes and its correlation with disease progression.

Ishaq also states that the criterion proposed by him is

not a new criterion for MSP extraction, rather, it is a

novel basis for identiﬁcation of a plane for measuring

corpus callosum area change. For convenience, this

minimum corpus callosum area plane will be short-

ened to “MCAP”.

It is important to note that for a single MRI vol-

ume the MCAP is not guaranteed to be unique, that is,

multiple planes in the brain may have the same mini-

mum corpus callosum area. Since all of these planes

restrict the neural transmission equally, identiﬁcation

of one of these planes is sufﬁcient for our purposes.

When searching for the MCAP, one must continu-

ously make use of an image registration implementa-

tion. As (spline-based) registration methods are usu-

ally computationally intensive, the implemented reg-

istration process is accelerated by employing the par-

allel capabilities of a GPU.

4 METHOD

Extracting the MCAP out of an MRI volume is a pro-

cess that consists out of several stages. The most im-

portant stage is image registration, that is used for cal-

culating the cross-sectional area of the corpus callo-

sum. All the necessary steps for ﬁnding the MCAP

are outlined in the following subsections.

4.1 Finding the MCAP

The goal is to extract a plane from an MRI volume

which embeds the corpus callosum cross-section with

the minimum area; also called the MCAP. This cross-

sectional area of the corpus callosum will be denoted

as A

, and the plane which embeds this minimal area

will be denoted as P

ext

. In other words, this means

that the area A

can be written as a function with P

ext

as its parameter:

ext

). (1)

This function must be minimized with respect to the

parameter P

ext

. In order to optimize Equation 1, the

value of A

must be calculated, what entails taking

the following three steps:

1. Extract a 2-D slice speciﬁed by the parameter P

ext

from an MRI volume. This entails resampling a

plane in the volume. The orientation and posi-

tion of this plane are parameterized over two ro-

tations (R

) around the X- and Y-axes respec-

tively, and one translation (T

) along the Z-axis.

Together, these parameters form the parameter

ext

= (R

); (2)

Shackleford reports these variables to take on val-

ues between −3.0 and 3.0 (degrees for R

and R

and millimeters for T

), as the corpus callosum

bridge is well deﬁned in this interval. The coor-

dinate system maps the anterior, superior and left

directions to the positive X, Y , and Z axes respec-

tively and is different from the usually used RAS

and LAS coordinate systems.

2. Segment the corpus callosum cross-section in the

slice extracted in step 1, by registering a 2-D tem-

plate with a segmented corpus callosum to the ex-

tracted slice;

3. Calculate the area (A

) of the corpus callosum by

integrating the determinant of the Jacobian of the

displacement ﬁeld over all the points on the tem-

plate which lie inside the corpus callosum (Da-

vatzikos et al., 1996).

Since the template is a vital part in ﬁnding the

MCAP, it is manually extracted from the MRI volume

using 3D Slicer, which is an open source application.

Ishaq mentions that one can also propose an al-

ternative framework which segments the whole cor-

pus callosum bridge in a given volume, by register-

ing it in 3-D to a pre-segmented template volume

and then ﬁnding MCAP by slicing the corpus callo-

sum bridge and measuring the corpus callosum area.

However, the corpus callosum is mostly a featureless

organ. Therefore, such a 3-D registration can po-

tentially cause anatomically different slices from the

template and target corpus callosums to map to each

other, while this is unlikely to happen in the current

solution.

4.2 Image Registration

The identiﬁcation of the MCAP relies heavily on im-

age registration. Image registration is an important

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

140

preprocessing step in medical image analysis. Medi-

cal images are used for diagnosis, treatment planning,

disease monitoring and image guided surgery and are

acquired using a variety of imaging modalities. There

are, therefore, potential beneﬁts in improving the way

these images are compared and combined. Comput-

erized approaches offer potential beneﬁts, particularly

by accurately aligning the information in the different

images and providing tools for visualizing the com-

bined images (Hill et al., 2001).

Image registration is a task to reliably estimate the

geometric transformation such that two images can be

precisely aligned. In this paper, the following termi-

nology will be used: the image that is not changed

during the registration process is called the reference

or ﬁxed image. The second image that is transformed

in such a manner that it increasingly resembles the

ﬁxed image, is called the template or moving image.

Any registration technique consists out of these

four components:

1. a transformation model, which relates the ﬁxed

and moving images;

2. a similarity measure, which measures the simi-

larity between ﬁxed and moving image;

3. an optimization technique, which determines the

optimal transformation parameters as a function

of the similarity function;

4. a regularization term, which is a technique that

evaluates a given candidate deformation and pe-

nalizes it if it is implausible.

Each of these components can be implemented

in different ways. Over the years, numerous algo-

rithms have been proposed. For more information

about some of these algorithms, look to Section 2.

The proposed framework will use sum of squared

difference as voxel-based similarity measure, restrict-

ing the framework to handle only mono-modality

problems. To be more speciﬁc, 2-D-2-D mono-modal

registration will be performed. A free-form deforma-

tion model, using B-splines, will be used to model

non-rigid deformations, a diffusion regularizer term

will penalize implausible deformations, and steepest

descent is the method used for optimization.

In order to improve robustness and speed of the

image registration framework, a hierarchical multires-

olution approach is adopted. A Gaussian pyramid of

both the ﬁxed and moving images will be built that

will contain the resampled versions of the images at

decreasing resolutions. Starting with the pair of im-

ages at the lowest resolution, registration is performed

using a coarse grid of control points. The registra-

tion results from a previous resolution level are used

at the higher resolution level and the registration is run

again, stopping only when the full image resolution is

reached. Adopting this approach, large deformations

can be recovered early at low resolution and more de-

tailed deformations are observed at the increasingly

ﬁner resolution levels.

5 IMPLEMENTATION

The GPU is an attractive platform to accelerate

compute-intensive algorithms (such as image regis-

tration) due to its ability to perform many arithmetic

operations in parallel. For this paper, the image reg-

istration implementation was modeled after the work

of Shackleford (Shackleford, 2011; Shackleford et al.,

2010; Sharp et al., 2010). Shackleford’s efforts re-

sulted in the creation of the Plastimatch framework.

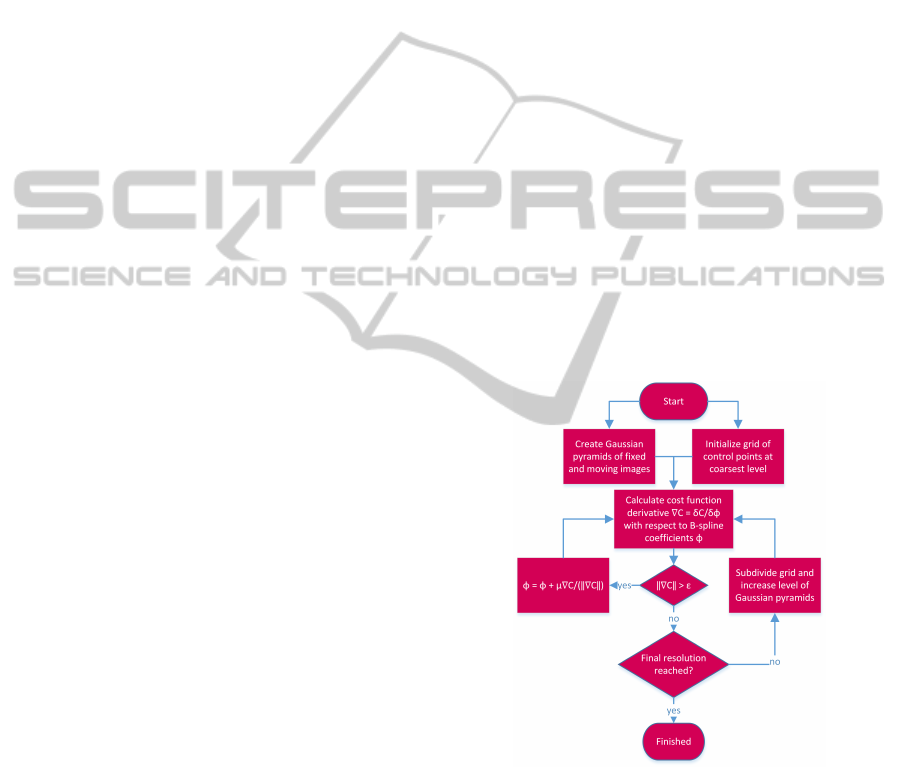
Figure 2 gives an overview of the implemented

image registration algorithm. Note that the cost func-

tion exists out of two terms: the similarity measure

and the regularizer. The total cost function is calcu-

lated using a GPU, but only the calculations concern-

ing the similarity measure are explained in this paper,

since this is the part where the execution time can be

signiﬁcantly improved.

Figure 2: Image registration algorithm outline.

With image registration, a displacement ﬁeld is

calculated that is used to warp the template in such a

manner that it resembles the ﬁxed image (in our case,

the extracted slice). The displacement ﬁeld is calcu-

lated using the grid of control points and the overall

registration process can be viewed as an optimization

problem as the similarity measure performed on the

two images, has to be minimized. One must also take

into consideration the regularization term which will

ComputingCorpusCallosumasBiomarkerforDegenerativeDisorders

141

penalize implausible deformations. This requires that

we evaluate:

1. C, the cost function corresponding to a given set

of B-spline coefﬁcients;

2. ∂C/∂Φ, the change in the cost function with re-

spect to the B-spline coefﬁcient values Φ at each

individual control point.

For simplicity, ∂C/∂Φ will be called cost function

gradient throughout the paper. As mentioned by

Shackleford, the B-spline interpolation and the gra-

dient calculation are the two most time-consuming

stages within the overall registration process. There-

fore, these two stages have been accelerated with

CUDA.

In the following subsections, we will ﬁrst outline

the free-form deformation model. Next, we describe

how this transformation method is used for generating

a displacement ﬁeld, which will be used for warping

the template image. Then, we will describe the imple-

mented data structures and how they are used in cal-

culating the cost function and its derivative. Finally,

some ﬁnal words on the image registration frame-

work’s organization.

5.1 Free-form Deformation Model

In most image processing applications, the pictures to

be manipulated are represented by a set of uniformly

spaced sampled values. Unser provided arguments in

favor of an approach that uses splines to retrieve these

sampled values. They were ﬁrst described by Schoen-

berg, where he laid the mathematical foundations for

the subject (Schoenberg, 1946). Splines are piecewise

polynomials with pieces that are smoothly connected

together. Of all the possible polynomial splines, cu-

bic splines tend to be the most popular in applications

(Unser, 1999), and are also used in this paper. Cubic

B-splines can be represented as follows:

(t) =











(t) = (1 −t)

/6,

(t) = (3t

− 6t

+ 4)/6,

(t) = (−3t

+ 3t

+ 3t + 1)/6,

(t) = t

/6.

(3)

The origins of free-form deformation can be

traced back to the area of computer aided design

(Sederberg and Parry, 1986; Barr, 1984), but it can

also be used in medical image analysis (Rueckert

et al., 1999). We have chosen for an FFD model based

on B-splines.

The basic idea of FFDs is to deform an object by

manipulating an underlying mesh of control points.

The resulting deformation controls the shape of a 3-D

(or 2-D) object and produces a smooth and C

con-

tinuous transformation (Rueckert et al., 1999). In

Figure 3: A grid of control points superimposed on the pix-

els of the template image. Both marked pixels are located at

the same relative offset within their respective tiles, so both

will use the same β

(u)β

(v) value.

contrast to thin-plate splines or elastic-body splines,

B-splines are locally controlled, which makes them

computationally efﬁcient even for a large number of

control points. In particular, the basis functions of

cubic B-splines have limited support, meaning that

changing a certain control point only affects the trans-

formation in the local neighborhood of that control

point.

5.2 Calculating the Displacement Field

In the case of image registration, the template will be

warped in each iteration, until it resembles the ﬁxed

image. The FFD transformation model uses a grid of

uniformly-spaced control points to calculate the dis-

placement ﬁeld for the template image, as shown in

Figure 3. This results in that the image is partitioned

into many, for example, equally sized 5 × 5 tiles. Ev-

ery vector of the displacement ﬁeld is inﬂuenced by

the 16 control points in the tile’s immediate neighbor-

hood and the B-spline basis function product evalu-

ated at the pixel. The latter is only dependent on the

pixel’s local coordinates within the tile. For exam-

ple, in Figure 3 one can see that both marked pixels

have the same local coordinates within their respec-

tive tiles, namely (2,2). This will result in the same

B-spline basis function product value at these two pix-

els. This property allows the pre-computation of all

the relevant B-spline basis function values once, in-

stead of recalculating these values for each individual

tile. More on this in the following subsection.

The B-spline interpolation used for the calculation

of the x-component of the displacement vector for a

certain pixel with coordinates (x,y) is

(x,y) =

∑

m=0

∑

l=0

(u)β

(v)φ

x,i+l, j+m

, (4)

where φ

is the spline coefﬁcient deﬁning the x-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

142

component of the displacement vector. The dimen-

sions n

and n

of the control point grid take the fol-

lowing form:



+ 3



, n



+ 3



, (5)

where m

and m

are respectively the X and Y dimen-

sions of the template image, and s

and s

are the con-

trol point spacing distances. The parameters i and j

are the indices of the tile, within which the pixel (x,y)

falls, that is

i =





− 1, j =





− 1. (6)

The local coordinates of the pixel within this tile, nor-

malized between [0,1], are

u =

−





, v =

−





. (7)

5.3 Optimized Data Structures

Implementing a data structure that exploits the sym-

metrical features that emerge as a result of the grid

alignment, makes the implementation of Equation 4

much faster. Shackleford considers the following op-

timizations:

• All pixels within a single tile use the same set of

16 control points to compute their respective dis-

placement vectors. This means that for each tile in

the image, the corresponding set of control point

indices can be pre-computed and stored in a look-

up table (LUT), called the index LUT.

• Equation 7 shows that for a tile of dimensions

= n

× n

, the number of β(u)β(v) combina-

tions is limited to n

values. Furthermore, as

shown in Figure 3, two pixels belonging to dif-

ferent tiles but with the same local coordinates,

will be subject to identical β(u)β(v) products.

This means that a look-up table, called the mul-

tiplier LUT, can be calculated containing the pre-

computed β(u)β(v) product for all the normalized

coordinate combinations.

For each pixel, the absolute coordinates (x,y)

within the image dimensions are used to calculate the

tile indices that the pixels falls within as well as the

pixel’s local coordinates within the tile, using Equa-

tions 6 and 7 respectively. These tile indices will be

used to access the index LUT, which will provide co-

ordinates of the 16 neighboring control points that

inﬂuence the pixel’s interpolation calculation. The

pixel’s local coordinates within the tile will be used

to retrieve the appropriate, pre-calculated β(u)β(v)

product from the multiplier LUT. Using these look-

up tables, the displacement ﬁeld calculation can be

considerably optimized.

5.4 Similarity Cost Function

Once the displacement ﬁeld is calculated, it is used to

warp the template image. Once warped, the template

image is compared to the ﬁxed image (both consisting

out of normalized values) by means of the similarity

measure. In our case, the similarity measure is the

sum of squared differences, that is

sim

∑

y=0

∑

x=0

(x,y) − I

(x + v

,y + v

))

, (8)

where N is the amount of pixels in the template im-

age, X and Y are the template image’s dimensions,

and (v

) form the displacement ﬁeld vector for the

template image pixel with coordinates (x,y). The sim-

ilarity part of the cost function will be called the sim-

ilarity cost function throughout the rest of this paper.

The gradient descent optimization requires the

partial derivatives of the similarity cost function with

respect to each control point (B-spline) coefﬁcient

value. The look-up tables introduced in the previous

section not only accelerate the B-spline interpolation

stage, it also accelerates the similarity cost function

gradient calculation. The similarity cost function gra-

dient can be considered as the change in the similarity

cost function with respect to the coefﬁcient values Φ

at each individual control point. This gradient can be

decomposed and can be computed independently, for

a given control point at the grid coordinates (κ, λ), as

∂C

sim

∂Φ

(κ,λ)

16 tiles

∑

(x,y)

∂C

∂

−→

v (x,y)

∂

−→

v (x,y)

∂Φ

, (9)

where the summation is performed over all the pix-

els (x,y) of the template image contained in the 16

tiles found in the control point’s local support region.

By means of this decomposition, the gradient’s de-

pendencies on the similarity cost function and spline

coefﬁcients can be independently evaluated. The ﬁrst

term, ∂C

sim

/∂

−→

v (x,y), depends only on the similar-

ity cost function. The second term, ∂

−→

v (x,y)/∂Φ, de-

scribes how the displacement ﬁeld changes with re-

spect to the control points. This last term is only

dependent on the B-spline parametrization and the

pixel’s location; it is computed as

∂

−→

v (x,y)

∂Φ

∑

l=0

∑

m=0

(u)β

(v). (10)

This only needs to be computed once, since it re-

mains constant over all the optimization iterations.

The pre-calculated β(u)β(v) product is available via

the multiplier LUT.

Since the SSD similarity measure is utilized, the

ﬁrst term (see Equation 9) can be written in terms of

ComputingCorpusCallosumasBiomarkerforDegenerativeDisorders

143

the template image’s spatial gradient ∇I

(x,y) as

∂C

sim

∂

−→

v (x,y)

= 2×(I

(x,y)−I

(x+v

,y+v

))∇I

(x,y).

(11)

Equation 11 shows that it depends on the intensity

values of the ﬁxed image and the (warped) template

image, I

and I

respectively, as well as the current

value of the displacement ﬁeld

−→

v . Meaning, that dur-

ing each iteration, the displacement ﬁeld will change

and that results in the modiﬁcation in the correspon-

dence between the ﬁxed and template images. This

also means that, unlike ∂

−→

v /∂Φ, ∂C

sim

/∂

−→

v needs to

be recalculated during each iteration of the optimiza-

tion. With both terms calculated, they can be com-

bined using the chain rule from Equation 9, which

can be written in terms of the control point coordi-

nates (κ,λ) as

∂C

sim

∂Φ

(κ,λ)

∑

16 tiles

(κ,λ)

∑

b=0

∑

a=0

∂C

sim

∂

−→

(x,y)

∑

m=0

∑

l=0









(12)

where a and b are the unnormalized local coordinates

of a pixel inside its respective tile, and x and y rep-

resent the absolute coordinates of a pixel within the

template image. Here, x and y can be deﬁned in terms

of the control point coordinates and summation in-

dices as follows:

x = s

(κ − l) + a, y = s

(λ − m) + b. (13)

For this paper, the method for calculating the sim-

ilarity cost function gradient has been implemented

in three versions: a na

ıve CPU and GPU version and

an optimized GPU version. The next two subsections

will describe these implemented versions.

5.4.1 Na

ıve CPU/GPU Implementation

The kernel described by Algorithm 1 calculates the

similarity cost function gradient vector ∂C

sim

/∂Φ for

a control point. As previously described, this gradient

calculation makes use of the ∂C

sim

/∂

−→

v and ∂

−→

v /∂Φ

terms, as described in Equation 9. The kernel is

launched with as many threads as there are control

points, where each thread calculates the ∂C

sim

/∂Φ

value for each control point. As shown in the pseudo-

code, the coordinates (κ,λ) are deferred from the

CUDA thread indices. Each control point’s gradient

is inﬂuenced by 16 neighboring tiles, and the template

pixel values that these tiles contain. Once the calcula-

tions are ﬁnished, the results are stored in the global

memory of the GPU.

Algorithm 1: Kernel that calculates the ∂C

sim

/∂Φ value for

a control point.

Require: First calculate ∂C

sim

/∂

−→

/* Iterate through the 16 tiles affecting this control

point to calculate ∂C

sim

/∂Φ. */

= A

= 0;

for m = 0 to 3 do

for l = 0 to 3 do

= κ − l; // X component of tile index

= λ − m; // Y component of tile index

for j = 0 to s

for i = 0 to s

/* Absolute x and y pixel coordinates of

template image */

x = (s

×t

) + i;

y = (s

×t

) + j;

if x and y fall within the bounds of the

template image then

U = β

(u)β

(v);

= A

+U × ∂C

sim

/∂

−→

(i);

= A

+U × ∂C

sim

/∂

−→

( j);

end if

end for

(∂C

sim

/∂Φ(κ,λ)).x = A

;

(∂C

sim

/∂Φ(κ,λ)).y = A

;

5.4.2 Optimized GPU Implementation

Although the implementation described in Section

5.4.1 is a good way to exploit the parallelization capa-

bilities of a GPU, it suffers from serious performance

deﬁciency as the kernel described in Algorithm 1 does

a lot of redundant load operations (Shackleford, 2011;

Shackleford et al., 2010; Sharp et al., 2010).

As can be seen in Algorithm 1, the gradient value

for each control point is inﬂuenced by its neighbors.

This also implies that when two different threads cal-

culate their respective contribution to a certain one

control point, and they both need to calculate the con-

tribution of one the same control point, they must each

load the same ∂C

sim

/∂

−→

v values from the same tile.

The only thing these two threads do different is that

they must each use different basis-function products

when computing the ∂

−→

v /∂Φ term to obtain their re-

spective contributions to the ∂C

sim

/∂Φ term. To gain

a visible view of the problem, consider the following

equations. Thread 1 calculates the following contri-

bution of a tile:

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

144

∑

∂C

sim

∂

−→

v (x,y)

(u)β

(v). (14)

Thread 2 calculates his contribution of the same tile,

but with different l and m values:

∑

∂C

sim

∂

−→

v (x,y)

(u)β

(v). (15)

In both Equations 14 and 15, the u and v values are

the normalized position of a pixel within the tile. One

can clearly see that although these two threads are ex-

ecuted independently of each other in parallel, each

thread will end up loading the same ∂C

sim

/∂

−→

v val-

ues, as they are handling the same tile.

This redundant loading of ∂C

sim

/∂

−→

v values can

be mitigated by implementing the following two

stages. The ﬁrst stage will read all the ∂C

sim

/∂

−→

v val-

ues of a certain tile from global memory into shared

memory. Any given pixel tile is inﬂuenced by (and

inﬂuences) 16 neighboring pixel tiles, meaning that

there are 16 different possible (l,m) combinations. For

a certain tile with a certain (l,m) combination, the fol-

lowing must be calculated

−→

(κ,λ,l,m)

∑

b=0

∑

a=0

∂C

sim

∂

−→

v (x,y, z)

(u)β

(v), (16)

where the values for x and y can be calculated using

Equation 13. The operation described in Equation

16 is performed for the 16 possible (l,m) combina-

tions, resulting in 16

−→

Z values per tile. This operation

will be implemented as a GPU kernel. Each of these

−→

Z values is a partial solution to the gradient com-

putation for a certain control point within the grid.

Therefore, we allocate for each control point within

the grid an array (or bins) that can hold up to 16 of

these partial gradient computation

−→

Z values. Once

the 16

−→

Z values for a certain tile are computed, each

of these values must be inserted into the correct con-

trol point’s bin of partial gradient computation

−→

Z val-

ues. In other words, when a tile computes the 16

−→

values, these values will not only be written to differ-

ent control points, but to different bin slots within the

control point. The second stage of the gradient com-

putation will simply sum up these 16

−→

Z values for

each control point.

The two proposed stages are implemented as GPU

kernels, but only the ﬁrst stage will be described as

the second stage simply sums up all the 16

−→

Z values

of the control point in question. The kernel described

in Algorithm 2 will be launched with 16 threads op-

erating on a single tile. Each one of these threads

will read a portion of the ∂C

sim

/∂

−→

v values if this tile

into shared memory, so that each of these 16 threads

doesn’t constantly have to read out of global mem-

ory. Once they have been read into shared memory,

each thread will compute the ∂C

sim

/∂Φ value with the

appropriate (l,m) values. When a thread ﬁnishes this

calculation, it puts the computed value into the correct

control point’s correct bin.

Algorithm 2: Optimized kernel design for calculating the

∂C

sim

/∂Φ value for a control point. Stage 1.

Require: First calculate ∂C

sim

/∂

−→

v , get the thread

block IDs (cpX,cpY ), get the thread IDs within the

thread block (t

)

/* Block IDs */

= κ;cp

= λ;

/* After reading ∂C

sim

/∂

−→

v into shared memory is

done (left out for brevity) */

synchthreads();

= A

= 0;

for j = 0 to s

for i = 0 to s

/* U = β

(u)β

(v) */

= A

+U × ∂C

sim

/∂

−→

(i);

= A

+U × ∂C

sim

/∂

−→

( j);

end for

/* dc d p buckets[s

× 16 × 2] contains the seper-

ate partial gradient contributions of all the control

point’s 16 neighbors. N

is the width of the control

point grid. */

if cp

and cp

fall within the bounds of the

control point grid then

= cp

+ (cp

;

bucketID = (3 − t

) + 4(3 −t

);

d p buckets[cp

][bID][0] = A

;

dc d p buckets[cp

][bID][1] = A

;

end if

5.5 Framework Organization

The implemented image registration framework uses

the GPU for calculations as shown in Figure 4. The

B-spline interpolation and the cost function gradient

are implemented on the GPU, while the optimization

stage is performed on CPU. During each iteration, the

optimizer, working on the CPU, calculates new pa-

rameters to update the control points so that the cost

function is minimized. When a minimum has been

found, the registration process stops.

When analyzing Figure 4, one can see that both

the evaluated cost function and its gradient must be

ComputingCorpusCallosumasBiomarkerforDegenerativeDisorders

145

Figure 4: Framework organization.

transferred from GPU to the CPU for every iteration

of the image registration process. Transfers between

the CPU and GPU memories are the most costly in

terms of time, but Shackleford observed in his ex-

periments that the CPU-GPU communication over-

head demands roughly 0.14% if the total algorithm

execution time. This fact allows the conclusion that

the CPU-GPU transfers do not affect the overall algo-

rithm performance.

6 RESULTS

We have implemented two items: an image regis-

tration framework and an application that uses this

framework for ﬁnding the MCAP. Both have been

thoroughly evaluated and the results are described in

the following subsections.

6.1 Image Registration Evaluation

Given that the method for extracting the corpus callo-

sum area relies heavily on deformable registration, the

quality of the registration directly affects the accuracy

of the area measurement. Several experiments have

been conducted in order to evaluate the deformable

registration that was implemented. Synthetic data has

been used to demonstrate the effectiveness and perfor-

mance of the registration framework, but our frame-

work has also been evaluated with medical data.

To evaluate the effectiveness and performance of

the registration framework, ground truth experiments

have been conducted. The precision and error intro-

duced by the algorithm that has to be evaluated, can

be assessed by comparing the results with the ground

truth. In this case, a synthetic image is deformed

using a known control point conﬁguration. This de-

Figure 5: Conducted experiment.

formed image will serve as the reference image, while

the original, undeformed image will act as the tem-

plate image. The quality of the registration can be

measured by comparing the displacement ﬁeld ob-

tained by the registration framework with the ground

truth displacement ﬁeld computed from the known

control point conﬁguration.

For the experiments, two synthetic images where

used as shown on the left side in Figure 5. Both

images have a checkerboard pattern and are of size

256 × 256, inspired by the experiments conducted by

Schwarz (Schwarz, 2007). For both images, a sepa-

rate control point conﬁguration was created that were

sinusoidal in both x- and y-direction and with a ﬁxed

control point spacing of 15 pixels. Using these con-

trol point conﬁgurations, the displacement ﬁelds were

calculated for each original image together with the

resulting warped images as shown on the right side of

Figure 5. Next, the registration framework is utilized

with various control point spacings ranging from 5 to

50 pixels with increments of 5.

We have conducted three experiments to evaluate

the accuracy of our registration framework. First, we

calculated the similarity of the images (using SSD)

after the registration process (Figure 6). The next

experiment calculated the Root Mean Square Error

(RMSE) between the ground truth displacement ﬁeld

and the displacement ﬁeld obtained from the registra-

tion process (Figure 7). Last, we calculated the mag-

nitude of difference (Figure 8). Each of these experi-

ments individually validated the accuracy of our reg-

istration framework, as they show that a control point

spacing of 15−20 pixels best recovers the applied de-

formation.

For this paper, three versions of the image reg-

istration implementation were written: a na

ıve CPU

and GPU implementation and an optimized GPU ver-

sion. All three implementations will generate the

same result, but will perform the registration at dif-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

146

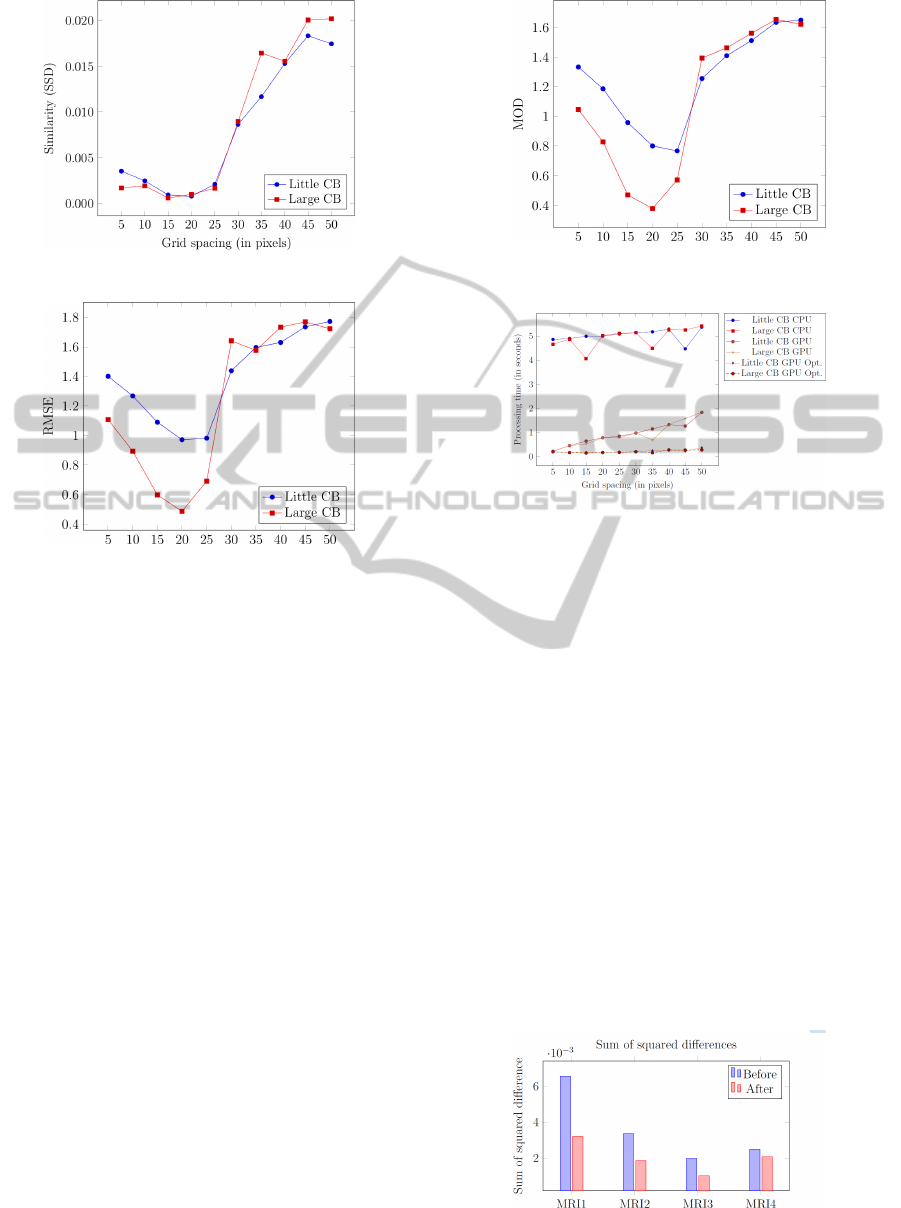
Figure 6: Similarity after registration.

Figure 7: RMSE of the generated displacement ﬁeld and the

ground truth.

ferent speeds. Figure 9 shows the impact of differ-

ent control point spacings on the three implemented

versions. Both the GPU and CPU versions of the

ıve implementation are susceptible to grid spacing,

because a coarse grid spacing means bigger tiles to

compute and a lot of redundant ∂C

sim

/∂

−→

v loads. The

performed experiments showed that when comparing

the GPU and CPU version of the na

ıve implementa-

tion, for a grid spacing of 5 pixels, the GPU version

performed about 21 times faster than the CPU. When

reaching a grid spacing of 50 pixels, it only performed

three times faster than the CPU version.

The optimized GPU version, however, is rather

agnostic to grid spacing. At a grid spacing of 10 pix-

els, the optimized version performed about 24 to 40

times faster than the na

ıve CPU version. When using

a grid spacing of 50 pixels, the optimized version cal-

culated its results about 20 times faster than its na

ıve

CPU counterpart. Since the image registration frame-

work is an essential part in ﬁnding the MCAP, it is

paramount that this part was properly optimized.

The deformable registration framework has also

been evaluated using medical data. To assess the qual-

ity of the registration, two measurements were used,

namely the sum of squared differences (SSD) mea-

surement and the correlation coefﬁcient (CC) mea-

surement, as shown by Figures 10 and 11 respec-

Figure 8: Magnitude of Difference of generated displace-

ment ﬁeld and ground truth.

Figure 9: Processing time of registration using CPU, GPU

and the optimized GPU versions.

tively. The results show that the resulting warped

images signiﬁcantly resemble their ﬁxed image coun-

terparts. We have used three MRI data sets retrieved

from the Open Access Series of Imaging Studies (OA-

SIS) project as well as an MRI volume obtained from

icoMetrix. The OASIS project is aimed at making

MRI data sets of the brain available to the scientiﬁc

community. The volume of icoMetrix has a size of

79 × 95 × 68 voxels, while the three volumes from

OASIS have a size of 128 × 256 × 256 voxels. How-

ever, the three volumes from OASIS are anisotropic

in nature. Each of the volumes have been resampled

so that they are isotropic, which results in a volume

of size 160 × 256 × 256. For each of these volumes,

we extracted a plane that roughly resembles the mid-

sagittal plane that would serve as the ﬁxed image.

Next, we also extracted from each volume a plane

that has been rotated over several degrees from the

central pixel of each volume’s extracted midsagittal

plane. The reason why we chose these planes is that

Figure 10: SSD between the ﬁxed image and the warped

moving image before and after the registration process.

ComputingCorpusCallosumasBiomarkerforDegenerativeDisorders

147

Figure 11: CC between the ﬁxed image and the warped

moving image before and after the registration process.

Figure 12: Graph of normalized CC areas of 8 MRI vol-

umes.

this is exactly what the implemented application will

do when searching for the MCAP.

6.2 MCAP Extraction Evaluation

Figure 12 shows a graph of normalized corpus callo-

sum areas for 8 MRI volumes in function of the opti-

mizer iterations. Seven of these MRI volumes came

from the OASIS project and the other one came from

icoMetrix. The results for each volume have been

normalized (i.e. starting at 1) with the rotation param-

eters and the translation parameter set to zero. The re-

sults show a distinct decrease and convergence of the

corpus callosum area for all examined volumes.

For the examined volumes, we register a percent-

age drop ranged from a minimum of 0.01%, a max-

imum of 13.6889% with a mean decrease in area of

6.6094% and a median decrease of 7.5012%. As

stated by Ishaq (Ishaq, 2008) and longitudinal study

performed by Juha (Juha et al., 2007), the minimiza-

tion in corpus callosum area is potentially signiﬁcant,

given that approximately 33% of the reduction in cor-

pus callosum area can be explained by atrophy.

7 CONCLUSIONS

The developed framework can automatically extract

the MCAP and simultaneously segment the corpus

callosum. This method, introduced by Ishaq, can aid

longitudinal studies. The method used, treats the cor-

pus callosum area as a function of the plane extrac-

tion parameters and it uses deformable registration to

generate a displacement ﬁeld that can be used for the

calculation of the corpus callosum area. The gathered

results show a clear decrease and convergence to the

plane with minimal corpus callosum area.

The obtained results cannot be compared to other,

existing methods, because none of the existing meth-

ods try to achieve the same objective, which is the

identiﬁcation of minimal corpus callosum area and

therefore, such a comparison would not be meaning-

ful. As stated by Ishaq, this work can beneﬁt future

studies on longitudinal analysis of the change in cor-

pus callosum area with the progression of different

neurological diseases.

Deformable registration is a crucial part in ﬁnd-

ing the MCAP. The algorithm for deformable regis-

tration has been described in detail. Free-form defor-

mation has been used, which allows to model ﬂexi-

ble deformations by means of a limited grid of con-

trol points, instead of manipulating each pixel indi-

vidually as is done in deformable registration meth-

ods based on dense deformation ﬁelds. A regulariza-

tion term is also used that will penalize deformations

that are implausible.

Finding an MCAP requires multiple image regis-

tration iterations. Therefore, the registration frame-

work has been optimized using CUDA. The intro-

duced algorithms, optimizations and data structures

reduce the complexity of the B-spline registration

process. Highly parallel and scalable designs for

computing both the sum of squared differences sim-

ilarity measure and its derivative with respect to the

B-spline parameterization were implemented. The

speed and robustness of the image registration pro-

cess were determined using both synthetic and medi-

cal data. The acceleration of the GPU process ranges

from 24 to 40 times faster than the na

ıve CPU imple-

mentation, depending on the grid spacing used for the

control points.

ACKNOWLEDGEMENTS

This research has been made possible thanks to the

collaboration with icoMetrix in Belgium.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

148

REFERENCES

Aylward, S., Jomier, J., Barre, S., Davis, B., and Ibanez, L.

(2007). Optimizing ITK’s Registration Methods for

Multi-processor, Shared-memory Systems. MICCAI

Workshop on Open Source and Open Data.

Barr, A. (1984). Global and Local Deformations of

Solid Primitives. SIGGRAPH Computer Graphics,

18(3):21–30.

Bookstein, F. and Green, D. (1993). A feature space for

derivatives of deformation. Information Processing

in Medical Imaging - Lecture Notes in Computer Sci-

ence, 687:1–16.

Christensen, G., Rabbitt, R., and Miller, M. (1996). De-

formable templates using large deformation kine-

matics. IEEE Transactions on Image Processing,

5(10):1435–1447.

Compston, A. and Coles, A. (2008). Multiple Sclerosis. The

Lancet, 372(9648):1502–1517.

Davatzikos, C., Vaillant, M., Resnick, S., Prince, J.,

Letovsky, S., and Bryan, R. (1996). A Computerized

Approach for Morphological Analysis of the Corpus

Callosum. Journal of Computer Assisted Tomogra-

phy, 20(1):88–97.

Duning, T. and Kloska, S. (2005). Dehydration con-

founds the assessment of brain atrophy. Neurology,

64(3):548–550.

Hill, D., Batchelor, P., Holden, M., and Hawkes, D. (2001).

Medical Image Registration. Physics in Medicine and

Biology, 46(3):R1–R45.

Hubel, D. (1995). Eye, brain and vision. WH Freeman.

Ishaq, O. (2008). Algorithms for Image Analysis of Corpus

Callosum Degeneration for Multiple Sclerosis. Mas-

ter’s thesis, Simon Fraser University.

Juha, M., Leszek, S., Sten, F., Jakob, B., Olof, F., and Maria,

K. (2007). Non-age-related Callosal Brain Atrophy in

Multiple Sclerosis: A 9-year Longitudinal MRI Study

Representing Four Decades of Disease Development.

Journal of Neurology, Neurosurgery, and Psychiatry,

78:375–380.

Metaxas, D. (1997). Physics-Based Deformable Models:

Applications to Computer Vision, Graphics and Med-

ical Imaging. Kluwer.

Rohde, G., Aldroubi, A., and Dawant, B. (2003). The adap-

tive bases algorithm for intensity-based nonrigid im-

age registration. IEEE Transactions on Medical Imag-

ing, 22(11):1470–1479.

Rueckert, D., Sonoda, L., Hayes, C., Hill, D., Leach, M.,

and Hawkes, D. (1999). Nonrigid Registration Us-

ing Free-Form Deformations: Application to Breast

MR Images. IEEE Transactions on Medical Imaging,

18(8).

Schoenberg, I. (1946). Contributions to the Problem of Ap-

proximation of Equidistant Data by Analytic Func-

tions. The Quarterly of Applied Mathematics, 4:45–

99.

Schwarz, L. (2007). Non-rigid Registration Using Free-

from Deformations. Master’s thesis, Technische Uni-

versit

at M

unchen.

Sederberg, T. and Parry, S. (1986). Free-form Deformation

of Solid Geometric Models. SIGGRAPH Computer

Graphics, 20(4):151–160.

Shackleford, J. (2011). High-Performance Image Registra-

tion Algorithms for Multi-Core Processors. PhD the-

sis, Drexel University.

Shackleford, J., Kandasamy, N., and Sharp, G. (2010). On

developing B-spline registration algorithms for multi-

core processors. Physics in Medicine and Biology,

55:6329–6351.

Sharp, G., Peroni, M., Li, R., Shackleford, J., and Kan-

dasamy, N. (2010). Evaluation of Plastimatch B-

Spline Registration on the EMPIRE10 Data Set. Med-

ical Image Analysis for the Clinic: A Grand Chal-

lenge, pages 99–108.

Simon, J. (2006). Brain Atrophy in Multiple Sclerosis:

What We Know and Would Like to Know. Multiple

Sclerosis, 12(6):679–687.

Simon, J., Simon, L., Campion, M., Rudick, R., Cookfair,

D., Herndon, R., Richert, J., Salazar, A., Fischer, J.,

Goodkin, D., Simonian, N., Lajaunie, M., Miller, D.,

Wende, K., Martens-Davidson, A., Kinkel, R., Mun-

schauer, F., and Brownscheidle, C. (2006). A Longi-

tudinal Study of Brain Atrophy in Relapsing Multiple

Sclerosis. Neurology, 12(6):679–687.

Szeliski, R. and Coughlan, J. (1997). Spline-Based Image

Registration. International Journal of Computer Vi-

sion, 22(3):199–218.

Thirion, J. (1998). Image matching as a diffusion process:

an analogy with Maxwell’s demons. Medical Imaging

Analysis, 2(3):243–260.

Thompson, P. and Toga, A. (1996). A surface-based

technique for warping three-dimensional images of

the brain. IEEE Transactions on Medical Imaging,

15(4):402–417.

Unser, M. (1999). Splines: A Perfect Fit for Signal and

Image Processing. IEEE Signal Processing Magazine,

16(6):22–38.

ComputingCorpusCallosumasBiomarkerforDegenerativeDisorders

149