
Interactive Control of Deformable-object Animations through Control
Metaphor Pattern Adherence
Shane Transue and Min-Hyung Choi
Department of Computer Science and Engineering, University of Colorado Denver, Denver, U.S.A.
Keywords:
Physically-based Simulation, Animation Control.
Abstract:
In this paper we present an adaptive and intuitive methodology for controlling the localized deformations
of physically simulated objects using an intuitive pattern-based control interface. To maximize the interac-
tive component presented in this approach we consolidate existing feedback mechanisms in deformable-body
control techniques to provide intuitive editing metaphors for stretching, bending, twisting, and compressing
simulated objects. The resulting movements created by these control metaphors are validated using imposed
behavior evaluation and the effectiveness of this approach is demonstrated through interactively generated
compound movements that introduce complex local deformations of objects in existing physical animations.
1 INTRODUCTION
Controlling the behaviors of deformable objects in
physically-based simulations is an area within com-
puter animation that has recently received extensive
attention. In this field, notable progress has been
made in the development of intuitive control tech-
niques that can be used to effectively generate and
target deformation behaviors in physical animations.
Effective approaches in this domain include goal ori-
ented behaviors derived from optimizations in inverse
dynamics (Murray-Smith, 2000) and constraint-based
techniques (Witkin and Welch, 1990). These ap-
proaches are based on methods that effectively con-
trol deformable-object behavior by interpolating be-
tween statically defined deformation states. This pro-
vides an artist with the ability to generate physically
plausible animations of deformable objects by defin-
ing this sequence of deformation states. Despite the
impressive results that can be achieved using these
techniques, there remains a segment within the do-
main of physically-based animation control that re-
quires the translation of high-level control behaviors
into the physical motions of simulated objects to de-
rive realistic deformations. The ability to effectively
interpret and map deformation behaviors to a simu-
lated object provides animation artists with a higher
level of control over the motions that can be expressed
in physical animations. Extending this precise control
to localized deformations, realistic motions from de-
formable models can be obtained (see Figure 1).
Figure 1: Natural deformation behavior derived from the
application of a twist control metaphor. Starting from the
rest state (top-left), the application of the twist control
metaphor produces a localized deformation (bottom-right).
In this paper we present an approach to uti-
lizing precisely controlled external forces to gener-
ate localized deformations in existing animations of
both Mass-Spring Systems (MSS) and Finite Element
Models (FEM) using high-level control metaphors.
Control metaphors introduce an abstraction for high-
level deformation patterns that can be imposed on de-
formable objects to obtain artist directed behaviors.
Unlike prior techniques where intermediate motion
is not explicitly controlled by an artist, we provide
294
Transue S. and Choi M..
Interactive Control of Deformable-object Animations through Control Metaphor Pattern Adherence.
DOI: 10.5220/0005311702940305
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 294-305
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

a set of controls that allow an artist to continuously
interact with the physical state of a simulated object.
Specifically, we look at how control metaphors can be
used to stretch, bend, twist, and compress localized
regions of simulated deformable objects. We then in-
tegrate this editing process into an intuitive animation
interface that allows for an artist to iteratively refine
deformation behaviors through the use of interactive
control widgets. The objective of our approach to de-
formation control is to provide a set of tools that can
be effectively used to generate deformations based on
predefined control metaphor behaviors and precisely
control deformations within existing animations. This
tool-set includes real-time simulation recording, the
ability to generate dynamic simulation previews, and
the introduction of interactive force curves for precise
deformation control with motion blending.
The effectiveness of our approach is explored
through the application of control metaphors to exist-
ing node-based models to generate explicit deforma-
tion behaviors. From the resulting animations gener-
ated with this proposed method, we illustrate that con-
trol metaphors can be used to effectivelyimpose phys-
ically plausible localized deformationsat any physical
time-step within an existing animation. To further il-
lustrate the utility of this proposed technique, we also
demonstrate that the subsequent application of control
metaphors can be used to define compound localized
deformation behaviors.
2 RELATED WORK
Several generalized control techniques in goal ori-
ented optimization (Popovi´c et al., 2000), dynamic
key-framing (Hildebrandt et al., 2012), space-time
optimization (Barbiˇc et al., 2009), and inversedynam-
ics (Jeon and Choi, 2007), (Twigg and James, 2008)
have been developed to provide effective techniques
for generating accurately controlled animations. The
common tie between these approaches is that they
are directed at the derivation of physically plausi-
ble motion defined between statically defined defor-
mation states. Similarly, recent developments in ex-
ample driven deformations by (Martin et al., 2011)
and methods using internal elasticity potentials intro-
duced by (Coros et al., 2012) can be used to direct
global deformations form predefined static deforma-
tion states or transformation goals. These approaches
represent a field of deformation control techniques
that utilize constraint-based optimizations that can be
used to effectively generate targeted deformation be-
haviors. However, these approaches lack flexibility
in the control of behaviors within intermediate states
generated during this optimization process. This can
be attributed to the to the difficulties in creating an
intuitive connection between artistic intent and opti-
mization control parameters.
To modify the deformation behavior between ex-
ample or goal states using current techniques, the so-
lution involves the introduction of additionalstatic ex-
amples that further refine the description of the de-
sired behavior (Chai and Hodgins, 2007). However
the introduction of these additional constraints in-
creases the number of required example deformation
states that an artist must provide. Upon doing so, an
artist must consider that the accuracy of these input
states can significantly affect the physical plausibility
of the resulting animation (Arikan and Forsyth, 2002).
In prior rigid-body control techniques based on
physical parameter optimization (Popovi´c et al.,
2000), these intermediate states can be derived from
global transformations. However, providing these
additional key-frames for deformable objects repre-
sents an additional challenge due to the inherent diffi-
culty in accurately defining static deformation states.
This problem is exacerbated for objects with complex
topologies or highly-dynamic models such as articu-
lated figures or cloth. While many of these introduced
techniques are well suited for generating the interme-
diate motions between static deformations, an artist is
left to provide these initial input states, a non-trivial
task. Additionally, the introduction of these new con-
straints requires a regeneration of all intermediate mo-
tions, thus eliminating prior deformation behaviors.
This is an undesirable effect if the original deforma-
tion behavior was close to the desired result.
Alternative techniques for interactively editing
deformable simulations proposed by (Barbiˇc et al.,
2012) and (Huang et al., 2011) aim to maintain the
original behavioralcharacteristics of a deformableob-
ject within the provided animation. This provides an
effective platform for interactively controlling defor-
mations and introduces the ability to alter object be-
haviors within existing animations.
These contributions substantially improve the in-
teractive editing process used by artists to control ob-
ject deformations while preserving existing animated
behaviors. Our work is related to these contributions
and aims to provide an interactive editing environ-
ment that can facilitate real-time editing of localized
deformations. We propose that generalized high-level
control metaphors can be used in cooperation with
existing techniques to both generate static deforma-
tion states as key-frames, introduce localized defor-
mations in existing animations, and provide tweaks
to existing cage-based animation techniques (Joshi
et al., 2007), (Ju et al., 2008).
InteractiveControlofDeformable-objectAnimationsthroughControlMetaphorPatternAdherence
295

3 METHOD OVERVIEW
The input to our interactive animation system is based
on MSS and FEM node-based deformation models
as individual rest state objects or as part of an exist-
ing physically-drivenanimation. In both instances the
dynamics model driving the deformation behavior is
orthogonal to our approach and does not contribute
to the requirements of our editing tools. Rather, the
only assumptions made about a provided nodal sys-
tem is that it is composed of n interconnected nodes
that define a shell or tetrahedral topology and can be
directly integrated into an existing dynamics model.
If an animated MSS or FEM model is provided, the
animation is discretized into states that correspond to
individual time-steps within the underlying dynam-
ics model driving the physical simulation. In using
precisely targeted external forces, we can effectively
limit the requirement of our approach to dynamics
models that support the application of these forces
to arbitrary nodes. In our implementation we utilize
the VegaFEM physics library (Barbiˇc and Schroeder,
2009) with an implicit Euler integration scheme.
The foundation of our editing approach is based
on the development of several components that are
required to facilitate this form of force-based editing
in an interactive environment. These requirements
include (1) reliable local coordinate systems for de-
formable models to facilitate targeted deformations,
(2) the ability to record physical simulations in real-
time, (3) the efficient generation of dynamic simula-
tion previews for interactive feedback, and (4) a set
of intuitive control metaphors that impose intuitive
pattern-based deformation behaviors. We consolidate
these components within an interactive editing envi-
ronment that allows an artist to effectively define new
animations and refine the deformation behaviors ex-
hibited by objects within existing animations. In this
section we provide the derivation for each of these
components and establish how each contributes to this
intuitive animation editing framework.
3.1 Local Coordinates
To provide an effective mapping between the imple-
mented control metaphors and the deformable objects
upon which they operate, we have introduced a ro-
bust technique for estimating local coordinate trans-
formations for deformable-bodies. Building on this
development, we introduce the notion of control co-
ordinates that allow metaphors to be directly targeted
to localized regions within a deformable object. As
these objects are simulated, these coordinate systems
maintain the application of a control metaphor to the
exact region defined by an artist. This allows us to
provide consistency in localized deformations, even
for objects that exhibit complex global trajectories. In
this section we provide an overviewof our method for
identifying a unique origin and orthogonal set of vec-
tors that can be used to represent the local coordinate
transformation of a deformable-body.
Initially considering the position of a deformable
object, we simply select the center of mass C as an
accurate representation of the objects global position.
To identify the orthogonal set of vectors that will rep-
resent the rotation of the deformable object we con-
sider two objectives: (1) the initial orientation should
be aligned to the objects geometric definition and (2)
the mapping should accurately represent the rotation
of the object, even during large scale deformations.
In our approach we have devised a two stage pro-
cess for identifying this coordinate system. In an ini-
tial pre-processing stage we calculateC and the orien-
tation of the coordinate system that best matches the
geometric representation of the object through Princi-
ple Component Analysis (PCA). As the objects defor-
mation changes during each simulation time-step, we
recalculate C and update the orthogonal axes vectors
to match the new rotation of the object. The com-
plete derivation of this local coordinate system utiliz-
ing PCA and averaged deformable mass distribution
is detailed in (Transue, 2014).
Figure 2: Local and control coordinate systems for a simple
deformable object. The selected node of the deformable
object represents the origin of the control coordinate system
and defines the localized region that will be influenced by
the external forces introduced by a control metaphor.
To produce a localized deformation using a con-
trol metaphor we must also provide an intuitive way
of selecting the affected region. Therefore to attach a
control metaphor to a deformable model at a specific
location, we employ a simple node selection tech-
nique. The selection of an individual node within the
object will weld a control metaphor to this node so it
can then be used to perform localized deformations.
The image in Figure 2 illustrates the selection of an
individual node that will define the location of the ap-
plied deformation behavior.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
296

3.2 Simulation Recording
The generation of new animations and the support for
modifying existing animations requires a complete set
of controls for both real-time recording and playback.
In our approach we provide the standard set of mul-
timedia controls as part of an interactive time-line
that allows an artist to effectively navigate through
the collection of frames within the active animation.
Providing the ability to use this interactive time-line
to scroll through object deformations throughout the
recorded animation presents a critical feedback sys-
tem that allows an artist to closely analyze each defor-
mation state of all animated objects. This presents an
artist with the ability to iteratively refine the motion
exhibited by the simulated objects until the desired
outcome has been reached. In our approach, the abil-
ity to refine the deformation behavior using real-time
playback allows for a higher level of artistic control
when compared to techniques that utilize inverse dy-
namics to generate a fixed result. This is simply due
to the interactive nature of our proposed approach.
3.3 Dynamic Simulation Previews
Unlike optimization techniques that require the use of
a secondary deformation state that an artist defines
as a dynamic key-frame of the object, our approach
does not explicitly define the final position of a de-
formable object but rather it is generated during the
application of the control metaphor. Therefore in us-
ing our method an artist does not immediately know
how the changes they have imposed on a deformable
object will affect the resulting motion of the object.
To address this problem we introduce the ability to
dynamically generate simulation previews. The im-
age in Figure 3 illustrates the dynamic preview of a
falling cloth model before and after a bend metaphor
has been applied.
Figure 3: Dynamic preview of a cloth model (for three se-
lected states) as a bend control metaphor is applied. The
original animation (left) illustrates the cloth with a uniform
decent due to gravity. The application of a bend metaphor
(right) provides a realistic animation of the falling cloth.
The generation of a simulation preview does not
affect the current animation but illustrates a select
number of future states for every object within the an-
imation. This provides an artist with immediate feed-
back as to how the current configuration of control
metaphors applied to various objects will affect both
local deformations and global trajectories of all ob-
jects within the animation.
4 CONTROL METAPHORS
The fundamental component that we introduce with
the proposed method of deformable object control is
the notion of high-level control metaphors. These
metaphors represent a mapping between a control
widget that specifies a motion, pattern, or behavior
and the physical implementation of that motion by a
simulated object or region within the objects surface.
This provides an artist with a generalized and exten-
sible control methodology for introducing localized
deformations in animated objects. In this section we
introduce the components that formally define a con-
trol metaphor and illustrate the flexibility of our pro-
posed technique by demonstrating that these compo-
nents can be easily interchanged to provide an exten-
sible set of deformation controls.
The implementation of a control metaphor is re-
sponsible for providing definitions to the following
components: (1) the identification of the control re-
gions that indicate the nodes are influenced by the
control, (2) the orientation of the external forces the
control produces, (3) the interactive widget that pro-
vides a visual representation of the controls behav-
ioral pattern, and (4) the definition of a force curve
that defines applied force magnitude over time.
The consolidation of these four components pro-
vides the formal basis of the abstract control metaphor
definition: given a control metaphor M, the composi-
tion of these components into a control metaphor is
defined as follows:
M = (R,O,V, F)
Where R represents the discrete set of bounding
volumes that identify the regions influenced by this
control, the set of normalized vectors O represents
the external force orientations applied to the object
in within each region, the set of three-dimensional
primitives V that provides the visual representation of
the control, and the scalar list F represents the force
magnitudes that define the application time and dura-
tion of the control. Providing a unique definition for
component allows for an unbound number of poten-
tial control metaphors with this extensible design.
Through the implementation of each component
we can derive high-level controls that can easily be
configured by an artist to introduce pattern-based de-
formations (such as bending, twisting, stretching, and
InteractiveControlofDeformable-objectAnimationsthroughControlMetaphorPatternAdherence
297

Figure 4: Illustrations (top and front views) of the widget that represents the bend control metaphor as seen within our
interactive editing environment. Each sphere identifies one of the control regions that are defined by the bend metaphor.
compression). Additionally, every control metaphor
instance contains a unique transformation that defines
its relative position and orientation to the geometry
of the controlled object. This allows an artist to in-
troduce both global and targeted localized deforma-
tions to define new animation or adjust the behaviors
of simulated objects within existing animations.
4.1 Control Regions
Control metaphors drive localized deformation pat-
terns based on the set of control regions R that de-
fine which nodes within a simulated object are influ-
enced by the introduced external forces. Specifically,
we aim to derive high level control patterns from a
collection of primitive regions such that each region
r ∈ R, in part, contributes to the global behavior of
the control. From this, we can define the control re-
gions of a pattern-based metaphor as a set of bound-
ing volumes that evaluate a boolean function for the
selection of the nodes involved in the deformation.
Depending on the complexity of the desired defor-
mation, a control metaphor may contain several con-
trol regions; however to avoid unnecessary complex-
ity in the usability of each control we utilize a lim-
ited number of geometric primitives to identify these
control regions. If a node resides within any of the
control regions within R, it will be highlighted in size
and color to indicate its participation within the defor-
mation (see Figure 4). This presents a clean interface
that effectively communicates which nodes contained
within a simulated model will drive the imposed de-
formation.
4.2 Force Orientation
The selection of the nodes that will contribute to a
localized deformation is interactively defined by the
set of artist configured control regions R. Therefore
for each control region r ∈ R, we must define an as-
sociated vector field o ∈ O that defines the orienta-
tions of the external forces applied to each node en-
capsulated within r. The orientations of the applied
external forces provide the defining characteristics of
the deformation pattern that will be imposed on the
controlled object, and can be defined through a sim-
ple force diagram. A control metaphor force diagram
simply provides the definition of the spatial configu-
ration of the regions that contain the vector fields that
define the orientations of the controls external forces.
While the definition of each regions vector field is
unbound, uniform vector fields are sufficient for the
derivation of most primitive deformation behaviors.
4.3 Visual Representation
To effectively communicate the location and orienta-
tion of how a deformation will be applied to a sim-
ulated object, we introduce a three-dimensional in-
teractive widget that defines the control regions and
structure of the control metaphor. In our approach
we provide an interactive widget for each control
metaphor that provides an artist with the ability to
configure the selection of the effected nodes, the ori-
entation of the applied forces, and the control position
of the deformation (Figure 4).
Each interactive widget is represented by a col-
lection of geometric primitives that allow an artist to
easily configure the properties of the applied control
metaphor. The configuration of these interactive con-
trol widgets is obtained by allowing an artist to per-
form adjustments by selecting the primitive compo-
nent within the widget and then modifying its parame-
ters (real-time interaction is facilitated though mouse-
based gestures). The parameter adjustments that we
provide for each control metaphor include the abil-
ity to scale and translate each component within the
widget. This provides a high-level of flexibility in an
artistic control of the provided control metaphors.
4.4 Force Curves
Control metaphors and the associated widgets we
have developed provide an intuitive way of effec-
tively imposing a behavioral pattern on a simulated
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
298

object within an interactive environment; however in
the context of physically-based animation several ad-
ditional parameters must be provided to completely
define the resulting deformation. These parameters
include the definition of the instance in time when the
external forces will be imposed, the duration of this
application, and the magnitudeof the forces applied to
the nodes within each control region of the metaphor.
Here we formally introduce the definition of a force
curve that provides the required functionality to de-
fine all of these properties through a simple interac-
tive curve editor. A force curve f is defined as a dis-
crete set of two-dimensional points that approximate
a function that defines the magnitude of the external
forces applied through a selected control metaphor. In
the instance where multiple control metaphors are ap-
plied to an individual object, each maintains its own
corresponding force curve. This provides an artist
with the ability to create several deformations exhibit-
ing unique characteristics on an individual object.
Time-line Discretization. Force curves approximate
a function that defines the magnitude of the exter-
nal forces required to generate a physical deformation
through control metaphors by supplyinga scalar value
that determines the strength of this deformation. To
provide these values in the context of a physical simu-
lation that employs a control metaphor,a force magni-
tude value must be provided for each simulation time-
step. This constraint is implicitly enforced through
the approximation of the curve that defines these mag-
nitude values. Let the set A represent the set of dis-
crete set of points that approximate the force curve
f and let (F
begin
,F
end
) represent the simulation time-
steps that correspond to the application of a control
metaphor. The following constraint is then placed on
the approximated representation of this force curve:
|A| = (F
end
− F
begin
). This will guarantee that for
each simulation time-step the magnitude of the ex-
ternal forces introduced by a control metaphor is de-
fined.
Curve Control. The implementation of the interac-
tive interface provided to an artist is based on an or-
thographic projection of a force curve approximated
by a Bezier curve. This representation also allows us
to provide control points that allow an artist to easily
control the shape of the approximated function. An
artist can interactively control the position of the end
and control points by simply dragging them to the de-
sired location. This provides an accurate method of
introduce precise definition of the specific instance an
artist would like interject a deformation. An illustra-
tion of the curve editor provided within our applica-
tion is illustrated in Figure 5.
Figure 5: Screenshot of the interactive force curve editor
that defines the magnitude of the applied forces over time.
With the proposed curve editing technique, com-
mon animation features such as motion blending
can be achieved. Motion blending can be achieved
through smooth gradients defined within the force
curve. These gradients translate to gradual deforma-
tions that can be used to blend multiple deformations
together smoothly. This also provides an artist with
the ability to refine imposed deformations by utilizing
multiple control metaphors to derive blended com-
pound deformations.
Force Magnitude-deformation Correlation. The
process of determining the magnitude of the applied
external forces required to derive the desired defor-
mation is a challenging process. In an effort to assist
an artist in the definition of the force curve that will
derive the desired behavior we employ dynamic pre-
views. As an artist modifies the force curve to gener-
ate a deformation, a dynamic preview can be gener-
ated to illustrate the resulting behavior. This provides
an interactive feedback loop to an artist to iterate on
the motion generated with our approach. Once the
desired deformation behavior has been achieved, the
simulation can be recorded to make the change to the
resulting animation. While this does not resolve the
possibility of introducing externalforces that generate
undesirable or unstable behaviors, it presents an itera-
tive process that allows an artist to visualizeand refine
the behaviors imposed by our control metaphors.
4.5 Deformation Controls
The definition of each component within this sec-
tion provides the basis upon which primitive defor-
mation behaviors can be created. The unique set of
components defined by a control metaphor can eas-
ily be defined to generate commonly required defor-
mation behaviors including bend operations, twisting,
InteractiveControlofDeformable-objectAnimationsthroughControlMetaphorPatternAdherence
299
stretching, and compression. In this section we pro-
vide the formal definition for these primitive pattern-
based motions and illustrate how these formaliza-
tions demonstrate the desired deformation behaviors
on primitive geometric objects.
Stretch Deformation. To derive the behavior im-
posed by the stretch control metaphor we simply as-
sert that this operation will attempt to separate two
regions within an objects geometric definition. These
individual regions are separated by a division plane
that effectivelysegments the bounded regions into left
and right selection intervals defined within two cylin-
drical control regions: {L
n
, R
n
}. The orientation of
the external forces is simply constrained to the X-axis
of the controls coordinate system. The node set L
n
external force orientation is defined by a negative unit
vector along this axis:
~
X
−
, and the orientation of the
forces acting upon the node set R
n
is defined by a
positive unit vector along this axis:
~
X
+
. Given these
components we formalize the definition of a generic
stretch control metaphor:
S = ({L
n
,R
n
}, {
~
X
−
,
~
X
+
}, V, F)
The visual component V of the stretch metaphor is
simply defined by the two cylindrical control regions
that correspond to the metaphors control regions. To
further refine the control provided to an artist, we pro-
vide an interactive means of refining the minimum
and maximum effect distance from the controls sepa-
ration plane and allow the radius of these cylindrical
regions to be dynamically adjusted. From this for-
mal definition we have also derived the components
required for a compression-based deformation. In the
application of this control, an artist can simply define
a negative force curve which will inverse the orienta-
tion of the applied forces, thus compressing the left
and right node sets to the origin of the control.
Twist Deformation. The implementation of the twist
control metaphor allows for separate regions of a
deformable-body, defined by a division plane, to be
rotated in opposing directions. The formal definition
of this control metaphor closely resembles the stretch
control with the exception of of the vector field de-
fined with the cylindrical control regions. Here we de-
fine these vector fields as a function of rotation about
the controls primary axis where R(L
n
) and R(R
n
) rep-
resent rotation functions operating on the nodes iden-
tified within each control region:
T = ({L
n
,R
n
}, {R
−
(L
n
),R
+
(R
n
)},V, F)
The visual component of this control metaphor is
identical to that of the stretch control and can be in-
teractively customized in the same way by adjusting
the nodes contained within the provided control re-
gions. The application of a negative force curve to
this control will effectively inverse the rotation func-
tions providing the orientations of the external forces.
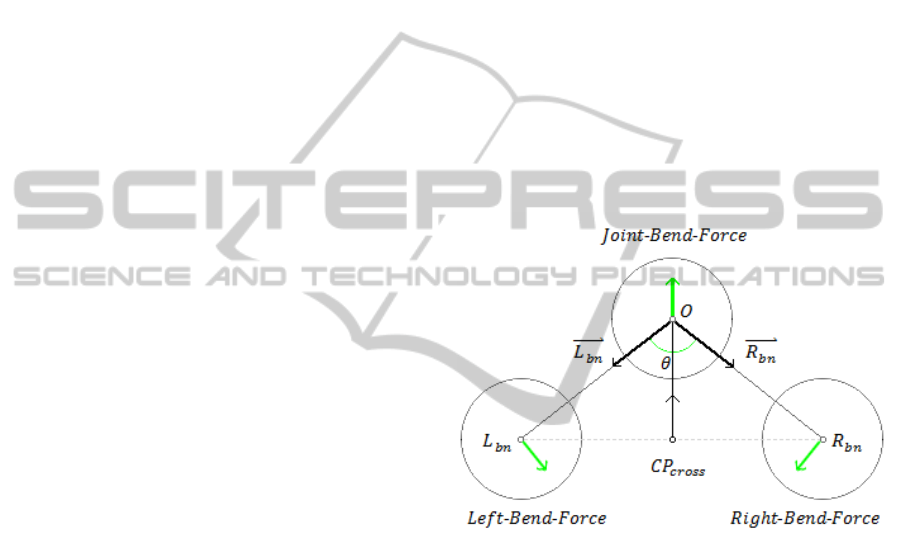
Bend Deformation. Considering the implementation
of a pivot-based bend deformation control, we define
three separate control regions, each containing an as-
sociated (uniform) force orientation vector field. The
Joint-Bend-Force (pivot force), denoted O, defines the
direction of the force that opposes the Left- (
~
L
bf
) and
Right- (
~
R
bf
) Bend-Forces to impose a bend deforma-
tion based on the selected nodes contained within the
controlled object. The opposing deformations cre-
ated by the imposed external forces combined with
the provided offset creates the desired deformation
behavior at the center of this control metaphor. An
illustration of the spherical control regions and force
orientations for this control is presented in Figure 6.
Figure 6: Force diagram illustrating the orientations of the
external forces that are applied within each of the three con-
trol regions used to generate a pivot-based bend deforma-
tion.
From this force diagram and the provided set of
spherical control regions, the formal definition of this
pivot-based bend control metaphor can be derived:
B = ({O,L
bn
,R
bn
}, {
~
O,
~
L
bf
,
~
R
bf
}, V, F)
The visual component V is composed of three
sphere-based control regions identified in the controls
force diagram. To provide the ability to further refine
the configuration of this control metaphor,we provide
a customizable joint-angle θ that defines the angle be-
tween the L
bn
and R
bn
node sets and allow the radius
of each control region to be adjusted. Additionally,
we provide the ability to extend the distance between
each of the control regions to adjust the length of the
resulting bend deformation.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
300

Figure 7: Screenshot of our interactive animation editing environment with media controls, time-line, and loaded scene con-
taining a high-resolution deformable dragon. Three bend metaphors have been applied to achieve the displayed deformations.
5 EDITING ENVIRONMENT
To facilitate the generation of new animations within
an interactive editing environment, our approach re-
lies on the animation studio software we have created
to facilitate the required functionalities listed in Sec-
tion 3. This editing environment provides the core
functionality required to view, generate, and record
physically-based animations. The ability to interac-
tively introduce control metaphors and edit deforma-
tion behaviors is facilitated through the main studio
interface of our animation editing application.
This implementation provides the ability to ani-
mate multiple objects within a scene, facilitates inter-
active deformation views, and manages configuration
of multiple control metaphors per simulated object.
The image in Figure 7 provides a screen-shot of our
application with a loaded animation. This interactive
interface is defined by three main components: (1) the
main scene viewports that allowan artist to effectively
view the deformation behaviors imposed by the se-
lected control metaphors, (2) the animation time-line
which allows for the recorded animation to be dynam-
ically viewed, and (3) the list of control metaphors
applied to the currently selected object.
The resulting deformations that we have obtained
were generated using our approach facilitated through
this provided editing interface. In the next sec-
tion look at several demonstrations of the localized
pattern-based deformations introduced by our pro-
posed control metaphors configured and employed
within this interactive editing environment.
6 RESULTS
To clearly demonstrate the utility and flexibility of our
approach we provide several illustrations of primitive
pattern-based motions, localized surface control, and
compound deformations obtained through the appli-
cation of multiple control metaphors. We show how
each of the introduced control metaphors can con-
tribute to a flexible animation tool-set that can al-
low artists the create new animations of deformable
models and refine the behaviors of simulated objects
within existing animations.
The implementations of our pattern-based control
metaphors introduce a basic set of deformation oper-
ations that provide the required foundation for creat-
ing complex animations of deformable models. These
results are based on the primitive deformation oper-
ations such as compression, bending, and twisting.
Here we demonstrate the resulting deformations that
can be obtained using these controls individually.
InteractiveControlofDeformable-objectAnimationsthroughControlMetaphorPatternAdherence
301
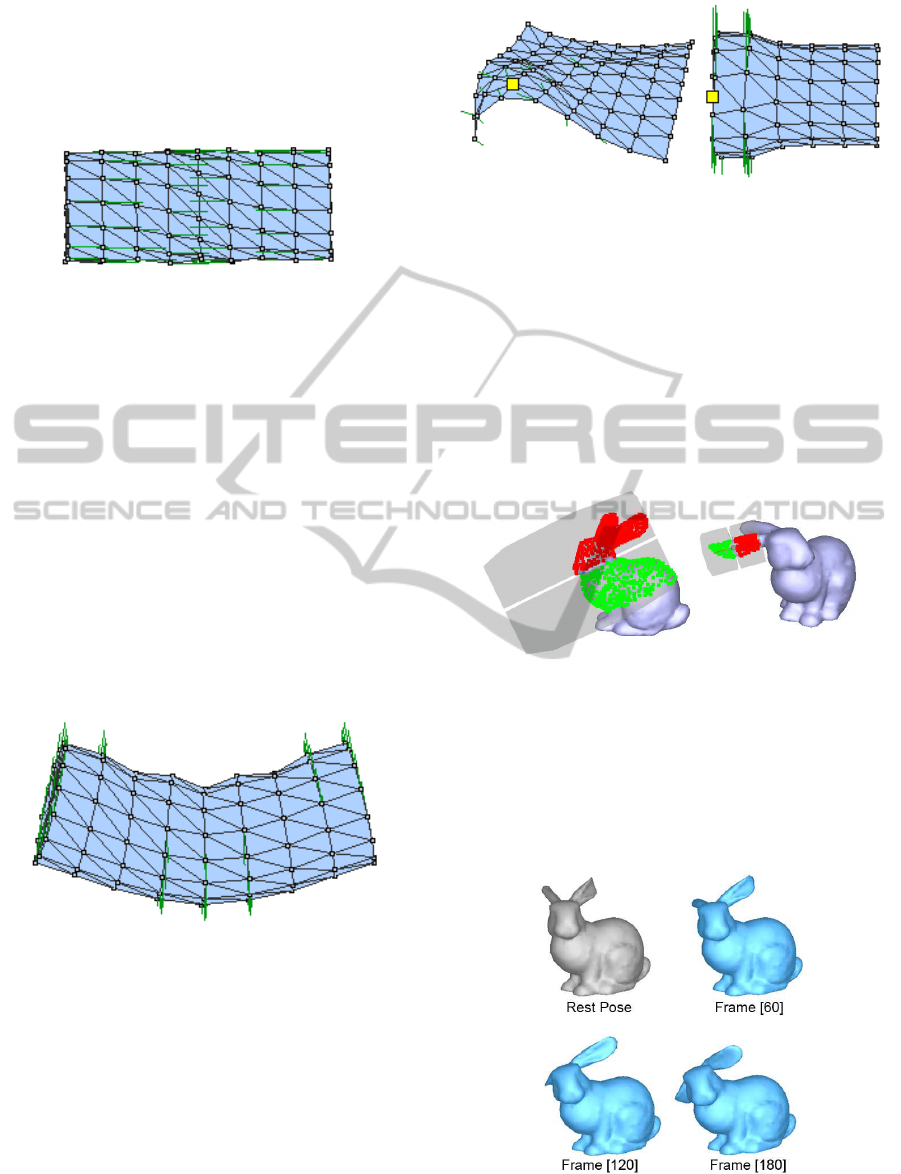
Compression Deformation Result. A compression
deformation can be derived by applying a stretch con-
trol metaphor with a negative force curve. The image
in Figure 8 illustrates how this metaphor can effec-
tively compress a tessellated cylindrical model.
Figure 8: Resulting application of a control metaphor im-
posing a compression behavior. The orange lines indicate
both the orientation and magnitude of the applied forces.
While the desired compression is obtained, we note
the slight twist to the topology of the models surface.
This effect is due to the uneven selection of the nodes
involved in this deformation. We discuss the poten-
tial deformation side-effects that can be created from
misaligned control metaphors in Section 7.4.
Bend Deformation Result. The application of a bend
control metaphor to a cylindrical model provides the
expected results when applied to the length of the ob-
ject. The image in Figure 9 illustrates the effective-
ness of this control metaphor in this instance. How-
ever, when performing a global deformation with a
bend metaphor,we ensure that the selected control re-
gions are balanced with respect to the bend pivot.
Figure 9: Global pivot-based bend deformation.
The success rate of applying this control metaphor to
an object to derive a global deformation is based on
the material stiffness coefficients that define the elas-
ticity of the model. When the bend control metaphor
is applied to a rigid model, an uneven distribution of
forces will incur an unintended torque on the object.
Localized Deformations. Control metaphors can ef-
fectively introduce localized deformations based on
the control coordinate system we have created to pro-
vide an artist with the ability to target a region within
a deformable model. The two examples illustrated in
Figure 10 illustrate these targeted deformations.
Figure 10: Twist (left) and stretch (right) control metaphors
applied to models to derive localized (to the position of the
enlarged node) deformation behaviors.
Compound Deformations. The process of apply-
ing multiple control metaphors to an individual de-
formable model provides the ability to derive com-
plex secondary behaviors within the topology of the
model. The illustration of the two control metaphors
applied to the Stanford bunny mesh in Figure 11 rep-
resents an application of two control metaphors used
to derive a compound deformation.
Figure 11: Control metaphor compound deformation. The
twist metaphor turns the rabbits head (left) and a bend
metaphor controls the rabbits ear (right).
The resulting deformation (see Figure 12) imposed by
the application of both control metaphors induces a
naturally blended motion between both operations. A
more complex compound deformation utilizing three
control metaphors is provided in Figure 13.
Figure 12: Compound deformation result created from the
control metaphors illustrated in Figure 11 (throughout 180
simulation time-steps).
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
302

Figure 13: Compound deformations of a dragon raising its wings and rotating its head. The imposed deformations are created
from the localized application of four control metaphors. The animated result is displayed left to right.
7 EVALUATION AND
DISCUSSION
The evaluation of an artists ability to effectively for-
malize and translate the result of a desired localized
behavior to an object within a physical simulation is
a challenging task. The applicability of the provided
set of control metaphors depends on several critical
factors including: (1) the artist’s ability to effectively
identify a node that represents the desired location of
the deformation, (2) the selection of an appropriate
predefined control metaphor, and (3) the process of
properly configuring the provided control widget to
derive to desired behavior. To objectively evaluate the
effectiveness of our approach, we analyze the integra-
tion of our force-based metaphor technique into the
existing set of deformable object control methodolo-
gies introduced in Section 2. In this section we de-
fine how our approach is framed to borrow key con-
cepts from these existing methods and identify how
our technique can contribute to an artists ability to
effectively generate localized deformation behaviors
within existing animations. Additionally, we also
consider drawbacks imposed by the set of reoccur-
ring problems (such as deformation oscillations and
induced torque) that are introduced when utilizing ex-
ternal forces to drive deformation behaviors.
7.1 Inverse-dynamics
Inverse dynamics is an animation technique that pro-
vides an artist with a high-level of control of an ob-
jects deformation states. The ability to define the ex-
act state that will be achieved by a deformable object
provides an artist with a powerful tool that can be used
to effectively produce targeted animations. This tech-
nique effectivelyreduces the time required to generate
a targeted animation of deformable object by simply
interpolating dynamic key-frames. This is achieved
by calculating the forces required to match the con-
straints imposed by the dynamic state of the object
for each key-frame during the animation. However,
utilizing a set of key-frames that define static states of
a deformable body as the input to a dynamic system
presents a large challenge to an artist: derive a set of
complex dynamic states for an object undergoing an
deformation such that the interpolated behavior will
represent a realistic and physically plausible motion.
While the task of defining the dynamic states of an
object (node position, velocity, etc.) may be achiev-
able for models with a simple geometric composi-
tion, objects with complex deformation states such as
cloth will present an artist with the challenging task
of deriving the intermediate states of this deforma-
tion. Manually obtaining this state with a high level of
fidelity for these complex objects is extremely chal-
lenging and generally requires an additional tool-set
(such as cage-based controls) to assist in this process.
Furthermore, even if the definitions of these dynamic
states are given, we are not guaranteed that the result-
ing motion provided by the interpolation process will
represent a fluid or natural behavior. This will lead an
artist to the process of iteratively refining the included
dynamic key-frames to obtain the desired behavior.
This is where we emphasize the ability of our
technique to generate physically plausible behaviors
based on high-level deformation patterns. The motion
naturally inspired by the application of external forces
can provide a resulting deformation behavior with a
high level of fidelity that can be used to define a dy-
namic key-frame. Additionally, our technique can be
used to address unrealistic motions that may be gener-
ated through the inverse-dynamics interpolation pro-
cess. This can be achieved by introducing a control
metaphor that acts upon the object within the existing
animation refine the resulting behavior. Therefore the
our method of creating localized deformations com-
plements this approach and can be used to improve
the quality of the generated animations.
7.2 Cage-based Control
Cage-based deformation control introduces the ability
to manipulate complex model topologies by utilizing
InteractiveControlofDeformable-objectAnimationsthroughControlMetaphorPatternAdherence
303

a reduced set of representative nodes that form an in-
flated cage around a deformable object. The nodes
of this superimposed cage can then be explicitly con-
trolled by an artist to implicitly direct the deforma-
tions of the complex underlying surface. The primary
concept introduced by cage-based deformation con-
trol techniques is that they greatly reduce the level of
control presented to an artist, thus the complexity of
the deformation editing process is greatly reduced.
This form of deformation control is generally uti-
lized as the solution to deriving physical plausible dy-
namic key-frames. However, this process does not ad-
dress the generation of physically-based motions over
time. This solution to deformation control must rely
on other techniques (such as an inverse-dynamics ap-
proach or rest-shape adaptation) to derive the inter-
mediate motion states required for an animation. This
is due to the fact that the key contribution from this
technique is a representative functional mapping be-
tween the nodes of the superimposed cage and the
nodes within the controlled deformable body.
This mapping however, provides an effective
means of imposing a high-level behavior on a com-
plex deformable model. We borrow the application
of this concept and extend it to represent dynamic be-
haviors imposed by our high-level control metaphors.
Therefore we can effectively provide a higher level
of control to an artist to accurately convey the be-
havior of the intended deformation. The control re-
gions defined within each control metaphor define
the bounded region that acts as dynamic cages that
closely adhere to the global trajectory of the simulated
object. This forms the basis of our control technique
for translating high-level deformation patterns to the
underlying representative geometry.
7.3 Rest-shape Adaptations
The development the technique pioneered by (Coros
et al., 2012) that utilizes internal elastic potential
between static deformation states to derive motion
from internal forces, introduces an effective means
of animating deformable objects through example-
and goal-oriented objectives. This technique effec-
tively eliminates reoccurring problems with external
force-based techniques (such as oscillations and in-
duced torque) and also introduces the notion of the an-
imated object developing a persona due to the intrin-
sic derivation of internal forces, making them seem
lifelike.
The lifelike effect introduced by this technique
however may not be desirable in all instances. In the
development of our force-based technique, we pro-
pose a more generalized method of applying defor-
mations to simulated objects. Throughthe subsequent
application of localized deformations using control
metaphors, our approach can approximate lifelike
movements of deformable objects (as shown in Fig-
ure 13); however the incurred artistic labor is more
extensive than that required by this rest-shape adap-
tation technique. In our approach, multiple control
metaphors are required.
7.4 Metaphor Alignment
The correct application of a control metaphor depends
on the intended result desired by an artist imposing
the behavior. To adhere to the original intent of the
control metaphor, it must be properly aligned with the
geometry of the simulated object it will deform. Even
with the simplified form of interactivecontrol widgets
provided to the user, the applied external forces can
fail to produce the intended deformation.
Control metaphors are subject to several condi-
tions that must be met for the desired behavior to be
achieved. This indicates that there are several factors
that can contribute to an invalid configuration of the
applied control metaphor that may lead to an undesir-
able or unstable deformation behavior. These factors
include: misaligned control widgets, an inadequate
external force magnitude, and the incorrect param-
eter configuration for the applied control metaphor.
The image in Figure 14 illustrates an instance where
a bend metaphor has not been properly aligned to the
underlying geometry of the simulated object. Specif-
ically, we note the lack of the selected nodes with
two of the provided control regions. Therefore, the
only external forces that will be applied to this ob-
ject reside within the joint set of this metaphor. The
resulting deformation will not match the intended re-
sult provided by this metaphor due to the misaligned
widget configuration.
Figure 14: Invalid alignment of an applied bend metaphor
where only one set of nodes is properly identified. This
will result in an incorrect deformation behavior due to the
incorrect widget orientation.
The implications of these requirements however
are not without their own merits. The flexibility pro-
vided to an artist through the selection of the local-
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
304

ized region, the orientation of the control, and config-
uration of the parameters specific to the applied con-
trol, can produce unwanted deformations; however
this also provides freedom to an artist to use the pro-
vided tool-set in alternativeways. As shown in the ex-
ample deformation in Figure (dragon result), the head
of the dragon can be turned using a bend deformation
rather than a twist control metaphor.
8 CONCLUSION
In this paper we have presented an effective way
to impose pattern-based deformations on simulated
MSS- or FEM-based deformable models. We have il-
lustrated that the targeted application of the proposed
high-level control metaphors can effectively generate
physically plausible deformations in new animations
and can be used to modify the behavior of objects
within existing animations.
In this results of this paper we have demonstrated
that in using the method of controlling targeted de-
formations we have introduced, localized deforma-
tions can effectively be imposed on simulated objects
and we preserve an artists ability to iteratively refine
the resulting behavior. We have also defined the out-
line of the interactive editing environment that was
used to create these desired deformations. Addition-
ally, through the subsequent application of the prim-
itive control metaphors introduced in our approach,
we have demonstrated that compound behaviors can
be effectively generated to create complex anima-
tions. Our deformation control technique has also
been compared to other leading approaches and we
have discussed the potential contributions and prob-
lems associated with this approach.
While this technique contains the commonly reoc-
curring challenges associated with the application of
external forces, the resulting deformation behaviors
provide physically plausible results that can be used
to effective generate realistic animations.
9 FUTURE WORK
The accurate control of deformable objects in simu-
lated environments for the generation of physically
plausible animations continues to present a challeng-
ing task. In this work we have identified a generalized
method for imposing pattern-based deformation be-
haviors on simulated objects; yet several of the promi-
nent reoccurring problems with the application of ex-
ternal forces remain, including oscillations, imposed
torque, and unbound force magnitudes.
REFERENCES
Arikan, O. and Forsyth, D. A. (2002). Interactive mo-
tion generation from examples. ACM Trans. Graph.,
21(3):483–490.
Barbiˇc, J., da Silva, M., and Popovi´c, J. (2009). Deformable
object animation using reduced optimal control. In
ACM SIGGRAPH 2009 Papers, pages 53:1–53:9.
Barbiˇc, J. and Schroeder, D. (2009). Vegafem.
Barbiˇc, J., Sin, F., and Grinspun, E. (2012). Interactive edit-
ing of deformable simulations. ACM Trans. Graph.,
31(4):70:1–70:8.
Chai, J. and Hodgins, J. K. (2007). Constraint-based mo-
tion optimization using a statistical dynamic model.
In ACM SIGGRAPH 2007 Papers, SIGGRAPH ’07.
Coros, S., Martin, S., Thomaszewski, B., Schumacher, C.,
Sumner, R., and Gross, M. (2012). Deformable ob-
jects alive! ACM Trans. Graph., 31(4):69:1–69:9.
Hildebrandt, K., Schulz, C., von Tycowicz, C., and Polth-
ier, K. (2012). Interactive spacetime control of de-
formable objects. ACM Trans. G., 31(4):71:1–71:8.
Huang, J., Tong, Y., Zhou, K., Bao, H., and Desbrun,
M. (2011). Interactive shape interpolation through
controllable dynamic deformation. Visualization and
Computer Graphics, IEEE Transactions on, 17(7).
Jeon, H. and Choi, M.-H. (2007). Interactive motion control
of deformable objects using localized optimal control.
In International Conference on Robotics and Automa-
tion, pages 2582–2587.
Joshi, P., Meyer, M., DeRose, T., Green, B., and Sanocki,
T. (2007). Harmonic coordinates for character articu-
lation. In ACM SIGGRAPH 2007, SIGGRAPH ’07.
Ju, T., Zhou, Q.-Y., van de Panne, M., Cohen-Or, D.,
and Neumann, U. (2008). Reusable skinning tem-
plates using cage-based deformations. In ACM SIG-
GRAPH Asia 2008 Papers, SIGGRAPH Asia ’08,
pages 122:1–122:10.
Martin, S., Thomaszewski, B., Grinspun, E., and Gross,
M. (2011). Example-based elastic materials. In SIG-
GRAPH 11, pages 72:1–72:8.
Murray-Smith, D. (2000). The inverse simulation approach:
a focused review of methods and applications. Math-
ematics and Comp. in Sim. (MATCOM), 53:239–247.
Popovi´c, J., Seitz, S. M., Erdmann, M., Popovi´c, Z.,
and Witkin, A. (2000). Interactive manipulation of
rigid body simulations. In Proc. 27th A. Conference
of Comp. Graph. and Interactive Techniques, SIG-
GRAPH 00, pages 209–217.
Transue, S. (2014). Interactive control of deformable-object
animations with intuitive motion pattern adherence.
Master’s thesis, University of Colorado Denver, Col-
orado.
Twigg, C. D. and James, D. L. (2008). Backward steps
in rigid body simulation. ACM Trans. Graph.,
27(3):25:1–25:10.
Witkin, A. and Welch, W. (1990). Fast animation and con-
trol of nonrigid structures. In Proceedings of the 17th
Annual Conference on Computer Graphics and Inter-
active Techniques, SIGGRAPH ’90, pages 243–252.
ACM.
InteractiveControlofDeformable-objectAnimationsthroughControlMetaphorPatternAdherence
305
