
A Measure of Texture Directionality
Manil Maskey and Timothy S. Newman
University of Alabama in Huntsville, Huntsville, AL, U.S.A.
Keywords:
Texture, Directionality, Orientedness, User Study.
Abstract:
Determining the directionality (i.e., orientedness) of textures is considered here. The work has three major
components. The first component is a new method that indicates if a texture is directional or not. The new
method considers both local and global aspects of a texture’s directionality. Local pixel intensity differences
provide most of the local aspect. A frequency domain analysis provides most of the global aspect. The second
component is a comparison study (based on the complete set of Brodatz textures) of the method versus the
known, competing methods for determining texture directionality. The third component is a user study of the
method’s utility.
1 INTRODUCTION
Image texture, while hard to well-define, involves
some local order repeating over a larger area
(Hawkins, 1970). In addition to having inherent fea-
tures such as the size and degree of regularity in rep-
etition, some textures also have orientation or other
inherent features. Texture features have been used ex-
tensively in a variety of computer vision and pattern
recognition applications. For example, Shiranita et
al. have used texture features to determine the quality
of meat (Shiranita et al., 1998). Gorkani and Picard
have used texture orientation to detect images of ur-
ban areas (Gorkani and Picard, 1994). Mudigonda
et al. have used texture features for detecting tissue
masses in mammograms (Mudigonda et al., 2001).
Texture features have also been extensively used to
retrieve matching images from large image databases
(Smith and Chang, 1996)(Saha et al., 2004)(Kekre
et al., 2010).
Research has shown that certain characteristics
of textures are readily perceived by human and ani-
mal vision. For example, studies (Hubel and Wiesel,
1968)(Blake and Holopigan, 1985) have found that
the visual cortex of monkeys includes numerous de-
tectors sensitive to orientation of structures in the
visual field. Textures also help in visually dif-
ferentiating surfaces (Beck, 1982)(Nothdurft, 1985).
In addition, orientations within textures offer tex-
ture segregation cues to the visual system (Noth-
durft, 1990)(Nothdurft, 1991). Additionally, Ware
and Knight (Ware and Knight, 1992) have performed
a user study that suggested that humans perceive there
to be a number of visual characteristics of textures,
such as regularity, size, and orientation.
In this paper, our focus is on determining if a tex-
ture is directional and on the use of directional tex-
tures. Directionality may be a useful feature for vision
and pattern recognition since it would allow for differ-
entiating between (i.e., classifying) textures. It may
also be useful in multimedia, visualization and graph-
ics applications. To support using texture directional-
ity as a texture discriminator, a new measure that can
determine the directionality status for a texture is in-
troduced and validated here. We also present the first
comparison study of texture directionality measures–
that study includes comparison of the new measure
against the existing measures, using user sentiment as
a baseline.
The rest of the paper is organized as follows.
Section 2 briefly discusses related work. Section 3
presents the new texture directionality measure. Sec-
tion 4 presents the comparison of the directionality
measures. Section 5 describes the user study. Sec-
tion 6 analyzes the results, and Section 7 provides the
conclusion and future work.
2 BACKGROUND
A number of frameworks for computing various types
of texture measures have been reported (e.g., (Haral-
ick, 1979)). In addition, some applications have used
such measures. For example, Chetverikov has mea-
432
Maskey M. and Newman T..
A Measure of Texture Directionality.
DOI: 10.5220/0005312904320438
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 432-438
ISBN: 978-989-758-090-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

sured texture regularity using a gray-level difference
histogram feature (Chetverikov., 1984) and later used
the measure in applications such as structural defect
detection (Chetverikov and Hanbury, 2002). Cao et
al. have derived a texture sharpness measure that is
used in quantifying sharpness of digital images (Cao
et al., 2009).
Our focus here is directional textures, so next we
discuss previous work on texture directionality.
2.1 Textures and Directionality
Tamura et al. (Tamura et al., 1978) conducted an
early study on the role of textures in human percep-
tion. They also introduced texture measures based on
spatial intensity variation, one of which aimed at esti-
mating overall directionality in an image. Their direc-
tionality measure was based on the sharpness of peaks
in a histogram of high magnitude gradient pixels. The
gradient values were estimated using mask-based hor-
izontal and vertical directional difference estimates at
each pixel. If a pixel’s gradient magnitude was above
a threshold, it was considered to be high magnitude.
They also reported user studies that considered the
correlation between human perception and their mea-
sures. The studies used 16 (of the 111) Brodatz image
archive textures of various types. All possible com-
binations of pairs of these 16 images were shown to
the participants, who then identified one texture from
each pair that best exhibited the directionality charac-
teristic. (Five other texture properties were also stud-
ied similarly.) Their study suggested that their direc-
tionality measure was highly correlated with the hu-
man responses.
Another texture directionality measure was de-
fined by Picard and Gorkani (Picard and Gorkani,
1992). Their measure was based on a steerable pyra-
mid defined with steerable filters like the ones de-
scribed by Freeman and Adelson (Freeman and Adel-
son, 1991). Picard and Gorkani’s pyramid had four
levels, where the lowest level was the actual tex-
ture. At each level, the steerable filters were used to
compute each pixel’s dominant orientation and orien-
tation “strength.” Then, orientation histograms were
constructed for each level based on the orientation
strength values. After smoothing, the histogram peaks
were found. Next, the orientation histograms for each
level were combined. Finally, the measure of texture
directionality was computed from this combination.
Picard and Gorkani applied their measure to all 111
Brodatz textures and subsequently validated the mea-
sure via user study on the same textures.
Abbadeni (Abbadeni, 2000) and colleagues (Ab-
badeni et al., 2000) have proposed a measure of tex-
ture directionality based on a variance statistic, the
auto-covariance function g. g expresses the covari-
ance between the original image and a shifted version
of that image, as shown in Eqn. 1:
g(δ
i
, δ
j
) =
1
c
i j
n
c
−δ
i
−1
∑
i=0
n
r
−δ
j
−1
∑
j=0
I (i, j) I (i + δ
i
, j + δ
j
),
(1)
where n
c
and n
r
are the number of columns and rows
in the image I, respectively, the δ terms represent
shifts, 0 ≤ δ
i
≤ n
c
− 1 and 0 ≤ δ
j
≤ n
r
− 1, and
c
i j
= (n
c
− δ
i
)(n
r
− δ
j
). The approach found the gra-
dient of the auto-covariance at each pixel. The pixels
whose gradient exceeded a threshold t were consid-
ered to be oriented. In addition, if a sufficient number
of pixels were considered to be oriented, then the im-
age was considered to be a texture with a dominant
orientation, denoted by Θ
d
, and a directionality value
N
Θ
d
, defined as shown in Eqn. 2:
N
Θ
d
=
∑
n
c
−1
i=0
∑
n
r
−1
j=0
Θ
d
(i, j)
(n
c
∗ n
r
) − N
Θ
nd
, (2)
where N
Θ
nd
is the number of non-oriented pixels. Ab-
badeni also performed a user study to validate the
measure.
Hagh-Shenas and Interrante (Hagh-Shenas and In-
terrante, 2005) have also described a texture direc-
tionality measure. It is based on the Discrete Fourier
Transform (DFT). It reduced DFT aliasing artifacts
by applying a Hanning window to the original texture
and then applying DFT on the Hanning-modified tex-
ture. Next, the DFT output was Gaussian-smoothed
and converted into polar coordinates. The 180
◦
-range
of frequency values in the polar coordinates were di-
vided into 18 equal intervals (through the DC point).
Each interval was also radially divided by 64 cir-
cles, generating, in all, 18x64 locations. The val-
ues at these locations were stored in an 18x64 matrix
called the Discrete Fourier Polar Coordinates Matrix
(DFPM). Using the DFPM, a directionality measure,
D
H
, was computed, as shown in Eqn. 3:
D
H
=
∑
n
i=1
(M(i) − f (i))
n ∗ M(i)
, (3)
where f(i) is the sum of the i
th
column in the DFPM,
M(i) is the maximum value in that column, and n=64
columns.
Sikora et al. (Sikora, 2001) and Wu et al. (Wu
et al., 1999) have used Gabor filter banks with scale
and orientation sensitive filters to design texture fea-
tures. These features were used to measure a concept
related to directionality, the structuredness, of an im-
age. Manjunath et al. (Manjunath et al., 2001) have
AMeasureofTextureDirectionality
433

also described texture descriptors that incorporate di-
rectional features for sub-regions of a texture. The
set of features over all the sub-images were then used
to formulate a feature vector for image indexing and
retrieval. Directionality of the texture itself was not
computed; hence, the texture is not classified as di-
rectional or non-directional.
Lastly, it should be noted that Healey and Enns
(Healey and Enns, 1999) have presented an overview
of the development of understandings and applica-
tions of texture in computer vision, graphics and vi-
sualization.
3 NEW TEXTURE
DIRECTIONALITY MEASURE
A focus of our work is determining if a texture sam-
ple is directional. In this section, we describe the pro-
cessing steps for our texture directional determination
scheme. Our scheme considers both local and global
aspects of directionality, which is one difference from
most prior work.
The scheme acts as a measure that indicates if a
texture is directional or non-directional. It examines
directional intensity variations in texture as an initial
step, then does a frequency domain analysis of the
texture. This examination of intensity variation along
predefined directions is aimed at identifying the more
certain highly directional and highly non-directional
textures first. Frequency domain analysis of the re-
maining textures provides more information on the
texture directionality.
Computing the measure consists of applying the
following steps to the texture sample.
Step 1. Compute pixel intensity differences along
the 0, 45, 90 and 135 degree directions (from the hori-
zontal) using a 3x3 neighborhood mask on each pixel
of the texture.
Step 2. Compute the mean pixel intensity differ-
ences along each direction.
Step 3. Compute the max and min pixel intensity
differences.
Step 4. Classify the texture as highly directional,
highly non-directional, or possibly directional, using
the following rules. If the difference, d, between the
max and min pixel intensity differences is greater than
a threshold t
1
, classify the texture as highly direc-
tional. If d is greater than another threshold t
2
, then
classify the texture as highly non-directional (we use
t
1
> t
2
). Classify all textures with t
2
≤ d ≤ t
1
as pos-
sibly directional. They need to be investigated further.
(Note: The local intensity variation approach taken
here is similar to the local binary pattern (LBP) con-
cept (Ojala et al., 2002). However, instead of using
the variation as a texture discrimination measure like
LBP does, we compute a global orientation measure
for the texture.)
Step 5. Stop if the texture was classified as highly
directional or highly non-directional. Otherwise, pro-
ceed to Steps 5a, 5b, and 5c:
Step 5a. Apply a Fourier transform. (Our ap-
proach uses the Fourier tranform to assess geometric
characteristics within a texture.)
Step 5b. Apply a Hough line transform to the out-
put of Step 5a to identify existence of lines. The
Hough transform is used to find structures in the
Fourier transformed texture. Presence of linear-like
structure in the Fourier transformed texture may in-
dicate that the texture is oriented. The Hough line
transform uses the line formulation shown in Eqn. 4:
xcosθ + ysinθ = ρ. (4)
Eqn. 4 specifies a line passing through (x, y) that is
perpendicular to the line from the origin to (ρ, θ) in
polar space. For each point (x,y) on that line, ρ and θ
are constant. The set of possible lines passing through
(x, y) is obtained by solving for ρ and θ. An accu-
mulator counts the number of times each (ρ, θ) com-
bination describes a credible line passing through a
pixel. Points that are collinear yield higher counts for
the (ρ, θ) parameters describing their common line.
Any time the accumulator count is high (we use 90
for our textures, which are size 128x128), we hypoth-
esize such a line is present.
Step 5c. If one or many lines exist in the output
of Step 5b, then classify the texture as a highly direc-
tional texture.
We use Hough processing after the Fourier step
to allow some textures with disconnected directional
components to be identified as directional (e.g., tex-
ture D102 from the Brodatz image archive); the lo-
cal pixel difference method does not deal well with
disconnected directional components. Furthermore,
our approach also allows textures with multiple dom-
inant directions to be detected as directional. Figure 1
shows such a texture, D102, with multiple dominant
directions. Figure 2 shows the Fourier transformation
of texture D102. The presence of straight lines in Fig-
ure 2 indicates that texture D102 is directional.
Since most prior texture directionality measures
have been based on a local texture model, they may
ignore some global aspects of texture directionality
that could be utilized in human visual perception. Our
measure, however, considers both local and global
texture directionality (via its use of local pixel differ-
ence and Fourier and Hough steps). One limitation is
that our measure only reports if the texture is oriented
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
434

Figure 1: D102.
Figure 2: Fourier transform of D102.
or not; it does not report direction (i.e., the angle of
texture’s orientation). We hope to address this limita-
tion in future work.
4 COMPARISON OF TEXTURE
DIRECTIONALITY MEASURES
We next report on our comparison study. It evalu-
ates our directionality measure versus the four prior
measures. In our comparison, we applied all the mea-
sures to the complete archive of 111 Brodatz textures.
Previously, only Picard and Gorkani have reported a
complete test, for their measure alone, on the entire
Brodatz archive. Thus, the report here represents the
first comprehensive comparison of the existing and
new texture directionality measures.
Table 1: List of consistently-classified textures.
Directional Non-directional
D1,D6,D11,D15,D18,D20, D2,D23,D28,D30,
D24,D25,D26,D34,D36,D37, D32,D33,D40,D41,
D47,D49,D50,D51,D52,D53, D54,D60,D62,D63,
D55,D56,D65,D68,D70,D72, D66,D67,D75,D88,
D76,D77,D78,D79,D83,D94, D89,D91,D100,
D95,D96,D105,D106 D109,D111
For the Abbadeni measure, we had to make two
assumptions due to incomplete information in their
paper: (1) the threshold for whether a pixel is ori-
(a) D1 (b) D6
(c) D2 (d) D23
Figure 3: Sample textures that are consistently- classified
(D1 and D6 directional; D2 and D23 non- directional).
ented, and (2) the criterion to determine a dominant
orientation. We determined these thresholds for our
work here as follows. (1) We have used the aver-
age orientation of all the pixels in the texture as the
threshold to determine which pixels are oriented. (2)
If more than half the texture’s pixels are oriented then
we consider that texture to have a dominant orienta-
tion. We label textures with a dominant orientation as
directional textures.
Table 1 lists textures from the Brodatz archive
that were classified consistently by the directional-
ity measures (i.e., the table shows the texture images
for which the five measures were in agreement). Ta-
ble 2 lists the Brodatz texture images for which the
five measures disagreed, with N and D used to de-
note classification as non-directional and directional,
respectively. We have computed the Pearson correla-
tion coefficient (Jackson, 2009) for only these incon-
sistencies to measure the correlation among all mea-
sures. The Pearson correlation coefficient here tests
the null hypothesis that there is no significant corre-
lation in data. Table 3 shows the correlation matrix,
using a 95% level of confidence value. We discovered
that our measure and Hagh-Shenas’s measure had the
best correlation. The second best correlation was our
measure with Picard and Gorkani’s measure.
5 USER STUDY
A subset of the Brodatz textures was used in our
user study, which we describe next. We consider the
study’s results as a ground truth to compare the tex-
ture directionality measures.
The study’s protocol, which was approved by the
AMeasureofTextureDirectionality
435
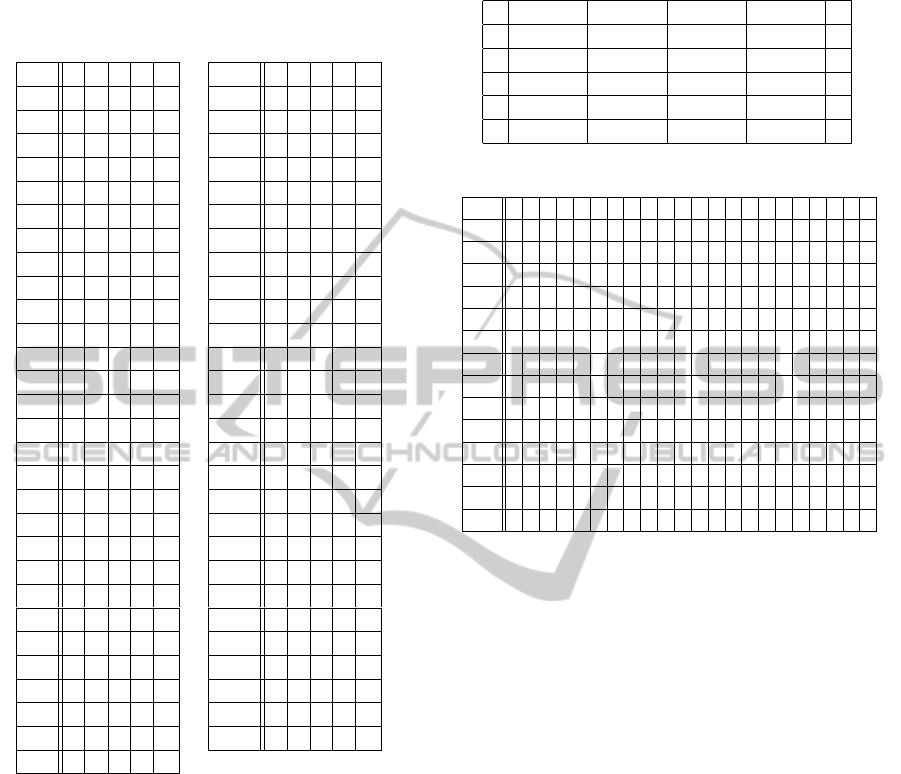
Table 2: Classification of remaining Brodatz textures by
measure (T= Tamura et al., H=Hagh-Shenas and Interrante,
P=Picard and Gorkani, A=Abbadeni et al., and M=My mea-
sure), with N indicating a non-directional classification and
a D indicating a directional one.
ID T H P A M
D3 D D D N D
D4 N D N N N
D5 N N N D N
D7 D D D D N
D8 N N D D N
D9 N D N N N
D10 N D D N N
D12 D D D D N
D13 D N D D N
D14 D N D D N
D16 N D D D N
D17 N D D D N
D19 N N N D N
D21 N D D D D
D22 N D D D D
D27 N N N D N
D29 N N N D N
D31 D N N N N
D35 D D D N D
D38 N N D D N
D39 N N N D N
D42 N N D D N
D43 N N D D N
D44 N D D D N
D45 N N D N N
D46 D N D D D
D48 N N D D N
D57 N D N N N
D58 N N N D N
ID T H P A M
D59 N N D D N
D61 N N N D N
D64 D D D N D
D69 D N D D N
D71 N D N N N
D73 N N N D N
D74 D N N N N
D80 N N D N N
D81 N D D N N
D82 N D D N N
D84 N N D D N
D85 N D D D D
D86 N D N D N
D87 N N D N N
D90 N N N D N
D92 N D N D N
D93 D N D N N
D97 N N D D D
D98 N N D N N
D99 N N N N D
D101 N D D N D
D102 N D D D D
D103 D D D N N
D104 D D D N N
D107 N N D N N
D108 N N D D N
D110 N N N D N
D112 N N N D N
institution’s Human Subjects Committee, involved
first providing a 2-3 minute overview about textures
to each participant. All participants considered the
same set of questions, with the study administered in
a computerized form. Participants were isolated from
each other.
5.1 Subjects
Twenty two individuals participated in the study.
Twelve were atmospheric science graduate students
and ten were environmental scientists.
5.2 User Study Task
In the study, participants were asked to perform a
task, which we describe next. Each participant com-
pleted classification of 15 Brodatz textures (shown
Table 3: Pearson Correlation Coefficient for inconsistent
classification.
T H P A M
T 1
H 0.17379 1
P 0.24871 0.25472 1
A -0.21738 -0.27275 -0.05432 1
M 0.20521 0.34405 0.28949 -0.03257 1
Table 4: User classification of the textures.
D9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
D14 0 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 1
D21 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 1 1 2 2 2 2 2
D25 2 2 2 2 1 1 0 2 2 2 2 2 2 2 2 2 2 2 1 1 2 0
D31 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
D34 2 2 2 2 1 1 2 1 1 1 1 2 2 1 1 1 1 1 1 1 2 2
D49 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
D53 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2
D58 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
D60 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
D65 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
D75 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 1 0 0
D78 0 1 1 1 2 0 0 1 1 0 1 1 1 1 1 0 1 1 2 1 1 0
D86 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
D97 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
in Figure 4) into one of three classes: highly direc-
tional, highly non-directional, and somewhat direc-
tional. Like Tamura, we selected these 15 at random,
5 per classification (from our measure). We used a
small subset rather than the complete set of Brodatz
textures to avoid user fatigue.
The overall results from the task are shown in
Table 4, where highly non-directional, highly direc-
tional, and somewhat directional textures are denoted
by 0, 2, and 1, respectively. The rows of the table
list individual textures. The columns of the table list
participant classifications.
Comparisons of classifications produced by the
user task against those from the existing direction-
ality measures are reported in Table 5. In the ta-
ble, the highly directional and somewhat directional
classes from the user task are grouped together. N and
ND represent directional and non-directional, respec-
tively. Our method concurs with the user study results
93% of the time. We believe that this is due to global
directionality being addressed by our method as well
as in human vision.
6 ANALYSIS
Next, we present a comparison of the directionality
measures performance. We do so using a comparison
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
436
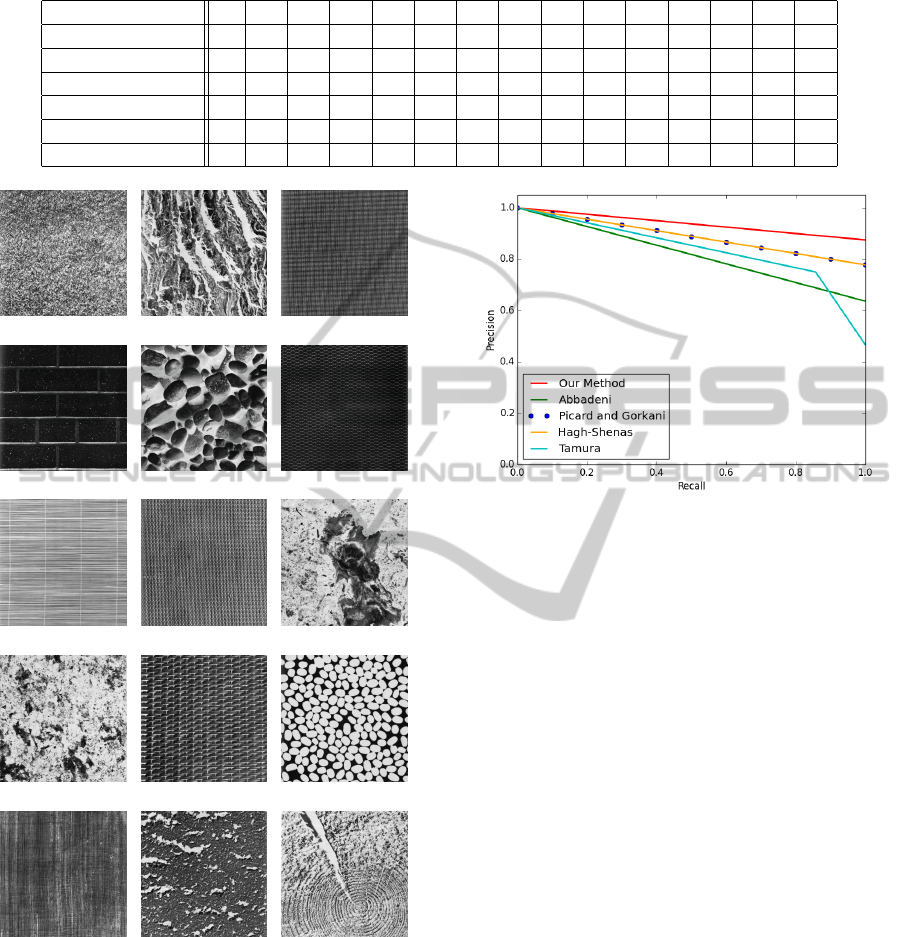
Table 5: Task 1 classifications vs. the classifications from the five measures.
D9 D14 D21 D25 D31 D34 D49 D53 D58 D60 D65 D75 D78 D86 D97
User Study ND ND D D ND D D D ND ND D ND D ND ND
Our Metric ND ND D D ND D D D ND ND D ND D ND D
Abbadeni ND D D D ND D D D D ND D ND D D D
Picard and Gorkani ND D D D ND D D D ND ND D ND D ND D
Hagh-Shenas D ND D D ND D D D ND ND D ND D D ND
Tamura ND D ND D D D D D ND ND D ND D ND ND
(a) D9 (b) D14 (c) D21
(d) D25 (e) D31 (f) D34
(g) D49 (h) D53 (i) D58
(j) D60 (k) D65 (l) D75
(m) D78 (n) D86 (o) D97
Figure 4: The Brodatz textures used in Task 1.
of classifiers mode, where the user study result is used
as the ground truth set and each measure is used as a
classifier. Classifier performance is considered here
using precision versus recall. Precision is the ratio of
the number of correct classifications to the total num-
ber of classifications. Recall is the ratio of the number
of correct classifications to the total number of correct
classifications.
Figure 5 shows the plot of precision versus re-
Figure 5: Precision versus recall comparison of texture ori-
entation measures.
call for all texture orientation measures using the user
study results as ground truth. The figure suggests that
our measure has high precision at all recall levels, in
particular that our new method’s precision exceeds
that of the existing measures.
7 CONCLUSIONS
In this paper we have presented a new texture direc-
tionality measure and validated the measure with user
studies. The measure allows determination of suitable
directional textures. We have also compared, for the
first time, the existing texture orientation measures us-
ing an identical set of images. In the future, we hope
to study other aspects of texture orientedness, such
as allowing for determination of which direction is a
dominant one in a directed texture.
REFERENCES
Abbadeni, N. (2000). Autocovariance-based perceptual tex-
tural features corresponding to human visual percep-
tion. In Proc., Int’l Conf. on Pattern Recognition ’00,
volume 3, pages 901–904.
Abbadeni, N., Zhou, D., and Wang, S. (2000). Computa-
tional measures corresponding to perceptual textural
AMeasureofTextureDirectionality
437

features. In Proc., Int’l Conf. on Image Processing
’00, volume 3, pages 897–900.
Beck, J. (1982). Textural Segmentation, in Organization
and Representation in Perception. Hillsdale, NY: Erl-
baum.
Blake, R. and Holopigan, K. (1985). Orientation selectiv-
ity in cats and humans assessed by masking. Vision
Research, 25(10):1459–1467.
Cao, F., Guichard, F., and Hornung, H. (2009). Measuring
texture sharpness of a digital camera.
Chetverikov., D. (1984). Measuring the degree of tex-
ture regularity. in proc. international conf. on pattern
recognition. In Proc., International Conf. on Pattern
Recognition, pages 80–82.
Chetverikov, D. and Hanbury, A. (2002). Finding defects in
texture using regularity and local orientation. Pattern
Recognition, 35(10):2165–2180.
Freeman, W. and Adelson, E. (1991). The design and use of
steerable filters. IEEE Trans. Pattern Anal. and Ma-
chine Intel., 13(9):891–906.
Gorkani, M. and Picard, R. (1994). Texture orientation for
sorting photos ”at a glance”. In Pattern Recognition,
1994. Vol. 1 - Conference A: Computer Vision amp;
Image Processing., Proceedings of the 12th IAPR In-
ternational Conference on, volume 1, pages 459–464
vol.1.
Hagh-Shenas, H. and Interrante, V. (2005). A closer look
at texture metrics. In Proc., 2nd Symp. on Applied
Perception in Graphics and Vis. (APGV ’05), pages
176–176.
Haralick, R. (1979). Statistical and structural approaches to
texture. Proceedings of the IEEE, 67(5):786–804.
Hawkins, J. K. (1970). Picture Processing and Psychopic-
torics. Academic Press, New York, NY, USA, as cited
by W. K. Pratt, Digital Image Processing 2nd Ed.,
1991, Wiley.
Healey, C. and Enns, J. (1999). Large datasets at a glance:
Combining textures and colors in scientific visual-
ization. IEEE Trans. Vis. and Computer Graphics,
5(2):145–167.
Hubel, D. and Wiesel, T. (1968). Receptive fields and func-
tional architecture of monkey striate cortex. Physiol-
ogy, 195:215–243.
Jackson, S. L. (2009). Research Methods and Statistics :
A Critical Thinking Approach. Wadsworth Cengage
Learning, Belmont, CA.
Kekre, H., Thepade, S. D., Jain, J., and Agrawal, N.
(2010). Article:iris recognition using texture features
extracted from haarlet pyramid. International Journal
of Computer Applications, 11(12):1–5. Published By
Foundation of Computer Science.
Manjunath, B., Ohm, J.-R., Vasudevan, V., and Yamada, A.
(2001). Color and texture descriptors. Circuits and
Systems for Video Technology, IEEE Transactions on,
11(6):703–715.
Mudigonda, N. R., Rangayyan, R. M., and Desautels,
J. L. (2001). Detection of breast masses in mam-
mograms by density slicing and texture flow-field
analysis. Medical Imaging, IEEE Transactions on,
20(12):1215–1227.
Nothdurft, C. (1985). Sensitivity for structure gradient
in texture discrimination tasks. Vision Research,
25:1957–1968.
Nothdurft, C. (1990). Texton segregation by associated dif-
ferences in global and local illuminance distribution.
In Proc., R Soc Lond Ser B Biol Sci, pages 295–320.
Nothdurft, C. (1991). Texture segmentation and pop-out
from orientation contrast. Vision Research, 31:1073–
1078.
Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-
tiresolution gray-scale and rotation invariant texture
classification with local binary patterns. Pattern Anal-
ysis and Machine Intelligence, IEEE Transactions on,
24(7):971–987.
Picard, R. and Gorkani, M. (1992). Finding perceptually
dominant orientations in natural textures. Spatial Vi-
sion, 8(2):221–253.
Saha, S., Das, A., and Chanda, B. (2004). Cbir using per-
ception based texture and colour measures. In Pat-
tern Recognition, 2004. ICPR 2004. Proceedings of
the 17th International Conference on, volume 2, pages
985–988 Vol.2.
Shiranita, K., Miyajima, T., and Takiyama, R. (1998). De-
termination of meat quality by texture analysis. Pat-
tern Recognition Letters, 19(14):1319 – 1324.
Sikora, T. (2001). The mpeg-7 visual standard for con-
tent description-an overview. Circuits and Systems for
Video Technology, IEEE Transactions on, 11(6):696–
702.
Smith, J. and Chang, S.-F. (1996). Automated binary texture
feature sets for image retrieval. In Acoustics, Speech,
and Signal Processing, 1996. ICASSP-96. Conference
Proceedings., 1996 IEEE International Conference
on, volume 4, pages 2239–2242 vol. 4.
Tamura, H., Mori, S., and Yamawaki, T. (1978). Textu-
ral features corresponding to visual perception. IEEE
Trans. Sys., Man and Cybernetics, 8(6):460–473.
Ware, C. and Knight, W. (1992). Orderable dimensions of
visual texture for data display: Orientation, size, and
contrast. In Proc., ACM Conf. on Human Factors in
Computing Sys. ’92, pages 203–209.
Wu, P., Manjunanth, B., Newsam, S., and Shin, H. (1999).
A texture descriptor for image retrieval and brows-
ing. In Content-Based Access of Image and Video
Libraries, 1999. (CBAIVL ’99) Proceedings. IEEE
Workshop on, pages 3–7.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
438
