
Probabilistic Modeling of Real-world Scenes in a Virtual Environment
Frank Dittrich, Stephan Irgenfried and Heinz Woern
Institute for Anthropomatics and Robotics (IAR),
Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany
Keywords:
Virtual Environment, Scene Modeling, Real-world Modeling, Synthetic Data, Probabilistic Modeling,
Probabilistic Graphical Models, Image Processing, Computer Vision.
Abstract:
In this paper we present an approach for the automated creation of real-world scenes in an virtual environment.
Here we focus on human-robot interaction and collaboration in the industrial domain, with corresponding vir-
tual object classes and inter-class constellations. As the basis for the sample generation process, we probabilis-
tically model essential discrete and continuous object parameters, by adapting a generic mixed joint density
function to distinct scene classes, in order to capture the specific inter- and intra-class dependencies. To pro-
vide a convenient way to assert these object interactions, we use a Bayesian Network for the representation of
the density function, where dependencies can directly be modeled by the network layout. For the conditioned
and uncertain descriptions of object translations, we use hierarchical Gaussian Mixture Models as geometrical
sampling primitives in the 3D space. In our paper, we show how the combination of a Bayesian Network with
these sampling primitives can directly be used for the automated collision avoidance of objects, during the
sampling process. For the illustration of the applicability and usefulness of our approach, we instantiate the
generic and abstract concept using an example with reduced complexity.
1 INTRODUCTION
The application of the here proposed approach for
probabilistic modeling of real-world scenes in virtual
environments is intended in research scenarios related
to safe human-robot cooperation (SHRC) and interac-
tion (SHRI) in the industrial domain. In our experi-
mental environment we allow for a shared workspace
with no spatial and temporal separation between hu-
man worker and industrial-grade components and
robots. In the context of SHRC and SHRI, we fo-
cus on the intuitive and natural human-robot interac-
tion, safety considerations and measures in a shared
work environment, the enabling of cooperative pro-
cesses and the interaction optimization.
All elements of our research spectrum thereby rely
on information related to activities in the workspace.
As a basis for the information generation on differ-
ent levels of abstraction, we use a multi-sensor setup
which delivers RGB-D data in a high frequency. This
sensor data is then further processed by low-level im-
age processing approaches for optical flow estimation
or pixel-wise object class segmentation, by mid-level
approaches for object class detection and human body
posture recognition and by high-level approaches for
gesture and action recognition. The results from the
different approaches are thereby interchanged, and
the hierarchical scene analysis represents the core of
our modular cognitive system for safe human-robot
collaboration, which is the basis for rational decision
making and system adaptation.
For the training of the machine vision compo-
nents of the modular system, we thereby need a large
amount of sensor data which depicts possible constel-
lation and parameterizations of the objects in the real-
world scene, with a high degree of variation, and in
multiple perspectives. The collection of such data,
using real-world sensors, is not a simple or even a
nearly impossible task, especially if ground truth data
is needed for the supervised training of the prediction
models. One way to avoid the collection of such data
by hand, is to use synthetic data. Here, the data is
created in a virtual environment, using virtual objects
and sensors. The parameterization of the objects and
the sensors is done automatically by an algorithm, and
the fast sampling of highly varying data with sensors
in various perspectives is automated and convenient.
One problem which arises when using synthetic
sensor data, is that one has to determine whether the
similarity between real-world data and the data pro-
duced by the virtual components is sufficient for the
specific prediction model. Here, similarity can be di-
165
Dittrich F., Irgenfried S. and Woern H..
Probabilistic Modeling of Real-world Scenes in a Virtual Environment.
DOI: 10.5220/0005313301650173
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 165-173
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

vided up into two classes. First the degree of realism
of the appearance of objects in a scene, which in case
of an RGB sensor would be the similarity of the syn-
thetic image and the output of a real camera sensor.
Second, the similarity of the statistics of object con-
stellations and parameterizations in the virtual and the
real world. In a scene or room which contains a ta-
ble, person, chair and laptop, we would expect certain
constellations to appear more often than others. The
chair would be most likely somewhere around the ta-
ble in close proximity, the human would be expected
to be somewhere in the room and the laptop would be
most likely on the table. Also a situation where the
person is standing in the table or the chair, would be
highly unlikely or just impossible.
In our approach we try to tackle the problem of
similarity of the second type. Our goal is to provide
a framework, where constellations and parameteri-
zations can be modeled probabilistically as a mixed
joint density function, by domain experts. In order
to produce similar statistics, when generating a large
amount of data, the joint density function is used for
the sampling of scene instances in a virtual environ-
ment, which are the basis for the generation of syn-
thetic sensor data.
The remainder of this paper is organized as fol-
lows. In Section 2 related work concerning the ap-
plication of synthetic data in machine vision applica-
tions is presented. In Section 3 the generic concep-
tional design of our probabilistic modeling scheme is
described. In Section 4, the application and useful-
ness of the generic concept is illustrated by a use case
with reduced complexity. Finally, in Section 5, a con-
clusion is drawn and hints for future work are given.
2 RELATED WORK
In this section we focus on work done by other au-
thors on the pros and cons of using artificially cre-
ated images and ground truth for evaluation of com-
puter vision algorithms. As stated by Rachkovskij
and Kussul (Rachkovskij and Kussul, 1998), Frasch
et. al (Frasch et al., 2011) and Kondermann (Konder-
mann, 2013), computer vision and machine learning
algorithm selection, training and evaluation requires
a representative set of image data to be processed to-
gether with the results expected from processing, the
ground truth. For computer vision applications, sam-
ple image data can either be captured with real-world
imaging sensors or created artificially based on direct
image statistics modeling or from 3D scenes using
computer graphics. Major drawbacks of using real
world sensor data for this task have been identified by
the aforementioned and other authors:
1. Creation of these datasets using real world sen-
sors is, for many applications, expensive in terms
of equipment and time or in case humans can be
injured or material can be damaged, even impos-
sible (Meister et al., 2012)(Geiger et al., 2012).
2. Manual effort has to be made to label objects in
the images and/or add high level context infor-
mation (Utasi and Benedek, 2012). Human ob-
servers have to annotate each frame with pixel-
wise ground truth information or at least control
the correctness of semi-automatic labeling.
3. Manually added ground truth information is
highly subjective as shown by Martin et al. (Mar-
tin et al., 2001) for the Berkeley Segmentation
Dataset and Benchmark BSDS300
1
. With the im-
age capturing of the real sensor, a lot of the infor-
mation present in the scene is lost for later pro-
cessing, especially contextual information or sur-
face data of occluded parts. A human annotating
a given image is interpreting the scene based on
his knowledge and may annotate it different to the
original scene.
4. It is not fully known, how well the sample data re-
flects the statistical characteristics of the real ap-
plication, especially in terms of edge cases(Frasch
et al., 2011). One would manually have to evalu-
ate the statistical properties of the whole dataset
and needs to know the setup of the real-world
scenes to gauge the coverage of real scenes statis-
tics by the sample dataset.
Although there are numerous drawbacks of using real
sensors to create sample data for vision and machine
learning applications, there are still much more of
these datasets used than synthetic ones (Frasch et al.,
2011). Regarding to Kondermann(Kondermann,
2013), this is the case because the data created ar-
tificially has been considered too unrealistic. For a
discussion on the impact of visual object appearance,
sensor models and light propagation in the scene for
creating synthetic datasets and ground truth we re-
fer to the work of Meister and Kondermann (Meister
and Kondermann, 2011). With the recent advances
made in the physical correct rendering in the field
of computer graphics, this prejudice is diminishing
and synthetic datasets are moving into focus of com-
puter vision researchers more and more(Frasch et al.,
2011). An approach how to evaluate driver assistance
systems using synthetic image data was presented by
von Neumann-Cosel, who described a simulation en-
vironment Virtual Test Drive (Neumann-Cosel et al.,
1
http://www.eecs.berkeley.edu/Research/Projects/CS/
vision/bsds/
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
166

2009) which is used to test and optimize a driver as-
sistance lane tracker in an virtual system-in-the-loop
environment. Similar did Haltakov et al. in (Haltakov
et al., 2013) to create camera images, depth maps and
ground truth for optical flow maps by extending the
Open Source driving simulator VDrift
2
. Shotton et al.
describe their work on how to use computer graphics
to create large depth data sample sets of human poses
based on motion capture data and discrete variation in
body size in (Shotton et al., 2011). Similar did Jie et
al. by augmenting real world images of pedestrians
with a synthetic image of a human for video surveil-
lance application(Jie et al., 2010).
3 BASIC CONCEPT
As described in Section 1, for the training of the ma-
chine vision components of our modular cognitive
system, we want to use synthetic data. In order to
produce good prediction results, not just for synthetic
testing data, but especially for real-world testing data,
we must provide training samples which are consis-
tent with the real-world.
3.1 Synthetic Data Creation
For the synthetic ground truth data generation, we
use the virtual robot experimentation platform V-REP
(E. Rohmer, 2013). This framework allows for a re-
mote access on parts of its functionality via a C/C++
API, and synthetic KINECT sensors are already in-
cluded. Also, the full version of the software is free
for educational and academic use. Here we can use
virtual representations of humans, furniture, robots
etc., in order to model scenes which are consistent
with our work environment and the application do-
main of our cognitive system. The choice of possible
object classes and constellations thereby define the
virtual scene type or domain.
We differentiate between static and dynamic ob-
jects, where in the first case the transformation, mean-
ing translation and rotation of the objects’ base coor-
dinate system, is static, or in the second case, can be
changed for every scene instance. For the creation of
synthetic data, we first transform all dynamic objects
and set up other possible parameters for all objects,
and then use virtual sensors in a distinct perspective
for the generation of the data. It should be men-
tioned, that in this paper and especially the presented
use case, we only use the depth information from vir-
tual RGB-D sensors. We consider V-REP not suited
2
http://vdrift.net/
Figure 1: Instantiation of a virtual scene in the SHRC and
SHRI domain, using the virtual robot experimentation plat-
form V-REP. Occurring object classes are human, mobile
and static robot, table, laptop, workpiece, rack and chair.
The transformations of the tables, the static robots and the
racks are static and constrain the subset of dynamic object
constellations which are consistent with the real world.
for creating synthetic RGB-images datasets due to its
lack in realism regarding illumination and surface ap-
pearance modeling as well as not supporting complex
light sources or shadows.
Fig.1 shows a scene instance in the domain of
SHRI or SHRC, where humans and (safe) static and
mobile robots are working in a shared workspace. All
tables, the static robots and all racks are thereby static
objects, and the human worker, mobile robot, laptop
and workpiece are dynamic objects. In this example
domain, all dynamic objects can be transformed, and
the posture of the human can also be set up with a
sample posture from a distinct choreography set. Ex-
amples for such choreographies are for instance walk-
ing, standing, working at a table or reaching for some-
thing. Our goal is now to generate scene instances
which are consistent with our definition of the real-
world. Also we want to generate samples, where the
statistical characteristics of our real-world are con-
tained, when sampling a large number scenes.
3.2 Probabilistic Scene Modeling
In the following, we want to show how to probabilis-
tically model the object parameters p
i
of all objects o
i
in a mixed joint density function (JDF). The parame-
ters are thereby restricted for all objects to the trans-
formation, with p = (x, α), where x = (x, y, z) depicts
the translation in the scene, and α is the scalar rota-
tion angle in the scene floor plane. In case of human
objects, the parameters are extended to p = (x, α, c),
where c is a discrete value which depicts the chore-
ography type. The sets O, O
S
, O
D
and O
H
depict the
indices of all objects, the static objects, the dynamic
objects and the objects which are in the human object
ProbabilisticModelingofReal-worldScenesinaVirtualEnvironment
167

class respectively, with O = O
S
∩ O
D
and O
H
⊆ O
D
.
Also, N
O
depicts the number of all, static, dynamic
and human objects respectively.
3.2.1 A Simple Approach
The easiest way to model a JDF over the object pa-
rameters P = (p
1
, p
2
, . . . , p
N
O
), would be a density
function with no dependencies between all parame-
ters, where all factors would be uniform:
f (P) =
∏
i∈O
f
X
(x
i
) f
Y
(y
i
) f
Z
(z
i
) f
α
(α
i
)
∏
j∈O
H
P
C
(c
j
).
(1)
The densities f
X
i
, f
Y
i
, f
Z
i
and f
α
i
are indepen-
dent of the specific object and uniform over
[0, X ], [0, Y], [0, Z] and [0, 2π] respectively, with
(X, Y, Z) as translation limits in the virtual space. The
distribution P
C
is also independent of the specific
human object and uniform over the the discrete set
{1, . . . , N
C
} of the N
C
choreographies.
In case of such a simple model, no expert knowl-
edge except the translation limits and available chore-
ographies would be encoded in the structure of the
density function. Fig.2 shows examples of erroneous
or highly unlikely constellations and parameteriza-
tions, which were generated when using this density
function for the sampling of scene instances. Look-
ing at these examples, expert knowledge could for in-
stance be, that static and dynamic objects can’t col-
lide, as illustrated in Fig.2, Left, Center, or that it is
in our real world, that chairs are always on the floor
and therefore never on a table Fig.2, Right. In case of
the latter, one could of course argue, that chairs some-
times appear on the tables in the real-world, even if it
is not very likely.
A prediction model trained on data created by this
density function, would therefore probably show a
very good generalization performance, while the col-
lisions samples would probably decrease the overall
performance, because of the training on erroneous
data. However, because of the complexity of the here
presented scene, it would also probably take a very
large number of samples, to gain good overall perfor-
mance measures, when granting maximum freedom
Figure 2: Examples where the simple modeling approach
(1) generates erroneous or highly unlikely constellations
and parameterizations. Left: Collision between dynamic
and static objects. Center: Collision between two dynamic
objects. Right: Transformation of a chair, which would be
considered by us as highly unlikely in the real world.
in the synthetic data creation process, especially when
special cases are as likely as common cases. Consid-
ering, that the creation of synthetic data and especially
the training of prediction models is very time consum-
ing, it is our goal to reduce the number of training
samples.
Based on these assumptions, we therefore try not
only to implement collision avoidance for static and
dynamic objects, but also want to adapt the scene
sampling process to the real-world. As described in
Section 1, this means that we want to adapt the sta-
tistical characteristics of the object constellations and
parameterizations to the real world. In case of the
chair, this could for instance mean, that a chair will
never be on a table, or that the probability of such
a constellation would be modeled as very less likely
than a chair standing on the floor and in close prox-
imity to a table. Hence the goal is, less scene sam-
ples, with the focus more on the common cases, and
less on the special and highly unlikely cases. Then, if
the expert knowledge reflects the real-world, a predic-
tion model trained on data created by such a density
function, would probably show a better overall per-
formance in real-world instances of this scene type,
than a prediction model trained on the density func-
tion presented in (1). Especially when a static ob-
ject layout is given, the subset of dynamic object con-
stellations which are consistent with the real world, is
highly constrained (Fig.1).
In the following section, we show how to imple-
ment such expert knowledge in a probabilistic model,
for the generation of consistent synthetic scenes.
3.2.2 A Sophisticated Approach
One way to model the statistical characteristics of the
real-world in a joint density function, would be using
an inductive approach, where one would record many
constellations and parameterizations of the real-world
objects and then train a Probabilistic Graphical Model
(PGM) based on that data. However, we don’t have
this data, so our approach is to use a Bayesian Net-
work (BN), which is also a PGM, and model the den-
sity function structure by hand, based on our expert
knowledge.
We will give a very short overview over the princi-
ple of BNs, in order to motivate the different parame-
ters and components, which is the basis for modeling
approach. A comprehensive description of BNs and
PGMs can be found in (Koller and Friedman, 2009).
A Bayesian Network represents a joint distribu-
tion or in our case a joint density function, where
a directed acyclic graph (DAG) is used for the de-
scription of the conditional dependencies of the ran-
dom variables. Here, the random variables are repre-
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
168
sented as graph nodes, and the directed graph edges
describe the conditional dependencies between the
random variables. A joint density with the same con-
ditional dependencies between the random variables
then factorizes into the following conditional density
functions (CDF):
f (x) =
N
V
∏
i=1
f
i
(x
i
|pa(x
i
)) , (2)
where x = (x
1
, x
2
, . . . , x
N
V
) describes the vector of
all N
R
random variables and f
i
(x
i
|pa(x
i
)) is the condi-
tional density function of the variable x
i
, conditioned
on the parents pa(x
i
) of x
i
, according to the DAG from
the BN. For the modeling of our joint density function
as a BN, we can therefore use the DAG structure and
the conditional density functions in order to imple-
ment our expert knowledge.
First we want to implement the translation of dy-
namic objects, in dependence or respectively condi-
tioned on the translation of other static and dynamic
objects. Fig.4 shows examples of distinct areas in
the virtual scene. The walking or driving area for
humans and mobile robots (Fig.4, Left), the area in
front of and on tables, and the area in front of racks
(Fig.4, Center), and the dynamic area conditioned on
the transformation of a dynamic object (Fig.4, Right).
In order to describe these areas or respectively a com-
bination of these areas probabilistically in a condi-
tional density function, and to later sample from these
CDFs, we need a probabilistic modeling of geometric
primitives.
As basis for this task, we use Gaussian Mixture
Models (GMM) where the components are uniformly
weighted and the means are equidistantly aligned
along a line, with the same diagonal covariance for
all components (Fig.3, Left). With this line model, it
is easy to form more complex 2D and 3D geometric
shapes (Fig.3, Right).
We now use the line models in order to probabilis-
tically describe the translation areas of every dynamic
object o
i
. For this we define a CDF:
f
i
(x|rel
T
(o
i
)) =
N
i
∑
j=1
w
a
j
f
A
j
(x|rel
T
(o
i
)) ,
N
j
∑
j=1
w
a
j
= 1 . (3)
The CDF f
i
(x|rel
T
(o
i
)) is defined as a weighted
sum of probabilistic area descriptions f
A
j
(x|rel(o
i
)).
Both, f
i
and the area descriptions f
A
j
are thereby con-
ditioned on rel
T
(o
i
), which depicts the transformation
parameters p of static and dynamic objects which are
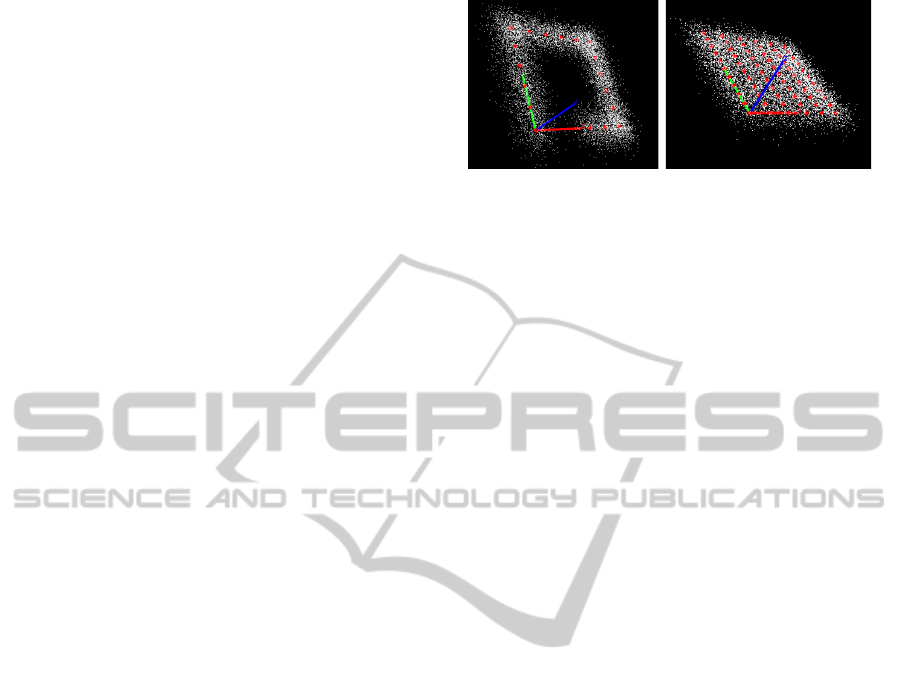
Figure 3: 10000 3D samples (white) created using a Gaus-
sian Mixture Model with uniform weighting of the compo-
nents, equidistant means (red) and the same diagonal co-
variance for all components. Left: Component means (red)
are aligned along a line. Right: Component means (red) are
aligned along a line, and the line is used to form a filled
rectangle in the 2D plane.
relevant for the translation areas of the object o
i
. The
components f
A
j
are thereby line models.
A laptop object can now be modeled as always on
top of one of the tables. Here we use area descriptions
f
A
j
which cover the tabletops in the correct height
(Fig.4, Center (dark red)), and are therefore depen-
dent on the position and transformation of a certain
table. By adapting the weights w
a
j
we could then also
model, that the laptop is more likely on certain tables.
A chair object can now be modeled as most likely
in front of one of the tables. Here we use area descrip-
tions f
A
j
which depict the areas in front of the tables
(Fig.4, Center (light red)), and also the walking and
driving area description (Fig.4, Left (dark grey)). The
chairs’ CDF is therefore dependent on all static ob-
jects. By adapting the weights w
a
j
we can now model,
that the chair is more likely in close proximity of a ta-
ble and less likely in the walking area, by assigning
small values to the weights from the walking area de-
scription. In addition we could model highly unlikely
case of a chair on a table, by adding the area descrip-
tions used in the laptop example, to the product of the
chairs’ CDF (3) and adapt the weights accordingly.
As described before, for all object classes other
than the human, we model the random parameters as
the object transformation p = (x, α) = (x, y, z, α), so
that the objects’ full CDF must be extended:
ˆ
f
i
(p|rel
T
(o
i
)) = f
i
(x|rel
T
(o
i
)) · u
0:2π
(α) , (4)
where u
0:2π
(α) depicts the uniform density func-
tion over the range of [0, 2π]. This means, that the
rotation is independent of the translation, and always
uniform over [0, 2π].
In case of the human, the random parameters
p
h
= (x, α, c) are mixed continuous and discrete, with
c ∈ {1, . . . , N
C
} depicting the choreography type. The
extended CDF for human objects has the form:
ProbabilisticModelingofReal-worldScenesinaVirtualEnvironment
169

Figure 4: Different types of translation sampling areas for dynamic object, which are determined by static and dynamic
objects. Left: The walking or driving area for humans and mobile robots (dark grey), which is dependent on the layout of all
static objects. Center: Areas which are related to tables (light and dark red) and racks (blue). Right: Dynamic area around a
mobile robot (green).
ˆ
f
i
(p
h
|rel
T
(o
i
)) = f
i
(x, c|rel
T
(o
i
)) · u
0:2π
(α) ,
f
i
(x, c|rel
T
(o
i
)) =
N
i
∑
j=1
w
a
j
f
A
j
(x|rel
T
(o
i
)) · P
c
j
(c)
,
(5)
where the choreography distribution P
c
j
(c) is de-
pendent on the area type, but independent of the ob-
ject translation. This means, that we want to model
semantics as expert knowledge about certain area
types. For instance, when in front of the rack, the hu-
man most likely performs reaching choreographies,
or when in the walking and driving area, the human
most likely performs the standing or walking chore-
ography.
In order to model all object parameters in a joint
density function, we define a BN using the object
CDFs. Here we consider the object parameters p
i
as
single random objects and model them as the nodes in
the DAG. We then add directed edges from the rele-
vant object nodes to the object node, consistent with
the relevant object parameters rel
T
(o
i
) for each object
node, and use the object CDFs
ˆ
f
i
(p
i
|rel
T
(o
i
)) as the
Figure 5: 10000 3D samples (white) created using a GMM
with uniform weighting of the components, equidistant
means (red) and the same diagonal covariance for all com-
ponents. Spherical objects (green, yellow, blue) in close
proximity to the sampling area define which of the compo-
nents of the GMM are activated for the sampling process,
by using a distance threshold based on the sphere dimen-
sion and the standard deviation of the GMM components.
factors in the joint density function definition. Static
object nodes are thereby always without parents, and
the parameters are static, so that density functions of
these objects are defines as 1 for the static parameters,
otherwise 0. The JDF over all object parameter P then
becomes:
f (P) =
∏
i∈O
D
ˆ
f
i
(p
i
|rel
T
(o
i
))
∏
i∈O
S
f
i
(p
i
), (6)
with
f (P
D
|P
S
) =
∏
i∈O
D
ˆ
f
i
(p
i
|rel
T
(o
i
)), (7)
where f (P
D
|P
S
) depicts the conditional JDF of all
dynamic object parameters P
D
, given the static object
parameters P
S
. Here, P
D
is considered as a free vari-
able and P
S
as a constant value.
So far we have jointly and probabilistically mod-
eled the transformation of the objects, and in case
of humans also the choreography semantics. What
is still missing is the modeling of the expert knowl-
edge, that objects don’t collide (Fig.2, Left, Center).
In order to model this, we first must be able to al-
ter the line models in case of an object entering the
sampling area. Fig.5 shows a rectangular line model
in the 2D plane, with distinct objects in the sampling
area, meaning samples drawn from this model could
collide with the object. Therefore in order to pre-
vent this from happening, we use a distance thresh-
olding scheme based on both object bounding boxes,
which can be spherical or rectangular shaped, and the
standard deviation of the model components, in order
to deactivate components which could produce col-
liding samples. For the deactivation of certain com-
ponents, we simply set their weight to zero and uni-
formly reweight the active components (Fig.5).
For this concept, we need a prioritization of the
objects, in order to define the transformation depen-
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
170

dencies between and within the object classes. There-
fore, we first define a priority over the classes, and
then over the single objects in the classes. For in-
stance, because of the higher priority, the transfor-
mation of human objects will always be sampled be-
fore a chair objects’ transformation is sampled, which
means, that the sampling of the chair transforma-
tion can be constrained by the position of the human.
Also, if the object human0 has a higher priority than
object human1 within the human object class, then the
transformation of human0 is sampled first. Therefore,
static objects must have the highest priority.
To model the collision avoidance in the BN, we
extend the defined CDFs by extending rel
T
(o
i
) with
the higher prioritized objects. This means, we add di-
rected edges from all higher prioritized object nodes
to the object o
i
. The resulting CDFs are then defined
by (4) and (5), with the extended conditioning and
with the adaptation of the single probabilistic area de-
scriptions f
A
j
(x|rel(o
i
)) based on the higher priori-
tized object transformations.
3.3 Virtual Scene Sampling
Based on the probabilistic model of the scene, we
can now generate virtual scene instances by sampling
from that model. The parameters of the static ob-
jects are thereby considered constant for all scene in-
stances, and are entered as evidence in the sampling
process.
In case of the simple approach (Section 3.2.1), be-
cause the parameters of all objects are modeled inde-
pendent, we sample each parameter individually us-
ing the uniform density functions f
X
, f
Y
, f
Z
and f
α
,
and the distribution P
C
.
In case of the sophisticated approach (Section
3.2.2), we use the Forward Sampling algorithm for
the sampling from the BN (Koller and Friedman,
2009). Because the evidence is always given only by
the static objects, which have no parents in the BNs
graph, we can use this algorithm with no extensions.
For the actual sampling, we then must sample from
each object CDF in the right order, which is given by
the object prioritization. This in turn means, that we
sample from the area descriptions which are GMMs
with multivariate normal components. For the sam-
pling from the multivariate normal density functions,
we used the implementation from (Press et al., 2007).
4 APPLICATION
For the illustration of our generic approach described
in Section 3.2.2, we instantiate the abstract formula-
Figure 6: Left: Sample configuration of the scene type
example (Section 4), which is consistent with the defined
scene knowledge. Right: Resulting Bayesian Network,
which is based on the probabilistic scene and expert knowl-
edge modeling of the use case. The nodes depict the ob-
ject parameter of the table (p
Table
), human (p
Hmn
), plant
(p
Plant
), and chair (p
Chair
), modeled as random objects.
tions using a simple non-complex scene type exam-
ple. Here, the object classes are table, human, lap-
top and plant, with one object instance per class. The
table is the only static object and is centered in the
room, all other objects are dynamic. The probabilis-
tic area descriptions f
A
j
are the area around the whole
table f
A
Table Surr
(Fig.4, Center), the room floor without
the table space and its surrounding area f
A
Room
(Fig.4,
Left) and the tabletop f
A
Table Top
(Fig.4, Center). As
scene experts we postulate, that the plant is always
on the table, the chair is always in close proximity to
the table and the human is either close to the table
or somewhere in the room. The prioritization is de-
fined in descending order: table, human, plant, chair.
For simplicity, the choreography semantics of the hu-
man is omitted in this example. Fig.6, Left depicts
a sample configuration of the scene objects, which is
consistent with the postulations.
Based on this expert knowledge about the scene
type, we now model the JDF of the parameters as a
Bayesian Network, which is depicted in Fig.6, Right.
The human object CDF is then defined as:
ˆ
f
Hmn
(p|o
Table
) = f
Hmn
(x|o
Table
) · u
0:2π
(α),
f
Hmn
(x|o
Table
) = 0.75 · f
A
Table Surr
(x|o
Table
)
+ 0.25 · f
A
Room
(x|o
Table
), (8)
where we state that the human is three times more
likely somewhere around the table than somewhere
else in the room, by setting the weights accordingly.
The first line of Fig.7 shows the results of the
scene sampling when using the model from the sim-
ple approach (Section 3.2.1). The independence of all
object parameters in the probabilistic model results in
completely random parameter configurations of the
scene objects, without expert knowledge encoded in
ProbabilisticModelingofReal-worldScenesinaVirtualEnvironment
171

Figure 7: The first line depicts constellations of four objects: table, human, chair and plant, in a virtual scene. The object
parameters are thereby sampled using the JDF from the simple approach (Section 3.2.1) The second line shows depth frames
created by a synthetic RGB-D sensor in the virtual environment, which observes the scene and thereby the sampled object
constellations. The third and fourth line show constellations and depth frames, of the same objects and virtual scene, respec-
tively. Here the sampling was conducted using the generic model from the sophisticated approach (Section 3.2.2), where the
object configurations were probabilistically modeled in accordance to the the scene type example in Section 4.
the possible object constellations and with object col-
lisions.
The third line of Fig.7 shows the results of the
scene sampling when using the before described so-
phisticated model. Because of the expert knowledge
implemented in the model, the chair is always close
to the table, the human is either close to the table or
somewhere in the broader surrounding area of the ta-
ble, and the plant is always on top of the table. Also
object collisions do not occur, except for the scene
sample depicted in the outermost right image, where
the human slightly collides with the table, which is
a consequence of the probabilistic modeling, where
collisions are highly unlikely but not impossible.
The second and fourth line of Fig.7 show depth
frames produced by a synthetic RGB-D sensor in the
virtual environment, which observes the scene and the
object constellations. In case of the second line, the
simple approach was used for scene sampling, and in
case of the fourth line, the sophisticated approach was
used for scene sampling.
It is the authors opinion, that when using synthetic
data for the training of statistical and machine learn-
ing approaches for computer vision tasks, it is im-
portant that the training samples are extracted from
virtual scenes which are in accordance with the real-
world context, where the trained approaches will be
deployed. For instance, in case of pixelwise object
class segmentation or detection, the features used for
training do not only contain information about the ob-
ject of interest, but also information about the back-
ground. When deployed in the real-world, the learned
background context should then fit to the background
presented to the classifier. Therefore, depth frame
samples based on the sophisticated approach (Fig.7,
Fourth line) should be favored over the samples based
on the simple approach (Fig.7, Second line), for clas-
sifier training. This motivates the usefulness of real-
world modeling in virtual environments for the sam-
pling of scene instances, or respectively, synthetic
training data.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
172

5 CONCLUSIONS
In this paper we presented a generic approach for the
probabilistic modeling of real-world scenes in a vir-
tual environment. Also, the sampling of consistent
scene instances was described, and both the modeling
and the sampling was illustrated and demonstrated us-
ing a simple scene type. The resulting synthetic data
was used to try to motivate the usefulness of the ap-
proach for the improved training of computer vision
approaches.
Future work will be the quantitative and qualita-
tive evaluation of the approach, using different scene
types and computer vision approaches, in order to
proof the conjectures.
REFERENCES
E. Rohmer, S. P. N. Singh, M. F. (2013). V-rep: a versa-
tile and scalable robot simulation framework. In Proc.
of The International Conference on Intelligent Robots
and Systems (IROS).
Frasch, J. V., Lodwich, A., Shafait, F., and Breuel, T. M.
(2011). A bayes-true data generator for evaluation of
supervised and unsupervised learning methods. Pat-
tern Recognition Letters, 32(11):1523–1531.
Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we
ready for autonomous driving? the kitti vision bench-
mark suite. In Computer Vision and Pattern Recogni-
tion (CVPR), 2012 IEEE Conference on, pages 3354–
3361.
Haltakov, V., Unger, C., and Ilic, S. (2013). Framework
for generation of synthetic ground truth data for driver
assistance applications. In German Association for
Pattern Recognition, editor, Proc. of the 35th German
Conference on Pattern Recognition GCPR 2013.
Jie, Y., Farin, D., Krueger, C., and Schiele, B. (2010). Im-
proving person detection using synthetic training data.
In Image Processing (ICIP), 2010 17th IEEE Interna-
tional Conference on, pages 3477–3480.
Koller, D. and Friedman, N. (2009). Probabilistic Graph-
ical Models: Principles and Techniques - Adaptive
Computation and Machine Learning. The MIT Press.
Kondermann, D. (2013). Ground truth design principles.
In Spampinato, C., Boom, B., and Huet, B., editors,
VIGTA ’13 Proceedings of the International Workshop
on Video and Image Ground Truth in Computer Vision
Applications, pages 1–4. ACM Press.
Martin, D., Fowlkes, C. C., Tal, D., and Malik, J. (2001). A
database of human segmented natural images and its
application to evaluating segmentation algorithms and
measuring ecological statistics. In Computer Vision,
2001. ICCV 2001. Proceedings. Eighth IEEE Interna-
tional Conference on, volume 2, pages 416–423.
Meister, S., J
¨
ahne, B., and Kondermann, D. (2012). Out-
door stereo camera system for the generation of real-
world benchmark data sets. Optical Engineering,
51(02):021107.
Meister, S. and Kondermann, D. (2011). Real versus realis-
tically rendered scenes for optical flow evaluation. In
Electronic Media Technology (CEMT), 2011 14th ITG
Conference on, pages 1–6.
Neumann-Cosel, K. v., Roth, E., Lehmann, D., Speth, J.,
and Knoll, A. (2009). Testing of image processing
algorithms on synthetic data. In Software Engineer-
ing Advances, 2009. ICSEA ’09. Fourth International
Conference on, pages 169–172.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-
nery, B. P. (2007). Numerical Recipes 3rd Edition:
The Art of Scientific Computing. Cambridge Univer-
sity Press.
Rachkovskij, D. A. and Kussul, E. M. (1998). Datagen:
a generator of datasets for evaluation of classification
algorithms. Pattern Recognition Letters, 19(7):537–
544.
Shotton, J., Fitzgibbon, A., Cook, M., Sharp, T., Finocchio,
M., Moore, R., Kipman, A., and Blake, A. (2011).
Real-time human pose recognition in parts from sin-
gle depth images. In Computer Vision and Pattern
Recognition (CVPR), 2011 IEEE Conference on.
Utasi,
´
A. and Benedek, C. (2012). A multi-view annota-
tion tool for people detection evaluation. In Spamp-
inato, C., editor, Proceedings of the 1st International
Workshop on Visual Interfaces for Ground Truth Col-
lection in Computer Vision Applications, pages 1–6,
New York and NY. ACM.
ProbabilisticModelingofReal-worldScenesinaVirtualEnvironment
173
